Найдите наибольшее и наименьшее: Найдите наибольшее и наименьшее значение функции у=5х-5 на промежутке {2;4}

Найдите наибольшее и наименьшее значения функции f. Алгебра Колмогоров 10-11 класс Упр 310 – Рамблер/класс

Найдите наибольшее и наименьшее значения функции f. Алгебра Колмогоров 10-11 класс Упр 310 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Опять эти функции(( Не понимаю я их! Поможете? Найдите наибольшее и наименьшее значения функции f на данном промежутке: 

a) f (х) = 2 sin х + cos 2х, (0; 2π];
 

ответы

Поможем)

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309

Привет! Поможете с решением?)
Скорость изменяется по закону 
(скорость измеряется в метрах в секунду). В какой момент времени (Подробнее…)

ГДЗ11 классКолмогоров А.Н.10 классАлгебра

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

10. Выпишите слово, в котором на месте пропуска пишется буква И. Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

10.
Выпишите слово, в котором на месте пропуска пишется буква (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Курс дифференциального и интегрального исчисления. Том 1

Курс дифференциального и интегрального исчисления. Том 1

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 1. Курс дифференциального и интегрального исчисления. Том I Фихтенгольц в 3 томах, Том 1. В книгах представленны все разделы современной высшей матиматеки, правила, задания и примеры их решения, теория и практика. Оглавление ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА 2. Упорядочение области рациональных чисел. 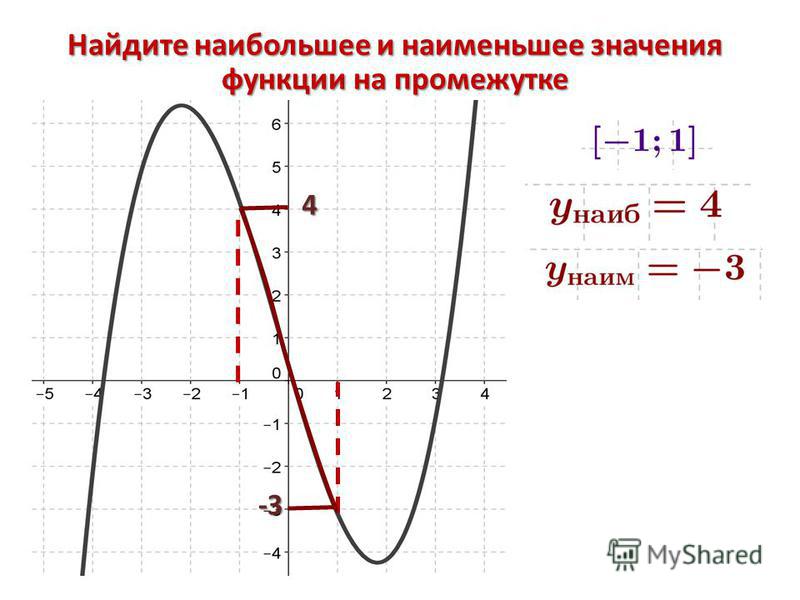3. Сложение и вычитание рациональных чисел. 4. Умножение и деление рациональных чисел. 5. Аксиома Архимеда. § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел 7. Упорядочение области вещественных чисел. 8. Вспомогательные предложения. 9. Представление вещественного числа бесконечной десятичной дробью. 10. Непрерывность области вещественных чисел. 11. Границы числовых множеств. § 3. Арифметические действия над вещественными числами 13. Свойства сложения. 14. Определение произведения вещественных чисел. 15. Свойства умножения. 16. Заключение. 17. Абсолютные величины. § 4. Дальнейшие свойства и приложения вещественных чисел 19. Степень с любым вещественным показателем. 20. Логарифмы. 21. Измерение отрезков. ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ § 1. Варианта и ее предел 23. Предел варианты. 24. Бесконечно малые величины. 25. Примеры. 26. Некоторые теоремы о варианте, имеющей предел. 27. Бесконечно большие величины. § 2. Теоремы о пределах, облегчающие нахождение пределов 29. Леммы о бесконечно малых. 30. Арифметические операция над переменными. 31. Неопределенные выражения. 32. Примеры на нахождение пределов. 33. Теорема Штольца и ее применения. § 3. Монотонная варианта 35. Примеры. 36. Число е. 37. Приближенное вычисление числа е. 38. Лемма о вложенных промежутках. § 4. Принцип сходимости. Частичные пределы 40. Частичные последовательности и частичные пределы. 41. Лемма Больцано — Вейерштрасса 42. Наибольший и наименьший пределы. ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ § 1. Понятие функции 44. Функциональная зависимость между переменными. Примеры. 45. Определение понятия функции. 46. Аналитический способ задания функции. 47. График функции. 48. Важнейшие классы функций. 49. Понятие обратной функции. 50. Обратные тригонометрические функции. 51. Суперпозиция функций. Заключительные замечания. § 2. Предел функции 53. Сведение к случаю варианты. 54. Примеры. 55. Распространение теории пределов. 56. Примеры. 57. Предел монотонной функции. 58. Общий признак Больцано—Коши. 59. Наибольший и наименьший пределы функции. § 3. Классификация бесконечно малых и бесконечно больших величин 61. Шкала бесконечно малых. 62. Эквивалентные бесконечно малые. 63. Выделение главной части. 64. Задачи. 65. Классификация бесконечно больших. § 4. Непрерывность (и разрывы) функций 67. Арифметические операции над непрерывными функциями. 68. Примеры непрерывных функций. 69. Односторонняя непрерывность. Классификация разрывов. 70. Примеры разрывных функций. 71. Непрерывность и разрывы монотонной функции. 72. Непрерывность элементарных функций. 73. Суперпозиция непрерывных функций. 74. Решение одного функционального уравнения. 75. Функциональная характеристика показательной, логарифмической и степенной функций. 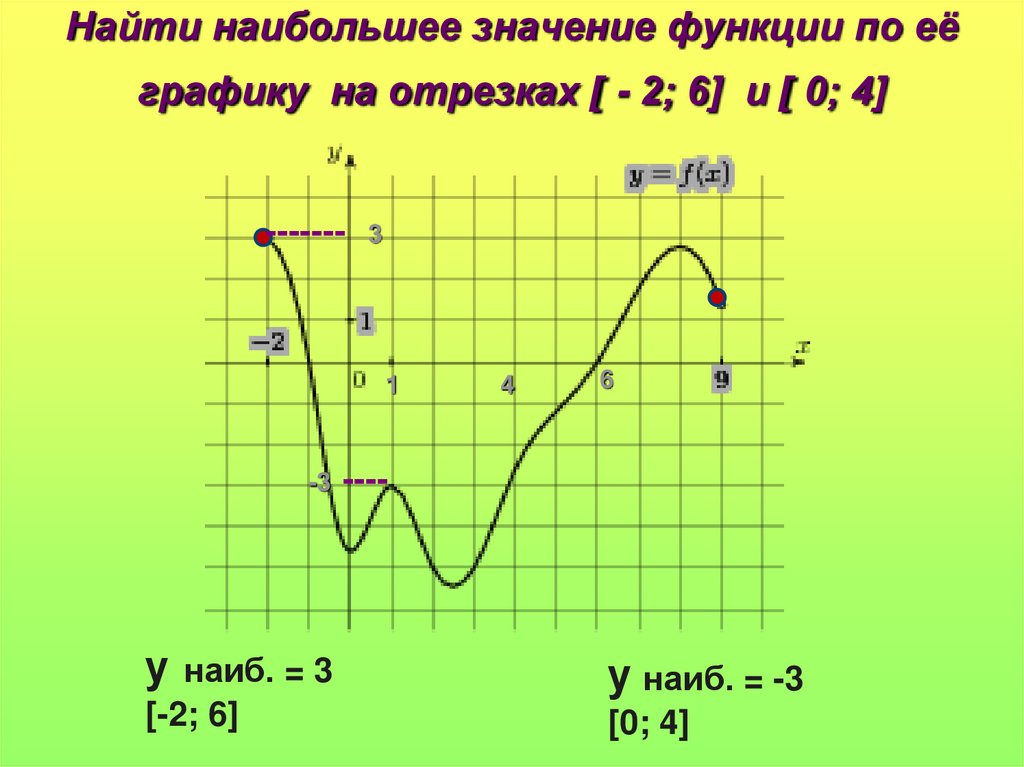76. Функциональная характеристика тригонометрического и гиперболического косинусов. 77. Использование непрерывности функций для вычисления пределов. 78. Степенно-показательные выражения. 79. Примеры. § 5. Свойства непрерывных функций 81. Применение к решению уравнений. 82. Теорема о промежуточном значении. 83. Существование обратной функции. 84. Теорема об ограниченности функции. 85. Наибольшее и наименьшее значения функции. 86. Понятие равномерной непрерывности. 87. Теорема Кантора. 88. Лемма Бореля. 89. Новые доказательства основных теорем. ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ § 1. Производная и ее вычисление 91. Задача о проведении касательной к кривой. 92. Определение производной. 93. Примеры вычисления производных. 94. Производная обратной функции. 95. Сводка формул для производных. 96. Формула для превращения функции. 97. Простейшие правила вычисления производных. 98. Производная сложной функции. 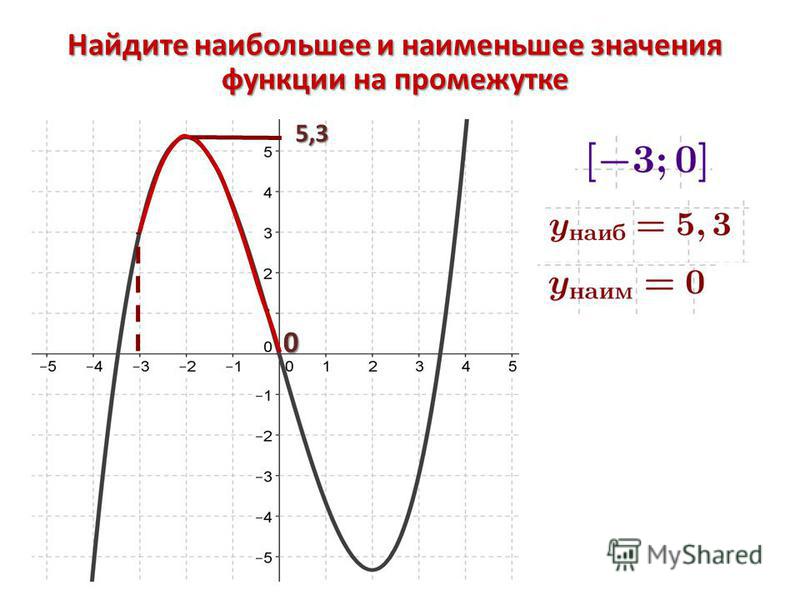100. Односторонние производные. 101. Бесконечные производные. 102. Дальнейшие примеры особых случаев. § 2. Дифференциал 104. Связь между диффереицируемостью и существованием производной. 105. Основные формулы и правила дифференцирования. 106. Инвариантность формы дифференциала. 107. Дифференциалы как источник приближенных формул. 108. Применение дифференциалов при оценке погрешностей. § 3. Основные теоремы дифференциального исчисления 110. Теорема Дарбу 111. Теорема Ролля. 112. Формула Лагранжа. 113. Предел производной. 114. Формула Коши. § 4. Производные и дифференциалы высших порядков 116. Общие формулы для производных любого порядка. 117. Формула Лейбница. 118. Примеры. 119. Дифференциалы высших порядков. 120. Нарушение инвариантности формы для дифференциалов высших порядков. 121. Параметрическое дифференцирование. 122. Конечные разности. § 5. Формула Тейлора 124. Разложение произвольной функции; дополнительный член в форме Пеано. 125. Примеры. 126. Другие формы дополнительного члена. 127. Приближенные формулы. § 6. Интерполирование 129. Дополнительный члеп формулы Лагранжа. 130. Интерполирование с кратными узлами. Формула Эрмита. ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ § 1. Изучение хода изменения функции 132. Условие монотонности функции. 133. Доказательство неравенств. 134. Максимумы и минимумы; необходимые условия. 136. Достаточные условия. Первое правило. 136. Примеры. 137. Второе правило. 138. Использование высших производных. 139. Разыскание наибольших и наименьших значений. 140. Задачи. § 2. Выпуклые (и вогнутые) функции 142. Простейшие предложения о выпуклых функциях. 143. Условия выпуклости функции. 144. Неравенство Иенсена и его приложения. 145. Точки перегиба. § 3. Построение графиков функций 147. Схема построения графика. Примеры. 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты. 149. Примеры. § 4. Раскрытие неопределенностей 151. Неопределенность вида oo/oo 152. Другие виды неопределенностей. § 5. Приближенное решение уравнений 154. Правило пропорциональных частей (метод хорд). 155. Правило Ньютона (метод касательных). 156. Примеры в упражнения. 157. Комбинированный метод. 158. Примеры и упражнения. ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 159. Функциональная зависимость между переменными. Примеры. 160. Функции двух переменных и области их определения. 161. Арифметическое n-мерное пространство. 162. Примеры областей в n-мерном пространстве. 163. Общее определение открытой и замкнутой области. 164. Функции n переменных. 165. Предел функции нескольких переменных. 166. Сведение к случаю варианты. 167. Примеры. 168. Повторные пределы. § 2. Непрерывные функции 170. Операции над непрерывными функциями. 171. Функции, непрерывные в области. Теоремы Больцано—Коши. 172. Лемма Больцано—Вейерштрасса. 173. Теоремы Вейерштрасса. 174. Равномерная непрерывность. 175. Лемма Бореля. 176. Новые доказательства основных теорем. § 3. Производные и дифференциалы функций нескольких переменных 178. Полное приращение функции. 179. Полный дифференциал. 180. Геометрическая интерпретация для случая функции двух переменных. 181. Производные от сложных функций. 182. Примеры. 183. Формула конечных приращений. 184. Производная по заданному направлению. 185. Инвариантность формы (первого) дифференциала. 186. Применение полного дифференциала в приближенных вычислениях. 187. Однородные функции. 188. Формула Эйлера. § 4. Производные и дифференциалы высших порядков 190. Теорема о смешанных производных. 191. Обобщение. 192. Производные высших порядков от сложной функции. 193. Дифференциалы высших порядков. 194. Дифференциалы сложных функций. 195. Формула Тейлора. § 5. Экстремумы, наибольшие и наименьшие значения 197. Достаточные условия (случай функции двух переменных). 198. Достаточные условия (общий случай). 199. Условия отсутствия экстремума. 200. Наибольшее и наименьшее значения функции. Примеры. 201. Задачи. ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ § 1. Формальные свойства функциональных определителей 203. Умножение якобианов. 204. Умножение функциональных матриц (матриц Якоби). § 2. Неявные функции 206. Существование неявной функции. 207. Дифференцируемость неявной функции. 208. Неявные функции от нескольких переменных. 209. Вычисление производных неявных функций. 210. Примеры. § 3. Некоторые приложения теории неявных функций 212. Метод неопределенных множителей Лагранжа. 213. Достаточные для относительного экстремума условия. 214. Примеры и задачи. 215. Понятие независимости функций. 216. Ранг матрицы Якоби. § 4. Замена переменных 218. Примеры. 219. Функции нескольких переменных. Замена независимых переменных. 220. Метод вычисления дифференциалов. 221. Общий случай замены переменных. 222. Примеры. ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ § 1. Аналитическое представление кривых и поверхностей 224. Примеры. 225. Кривые механического происхождения. 226. Кривые на плоскости (в полярных координатах). Примеры. 227. Поверхности и кривые в пространстве. 228. Параметрическое представление. 229. Примеры. § 2. Касательная и касательная плоскость 231. Примеры. 232. Касательная в полярных координатах. 233. Примеры. 234. Касательная к пространственной кривой. Касательная плоскость к поверхности. 235. Примеры. 236. Особые точки плоских кривых. 237. Случай параметрического задания кривой. § 3. Касание кривых между собой 239. Примеры. 240. Характеристические точки. 241. Порядок касания двух кривых. 242. Случай неявного задания одной из кривых. 243. Соприкасающаяся кривая. 244. Другой подход к соприкасающимся кривым. § 4. Длина плоской кривой 246. Направление на кривой. 247. Длина кривой. Аддитивность длины дуги. 248. Достаточные условия спрямляемости. Дифференциал дуги. 249. Дуга в роли параметра. Положительное направление касательной. § 5. Кривизна плоской кривой 251. Круг кривизны и радиус кривизны. 252. Примеры. 253. Координаты центра кривизны. 254. Определение эволюты и эвольвенты; разыскание эволюты. 255. Свойства эволют и эвольвент. 256. Разыскание эвольвент. ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ

Программа C++ для поиска наибольшего и наименьшего элемента массива

Это программа C++ для поиска наибольшего и наименьшего элементов в массиве.

Описание проблемы

Программа берет массив и выводит наибольший и наименьший элементы массива.

Проблема Решение

1. Программа получает массив элементов.
2. С помощью цикла for находится самый большой и самый маленький элемент.
3. Результат распечатывается.
4. Выйти.

Программа C++/исходный код

Вот исходный код программы C++ для поиска наибольшего и наименьшего элементов в массиве. Вывод программы показан ниже.

1.  #include 

2.  использование пространства имен std; 

3.  int main () 

4.  { 

5.  int arr[10], n, i, max, min; 

6.  cout << "Введите размер массива: "; 

7.  cin >> n; 

8.  cout << "Введите элементы массива: "; 

9.  для (i = 0; i < n; i++) 

10.  cin >> arr[i]; 

11.  макс = обр[0]; 

12.  для (i = 0; i < n; i++) 

13.  { 

14.  если (max < arr[i]) 

15.  max = arr[i] 

16.  } 

17.  мин = обр[0]; 

18.  для (i = 0; i < n; i++) 

19.  { 

20.  если (min > arr[i]) 

21.  min = arr[i] 

22.  } 

23.  cout << "Самый большой элемент: " << max; 

24.  cout << "Наименьший элемент: " << min; 

25.  возврат 0; 

26.  } 

Объяснение программы

1. Сначала пользователю предлагается ввести размер массива, и он сохраняется в переменной «n».
2. Объявлен массив «arr» с типом данных integer размером 10.
3. Элементы массива запрашиваются для ввода и сохраняются в «arr» с использованием цикла for.
4. Значение индекса 0 в arr присваивается переменной max.
5. Используя цикл for и инициализируя «i» равным 0, находится самый большой элемент.
6. Если max меньше arr[i], то значение arr[i] присваивается max. i увеличивается на каждой итерации.
7. Цикл продолжается до тех пор, пока «i» не станет меньше «n».
8. Аналогично находится наименьший элемент.
9. Значение индекса 0 в arr присваивается переменной min.
10. С помощью цикла for наименьшему элементу присваивается значение min.
11. Результат распечатывается.

реклама

реклама

Тестовые случаи времени выполнения

 Случай 1:
Введите размер массива: 5
Введите элементы массива: 1 2 3 4 5
Самый большой элемент: 5
Наименьший элемент: 1

Случай 2:
Введите размер массива: 3
Введите элементы массива: 36 136 0
Самый большой элемент: 136
Наименьший элемент: 0

Случай 3:
Введите размер массива: 10
Введите элементы массива: 24 56 12 8 50 69244 81 52 73
Самый большой элемент: 244
Наименьший элемент: 8 

Sanfoundry Global Education & Learning Series – Программы C++.

Чтобы попрактиковаться во всех программах на C++, вот полный набор из 1000+ примеров программирования на C++ .

Следующие шаги:

• Получите бесплатный сертификат о заслугах в программировании на C++
• Примите участие в конкурсе по сертификации программирования на C++
• Стать лучшим специалистом по программированию на C++
• Пройдите тесты по программированию на C++
• Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
• Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Категории Программы C++, Программы C++ — Массив

реклама

реклама

Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест

Маниш Бходжасиа, ветеран технологий с более чем 20-летним опытом работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.

Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.

Поиск наименьшего и наибольшего значения в диапазоне в Excel. Учебное пособие по Excel

Предположим, у нас есть таблица Excel с тремя столбцами: годовой оклад, сумма кредита и срок кредита.

В этой таблице не так много строк, и если кто-то захочет, чтобы мы назвали ему наименьшее число в каждом столбце, мы, вероятно, могли бы просто пойти и найти эти ячейки «невооруженным глазом».

Тем не менее, уже одно это кажется большой работой. А теперь представьте, что наш стол стал еще больше. К счастью, есть несколько способов найти нужные нам значения. В данном случае наименьшее и наибольшее число.

Наименьшее и наибольшее число с фильтром

Первый вариант заключается в том, что мы выбираем первые три столбца в нашей первой строке (тот, который содержит имена наших столбцов), переходим на вкладку Данные , затем на Сортировка и фильтр , а затем нажмите Фильтр : 

Мы заметим, что наши ячейки в первой строке теперь имеют раскрывающийся список.

Если мы выберем кнопку раскрывающегося списка в ячейке A1 , мы заметим несколько вариантов в нашем распоряжении:

Сразу видно, что у нас есть две нужные опции:

• Сортировать от меньшего к большему
• Сортировать от большего к меньшему

Если мы нажмем на первый вариант, мы заметим, что наш первый столбец теперь упорядочен от наименьшей годовой зарплаты к наибольшей.

Логически, так как мы выбрали только раскрывающийся список из столбца A это столбец, из которого были упорядочены эти значения.

Теперь мы знаем самое высокое и самое низкое значение. Мы можем сделать то же самое и для других столбцов.

Наименьшее и наибольшее число с условным форматированием

Еще один способ найти наибольшее и наименьшее значение — это параметр Гистограммы в условном форматировании.

Мы выберем столбец B , а затем перейдем к Условное форматирование >> Панели данных , а затем выберем первый вариант в Градиентная заливка .

Ячейки в столбце B теперь будут заполняться автоматически, при этом наименьшее значение будет наименее заполненным синим цветом, а наибольшее значение будет полностью окрашено.

Этот вариант очень удобен, когда мы работаем с небольшим набором данных или хотим показать наши данные с помощью более качественной графики, но довольно сложно найти таким образом наименьшее и наибольшее значения при работе с большим набором данных.

Наименьшее и наибольшее число с функциями

Самый простой способ найти наименьшее и наибольшее значения в нашем диапазоне — использовать функции. Предположим, что мы хотим найти наименьшее значение в нашем столбце C (Срок кредита).

Мы перейдем к одной ячейке ниже нашей последней заполненной ячейки в столбце (в нашем случае ячейка C21 ).

Также проще перейти к последней ячейке в нашем диапазоне. Мы просто нажимаем CTRL + стрелка вниз , и Excel направляет нас к последней ячейке в нашем диапазоне.

После того, как мы нашли нашу ячейку, мы перейдем на вкладку Главная , на подвкладку Редактирование , нажмите стрелку рядом с Автосумма, нажмите Мин (вычисляет наименьшее значение) или Max (вычисляет наибольшее значение), а затем нажмите ENTER .

Если мы нажмем Min , нам автоматически будет представлена ​​функция, которую Excel подготовил для нас:

Как мы видим, наша функция выглядит нормально. Мы нажмем ENTER и затем нам будет представлен результат, который в данном случае является числом 18.

Чтобы найти наибольшее значение, мы должны изменить нашу функцию с MIN на MAX .

Наименьшее и наибольшее число с VBA

Поскольку мы не решили проблему наименьшего и наибольшего значения в столбце B , мы сделаем это с помощью кода VBA. Для этого мы определим ячейку E1 как Наименьшую сумму кредита, а ячейку F1 — как Наибольшую сумму кредита .

Мы введем наименьшее значение столбца B в ячейку E2 и наибольшее значение столбца B в ячейку Ф2 .

Наш код VBA будет следующим:

Sub Return_lowest_number() Dim ws As рабочий лист Установите ws = Рабочие листы («Ссудная таблица») ws.Range("E2") = Application.WorksheetFunction.Min(ws.Range("B2:B20")) Конечный переходник

Sub Return_lowest_number()     Dim ws As Worksheet     Set ws = Worksheets("Таблица займов")     ws.Range("E2") = Application.WorksheetFunction.Min(ws.Range("B2:B20 )) Конец Sub

В первой части кода мы объявляем переменную. Dim — это сокращение от «размерность», и мы используем его, когда хотим объявить переменную, которая будет запомнена и может быть использована позже в нашем коде.

В нашем примере мы создаем переменную ws , которая будет определена как рабочий лист.

На следующем шаге мы устанавливаем нашу переменную для ссылки на наш рабочий лист. Наш рабочий лист называется Loan table, поэтому мы установим нашу переменную ws , чтобы совпадать с этим именем.

Наконец, мы вызываем нашу переменную, а затем ставим точку («.»), что позволит нам вызывать определенную ячейку из нашего рабочего листа. На этом этапе мы определяем ячейку, в которую мы хотим ввести данные, а затем определяем сами данные. Наша нужная ячейка — ячейка E2 .

Мы хотим, чтобы наша ячейка E2 была равна минимальному значению диапазона в столбце B . С другой стороны уравнения, мы сначала вызываем приложение , чтобы мы могли также вызвать функцию рабочего листа . Затем мы вызываем функцию Min , чтобы вернуть минимальное значение нашего диапазона.

Затем мы хотим определить наш диапазон. Наш диапазон, очевидно, будет расположен на нашем листе, и мы вызываем нашу переменную для листа, а затем вызываем диапазон наших данных, который равен B2:B20 .

Когда мы запустим наш код с F5 , мы получим результат в ячейке E2 следующим образом:

Чтобы вернуть наибольшее значение, т. е. наибольшую сумму кредита, мы должны внести некоторые коррективы в наш код. Мы создадим еще один код под нашим первым, и он будет выглядеть так:

.

Sub Return_largest_number() Dim ws As рабочий лист Установите ws = Рабочие листы («Ссудная таблица») ws.Range("F2") = Application.WorksheetFunction.Max(ws.Range("B2:B20")) Конечный переходник

Sub Return_largest_number()     Dim ws As Worksheet     Set ws = Worksheets("Таблица займов")     ws.Range("F2") = Application.WorksheetFunction. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт