Вектора онлайн калькулятор: Онлайн калькулятор. Скалярное произведение векторов

Калькулятор для расчета емкости АКБ для ИБП

Расчет емкости аккумуляторной батареи для UPS и время работы источника бесперебойного питания

Если вы владелец дорогого электрооборудования, которое требует стабильного и бесперебойного питания — без ИБП вам не обойтись.

Насколько проще была бы наша жизнь, если бы существовал универсальный источник бесперебойного питания на все случаи жизни?

На практике же, каждый пользователь предъявляет к источнику бесперебойного питания конкретные требования, которые зависят от назначения, типа и количества техники, которая будет подключена к ИБП.

Специалисты компании LogicPower считают, что к выбору UPS для дома или бизнеса необходимо подходить рационально. Калькулятор ИБП избавит вас от разочарований и лишних трат, если вы неправильно подберете мощность, тип ИБП или емкость аккумулятора.

Типы источников бесперебойного питания

Smart ИБП с двойным преобразованием применяют для высокочувствительной техники с большим количеством «электронной начинки».

Преимущества ИБП on-line:

• широкий диапазон входных напряжений (110-300V) при минимальном отклонении на выходе (220V±1%)
• скорость переключения режимов работы у бесперебойников смарт онлайн равна нулю
• модели Smart ИБП online с одинаковой мощностью можно параллельно соединять между собой
• возможность удаленного управления и контроля параметров работы инверторов напряжения.

ИБП линейно-интерактивные пользуются широким спросом у владельцев персональных компьютеров.

Преимущества линейно-интерактивных ИБП:

• линейно-интерактивные бесперебойники LogicPower имеют доступную стоимость при высоком качестве сборки и внутреннего наполнения
• встроенная функция AVR позволяет использовать UPS линейно-интерактивный как стабилизатор напряжения для компьютера
• время автономной работы от аккумулятора от 10 до 30 минут, что позволяет сохранить необходимые файлы и корректно отключить ПК

ИБП с правильной синусоидой в паре с внешним аккумулятором используют для обеспечения бесперебойного питания 24/7 систем автономного отопления, водоснабжения, видеонаблюдения и т. д.

Преимущества UPS с чистой синусоидой:

• источники бесперебойного питания с правильной синусоидой имеют широкий спектр защитных функций от: короткого замыкания, скачков напряжения, сетевых помех, разряда и избыточного заряда батарей, высокого/низкого напряжения
• скорость переключения у бесперебойников с чистой синусоидой на работу от аккумулятора и обратно – меньше секунды

ИБП гибридный MPPT с правильной синусоидой чаще всего используют для автономных систем бесперебойного питания на основе солнечных батарей. ИБП данного типа совместимы и с традиционными, и с альтернативными источниками электрической энергии.

Преимущества гибридных источников бесперебойного питания с MPPT контроллером:

• ИБП гибридный автоматически регулирует ток заряда внешней батареи при помощи микропроцессорного управления
• гибридный инвертор имеет высокую производительность, КПД – 98%
• UPS обеспечивает максимально точный контроль параметров работы и распределения вырабатываемой энергии

Онлайн калькулятор ИБПпоможет произвести быстрый и точный расчет необходимой вам мощности источника бесперебойного питания с учетом суммарной мощности, подключенного к нему оборудования* и коэффициента запаса.

*Для расчетов берется мощность каждой единицы оборудования, указанная производителем в технической документации

Как выбрать аккумулятор для источника бесперебойного питания?

После того как вы определитесь с типом и мощностью источника бесперебойного питания, необходимо правильно подобрать аккумуляторную батарею.

Главный критерий выбора – необходимое вам время резервного питания электрооборудования от аккумуляторной батареи.

Типы аккумуляторов для ИБП

Аккумуляторы свинцово-кислотные AGМ герметичные необслуживаемые батареи пользуются широким спросом благодаря доступной стоимости. Кроме цены необслуживаемые АКБ данного типа имеют следующие преимущества: высокая надежность, стабильное напряжение, широкий диапазон рабочих температур. Рассчитаны на 400 циклов заряд/разряд

Мультигелевые аккумуляторные батареи – это модернизированные AGM аккумуляторы, которые имеют увеличенный ресурс циклов работы – 800.

Аккумуляторы гелевые GeL – благодаря вязкой структуре электролита не боятся низких температур и отлично работают при низком заряде батареи. Ресурс циклов заряд/разряд – 1200

Литий железо фосфатные АКБ отличаются устойчивостью к высоким и низким температурам окружающей среды, имеют хорошую производительность, минимальный уровень токсичности, компактные размеры и малый вес. Аккумуляторы Lifepo4 выдерживают более 7000 циклов

Онлайн калькулятор емкости аккумулятора для ИБП поможет правильно подобрать АКБ

Остались вопросы?

Технические эксперты LogicPower дадут квалифицированную консультацию и помогут Вам с выбором оборудования для систем бесперебойного питания

0(800) 211-405

LogicPower – стандарт напряжения!

Вектор ab: Онлайн калькулятор. Координаты вектора по двум точкам — ЭкоДом: Дом своими руками

Содержание

Проекция вектора онлайн

Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр_ab = |b|cos(a,b) или

где a•b — скалярное произведение векторов, |a| — модуль вектора a.

Инструкция. Для нахождения проекции вектора Пp_ab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.

Заданы:

две координаты вектора

три координаты вектора

a:
;
;

b:
;

;

Классификация проекций вектора

Виды проекций по определению проекция вектора

1. Геометрическая проекция вектора AB на ось (вектор) называется вектор A’B’, начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
2. Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A’B’, взятая со знаком + или -, в зависимости от того, имеет ли вектор A’B’ то же направление, что и ось (вектор).

Виды проекций по системе координат

1. проекции на плоскости (система координат OX,OY). Пример: a(2;-3), a=2i-3j
   
2. проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k
   
3. проекции в N-мерном пространстве

Свойства проекции вектора

1. Геометрическая проекция вектора есть вектор (имеет направление).
2. Алгебраическая проекция вектора есть число.

Теоремы о проекциях вектора

Теорема 1. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.

AC’=AB’+B’C’

Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр_ab = |b|·cos(a,b)

Виды проекций вектора

1. проекция на ось OX.
2. проекция на ось OY.
3. проекция на вектор.

Проекция на ось OX	Проекция на ось OY	Проекция на вектор
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).

1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)

2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).

3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).

Пример 1. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60^о. Если OE есть единица масштаба, то |b|=4, так что .

Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.

Пример 2. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120^o. Длина |b| вектора b равна 4, поэтому пр_ab=4·cos120^o = -2.

Действительно, длина вектора равна 2, а направление противоположно направлению оси.

Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).

Координаты вектора: MN(4-1;5-1) = MN(3;4)

Тогда модуль вектора MN равен:

Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.

M’N’(3;0)

Пример 4. Найти проекцию вектора c на вектор d;

с = АС = (-2;-1;3), d = CB(-5;-3;3)

Найдем проекцию вектора AC на вектор BC

Пример 5. Найти проекцию пр_b(-2a+4b)

где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π

Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n

Найдем модуль вектора 4m-n.

а) Рассмотрим треугольник со сторонами a,b,c. По теореме косинусов:

a² = b² + c² – 2bc∙cos(b,c), откуда

или

б) Рассмотрим второй вариант решения.

Поскольку угол между векторами π, т.е. 180^о, то векторы лежат на одной оси.

Таким образом, 4m-n = 4*1 – 1 = 3.

Находим проекцию.

пр_b(-2a+4b) = пр

b(12m+2n) =

Сумма двух векторов.

Законы сложения векторов. Сумма нескольких векторов. Правило параллелограмма. Вычитание векторов 9

Тема 24.

Сумма векторов. Разность векторов.

Рассмотрим пример. Пусть материальная точка переместилась из точки A в точку B, а затем из точки B в точку C. В результате этих перемещений, которые можно представить векторами AB⃗ и BC⃗, материальная точка переместилась из точки A в точку C. Поэтому результирующее перемещение можно представить вектором AC⃗. Поскольку перемещение из точки A в точку C складывается из перемещения из A в B и перемещения из B в C, то вектор AC⃗ естественно назвать суммой векторов AB⃗ и BC⃗:AC⃗=AB⃗+BC⃗.

Рассмотренный пример приводит нас к понятию суммы двух векторов.

Пусть a⃗ и b⃗ – два вектора. Отметим произвольную точку A и отложим от этой точки вектор AB⃗ равный a⃗. Затем от точки B отложим вектор BC⃗, равный b⃗. Вектор AC⃗ называется суммой векторов a⃗ и b⃗.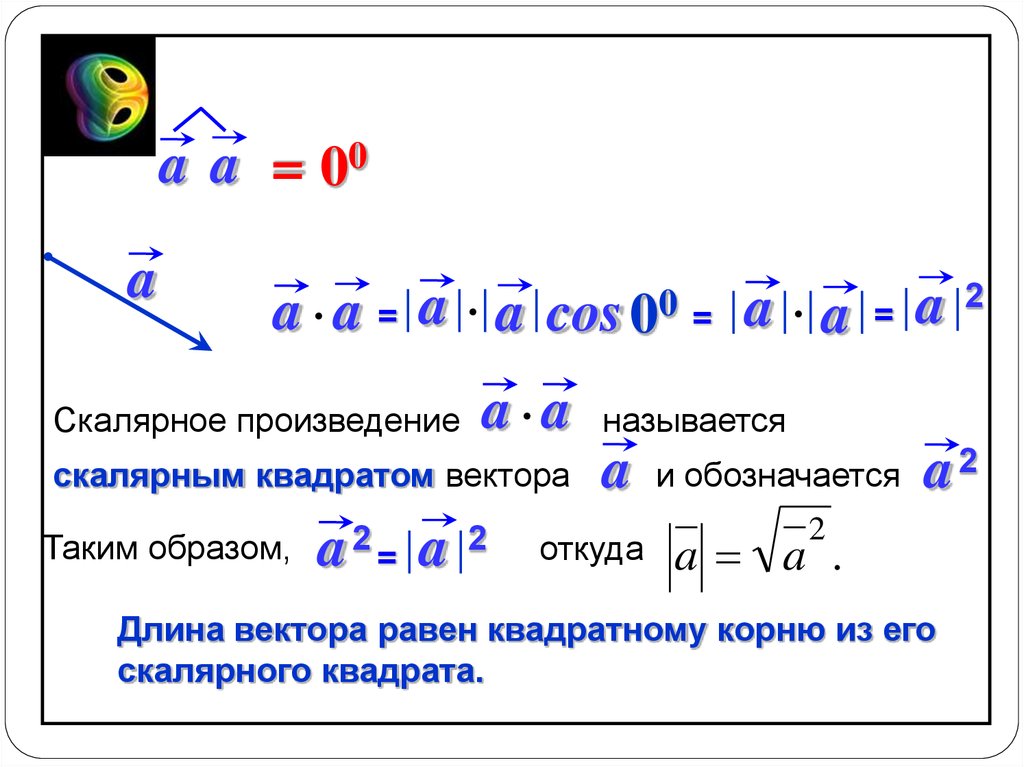 Это правило сложения векторов называется правилом треугольника. Рисунок это поясняет.

Сумма векторовa⃗ и b⃗ обозначается так: a⃗+b⃗.

Складывая по правилу треугольника произвольный вектор a⃗ с нулевым вектором, получаем, что для любого вектора a⃗ справедливо равенство

a⃗+0⃗=a⃗

Правило треугольника можно сформулировать также следующим образом: если A, B и C – произвольные точки, то AB⃗+BC⃗=AC⃗.

Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.

Теорема

Для любых векторов a⃗,b⃗ и c⃗ справедливы равенства:

1. a⃗+b⃗=b⃗+a⃗ (переместительный закон).

2. a⃗+b⃗+c⃗=a⃗+b⃗+c⃗ (сочетательный закон).

Докажем первое равенство.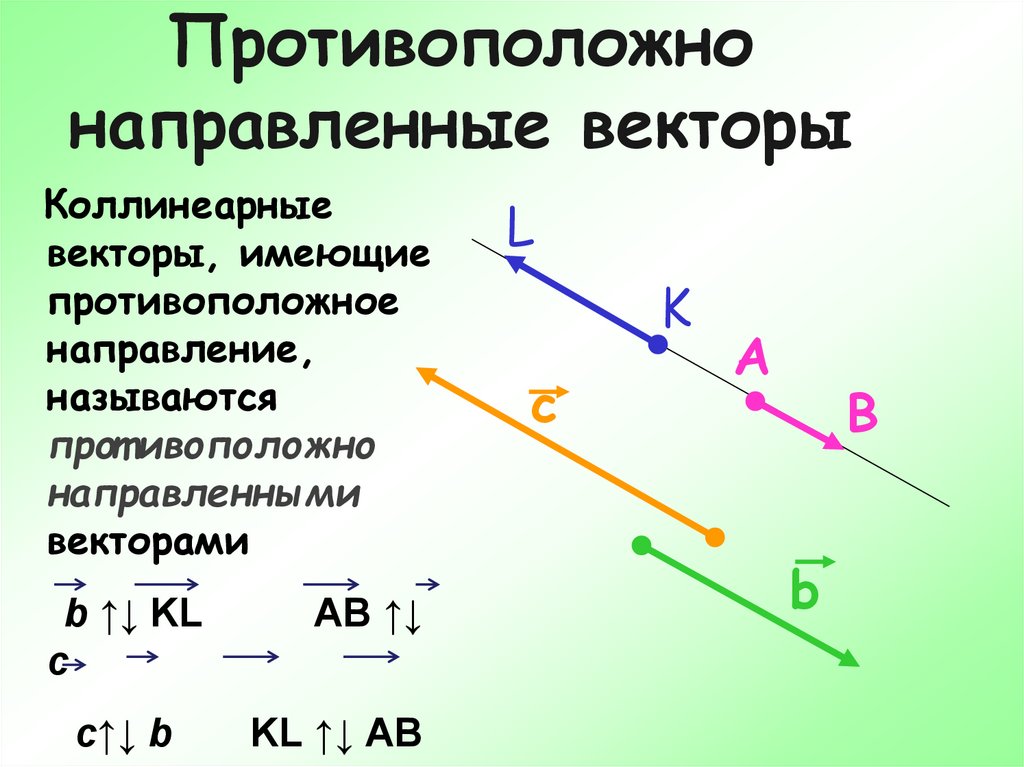 Рассмотрим случай, когда векторы a⃗ и b⃗ не коллинеарны. От произвольной точки A отложим векторы ABAD и на этих векторах построим параллелограмм ABCD. По правилу треугольника AC⃗=AB⃗+BC⃗=a⃗+b⃗. Аналогично AC⃗=AD⃗+DC⃗=b⃗+a⃗. Отсюда следует, что a⃗+b⃗=b⃗+a⃗.

При доказательстве первого свойства мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы a⃗ и b⃗, нужно отложить от какой-нибудь точки A векторы AB⃗=a⃗ и AD⃗=b⃗ и построить параллелограмм ABCD. Тогда вектор AC⃗ равен a⃗+b⃗. Правило параллелограмма часто используется в физике, например при сложении двух сил.

Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Например, от произвольной точки A отложен вектор AB⃗=a⃗, затем от точки B отложен вектор BC⃗=b⃗ и, наконец, от точки С отложен вектор CD⃗=c⃗. В результате получается вектор AD⃗=a⃗+b⃗+c⃗.

Аналогично можно построить сумму четырех, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.

Разностью векторов a⃗ и b⃗ называется такой вектор, сумма которого с вектором b⃗ равна вектору a⃗.

Разность векторов a⃗ и b⃗ обозначается так:a⃗-b⃗.

Рассмотрим задачу о построении двух векторов.

Даны векторы a⃗ и b⃗. Построить вектор a⃗-b⃗.

Отметим на плоскости произвольную точку O и отложим от этой точки векторы OA⃗=a⃗ и OB⃗=b⃗.

По правилу треугольника OB⃗+BA⃗=OA⃗ или b⃗+BA⃗=a⃗. Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗. По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.

Пусть a⃗ – произвольный ненулевой вектор. Вектор a1⃗ называется противоположным вектору a⃗, если векторы a⃗ и a1⃗ имеют равные длины и противоположно направлены.

Вектор, противоположный вектору a⃗, обозначается так: -a⃗. Очевидно, что a⃗+-a⃗=0⃗.

Теорема

Для любых векторов a⃗ и b⃗ справедливо равенство a⃗-b⃗=a⃗+-b⃗.

Сегодня мы научились складывать и вычитать векторы. Узнали правило треугольника, правило параллелограмма и правило многоугольника.

Векторов

Это вектор:

Вектор имеет величин (размер) и направлений :

Длина линии показывает ее величину, а стрелка указывает направление.

Мы можем добавить два вектора, соединив их лоб в лоб:

И неважно в каком порядке мы их складываем, получаем один и тот же результат:

Пример: Самолет летит, указывая на север, но ветер дует с северо-запада.

Два вектора (скорость, создаваемая пропеллером, и скорость ветра) приводят к несколько более низкой скорости относительно земли в направлении немного к востоку от севера.

Если смотреть на самолет с земли, то может показаться, что он немного скользит вбок.

Вы когда-нибудь видели такое? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают объяснить это.

Скорость, ускорение, сила и многое другое являются векторами.

Вычитание

Мы также можем вычесть один вектор из другого:

• Сначала мы меняем направление вектора, который хотим вычесть,
• , затем добавьте их как обычно:

а − б

Обозначение

Вектор часто записывается жирным шрифтом , например a или b .

Вектор также можно записать в виде букв его головы и хвоста со стрелкой над ними, например:

Расчеты

Теперь.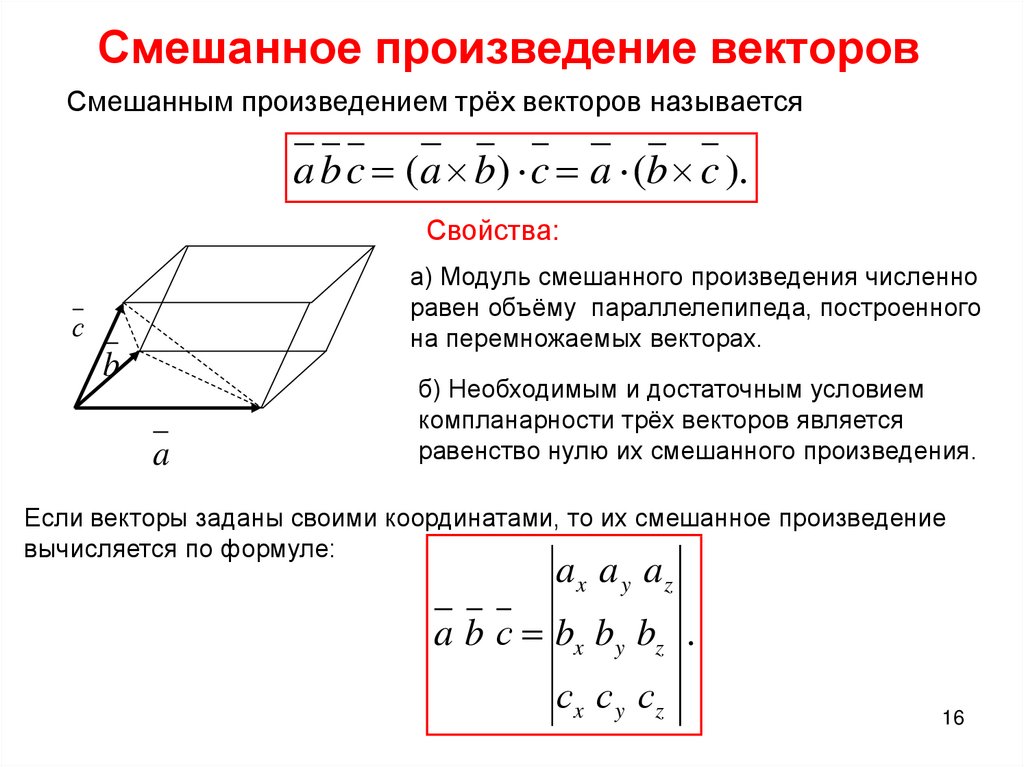 .. как мы будем производить расчеты?

Самый распространенный способ — сначала разбить вектор на части x и y, например:

Вектор a разбит на
два вектора a _x и a _y

(Позже мы увидим, как это сделать.)

Добавление векторов

Затем мы можем сложить векторы по добавление частей x и добавление частей y :

Вектор (8, 13) и вектор (26, 7) в сумме дают вектор (34, 20)

Пример: сложить векторы

a = (8, 13) и b = (26, 7)

c = a + b

c = (1, c = 1, 8, ) (26, 7) = (8+26, 13+7) = (34, 20)

Когда мы разбиваем такой вектор, каждая его часть называется компонентой :

Вычитание векторов

Чтобы вычесть, сначала инвертируйте вектор, который мы хотим вычесть, затем сложите.

Пример: вычесть

k = (4, 5) из v = (12, 2)

a = v + − k

= (1, 2) + a (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)

Величина вектора

Величина вектора показана двумя вертикальными чертами по обе стороны от вектора:

| и |

ИЛИ можно написать двойными вертикальными черточками (чтобы не путать с абсолютным значением):

|| и ||

Для расчета используем теорему Пифагора:

| и | = √( х ² + у ² )

Пример: какова величина вектора

b = (6, 8) ?

| б | = √( 6 ² + 8 ² ) = √( 36+64) = √100 = 10

Вектор с величиной 1 называется единичным вектором.

Вектор против скаляра

Скаляр имеет величину (размер) только .

Скаляр: просто число (например, 7 или −0,32) … определенно не вектор.

Вектор имеет величину и направление и часто пишется жирным шрифтом , поэтому мы знаем, что это не скаляр:

• , поэтому c — это вектор, он имеет величину и направление
• , но c — это просто значение, например 3 или 12,4

Пример: k

b на самом деле скаляр, умноженный на k вектор b .

Умножение вектора на скаляр

Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.

Пример: умножить вектор

m = (7, 3) на скаляр 3

a = 3 м = (3×7, 3×3) = (21, 9)

Он по-прежнему указывает в том же направлении, но в 3 раза длиннее

(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз. )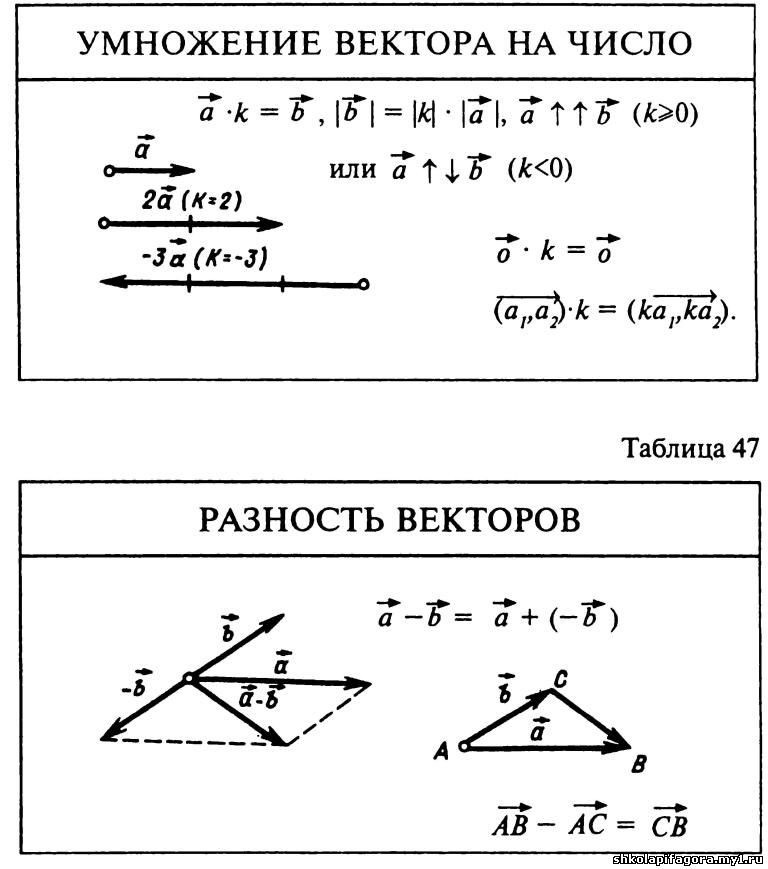

 

Умножение вектора на вектор (скалярное произведение и векторное произведение)

Как нам умножить два вектора вместе? Существует более чем один способ! Скаляр или скалярное произведение (результатом является скаляр). Вектор или векторное произведение (результатом является вектор). (Дополнительную информацию см. на этих страницах.)

 

Более двух измерений

Векторы также прекрасно работают в 3-х и более измерениях:

Вектор (1, 4, 5)

Пример: сложите векторы

и = (3, 7, 4) и b = (2, 9, 11)

c = a + b

c = (3, 7, 4) + (2, 9, 11) = (3+2 , 7+9, 4+11) = (5, 16, 15)

Пример: какова величина вектора

w = (1, −2, 3) ?

| с | = √( 1 ² + (−2) ² + 3 ² ) = √( 1+4+9) = √14

Вот пример с 4-мя измерениями (но рисовать сложно!):

Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)

(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1,-2,-3,-4)
= ( 3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)

 

Величина и направление

Мы можем знать величину и направление вектора, но нам нужны его длины x и y (или наоборот):

Вектор a в полярных координатах Координаты		Вектор a в декартовых координатах Координаты

Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткий обзор:

Из полярных координат (r, θ ) в декартовы координаты (x,y)		От декартовых координат (x,y) до полярных координат (r,θ)
x = r × cos( θ ) y = r × sin( θ )		г = √ ( х 2 + у 2 ) θ = тангенс -1 (г/х)

 

 

Пример

Сэм и Алекс тянут коробку.

• Сэм тянет с силой 200 ньютонов под углом 60°
• Алекс тянет с усилием 120 ньютонов под углом 45°, как показано

Что такое объединенная сила и ее направление?

 

Сложим два вектора с головы до хвоста:

Первое преобразование из полярной системы в декартову (до 2 десятичных знаков):

Вектор Сэма:

• x = r × cos( θ ) = 200 × cos(60°) = 200 × 0,5 = 100
• y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173,21

Вектор Алекса:

• x = r × cos( θ ) = 120 × cos(−45°) = 120 × 0,7071 = 84,85
• y = r × sin( θ ) = 120 × sin(−45°) = 120 × -0,7071 = −84,85

Теперь у нас есть:

Добавьте их:

(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)

Этот ответ верный, но давайте обратимся к полярному, поскольку вопрос был полярным:

• r = √ (x ² + y ² ) = √ (184,85 ² + 88,36 ² ) = 900,4

20407

• θ = тангенс ^-1 ( y / x ) = тангенс ^-1 ( 88,36 / 184,85 ) = 25,5°

И у нас есть этот (округленный) результат:

А для Сэма и Алекса это выглядит так:

Они могли бы получить лучший результат, если бы стояли плечом к плечу!

 

 

Точечный продукт

Вектор имеет величину (длину) и направление :

Вот два вектора:

Они могут быть умножены на с использованием « скалярного произведения » (см. также Перекрестное произведение).

Расчет

Скалярный продукт записывается с использованием центральной точки:

a · b
Это означает скалярное произведение а и б

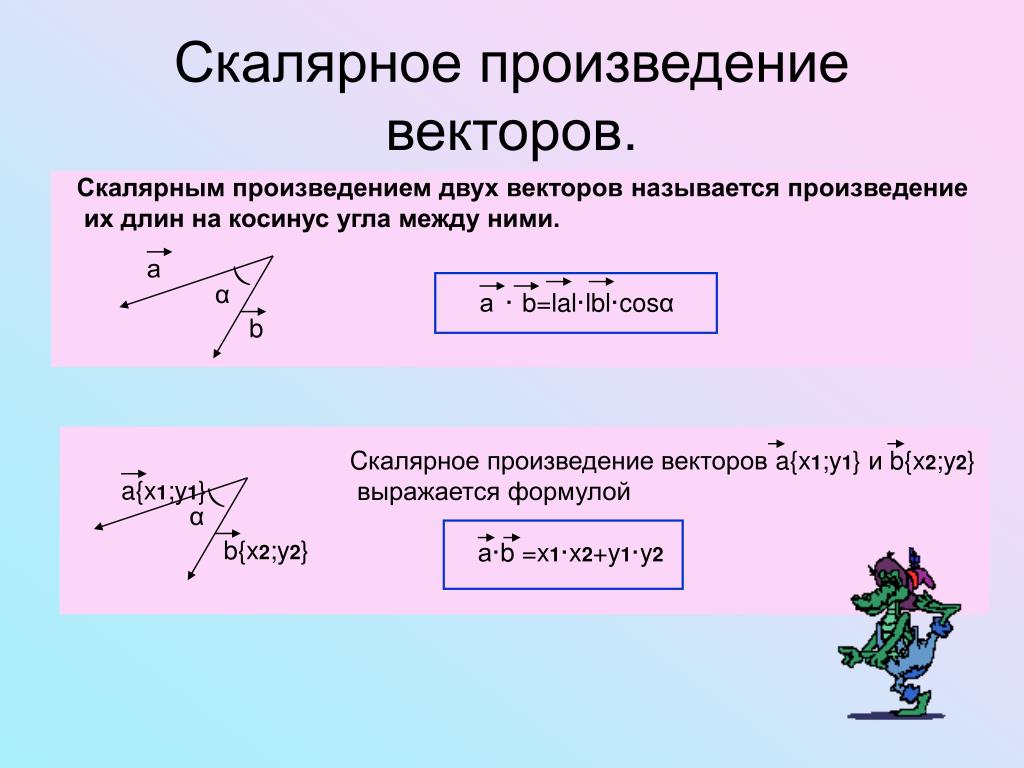
Мы можем вычислить скалярное произведение двух векторов следующим образом:

а · б = | и | × | б | × cos(θ)

Где:
| и | величина (длина) вектора a
| б | — величина (длина) вектора b
θ — угол между a и b

Итак, мы умножаем длину на a умножить на длину b , затем умножить на косинус угла между a и b

 

ИЛИ мы можем рассчитать это так:

a · b = a _x x b _x + a _y x b _y

Итак, мы умножаем x, умножаем y, а затем складываем.

Оба метода работают!

И результат номер (называемый «скаляром», чтобы показать, что это не вектор).

Пример: вычислить скалярное произведение векторов

a и b :

a · b = | и | × | б | × cos(θ)

a · b = 10 × 13 × cos(59,5°)

a · b = 10 × 13 × 0,5075…

a · b 90,008 = 65,008 = 66 (округлено)

ИЛИ мы можем вычислить это так:

a · b = а _х х б _х + а _у х б _у

а · б = -6 х 5 + 8 х 12

2

а · 8

a · b = 66

Оба метода дали один и тот же результат (после округления)

Также обратите внимание, что мы использовали минус 6 для _x (оно движется в отрицательном направлении x)

Примечание: вы можете использовать векторный калькулятор
чтобы помочь вам.

Почему cos(θ) ?

Хорошо, чтобы умножить два вектора, имеет смысл перемножить их длины вместе , но только тогда, когда они указывают в одном направлении .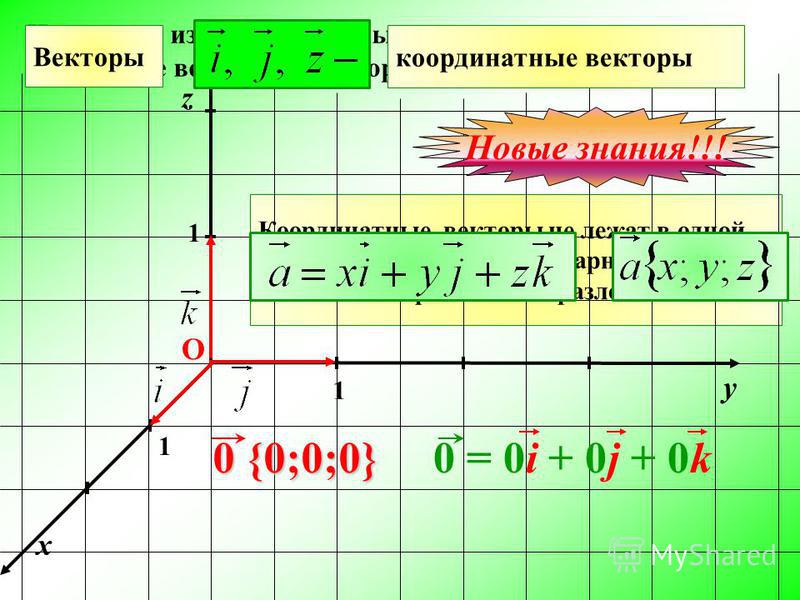

Итак, мы делаем одну «точку в том же направлении», что и другая, умножая на cos(θ):

Возьмем компонент a , лежащий рядом с b		Как пролить свет, чтобы увидеть где лежит тень

ТОГДА умножаем !

Это работает точно так же, если мы «проецируем» b вместе с на , а затем умножаем: Потому что не имеет значения, в каком порядке мы делаем умножение: | и | × | б | × потому что (θ) = | и | × соз (θ) × | б |

Прямоугольные

Когда два вектора расположены под прямым углом друг к другу, скалярное произведение равно ноль .

Пример: рассчитать скалярный продукт для:

a · b = | и | × | б | × cos(θ)

а · б = | и | × | б | × cos(90°)

a · b = | и | × | б | × 0

а · б = 0

, или мы можем вычислить его следующим образом:

a · b = a _x x b _x + a _y x b _y

1 6 · 1 -2 x 1900 900 × 9

а · б = -144 + 144

а · б = 0

Это может быть удобным способом узнать, находятся ли два вектора под прямым углом.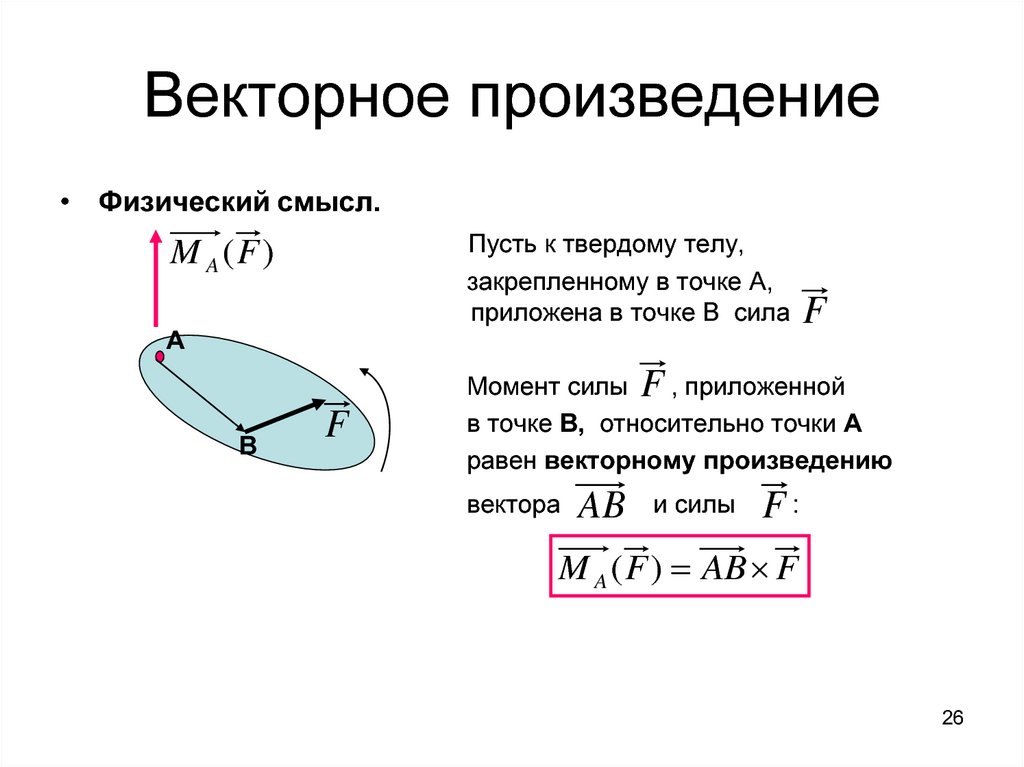

Три или более измерений

Все это прекрасно работает и в 3-х (или более) измерениях.

И действительно может быть очень полезным!

Пример: Сэм измерил концы двух полюсов и хочет узнать

угол между ними :

У нас есть 3 измерения, поэтому не забудьте z-компоненты:

a · b = а _x × b _x + a _y × b _y + a _z × b _z

× 1 + 1 × 99008

а · б = 36 + 16 + 70

а · б = 122

 

Теперь о другой формуле:

a · b = | и | × | б | × cos(θ)

Но что такое | и | ? Это величина или длина вектора a . Мы можем использовать Пифагор:

• | и | = √(4 ² + 8 ² + 10 ² )
• | и | = √(16 + 64 + 100)
• | и | = √180

Аналогично для | б |:

• | б | = √(9 ² + 2 ² + 7 ² )
• | б | = √(81 + 4 + 49)
• | б | = √134

И мы знаем из вычислений выше, что a · b = 122, поэтому:

a · b = | и | × | б | × cos(θ)

122 = √180 × √134 × cos(θ)

cos(θ) = 122 / (√180 × √134)

cos(θ) = 0,7855.

Рассчитать норму вектора онлайн — функция vector_norm

Векторная норма, расчет онлайн

Резюме:

Векторный калькулятор позволяет рассчитать норму вектора онлайн.

vector_norm online

---

Описание:

Векторный калькулятор позволяет определить норму вектора по координатам . Вычисления производятся в точной форме, они могут включать числа, но также и буквы. 92)`

Векторный калькулятор способен вычислить норму вектора знает его координаты, которые являются числовыми или символьными.

Позвольте `vec(u)`(1;1) вычислить норму вектора `vec(u)`, введите vector_norm(`[1;1]`) , после вычисления возвращается норма, равная `sqrt(2)`.

92)`.

Векторный калькулятор позволяет вычислить норму вектора знает его координаты, которые являются числовыми или буквенными.

Пусть `vec(u)`(1;1;1) для вычисления нормы вектора `vec(u)`, введите vector_norm(`[1;1;1]`) , после вычисления возвращается норма, равная `sqrt(3)`.

92)` возвращается.

Вычисление нормы вектора в пространстве любой размерности

Векторный калькулятор используется по тому же принципу для вычисления нормы вектора в пространстве любой размерности.

Синтаксис:

vector_norm(vector)

---

Примеры:

vector_norm(`[1;1]`), возвращает `sqrt(2)`

Расчет онлайн с помощью vector_norm (вычисление нормы вектора)

См.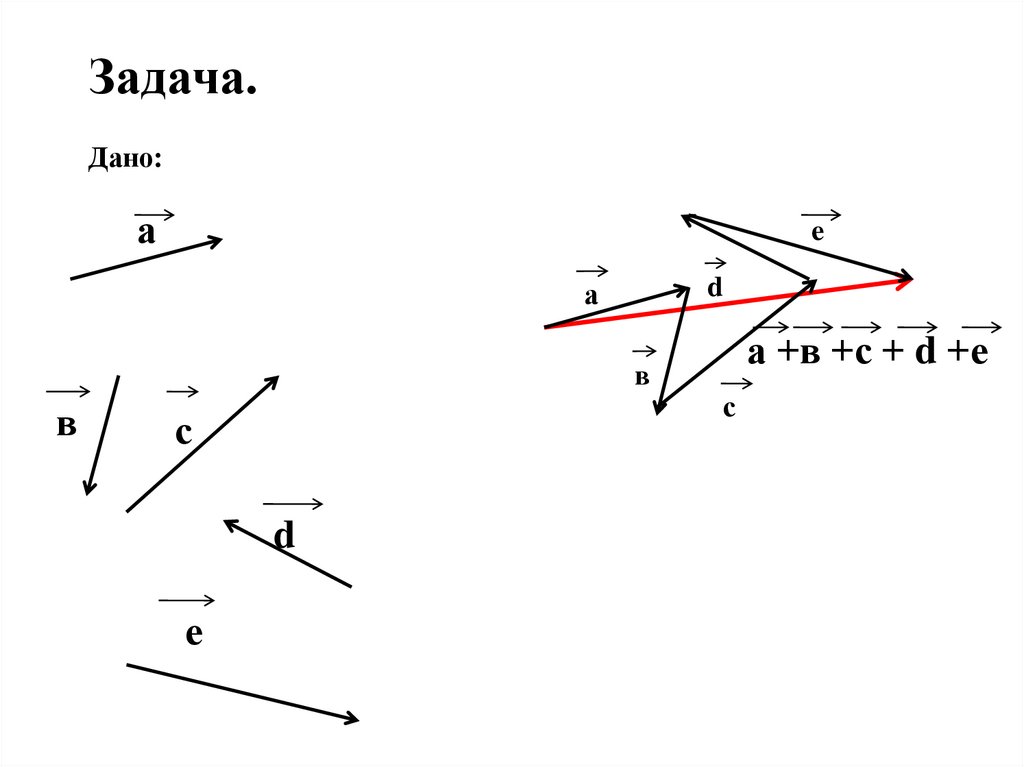 также

Список связанных калькуляторов:

• Векторный калькулятор : vector_calculator. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
• Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
• Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
• Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
• Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
• Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
• Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.
• Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
• Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
• Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.

---

Список связанных упражнений:

• Вычисление расстояния между двумя точками. Целью этого исправленного упражнения является вычисление расстояния между двумя точками по их координатам.

---

Напоминания о курсах, калькуляторы, упражнения и игры: Векторы

 

Модуль вектора | Онлайн-калькулятор, формулы, упражнения и многое другое

Вычисление модуля вектора — это операция, которую вам придется использовать во многих математических упражнениях, таких как вычисление скалярного произведения двух векторов. Ниже представлен калькулятор, позволяющий получить модуль вектора из его составляющих (v ₁ , v ₂ ) или положение двух его точек A (x ₁ , y ₁ ) и B (x ₂ , y ₂ )

наш калькулятор векторных данных, которые вы знаете, и нажмите кнопку расчета, чтобы получить его модуль. Кроме того, если вы хотите научиться вычислять модуль вектора , мы покажем вам, как это делается.

Разделы статьи

• Что такое модуль вектора?
• Как вычислить модуль вектора с его компонентами
• Вычислить модуль вектора по координатам двух точек.
• Модуль суммы двух векторов

Что такое модуль вектора?

Когда мы говорим о модуле вектора, мы имеем в виду длину сегмента, который лежит между его концами A и B :

При вычислении модуля мы всегда будем получать положительное значение или равное до нуля , если это нулевой вектор.

Как вычислить модуль вектора с его компонентами

Вектор определяется своими компонентами, и из этих компонентов мы можем вычислить его модуль, применяя следующую формулу :

В основном вам нужно вычислить квадратный корень из суммы каждого компонента в квадрате.

Например, мы собираемся вычислить квадратный корень из двух векторов

= (3, 0) y = (5, 5):

Если вектор трехмерный Формула для расчета его модуля точно такая же, но с добавлением квадрата третьего компонента. То есть вам придется применить это уравнение:

В случае вектора в R3 Если компоненты x, y и z возведены в квадрат, мы вычислим квадратный корень из суммы квадратов компонентов x, y и z.

Вычислить модуль вектора по координатам двух точек.

Для существует второй метод получения модуля вектора по координатам двух его точек . Нам нужно только применить следующую формулу:

Как решенное упражнение, мы собираемся вычислить модуль вектора, точками которого являются A(2, 1) и B(-3, 2) . Применяем формулу, которая у нас есть как раз на изображении над этими линиями и имеем вот что:

¿Y как вычисляется если координаты трехмерные? ? В случае, когда каждая из точек вектора имеет координаты x, y, z, тогда формула для использования такова: учитывает эту третью координату оси Z.

Модуль суммы двух векторов

Для вычислить модуль суммы двух векторов мы должны:

• Вычислить квадрат модуля каждого вектора
• Вычислить скалярное произведение двух векторов

Получив его, мы применяем следующую математическую формулу:

Если у вас есть какие-либо сомнения относительно того, как получить модуль вектора из его компонентов или координат, оставьте нам комментарий, и мы будем рады вам помочь.