Найдите наименьшее общее кратное чисел 21 и 18: Найдите наименьшее общее кратное чисел разложив их на простые множители 21 и 18, 24 и…

2

Найдите наименьшее общее кратное » задачи

НОД и НОК »

• Найдите наименьшее общее кратное чисел если a)c=2*2*2*3*5*7 n=2*2*3*3*5*7

  
  б) p=2*3*5*5*7*7*11 q=2*3*3*5*7*11*13
  НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ ЧИСЛА:
  А)3 и 8
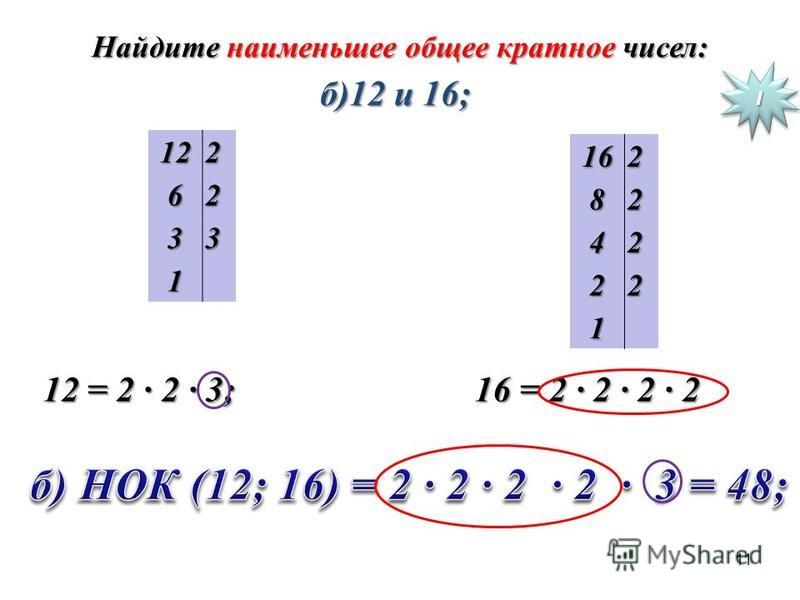
  б)24 и 18
  в)80 и 120
  г)253 и 207
  д)50 и 49
  е)120, 180 и 200
  Решение: Первый способ найти НОК:
  Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
  Кратное числа А обозначаем большой буквой «К».
  Пример:
  К (6) = {12, 18, 24, 30,}
  К (8) = {8, 16, 24, 32,}
   
  Число 24 является общим, значит оно и является наименьшим общим кратным. 
  Второй способ:
  1) Разложить данные числа на простые множители.
  2) Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
  60 = 2 · 2 · 3 · 5
  24 = 2 · 2 ·2· 3
  3) Подчеркнуть в разложениименьшегочисла (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
  НОК (24, 60) = 2 · 2 · 3 · 5 ·2
  4) Полученное произведение записать в ответ.
  Ответ: НОК (24, 60) = 120
  а) c=2*2*2*3*5*7
  n=2*2*3*3*5*7
  НОК(c,n)=2*2*2*3*5*7=840
  б)  p=2*3*5*5*7*7*11
  q=2*3*3*5*7*11*13
  НОК(p,q)=2*3*3*5*5*7*7*11*13=3153150
  НОК
  а) 24
  б) 72
  в) 240
  г) 2277
  д) 2450
  е) 1800
  

• Найдите наименьшее общее кратное:

  
  а)56и70; б)78и792; в)320и720; г)252и840; д)42и63; е)120и324; ж)675и945; з)924и396.
  Решение: А) 56 = 2 * 2 * 2 * 7
  70 = 2 * 5 * 7
  НОК (56 и 70) = 2 * 2 * 2 * 5 * 7 = 280
  б) 78 = 2 * 3 * 13
   792 = 2 * 2 * 2 * 3 * 3 * 11
  НОК (78 и 792) = 2 * 2 * 2 * 3 * 3 * 11 * 13 = 10 296
  в) 320 = 2 * 2 * 2 * 2 * 2 * 2 * 5
  720 = 2 * 2 * 2 * 2 * 3 * 3 * 5
  НОК (320 и 720) = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 5 = 2 880
  г) 252 = 2 * 2 * 3 * 3 * 7
  840 = 2 * 2 * 2 * 3 * 5 * 7
  НОК (252 и 840) = 2 * 2 * 2 * 3 * 3 * 5 * 7 = 2 520
  д) 42 = 2 * 3 * 7
  63 = 3 * 3 * 7
  НОК (42 и 63) = 2 * 3 * 3 * 7 = 126
  е) 120 = 2 * 2 * 2 * 3 * 5
  324 = 2 * 2 * 3 * 3 * 3 * 3
  НОК (120 и 324) = 2 * 2 * 2 * 3 * 3 * 3 * 3 * 5 = 3 240
  ж) 675 = 3 * 3 * 3 * 5 * 5
  945 = 3 * 3 * 3 * 5 * 7
  НОК (675 и 945) = 3 * 3 * 3 * 5 * 5 * 7 = 4 725
  з) 924 = 2 * 2 * 3 * 7 * 11
  396 = 2 * 2 * 3 * 3 * 11
  НОК (924 и 396) = 2 * 2 * 3 * 3 * 7 * 11 = 2 772

• Найдите наименьшее общее кратное данных чисел и вставьте его вместо звёздочек

  
  Н О К ( 12121278,151515)=*
  НОК (242424, 181818)=*
  Решение: 12121278 = 2 · 3 · 13 · 19 · 8179
  151515 = 3 · 3 · 5 · 7 · 13 · 37
   НОК (12121278; 151515) = 2 · 3 · 13 · 19 · 8179 · 3 · 5 · 7 · 37 = 47091165030
  242424 = 2 · 2 · 2 · 3 · 3 · 7 · 13 · 37
  181818 = 2 · 3 · 3 · 3 · 7 · 13 · 37
  НОК (242424; 181818) = 2 · 2 · 2 · 3 · 3 · 7 · 13 · 37 · 3 = 727272
  

• а) найдите наименьшее общее кратное и наибольший общий делитель чисел

  
  1)8 и 36 2)12 и 84 3)26 и 169 4)196и 294 5)210 и 84 6)70 60 и 90
  б) найдите наименьшее общее кратное и наибольший общий делитель чисел
  1)555 325 и 275 2)180 270 и 450 3)192 288 и 512 4)128 192 и 224

  
  Решение: 1) 8 и 36 — общее кратное 72, общий делитель — 4
  2)12 и 84 — 84, 12
  3)26 и 169 — 338, 13
   4)196 и 294 — 588, 98
   5)210 и 84 — 420, 42
   6) 70 и 60 и 90 1260 10
   
   
   
    

• 310 Найдите наименьшее общее кратное чисел, разложив их на простые множители:1) 21 и 18 2) 24 и 32 3)16 и 20 4) 20 и 35 5)75 и 90 6)6 и 13 7)14 и 18 8)28 и 42 9)21 и 33 10)12,30 и 75 11)15,42 и 105 12)21,28 и 35.

  
  Решение: 1) 21=3*7
      18=2*3*3
  Значит, НОК = 2*7*3*3=126
  2) 24 = 2*2*2*3
      32 = 2*2*2*2*2
  Значит, НОК = 96
  3) 16 = 2*2*2*2
      20 = 2*2*5
  Значит, НОК = 80
  То есть, чтобы получить НОК, нужно расписать каждое число на простые множители, в записи с наименьшим числом вычеркнуть повторяющиеся цифры и то, что у нас осталось домножить на то, что в наибольшем числе, аналогично можно выполнить другие, удачи
  

• Номер 3

  
  Найдите наименьшее общее кратное,
  А)32 и 48
  Б)4, 7, 12.
  Номер 4
  Какую цифру следует поставить в записи 34*, чтобы получившееся число делилось одновременно на 3 и 5?
  Номер 5
  Найдите сумму всех трехзначных чисел, кратных одновременно 77 и 5
  Решение: 3
  32=2*2*2*2*2  48=2*2*2*2*3  НОД(32;48)=2*2*2*2=16
  7=1*7  4=1*4  12=2*2*3  НОД(4;7;12)=1
  4
  На 5 делятся числа, которые оканчиваются 0 или 5
  На 3 делятся числа, сумма цифр которых делится на 3
  Значит число 345
  5
  Должны делится на 7,11 и оканчиваться 0 или 5
  Их всего 2:385 и 770
  385+770=1155
  

• Найдите наименьшее общее кратное чисел 1)36,90,200; 2)56,240,350; 3)72,108,144; 4)90,60,135; 5)100,80,120; 6)35,68,187.

  
  Решение: 1) 36=2*2*3*3; 90=2*3*3*5; 200=2*2*2*5*5; НОК(36;90;200)=2*2*2*5*5*3*3=200*9=1800; 2) 56=2*2*2*7; 240=2*2*2*2*3*5; 350=2*5*5*7; НОК(56;240;350)=2*2*2*2*3*5*5*7=240*35=8400; 3) 72=2*2*2*3*3; 108=2*2*3*3*3; 144=2*2*2*2*3*3; НОК(72;108;144)=2*2*2*2*3*3*3=144*3=432; 4) 90=2*3*3*5; 60=2*2*3*5; 135=3*3*3*5; НОК(60;90;135)=3*3*3*5*2*2*=135*4= 540; 5) 100=2*2*5*5; 80=2*2*2*2*5 120=2*2*2*3*5; НОК(80;100;120)=2*2*2*3*5*2*5= 120*10=1200; 6) 35=5*7; 68=2*2*17 187=11*17; НОК(35;68;187)=2*2*17*5*7*11=35*68*11=26180;

• 1) Найдите наименьшее общее кратное чисел a и b, если a=2*2*2*3*7*7, b= 3*3*7*7*7*11*11.

  
  Варианты ответов:
  1. 1
  2. 3*7*7
  3. 2*2*2*3*3*7*7*7*11*11
  4. 2*2*3*3*7*7

  2) Известно, что a — чётное число, а b — нечётное число. Какое из следующих чисел является чётным числом?
  1. a*b
  2. a+b
  3. (a+1)*b
  4. a+b+2
  Решение: 1) Найдите наименьшее общее кратное чисел a и b, если a=2*2*2*3*7*7, b= 3*3*7*7*7*11*11.
  —
  Определение:   Наименьшим общим кратным натуральных чисел a и b называют  наименьшее натуральное число, которое кратно и a, и   b.(т. е. делится и на то, и на другое)
    Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
    1) разложить их на простые множители — в данном примере это уже сделано.
    2) выписать множители, входящие в разложение одного из чисел;
  2*2*2*3*7*7 
    3) домножить их на множители из разложенных на множители  других чисел, которых в первом нет: 
  2*2*2*3*3*7*7*7*11*11.
  Из данных вариантов теперь сможете выбрать верный ответ. 
  2) Известно, что a — чётное число, а b — нечётное число. Какое из следующих чисел является чётным числом?
  Чётное число — целое число, которое делится на 2 без остатка: 
  1. a*b произведение четного числа на нечетное дает четное число —
   в произведении аb есть множитель 2- один из множителей числа а, оно четное.  
  Почему остальные варианты не являются четными, теперь сумеете ответить самостоятельно.

• Найдите наибольший общий делитель чисел:

  
  1) 72 и 120;
  2) 792 и 1188;
  3) 924 и 396.
  Найдите наименьшее общее кратное чисел:
  1) 56 и 70;
  2) 78 и 792;
  3) 320 и 720;
  4) 252 и 840.
  Решение: НОД (72; 120) = 2 * 2 * 2 * 3 = 24 — наибольший общий делитель72 = 2 * 2 * 2 * 3 * 3          72 : 24 = 3120 = 2 * 2 * 2 * 3 * 5          120 : 24 = 5
  НОД (792; 1188) = 2 * 2 * 3 * 3 * 11 = 396 — наибольший общий делитель792 = 2 * 2 * 2 * 3 * 3 * 11              792 : 396 = 21188 = 2 * 2 * 3 * 3 * 3 * 11            1188 : 396 = 3
  НОД (924; 396) = 2 * 2 * 3 * 11 = 132 — наибольший общий делитель924 = 2 * 2 * 3 * 7 * 11           924 : 132 = 7396 = 2 * 2 * 3 * 3 * 11           396 : 132 = 3
  НОД (42; 105) = 3 * 7 = 21 — наибольший общий делитель42 = 2 * 3 * 7               42 : 21 = 2   105 = 3 * 5 * 7             105 : 21 = 5
  НОД (588; 252) = 2 * 2 * 3 * 7 = 84 — наибольший общий делитель588 = 2 * 2 * 3 * 7 * 7            588 : 84 = 7252 = 2 * 2 * 3 * 3 * 7            252 : 84 = 3
  НОД (680; 612) = 2 * 2 * 17 = 68 — наибольший общий делитель680 = 2 * 2 * 2 * 5 * 17         680 : 68 = 10612 = 2 * 2 * 3 * 3 * 17         612 : 68 = 9Чтобы найти НОД, нужно разложить числа на простые множители и найти произведение их совместных простых множителей, взятых с наименьшим показателем степени.
  Пары взаимно простых чисел:  12 и 33; 12 и 25; 14 и 33; 14 и 25; 33 и 25.12 = 2 * 2 * 314 = 2 * 733 = 3 * 1125 = 5 * 5Взаимно простые числа — это числа, у которых нет совместных простых множителей, кроме единицы.

• а) найдите наименьшее общее кратное 21 и 176. б) трех наименьших двузначных чисел, кратных 9. в) придумайте состваное число, которое было бы взаимно простым с каждым из чисел 39,85 и 154. г) наименьшее общее кратное чисел a и b равно b. Найдите наибольший общий делитель этих чисел. д) наибольший общий делитель двух чисел равен 4, а их наименьшее общее кратное ровно 120. Одно из чисел равно 24. Найдите второе число.

  
  Решение: а) 21=3*7

    176=2*2*2*2*11 => 21 и 176 — взаимно простые числа и НОК (21;176)=21*176=3696

  б) НОК(18;27;36)=2*3*3*3*2=108

  18=2*3*3

  27=3*3*3

  36=2*2*3*3

  в) 39=3*13

  85=5*17

  154=2*7*11

  например составное число 361=19*19, будет взаимно простым с каждым из чисел

  г) НОК (а;b)=b. значит a<b => НОД (а;b)=а

  д) НОД=4=2*2; НОК=120=2*2*2*3*5

  24=2*2*2*3 => второе число: 2*2*5=20

789 10 11 > >>

LCM из 18 и 21

1. Главная
2. Математические функции
3. LCM Калькулятор
4. lcm из 18 и 21

LCM из 18 и 21 дает более полное представление о том, как найти более полную работу, чем 126. lcm 18 и 21 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.

что такое lcm 18 и 21?
lcm (18   21) = (?)
18 => 2 x 3 x 3
21 => 3 x 7

= 3 x 2 x 3 x 7
= 126

где
18 — натуральное число,
21 — целое положительное число,
126 — lcm 18 и 21,
{3} в {2 x 3 x 3, 3 x 7} — это общие делители 18 и 21,
{2 x 3 x 7} в {2 x 3 x 3, 3 x 7} являются необычными делителями 18 и 21.

Использование в математике: LCM 18 и 21
Ниже приведены некоторые математические приложения, в которых можно использовать lcm 18 и 21:

1. найти наименьшее число, которое точно делится на 18 и 21.
2. , чтобы найти общий знаменатель двух дробей, имеющих 18 и 21 в знаменателях при сложении или вычитании разнородных дробей.

Использование в задачах реального мира: 18 и 21 lcm
В контексте задач реального мира lcm 18 и 21 помогает найти точное время, когда два похожих и повторяющихся события с разным расписанием происходит одновременно. Например, задачи реального мира включают lcm в ситуациях, когда нужно определить, в какое время колокола A и B звонят вместе, если колокол A звонит через 18 секунд, а колокол B звонит через 21 секунду несколько раз. Ответ заключается в том, что все колокола A и B звонят вместе за 126 секунд в первый раз, за ​​252 секунды во второй раз, за ​​378 секунд в третий раз и так далее.

Важные примечания: 18 и 21 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm 18 и 21:

1. Общие простые множители и оставшиеся простые множители 18 и 21 следует умножить, чтобы найти наименьшее общее кратное 18 и 21 при решении lcm методом простых множителей.
2. Результаты lcm 18 и 21 и lcm 21 и 18 идентичны, это означает, что порядок заданных чисел в вычислении lcm не влияет на результаты.

Для значений, отличных от 18 и 21, используйте этот инструмент ниже:

В приведенном ниже решенном примере с пошаговой работой показано, как найти LCM 18 и 21 с помощью метода простых множителей и метода деления.

Пример решения с использованием метода простых множителей:
Что такое НОК 18 и 21?

шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 18
B = 21

Что нужно найти:
найти lcm чисел 18 и 21

Шаг 2 Найти простые делители чисел 18 и 21:
Простые делители числа 18 = 2 x 3 x 3
Простые делители of 21 = 3 x 7

Шаг 3 Определите повторяющиеся и неповторяющиеся простые делители чисел 18 и 21:
{3} – наиболее повторяющийся делитель, а {2 x 3 x 7} – неповторяющиеся делители чисел 18 и 21.