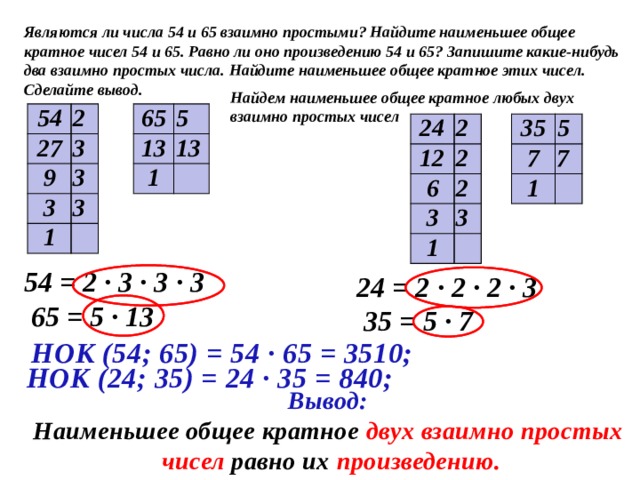
Найдите наименьшее общее кратное чисел 30 и 40: Как найти НОК чисел 18 и 45. 30 и 40. 210 и 350. 20 70…

2

Найдите наименьшее общее кратное » задачи

НОД и НОК »

• Найдите наименьшее общее кратное число

  
  28,35и70
  18,24и27
  36,54и81
  88,132и198
  
  Решение: В 1 строчке28
  в 2 строчке18
  в 3 сирочке36
  в 4 строске 88

  1) 28 = 2·2·7
    35 = 5·7
    70 = 2· 5·7
  НОК (28; 35; 70) = 2·2·7·5=350
  2) 18 = 2·3·3
    24 = 2·2·2·3
    27 = 3·3·3
  нОК ( 18; 24; 81) = 2·3·3·2·2·3=216
  3) 36=2·2·3·3
    54 = 2·3·3·3
    81 = 3·3·3·3
  НОК( 36;54;81) = 2·2·3·3·3·3=324
  4) 88 = 2·2·2·11
    132 = 2·2·3·11
    198 = 2·3·3·11
  НОК(88; 132; 198) = 2·2·2·11·3·3=792 

• Найдите наименьшее общее кратное чисел: 25, 75, и 120; 81, 90 и 135

  
  Решение: НОК(25,75,120)=2*2*2*3*5*5=600
  25|5 75|3 120|2
    5|5 25|5 60|2
    1| 5|5 30|2
    1| 15|3
    5|5
    1|
  НОК(81,90,135)=3*3*3*3*5*2=810
  81|3 90|2 135|3
  27|3 45|3 45|3
    9|3 15|3 15|3
    3|3 5|5 5|5
    1| 1| 1|

• Найдите наименьшее общее кратное число 8 и 16

  
  
  Решение: 8 и 8 делится на 8 и 16 делится на 8!

  8 2 16 2 
  4 2 8 2
  2 2 4 2
    2 2 
  1 1
  НОК(8;16)=2*2*2*2=16

• Найдите наименьшее общее кратное чисел 6,24,36

  
  Решение: Кратное 6: 1,2,3,6
  24: 1,2,3,4,6,8,12,24
  36: 1,2,3,4,6,9,12,18,36

  6|2. 24|2. 36|2
  3|3. 12|2. 18|2
  1|. 6|2. 9|3
  3|3. 3|3
  1|. 1|. НОК(6,24 и 36)= ( под этими столбиками выписываете цифры справа. Нок жадный поэтому к 2*3 прибавляете столько цифр из других столбиков, сколько ему не хватает для счастья, должно получиться: 2*3*2*2*3))=72
  

• Найдите наименьшее общее кратное чисел 60,84,48

  
  Решение: 1680
  1680:60=28
  1680:84=20
  1680:48=35

  60 = 2 * 2 * 3 * 5

  84 = 2 * 2 * 3 * 7

  48 = 2 * 2 * 2 * 2 * 3

  НОК (60; 84; 48) = 2*2*2*2*3*5*7 = 1680 — наименьшее общее кратное

  1680 : 60 = 28     1680 : 84 = 20          1680 : 48 = 35

  160 = 2 * 2 * 2 * 2 * 2 * 5

  96 = 2 * 2 * 2 * 2 * 2 * 3

  НОД (160; 96) = 2*2*2*2*2 = 32 — наибольший общий делитель

  160 : 32 = 5           160 : 96 = 3

• Найдите наименьшее общее кратное чисел: а) 18 и 45; б) 30 и 40

  
  
  Решение: А) Раскладываем на простые множители
  18|2 45|3
  9 |3 15 |3
  3 |3 5 |5
  1 | 1 |
  Понятно, как оформлять
  берем каждый множитель в наибольшей степени
  НОК(18; 45): 2 * 3*3*5 = 90
  б) Теперь пишем попроще, а оформить можно как в А
  30:2=15 40:2=20
  15:3=5 20:2=10
  5:5=1 10:2=5
  5:5=1
  НОК(30;40):2*2*2*3*5=120

• Найдите наименьшее общее кратное чисел и наименьший общий делитель чисел 56 и 70, 78 и 792, 320 и 720, 252и 840

  
  Решение: 56 = 2 * 2 * 2 * 7

  70 = 2 * 5 * 7

  НОК (56; 70) = 2 * 2 * 2 * 5 * 7 = 280 — наименьшее общее кратное

  НОД (56; 70) = 2 * 7 = 14 — наибольший общий делитель

  78 = 2 * 3 * 13

  792 = 2 * 2 * 2 * 3 * 3 * 11

  НОК (78; 792) = 2 * 2 * 2 * 3 * 3 * 11 * 13 = 10296 — наименьшее общее кратное

  НОД (78; 792) = 2 * 3 = 6 — наибольший общий делитель

  320 = 2 * 2 * 2 * 2 * 2 * 2 * 5

  720 = 2 * 2 * 2 * 2 * 3 * 3 * 5

  НОК (320; 720) = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 5 = 2880

  НОД (320; 720) = 2 * 2 * 2 * 2 * 5 = 80 — наибольший общий делитель

  252 = 2 * 2 * 3 * 3 * 7

  840 = 2 * 2 * 2 * 3 * 5 * 7

  НОК (252; 840) = 2 * 2 * 2 * 3 * 3 * 5 * 7 = 2520 — наименьшее общее кратное

  НОД (252; 840) = 2 * 2 * 3 * 7 = 84 — наибольший общий делитель

• Найдите наименьшее общее кратное чисел и наименьший общий делитель чисел 56 и 70, 78 и 792, 320 и 720, 252и 840

  
  Решение: 56 = 2 * 2 * 2 * 770 = 2 * 5 * 7НОК (56; 70) = 2 * 2 * 2 * 5 * 7 = 280 — наименьшее общее кратноеНОД (56; 70) = 2 * 7 = 14 — наибольший общий делитель78 = 2 * 3 * 13792 = 2 * 2 * 2 * 3 * 3 * 11НОК (78; 792) = 2 * 2 * 2 * 3 * 3 * 11 * 13 = 10296 — наименьшее общее кратноеНОД (78; 792) = 2 * 3 = 6 — наибольший общий делитель320 = 2 * 2 * 2 * 2 * 2 * 2 * 5720 = 2 * 2 * 2 * 2 * 3 * 3 * 5НОК (320; 720) = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 5 = 2880НОД (320; 720) = 2 * 2 * 2 * 2 * 5 = 80 — наибольший общий делитель252 = 2 * 2 * 3 * 3 * 7840 = 2 * 2 * 2 * 3 * 5 * 7НОК (252; 840) = 2 * 2 * 2 * 3 * 3 * 5 * 7 = 2520 — наименьшее общее кратноеНОД (252; 840) = 2 * 2 * 3 * 7 = 84 — наибольший общий делитель

• Найдите наименьшее общее кратное чисел 6и10; 9 и 12;14 и 28;8и9;32и48;8,9 и 15

  
  
  Решение: Наименьшее общее кратное (НОК) двух целых чисел — это наименьшее натуральное число, которое делится оба числа без остатка.
  Для нахождения НОК каждое из чисел раскладывается на множители. НОК равен произведению меньшего из двух чисел, и множителей второго числа, которые отсутствуют в первом. Если множители не повторяются, то НОК равен произведению исходных чисел.

  НОК(6,10)=6*5=30
  6=2*3
  10=2*5

  НОК(9,12)=9*2*2=36
  9=3*3
  12=2*2*3

  НОК(14;28)=14*2=28
  14=2*7
  28=2*2*7

  НОК(8;9)=8*9=72
  8=2*2*2
  9=3*3

  НОК(32;48)=32*3=96
  32=2*2*2*2*2
  48=2*2*2*2*3

  НОК(8;9;15)=8*9*5=360
  8=2*2*2
  9=3*3
  15=3*5

• Найдите наименьшее общее кратное НОК(6,10) НОК(9,12) НОК(14,28) НОК(8,9) НОК(32,48) НОК(8,19и15)

  
  Решение: 6=2*3, 10=2*5, НОК = 2*3*5 = 30
  9=3*3, 12=2*2*3. НОК = 3*3*2*2= 36
  14=2*7, 28=2*2*7. НОК = 2*7*2= 28
  8= 2*2*2, 9=3*3, НОК= (числа взаимно простые, у них нет общих множителей. поэтому НОК=8*9 = 72)
  32=2*2*2*2*2, 48=2*2*2*2*3 НОК = 2*2*2*2*2*3 = 96
  8=2*2*2. 19=19*1, 15=3*5 НОК=8*19*15= 2280

  НОК(6,10) 2*3 2*5
  2*3*5=30
  НОК(9,12) 3*3 2*2*3
   2*2*3*3=36
  НОК(14,28) одно кратно другому
  28
  НОК(8,9) взаимопростые
  8*9=72
  НОК(32,48) 2*2*2*2*2 2*2*2*2*3 
  2*2*2*2*2*3=96
  НОК(8,19и15) взаимопростые
  8*19*15=2280

123 4 5 > >>

LCM 30, 40 и 50

Калькуляторы Учебные материалы по математике

1. Главная страница
2. Математические функции
3. Калькулятор LCM
4. LCM 30, 40 и 50

LCM 30, 40 и 50 равно 600. Всесторонняя работа дает понимание того, как найти, что больше 600. это lcm 30, 40 и 50 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.

что такое lcm 30, 40 и 50?
lcm (30   40   50) = (?)
30 => 2 x 3 x 5
40 => 2 x 2 x 2 x 5
50 => 2 x 5 x 5

= 2 x 5 x 3 x 2 x 2 x 5
= 600
lcm (30, 40 и 50) = 600
600 — lcm 30, 40 и 50.

, где
30 — целое положительное число, 4900 положительное целое число,
 600 — это lcm чисел 30, 40 и 50; , 40 и 50,
{3, 2, 2, 5} в {2 х 3 х 5, 2 х 2 х 2 х 5, 2 х 5 х 5} — остальные оставшиеся множители 30, 40 и 50.

Использование в математике: НОК 30, 40 и 50
Ниже приведены некоторые математические приложения, в которых можно использовать МОК 30, 40 и 50:

1. найти наименьшее число, которое точно делится на 30, 40 и 50.
2. , чтобы найти общие знаменатели для дробей, имеющих 30, 40 и 50 в качестве знаменателей при сложении или вычитании разнородных дробей.

Использование в реальных задачах: 30, 40 и 50 lcm
В контексте задач реального мира lcm, lcm 30, 40 и 50 помогает найти точное время, когда три одинаковых и повторяющихся с разным графиком времени происходят вместе в одно и то же время. Например, в реальных задачах используется lcm в ситуациях, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 30 секунд, B звонит через 40 секунд и C повторяется через 50 секунд. Ответ заключается в том, что все колокола A, B и C звонят вместе в 600 секунд в первый раз, в 1200 секунд во второй раз, в 1800 секунд в третий раз и так далее.

Важные примечания: 30, 40 и 50 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 30, 40 и 50:

1. Повторяющиеся и неповторяющиеся простые множители 30, 40 и 50 следует умножить, чтобы найти наименьшее общее кратное 30, 40 и 50, при решении lcm методом простых множителей.
2. Результаты lcm 30, 40 и 50 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.

Для значений, отличных от 30, 40 и 50, используйте этот инструмент ниже:

В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm для 30, 40 и 50, используя либо метод простых множителей, либо метод специального деления.

.

Пример решения с использованием метода простых множителей:
Что такое НОК 30, 40 и 50?

шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 30
B = 40
C = 50

Что нужно найти:
найдите lcm числа 30, 40 и 50

шаг 2 Найдите простые множители числа 30, 4:
Простые множители 30 = 2 x 3 x 5
Простые множители 40 = 2 x 2 x 2 x 5
Простые множители 50 = 2 x 5 x 5

шаг 3 Определите повторяющиеся и неповторяющиеся простые множители числа 30 , 40 и 50:
{2, 5} — наиболее повторяющиеся множители, а {3, 2, 2, 5} — неповторяющиеся множители 30, 40 и 50.

шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 30, 40 и 50:
= 2 x 5 x 3 x 2 x 2 x 5
= 600

lcm(20 и 30) = 600

Отсюда ,
lcm 30, 40 и 50 равно 600

Пример решения с использованием специального метода деления:

Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 30, 40 и 50.

Шаг 1 Адресуйте входные параметры, значения и наблюдайте, что нужно найти:
Входные параметры и значения:
Целые числа: 30, 40 и 50

Что нужно найти:
lcm (30, 40, 50) = ?

шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми. Формат:
30, 40 и 50

шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (30, 40 и 50), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами. Перенесите целое число на следующую строку, если какое-либо целое число из 30, 40 и 50 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:

2	30	40	50
2	15	20	25
2	15	10	25
3	15	5	25
5	5	5	25
5	1	1	5
	1	1	1

шаг 4 Умножьте делители, чтобы найти lcm 30, 40 и 50:
= 2 x 2 x 2 x 3 x 5 x 5 ) = 600

Наименьшее общее кратное для трех чисел 30, 40 и 50 равно 600

НОК чисел 30, 35 и 40

Калькуляторы Учебные ресурсы по математике

1. Главная страница
2. Математические функции
3. Калькулятор LCM
4. LCM 30, 35 и 40

LCM 30, 35 и 40 равно 840. Всесторонняя работа дает представление о том, как найти, что больше из 840. это lcm 30, 35 и 40 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.

что такое lcm 30, 35 и 40?
lcm (30   35   40) = (?)
30 => 2 x 3 x 5
35 => 5 x 7
40 => 2 x 2 x 2 x 5

= 2 x 5 x 3 x 7 x 2 x 2
= 840
lcm (30, 35 и 40) = 840
840 lcm 30, 35 и 40.

где
30 — целое положительное число,
,
840 — lcm 30, 35 и 40,
{2, 5} в {2 x 3 x 5, 5 x 7, 2 x 2 x 2 x 5} — наиболее повторяющиеся множители 30, 35 и 40 ,

{3, 7, 2, 2} в {2 х 3 х 5, 5 х 7, 2 х 2 х 2 х 5} — остальные множители 30, 35 и 40.

Использование в математике : LCM 30, 35 и 40
Ниже приведены некоторые математические приложения, в которых можно использовать lcm 30, 35 и 40:

1. для нахождения наименьшего числа, которое точно делится на 30, 35 и 40
2. , чтобы найти общие знаменатели для дробей, имеющих 30, 35 и 40 в качестве знаменателей при сложении или вычитании разнородных дробей.

Использование в реальных задачах: 30, 35 и 40 lcm
В контексте реальных задач lcm, lcm 30, 35 и 40 помогает найти точное время, когда три похожих и повторяющихся с разное расписание происходит вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуациях, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 30 секунд, B звонит через 35 секунд и C повторяется через 40 секунд. Ответ заключается в том, что все колокола A, B и C звонят вместе в 840 секунд в первый раз, в 1680 секунд во второй раз, в 2520 секунд в третий раз и так далее.

Важные примечания: 30, 35 и 40 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 30, 35 и 40:

1. Повторяющиеся и неповторяющиеся простые множители 30, 35 и 40 следует умножить, чтобы найти наименьшее общее кратное 30, 35 и 40, при решении lcm методом простых множителей.
2. Результаты lcm 30, 35 и 40 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.

Для значений, отличных от 30, 35 и 40, используйте этот инструмент ниже:

В приведенном ниже примере решения с пошаговой работой показано, как найти lcm числа 30, 35 и 40, используя либо метод простых множителей, либо метод специального деления. .

Пример решения с использованием метода простых множителей:
Чему равно НОК 30, 35 и 40?

шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 30
B = 35
C = 40

Что нужно найти:
найти lcm числа 30, 35 и 40

шаг 5, 4 числа 3:
Простые множители 30 = 2 x 3 x 5
Простые множители 35 = 5 x 7
Простые множители 40 = 2 x 2 x 2 x 5

шаг 3 Определите повторяющиеся и неповторяющиеся простые делители 30, 35 и 40:
{2, 5} — наиболее повторяющиеся факторы, а {3, 7, 2, 2} — неповторяющиеся факторы 30, 35 и 40.

Шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 30, 35 и 40:
= 2 x 5 x 3 x 7 x 2 x 2
= 840
lcm(20 и 30) = 840

Отсюда ,
lcm 30, 35 и 40 is 840

Пример решения с использованием специального метода деления:

Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 30, 35 и 40.

Шаг 1 Адресуйте входные параметры, значения и наблюдайте, что нужно найти:
Входные параметры и значения:
Целые числа: 30, 35 и 40

Что нужно найти:
lcm (30, 35, 40) = ?

шаг 2 Расположите заданные целые числа по горизонтали, разделив их пробелами или запятыми:
30, 35 и 40

шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (30, 35 и 40), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами.