Найти сумму векторов с помощью онлайн калькулятора
Операции над векторами
Вектором называется отрезок определенной длины с указанием стрелкой его направления в пространстве. В сложных строительных, электротехнических и других инженерных расчетах приходится выполнять такую операцию, как сложение векторов.
Сумму векторов можно найти способом геометрического сложения.
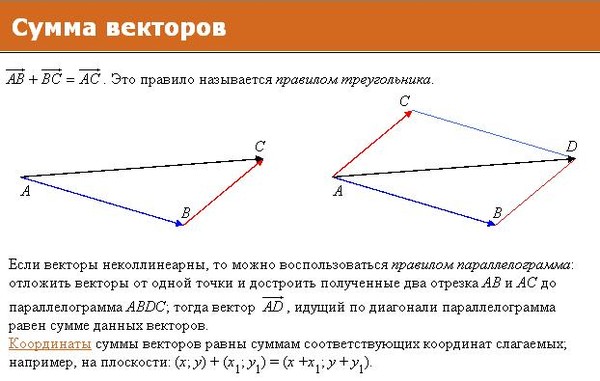
1. При геометрическом сложении один из расположенных в двухмерном или трехмерном пространстве векторов путем параллельного смещения переносится своим началом в конец другого вектора. Суммарным вектором будет вектор, начало которого совпадает с началом 1-го вектора, а конец — с концом 2-го. Сложение векторов производится по правилу треугольника или параллелограмма. При сложении векторов по правилу параллелограмма оба вектора откладываются от одной точки, затем достраивается параллелограмм, стороны которого параллельны заданным векторам. Суммарным вектором является диагональ параллелограмма, идущая от общего начала исходных векторов к противоположной вершине.
2.Рассчитать сумму векторов можно с помощью системы уравнений.
Суммой векторов а и b является вектор с, каждый элемент которого равняется попарной сумме соответствующих элементов векторов а и b.
Для двухмерного пространства сумму векторов с координатами a = {ax ; ay} и b = {bx ; by} вычисляем по формуле:
a + b = {ax + bx; ay + by}
Для трехмерного пространства сумму векторов, имеющих координаты a = {ax ; ay ; az} и b = {bx ; by ; bz} находим по формуле:
a + b = {ax + bx; ay + by; az + bz}
Для n-мерного пространства сумму вектора a = {a1 ; a2 ; … ; an} и вектора b = {b1 ; b2 ; … ; bn
} определяем таким же способом:a + b = {a1 + b1; a2 + b2; . .. ; an + bn}
.. ; an + bn}
Сумма противоположных векторов a и (- а) равняется 0.
С помощью онлайн калькулятора можно легко получить уравнение, представляющее сумму заданных векторов. Для этого необходимо ввести заданные координаты каждого из векторов, расположенных в трехмерном пространстве (либо два исходных значения каждого из векторов в двухмерном пространстве) и нажать кнопку Рассчитать.
| Первый вектор a1i | |
| Первый вектор b1j | |
| Первый вектор c1k | |
| Второй вектор a2i | |
| Второй вектор b2j | |
| Второй вектор c2 | |
| Сумма векторов | |
вектор
Векторы — что это, определение и ответ
ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
Вектор – отрезок, у которого есть начало и конец, то есть указано его направление.
Вектор обозначается через точки начала и конца вектора, например \(\overrightarrow{АВ}\) (первая буква – начало вектора, вторая – конец) или, если мы хотим обозначить вектор без указания точек, пишем просто \(\overrightarrow{a}\).
Точка тоже может быть вектором, в таком случае вектор называют нулевым, т.к. его началом и концом является одна и та же точка. Обозначаем нулевой вектор как, например, \(\overrightarrow{\text{MM}}\) или \(\overrightarrow{0}\).
Длина или модуль вектора – это длина отрезка (как если бы у него не было направления).
Длина вектора \(\overrightarrow{АВ}\) обозначается как \(\left| \overrightarrow{АВ} \right|\), длина вектора \(\overrightarrow{a}\ \)как \(\left| \overrightarrow{a} \right|\), а длина нулевого вектора всегда равна нулю:
\(\left| \overrightarrow{АВ} \right| = 7\)
\(\left| \overrightarrow{a} \right| = 3\)
\(\left| \overrightarrow{\text{MM}} \right| = \left| \overrightarrow{0} \right| = 0\)
РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Коллинеарные векторы – это векторы, которые лежат на параллельных прямых или на одной прямой. Нулевой вектор коллинеарен любому вектору.
Нулевой вектор коллинеарен любому вектору.
Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону.
Обозначается как \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) сонаправлен вектору \(\overrightarrow{b}\))
Противоположно направленные векторы – это коллинеарные векторы, которые направлены в противоположные стороны.
Обозначаются как \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) противоположно напрвлен вектору \(\overrightarrow{b}\))
Равные векторы – это сонаправленные векторы, у которых равны длины, т.е. у них одинаковые и направление, и длина.
Например:
\(\overrightarrow{АВ}\) и \(\overrightarrow{a}\) – коллинеарны, при этом противоположно направлены, т.к. лежат параллельных прямых и направлены в разные стороны:
\(\overrightarrow{АВ} \uparrow \downarrow \overrightarrow{a}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – коллинеарны, при этом сонаправлены, т.
 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:
\(\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – равны, т.к. сонаправлены (из п.2) и равны по модулю:
\(\left. \ \frac{\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}}{\overrightarrow{\left| \text{CD} \right|} = 5 = \left| \overrightarrow{b} \right|} \right\} \Longrightarrow \overrightarrow{\text{CD}} = \overrightarrow{b}\)
\(\overrightarrow{М}\) коллинеарен всем векторам, и может являться им как сонаправленным, так и противоположно направленным, т.к. \(\overrightarrow{М} = \overrightarrow{0}\).
СВОЙСТВА НЕНУЛЕВЫХ КОЛЛИНЕАРНЫХ ВЕКТОРОВ:
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{b} \upuparrows c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{b} \upuparrows c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
\ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) и \(\overrightarrow{b} \uparrow \downarrow c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}} \right\} \Longrightarrow \overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}\), то \(\overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ТОЧКИ:
Говорят, что вектор отложен от точки, если она является его началом. Например, \(\overrightarrow{АВ}\) отложен от точки А, \(\left| \text{CD} \right|\) отложен от точки С и так далее. Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
От любой точки можно отложить вектор, равный данному и при том только один.
Например, возьмем точку М и два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Мы можем отложить от точки М вектора, равные \(\overrightarrow{a}\) и \(\overrightarrow{b}\) всего один раз. Делается это параллельным переносом:
Таким образом \(\overrightarrow{a} = \overrightarrow{a’}\), и \(\overrightarrow{b} = \overrightarrow{b’}\), при этом \(\overrightarrow{a’}\ и\ \overrightarrow{b’}\) отложены от точки М.
СЛОЖЕНИЕ ВЕКТОРОВ:
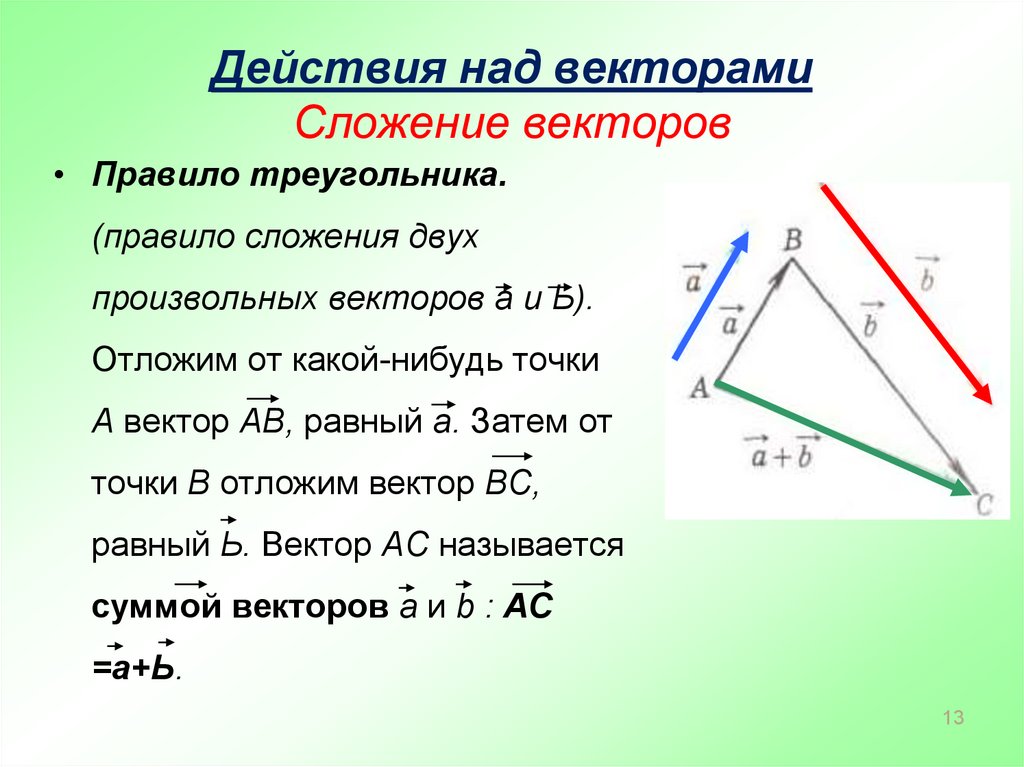
При сложении векторов нужно учитывать их направления, поэтому проще всего складывать вектора визуально. Существуют два самых простых способа сложить два вектора – это правило треугольника и правило параллелограмма.
ПРАВИЛО ТРЕУГОЛЬНИКА
Если нужно найти сумму двух векторов, по правилу треугольника нужно:
Параллельным переносом перенести начало одного вектора в конец другого.

Пусть эти векторы будут сторонами треугольника, тогда третья его сторона – их сумма.
Обозначить направление получившегося вектора суммы – от начала первого вектора в конец второго (стрелка к стрелке).
Пример №1:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:
Перенесем вектор \(\overrightarrow{b}\) так, чтобы он начинался там, где заканчивается вектор \(\overrightarrow{a}\).
Соединим эти векторы в треугольник, третьей стороной которой будет вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
Направление вектора \(\overrightarrow{c}\) будет идти от начала \(\overrightarrow{a}\) до конца \(\overrightarrow{b}\) (стрелка к стрелке)
ПРАВИЛО ПАРАЛЛЕЛОГРАММА:
Если нужно найти сумму двух векторов, по правилу параллелограмма нужно:
Параллельным переносом перенести начала этих векторов в одну точку.

Пусть эти векторы будут сторонами параллелограмма, тогда диагональ этого параллелограмма – их сумма.
Обозначить направление получившегося вектора суммы – от начала векторов в противоположный конец параллелограмма (по диагонали).
Пример №2:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:
Перенесем оба вектора параллельным переносом так, чтобы они начинались из одной точки.
Представим, что они являются сторонами параллелограмма.
Диагональ этого параллелограмма, которая начинается в точке начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – это вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ:
Переместительное свойство:
\(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)
Сочетательное свойство:
\((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)
СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ:
Чтобы сложить несколько векторов, нужно ставить их друг за другом, сохраняя их направление (используя параллельный перенос), тогда их суммой будет являться вектор, начала которого – это начало первого вектора, а конец – конец последнего вектора (как в правиле треугольника).
Пример №3:
Найдите сумму векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\):
Поставим эти векторы как бы по порядку сохраняя их длину и направление. По переместительному свойству неважно, в каком порядке мы будем располагать вектора. Соединим их, например, в таком порядке — \(\overrightarrow{d}\), \(\overrightarrow{e}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{a}\).
Проведем вектор их суммы от начала первого вектора в конец второго:
ВЫЧИТАНИЕ ВЕКТОРОВ:
Вычесть вектор – это то же самое, что прибавить отрицательный вектор:
\(\overrightarrow{a}\ –\ \overrightarrow{b} = \overrightarrow{a} + (–\overrightarrow{b})\)
То есть и при вычитании можно использовать правила сложения. Главное – найти противоположный вектор.
Главное – найти противоположный вектор.
Само словосочетание «противоположный вектор» говорит о том, что такие вектора направлены в разные стороны.
Значит вычесть вектор – значит прибавить вектор с противоположным ему направлением.
Мы можем проверить это свойство алгебраически. Мы знаем, что противоположные числа в сумме дают 0:
\(a + (–a) = a\ –\ a = 0\)
Тогда и сумма противоположных векторов дадут 0 (т.е. если мы «пойдем» от начала до конца \(\overrightarrow{a}\) и обратно по –\(\overrightarrow{a}\), то мы вернемся снова в начало \(\overrightarrow{a}\)):
Значит и для векторов справедливо это свойство:
\(\overrightarrow{a}\ + (–\ \overrightarrow{a}) = 0\)
Пример №4:
Найдите \(\overrightarrow{f} = \overrightarrow{a}\ –\ \overrightarrow{b} + \overrightarrow{c}\ –\ \overrightarrow{d}\ –\ \overrightarrow{e}\), если
Можем использовать сложение векторов, если мы найдем отрицательные векторы.
 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
Теперь сложим все векторы, учитывая отрицательные:
ПРОИЗВЕДЕНИЕ ВЕКТОРА И ЧИСЛА:
Произведением ненулевого вектора и числа является вектор, коллинеарный данному, длина которого равна произведению длины данного вектора и числа:
\(k \bullet \overrightarrow{a} = \overrightarrow{\text{ka}}\)
где k – это число, при этом:
\(\overrightarrow{a} \upuparrows \overrightarrow{\text{ka}}\) при \(k > 0\)
\(\overrightarrow{a} \uparrow \downarrow \overrightarrow{\text{ka}}\) при \(k < 0\)
Произведением любого вектора на ноль является нулевой вектор.
Пример №5:
Найдите 5\(\overrightarrow{a}\) и –2\(\overrightarrow{a}\) , если:
1. Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
\(5\overrightarrow{a} = \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a}\):
\(5\overrightarrow{a} \upuparrows \overrightarrow{a}\), т.к 5 > 0
2. Аналогично поступим и с отрицательным числом, только теперь уже складываем противоположные векторы:
\(–2\overrightarrow{a} \uparrow \downarrow \overrightarrow{a}\), т.к –2 < 0
СВОЙСТВА ПРОИЗВЕДЕНИЯ ВЕКТОРА И ЧИСЛА:
Сочетательное свойство:
\(kl \bullet \overrightarrow{a} = k(l\overrightarrow{a}) \)
Распределительный закон:
\(\overrightarrow{a}(k + l) = k\overrightarrow{a} + l\overrightarrow{a}\)
и
\(k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}\)
ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ:
Используя векторы и связанные с ними свойства можно решать различные геометрические задачи.
Пример №6:
Точка С – середина отрезка АВ, О – произвольная точка на плоскости. Докажите, что
\(ОС = \frac{1}{2}(АО + ОВ)\)
По правилу треугольника:
\(\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{АС}\)
\(\overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС}\)
Сложим два этих выражения, получим:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
При этом \(\overrightarrow{АС}\) и \(\overrightarrow{ВС}\) – противоположные векторы, т.к. равны по модулю (точка С середина АВ), и имеют противоположное направление, значит:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + 0\)
\(ОС = \frac{1}{2}(АО + ОВ)\)
Что и требовалось доказать.
Пример №7:
ABCD – трапеция. Точки M и N середины оснований BC и AD соответственно. Точка О – точка пересечения прямых AB и CD. Докажите, что О, M и N лежат на одной прямой.
Треугольники OAD и OBC подобны по двум углам:
\(\left. \ \frac{\angle\text{OBC} = \angle OAD\ как\ соответствующие\ углы}{\angle O\ — \ общий} \right\}\Delta\text{OAD}\sim\text{ΔOBC}\)
\(\frac{\text{OA}}{\text{OB}} = \frac{\text{OD}}{\text{OC}} = k\)
При этом соответствующие стороны коллинеарны, значит можем выразить их как произведение числа и вектора:
\(\overrightarrow{\text{OA}} \upuparrows \overrightarrow{\text{OB}} \Longrightarrow \overrightarrow{\text{OA}} = k\overrightarrow{\text{OB}}\)
\(\overrightarrow{\text{OD}} \upuparrows \overrightarrow{\text{OC}} \Longrightarrow \overrightarrow{\text{OD}} = k\overrightarrow{\text{OC}}\)
В данной задаче можем выразить \(\overrightarrow{\text{OM}}\) и \(\overrightarrow{ON}\) как
\(\overrightarrow{\text{OM}} = \frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}(\overrightarrow{\text{OA}} + \overrightarrow{\text{OD}})\)
т.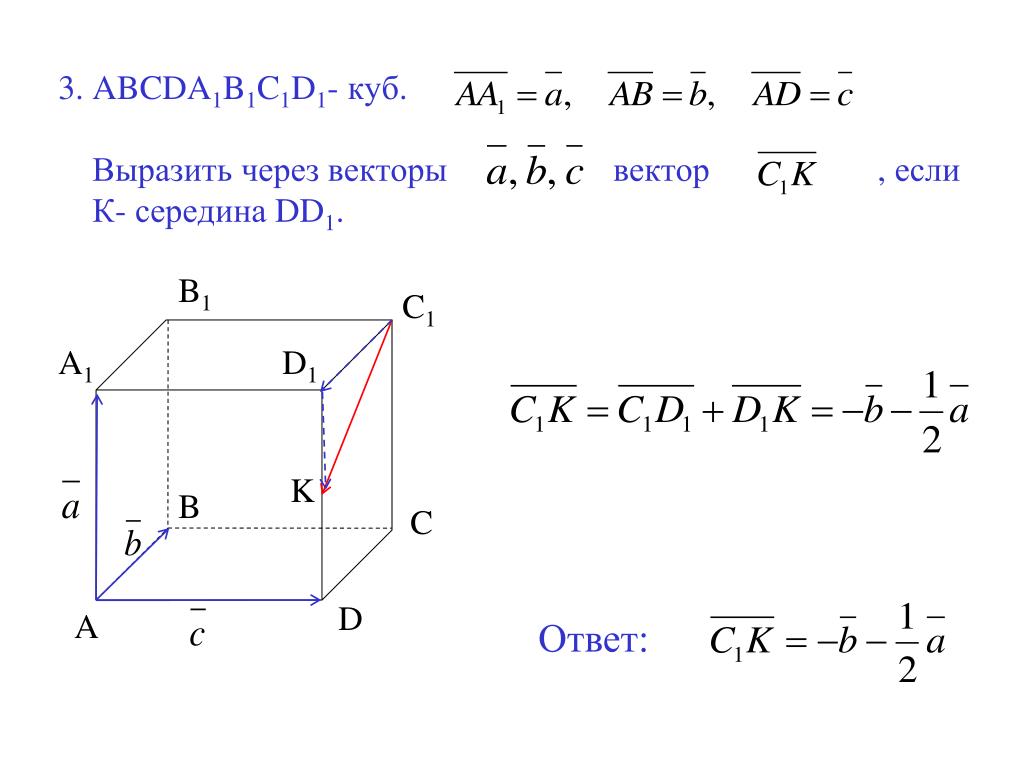 к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
Соединим выразим вектор \(\overrightarrow{\text{ON}}\) через \(\overrightarrow{\text{OA}}\) и \(\overrightarrow{\text{OD}}\) из пункта 3:
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OD}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( k\overrightarrow{\text{OB}} + k\overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}k\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = k(\frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)) = k\overrightarrow{\text{OM}}\)
Если вектор \(\overrightarrow{\text{ON}}\) можно представить как произведение числа k с вектором \(\overrightarrow{\text{OM}}\), значит \(\overrightarrow{\text{ON}}\) и \(\overrightarrow{\text{OM}}\) коллинеарны, а значит лежат на одной прямой (они не могут быть параллельны, т.
 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).
Что и требовалось доказать.
(@)Вопрос
Обновлено: 09.07.2019
DC PANDEY-BASIC MATHEMATICS-Exercise
14 видеоРЕКЛАМА
Text Solution
A
3
A
=тангенс −1 (0,472) =25,3∘B
√25ед. , α=tan−1(0,472)=25,3∘
C
√37ед. 2 √37единица, α =tan−1(1)=45∘
Ответ
Правильный ответ C
Решение
В соответствии с вопросом нарисуем следующий рисунок.
Результат векторов A и B
R=√A2+B2+2ABcosθ
=√16+9+2×4×3cos60∘=√37unit
∴Направление вектора суммы ,
tanα=BsinθA+Bcosθ=3sin60 ∘4+3cos60∘=0,472
α=tan−1(0,472)=25,3∘
Таким образом, результат |A|и|B| составляет √37 единиц под углом 25,3∘ от A в направлении, показанном на рисунке.
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Аб Падхаи каро бина адс ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
3. Найдите единичный вектор в направлении, параллельном сумме векторов vec a=2hat i+4hat j-5hat k и vec b=hat i+2hat j+3hat k найдите также направляющие косинусы этого вектора.
Найдите вычитание векторов A и B, как показано на рисунке, а также найдите направление вектора вычитания, учитывая A=4 единицы и b=3 единицы.
31087271
Найдите конинусы направлений вектора (5i+2j+6k). Также запишите значение суммы квадратов направленных косинусов этого вектора.
34887524
Найдите направленные косинусы вектора (5ˆi+2ˆj+6k). Также запишите значение суммы квадратов направленных косинусов этого вектора.
39182758
→i+2→j+3→k,−→i+2→j+→k और 3→i+→j में इकाई सदिश ज्ञात करें|
152622103
के योगफल भी इकाई सदिश हो।
152622315
Найти единичный вектор в направлении, параллельном сумме векторов →a=2i+4j−5k и →b=i+2j+3k, найти также направляющие косинусы этого вектора.
234812230
Если сумма двух единичных векторов также является единичным вектором. Найдите величину их разности?
576402881
Найдите единичный вектор в направлении суммы векторов →a=2ˆi−ˆj+k и ¯b=2ˆj+k.
642810353
Если сумма двух единичных векторов также является единичным вектором. Найдите величину их разности?
643080922
Текст Решение
Найдите сумму векторов A и B, как показано на рисунке, а также найдите направление вектора суммы. Учитывая A = 4 единицы и B = 3 единицы.
643192803
Найдите вычитание векторов A и B, как показано на рисунке, а также найдите направление вектора вычитания, учитывая A=4 единицы и b=3 единицы.
643192806
Найдите единичный вектор, параллельный сумме векторов →a = 2i+4j−5k и →b = hati+2hatj+3hatk. Также найдите его направляющие косинусы.
643225349
ਵੈਕਟਰਾਂ →a=2→i+2→j−5→k ਅਤੇ →b=2→i+→j+3→k ੀ ਦਿਸ਼ਾ ਵੱਲ ਇਕਾਈ ਵੈਕਟਰ ਪਤਾ ਕਰੋ।
643581426
Найти единичный вектор в направлении суммы векторов
¯a=2¯i+2¯j−5¯kand¯b=2¯i+¯j+3¯k.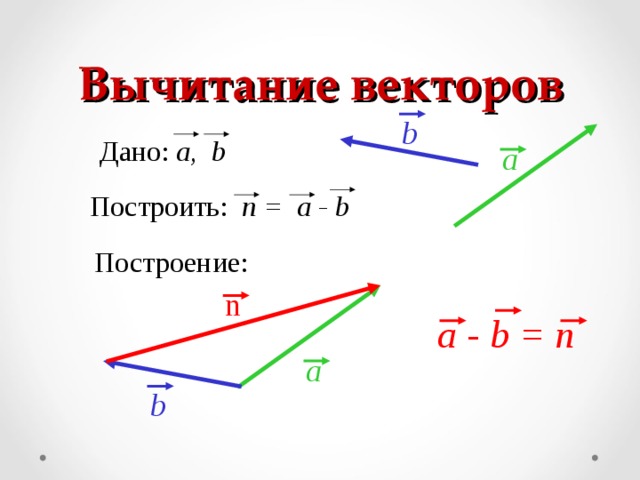
644424513
Найдите сумму трех векторов?
Дата последнего обновления: 19 апреля 2023 г.
Подсказка: Во-первых, давайте предположим, что эти три вектора выражены через i, j и k. Чтобы решить вопрос, нам нужно добавить все компоненты i векторов по отдельности, затем компоненты j и, наконец, компоненты k всех трех векторов.
Полный пошаговый ответ:
Здесь допустим три вектора.
Первый вектор: $a = {x_1}i + {y_1}j + {z_1}k$, второй вектор: $b = {x_2}i + {y_2}j + {z_2}k$, а третий вектор равен $c = {x_3}i + {y_3}j + {z_3}k$.
Применим сложение двух векторов a и b. Для этого нам нужно добавить все компоненты i векторов отдельно, затем компоненты j и, наконец, компоненты k всех трех векторов.
Следовательно,
$ \Rightarrow a + b = \left( {{x_1}i + {y_1}j + {z_1}k} \right) + \left( {{x_2}i + {y_2}j + {z_2 }k} \right)$
$ \Rightarrow a + b = \left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left ( {{z_1} + {z_2}} \right)k$
Теперь добавим вектор c с приведенным выше выражением.
$ \Rightarrow a + b + c = \left[ {\left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left ( {{z_1} + {z_2}} \right)k} \right] + \left( {{x_3}i + {y_3}j + {z_3}k} \right)$
Это равно
$ \Rightarrow a + b + c = \left( {{x_1} + {x_2} + {x_3}} \right)i + \left( {{y_1} + {y_2} + {y_3}} \right)j + \left( {{z_1} + {z_2} + {z_3}} \right)k$
Следовательно, сумма трех векторов $a = {x_1}i + {y_1}j + {z_1}k$, $b = {x_2}i + {y_2}j + {z_2}k$ и $c = {x_3}i + {y_3}j + {z_3}k$ равно $a + b + c = \left( {{x_1} + {x_2} + {x_3}} \right)i + \left( {{y_1 } + {y_2} + {y_3}} \right)j + \left( {{z_1} + {z_2} + {z_3}} \right)k$ .
Примечание: Сложение векторов отличается от обычного сложения, поскольку векторы имеют направление. Здесь i, j и k представляют направления x, y и z соответственно. Таким образом, при сложении или вычитании векторов мы должны складывать или вычитать значение только того же направления. Мы также должны быть осторожны со знаком. Следовательно, мы должны позаботиться о квадранте, в котором лежит вектор.
Мы можем напрямую сложить три вектора заданного вопроса.
Первый вектор: $a = {x_1}i + {y_1}j + {z_1}k$, второй вектор: $b = {x_2}i + {y_2}j + {z_2}k$, а третий вектор равен $c = {x_3}i + {y_3}j + {z_3}k$.
Применим сложение двух векторов a и b. Для этого нам нужно добавить все компоненты i векторов отдельно, затем компоненты j и, наконец, компоненты k всех трех векторов.
Следовательно,
$ \Rightarrow a + b + c = \left( {{x_1}i + {y_1}j + {z_1}k} \right) + \left( {{x_2}i + {y_2}j + {z_2}k} \right) + \left( {{x_3}i + {y_3}j + {z_3}k} \right)$
$ \Rightarrow a + b + c = \left( {{x_1} + {x_2} + {x_3}} \right)i + \left( {{y_1} + {y_2} + { y_3}} \right)j + \left( {{z_1} + {z_2} + {z_3}} \right)k$
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с конверсией химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики. Химия класса 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении А.

 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:

 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие: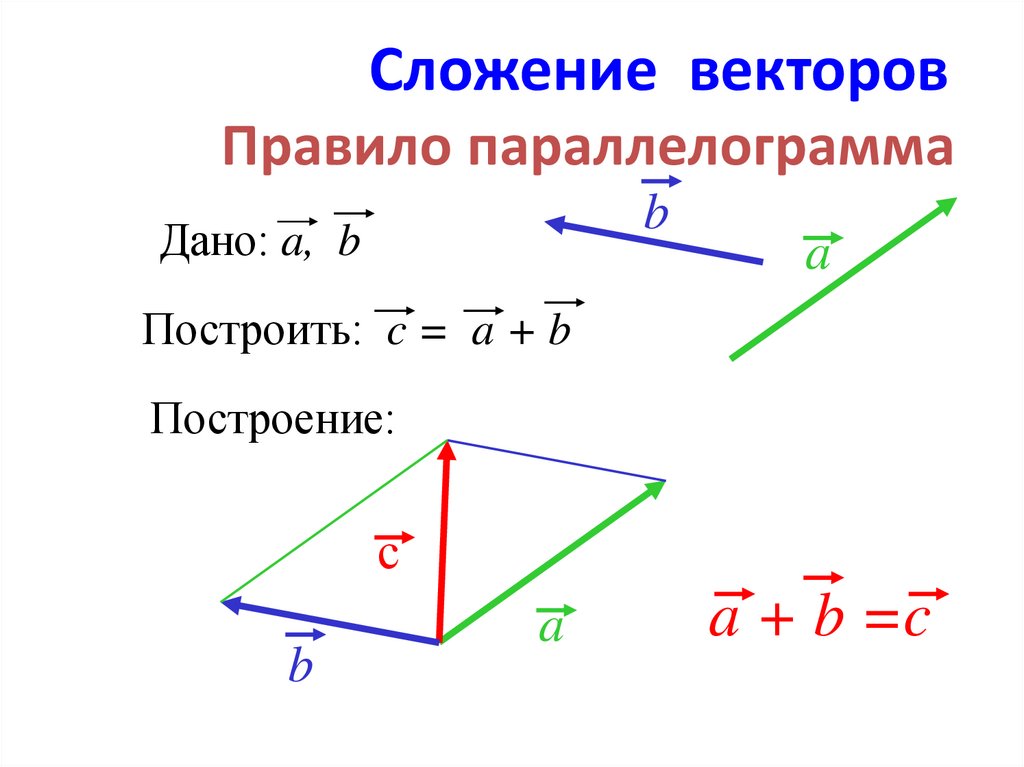 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).