Угловой коэффициент прямой
Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где k – это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:
Подробнее об этой формуле рассказано в этой статье!
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:
*Оба катета равны шести (это их длины).
Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Ответ: 1
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (5;0) и (0;5). Значит,
Приведём формулу к виду y = kx + b
Получили, что угловой коэффициент k = – 1.
Ответ: –1
Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Ответ: 40/3
Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Значит,
Приведём к виду y = kx + b:
Получили, что угловой k = 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Ответ: 18
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Значит,
Приведём к виду y = kx + b
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).
Искомая ордината равна –12.
Ответ: –12
Найдите ординату точки пересечения прямой, заданной уравнением
3х + 2у = 6, с осью Oy.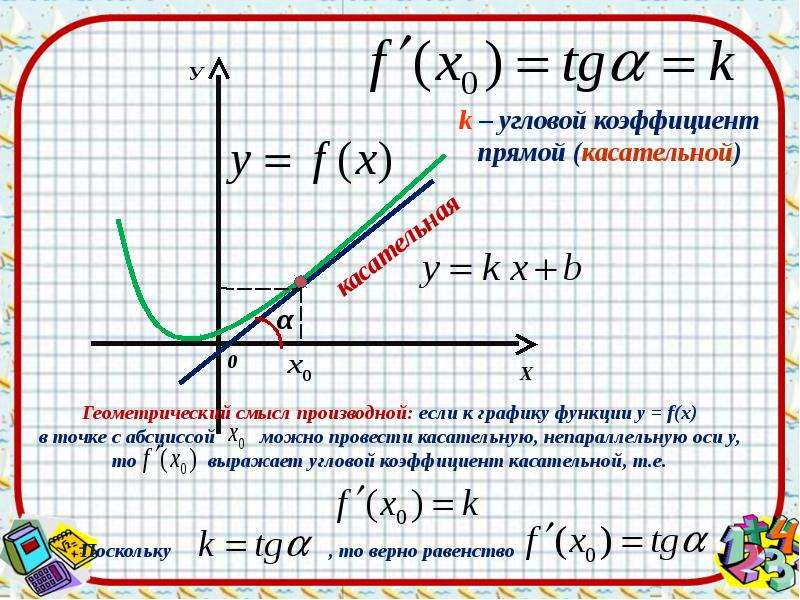
Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу равна 3.
*Решается система:
Ответ: 3
Найдите ординату точки пересечения прямых, заданных уравнениями
3х + 2у = 6 и у = – х.
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х вместо у:
Ордината равна минус шести.
Ответ: – 6
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Посмотреть решение
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Посмотреть решение
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Посмотреть решение
Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Посмотреть решение
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).
Посмотреть решение
Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.
Посмотреть решение
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.
Посмотреть решение
Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению.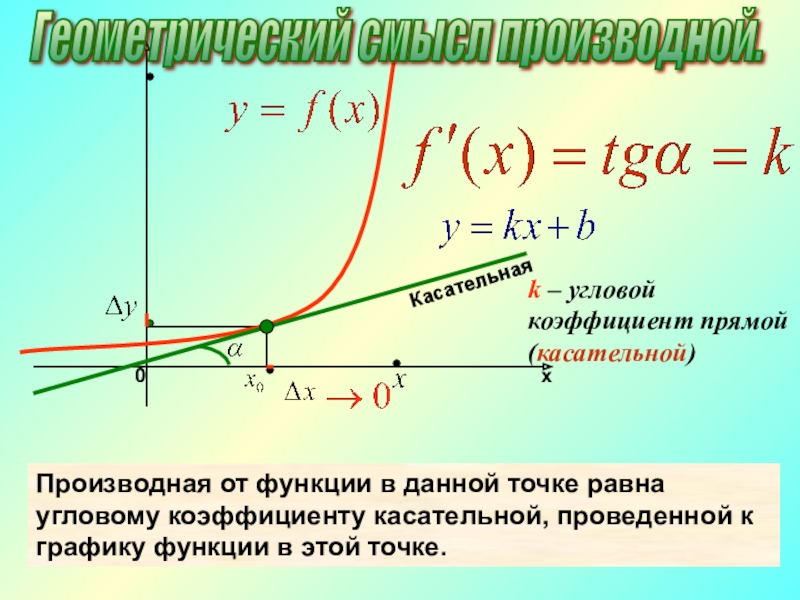 Надеюсь, это удалось.
Надеюсь, это удалось.
1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике.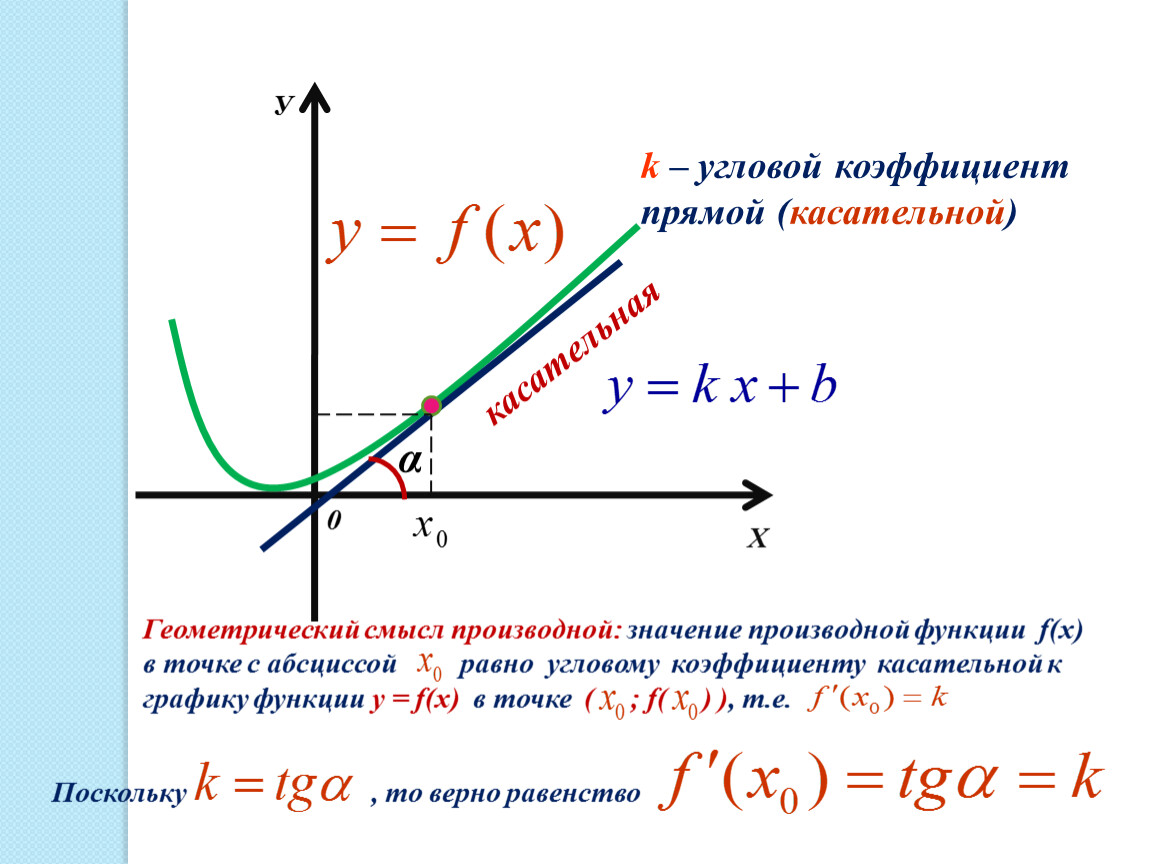 Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
>> Угол наклона прямой от 0 до 90 градусов <<
>> Угол наклона прямой от 90 до 180 градусов <<
В данных двух случаях, по свойству тангенса:
То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Калькулятор уклона
Калькулятор Использование
Наклон линии представляет собой ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как подъем относительно пробега. Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии является мерой ее крутизны.
Решения для калькулятора уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения для уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения уклона y = mx + b
- Стандартная форма Ax + By = C
- y-пересечение, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать уклон линии
Рассчитать уклон, м , используя формулу для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \] Здесь вам нужно знать координаты 2-х точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Как найти наклон линии
- Найти разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти наклон
Δу = у 2 — у 1
Δх = х 2 — х 1
м = Δy/Δx
Пример: Найдите уклон
Допустим, вы знаете две точки на прямой, и их координаты (2, 5) и (9, 19). Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy равна
- Разница между координатами x Δx равна
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δу = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( m = \dfrac {14} {2} \)
\(m = 7 \)
Уравнения линии с наклоном
Существует 3 распространенных способа записи уравнений линии с наклоном:
- Точечный наклон форма
- Форма пересечения уклона
- Стандартная форма
Точечный уклон формы записывается как
y — y 1 = м (x — x
Используя координаты одной из точек на линии, вставьте значения в x1 и y1 точек, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы вычислили как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
y — 5 = 7(x — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения уклона записывается как
y = м x + b
Возьмите уравнение формы уклона точки и умножьте его на 7 x и 7 на 2.
y — 5 = 7(x — 2) )
y — 5 = 7x — 14
Продолжайте работать над уравнением так, чтобы y было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме точки пересечения:y = 7x — 9
Стандартная форма уравнения для линии записывается как
Ax + By = C
Вы также можете увидеть стандартную форму, записанную как Ax + By + C = 0 в некоторых ссылках.
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Наклон форма перехвата y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найти наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.
 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Как найти точку пересечения с осью y
Точка пересечения с осью y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
y = 3(0) — 6
y = -6
Точка пересечения с осью y равна -6
Как найти точку пересечения с осью x =0. Это точка пересечения прямой с осью x.
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
x = 2
Х-отрезок равен 2
Наклон параллельных прямых
Если известен наклон прямой, любая параллельная ей линия будет иметь одинаковый наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии образуют угол 90° при пересечении.
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число. 4 — целое число, поэтому его знаменатель равен 1. Обратное число 4/1 равно 1/4.
- Отрицательная инверсия наклона -4 равна наклону 1/4.
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее исследование
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
Как найти наклон линии
Все математические ресурсы GRE
13 диагностических тестов 452 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 Следующая →
Справка по математике GRE » Геометрия » Координатная геометрия » Линии » Другие линии » Как найти наклон линии
См. следующий график:
следующий график:
Какой наклон изображенной линии?
Возможные ответы:–1
–1/3
1/3
3
–3
Правильный ответ :–3
Объяснение:Можно использовать либо формулу наклона m = (y 2 – y 1 )/(x 2 – x 1 ), либо стандартное линейное уравнение y = mx + b для решения уклон, м. Расчетом или наблюдением можно определить, что наклон равен –3.
Сообщить об ошибке
Каков наклон уравнения 4 x + 3 y = 7?
Возможные ответы:3/4
–3/4
–4/3
4/3
–7/3
Правильный ответ:–4/3
Объяснение:Мы должны представить это уравнение в виде y = м x + b , где м — уклон.
Начнем с 4 x + 3 y = 7.
Изолируем член y : 3 y = 7 – 4 x 9000 5
Разделить на 3: y = 7/3 – 4/3 * x
Переставьте члены: y = –4/3 * x + 7/3, поэтому наклон равен –4/3.
Сообщить об ошибке
Каков наклон уравнения?
Возможные ответы: Правильный ответ: Объяснение:Чтобы найти наклон линии, вы должны преобразовать уравнение в форму пересечения наклона. В этом случае уравнение будет , что означает, что наклон равен .
Сообщить об ошибке
Каков наклон линии?
Возможные ответы: Правильный ответ: Объяснение:Чтобы найти наклон, представим уравнение в форме пересечения наклона. В этом случае имеем , что указывает на то, что наклон равен .
Сообщить об ошибке
Каков наклон линии, проходящей через точку, если она определяется:
?
Возможные ответы: Правильный ответ: Объяснение: Поскольку уравнение определено как есть, вы знаете, что точка пересечения по оси Y равна . В этом суть. Чтобы найти наклон линии, вам просто нужно использовать две имеющиеся у вас точки и найти уравнение:
В этом суть. Чтобы найти наклон линии, вам просто нужно использовать две имеющиеся у вас точки и найти уравнение:
Сообщить об ошибке
Какое из следующего может быть уравнением для красной линии, изображенной выше?
Возможные ответы: Правильный ответ: Объяснение:Об этом чертеже необходимо отметить два ключевых факта. Во-первых, линия явно имеет отрицательный наклон, учитывая, что она идет «под гору», если смотреть на нее слева направо. Во-вторых, он имеет положительную точку пересечения по оси y. Таким образом, вы знаете, что коэффициент для термина должен быть отрицательным, а числовой коэффициент для точки пересечения оси Y должен быть положительным. Это происходит только в уравнении . Поэтому это единственный возможный вариант.
Сообщить об ошибке
Каков наклон линии, определяемой уравнением:
Возможные ответы: Правильный ответ:900 05 Объяснение:
Такой вопрос на самом деле довольно прост.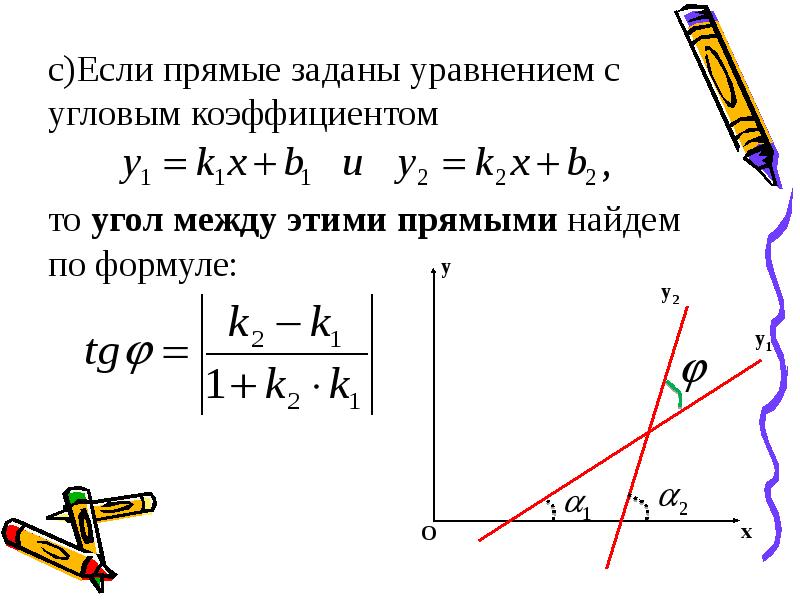 Все, что вам нужно сделать, это переписать уравнение в форме пересечения наклона, то есть:
Все, что вам нужно сделать, это переписать уравнение в форме пересечения наклона, то есть:
Следовательно, начнем упрощать:
Становится…
Затем…
Наконец, разделите обе стороны на :
Коэффициент для члена – это ваш наклон:
Сообщить об ошибке
Каков наклон линии 3 = 8y — 4x?
Возможные ответы:0,5
-2
2
-0,5
Правильный ответ:0,5
Объяснение:Решите уравнение для y. y=mx+b, где m — уклон
Сообщить об ошибке
Найти наклон линии 6X – 2Y = 14
Возможные ответы:
3
-6
12
-3
Правильный ответ:3
Объяснение:Представьте уравнение в форме точки пересечения наклона:
y = mx + b
-2y = -6x +14
y = 3x – 7
Наклон линии представлен буквой M; следовательно, наклон линии равен 3,9.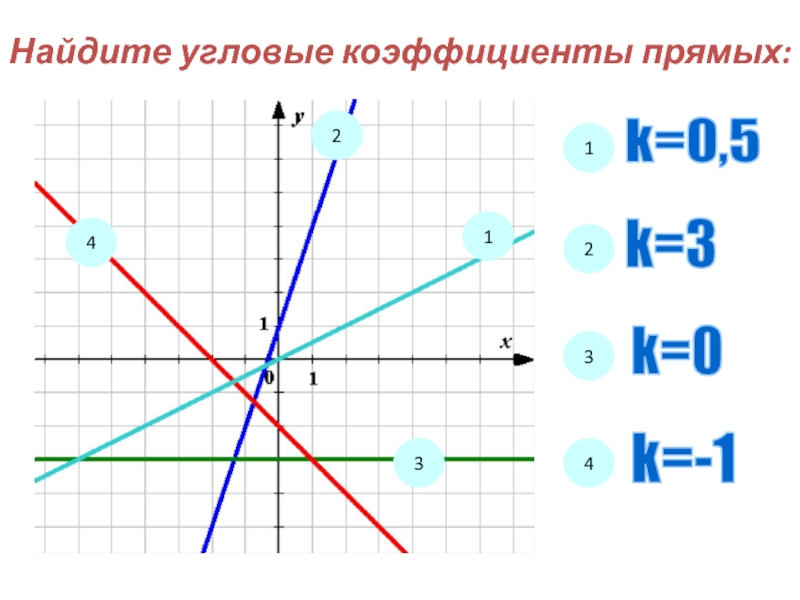

 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3