Найдите высоту правильной треугольной пирамиды стороны основания 2: Найдите высоту правильной треугольной пирамиды стороны основания 2, а объем равен 3в корне

ЕГЭ Профиль №2. Пирамида

Задача 1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. Ответ ОТВЕТ: 340.
Задача 2. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды. Ответ ОТВЕТ: 360.
Задача 3. Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1. Ответ ОТВЕТ: 1,5.
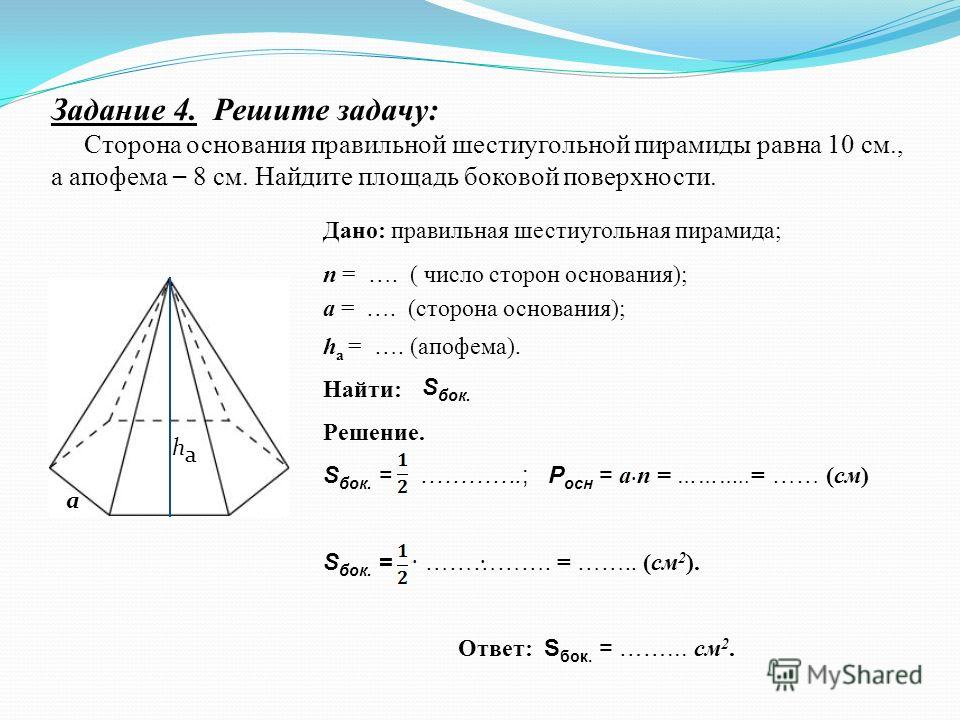
Задача 4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза? Ответ ОТВЕТ: 8.
Задача 5. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды. Ответ ОТВЕТ: 4.
Задача 6. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна \(\sqrt 3 \). Ответ ОТВЕТ: 0,25.
Задача 7. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен \(\sqrt 3 \). Ответ ОТВЕТ: 3.
Задача 8. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? Ответ ОТВЕТ: 4.
Задача 9. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем. Ответ ОТВЕТ: 256.
Задача 10. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60o. Высота пирамиды равна 6. Найдите объем пирамиды. Ответ ОТВЕТ: 48.
Задача 11. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. Ответ ОТВЕТ: 4,5.
Задача 12. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды. Ответ ОТВЕТ: 6.
Задача 13. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC. Ответ ОТВЕТ: 3.
Задача 14. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. Ответ ОТВЕТ: 3.
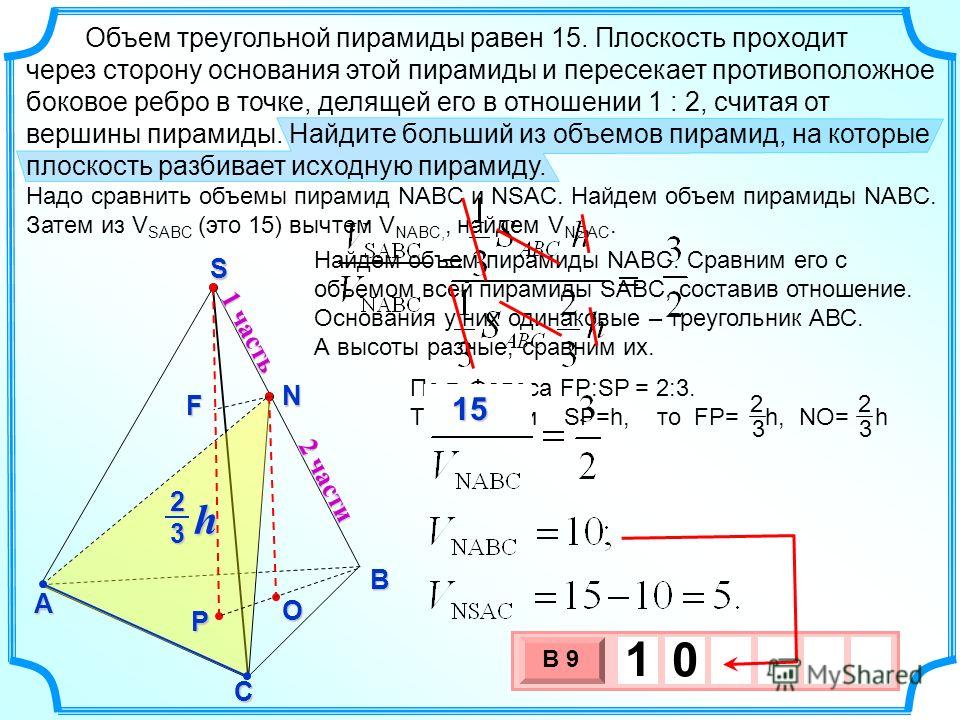
Задача 15. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. Ответ ОТВЕТ: 10.
Задача 16. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза? Ответ ОТВЕТ: 4.
Задача 17. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4. Ответ ОТВЕТ: 96.
Задача 18. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза? Ответ ОТВЕТ: 9.
Задача 19. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4. Ответ ОТВЕТ: 60.
Задача 20. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза? Ответ ОТВЕТ: 4.

Задача 21. Ребра правильного тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер. Ответ ОТВЕТ: 0,25.
Задача 22. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4. Ответ ОТВЕТ: 24.
Задача 23. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды. Ответ ОТВЕТ: 13.
Задача 24. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды. Ответ ОТВЕТ: 12.
Задача 25. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро. Ответ ОТВЕТ: 7.
Задача 26. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45o. Найдите объем пирамиды. Ответ ОТВЕТ: 48.
Задача 27. Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. Ответ ОТВЕТ: 2.
Задача 28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. Ответ ОТВЕТ: 2.
Задача 29. Найдите объем параллелепипеда    ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3. Ответ ОТВЕТ: 18.
Задача 30. Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3. Ответ ОТВЕТ: 1.
Задача 31. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3. Ответ ОТВЕТ: 27.
Задача 32. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 54, AC = 144. Найдите боковое ребро SA. Ответ ОТВЕТ: 90.
Задача 33. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SB = 10, BD = 12. Найдите длину отрезка SO. Ответ ОТВЕТ: 8.
Задача 34. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 16, SB = 34. Найдите длину отрезка BD. Ответ ОТВЕТ: 60.
Задача 35. В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности. Ответ ОТВЕТ: 3.
Задача 36. В правильной треугольной пирамиде SABC N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN. Ответ ОТВЕТ: 2.
Задача 37. В правильной треугольной пирамиде SABC L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB. Ответ ОТВЕТ: 1.
Задача 38. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS. Ответ ОТВЕТ: 1.
Задача 39. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке R. Площадь треугольника ABC равна 30, RS = 21. Найдите объем пирамиды. Ответ ОТВЕТ: 210.
Задача 40. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P. Объем пирамиды равен 1, PS = 1. Найдите площадь треугольника ABC. Ответ ОТВЕТ: 3.
Задача 41. В правильной четырехугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 5, сторона основания равна \(3\sqrt 2 \). Найдите объем пирамиды. Ответ ОТВЕТ: 24.
Задача 42. В правильной четырехугольной пирамиде все ребра равны 1. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых ребер. Ответ ОТВЕТ: 0,25.
Задача 43. В правильной треугольной пирамиде боковое ребро равно5, а сторона основания  равна \(3\sqrt 3 \). Найдите высоту пирамиды. Ответ ОТВЕТ: 4.

Реклама

Поддержать нас

Стереометрия на ЕГЭ. Приемы и секреты.

Вы уже знаете, что задачи по стереометрии в первой части ЕГЭ на самом деле простые. Правильный чертеж, элементарная логика, внимательность, плюс некоторые приемы, о которых мы рассказали в первой части статьи и еще расскажем — вот и всё, что вам нужно. Перейдем сразу к практике.

. Объем параллелепипеда равен . Найдите объем треугольной пирамиды .

Мы помним, что объем параллелепипеда равен . А объем пирамиды равен . Иными словами, если у параллелепипеда и пирамиды одинаковые основания и одинаковые высоты, то объем пирамиды будет в три раза меньше, чем объем параллелепипеда. А у нашей пирамиды еще и площадь основания в два раза меньше. Значит, ее объем в шесть раз меньше объема параллелепипеда.

Ответ: .

. Объем куба равен . Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Об одном из способов решения этой задачи мы уже рассказали. Посчитайте, сколько нужно четырехугольных пирамидок, чтобы сложить из них такой кубик.

Есть и второй способ. Если бы пирамида и куб имели одинаковые высоты, объем пирамиды был бы в раза меньше объема куба (поскольку площади основания у них одинаковые). А у нашей пирамиды высота в два раза меньше, чем у куба. Значит, ее объем будет в раз меньше, чем у куба.

Ответ: .

. Радиусы трех шаров равны , и . Найдите радиус шара, объем которого равен сумме их объемов.

На самом деле это задача по алгебре, причем элементарная. Объем шара равен . Осталось решить уравнение:

Как извлечь кубический корень из этого числа? Очень просто — разложите его на множители.

Ответ: .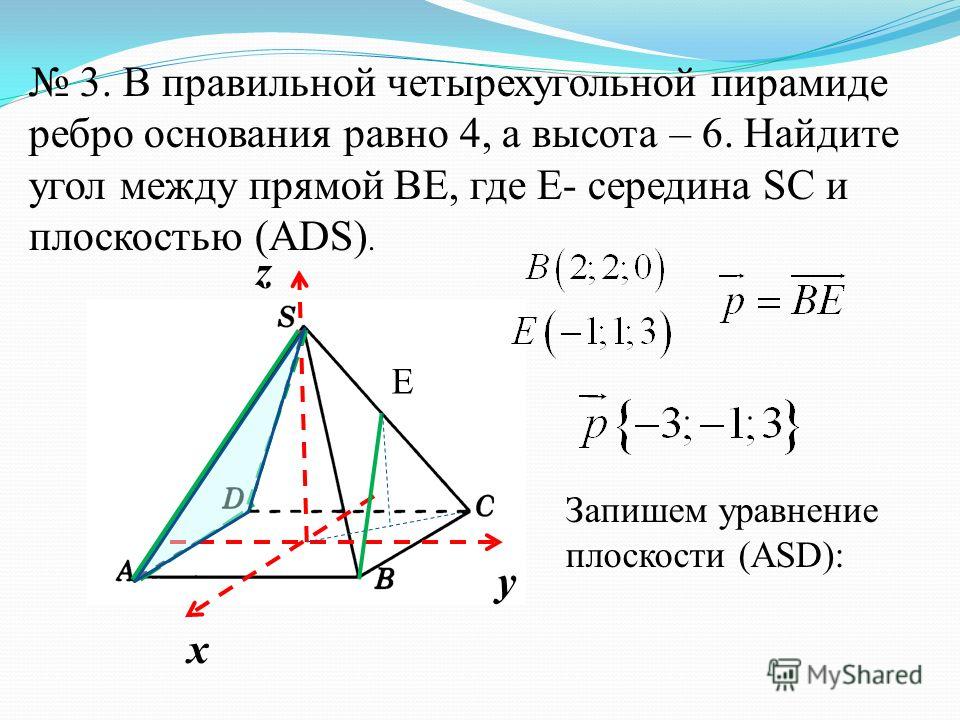

. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны , а объем равен .

Мы говорили, что в основании правильной треугольной пирамиды лежит правильный треугольник. У него все углы равны и все стороны тоже равны. Площадь его проще всего найти по формуле
. Она равна . Поскольку ,
высота равна .

. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом градусов. В ответе укажите .

Если вы вдруг забыли, что такое образующая, — смотрите нашу таблицу с формулами. А что значит «наклонена к плоскости основания»? Вспомним, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость, то есть угол .

Из прямоугольного треугольника находим, что . Объем конуса найдем по известной формуле и поделим на .
Ответ: .

. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами , а боковые ребра равны и наклонены к плоскости основания под углом градусов.

Нарисуйте вид сверху, то есть правильный шестиугольник. У него все стороны равны, все углы тоже равны.

Как найти площадь правильного шестиугольника, если специальную формулу вы не знаете? Проще всего разбить его на одинаковых равносторонних треугольников. Формула площади равностороннего треугольника вам известна:
.

Итак, площадь основания равна . Осталось найти высоту.

Высота призмы — это отрезок, перпендикулярный ее основаниям. Из прямоугольного треугольника АСН находим:
.

Ответ: .

. Диагональ прямоугольного параллелепипеда равна и образует углы , и градусов с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Мы уже говорили, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Обозначим вершины параллелепипеда.

Проекцией диагонали на нижнее основание будет отрезок . Пусть диагональ образует угол градусов именно с плоскостью нижнего основания.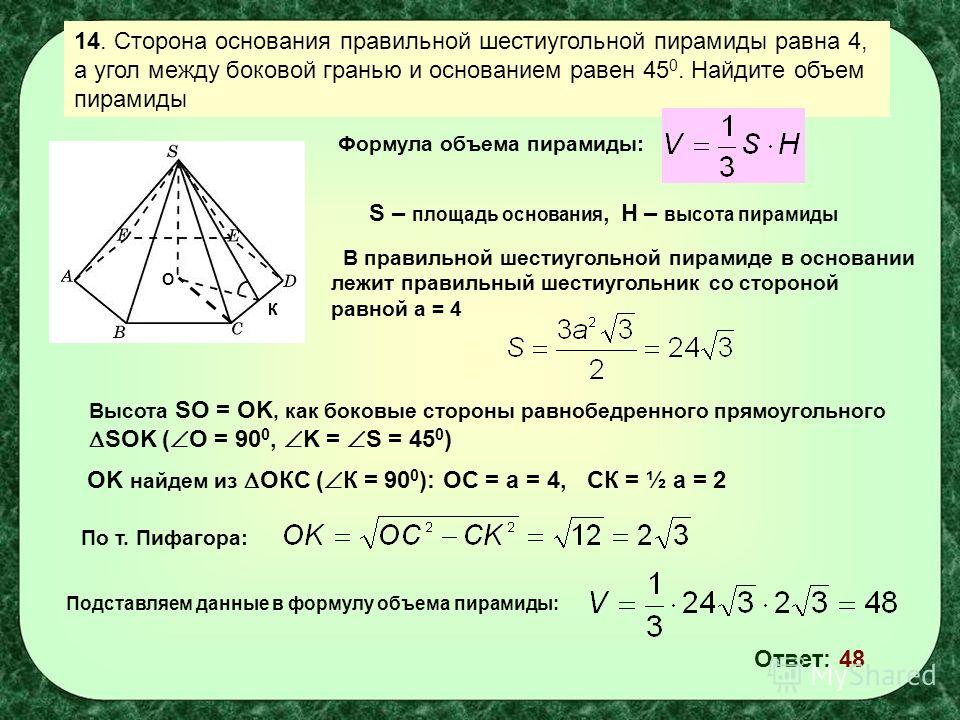
Рассмотрим прямоугольный треугольник . По теореме Пифагора, . Итак, мы нашли высоту параллелепипеда.

Проекцией на переднюю грань будет отрезок .
Из прямоугольного треугольника найдем . Мы нашли ширину параллелепипеда. А его длина (то есть отрезок ) находится аналогично. Она тоже равна . Объем параллелепипеда равен .

Ответ: .

.

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно . Найдите объем пирамиды.

Если решать «в лоб», считая, что — основание, то у нас получится задача по стереометрии из второй части ЕГЭ. Но зачем такие сложности? Развернем пирамиду.

Объем пирамиды равен . В основании лежит равнобедренный прямоугольный треугольник, площадь которого равна . Тогда объем пирамиды равен .

Ответ: .

. Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен . Найдите объем шестиугольной пирамиды.

У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Разные только площади основания. Нарисуем вид снизу.

Видим, что площадь основания треугольной пирамиды в раз меньше, чем у шестиугольной.

Ответ: .

Если в условии задачи по стереометрии дан рисунок — значит, повезло. Рисунок — это уже половина решения. А если его нет? Значит, рисуйте сами, как умеете. Отговорки «не умею» или «рисование у нас было только в детском саду» — не принимаются. Вам ведь не девочку на шаре надо изобразить, а намного более простые объекты 🙂

. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите .

Обратите внимание, что . Значит, сторона куба является диаметром шара. Осталось понять, какая часть шара лежит внутри куба.

Правильный ответ: .

. Вершина куба со стороной является центром сферы, проходящей через точку . Найдите площадь части сферы, содержащейся внутри куба. В ответе запишите величину .

Здесь главное — понять, какая часть шара лежит внутри куба. Порисуйте кубики и шарики. Пока есть возможность, возьмите яблоко (оно почти шарообразной формы), потренируйтесь. Жаль, что на ЕГЭ вам не выдадут килограмма яблок для отработки пространственного мышления.

Правильный ответ: .

Если вы его не получили, смотрите подсказку в конце статьи.

. Объем треугольной пирамиды равен . Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении , считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Прежде всего, что значит «точка делит боковое ребро в отношении , считая от вершины»? Это значит, что она делит его на отрезки, длины которых и .

Плоскость делит пирамиду на две. У пирамид и общее основание . Ясно, что отношение их объемов равно отношению высот.

Проведем перпендикуляры и к плоскости основания пирамиды. — высота пирамиды ABC\mkern -2muS, — высота пирамиды . Очевидно, что отрезок параллелен отрезку , поскольку два перпендикуляра к одной плоскости параллельны друг другу. Через две параллельные прямые можно провести плоскость, причем только одну. Итак, точки и лежат в одной плоскости, то есть мы от стереометрической задачи перешли к плоской, планиметрической.

Треугольники и подобны, .

Значит, . Объем пирамиды равен объема пирамиды .

Ответ: .

. Ребра тетраэдра равны . Найдите площадь сечения, проходящего через середины четырех его ребер.

Прежде всего, все ребра равны, значит, тетраэдр — правильный. В его основании лежит равносторонний треугольник, а вершина проецируется в центр этого треугольника.

Как вы думаете, какая фигура получится в сечении?

Заметим, что отрезок параллелен (поскольку является средней линией треугольника . И отрезок тоже параллелен , потому что является средней линией треугольника . Значит, параллелен . Аналогично параллелен . Мы помним, что средняя линия треугольника не только параллельна основанию — она равна половине основания. А у нашего тетраэдра все ребра равны. Значит, — ромб, все стороны которого равны . Уже хорошо.

Мы уже сказали, что у правильного тетраэдра вершина (точка ) проецируется в центр основания (точка ). В основании — правильный треугольник. Значит, точка будет точкой пересечения биссектрис, медиан и высот этого треугольника, и тогда перпендикулярен .

Вспомним теорему о трех перпендикулярах. является проекцией на плоскость основания, следовательно, отрезок тоже перпендикулярен . И тогда — квадрат. Его площадь равна .

А теперь — самые сложные задачи по стереометрии из первой части варианта ЕГЭ. Для их решения существуют секретные приемы. Конечно же, лучше знать их заранее, чем изобретать на экзамене.

. Объем тетраэдра равен . Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

Можно долго искать формулу объема октаэдра (а именно он там и находится, в серединке), а можно поступить умнее. Помните, как в задаче мы считали площадь неудобно расположенных фигур?

Здесь проще всего посчитать площадь квадрата со стороной , в который вписан данный треугольник. И вычесть из нее площади трех прямоугольных треугольников. Видите их на рисунке?

В нашей задаче про тетраэдр и многогранник можем поступить аналогично. Как получился этот многогранник в серединке? От исходного тетраэдра отрезали четыре маленьких тетраэдра, объем каждого из которых в раз меньше, чем объем большого (об этом мы уже говорили). Получаем: .

Ответ: .

. Объем параллелепипеда равен . Найдите объем треугольной пирамиды .

Обратите внимание, нарисован куб, а написано — параллелепипед. Мы знаем, что его объем равен , но не знаем, чему равны его длина, ширина и высота. Обозначим их и . Не так-то просто найти площадь основания и высоту пирамиды . Так может, и не надо этого делать? Есть более удобный способ — тот же, что и в предыдущей задаче. Ведь пирамида получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — , , и . А объем каждой из них легко посчитать — мы делали это в первой задаче этой статьи. Например, объем пирамиды равен объема параллелепипеда. Объем четырех всех пирамид, которые отрезали, равен объема параллелепипеда. Значит, объем пирамиды равен объема параллелепипеда.

Ответ: .

Поздравляем! Задачи по стереометрии из первой части ЕГЭ по математике освоены — от простых до самых сложных. Заходите чаще на наш сайт.

Подсказка к задаче :

Как найти высоту в четырехугольной пирамиде. Как найти высоту правильной четырехугольной пирамиды

Треугольная пирамида — это пирамида, в основе которой находится треугольник. Высота этой пирамиды — это перпендикуляр, который опущен из вершины пирамиды на ее основания.

Нахождение высоты пирамиды

Как найти высоту пирамиды? Очень просто! Для нахождения высоты любой треугольной пирамиды можно воспользоваться формулой объема: V = (1/3)Sh, где S — это площадь основания, V — объем пирамиды, h — ее высота. Из этой формулы вывести формулу высоты: для нахождения высоты треугольной пирамиды, нужно умножить объем пирамиды на 3, а потом поделить получившееся значение на площадь основания, это будет: h = (3V)/S. Поскольку основание треугольной пирамиды — это треугольник, можно воспользоваться формулой подсчета площади треугольника. Если нам известны: площадь треугольника S и его сторона z, то по формуле площади S=(1/2)γh: h = (2S)/γ, где h — это высота пирамиды, γ — это ребро треугольника; угол между сторонами треугольника и сами две стороны, то по такой формуле: S = (1/2)γφsinQ, где γ, φ — это стороны треугольника, находим площадь треугольника. Значение синуса угла Q нужно посмотреть в таблице синусов, которая есть в Интернете. Далее подставляем значение площади в формулу высоты: h = (2S)/γ. Если в задании требуется вычислить высоту треугольной пирамиды, то объем пирамиды уже известен.

Правильная треугольная пирамида

Найдите высоту правильной треугольной пирамиды, то есть пирамиды, в которой все грани — это равносторонние треугольники, зная величину ребра γ. В этом случае ребра пирамиды — это стороны равносторонних треугольников. Высота правильной треугольной пирамиды будет: h = γ√(2/3), где γ — это ребро равностороннего треугольника, h — это высота пирамиды. Если площадь основания (S) неизвестна, а даны лишь: длина ребра (γ) и объем (V) многогранника, то необходимую переменную в формуле из прежнего шага нужно заменить ее эквивалентом, который выражен через длину ребра. Площадь треугольника (правильного) равна 1/4 от произведения длины стороны этого треугольника, возведенную в квадрат на квадратный корень из 3. Подставляем эту формулу вместо площади основания в предыдущую формулу, и получаем такую формулу: h = 3V4/(γ 2 √3) = 12V/(γ 2 √3). Объем тетраэдра можно выразить через длину его ребра, то из формулы для вычисления высоты фигуры можно убрать все переменные и оставить только сторону треугольной грани фигуры. Объем такой пирамиды можно вычислить, поделив на 12 из произведения возведенную в куб длину его грани на квадратный корень из 2.

Подставляем это выражение в предыдущую формулу, получаем такую формулу для вычисления: h = 12(γ 3 √2/12)/(γ 2 √3) = (γ 3 √2)/(γ 2 √3) = γ√(2/3) = (1/3)γ√6. Также правильную треугольную призму можно вписывать в сферу, и зная только радиус сферы (R) можно найти и саму высоту тетраэдра. Длина ребра тетраэдра равна: γ = 4R/√6. Заменим переменную γ этим выражением в предыдущей формуле и получаем формулу: h = (1/3)√6(4R)/√6 = (4R)/3. Такую же формулу можно иметь, зная радиус (R) окружности, вписанной в тетраэдр. В таком случае длина ребра треугольника будет равна 12 соотношениям между квадратным корнем из 6 и радиусом. Подставляем это выражение в предыдущую формулу и имеем: h = (1/3)γ√6 = (1/3)√6(12R)/√6 = 4R.

Как найти высоту правильной четырехугольной пирамиды

Чтобы ответить на вопрос, как найти длину высоты пирамиды, необходимо знать, сто такое правильная пирамида. Четырехугольная пирамида — это пирамида, в основе которой находится четырехугольник. Если в условиях задачи мы имеем: объем (V) и площадь основания (S) пирамиды, то формула для вычисления высоты многогранника (h) будет такая — разделить объем, умноженный на 3 на площадь S: h = (3V)/S. При квадратном основании пирамиды с известными: заданным объемом (V) и длиной стороны γ, замените площадь (S) в предыдущей формуле на квадрат длины стороны: S = γ 2 ; H = 3V/γ 2 . Высота правильной пирамиды h = SO проходит как раз через центр окружности, которая описанная около основания. Поскольку основание данной пирамиды — это квадрат, то точка О — это точка пересечения диагоналей AD и BC. Мы имеем: OC = (1/2)BC = (1/2)AB√6. Далее, мы в прямоугольном треугольнике SOC находим (по теореме Пифагора): SO = √(SC 2 -OC 2). Теперь Вы знаете, как найти высоту правильной пирамиды.

Пирамида — это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение «высота пирамиды» очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.

Части пирамиды

Каждая пирамида состоит из следующих элементов:

• боковые грани, которые имеют по три угла и сходятся в вершине;
• апофема представляет собой высоту, которая опускается из ее вершины;
• вершина пирамиды — это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
• основание — это многоугольник, на котором не лежит вершина;
• высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.

Как найти высоту пирамиды, если известен ее объем

Через формулу объема пирамиды V = (S*h)/3 (в формуле V — объем, S — площадь основания, h — высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см 2 , тогда как ее объем составляет 125 см 3 . Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.

Как найти высоту пирамиды, если известна длина диагонали и ее ребра

Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а — гипотенуза, а в нашем случае ребро пирамиды; b — первый катет или половина диагонали и с — соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² — b².

Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра — 30 см. Необходимо найти высоту. Решаем: c² = 30² — 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.

Как найти высоту усеченной пирамиды

Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды — это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания — d2, а ребро имеет длину — l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.

Теперь рассмотрим все это дело на практике. Перед нами задача. Усеченная пирамида имеет в основании квадрат, длина диагонали большего основания равняется 10 см, в то время как меньшего — 6 см, а ребро равняется 4 см. Требуется найти высоту. Для начала находим один катет: а = (10-6)/2 = 2 см. Один катет равен 2 см, а гипотенуза — 4 см. Получается, что второй катет или высота будет равна 16-4 = 12, то есть h = √12 = около 3,5 см.

Политика конфиденциальности

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.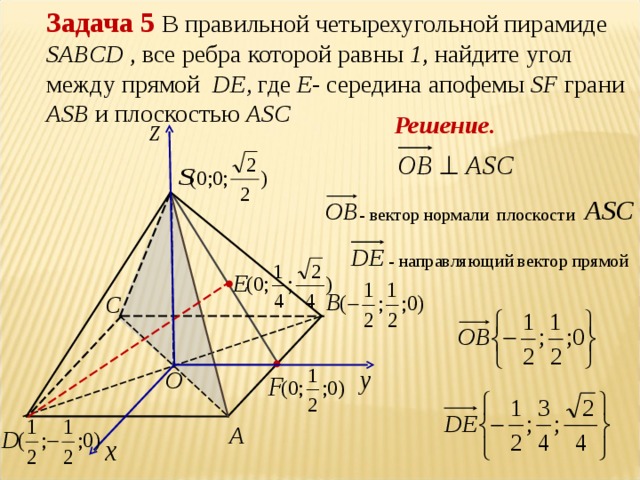

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Здесь разберём примеры связанные с понятием объёма. Для решения подобных заданий обязательно нужно знать формулу объёма пирамиды:

S

h – высота пирамиды

Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:

Вершина правильной пирамиды проецируется в центр её основания

Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):

Можете на блоге, где разбирались задачи связанные с нахождением объёма пирамиды. Рассмотрим задачи:

27087.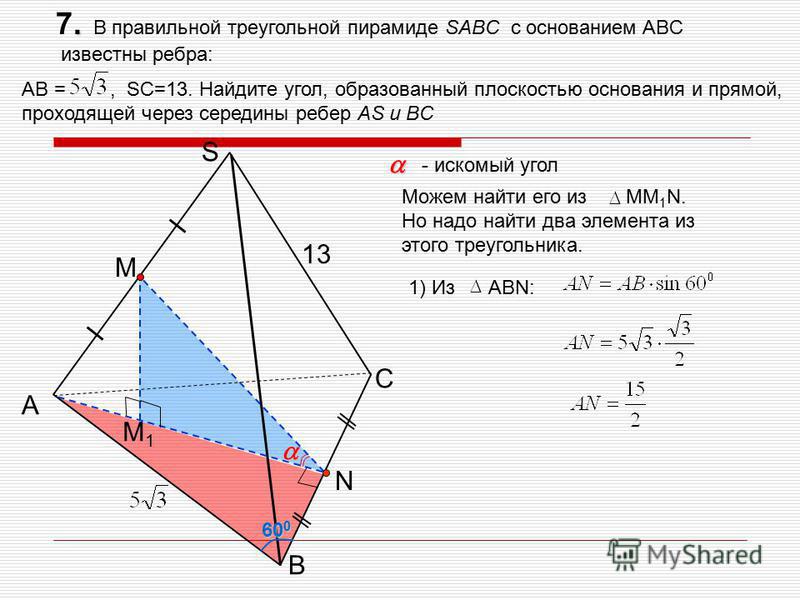 Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.

S – площадь основания пирамиды

h – высота пирамиды

Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Ответ: 0,25

27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.

Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:

S – площадь основания пирамиды

h – высота пирамиды

Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.

Для нахождения площади основания воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:

Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:

Высота равна трём.

Ответ: 3

27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):

Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:

Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:

Следовательно:

Таким образом, объём пирамиды равен:

Ответ: 256

27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:

Найдём площадь квадрата (основания пирамиды):

Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:

Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.

Таким образом, можем вычислить чему равно боковое ребро пирамиды:

Ответ: 13

245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Как уже неоднократно было сказано – объём пирамиды вычисляется по формуле:

S – площадь основания пирамиды

h – высота пирамиды

Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём.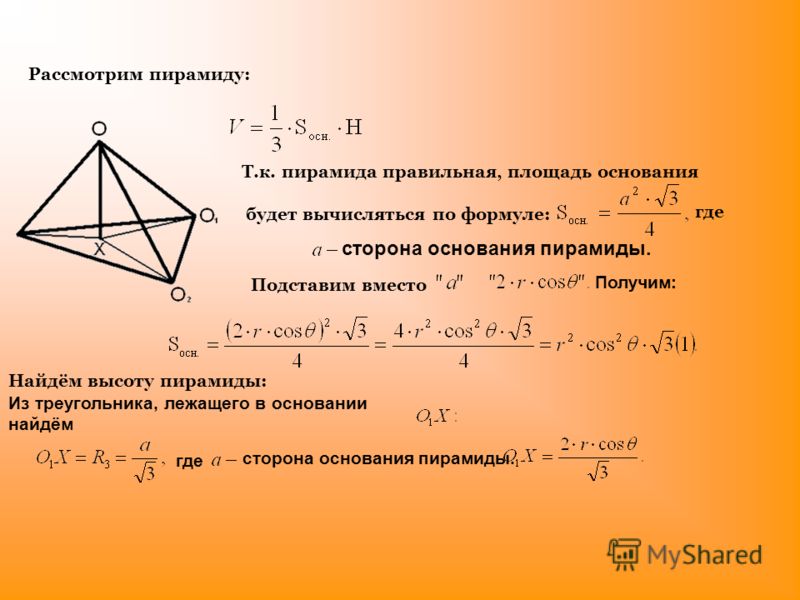 Основания пирамиды – это многоугольник, площадь которого равна:

Таким образом:

Ответ: 27

27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Пирамида — это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение «высота пирамиды» очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.

Части пирамиды

Каждая пирамида состоит из следующих элементов:

• боковые грани, которые имеют по три угла и сходятся в вершине;
• апофема представляет собой высоту, которая опускается из ее вершины;
• вершина пирамиды – это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
• основание – это многоугольник, на котором не лежит вершина;
• высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.

Как найти высоту пирамиды, если известен ее объем

Через формулу объема пирамиды V = (S*h)/3 (в формуле V — объем, S – площадь основания, h — высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см 2 , тогда как ее объем составляет 125 см 3 . Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.

Как найти высоту пирамиды, если известна длина диагонали и ее ребра

Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а – гипотенуза, а в нашем случае ребро пирамиды; b – первый катет или половина диагонали и с – соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² — b².

Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра – 30 см. Необходимо найти высоту. Решаем: c² = 30² — 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.

Как найти высоту усеченной пирамиды

Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды – это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания – d2, а ребро имеет длину – l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.

Вопрос Видео: Определение высоты треугольной пирамиды

Стенограмма видео

𝑀𝐴𝐵𝐶 — правильная пирамида, основанием которой 𝐴𝐵𝐶 является равносторонний треугольник со стороной 32 сантиметра. Если длина ее бокового ребра равна 88 сантиметрам, найдите высоту пирамиды с точностью до сотых.

Начнем с эскиза этой пирамиды 𝑀𝐴𝐵𝐶. Нам говорят, что 𝐴𝐵𝐶 — равносторонний треугольник, поэтому все его стороны будут иметь длину 32 сантиметра. Нам также говорят, что боковой край равен 88 сантиметрам. Так, например, мы могли бы сказать, что это означает, что длина 𝑀𝐴 составляет 88 сантиметров. Высота этой пирамиды — это перпендикулярное расстояние от вершины 𝑀 до центра тяжести основания. Давайте заметим, что мы могли создать этот прямоугольный треугольник внутри пирамиды. Мы хотим вычислить ℎ, перпендикулярную высоту. Мы знаем, что боковое ребро равно 88 сантиметрам. Итак, если бы мы могли определить эту длину от вершины 𝐴 до центроида основания, то мы смогли бы вычислить значение ℎ. Итак, давайте рассмотрим, как мы можем рассчитать это расстояние от 𝐴 до центроида.

Создадим двухмерный рисунок основания пирамиды, который представляет собой равносторонний треугольник 𝐴𝐵𝐶. Определим это расстояние от вершины 𝐴 до центроида как 𝑥 сантиметров в пирамиде. Ну а в основании пирамиды, именно вот на этом равностороннем треугольнике. Если бы мы продолжили эту розовую линию, мы бы создали медиану равностороннего треугольника, потому что центр тяжести треугольника формируется в точке пересечения трех медиан треугольника. Итак, нам нужно сделать две вещи. Во-первых, нам нужно определить длину медианы, а затем нам нужно определить длину 𝑥.

Первое свойство, которое мы можем использовать и запомнить, состоит в том, что медиана равностороннего треугольника является серединным перпендикуляром. Итак, это означает, что 𝐵𝐶 разделена на две конгруэнтные части, и эта медиана пересекается с 𝐵𝐶 под прямым углом. Итак, учитывая, что мы знаем длину стороны этого равностороннего треугольника, у нас на самом деле достаточно информации, чтобы применить теорему Пифагора для определения длины медианы. Поскольку длина стороны равностороннего треугольника равна 32 сантиметрам, то 𝐴𝐵 равно 32 сантиметрам. Длина от 𝐵 до середины 𝐵𝐶 должна составлять половину 32 сантиметров, то есть 16 сантиметров. Мы можем определить длину от 𝐴 до середины 𝐵𝐶 как 𝑚 сантиметров.

Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов двух других сторон. Итак, в этом треугольнике у нас есть две длины сторон 16 сантиметров и 𝑚 сантиметров, которые могут быть 𝑎 и 𝑏, а гипотенуза равна 32 сантиметрам. Подставляя эти значения в теорему Пифагора, мы получаем 16 в квадрате плюс 𝑚 в квадрате равно 32 в квадрате. Вычисляя квадраты, мы имеем 256 плюс 𝑚 в квадрате равно 1024. Переставляя это путем вычитания 256, мы получаем 𝑚 в квадрате равно 768. Взяв квадратный корень из обеих сторон, мы получаем, что 𝑚 равно квадратному корню из 768. Мы можно оставить как квадратный корень из 768 или еще больше упростить до 16 корня из трех. Если мы преобразуем это в десятичное число, то мы пока не будем его округлять, потому что нам нужно будет использовать его в следующих вычислениях.

Итак, теперь мы подсчитали, что длина медианы составляет 16 корней из 3 сантиметров. Нам еще нужно вычислить это расстояние 𝑥, которое является долей медианы. И на самом деле именно теорема о центроиде говорит нам об этой пропорции. Эта теорема говорит нам, что расстояние от каждой вершины до центроида составляет две трети длины медианы от этой вершины. Итак, мы имеем здесь то, что 𝑥 — это две трети корня из 16 на три сантиметра. Затем мы можем умножить две трети и 16 корней из трех, и это даст нам 32 корня из трех на три сантиметра. Итак, наконец, мы выяснили, что 𝑥 — это корень 32 из трех на три сантиметра.

Когда мы вернемся к пирамиде, мы увидим, что внутри этой пирамиды у нас теперь есть прямоугольный треугольник, две длины которого нам известны, и мы можем вычислить высоту ℎ. Мы можем освободить место для этого вычисления. Может быть полезно нарисовать этот треугольник изнутри пирамиды. Итак, здесь у нас есть треугольник с гипотенузой 88 сантиметров, основанием из 32 корней три на три сантиметра и длиной стороны ℎ. Применяя здесь теорему Пифагора, мы получим ℎ в квадрате плюс 32 корня из трех в квадрате равно 88 в квадрате. Когда мы возводим здесь значения в квадрат, если мы возьмем этот термин 32, корень три из трех и возведем его в квадрат, в числителе мы получим 32 в квадрате, умноженное на корень из трех в квадрате, что равно трем, деленным на три в квадрате.

3072 более девяти на самом деле можно упростить до 1024 более трех. В правой части 88 в квадрате равно 7744. Затем мы переставляем, вычитая 1024 на три с обеих сторон, в результате чего ℎ в квадрате равно 22208 на три. Затем мы извлекаем квадратный корень из обеих сторон, что дает нам ℎ равно квадратному корню из 22208 на три. На этом этапе мы затем проверяем, как должен быть дан ответ. А так как нас просят дать ответ с точностью до сотой, то нам нужно найти десятичную аппроксимацию. Это будет 86,0387 и так далее сантиметров. Округлив это число до сотых, мы получим ответ, что высота этой пирамиды составляет 86,04 сантиметра с точностью до сотых.

Формула треугольной пирамиды. Что такое формула треугольной пирамиды? Примеры

Треугольная пирамида имеет треугольное основание, и все три треугольные грани сходятся в вершине. Существует частный случай треугольной пирамиды, называемый тетраэдром, у него есть равносторонние треугольники для каждой из граней. Формула треугольной пирамиды состоит из объема и площади поверхности треугольной пирамиды, которая вычисляет три стороны треугольной формы, высоту и высоту наклона. На следующем рисунке показано, как выглядит треугольная пирамида:

Что такое формула треугольной пирамиды?

Пирамида с треугольным основанием, три треугольные грани которого сходятся на вершине. Формула треугольной пирамиды включала в себя как объем, так и площадь поверхности пирамиды. Формула объема треугольной пирамиды вычисляет площадь основания и высоту, тогда как площадь поверхности треугольной пирамиды вычисляет площадь основания, периметр и наклонную высоту. Ниже приведены формулы для объема и площади поверхности треугольной пирамиды, которые используются в формуле треугольной пирамиды: 

Объем = 1/3 × площадь основания × высота

Площадь поверхности = площадь основания +1/2 (периметр × высота наклона)

Формула треугольной пирамиды

Формулы площади поверхности треугольной пирамиды:

Объем = 1/3 × площадь основания × высота

Площадь поверхности = площадь основания + 1/2 (периметр × высота наклона)

Разбейте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Примеры использования формулы треугольной пирамиды

Пример 1. Найдите объем треугольной пирамиды с площадью основания 10 см ² и высотой 5 см.

Решение:

Дано: площадь основания = 10 см ² , высота = 5 см.

Используя формулу объема треугольной пирамиды

Объем = 1/3 × площадь основания × высота

= 1/3 × 10 × 5

= 16,67 см ³

Следовательно, объем треугольной пирамиды равен 16,67 см ³

Пример 2: Треугольная пирамида имеет площадь основания 15 единиц ²  и сумму длин ребер 60 единиц. Вычислите площадь поверхности треугольной пирамиды, если высота наклона равна 20 единицам.

Решение:
Дано: площадь основания = 15 единиц ² , периметр = 60 единиц.

Используя формулу площади поверхности треугольной пирамиды

Площадь поверхности = площадь основания + 1/2 (периметр × высота наклона)

= 15 + 1/2 (60 × 20)
= 15 + 600
= 615 единиц ²

Следовательно, площадь поверхности треугольной пирамиды равна 615 единиц ²

Пример 3. Найдите площадь поверхности треугольной пирамиды, площадь треугольников основания которой составляет 24 квадратных единицы, периметр треугольника – 12 единиц, а наклонная высота пирамиды – 18.

Решение:

Площадь оснований треугольников = 24 квадратных единицы.

Периметр треугольника =12 единиц.

Наклонная высота пирамиды =18 ед.

Используя формулу площади поверхности треугольной пирамиды

Площадь поверхности треугольной пирамиды = Площадь основания + 1/2 (периметр × высота наклона)

= 24 + 1/2 (12 × 18)

= 132 ед. ²

Следовательно, площадь поверхности треугольной пирамиды 132 ед. ²

Часто задаваемые вопросы о формуле треугольной пирамиды

Что подразумевается под формулой треугольной пирамиды?

Треугольная пирамида имеет треугольное основание, и все три треугольные грани сходятся в вершине. Формула треугольной пирамиды включала в себя как объем, так и площадь поверхности пирамиды. Формула объема треугольной пирамиды вычисляет площадь основания и высоту, тогда как площадь поверхности треугольной пирамиды вычисляет площадь основания, периметр и наклонную высоту. Ниже приведены формулы для объема и площади поверхности треугольной пирамиды, которые используются в формуле треугольной пирамиды: 

Объем = 1/3 × площадь основания × высота

Площадь поверхности = площадь основания + 1/2 (периметр × высота наклона)

Как найти площадь поверхности треугольной пирамиды?

Формула площади поверхности пирамиды рассчитывается путем сложения площадей всех треугольных граней пирамиды. что составляет площадь основания +1/2 (периметр × наклонная высота). Размерами, необходимыми для определения площади поверхности треугольной пирамиды, являются сторона, высота и наклонная высота.

Как найти объем треугольной пирамиды?

Формула для расчета объема треугольной пирамиды: Объем = 1/3 × площадь основания × высота. Размерами, необходимыми для определения площади поверхности треугольной пирамиды, являются сторона, высота и наклонная высота.

Используя формулу треугольной пирамиды, найдите объем с площадью основания 15 см

Дано: площадь основания = 15 см ² , высота = 4 см.

Использование формулы объема треугольной пирамиды

Объем = 1/3 × площадь основания × высота

= 1/3 × 15 × 4

= 20 см ³

Следовательно, объем треугольной пирамиды равен 20 см ³

5 Площадь поверхности Треугольная пирамида

Площадь поверхности треугольной пирамиды равна сумме площадей всех граней треугольной пирамиды. В основном треугольная пирамида имеет треугольное основание и ограничена тремя боковыми треугольными гранями, которые сходятся в одной вершине. У треугольной пирамиды все грани треугольники. Эта пирамида имеет 4 грани, 6 ребер и 4 угла или вершины. Ниже приведены несколько типов треугольной пирамиды:

• Правильная треугольная пирамида — все грани представляют собой равносторонние треугольники и известны как тетраэдры.
• Прямоугольная треугольная пирамида — основанием является равносторонний треугольник, а остальными гранями являются равнобедренные треугольники.
• Неправильная треугольная пирамида — основанием является разносторонний или равнобедренный треугольник.

1.	Какова площадь поверхности треугольной пирамиды?
2.	Площадь поверхности треугольной пирамиды Формула
3.	Как рассчитать площадь поверхности треугольных пирамид?
4.	Площадь боковой поверхности треугольной пирамиды
5.	Часто задаваемые вопросы о площади поверхности треугольной пирамиды Формула

Какова площадь поверхности треугольной пирамиды?

Площадь поверхности любой трехмерной геометрической формы представляет собой сумму площадей всех граней или поверхностей этого замкнутого твердого тела. Треугольная пирамида имеет четыре треугольные грани. Таким образом, формула расчета площади поверхности треугольной пирамиды включает площадь основания, периметр основания и наклонную высоту любой стороны пирамиды. Площадь поверхности всегда измеряется в квадратных единицах, таких как см ² , м ² , фут ² или локти ² . Площадь поверхности треугольной пирамиды равна \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\!\times\!\text {Наклонная высота} ) \end{выравнивание}\).

Площадь поверхности треугольной пирамиды Формула

Формула площади поверхности треугольной пирамиды рассчитывается путем сложения площадей всех треугольных граней пирамиды. Площадь поверхности прямоугольной пирамиды равна \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\!\times\!\text {Наклон Высота}) \end{выравнивание}\).

После подстановки значений получаем выражение площади поверхности по формуле треугольной пирамиды как 1/2(a × b) + 3/2(b × s).

Где

• b — сторона треугольной пирамиды.
• а — высота основания треугольника
• с — наклонная высота треугольной пирамиды.
• 1⁄2(a × b) — площадь основания треугольных граней.
• 3⁄2(b × s) — это произведение периметра и наклонной высоты пирамиды.

Как рассчитать площадь поверхности треугольных пирамид?

Площадь поверхности треугольной пирамиды можно рассчитать, представив 3D-форму в 2D-сетку, чтобы фигуры было легче увидеть. После расширения 3D-формы в 2D-форму мы получим четыре треугольника.
Следующие шаги используются для вычисления площади поверхности треугольной пирамиды:

• Шаг 1: Найдите площадь треугольников с основаниями: Площадь треугольников с основаниями равна (1/2 × основание треугольника × высота треугольника). треугольник), который становится основанием × высота.
• Шаг 2: Найдите периметр треугольных граней: Периметр треугольника равен сумме всех сторон треугольника, которая равна \((сторона)_{1}\) + \((сторона)_{2} \) + \((сторона)_{3}\).
• Шаг 3: Найдите наклонную высоту треугольных граней: Наклонная высота треугольной пирамиды обычно обозначается буквой «s».
• Шаг 4: Сложите все области вместе. Таким образом, формула площади поверхности треугольной пирамиды равна 1/2 (a × b) + 3/2 (b × s) в квадратных единицах.

Площадь боковой поверхности треугольной пирамиды

Площадь боковой поверхности — это площадь неосновных граней, или можно сказать, что только площадь боковой поверхности любого объекта рассчитывается путем удаления базовой площади. Площадь боковой стороны треугольной пирамиды можно рассчитать, удалив площадь основания треугольника из произведения периметра основания и наклонной высоты пирамиды.

Таким образом, площадь боковой поверхности прямоугольной треугольной пирамиды равна 1/2 (периметр основания × высота наклона), которая затем становится равной 3/2 (сторона × высота наклона).

Где

• b — сторона пирамиды.
• s — наклонная высота основания.

Примеры площади поверхности треугольной пирамиды Формула

1. Пример 1: Каждая сторона треугольной пирамиды имеет длину 3 единицы, высота треугольника с основанием равна 6, а высота наклона равна 5. Найдите общую площадь поверхности.

   Решение

   Площадь поверхности треугольной пирамиды со стороной а равна

   Площадь поверхности = 1⁄2(a × b) + 3⁄2(b × s)

   Подставляя значения, получаем,

   Площадь поверхности = 1⁄2(6 × 3) + 3⁄2( 3 × 5)

   Площадь поверхности = (9) + (22,5) = 31,5 ед.

2. Пример 2: Найдите площадь поверхности треугольной пирамиды, площадь основания которой равна 24 единицам ² , периметр равен 12 единицам, а наклонная высота пирамиды равна 18.

   Решение

   Площадь поверхности треугольной пирамиды со стороной a равна

   Площадь поверхности = 1/2(a × b) + 3⁄2(b × s)

   Площадь поверхности треугольной пирамиды = \(\begin{align} \text {Площадь основания}+\!\frac{1}{2} \text {(Периметр}\! \times\!\text {Наклонная высота}) \end{align}\)

   Подставляем значения в формулу,

   Площадь поверхности треугольной пирамиды = \(\begin{align} \text {24}+ \!\frac{1}{2} \text {(12}\!\times\!\text {18}) \end{align}\)

   = 132 кв.

   Ответ: Площадь поверхности треугольной пирамиды 96 единиц ² .

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по площади поверхности треугольной пирамиды Формула

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади поверхности треугольной пирамиды Formula

Как найти площадь поверхности треугольной пирамиды?

Формула площади поверхности пирамиды рассчитывается путем сложения площадей всех треугольных граней пирамиды. что равно 1/2(a × b) + 3/2(b × s). Где b — сторона пирамиды, a — высота треугольника в основании, s — наклонная высота пирамиды.

Какова формула объема треугольной пирамиды?

Объем треугольной пирамиды можно найти по формуле 1/3 × Площадь основания × Высота.

Как найти площадь основания прямоугольной пирамиды?

Площадь основания прямоугольной треугольной пирамиды равна 1/2 × высота треугольника с основанием × нижний край треугольника с основанием.

Что такое боковая поверхность треугольной пирамиды?

Боковая поверхность треугольной пирамиды рассчитывается в соответствии с приведенными ниже шагами.

• Шаг 1: Найдите заданные параметры.
• Шаг 2: Умножьте 1/3 на периметр основания треугольника и наклонную высоту треугольной пирамиды.
• Шаг 3: Запишите результат в квадратах.

Как найти общую площадь поверхности треугольной пирамиды, зная площадь ее боковой поверхности и площадь основания?

Формула для расчета общей площади поверхности треугольной пирамиды: 1/2(a × b) + 3/2(b × s).