ТЕОРИЯ
1. Справочный материал
2. Решение неравенств
Определение и основные свойства неравенств.
Определения:
где a и
b могут быть числами или функциями.
Символы <(≤), >(≥) называются знаками неравенства и читаются соответственно :
меньше(меньше или равно) ,больше(больше или равно).
Неравенства , которые записываются с помощью знаков > и <,называются строгими,
а неравенства, в записи которых участвуют знаки ≥ и ≤,- нестрогими.
Неравенства вида a<x<b (a≤x≤b) называются двойными неравенствами
и читаются соответственно :x больше a,но меньше b (x больше или равно a,но меньше или равно b ).
Различают два вида неравенств: числовые (2>0,7 ;½<6) и неравенства с переменной (5x-40>0 ; x²-2x<0).
Свойства числовых неравенств :
- Если
a>b , то
b<a; если a<b,
то
b>a.
- Если a<b и b<c, то a<c.
- Если a<b и c-любое число, то a +c<b+c.
- Если a<b и c>0,то ac<bc. Если a<b и c<0,то ac>bc.
- Если a<b и c<d,то a +c<b +d.
Числовые промежутки
| Неравенство |
Числовой промежуток |
Название промежутка |
Геометрическая интерпретация |
| замкнутый промежуток(отрезок) с концами a и b ,a<b |
|
||
|
|
открытый промежуток (интервал) с концами a и b ,a<b |
|
|
|
|
|
полуоткрытые промежутки (полуинтервалы) концами a и b ,a<b |
|
|
|
|
бесконечные промежутки (лучи) |
|
|
|
|
бесконечные промежутки (открытые лучи) |
|
| бесконечный промежуток (числовая прямая) |
Вверх
Основные
определения и свойства.
Определения:
Решением неравенства с одной переменной называется значение переменной,
которое обращает его в верное числовое неравенство.
Решить неравенство — значит найти все его решения или доказать, что решений нет.
Неравенства, имеющие одни и те же решения, называются равносильными.
Неравенства, не имеющие решений, также считают равносильными.
При решении неравенств используются следующие свойства:
1) Если из одной части неравенства перенести в
другую слагаемое с противоположным знаком,
то получится равносильное ему неравенство.
2) Если обе части неравенства умножить или
разделить на одно и то же положительное число,
то получится равносильное ему неравенство.
3) Если обе части неравенства умножить или
разделить на одно и то же отрицательное число,
изменив при этом знак неравенства на противоположный,
то получится равносильное ему неравенство.
Многие неравенства в процессе преобразований сводятся к линейным неравенствам.
Неравенства вида ах>b ( ах <b ,ax≤b или ax≥b), где а и b — некоторые числа,
называют
линейными неравенствами с одной
переменной.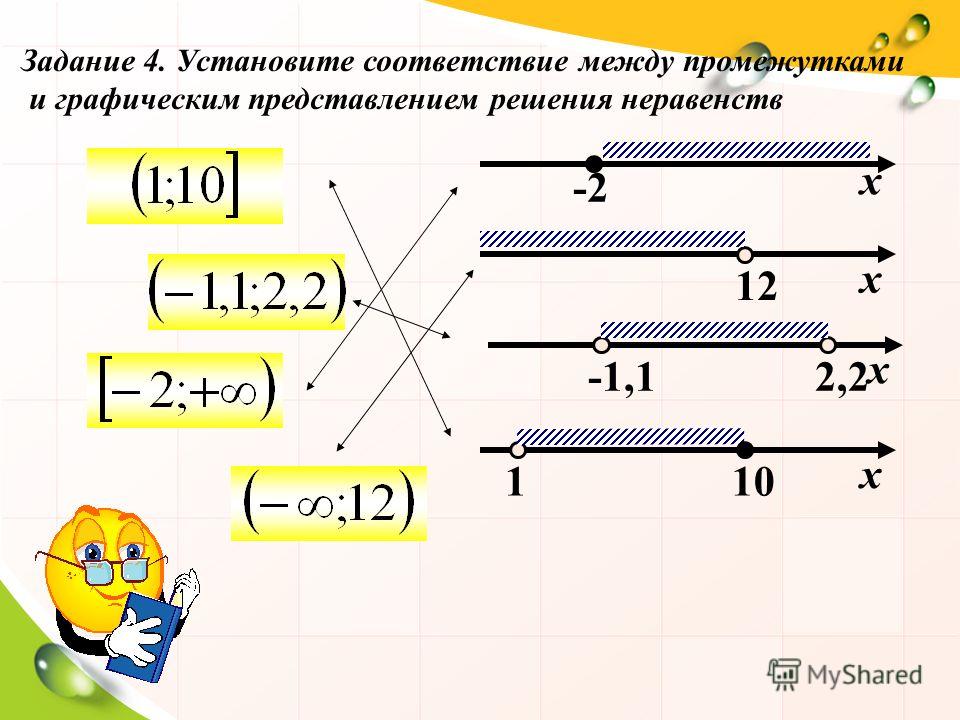
Если a>0 ,то неравенство ax>b
и множество решений неравенства есть промежуток
Если a<0 ,то неравенство ax>b равносильно неравенству
и множество решений неравенства есть промежуток
неравенство примет вид 0∙x>b, т.е. оно не имеет решений ,если b≥0,
и верно при любых x ,если b<0
.Аналитический способ решения неравенств с одной переменной.
Алгоритм решения неравенства с одной переменной
- Преобразовать обе части неравенства.
- Привести подобные слагаемые.
- Привести неравенства к простейшему виду, на основании свойств неравенств.
- Записать ответ.
Приведем примеры решения неравенств .
Пример 1. Решить неравенство 3x≤15.
Решение:
Обе части неравенства
Множество решений
неравенства представляет собой числовой промежуток (-∞;5].
Ответ :(-∞;5]
Пример 2. Решить неравенство -10x≥34.
Решение:
Обе части неравенстваразделим на отрицательное число -10 ,
при этом знак неравенства изменим на противоположный (свойство 3) : x≤-3,4.
Множество решений неравенства представляет собой промежуток (-∞;-3,4].
Ответ : (-∞;-3,4].
Пример 3. Решить неравенство 18+6x>0.
Решение:
Перенесем слагаемое 18 с противоположным знаком в левую часть неравенства (свойство 1): 6x>-18.
Разделим обе части на 6 (свойство 2) :
x>-3.
Множество решений неравенства представляет собой промежуток (-3;+∞).
Ответ : (-3;+∞).
Пример 4.Решить неравенство 3(x-2)-4(x+2)<2(x-3)-2.
Решение:
Раскроем скобки : 3x-6-4x-8<2x-6-2.
Перенесем члены ,содержащие неизвестное ,в левую часть ,
а члены не содержащие неизвестное , в правую часть (свойство 1):
3x-4x-2x<6+8-6-2.
Приведем подобные члены: -3x<6.
Разделим обе части на -3 (свойство 3) :
x>-2.
Множество решений неравенства представляет собой промежуток (-2;+∞).
Ответ
: (-2;+∞).
Пример 5. Решить неравенство
Решение:
Умножим обе части неравенства на наименьший общий знаменатель дробей,
входящих в неравенство, т. е. на 6 (свойство 2).
Получим:
,2x-3x≤12.
Отсюда , —x≤12 , x≥-12.
Ответ : [-12;+∞).
Пример 6. Решить неравенство 3(2-x)-2>5-3x.
Решение:
Упростим неравенство ,раскрыв скобки:
6-3x-2>5-3x, 4-3x>5-3x, -3x+3x>5-4.
Приведем подобные члены в левой части неравенства и запишем
результат в виде 0∙x>1.
Полученное неравенство не имеет решений, так как при любом значении x
оно обращается в числовое неравенство 0 < 1, не являющееся верным.
Значит, не имеет решений и равносильное ему заданное неравенство.
Ответ : решений нет.
Пример 7.Решить неравенство 2(x+1)+5>3-(1-2x).
Решение:
Упростим неравенство ,раскрыв скобки:
2x+2+5>3-1+2x, 2x+7>2+2x,2x-2x>2-7, 0∙x>-5.
Полученное неравенство является верным при любом значении x,
так как левая часть при любом x равна нулю, а 0>-5.
Множеством решения неравенства является промежуток (-∞;+∞).
Ответ
:
(-∞;+∞).
Пример 8. При каких значениях x имеет смысл выражение:
a)
b)
Решение:
а)По определению арифметического квадратного корня
должно выполнятся следующее неравенство 5x-3≥0.
Решая, получаем 5x≥3, x≥0,6.
Итак, данное выражение имеет смысл при всех x из промежутка [0,6;+∞).
Ответ : [0,6;+∞).
б)С учетом свойств арифметического квадратного корня и знаменателя дроби
должно выполнятся следующее неравенство 2-3x>0.
Отсюда ,-3x>-2
(свойство 3), x<2/3.
Данное выражение имеет смысл при всех x из промежутка (-∞;2/3).
Ответ :(-∞;2/3).
Пример 9.При каких значениях a квадратное уравнение x-8x2-4a=0 имеет два корня ?
Решение:
Квадратное уравнение будет иметь два корня ,если дискриминант D будет больше нуля.
D=(-8)2-4∙(-4a)=64+16a,
64+16a>0,
16a>-64,
a>-4.
Таким образом , при всех значениях a из промежутка (-∞;-4)
данное квадратное уравнение будет иметь два корня.
Ответ
:
при всех
a из промежутка
(-∞;-4)
.
Пример 10.Решите задачу:
В одном бассейне налито 100 л воды, а во втором 150 л воды.
Каждый час в первый бассейн вливается 15 л воды, а во второй — 5 л воды.
В какие моменты времени в первом бассейне будет больше воды, чем во втором?
Решение:
Пусть за x ч в первый бассейн вольется 15x л воды и в нем станет 100+15x л воды.
Тогда через x ч во втором бассейне будет 150+5x л воды.
Надо найти такие значения x , для которых выполняется неравенство
100+15x>150+5x.
Преобразовав ,получаем
15x-5x>150-100,
10x>50,
x>5.
Итак ,в первом бассейне окажется больше воды ,чем во втором, при x>5,
т.е. после 5ч с начала вливания воды.
Ответ : после 5ч с начала вливания воды.
Пример 11. При каких значениях x значения функции Y=-1/3x+8 принадлежит промежутку (-1,1)?
Решение: -1<-1/3x+8<1,
-9<-1/3x<7,
27>x>21,
21<x<27.
Ответ : (21;27).
Вопросы.
1. Что называется неравенством первой степени с одним неизвестным?
2. Что называется решением неравенства с одним неизвестным?
3.
Что значит решить неравенство с одним неизвестным?
4. Каким способом можно решить неравенство первой степени с одним неизвестным?
.Графический способ решения неравенств с одной переменной.
Покажем, как можно, применяя графический метод, решить неравенства вида
kx+ b> 0 (1)
или
kx + b<0, (2)
где k и b — заданные числа и k≠0.
В декартовой системе координат Оху рассмотрим прямую
y = kx + b. (3)
На рис. 1 изображена такая прямая при
k>
0, а на рис.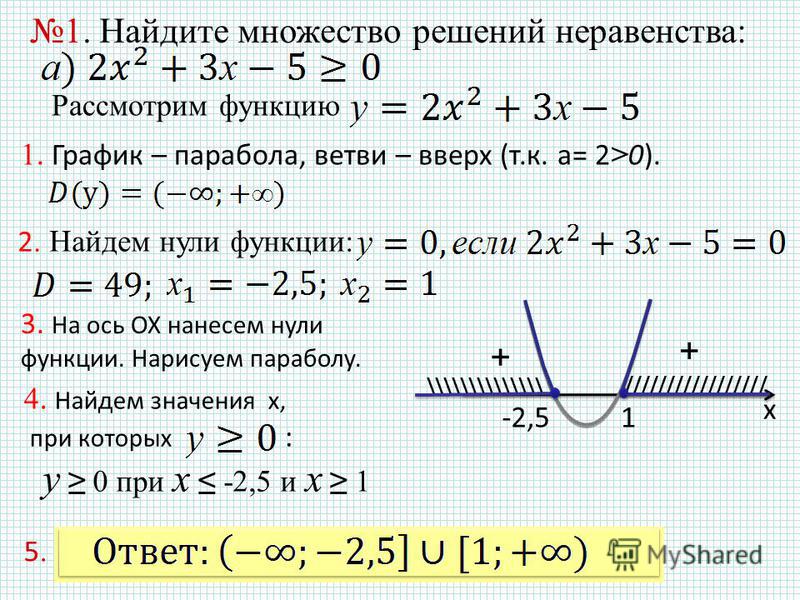
2 изображена такая прямая при
k<0.
рис1. рис.2.
Решить неравенство (1) — это значит найти все решения х,
для которых прямая y = kx-b расположена выше оси х.
Здесь важную роль играет точка А пересечения прямой (3) с осью х.
Абсциссу точки А
обозначим
через
xo.
Так как ее ордината равна нулю, то
xo
удовлетворяет уравнению
O = kxo + b, откуда
xo=-b/k.
Обратимся к рис. 1, соответствующему случаю k> 0. Мы видим , что прямая y = kx+b
расположена выше оси
х
для всех х,
находящихся правее
точки xo, т. е. для всех х из интервала (-∞,
+ ∞), и
расположена ниже оси
х
для
всех х,
находящихся левее точки
xo,
т. е. для всех х
из интервала (—∞,xo).
Итак, при k> 0 неравенство (1) выполняется на интервале (xo, + ∞), а неравенство (2) —на интервале (—∞,xo).
При k<0, как это видно из рис. 2, неравенство (1) выполняется на интервале (—∞,xo),
а неравенство (2) — на интервале (xo, + ∞).
Пример 1. Решить, применяя графический метод, неравенства
2X+1 >0, (4)
2X+1 <0. (5)
Решение :
Начертим в декартовой системе координат Оху прямую
у = 2X+1.
(6)
рис3.
Для этого нужно знать две ее точки. В качестве первой точки возьмем точку пересечения прямой с осью х. Она все равно будет нужна. Полагая в формуле (6) у = 0, получим уравнение
0 = 2х+1.
Его решение есть абсцисса точки А пересечения прямой с осью х. Итак, А ( —1/2 ,0).
В качестве второй точки можно взять точку В
пересечения
прямой с осью у.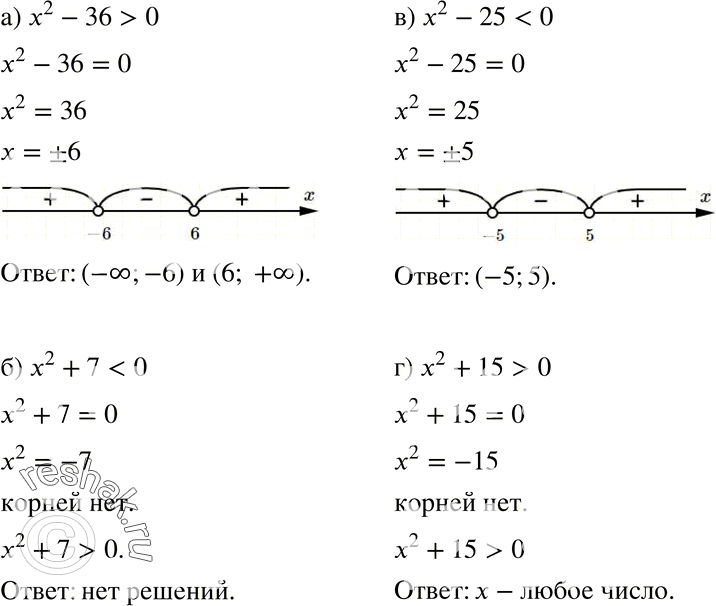
2+5x больше 0
х(х+5) больше 0
т.к х меньше 0, то и х+5 меньше 0, значит х меньше (-5)
это второй промежуток решения : от — бесконечности до -5 (не включая -5)
3) 0 — легко подставить и понять, что решением не является
ответ: объединение двух промежутков: от — бескон. до -5 и от 5 до +бескон.
Ответ
Ответ разместил: Vova50915091
x²- 5x — 6 > 0
x²- 5x — 6 = 0
x₁ = 6; x₂ = -1
-1 6>
x ∈ (-∞; -1)U(6; ∞)
Ответ
Ответ разместил: sonya408
x²-5x-6≥0=x∈(-∞;-1]∪[6;+∞)
Объяснение:
x²-5x-6≥0=
x²+x-6x-6≥0
x(x+1)-6(x+1)≥0
(x+1)(x-6)≥0
(x+1≥0
(x-6≥
(x+1≤0
(x-6≤0
(x≥-1
(x≥6
(x≤-1
(x≤6
x∈[6;+∞)
x∈(-∞;-1]
Ответ
Ответ разместил: NeekaFox
Решение во вложении
*******************************************
Ответ
Ответ разместил: irfanmirzoev2
Решите неравенство (x² -5x +4) / (5 -x²) > 0 .
(x² -5x +4) / (5 -x²) >0⇔(x² -5x +4) / (x² -5)< 0⇔(x -1)(x — 4) / (x+√5)(x -√5)< 0 ⇔ (x -1)(x -4) * (x+√5)(x -√5)< 0⇔ (x+√5) (x -1)(x -√5) (x -4) < 0
Решаем по методу интервалов :
+ — + — +
( -√5 ) (1) ( √5 ) (4)
ответ : x ∈ ( -√5 ; 1) ∪ ( √5 ; 4) .
Ответ
Ответ разместил: albinasaydilova
смотри вложения если что-то не поймешь напиши в сообщения
Ответ
Ответ разместил: margosha2810
Удачи закончить учебный год на отлично
Другие вопросы по: Алгебра
Изменение электрического заряда конденсатора в колебательном контуре происходит по закону q=0,2cos*πt/25. чему равна частота колебаний заряда?…
27.02.2019 09:20
Ответов: 3
Ширина атлантического океана в километрах…
28.02.2019 14:20
Ответов: 3
Из букв в словах ( марс и уран)запишите перечислением элементов: 1) множество а и b.
2-5x-7< 0…
Популярные вопросы
Ккаким формам жизни относятся бактерии и сине зеленые водоросли?…
28.02.2019 19:30
Ответов: 3
Составь предложение из рассыпавшихся слов: рождается, существо, как, социальное, как, человек, биологическое, развивается…
01.03.2019 00:00
Ответов: 1
Галинка зліпила 160 вареників з м’ясом і з картоплею причому вареники з м’ясом становоли 5/8 усіх вареників. скільки вареників з м’ясом зробила галинка?…
02.03.2019 14:30
Ответов: 2
Чему равна кинетическая энергия автомобиля массой m=1,0 т, проезжающего каждую минуту путь s=1,2 км?…
02.03.2019 17:00
Ответов: 3
При погружении в жидкость на тело объемом 2 дм3 действует архимедова сила 14,2 н. какая это жидкость?…
04.03.2019 12:50
Ответов: 3
Составь схемы цепей питания. характерной для саванны…
08.03.2019 04:30
Ответов: 3
Что надо делать, чтобы не повредить зрение?.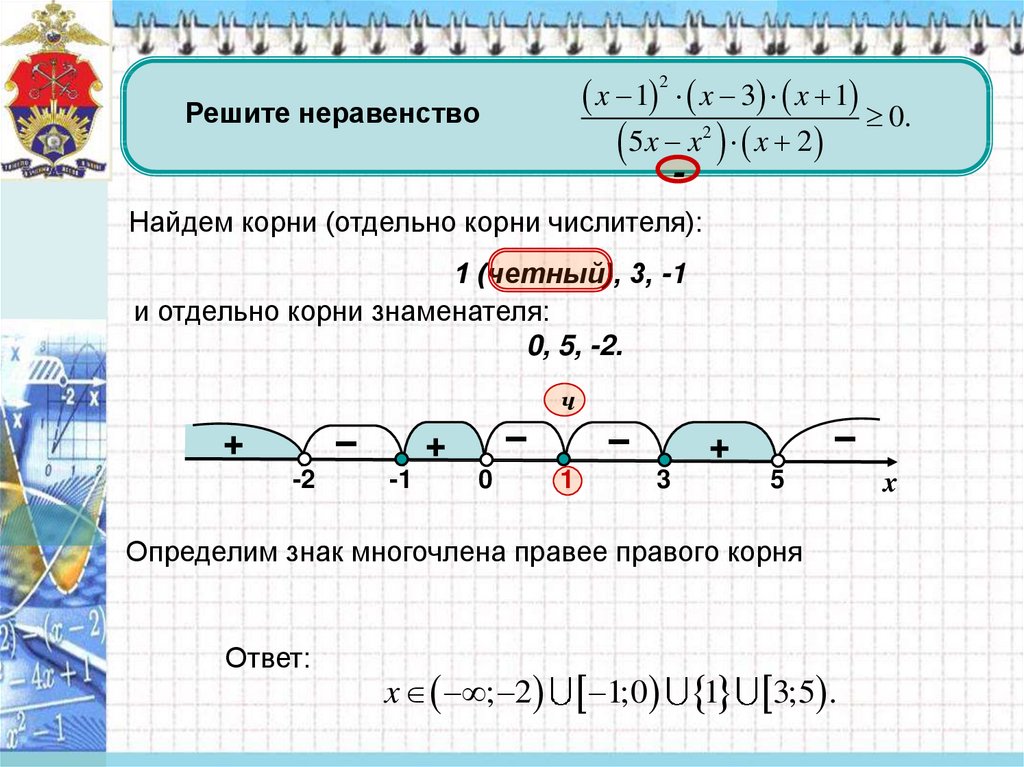
2+5x больше 0
х(х+5) больше 0
т.к х меньше 0, то и х+5 меньше 0, значит х меньше (-5)
это второй промежуток решения : от — бесконечности до -5 (не включая -5)
3) 0 — легко подставить и понять, что решением не является
ответ: объединение двух промежутков: от — бескон. до -5 и от 5 до +бескон.
Ответ
Ответ разместил: missm0541
x²- 5x — 6 > 0
x²- 5x — 6 = 0
x₁ = 6; x₂ = -1
-1 6>
x ∈ (-∞; -1)U(6; ∞)
Ответ
Ответ разместил: лав35
x²-5x-6≥0=x∈(-∞;-1]∪[6;+∞)
Объяснение:
x²-5x-6≥0=
x²+x-6x-6≥0
x(x+1)-6(x+1)≥0
(x+1)(x-6)≥0
(x+1≥0
(x-6≥
(x+1≤0
(x-6≤0
(x≥-1
(x≥6
(x≤-1
(x≤6
x∈[6;+∞)
x∈(-∞;-1]
Ответ
Ответ разместил: Браство
Решение во вложении
*******************************************
Ответ
Ответ разместил: Colaps
смотри вложения если что-то не поймешь напиши в сообщения
Ответ
Ответ разместил: школа21002100
Удачи закончить учебный год на отлично
Другие вопросы по: Алгебра
Напишите сумму: в)x+32 и y+13 г)m-98 и n+56.
..
28.02.2019 23:10
Ответов: 3
Из овечьей шерсти скатали валенки. сравните массы шерсти и валенок, если отходов не было. что изменилось?…
01.03.2019 02:40
Ответов: 3
Какое из слов: золотой, серебряный, медный ,стеклянный-может быть нарицательным существительным?…
01.03.2019 04:30
Ответов: 3
Василиса премудрая сшила из одинаковых лоскутов, каждый площадью 9дм в квадрате, покрывало квадратной формы со стороной 24дм. на каждом лоскуте она вышила город с 5 теремами. сколь…
02.03.2019 10:40
Ответов: 1
Вода массой 400г и карбонат кальция массой 250г. образуют суспензию. рассчитайте количество и массовую долю карбоната кальция в суспензии…
02.03.2019 19:20
Ответов: 3
Определите массу кислорода, воздуха, необходимо для полного сгорания этилового спирта массой 69 грамм…
02.03.2019 21:00
Ответов: 1
Знаешь правильный ответ?
Решите неравенство x^2-5x+4/5-x^2> 0.
..
Популярные вопросы
Сочинение на тему»о чем расказывает слово»…
28.02.2019 06:20
Ответов: 1
Напишите на тему «какая книга меня больше всего поразила»….
01.03.2019 12:50
Ответов: 2
Решить =)в автоцистернах 32т бензина. количество бензина первой цистерны состовляют 7 количества бензина второй цистерны. сколько тонн было 9 в каждой из этих двух решить…
01.03.2019 19:30
Ответов: 2
Узнать свою массу и площадь ботинка, вычислить, какое давление вы производите при ходьбе и стоя на месте…
02.03.2019 20:20
Ответов: 2
Когда брат полил 5 грядок а сестра 3 грядки им осталось полить 4 грядки сколько всего грядок должны полить дети? как написать условие и как решать…
03.03.2019 22:40
Ответов: 1
Восновании пирамиды abcd, все боковые ребра которой равны корень из 74 см, лежит прямоугольник со сторонами ab=8 см и bc=6 см.
найдите площадь сечения msn, если оно перпендикулярно…
07.03.2019 16:10
Ответов: 1
Составить 10 предложений на тему не и ни…
08.03.2019 04:20
Ответов: 1
Расставь скобки и знаки действий, что бы получилось верное равенство: 5 5 5 5 5 = 550….
08.03.2019 07:00
Ответов: 3
1) с какого опыта можно доказать , что, тела состоящие из различных веществ при одинаковой массе имеют разные объемы? ? 2) почему в таблицах плотности указывают температуру , при к…
08.03.2019 08:50
Ответов: 3
Найти число корней уравнения 5[х]+27{х}=2012, где [х] — целая часть числа х, а {х} — дробная часть числа х….
08.03.2019 09:10
Ответов: 2
Больше вопросов по предмету: Алгебра Случайные вопросы
3
Решение сложных неравенств | Начальная алгебра
Результаты обучения
- Описывать множества как пересечения или объединения
- Использование обозначения интервалов для описания пересечений и объединений
- Использование графов для описания пересечений и объединений
- Решение сложных неравенств — ИЛИ
- Решите сложные неравенства в форме или и выразите решение графически и с интервалом г.
- Решение составных неравенств — И
- Выразите решения неравенств графически и с помощью записи интервалов
- Найдите решения составных неравенств в форме [латекс]a
- Решение абсолютных неравенств
- Решение одношаговых и многошаговых неравенств, содержащих абсолютные значения
- Определить случаи, когда нет решений абсолютных неравенств г.
Используйте интервальную запись для описания наборов чисел как пересечений и объединений
Когда два неравенства соединяются словами и , решение составного неравенства происходит, когда оба неравенства верны одновременно. Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда либо неравенств верно. Решение представляет собой комбинацию или объединение двух отдельных решений.
В этом разделе мы научимся решать сложные неравенства, которые соединяются словами И и ИЛИ. Во-первых, это поможет увидеть некоторые примеры неравенств, интервалов и графиков составных неравенств. Это поможет вам правильно описать решения сложных неравенств.
Диаграммы Венна используют концепцию пересечений и объединений, чтобы показать, сколько общего у двух или более объектов. Например, эта диаграмма Венна показывает пересечение людей, которые разбивают вам сердце, и тех, кто ежедневно расшатывает вашу уверенность. Очевидно, Сесилия обладает обоими этими качествами; поэтому она является пересечением двух.
В математических терминах рассмотрим неравенство [latex]x\lt6[/latex] и [latex]x\gt2[/latex]. Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал?
На словах x должно быть меньше 6 , и в то же время должно быть больше 2, очень похоже на приведенную выше диаграмму Венна, где Сесилия одновременно разбивает вам сердце и ежедневно подрывает вашу уверенность.
Давайте посмотрим на график, чтобы увидеть, какие числа возможны с этими ограничениями.
Числа, общие для обеих линий на графике, называются пересечением двух неравенств [latex]x\lt6[/latex] и [latex]x\gt2[/latex]. Это называется ограниченным неравенством и записывается как [latex]2\lt{x}\lt6[/latex]. Подумайте об этом на минуту. x должно быть меньше 6 и больше двух — значения x попадут между двумя числами . В записи интервала это выглядит как [латекс]\влево(2,6\вправо)[/латекс]. График будет выглядеть так:
С другой стороны, если вам нужно представить две вещи, которые не имеют общих элементов или признаков, вы можете использовать объединение. На следующей диаграмме Венна показаны две вещи, которые не имеют общих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции.
В математических терминах, например, [latex]x>6[/latex] или [latex]x<2[/latex] — это неравенство, к которому присоединено слово или .
Используя интервальную запись, мы можем описать каждое из этих неравенств отдельно:
[латекс]x\gt6[/латекс] совпадает с [латекс]\left(6, \infty\right)[/латекс] и [латекс]х<2[/латекс] совпадает с [латекс ]\влево(\infty, 2\вправо)[/латекс]. Если мы описываем решения неравенств, какой эффект имеют или ? Мы говорим, что решения – это либо действительные числа, меньшие двух 91 865, либо 91 866 действительных чисел, большие 6. Вы понимаете, почему нам нужно записывать их как два отдельных интервала? Давайте посмотрим на график, чтобы получить четкое представление о том, что происходит.
Если вы поместите оба этих неравенства на график, мы увидим, что они не имеют общих чисел. Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:
[латекс]\влево(\infty, 2\вправо)\чашка\ left(6, \infty\right)[/latex]
Общепринято строить интервалы, начиная с крайнего левого значения на числовой прямой в качестве левого значения, например [latex]\left(2,6 \right)[/latex], где 2 меньше 6.
Число справа должно быть больше числа слева.
Пример
Нарисуйте график составного неравенства [latex]x\gt3[/latex] или [latex]x\le4[/latex] и опишите множество значений x , которые удовлетворяют ему с интервал.
Показать решение
Примеры
Нарисуйте график сложного неравенства: [latex]x\lt5[/latex] и [latex]x\ge-1[/latex] и опишите множество x — значения, которые будут ему удовлетворять с интервалом.
Показать решение
Примеры
Нарисуйте график составного неравенства [латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс] и опишите множество x — значения, которые будут удовлетворять его с интервалом.
Показать решение
В следующем видео представлены два примера того, как рисовать неравенства с участием И, а также записывать соответствующие интервалы.
Решение составных неравенств в форме или
Как мы видели в предыдущем разделе, решение составного неравенства, состоящего из двух неравенств, соединенных словом или , представляет собой объединение решений каждого неравенства. Объединения позволяют нам создать новый набор из двух элементов, которые могут иметь или не иметь общих элементов.
В этом разделе вы увидите, что некоторые неравенства необходимо упростить, прежде чем их решение можно будет записать или изобразить в виде графика.
В следующем примере вы увидите пример решения одношагового неравенства в форме ИЛИ. Обратите внимание, как каждое неравенство обрабатывается независимо до конца, где решение описывается в терминах обоих неравенств. Для решения составных неравенств вы будете использовать те же свойства, что и для решения обычных неравенств.
Не забывайте применять свойства неравенства при решении сложных неравенств.
В следующем примере используется деление на отрицательное значение, чтобы изолировать переменную.
Пример
Найдите y . [latex]2y+7\lt13\text{ или }−3y–2\lt10[/latex]
Показать решение
В последнем примере окончательный ответ включал решения, интервалы которых перекрывались, в результате чего ответ включал все числа на числовой прямой. На словах мы называем это решение «все действительные числа». Любое действительное число даст истинное утверждение либо для [latex]y<3\text{, либо для }y\ge -4[/latex], если его заменить на 9.1865 х .
Пример
Решите для z . [латекс]5z-3\gt-18[/латекс] или [латекс]-2z-1\gt15[/латекс]
Показать решение
Следующее видео содержит пример решения составного неравенства с участием ИЛИ и построения соответствующего графика.
В следующем разделе вы увидите примеры решения сложных неравенств, содержащих числа и .
Решить сложные неравенства в форме
и и представить решение графическиРешение составного неравенства, состоящего из двух неравенств, соединенных словом и , есть пересечение решений каждого неравенства. Другими словами, оба утверждения должны быть истинными одновременно. Решением составного неравенства и являются все решения, общие для этих двух неравенств. Как мы видели в предыдущих разделах, именно здесь два графика перекрываются.
В этом разделе мы увидим больше примеров, когда мы должны упростить сложные неравенства, прежде чем мы сможем выразить их решения графически или с интервалом.
Пример
Решить для x : [латекс] \displaystyle {5}{x}-{2}\le{3}\text{ и }{4}{x}{+7}>{3} [/latex]
Показать решение
Составные неравенства в форме [латекс]a
Вместо того, чтобы разбивать составное неравенство в форме [латекс]a
В видео ниже вы увидите еще один пример решения неравенства в форме [latex]a Чтобы решить неравенства типа [latex]a Решение составного неравенства с числами и всегда совпадает с решением каждого неравенства. Есть три возможных исхода сложных неравенств, соединенных словами и : В приведенном ниже примере составное неравенство не имеет решения, поскольку неравенства не пересекаются. Давайте применим то, что вы знаете о решении уравнений, содержащих абсолютные значения, и то, что вы знаете о неравенствах, для решения неравенств, содержащих абсолютные значения. [латекс]\влево|х\вправо|\leq 4[/латекс] Это неравенство читается как «абсолютное значение x меньше или равно 4». Если вас попросят решить для x , вы хотите узнать, какие значения x отстоят на 4 единицы или менее от 0 на числовой прямой. Вы могли бы начать с размышлений о числовой прямой и о том, какие значения x удовлетворяют этому уравнению. 4 и [латекс]−4[/латекс] находятся на расстоянии четырех единиц от 0, поэтому они являются решениями. 3 и [латекс]-3[/латекс] также являются решениями, потому что каждое из этих значений меньше, чем на 4 единицы от 0. Так же как 1 и [латекс]-1[/латекс], 0,5 и [латекс]-0,5[ /latex] и так далее — существует бесконечное количество значений для x , которые будут удовлетворять этому неравенству. График этого неравенства будет иметь две замкнутые окружности, 4 и [латекс]−4[/латекс]. Расстояние между этими двумя значениями на числовой прямой окрашено в синий цвет, поскольку все эти значения удовлетворяют неравенству. Решение можно записать так: Неравенство: [латекс]-4\leq x\leq4[/латекс] Интервал: [латекс]\влево[-4,4\вправо][/латекс] Ситуация немного отличается, когда знак неравенства стоит «больше» или «больше или равно». Рассмотрим простое неравенство [латекс]\влево|х\вправо|>3[/латекс]. Опять же, вы могли бы подумать о числовой прямой и о том, какие значения числа x больше, чем на 3 единицы от нуля. На этот раз 3 и [латекс]−3[/латекс] не включены в решение, поэтому оба этих значения отмечены незакрашенными кружками. 2 и [латекс]-2[/латекс] не будут решениями, потому что они не более чем в 3 единицах от 0. Но 5 и [латекс]-5[/латекс] будут работать, как и все значения, расширяющие слева от [латекс]−3[/латекс] и справа от 3. График будет выглядеть так, как показано ниже. Решение этого неравенства можно записать так: Неравенство : [латекс]x<−3[/латекс] или [латекс]x>3[/латекс]. Интервал: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex] В следующем видео вы увидите примеры решения и выразить решение абсолютных неравенств с использованием И и ИЛИ. Для любого положительного значения a и x, одной переменной или любого алгебраического выражения: Рассмотрим еще несколько примеров неравенств, содержащих абсолютные значения. Как и в случае с уравнениями, могут быть случаи, когда неравенство не имеет решения. Составное неравенство — это утверждение из двух утверждений о неравенстве, связанных вместе либо словом , либо словом , либо словом и . Иногда составное неравенство и отображается символически, например [latex]a Случай 1: Описание Решением могут быть все значения между двумя конечными точками Неравенства [latex]x\le{1}[/latex] и [latex]x\gt{-1}[/latex] или в виде ограниченного неравенства: [latex]{-1}\lt{x}\le {1}[/латекс] Интервал [латекс]\влево(-1,1\вправо][/латекс] Графики Случай 2: Описание Решение может начинаться в точке на числовой прямой и продолжаться в одном направлении. 
Неравенства [латекс]x\gt3[/латекс] и [латекс]x\ge4[/латекс] Интервал [латекс]\влево[4,\infty\вправо)[/латекс] Графики Случай 3: Описание В тех случаях, когда два неравенства не перекрываются, составное неравенство не имеет решения Неравенства [латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс] Интервалы [латекс]\влево(-\infty,-3\вправо)[/латекс] и [латекс]\влево(3,\infty\вправо)[/латекс] График Решение неравенств, содержащих абсолютные значения
Начнем с простого неравенства.
Написание решений неравенств с абсолютными значениями
Неравенство абсолютного значения Эквивалентное неравенство Обозначение интервала [латекс]\влево|{х}\вправо|\ле{а}[/латекс] [латекс]{-a}\le{x}\le{a}[/латекс] [латекс]\влево[-а, а\вправо][/латекс] [латекс]\левый| х \право|\lt{a}[/латекс] [латекс]{-a}\lt{x}\lt{a}[/латекс] [латекс]\влево(-а, а\вправо)[/латекс] [латекс]\левый| х \право|\ge{ а}[/латекс] [латекс]{x}\le\text{−a}[/latex] или [латекс]{x}\ge{ a}[/latex] [латекс]\влево(-\infty,-a\вправо]\чашка\влево[a,\infty\вправо)[/латекс] [латекс]\левый| х \right|\gt\text{a}[/latex] [латекс]\displaystyle{x}\lt\text{−a}[/latex] или [латекс]{x}\gt{a}[/latex] [латекс]\влево(-\infty,-a\вправо)\чашка\влево(a,\infty\вправо)[/латекс] 
Определите случаи неравенств, содержащих абсолютные значения, которые не имеют решений
Резюме
