1 й замечательный предел: Первый замечательный предел. Примеры решения.

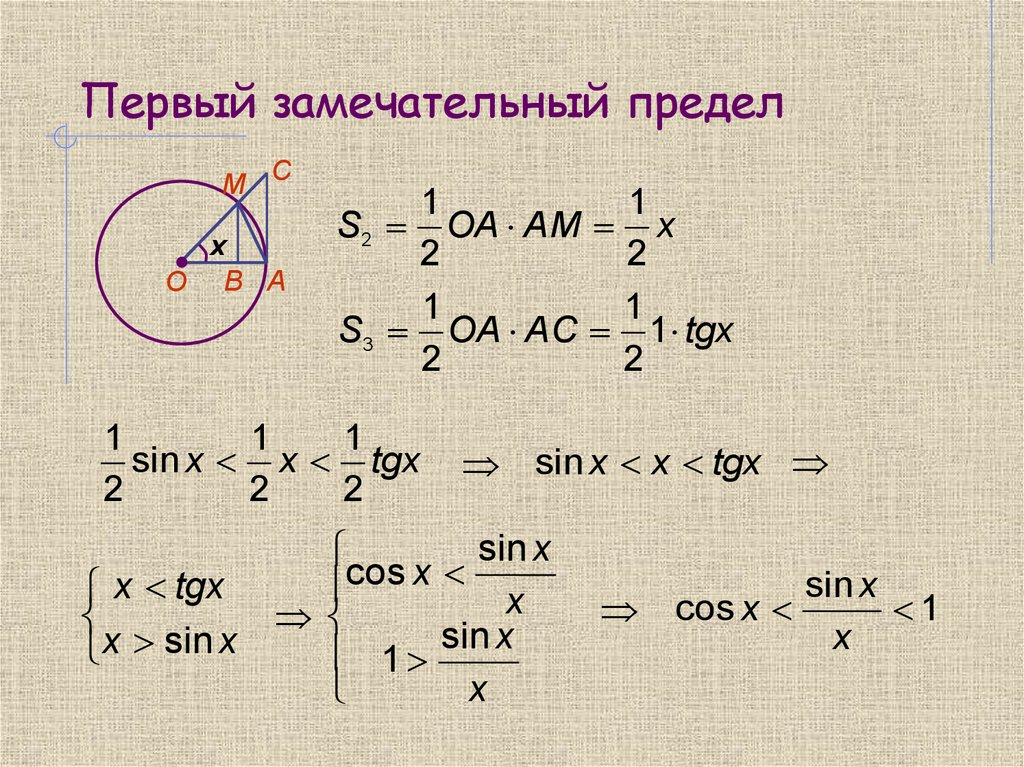
20 Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы  и  и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:  (1)(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

21 Второй замечательный предел

 или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: , поэтому

.

Если , то . Поэтому, согласно пределу , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что  для вещественного x.    

Следствия

5.  для , 

23 Сравнение функций.

Определение 15 (символ О).

 Если для функций f(x), g(x) существуют постоянные c>0, >0, такие, что |f(x)| c |g(x)| при |x-a|<, x a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x a.

Данное определение переносится и на случай, когда x, x.

Пример 12.

1. Так как |1/x²|  |1/x| при |x|  1, то 1/x² = O(1/x) при x ;

2. 1/x = O(1/x²) при x 0 так как |1/x| 1/x² при |x| 1.

Запись f=O(1) при x a означает, что функция f(x) ограничена в некоторой окрестности точки a.

Определение 16 (функции одного порядка). Если f=O(g) и g=O(f) при x a 

 f и g — одного порядка при x a.

Пример 13. Функции f(x) = x(2+sin 1/x) g(x) = x x  0 являются бесконечно малыми одного порядка при x a , так как

f/g = (x(2+sin 1/x))/x = 2+sin 1/x = |2+sin 1/x|  3  f=O(g), g/f = 1/|2+sin 1/x|  1 g=O(f).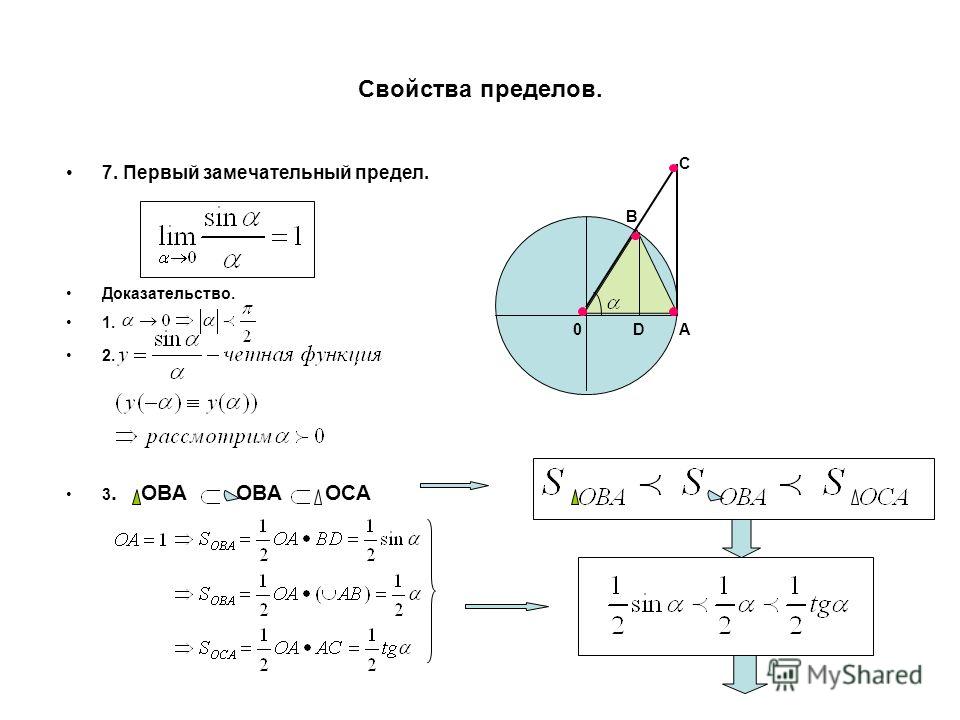

Определение 17 (эквивалентные функции). Функции f(x) и g(x) называются эквивалентными при x a, если (x): f(x) =  (x)g(x), где lim_x a (x) = 1.

Иначе говоря функции эквивалентны при x a, если предел их отношения при 

xa равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x 0

(1)

tg x ~ x, x  0, arcsin x ~ x, x  0, arctg x~ x, x  0

e^x—1~ x, x 0

ln (1+x)~ x, x0

(2)

m—1~ mx, x0

(3)

Следующая теорема удобна для применения на практике при вычислении пределов.

Теорема 7. Пусть f(x)~ f1(x), g(x)~ g1(x) при x a Тогда если существует предел

lim_x af1(x)/g1(x),

то существует

lim_x af(x)/g(x),

причем

lim_x af1(x)/g1(x) = lim_x af(x)/g(x).

Пример 14. Найти предел

lim_x 0(ln cos x)/sin x2

Решение. Для решения воспользуемся асимптотическими равенствами (1), (2)

lim_x 0(ln cos x)/sin x2 = lim_x 0 (ln(1-2sin²

x/2))/x2 =

= lim_x 0(-2sin²x/2)/x2 = -2lim_x 0(x2/4)/x2 = -1/2.

Определение 18 (символ о). Говорят, что функция f является бесконечно малой по сравнению с g при x a, и пишут f=o(g), x a, если выполнено соотношение f(x) = (x)g(x), где lim_x a (x) = 0. Иначе говоря lim_x a f(x)/g(x) = lim_x a (x) = 0.

Пример 15.

1. x2 = o(x) при x  0, так как lim_x  0x2/x = lim_x  0x = 0;

2. 1/x2 = o(1/x) при x  так как lim_x x/x2 = lim_x 1/x = 0

Справедлива теорема.

Теорема 8. Для того, чтобы функции f(x), g(x) были эквивалентными при xa необходимо и достаточно, чтобы при x a выполнялось хотя бы одно из условий

f(x) = g(x)+o(g(x))

или

g(x) = f(x)+o(f(x)).

Заметим, что функции g(x) в первом условии и соответственно функция f(x) во втором называются главной частью функции f(x) (g(x)).

Пример 16.

1. Функция x – главная часть функции sin x при x 0, так как sin x = x+o(x) при x 0;

2. Если P_n(x) = a_nxⁿ+…+a₁x+a₀, a_n 0, то функция a_nxⁿ является главной частью P_n(x) при x, так как P_n(x) = a_nxⁿ+o(xⁿ) при x.

Метод выделения главной части бесконечно малых применяется к вычислению пределов.

Пример 17. Найти предел

Решение. Используя асимптотическое равенство (3) и асимптотическое равенство (1), а также учитывая, что x2 = o(x) при x 0 (см. пример 15) и f=o(x2) является функцией o(x) при x 0, найдем

Определение 19.

 Если f=o(g) при x a и g(x) — бесконечно малая при x a, то говорят, что f(x) — бесконечно малая более высокого по сравнению с g(x) порядка при x a.

Пример 18. x²— бесконечно малая более высокого порядка по сравнению с x при x 0

Определение 20. Если f(x), g(x) -бесконечно большие при x a и f=o(g) при x a, то говорят, что g — бесконечно большая более высокого порядка по сравнению с f .

Пример 19. Функции f=x3+x2+2x+1, g=x4+3x2 -бесконечно большие при x, и так как lim_x f/g=0, то g — бесконечно большая более высокого порядка по сравнению с f

Отметим некоторые правила обращения с символами o(), O().

Предложение 2.

1. o(f)+o(f) = o(f)

2. o(f) тем более есть O(f)

3. O(f)+O(f) = O(f)

4. Если g 0

   , то o(f)/g=o(f/g), O(f)/g=O(f/g).

Второй замечательный предел — МегаЛекции

Первый замечательный предел

Рассмотрим следующий предел:

Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

Данный математический факт носит название Первого замечательного предела.

– тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция.

Важно лишь, чтобы она стремилась к нулю.

Примеры:
, , ,

Здесь , , , , и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

Теперь только осталось избавиться от трехэтажности дроби:

 

Пример 2

Найти предел

Опять мы видим в пределе дробь и синус.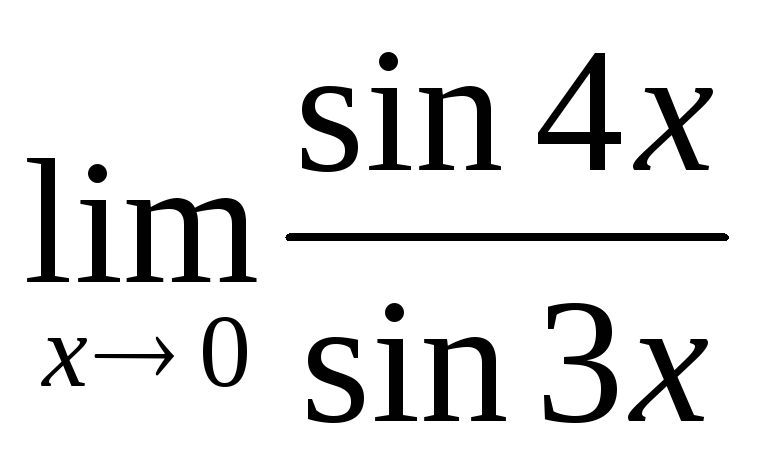 Пробуем подставить в числитель и знаменатель ноль:

Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :

Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

Собственно, ответ готов:

Пример 3

Найти предел

Подставляем ноль в выражение под знаком передела:

Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле ( В данном случае:

Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел

Пробуем подставить ноль в числитель и знаменатель:

Получена неопределенность (косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

Постоянные множители вынесем за значок предела:

Организуем первый замечательный предел:

Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

Избавимся от трехэтажности:

Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

 

Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка: – это иррациональное число.

В качестве параметра может выступать не только переменная , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение , Нетрудно заметить, что при основание степени , а показатель – , то есть имеется, неопределенность вида :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель:

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :

Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел .
Легко заметить, что в данном примере . Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :

Наконец-то долгожданное устроено, с чистой совестью превращаем его в букву :

Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово.

---

Воспользуйтесь поиском по сайту:

теория и примеры 1 замечательный предел примеры решения

Теперь со спокойной душой переходим к рассмотрению замечательных пределов .
имеет вид .

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.

Необходимо вычислить предел

Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.

Согласно нашему правилу №1 подставим вместо х ноль:

Получаем неопределенность .

Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:

Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:

Подставим решение первого замечательного примера и получаем:

Упрощаем дробь:

Ответ: 7/3.

Как видите – все очень просто.

Имеет вид , где e = 2,718281828… – это иррациональное число.

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .

Необходимо вычислить предел

Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.

Как всегда воспользуемся правилом №1 – подставим вместо х:

Видно, что при х основание степени , а показатель – 4x > , т.е. получаем неопределенность вида :

Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:

Не забываем выделять наш замечательный предел:

Вот такие действительно замечательные пределы !
Если у вас остались какие то вопросы по первому и второму замечательным пределам , то смело задавайте их в комментариях.
Всем по возможности ответим.

Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.

Мало информации? — Вы можете !

Можно писать математические вычисления в блокнотах. В блокноты с логотипом (http://www.blocnot.ru) индивидуальным писать намного приятней.

Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.

Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:

Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.

Пример 1. Найти предел .

Решение. Подстановка вместо x нуля приводит к неопределённости:

.

В знаменателе — синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:

.

В знаменателе — синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .

И приходим к разновидности первого замечательного предела:

потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.

Умножаем икс на три и тут же делим:

.

В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:

Теперь можем окончательно решить данный предел:

.

Пример 2. Найти предел .

Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:

.

Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:

.

Пример 3. Найти предел .

Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:

.

Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:

.

Пример 4. Найти предел .

Решение. Вновь получаем неопределённость «нуль делить на нуль»:

.

Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:

Пример 5. Найти предел .

Решение. И вновь неопределённость «нуль делить на нуль»:

Помним из тригонометрии, что тангенс — это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:

.

Пример 6. Найти предел .

Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.

Первый замечательный предел выглядит следующим образом: lim x → 0 sin x x = 1 .

В практических примерах часто встречаются модификации первого замечательного предела: lim x → 0 sin k · x k · x = 1 , где k – некоторый коэффициент.

Поясним: lim x → 0 sin (k · x) k · x = п у с т ь t = k · x и з x → 0 с л е д у е т t → 0 = lim t → 0 sin (t) t = 1 .

Следствия первого замечательного предела:

1. lim x → 0 x sin x = lim x → 0 = 1 sin x x = 1 1 = 1

1. lim x → 0 k · x sin k · x = lim x → 0 1 sin (k · x) k · x = 1 1 = 1

Указанные следствия достаточно легко доказать, применив правило Лопиталя или замену бесконечно малых функций.

Рассмотрим некоторые задачи на нахождение предела по первому замечательному пределу; дадим подробное описание решения.

Пример 1

Необходимо определить предел, не используя правило Лопиталя: lim x → 0 sin (3 x) 2 x .

Решение

Подставим значение:

lim x → 0 sin (3 x) 2 x = 0 0

Мы видим, что возникла неопределенность нуль делить на нуль. Обратимся к таблице неопределенностей, чтобы задать метод решения. Сочетание синуса и его аргумента дает нам подсказку об использовании первого замечательного предела, однако для начала преобразуем выражение. Произведем умножение числителя и знаменателя дроби на 3 x и получим:

lim x → 0 sin (3 x) 2 x = 0 0 = lim x → 0 3 x · sin (3 x) 3 x · (2 x) = lim x → 0 sin (3 x) 3 x · 3 x 2 x = = lim x → 0 3 2 · sin (3 x) 3 x

Опираясь на следствие из первого замечательного предела, имеем: lim x → 0 sin (3 x) 3 x = 1 .

Тогда приходим к результату:

lim x → 0 3 2 · sin (3 x) 3 x = 3 2 · 1 = 3 2

Ответ: lim x → 0 sin (3 x) 3 x = 3 2 .

Пример 2

Необходимо найти предел lim x → 0 1 — cos (2 x) 3 x 2 .

Решение

Подставим значения и получим:

lim x → 0 1 — cos (2 x) 3 x 2 = 1 — cos (2 · 0) 3 · 0 2 = 1 — 1 0 = 0 0

Мы видим неопределенность нуль делить на нуль. Произведем преобразование числителя с использованием формул тригонометрии:

lim x → 0 1 — cos (2 x) 3 x 2 = 0 0 = lim x → 0 2 sin 2 (x) 3 x 2

Видим, что теперь здесь возможно применение первого замечательного предела:

lim x → 0 2 sin 2 (x) 3 x 2 = lim x → 0 2 3 · sin x x · sin x x = 2 3 · 1 · 1 = 2 3

Ответ: lim x → 0 1 — cos (2 x) 3 x 2 = 2 3 .

Пример 3

Необходимо произвести вычисление предела lim x → 0 a r c sin (4 x) 3 x .

Решение

Подставим значение:

lim x → 0 a r c sin (4 x) 3 x = a r c sin (4 · 0) 3 · 0 = 0 0

Мы видим неопределенность делить нуль на нуль. Произведем замену:

a r c sin (4 x) = t ⇒ sin (a r c sin (4 x)) = sin (t) 4 x = sin (t) ⇒ x = 1 4 sin (t) lim x → 0 (a r c sin (4 x)) = a r c sin (4 · 0) = 0 , значит t → 0 при x → 0 .

В таком случае, после замены переменной, предел принимает вид:

lim x → 0 a r c sin (4 x) 3 x = 0 0 = lim t → 0 t 3 · 1 4 sin (t) = = lim t → 0 4 3 · t sin t = 4 3 · 1 = 4 3

Ответ: lim x → 0 a r c sin (4 x) 3 x = 4 3 .

Для более полного понимания материала статьи следует повторить материал темы «Пределы, основные определения, примеры нахождения, задачи и решения».

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формула второго замечательного предела имеет вид lim x → ∞ 1 + 1 x x = e . Другая форма записи выглядит так: lim x → 0 (1 + x) 1 x = e .

Когда мы говорим о втором замечательном пределе, то нам приходится иметь дело с неопределенностью вида 1 ∞ , т.е. единицей в бесконечной степени.

Рассмотрим задачи, в которых нам пригодится умение вычислять второй замечательный предел.

Пример 1

Найдите предел lim x → ∞ 1 — 2 x 2 + 1 x 2 + 1 4 .

Решение

Подставим нужную формулу и выполним вычисления.

lim x → ∞ 1 — 2 x 2 + 1 x 2 + 1 4 = 1 — 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 — 0 ∞ = 1 ∞

У нас в ответе получилась единица в степени бесконечность. Чтобы определиться с методом решения, используем таблицу неопределенностей. Выберем второй замечательный предел и произведем замену переменных.

t = — x 2 + 1 2 ⇔ x 2 + 1 4 = — t 2

Если x → ∞ , тогда t → — ∞ .

Посмотрим, что у нас получилось после замены:

lim x → ∞ 1 — 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t — 1 2 t = lim t → ∞ 1 + 1 t t — 1 2 = e — 1 2

Ответ: lim x → ∞ 1 — 2 x 2 + 1 x 2 + 1 4 = e — 1 2 .

Пример 2

Вычислите предел lim x → ∞ x — 1 x + 1 x .

Решение

Подставим бесконечность и получим следующее.

lim x → ∞ x — 1 x + 1 x = lim x → ∞ 1 — 1 x 1 + 1 x x = 1 — 0 1 + 0 ∞ = 1 ∞

В ответе у нас опять получилось то же самое, что и в предыдущей задаче, следовательно, мы можем опять воспользоваться вторым замечательным пределом. Далее нам нужно выделить в основании степенной функции целую часть:

x — 1 x + 1 = x + 1 — 2 x + 1 = x + 1 x + 1 — 2 x + 1 = 1 — 2 x + 1

После этого предел приобретает следующий вид:

lim x → ∞ x — 1 x + 1 x = 1 ∞ = lim x → ∞ 1 — 2 x + 1 x

Заменяем переменные. Допустим, что t = — x + 1 2 ⇒ 2 t = — x — 1 ⇒ x = — 2 t — 1 ; если x → ∞ , то t → ∞ .

После этого записываем, что у нас получилось в исходном пределе:

lim x → ∞ x — 1 x + 1 x = 1 ∞ = lim x → ∞ 1 — 2 x + 1 x = lim x → ∞ 1 + 1 t — 2 t — 1 = = lim x → ∞ 1 + 1 t — 2 t · 1 + 1 t — 1 = lim x → ∞ 1 + 1 t — 2 t · lim x → ∞ 1 + 1 t — 1 = = lim x → ∞ 1 + 1 t t — 2 · 1 + 1 ∞ = e — 2 · (1 + 0) — 1 = e — 2

Чтобы выполнить данное преобразование, мы использовали основные свойства пределов и степеней.

Ответ: lim x → ∞ x — 1 x + 1 x = e — 2 .

Пример 3

Вычислите предел lim x → ∞ x 3 + 1 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 .

Решение

lim x → ∞ x 3 + 1 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x — 1 x 3 3 2 x — 5 x 4 = = 1 + 0 1 + 0 — 0 3 0 — 0 = 1 ∞

После этого нам нужно выполнить преобразование функции для применения второго замечательного предела. У нас получилось следующее:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = 1 ∞ = lim x → ∞ x 3 — 2 x 2 — 1 — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = = lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5

lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = = lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5

Поскольку сейчас у нас есть одинаковые показатели степени в числителе и знаменателе дроби (равные шести), то предел дроби на бесконечности будет равен отношению данных коэффициентов при старших степенях.

lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 2 x 2 + 2 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = = lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 6 2 = lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 3

При замене t = x 2 + 2 x 2 — 1 — 2 x 2 + 2 у нас получится второй замечательный предел. Значит, что:

lim x → ∞ 1 + — 2 x 2 + 2 x 3 + 2 x 2 — 1 x 3 + 2 x 2 — 1 — 2 x 2 + 2 — 3 = lim x → ∞ 1 + 1 t t — 3 = e — 3

Ответ: lim x → ∞ x 3 + 1 x 3 + 2 x 2 — 1 3 x 4 2 x 3 — 5 = e — 3 .

Выводы

Неопределенность 1 ∞ , т.е. единица в бесконечной степени, является степенной неопределенностью, следовательно, ее можно раскрыть, используя правила нахождения пределов показательно степенных функций.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.

Формула

Формула первого замечательного предела имеет вид: $$ \lim_{\alpha\to 0} \frac{\sin\alpha}{\alpha} = 1 $$

Замечаем, что при $ \alpha\to 0 $ получается $ \sin\alpha \to 0 $, тем самым в числетеле и в знаменателе имеем нули. Таким образом формула первого замечательного предела нужна для раскрытия неопределенностей $ \frac{0}{0} $. 2+1 = 1 $, при $ x\to 0 $. Не выполнено второе условие, поэтому применять формулу НЕЛЬЗЯ!

Следствия

Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.

$$ \lim_{\alpha\to 0} \frac{\alpha}{\sin\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{\sin(a\alpha)}{\sin(b\alpha)} = \frac{a}{b} $$

$$ \lim_{\alpha\to 0} \frac{tg\alpha}{\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{\arcsin\alpha}{\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{arctg\alpha}{\alpha} = 1 $$

Примеры решений

Рассмотрим первый замечательный предел, примеры решения которого на вычисление пределов содержащих тригонометрические функции и неопределенность $ \bigg[\frac{0}{0}\bigg] $

Пример 1

Вычислить $ \lim_{x\to 0} \frac{\sin2x}{4x} $

Решение

Рассмотрим предел и заметим, что в нём присутствует синус. Далее подставим $ x = 0 $ в числитель и знаменатель и получим неопределенность нуль делить на нуль: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \frac{0}{0} $$ Уже два признака того, что нужно применять замечательный предел, но есть небольшой нюанс: сразу применить формулу мы не сможем, так как выражение под знаком синуса отличается от выражения стоящего в знаменателе. А нам нужно, чтобы они были равны. Поэтому с помощью элементарных преобразований числителя мы превратим его в $ 2x $. Для этого мы вынесем двойку из знаменателя дроби отдельным множителем. Выглядит это так: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \lim_{x\to 0} \frac{\sin2x}{2\cdot 2x} = $$ $$ = \frac{1}{2} \lim_{x\to 0} \frac{\sin2x}{2x} = \frac{1}{2}\cdot 1 = \frac{1}{2} $$ Обратите внимание, что в конце $ \lim_{x\to 0} \frac{\sin2x}{2x} = 1 $ получилось по формуле. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. 4} = 1 $$

Пример 4

Вычислить $ \lim_{x\to0} \frac{\sin2x}{tg3x} $

Решение

Вычисление начнём с подстановки $ x=0 $. В результате получаем неопределенность $ \frac{0}{0} $. Предел содержит синус и тангенс, что намекает на возможное развитие ситуации с использованием формулы первого замечательного предела. Преобразуем числитель и знаменатель дроби под формулу и следствие: $$ \lim_{x\to0} \frac{\sin2x}{tg3x} = \frac{0}{0} = \lim_{x\to0} \frac{\frac{\sin2x}{2x}\cdot 2x}{\frac{tg3x}{3x}\cdot 3x} = $$ Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей $$ = \lim_{x\to0} \frac{1\cdot 2x}{1\cdot 3x} = \frac{2}{3} $$

Ответ

$$ \lim_{x\to0} \frac{\sin2x}{tg2x} = \frac{2}{3} $$

В статье: «Первый замечательный предел, примеры решения» было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.

День дурака 1 апреля

«Откуда происходит обычай делать первоапрельские шутки?» Этот вопрос был задан в 1708 году в издании с чудесным названием «Британский Аполлон, или Любопытные развлечения для изобретательных». Одна из теорий состоит в том, что День дурака был просто результатом того, что он пришелся на конец зимы и приход весны. Это время обновления и возрождения было отмечено весельем и весельем, мало чем отличающимся от римского праздника Хиларии в конце марта, который отмечался переодеванием, весельем и весельем.

Безусловно, День дурака обладает всеми характеристиками такого праздника обновления, раздвигая границы повседневного поведения, но вызывая в результате беспорядок, установленный в строгих временных рамках. Например, традиционно в День дурака все розыгрыши должны прекращаться ровно в 12 часов дня, и любой, кто шутит после полудня, считается «первоапрельским шутом».

Согласно другой теории, День дурака возник во Франции 16 века, где начало Нового года первоначально отмечалось 1 апреля. После введения григорианского календаря Новый год был перенесен на 1 января, что не было повсеместно популярным. Те, кто принял новый календарь, подшучивали над теми, кто этого не сделал, и называли своих жертв «первоапрельскими дураками».

В британском фольклоре День смеха ассоциируется с Готэмом в Ноттингемшире и событием 13 века. Согласно легенде, король Джон решил «приобрести» часть земли Готэма для охотничьего домика. Естественно, это не понравилось горожанам, и поэтому они придумали хитрый план, чтобы отговорить короля. Они решили «валять дурака», поэтому, когда люди короля прибыли в город, они обнаружили, что горожане занимаются разными безумными вещами, такими как попытки утопить рыбу. Этого было достаточно, чтобы люди короля посоветовали королю выбрать другое место для своей ложи, поскольку Готэм явно был полон сумасшедших. С тех пор, согласно легенде, День дурака отмечается в память об их шутках.

Если это так, то вы ожидаете найти ссылки на День дурака с тех пор, тогда как первое упоминание не было до 1686 года, когда писатель Джон Обри упомянул «святой день дураков».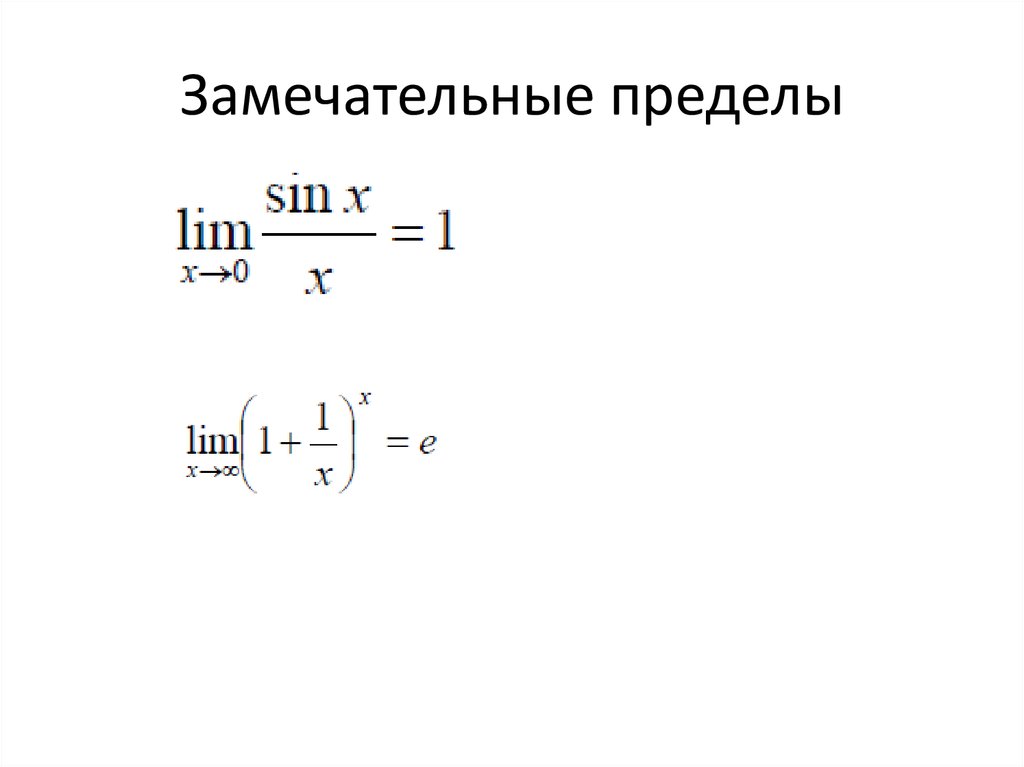 Однако похоже, что к этому времени в Британии уже прочно утвердились традиции первоапрельских праздников. В выпуске «Dawks’s News-Letter» от 2 апреля 1698 года сообщалось, что «вчера, первого апреля, несколько человек были отправлены в Тауэрский ров, чтобы посмотреть, как львов моют».

Это маловероятное событие было популярным розыгрышем в Лондоне в 18-м и 19-мвв. Ничего не подозревающих доверчивых людей пригласили на ежегодную церемонию омовения львов в лондонском Тауэре. Они отправятся в Башню, только узнают, что, конечно же, такой церемонии не было, и их послали с дурацким поручением.

Идея Дня дурака быстро распространилась по всей Британии в 18 веке. Он был особенно популярен в Шотландии, где он стал двухдневным мероприятием, начавшимся с «охоты на гуся», что означает «кукушка» или «дурак». Это повлекло за собой отправку людей с ложными поручениями, часто с посланиями следующего содержания: «Не смейся, не улыбайся. Охотьтесь на гука еще милю. Получатель отправлял посланника другому человеку с тем же сообщением и так далее. За этим последовал Tailie Day, который довольно причудливо включал в себя розыгрыши над задницами людей, например, прикреплял к ним воображаемые хвосты или записки «пни меня».

В настоящее время, когда кто-то разыгрывает первоапрельскую шутку, шутник обычно кричит «Первоапрельская шутка!». Розыгрыши могут быть очень простыми, например, отправка людей в погоню за дикими гусями, или довольно сложными, как показано в некоторых из следующих примеров.

Некоторые люди могут помнить знаменитую первоапрельскую шутку 1957 года, когда программа BBC «Панорама» показывала, как швейцарские фермеры собирают спагетти со спагетти-деревьев. BBC получила так много запросов от зрителей, которые спрашивали, где они могут купить растение для спагетти, что на следующий день им пришлось признаться в розыгрыше!

Би-би-си наслаждается хорошим розыгрышем, и в 1965 году они снова затеяли его с другим известным розыгрышем: обоняние-видение. Было объявлено о судебном процессе, согласно которому запахи должны были транслироваться вместе с обычными телешоу. Судя по всему, многие зрители объявили суд большим успехом!

Затем, в 2008 году, шутники на BBC сообщили, что во время съемок сериала «Чудеса эволюции» они засняли летающих пингвинов. Ведущий Терри Джонс из «Монти Пайтона» был показан прогуливающимся с пингвинами в Антарктиде, а затем после их полета в тропические леса Амазонки, где пингвины «проведут зиму, греясь на тропическом солнце». Видео стало вирусным в Интернете.

Газета The Guardian вступила в дело 1 апреля 1977 года, опубликовав семистраничное приложение о полностью вымышленном островном государстве Сан-Серрифе.

И в этом новом цифровом мире давайте не будем забывать об интернет-гиганте Google с его ежегодными первоапрельскими шутками!

Не могу рассказать вам, насколько замечателен SplashLearn

Робин Микер

Родитель, K, 3-й и 7-й классы

Время, потраченное Стерлингом: 17 часов

Задачи, на которые ответил Стерлинг: 4,287

Персонажи, разблокированные Стерлингом: 349

У меня трое мальчиков, старшему 12 лет, он учится в 7-м классе, среднему ребенку 8 лет, он учится в 3-м классе, и самый младший, которому 6 лет, и он находится в детском саду.

Я купил SplashLearn для четвертого класса, когда мой семиклассник учился в четвертом классе (3 года назад). Сначала я скачал бесплатную версию и сразу в нее влюбился. Я был так впечатлен тем, что он точно соответствовал математике, которую мой ребенок делал в школе. Помню, через пару недель мой ребенок пришел домой и спросил меня о дистрибутивных, коммутативных и ассоциативных свойствах. Я понятия не имел. Я обратился к SplashLearn как к опоре, и это очень помогло. Я сел с ним и угадал несколько, чтобы он сказал мне правильные ответы и почему. Мне нравятся эти функции, потому что они учат вас, почему вы даете неправильный ответ. В следующем году мы купили версию SplashLearn для 5-го класса. И я любил это так же сильно. Я чувствовал, что это идеально согласуется с тем, чему мой ребенок учился в школе. К тому времени мой средний ребенок учился в школе, и в итоге мы купили уровни для 4-го, 5-го, детского сада, 1-го и 2-го классов. Затем вы выпустили полный набор, в котором были классы от k до 5th. Я купил это для моего третьего ребенка, который сейчас в детском саду, и ему это нравится. Я был так занят событиями и жизнью, что у меня не было времени сесть и поработать с моим тогдашним Дошкольником на iPad. Признаюсь, SplashLearn помогал мне в качестве няни, когда мне нужно было время от времени его чем-то занять. Ему нравилось играть, поэтому он не возражал. Когда он был в дошкольном возрасте, он прошел уровень детского сада. (Он всегда был хорош в математике). Но в итоге он научился вещам, которым я его даже не учил. Я понял, что он учился этому на SplashLearn, и несколько раз его старшие братья учили его, как делать раздел с помощью SplashLearn. Всем родителям маленьких детей я рекомендую это приложение.

Мне нравится, как он отправляет отчеты об успеваемости по электронной почте, и я могу видеть, как далеко они продвинулись в учебном году. Например, я вижу, что моему детскому саду осталось всего 9 уровней до окончания всего 1-го класса.

Что касается K-5 Suite , нам нравится океанский аквариум против джунглей. Хотелось бы видеть больше разных видов экзотических рыб, т.е. Рыбка фугу, которая надувается, когда вы щелкаете по ней. Или морских коньков или рыб-попугаев. Или моллюсков, которые открываются и закрываются. Мы также хотели бы видеть возможность покупать фоновые предметы, такие как замки из песка, больше коралловых рифов, затонувшие сундуки с сокровищами или корабли. Было бы неплохо иметь возможность поворачивать аквариум, чтобы рассмотреть его со всех сторон. В 1 классе тоже хотелось бы увидеть дополнительные игры, а не только аквариум и джунгли.

4-й класс SplashLearn

Несмотря на то, что мой средний ребенок учится в 3-м классе, он занимается математикой в ​​4-м классе. Мне нравится раздел длинного деления, где он помогает вводить числа, чтобы вы могли видеть, находитесь ли вы на правильном пути. Это отличный инструмент для детей, которые учатся и не всегда могут вспомнить следующий шаг. Мне нравится блокнот и возможность решить проблему без дополнительной бумаги.

Игры в приложении для 4-го класса, моим детям плевать на падение каракулей, потому что они говорят, что вы слишком легко теряете жизни. Автомобильная гонка слишком сложна, потому что слишком сложно объезжать другие машины, и вы слишком легко умираете. На самом деле нам нравится давняя игра-ловушка для мышей, потому что в ней очень тяжело терять жизни. Нам нравится аквариум. Мы считаем, что игры должны быть немного более детализированными и менее архаичными. Я как родитель считаю, что должно быть ограничение по времени, в течение которого ребенок может находиться в аквариуме или в играх, прежде чем ребенок выйдет из него и ему придется вернуться к математической части.

Моему 3-класснику (играющему на уровне 4-го класса) больше всего понравился голубой мальчик-космонавт. Однако он работал над красным мальчиком, и когда он изменил внешний вид своего игрока, мы потеряли весь его успех. Это вызвало массу слез и разочарования в нашем доме. Мы считаем, что у ребенка должна быть возможность изменить внешний вид своего игрока, не теряя при этом все полученные космические корабли.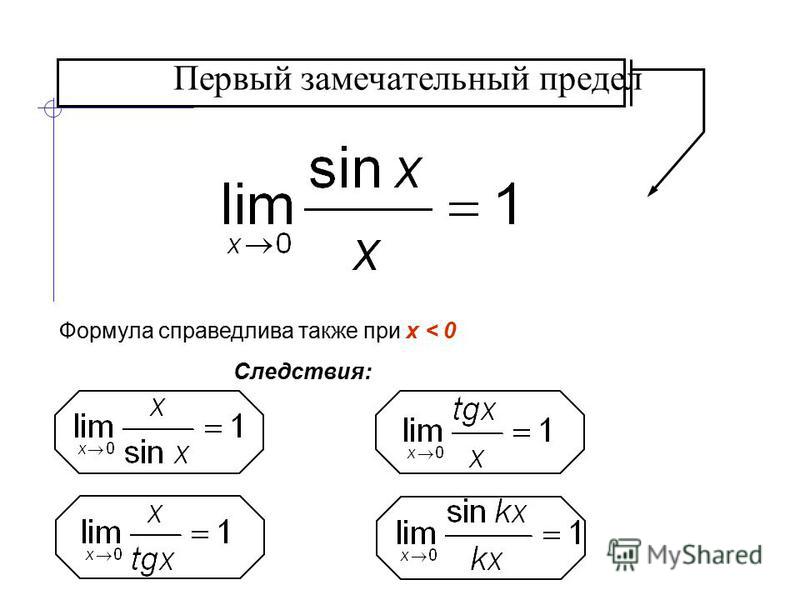

Идея игры

Мой ребенок предложил сделать игру, в которой вы находитесь на ракетном корабле и летите в космосе. У вас есть минута, чтобы увернуться от космических камней и метеоров и приземлиться на посадочную площадку. Если вы не приземлитесь успешно в течение этой минуты, вам придется вернуться и сделать больше работы, чтобы получить еще одну жизнь.

В общем, нам нравится SplashLearn. Я хотел бы, чтобы оценки продолжались до более высоких уровней, чтобы охватить детей среднего школьного возраста. Хотелось бы больше алгебры.

Спасибо за разработку SplashLearn. Я всегда рекомендую его всем знакомым матерям детей. Я также рекомендовал его учителям моих детей. Я не знаю, есть ли у вас способ для учителей, чтобы 25-30 учеников вошли в систему, но я думаю, что это отличный инструмент для учителей.

1-й Всемирный день связи, 1967

PAUL VI

MESSAGE OF THE HOLY FATHER
FOR THE WORLD SOCIAL COMMUNICATIONS DAY

Theme: Church and Social Communication:
First World Communication Day
   

We address you , дорогие братья и сыновья, приближается Всемирный день связи, который впервые состоится в воскресенье, седьмого мая.

Церковь, понимая, «что она действительно и неразрывно связана с человечеством и его историей» (1), желает посредством этой инициативы, предложенной Вторым Ватиканским Вселенским Собором, привлечь внимание своих чад и всех мужчин доброй воли к обширному и сложному феномену современных средств социальной коммуникации, таких как пресса, кино, радио и телевидение, которые составляют одну из наиболее характерных черт современной цивилизации.

Благодаря этим замечательным приемам общественная жизнь человека приобрела новые измерения: время и пространство были покорены, и человек стал как бы гражданином мира, сопричастным и свидетелем самых отдаленных событий и перипетий весь человеческий род. Как сказал Собор, «уже можно говорить об истинной социальной и культурной трансформации, которая оказывает влияние и на религиозную жизнь человека» (2). Этому преобразованию в значительной степени способствовали средства социальной коммуникации, иногда решающим образом, мы уже сейчас приближаемся к новым удивительным событиям, таким как всемирное телевидение через искусственные спутники. Во всем этом Мы видим развертывание и осуществление чудного замысла Промысла Божия, открывающего человеческому гению все новые пути достижения своего совершенства и достижения своей конечной цели.

Поэтому следует полностью отдать должное вкладу печати, кино, радио и телевидения, а также других средств общественной коммуникации в обогащение культуры, в распространение различных художественных форм, к отдыху, к взаимному познанию и взаимопониманию между народами, а также к распространению евангельской вести.

Однако, хотя масштабы этого явления, охватившего теперь и отдельных людей, и все сообщество людей, вызывают восхищение и удовлетворение, они также дают повод для размышлений и беспокойства. Эти инструменты, по самой своей природе предназначенные для распространения мысли, человеческого выражения, имиджа, информации и гласности, не только воздействуют на общественное мнение и, следовательно, на образ мыслей и действия отдельных лиц и общества. группы, но и оказывают давление на умы, оставляя глубокий след в сознании и совести человека, которого теснит и почти подавляет множество противоречивых призывов.

Нельзя игнорировать опасность и ущерб, которые эти средства, какими бы благородными они сами по себе ни были, могут нанести отдельным лицам и обществу, если они не используются человеком с чувством ответственности, с честным намерением и в соответствии с объективным моральным порядком. .

Чем больше сила и амбивалентная эффективность этих средств, тем с большей осторожностью и ответственностью они должны применяться.

Поэтому с чувством уважения, дружбы и уверенности, что Мы интерпретируем ожидания и тревоги честных людей во всем мире, мы обращаемся ко всем, кто посвящает свои способности и свою работу этому чувствительному и важному сектору современной жизни. Мы питаем надежду, что благородная служба, которую они призваны оказывать своим братьям, всегда будет соответствовать благородству миссии, делающей их посредниками и как бы хозяевами и наставниками между истиной и общественностью. реальность внешнего мира и внутренние пределы совести.

Точно так же, как они имеют право не подвергаться чрезмерному идеологическому, политическому и экономическому давлению, которое ограничивает их справедливую и ответственную свободу выражения мнений, их выступления перед публикой требуют уважения достоинства человека и общества. Пусть каждое их усилие будет направлено на распространение истины в умах людей, верность тому, что хорошо в их сердцах, и последовательность в их действиях. Таким образом, они будут способствовать возвышению человечества и будут играть конструктивную роль в построении нового общества, которое будет более свободным, более бдительным, более ответственным, более братским и более благородным (3).

Особое внимание мы уделяем молодому поколению. Не без трудностей, а иногда и с явными или реальными промахами, они стремятся направить свою настоящую и будущую жизнь. Они должны быть в состоянии сделать свой выбор в духе свободы и с чувством ответственности. Препятствовать или сбивать с пути ложными взглядами их напряженные усилия означало бы обманывать их справедливые ожидания, сбивать с толку их благородные устремления и убивать их великодушные порывы.

С отеческим сердцем Мы вновь обращаемся с настоятельным призывом к достойным членам профессионального мира социальных коммуникаций, особенно к тем из них, кто славится именем христиан, прося их нести «свидетельство в деле «Мира», что во всех своих временных выражениях должно быть верным эхом вечного, нетварного Слова, Слова Отца, Света разумов, Истины, так облагораживающей нас» (4).

Необходимо, однако, чтобы усилия работников в области социальных коммуникаций были поддержаны сплоченным сотрудничеством всех, ибо это ответственность всех, кто подвергается испытанию: ответственность родителей, которые являются первыми , незаменимые воспитатели своих детей; учителя, задачей которых является научить своих учеников знанию и пониманию языка современной техники, показывая им, как правильно оценивать то, что выдвигается, как пользоваться этими средствами разумно, с умеренностью и самодисциплиной. В игру вступает ответственность молодых людей, поскольку они призваны в высшей степени использовать эти инструменты в своем личном образовании, а также в укреплении братства и мира между людьми. Государственные органы также выполняют свои обязанности по продвижению и защите общего блага с должным уважением к подлинной свободе. Наконец, это забота всех читателей, зрителей и слушателей, поскольку они призваны тщательно и мудро выбирать свои ежедневные газеты и свои периодические издания, свои кинофильмы и свои передачи; они должны помочь сделать общение благороднее и выше, достойнее, то есть ответственных и зрелых людей.

Наиболее полезна и похвальна поэтому всякая серьезная инициатива, направленная на формирование у читателя и зрителя критического суждения и на побуждение его оценивать новости, идеи и образы, которые ему преподносятся, не только под эстетическим углом зрения. и технические аспекты, но и с человеческой, моральной и религиозной точки зрения, имея в виду высшие ценности жизни.

Церковь тоже хочет внести свой вклад в упорядоченное развитие мира социальных коммуникаций: вклад вдохновения, ободрения, увещевания, руководства и сотрудничества.

Именно по этой причине Второй Ватиканский Вселенский Собор сделал это предметом изучения: Соборное Постановление о средствах общественного общения и соответствующее пастырское наставление, которое сейчас готовится, свидетельствуют о материнской заинтересованности Церкви в содействии человеческих ценностей, которые христианство, охватывая их всем сердцем, делает более жизненными и благородными, христианство направляет их к высшей цели человека, приводя к тому, что реальный, плодотворный нравственный и духовный прогресс идет рука об руку с замечательным техническим прогрессом.

Поэтому мы выражаем надежду, что этот «День» может стать поводом для обдуманного обращения, направленного на пробуждение совести и объединенных усилий со стороны всех в таком важном деле. Мы увещеваем Наших сыновей и дочерей предпринимать щедрые действия, в молитвенном единстве намерений со своими Пастырями и со всеми, кто готов дать свое долгожданное сотрудничество, чтобы с Божьей помощью и заступничеством Пресвятой Богородицы они могли достичь тех, результатов, на достижение которых направлено празднование Всемирного дня связи на благо человечества.