Что такое модули в алгебре
Что такое модули в алгебре
Ошибка исполнения CGI приложения
Русское описание
Пользователь превысил лимит на количество одновременно исполняемых CGI. В данный момент исполнение невозможно. Попробуйте позже.
English description
Site has exceeded maximum processes limit Execution of CGI is impossible, try again later.
В случае, если вы не можете решить проблему самостоятельно — напишите о ней на support@agava. com (Unix хостинг) или w-support@agava. com (Windows хостинг)
Попробуйте позже.
Www. grandars. ru
09.11.2018 18:10:38
2018-11-09 18:10:38
Источники:
Https://www. grandars. ru/student/vysshaya-matematika/modul-chisla. html
Модули — Математика — Теория, тесты, формулы и задачи — Обучение Математике, Онлайн подготовка к ЦТ и ЕГЭ. » /> » /> .keyword { color: red; }
Что такое модули в алгебре
Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:
Из определения следует, что:
Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Основные свойства модуля:
Некоторые методы решения уравнений с модулями
Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:
Предпочтительным способом решения будет переход к совокупности:
А для уравнений вида:
Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак.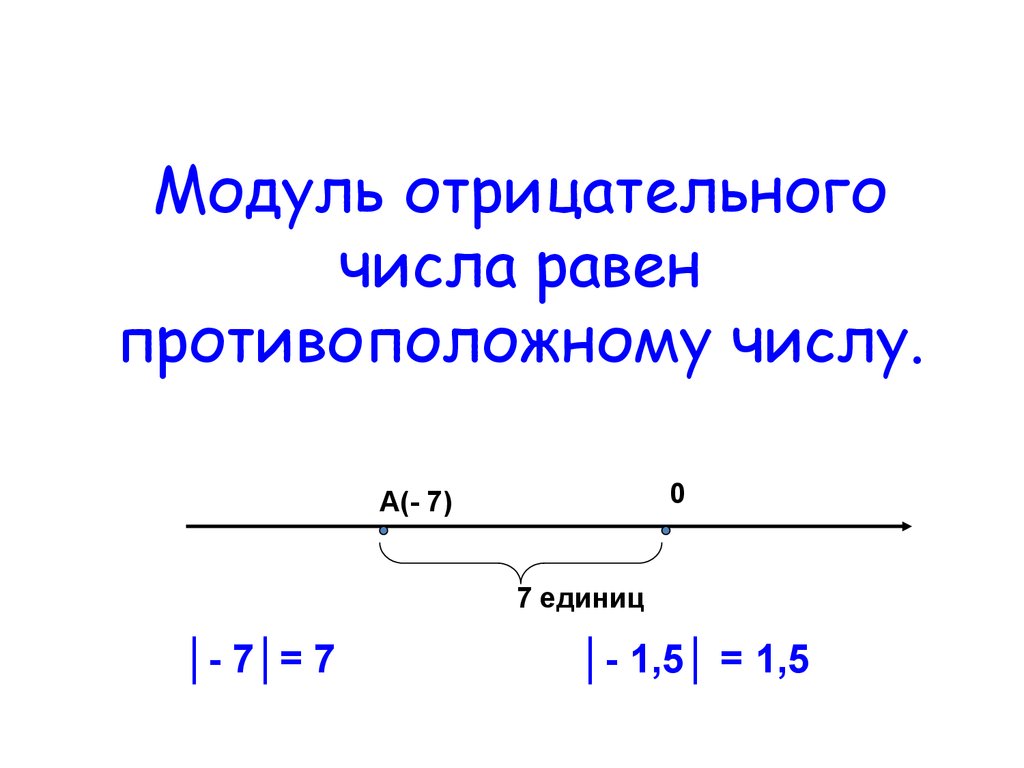 В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:
В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:
Для решения уравнений в которых содержится более чем один модуль применяется Метод интервалов, который состоит в следующем:
- Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем. Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять. Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.

Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Что такое модули в алгебре.
Educon. by
04.02.2017 14:39:18
2017-02-04 14:39:18
Источники:
Https://educon. by/index. php/materials/math/moduli
Модуль числа. Свойства модуля » /> » /> .keyword { color: red; }
Что такое модули в алгебре
Обозначим на координатной прямой две точки, которые соответствуют числам « −4 » и 2 .
Точка « A », соответствующая числу « −4 », находится на расстоянии 4 единичных отрезков от точки 0 (начала отсчёта), то есть длина отрезка « OA » равна 4 единицам.
Число 4 (длина отрезка « OA ») называют модулем числа « −4 ».
Обозначают Модуль числа так: |−4| = 4
Читают символы выше следующим образом: «модуль числа минус четыре равен четырём».
Точка « B », соответствующая числу « +2 », находится на расстоянии двух единичных отрезков от начала отсчёта, то есть длина отрезка « OB » равна двум единицам.
Число 2 называют модулем числа « +2 » и записывают: |+2| = 2 или |2| = 2 .
Если взять некоторое число « a » и изобразить его точкой « A » на координатной прямой, то расстояние от точки « A » до начала отсчёта (другими словами длина отрезка « OA ») и будет называться модулем числа « a ».
Запомните!
Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным.
Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи.
Модуль числа.
Math-prosto. ru
22.03.2017 3:02:16
2017-03-22 03:02:16
Источники:
Https://math-prosto. ru/ru/pages/modulus/modulus_of_number/
Модуль числа – что это такое: что значит абсолютная величина
В школе на уроке математики каждый год ученики разбирают новые темы. 6 класс обычно изучает модуль числа – это важное понятие в математике, работа с которым встречается далее в алгебре и высшей математики. Очень важно изначально правильно понять объяснение термина и разобраться в этой теме, чтобы успешно проходить прочие темы.
Оглавление
- Величины в математике
- Что такое модуль числа?
- Полезное видео: что такое модуль действительного числа?
- Свойства
- В уравнениях
- Полезное видео: модуль действительного числа и его свойства
- Вывод
Величины в математике
Для начала следует понимать, что абсолютная величина – это параметр в статистике (измеряется количественно), который характеризует изучаемое явление по его объему.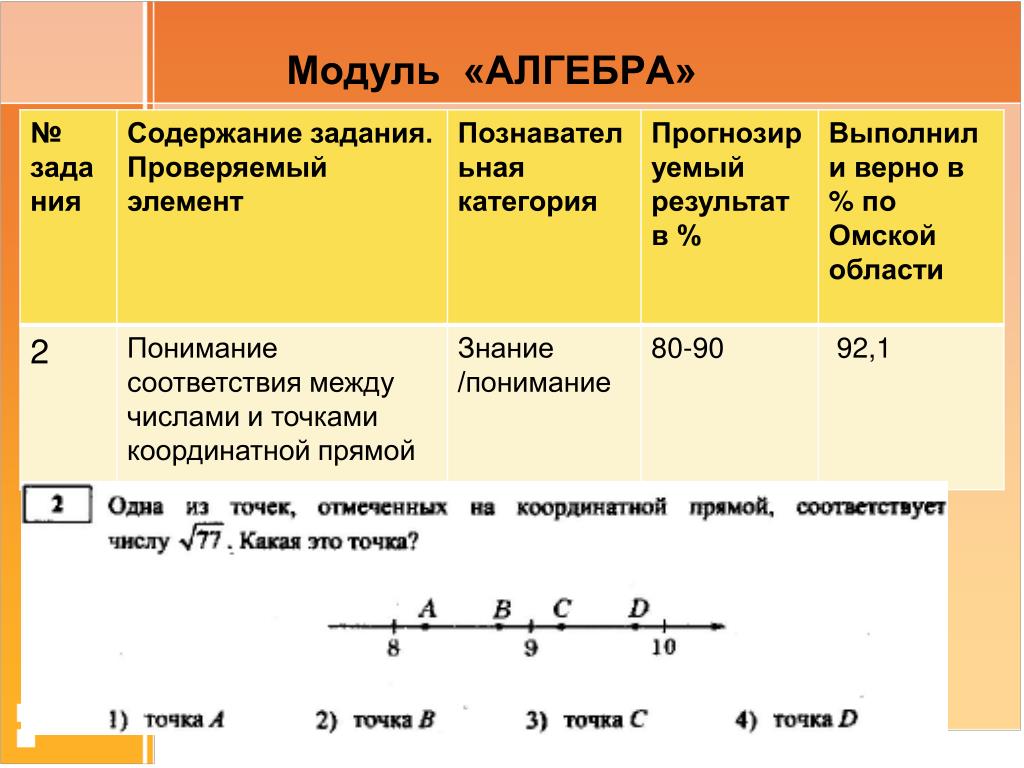 При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:
При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:
- суммарные – подходят для группы единиц или полностью всей совокупности;
- индивидуальные – подходят только для работы с единицей некой совокупности.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Понятия широко используются в статистических измерениях, результатом которых являются показатели, характеризующие абсолютные размеры у каждой единицы некоего явления. Измеряются они в двух показателях: натуральном, т.е. физические единицы (шт., люди) и условно-натуральном. Модуль в математике является отображением данных показателей.
Модуль числа
Что такое модуль числа?
Важно! Данное определение «module» с латыни переводиться как «мера» и означает абсолютную величину любого натурального числа.
Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.
Для того, чтобы определить данный показатель у числа, следует не учитывать его знак (минус, плюс), но при этом следует помнить то, что он никогда не может быть отрицательным. Данное значение на бумаге выделяется графически в виде квадратных скобок — |a|. При этом, математическое определение такое:
|х| = х, если х больше или равен нулю и -х, если меньше нуля.
Английский ученый Р. Котес был тем человеком, кто впервые применил данное понятие в математических расчетах. А вот К. Вейерштрасс, математик из Германии, придумал и ввел в использование графический символ.
Это интересно! Как разложить на множители квадратный трехчлен: формула
В геометрии module можно рассмотреть на примере координатной прямой, на которое нанесены 2 произвольные точки. Предположим, одна — А имеет значение 5, а вторая В — 6. При подробном изучении чертежа станет ясно, что расстояние от А до В – 5 единиц от нуля, т.е. начала координат, а точка В размещена от начала координат на 6 единиц. Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.
Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.
Полезное видео: что такое модуль действительного числа?
Свойства
Как у любого математического понятия, у module есть свои математические свойства:
- Он всегда положительный, поэтому модулем положительного значения будет оно само, например, модуль числа 6 и -6 равен 6. Математически это свойство можно записать как |a| = a, при a> 0;
- Показатели противоположных чисел равны между собой. Это свойство понятнее в геометрическом изложении, поскольку на прямой данные числа располагаются в разных местах, но при этом от начала отсчета их отделяет равное количество единиц. Математически это записывается так: |а| = |-а|;
- Модуль нуля равен нулю, при условии, что действительное число – это ноль.
 Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0;
Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0; - Если требуется найти модуль двух умножающихся цифр, стоит понимать, что он будет равен полученному произведению. Другими словами, произведение величин А и В = АВ, при условии, что они положительные или же отрицательные, и тогда произведение равняется -АВ. Графически это можно записать как |А*В| = |А| * |В|.
Это интересно! Считаем правильно: как находить процент от суммы и числа
Успешное решение уравнений с модулем зависит от знания данных свойств, которое поможет любому правильно вычислять и работать с данным показателем.
Свойства модуля
Важно! Показатель не может быть отрицательным, поскольку он определяет расстояние, которое всегда положительное.
В уравнениях
В случае работы и решения математических неравенств, в которых присутствует module, всегда необходимо помнить, что для получения итогового правильного результата следует раскрыть скобки, т. е. открыть знак module. Зачастую, в этом и есть смысл уравнения.
е. открыть знак module. Зачастую, в этом и есть смысл уравнения.
При этом стоит помнить, что:
- если в квадратных скобках записано выражение, его необходимо решить: |А + 5| = А + 5, при А больше или равным нулю и 5-А, в случае А меньше нуля;
- квадратные скобки чаще всего должны раскрываться независимо от значений переменной, например, если в скобках заключено выражение в квадрате, поскольку при раскрытии в любом случае будет положительное число.
Это интересно! Уроки математики: умножение на ноль — главное правило
Очень легко решаются уравнения с module путем занесения значений в систему координат, поскольку тогда легко увидеть визуально значения и их показатели.
Полезное видео: модуль действительного числа и его свойства
Вывод
Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.
Модуль числа — Математика и Английский
Модуль 5 математика
Обозначим на координатной прямой две точки, которые соответствуют числам « −4 » и 2 .
Точка « A », соответствующая числу « −4 », находится на расстоянии 4 единичных отрезков от точки 0 (начала отсчёта), то есть длина отрезка « OA » равна 4 единицам.
Число 4 (длина отрезка « OA ») называют модулем числа « −4 ».
Обозначают Модуль числа так: |−4| = 4
Читают символы выше следующим образом: «модуль числа минус четыре равен четырём».
Точка « B », соответствующая числу « +2 », находится на расстоянии двух единичных отрезков от начала отсчёта, то есть длина отрезка « OB » равна двум единицам.
Число 2 называют модулем числа « +2 » и записывают: |+2| = 2 или |2| = 2 .
Если взять некоторое число « a » и изобразить его точкой « A » на координатной прямой, то расстояние от точки « A » до начала отсчёта (другими словами длина отрезка « OA ») и будет называться модулем числа « a ».
Запомните!
Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным.
Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи.
Точка B, соответствующая числу 2 , находится на расстоянии двух единичных отрезков от начала отсчёта, то есть длина отрезка OB равна двум единицам.
Math-prosto. ru
24.06.2019 15:00:17
2019-06-24 15:00:17
Источники:
Https://math-prosto. ru/ru/pages/modulus/modulus_of_number/
Модуль числа, определение и свойства » /> » /> .keyword { color: red; }
Модуль 5 математика
Разберем сегодня, что значит модуль числа, как считать модуль и как обозначается модуль в математике. А также его свойства и, конечно же, примеры.
О чем эта статья:
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным.
2. Модуль положительного числа равен самому числу.
- |a| = a, если a > 0
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
- |0| = 0, если a = 0
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
- |a b| = |a| |b|, когда
−(a · b), когда a · b
7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.
Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Отметим на числовой прямой точки, удовлетворяющие этому условию.
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.
Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:
Ответ в данном случае будет таким: (−11; −3).
Решим неравенство: |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.
При этом, √ a 2 = |a|.
По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .
Оно равно a при а > 0 и −а, при а
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.
При этом, √ a 2 = |a|.
По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .
Оно равно a при а > 0 и −а, при а
Точка В, которая соответствует числу 3, находится на расстоянии 3 единичных отрезков от точки O то есть от начала отсчёта.
Skysmart. ru
19.09.2017 11:28:58
2017-09-19 11:28:58
Источники:
Https://skysmart. ru/articles/mathematic/modul-chisla
Математика 6 Мерзляк Тест 5 Ответы. 14 вопросов 4 варианта » /> » /> .keyword { color: red; }
14 вопросов 4 варианта » /> » /> .keyword { color: red; }
Модуль 5 математика
Математика 6 Мерзляк Тест 5 (вариант 1) + ОТВЕТЫ (варианты 1-4) на тему «Сравнение, сложение, вычитание рациональных чисел. Модуль числа». Тестовые задания используются в комплекте с учебником «
Тест 5. Сравнение, сложение, вычитание
Рациональных чисел. Модуль числа.
(УМК Мерзляк) Вариант 1
Сколько целых чисел удовлетворяют неравенству –7
1) 10 2) 12 3) 11 4) 9 Укажите число, имеющее наименьший модуль.
1) –15,78 2) 7,5 3) 56,567 4) –3у Вычислите |–9| + |9|.
1) –18 2) 0 3) 18 4) 9 Укажите верное неравенство.
1) 8,6 –100 4) –3,8 > –3,2 Решите уравнение |х| = –8.
1) –8,8 2) 8 3) –8 4) корней нет Вычислите –6,2 + 2,6.
1) –8,8 2) –3,6 3) 3,6 4) 8,8 Вычислите 2,3 – 4,42.
1) 2,12 2) 6,72 3) –2,12 4) –6,72 Укажите верное утверждение.
1) –7 – целое число;
2) противоположные числа имеют одинаковые модули;
3) точка с положительной координатой может лежать левее нуля;
4) сумма двух отрицательных чисел может равняться нулю Температура воздуха в 9 часов утра составляла –9°.
1) –19° 2) 1° 3) 5° 4) –5° Между какими соседними целыми числами на координатной прямой расположено число –7 3 /5 ?
1) –8 и –7 2) –7 и –6 3) –6 и –5 4) 7 и 8 Какие числа удалены от числа 6 на 8 единиц?
1) 14 2) –2 3) –2 и 14 4) 7 Найдите значение а, при котором корнями уравнения |х – а + 5| = 7 являются противоположные числа. Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству 5 Математика 6 Мерзляк Тест 5
Вариант 1. ОТВЕТЫ:
№ 1. Сколько целых чисел удовлетворяют неравенству –7 Ответ: 3) 11.
№ 2. Укажите число, имеющее наименьший модуль. Ответ: 4) –3у.
№ 3. Вычислите |–9| + |9|. Ответ: 3) 18.
№ 4. Укажите верное неравенство.
№ 5. Решите уравнение |х| = –8. Ответ: 4) корней нет
Ответ: 4) корней нет
№ 6. Вычислите –6,2 + 2,6. Ответ: 2) –3,6.
№ 7. Вычислите 2,3 – 4,42. Ответ: 3) –2,12.
№ 8. Укажите верное утверждение. Ответ: 1) –7 – целое число; 2) противоположные числа имеют одинаковые модули.
№ 9. Температура воздуха в 9 часов утра составляла –9°. К 10 часам она изменилась на –3°, к 11 часам – на 5°, к 12 часам – на 2°. Найдите температуру воздуха в 12 часов. Ответ: 4) –5°.
№ 10. Между какими соседними целыми числами на координатной прямой расположено число –7 3 /5 ? Ответ: 1) –8 и –7.
№ 11. Какие числа удалены от числа 6 на 8 единиц? Ответ: 3) –2 и 14.
№ 12. Найдите значение а, при котором корнями уравнения |х – а + 5| = 7 являются противоположные числа. Ответ: 5.
№ 13. Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству 5 Ответ: (См. рис. в спойлере)
№ 14. Длина отрезка АВ равна 8,7. Известно, что А(–4,9). Найдите координату точки Б, если точка В находится ближе к началу отсчета, чем точка А. Ответ: 3,8.
Математика 6 Мерзляк Тест 5
ОТВЕТЫ на все варианты
Вы смотрели: Математика 6 Мерзляк Тест 5 с ответами «Сравнение, сложение, вычитание рациональных чисел. Модуль числа». Цитаты из пособия для учащихся «Тесты по математике 6 класс к новому учебнику А. Г. Мерзляк ФГОС / Т. М. Ерина — М.: Издательство Экзамен» использованы в учебных целях. Ответы опубликованы на все 4 варианта и адресованы родителям.
Похожие записи
Алгебра 9 Мерзляк С-27 В1
Самостоятельная работа № 27 по алгебре в 9 классе «Сумма n первых членов арифметической прогрессии» с.
Математика 6 Мерзляк Тест 5 (вариант 1) + ОТВЕТЫ (варианты 1-4) на тему «Сравнение, сложение, вычитание рациональных чисел.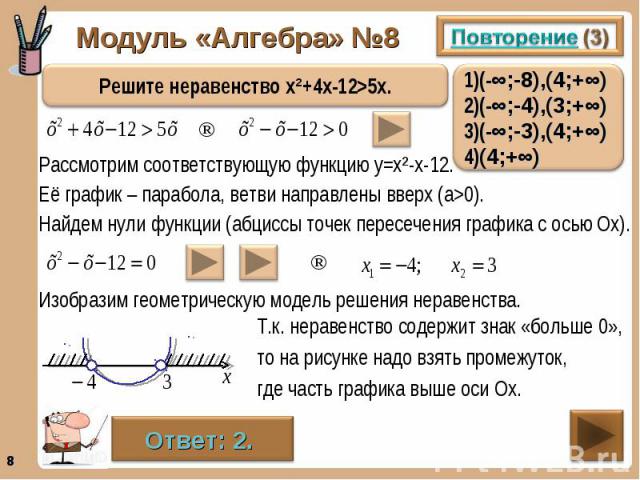 Модуль числа». Тестовые задания используются в комплекте с учебником «Математика 6 класс» авторов: А. Г. Мерзляк и др.
Модуль числа». Тестовые задания используются в комплекте с учебником «Математика 6 класс» авторов: А. Г. Мерзляк и др.
Сколько целых чисел удовлетворяют неравенству –7
1) 10 2) 12 3) 11 4) 9 Укажите число, имеющее наименьший модуль.
1) –15,78 2) 7,5 3) 56,567 4) –3у Вычислите |–9| + |9|.
1) –18 2) 0 3) 18 4) 9 Укажите верное неравенство.
1) 8,6 –100 4) –3,8 > –3,2 Решите уравнение |х| = –8.
1) –8,8 2) 8 3) –8 4) корней нет Вычислите –6,2 + 2,6.
1) –8,8 2) –3,6 3) 3,6 4) 8,8 Вычислите 2,3 – 4,42.
1) 2,12 2) 6,72 3) –2,12 4) –6,72 Укажите верное утверждение.
1) –7 – целое число;
2) противоположные числа имеют одинаковые модули;
3) точка с положительной координатой может лежать левее нуля;
4) сумма двух отрицательных чисел может равняться нулю Температура воздуха в 9 часов утра составляла –9°. К 10 часам она изменилась на –3°, к 11 часам – на 5°, к 12 часам – на 2°. Найдите температуру воздуха в 12 часов.
1) –19° 2) 1° 3) 5° 4) –5° Между какими соседними целыми числами на координатной прямой расположено число –7 3 /5 ?
1) –8 и –7 2) –7 и –6 3) –6 и –5 4) 7 и 8 Какие числа удалены от числа 6 на 8 единиц?
1) 14 2) –2 3) –2 и 14 4) 7 Найдите значение а, при котором корнями уравнения |х – а + 5| = 7 являются противоположные числа. Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству 5 Математика 6 Мерзляк Тест 5 Вариант 1. ОТВЕТЫ:
Изобразите на координатной прямой множество чисел, удовлетворяющих неравенству 5 Математика 6 Мерзляк Тест 5 Вариант 1. ОТВЕТЫ:
1 8,8 2 3,6 3 3,6 4 8,8.
Xn—b1agatflbfbtgq5jm. xn--p1ai
22.02.2018 4:26:18
2018-02-22 04:26:18
Источники:
Https://xn--b1agatflbfbtgq5jm. xn--p1ai/matematika-6-merzljak-test-5/
абстрактная алгебра — Что такое $R$-модуль?
Спросил
Изменено 10 лет, 4 месяца назад
Просмотрено 7к раз
$\begingroup$
Из Википедии:
«Если $R$ коммутативен, то левые $R$-модули совпадают с правыми $R$-модулями и называются просто $R$-модулями.»
Определение левого $R$-модуля: $M$ — левый $R$-модуль, если $M$ — абелева группа и $R$ — кольцо, действующее на $M$ такое, что
(i) $r(m_1 + m_2) = rm_1 + rm_2$
(ii) $(r_1 + r_2 ) m = r_1 m + r_2 m$
(iii) $1m = m$
(iv) ) $r_1 (r_2m) = (r_1 r_2) m$
Я не понимаю, при чем здесь коммутативность $R$, когда модуль бывает левым и правым. Если $R$ коммутативно, это означает, что $r_1 r_2 = r_2 r_1$. Как же из этого следует, что $rm = mr$? $M$ не является подмножеством $R$, это может быть что угодно, так как же коммутативность $R$ заставляет элементы $M$ и $R$ также коммутировать?
Если $R$ коммутативно, это означает, что $r_1 r_2 = r_2 r_1$. Как же из этого следует, что $rm = mr$? $M$ не является подмножеством $R$, это может быть что угодно, так как же коммутативность $R$ заставляет элементы $M$ и $R$ также коммутировать?
- абстрактная алгебра
- модули
$\endgroup$
3
$\begingroup$
Определение правого модуля $R$ аналогично, за исключением того, что элементы $R$ записываются справа, а аксиомы становятся
(i) $(m_1 + m_2)r = m_1r + m_2r$
(ii ) $m(r_1 + r_2 ) = mr_1 + mr_2 $
(iii) $m1 = m$
(iv) $(mr_1) r_2 = m(r_1 r_2)$
Если $R$ — коммутативное кольцо и $M$ — левый $R$-модуль, то мы можем определить правый $R$-модуль $M’$, который является той же абелевой группой, что и $M$, и с по существу тем же действием, но с элементами $R $ действует справа: а именно, если $rm$ является результатом действия $r\in R$ на $m\in M$, то мы определяем действие $R$ на $M’$ как $mr = rm $.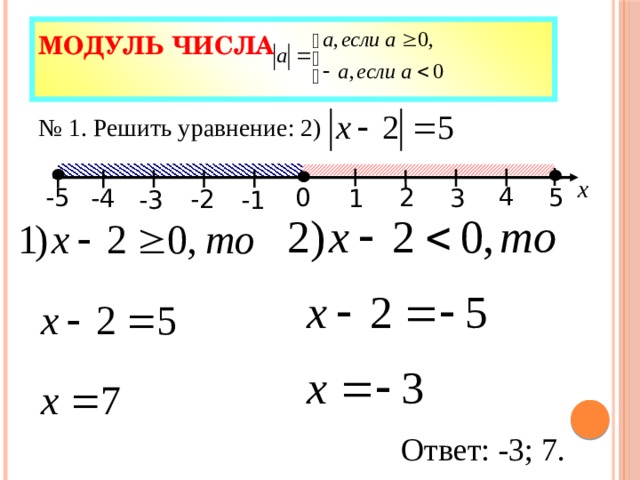 (То есть вопрос не в том, «истинно» ли $mr=rm$; скорее, мы определяем, что это так.) Тогда можно проверить, что $M’$ удовлетворяет аксиомам, и существует ничего не теряется при переходе от $M$ к $M’$ или наоборот. Коммутативность необходима для аксиомы (iv). Именно это имеется в виду в Википедии.
(То есть вопрос не в том, «истинно» ли $mr=rm$; скорее, мы определяем, что это так.) Тогда можно проверить, что $M’$ удовлетворяет аксиомам, и существует ничего не теряется при переходе от $M$ к $M’$ или наоборот. Коммутативность необходима для аксиомы (iv). Именно это имеется в виду в Википедии.
Однако следует быть осторожным. Если $M$ — левый $R$-модуль, то $M$ как абелевой группе может быть задано действие правого $R$-модуля, которое не получается из действия левого таким образом, даже если $R$ коммутативный. Поэтому в некоторых контекстах, где рассматривается более одного действия, может быть полезно обозначить левый и правый модули даже коммутативных колец.
$\endgroup$
$\begingroup$
Учитывая кольцо $R$, напротив 9{оп}$; в этом случае левый и правый $R$-модули «одинаковы».
[Редактировать: мой ответ не добавляет ничего нового к ответу Джонаса, но я думаю, что термин напротив кольца заслуживает упоминания в этой теме. ]
]
$\endgroup$
$\begingroup$
Что хочет сказать Википедия:
Если $R$ — коммутативное кольцо, а $M$ — правый $R$-модуль, то закон $r\cdot m:=mr$ определяет структуру левого $R$-модуля на $M$.
Итак, все утверждения о правых $R$-модулях очень легко превратить в утверждения о левых $R$-модулях, написав умножение слева. Следовательно, мы ничего не теряем, если будем изучать только левые $R$-модули.
Убедитесь, что вы понимаете, что обычно это не так, если $R$ некоммутативен.
$\endgroup$
$\begingroup$
Для правого модуля умножение обычно записывается со скаляром справа, и аксиома (iv) принимает вид $(mr_1)r_2=m(r_1r_2)$. Если бы вы записали произведение со скаляром слева, аксиома (iv) стала бы весьма неудобной: $r_1(r_2m)=(r_2r_1)m$. Но, конечно, если $R$ коммутативно, это не имеет значения.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
модулей / Бенджамин Р. Брей
Опубликовано в математике 13 мая 2020 г.
Содержание
- Векторное пространство над полем
- Модуль над кольцом
- Модули над кольцом многочленов F[x]\FF[x]F[x]
- Гомоморфизмы модулей
- Кольцо модульных эндоморфизмов
- Частные модули
- Бесплатные модули
- Универсальное свойство бесплатных модулей
Векторное пространство над полем
Векторные пространства над полем — это частный случай более общего понятия модулей над кольцом. Обычно в учебниках векторное пространство определяется как множество, снабженное двумя операциями, которые подчиняются длинному списку аксиом:0005
(абстрактное) векторное пространство (V,F,+,⋅)(V,\mathbb{F},+,\cdot)(V,F,+,⋅) состоит из
- поля F\ mathbb{F}F, элементы которого называются скалярами
- Набор ВВВ, элементы которого называются (абстрактными) векторами
- Правило (+):V×V→V(+) : V \times V \rightarrow V(+):V×V→V для сложения векторов , удовлетворяющее
- (ассоциативность) u+(v+w)=(u+v)+wu+(v+w)=(u+v)+wu+(v+w)=(u+v)+w
- (коммутативность) u+v=v+uu+v = v+uu+v=v+u
- (аддитивная идентичность) существует 0∈V0 \in V0∈V с v+0=vv + 0 = vv+0=v для всех v∈Vv \in Vv∈V
- (аддитивная обратная) для всех v∈Vv \in Vv∈V существует (−v)∈V(-v) \in V(−v)∈V с v+(−v)=0v + (-v) = 0в+(-в)=0
- Правило (⋅): F×V→V(\cdot) : \mathbb{F} \times V \rightarrow V(⋅):F×V→V для скалярного умножения , удовлетворяющее
- (скалярное тождество) 1F⋅v=v1_F \cdot v = v1F⋅v=v для всех v∈Vv \in Vv∈V
- (совместимость) (αβ)v=α(β(v))(\alpha\beta) v = \alpha(\beta(v))(αβ)v=α(β(v))
- (распределяет по сложению векторов) α(v+w)=αv+αw\alpha (v + w) = \alpha v + \alpha wα(v+w)=αv+αw
- (распределяет по добавлению поля) (α+β)v=αv+βv(\alpha + \beta) v = \alpha v + \beta v(α+β)v=αv+βv
Мы можем сформулировать эти свойства более кратко, заметив, что свойство III эквивалентно требованию, чтобы (V,+)(V,+)(V,+) образовывала коммутативную группу.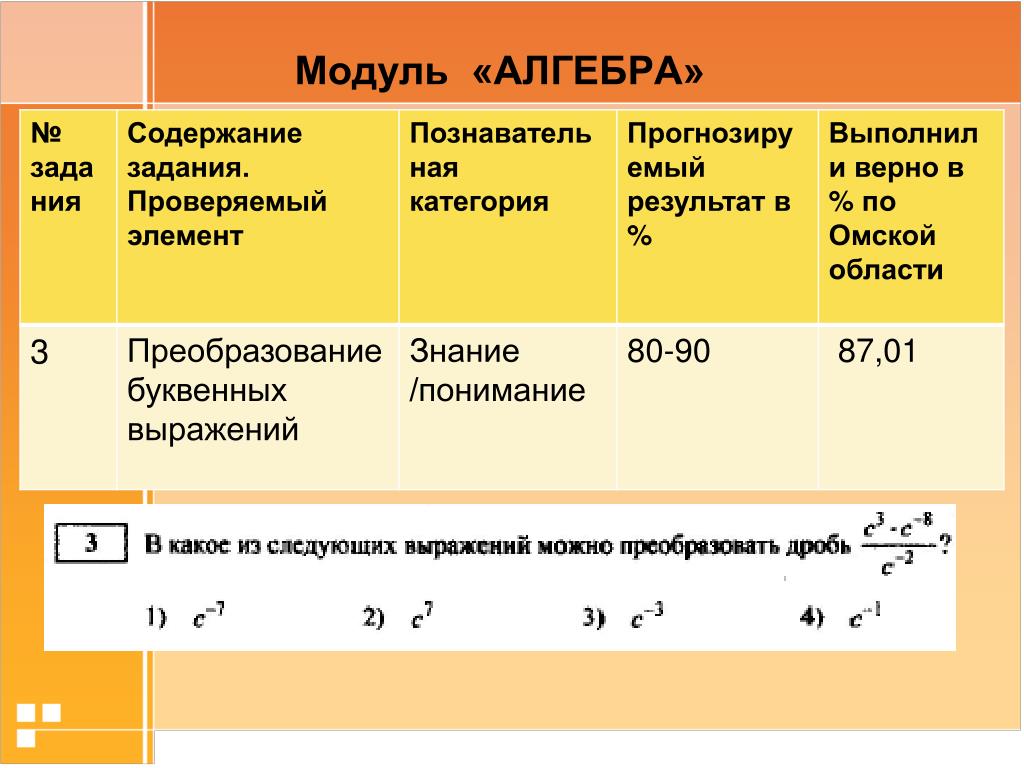
(абстрактное) векторное пространство над полем F\FFF является коммутативной группой (V,+)(V,+)(V,+) вместе с правилом (⋅):F×V→V(\cdot ) : \FF \times V \rightarrow V(⋅):F×V→V, удовлетворяющий
- (скалярное тождество) 1F⋅v=v1_F \cdot v = v1F⋅v=v для всех v∈Vv \in Vv∈V
- (совместимость) (αβ)v=α(β(v))(\alpha\beta) v = \alpha(\beta(v))(αβ)v=α(β(v))
- (распределяет над сложением) α(v+w)=αv+αw\alpha (v + w) = \alpha v + \alpha wα(v+w)=αv+αw
- (распределяет по добавлению поля) (α+β)v=αv+βv(\alpha + \beta) v = \alpha v + \beta v(α+β)v=αv+βv
Определения 1a и 1b представляют множество VVV в качестве основного объекта интереса, отодвигая скаляры F\FFF на второй план. Ключ к пониманию модулей состоит в том, чтобы перевернуть эту презумпцию с ног на голову, вместо этого рассматривая F\FFF как выделенный объект.
Частичным применением масштабного оператора (⋅): F×V→V(\cdot) : \FF \times V \rightarrow V(⋅):F×V→V, каждый скаляр α∈F\alpha \in \ FFα∈F соответствует линейному отображению φa:v↦αv\varphi_a : v \mapsto \alpha vφa:v↦αv из VVV в себя. Линейные отображения в себя на VVV образуют кольцо эндоморфизмов (End(V),+,∘)(\End(V), +, \circ)(End(V),+,∘), операции которого суть поточечное сложение и функция сочинение. Аксиомы векторного пространства гарантируют, что отображение φ⊡:F→(V→V)\varphi_\boxdot : \FF\rightarrow (V \rightarrow V)φ⊡:F→(V→V) из элементов поля в линейное само -maps является кольцевым гомоморфизмом. Мы приходим к нашему третьему и последнему определению,
Линейные отображения в себя на VVV образуют кольцо эндоморфизмов (End(V),+,∘)(\End(V), +, \circ)(End(V),+,∘), операции которого суть поточечное сложение и функция сочинение. Аксиомы векторного пространства гарантируют, что отображение φ⊡:F→(V→V)\varphi_\boxdot : \FF\rightarrow (V \rightarrow V)φ⊡:F→(V→V) из элементов поля в линейное само -maps является кольцевым гомоморфизмом. Мы приходим к нашему третьему и последнему определению,
(абстрактное) векторное пространство над полем F\FFF является коммутативной группой (V,+)(V,+)(V,+) вместе с кольцевым гомоморфизмом φ:F→End(V)\varphi : \FF \rightarrow \mathrm{Конец}(V)φ:F→Конец(V).
Кольцевой гомоморфизм определяет аддитивные и мультипликативные групповые действия на VVV скалярами из поля F\FFF.
Модуль над кольцом
Для модулей требуется только, чтобы множество, действующее на VVV, было кольцом, а не полем.
А модуль над кольцом RRR является коммутативной группой (M,+)(M,+)(M,+) вместе с кольцевым гомоморфизмом φ:R→End(M)\varphi : R \rightarrow \End(M)φ: R→End(M), определяющий действие RRR на MMM, где End(M)\End(M)End(M) — множество гомоморфизмов групп M→MM \rightarrow MM→M.
Модули над кольцом RRR для краткости называются RRR-модулями . RRR-модуль называется левым , если он возникает из левого действия, и правым в противном случае. Что касается векторных пространств, мы могли бы развернуть это определение в список аксиом, но это запутало бы истинное назначение модулей: многие математические объекты являются кольцами, а модули позволяют нам изучать кольца по их действию на множестве (так же, как мы можем изучать группы через их представления).
Пусть МММ — RRR-модуль. RRR-подмодуль в МММ — это замкнутая относительно действия кольца подгруппа N⩽(M,+)N \подгруппа (M,+)N⩽(M,+), rn∈Nrn \in Nrn∈N при r∈ Rr \in Rr∈R, n∈Nn \in Nn∈N.
Ниже перечислены несколько важных примеров модулей.
- Если F\FFF является полем, то F\FFF-модули и F\FFF-векторные пространства идентичны.
- Каждое кольцо RRR является RRR-модулем над собой. В частности, каждое поле F\FFF является F\FFF-векторным пространством.
 Подмодули RRR как поля над собой являются идеалами. 9\infty(\mathcal{M})C∞(M)-модуль.
Подмодули RRR как поля над собой являются идеалами. 9\infty(\mathcal{M})C∞(M)-модуль. - Для кольцевого RRR каждая RRR-алгебра имеет естественную (левую/правую) структуру RRR-модуля, заданную (левым/правым) кольцевым действием RRR на AAA.
(Z\ZZZ-модули) По определению каждый Z\ZZZ-модуль является коммутативной группой. Аналогично, каждая коммутативная группа (G,+)(G,+)(G,+) становится Z\ZZZ-модулем при действии кольца, определенном для n∈Zn \in \ZZn∈Z, g∈Gg \in Gg∈ G на n⋅g={−a+a+⋯+a−(n раз), если n>0−0, если n=0-a-a-⋯-a(-n раз), если n<0 п \cdot g = \begin{case} \hphantom{-}a + a + \cdots + a \quad \hphantom{-}\text{(} n \text{ раз)} & \text{если } n > 0 \\ \hphantom{-}0 & \text{if} n = 0 \\ -a — a — \cdots — a \quad \text{(} {-}n \text{ раз)} & \text{если} n < 0 \end{случаи} n⋅g=⎩⎨⎧−a+a+⋯+a−(n раз)−0−a−a−⋯−a(−n раз)если n>0если n=0если n<0 Мы заключаем, что Z\ZZZ-модулей и коммутативных групп 9{\ макс (п, м)} p_j q_ {kj} [p+q]k=pk+qk[p⋅q]k=j=0∑max(n,m)pjqk−j
Подумайте, что означает, что F\FFF-векторное пространство VVV является F[x]\FF[x]F[x]-модулем. k v
\end{выровнено}
φ(p)v=φ(k=1∑mpkxk)v=k=1∑mpkφ(x)kv Аналогично любой выбор ϕ(x)∈End(V)\phi (x) \in \End(V)ϕ(x)∈End(V) дает допустимый кольцевой гомоморфизм, выявляющий биекцию между F[x]\FF[x]F[x]-модулями и парами (V,T ∈End(V))(V, T \in \End(V))(V,T∈End(V)). { F[x]-модули V }⟷{F-векторные пространства V с алинейным отображением T:V→V}
\bigg\{ \;\mathbb{F}[x]\text{-modules} V\; \bigg\}
\longleftrightarrow
\bigg\{ \substack{\small\text{$\mathbb{F}$-векторные пространства $V$ с }\\\small \text{линейным отображением $T : V \rightarrow V$}} \bigg\ }
{F[x]-модули V}⟷{F-векторные пространства V с алинейным отображением T:V→V} В общем случае существует множество различных структур F[x]\FF[x]F[x]-модулей задано F\FFF-векторное пространство VVV, каждое из которых соответствует линейному выбору T:V→VT : V \rightarrow VT:V→V.
k v
\end{выровнено}
φ(p)v=φ(k=1∑mpkxk)v=k=1∑mpkφ(x)kv Аналогично любой выбор ϕ(x)∈End(V)\phi (x) \in \End(V)ϕ(x)∈End(V) дает допустимый кольцевой гомоморфизм, выявляющий биекцию между F[x]\FF[x]F[x]-модулями и парами (V,T ∈End(V))(V, T \in \End(V))(V,T∈End(V)). { F[x]-модули V }⟷{F-векторные пространства V с алинейным отображением T:V→V}
\bigg\{ \;\mathbb{F}[x]\text{-modules} V\; \bigg\}
\longleftrightarrow
\bigg\{ \substack{\small\text{$\mathbb{F}$-векторные пространства $V$ с }\\\small \text{линейным отображением $T : V \rightarrow V$}} \bigg\ }
{F[x]-модули V}⟷{F-векторные пространства V с алинейным отображением T:V→V} В общем случае существует множество различных структур F[x]\FF[x]F[x]-модулей задано F\FFF-векторное пространство VVV, каждое из которых соответствует линейному выбору T:V→VT : V \rightarrow VT:V→V.
F[x]\FF[x]F[x]-подмодули F[x]\FF[x]F[x]-модуля~VVV — это в точности TTT-инвариантные подпространства VVV, где T∈End (V)T \in \End(V)T∈End(V) обозначает действие xxx.
Каждый F[x]\FF[x]F[x]-подмодуль ВВВ замкнут относительно действия кольцевых элементов, в том числе ТТТ. Точно так же каждое TTT-инвариантное подпространство замкнуто относительно кольцевых действий, которые все являются полиномами в TTT.
Модули гомоморфизмов
Гомоморфизм RRR-модулей — это отображение ϕ:M→N\phi : M \rightarrow Nϕ:M→N между модулями, которое сохраняет структуру RRR-модуля, сохраняя сложение и коммутируя с кольцевым действием на MMM, ϕ (x+y)=ϕ(x)+ϕ(y)∀ x,y∈Mϕ(r⋅x)=r⋅ϕ(x)∀ x∈M,r∈R
\begin{выровнено}
\phi(x + y) &= \phi(x) + \phi(y) & \forall\, x,y \in M \\
\phi(r \cdot x) &= r \cdot \phi(x) & \forall\, x \in M, r \in R
\end{выровнено}
ϕ(x+y)ϕ(r⋅x)=ϕ(x)+ϕ(y)=r⋅ϕ(x)∀x,y∈M∀x∈M,r∈R 9{-1}\{0_S\}kerϕ=ϕ−1{0S} как аддитивный групповой гомоморфизм. Биективный гомоморфизм RRR-модулей является -изоморфизмом . Для любого кольца RRR множество HomR(M,N)\Hom_R(M,N)HomR(M,N) гомоморфизмов между двумя RRR-модулями образует коммутативную группу относительно поточечного сложения, (ϕ+ψ)(m) =ϕ(m)+ψ(m)(\phi + \psi)(m) = \phi(m) + \psi(m)(ϕ+ψ)(m)=ϕ(m)+ψ(m) для ϕ,ψ∈HomR(M,N)\phi, \psi \in \Hom_R(M,N)ϕ,ψ∈HomR(M,N). Более того,
Более того,
Для коммутативного кольца RRR группа HomR(M,N)\Hom_R(M,N)HomR(M,N) образует RRR-модуль относительно действия кольца R→End(HomR(M,N))R \rightarrow \End(\Hom_R(M,N))R→End(HomR(M,N)) определяется как (r⋅ϕ)(m)≡r⋅ϕ(m)∀ r∈R,m∈M ,ϕ∈HomR(M,N) \begin{выровнено} (r \cdot \phi)(м) &\эквив г \cdot \phi(m) &\forall\, r \in R, m \in M, \phi \in \Hom_R(M,N) \end{выровнено} (r⋅ϕ)(m)≡r⋅ϕ(m)∀r∈R,m∈M,ϕ∈HomR(M,N)
Коммутативность RRR гарантирует, что (r⋅ϕ)∈HomR(M,N)(r\cdot \phi) \in \Hom_R(M,N)(r⋅ϕ)∈HomR(M,N), поскольку ( r⋅ϕ)(s⋅m)=r⋅ϕ(s⋅m)(по определению)=rs⋅ϕ(m)(ϕ является гомоморфизмом)=sr⋅ϕ(m)(коммутативность)=s⋅(r ⋅ϕ(m))(по определению) \begin{выровнено} (r \cdot \phi)(s \cdot m) &= r \cdot \phi(s \cdot m) & \text{(по определению)} \\ &= rs \cdot \phi(m) & \text{(} \phi \text{ является гомоморфизмом)} \\ &= sr \cdot \phi(m) & \text{(коммутативность)} \\ &= s \cdot (r \cdot \phi(m)) & \text{(по определению)} \end{выровнено} (r⋅ϕ)(s⋅m)=r⋅ϕ(s⋅m)=rs⋅ϕ(m)=sr⋅ϕ(m)=s⋅(r⋅ϕ(m))(по определению) (ϕ — гомоморфизм) (коммутативность) (по определению)
Кольцо модульных эндоморфизмов
эндоморфизма HomR(M,M)\Hom_R(M,M)HomR(M,M) образуют кольцо с единицей, где (ϕ+ψ)(m)=ϕ(m)+ψ(m)(поточечное сложение) (ϕψ)(m)=(ϕ∘ψ)(m)(композиция)1HomR(M,M)=IdM(мультипликативная тождественность)
\begin{выровнено}
(\phi + \psi)(m) &= \phi(m) + \psi(m) & \text{(поточечное сложение)} \\
(\phi \psi)(м) &= (\phi \circ \psi)(м) & \text{(состав)} \\
1_{\Hom_R(M,M)} &= \mathrm{Id}_M & \text{(мультипликативная идентичность)}
\end{выровнено}
(ϕ+ψ)(m)(ϕψ)(m)1HomR(M,M)=ϕ(m)+ψ(m)=(ϕ∘ψ)(m)=IdM(поточечное сложение) (композиция)(мультипликативная идентичность) Мы пишем EndR(M)=HomR(M,M)\End_R(M) = \Hom_R(M,M)EndR(M)=HomR(M,M) для кольцо эндоморфизма МММ.
Пусть МММ — модуль над коммутативным кольцом RRR. Кольцо эндоморфизмов EndR(M)\End_R(M)EndR(M) образует RRR-алгебру при том же кольцевом действии r↦φ(φr:m↦rm)r \stackrel{\varphi}{\mapsto} ( \varphi_r : m \mapsto rm)r↦φ(φr:m↦rm), что определяет MMM как RRR-модуль.
Обычно это свойство формулируется без ссылки на гомоморфизмы колец, но в этих примечаниях мы хотим подчеркнуть, что изучение модулей — это действительно изучение . Однако есть по крайней мере одна тонкость: определяя MMM как RRR-модуль, мы требовали, чтобы φ⊡:R→End(M,+)\varphi_\boxdot : R \rightarrow \End(M,+)φ⊡ :R→End(M,+) — гомоморфизм колец из RRR в аддитивные групповые эндоморфизмы на (M,+)(M,+)(M,+). Теперь мы спрашиваем, является ли каждый φr\varphi_rφr также гомоморфизмом RRR-модулей.
Во-первых, аддитивный групповой гомоморфизм φr∈End(M,+)\varphi_r \in \End(M,+)φr∈End(M,+) также является модульным гомоморфизмом, так как для r,s∈Rr,s \in Rr,s∈R и m∈Mm \in Mm∈M, φr(s⋅m)=r⋅(s⋅m)(по определению)=(rs)⋅m1(ассоциативность скаляров)=s⋅( r⋅m)(ассоциативность скаляров)=s⋅φr(m)(по определению)
\begin{выровнено}
\varphi_r(s\cdot m)
&= r \cdot (s \cdot m) &\text{(по определению)} \\
&= (rs) \cdot m_1 &\hspace{4em}\text{(ассоциативность скаляров)}\\
&= s \cdot (r \cdot m) &\text{(ассоциативность скаляров)}\\
&= s \cdot \varphi_r(m) &\text{(по определению)}
\end{выровнено}
φr(s⋅m)=r⋅(s⋅m)=(rs)⋅m1=s⋅(r⋅m)=s⋅φr(m)(по определению)(ассоциативность скаляров)( ассоциативность скаляров)(по определению) Далее, φ⊡:R↦EndR(M)\varphi_\boxdot : R \mapsto \End_R(M)φ⊡:R↦EndR(M) посылает r↦φrr \mapsto \varphi_rr↦φr — кольцевой гомоморфизм. φr1+r2(m)=(r1+r2)⋅m(по определению)=r1⋅m+r2⋅m(дистрибутивность скаляров)=φr1(m)+φr2(m)(по определению)φr1r2(m)= (r1r2)⋅m(по определению)=r2⋅(r1⋅m)(R коммутативный)=(φr2∘φr1)(m)(по определению)
\begin{выровнено}
\varphi_{r_1 + r_2}(м)
&= (r_1 + r_2) \cdot m &\text{(по определению)} \\
&= r_1 \cdot m + r_2 \cdot m &\text{(дистрибутивность скаляров)} \\
&= \varphi_{r_1}(m) + \varphi_{r_2}(m) &\text{(по определению)} \\
\varphi_{r_1 r_2}(м)
&= (r_1 r_2) \cdot m & \text{(по определению)} \\
&= r_2 \cdot (r_1 \cdot m) &\text{($R$ коммутативный)} \\
&= (\varphi_{r_2} \circ \varphi_{r_1})(m) &\text{(по определению)}
\end{выровнено}
φr1+r2(m)φr1r2(m)=(r1+r2)⋅m=r1⋅m+r2⋅m=φr1(m)+φr2( m)=(r1r2)⋅m=r2⋅(r1⋅m)=(φr2∘φr1)(m)(по определению)(дистрибутивность скаляров)(по определению)(по определение)(R коммутативный)(по определению) Наконец, каждый φr\varphi_rφr коммутирует с каждым элементом ϕ∈EndR(M)\phi \in \End_R(M)ϕ∈EndR(M), (φr∘ϕ) (m)=φr(ϕ(m))(композиция)=r⋅ϕ(m)(по определению)=ϕ(r⋅m)(модульный гомоморфизм)=ϕ(φr(m))(по определению)
\begin{выровнено}
(\ varphi_r \circ \phi)(м)
&= \varphi_r (\phi(m)) &\text{(композиция)} \\
&= r \cdot \phi(m) &\text{(по определению)}\\
&= \phi(r \cdot m) &\text{(модульный гомоморфизм)}\\
&= \phi( \varphi_r(m)) &\text{(по определению)}
\end{выровнено}
(φr∘ϕ)(m)=φr(ϕ(m))=r⋅ϕ(m)=ϕ(r⋅m)=ϕ(φr(m))(состав)(по определению) (модульный гомоморфизм)(по определению)
φr1+r2(m)=(r1+r2)⋅m(по определению)=r1⋅m+r2⋅m(дистрибутивность скаляров)=φr1(m)+φr2(m)(по определению)φr1r2(m)= (r1r2)⋅m(по определению)=r2⋅(r1⋅m)(R коммутативный)=(φr2∘φr1)(m)(по определению)
\begin{выровнено}
\varphi_{r_1 + r_2}(м)
&= (r_1 + r_2) \cdot m &\text{(по определению)} \\
&= r_1 \cdot m + r_2 \cdot m &\text{(дистрибутивность скаляров)} \\
&= \varphi_{r_1}(m) + \varphi_{r_2}(m) &\text{(по определению)} \\
\varphi_{r_1 r_2}(м)
&= (r_1 r_2) \cdot m & \text{(по определению)} \\
&= r_2 \cdot (r_1 \cdot m) &\text{($R$ коммутативный)} \\
&= (\varphi_{r_2} \circ \varphi_{r_1})(m) &\text{(по определению)}
\end{выровнено}
φr1+r2(m)φr1r2(m)=(r1+r2)⋅m=r1⋅m+r2⋅m=φr1(m)+φr2( m)=(r1r2)⋅m=r2⋅(r1⋅m)=(φr2∘φr1)(m)(по определению)(дистрибутивность скаляров)(по определению)(по определение)(R коммутативный)(по определению) Наконец, каждый φr\varphi_rφr коммутирует с каждым элементом ϕ∈EndR(M)\phi \in \End_R(M)ϕ∈EndR(M), (φr∘ϕ) (m)=φr(ϕ(m))(композиция)=r⋅ϕ(m)(по определению)=ϕ(r⋅m)(модульный гомоморфизм)=ϕ(φr(m))(по определению)
\begin{выровнено}
(\ varphi_r \circ \phi)(м)
&= \varphi_r (\phi(m)) &\text{(композиция)} \\
&= r \cdot \phi(m) &\text{(по определению)}\\
&= \phi(r \cdot m) &\text{(модульный гомоморфизм)}\\
&= \phi( \varphi_r(m)) &\text{(по определению)}
\end{выровнено}
(φr∘ϕ)(m)=φr(ϕ(m))=r⋅ϕ(m)=ϕ(r⋅m)=ϕ(φr(m))(состав)(по определению) (модульный гомоморфизм)(по определению)
По определению каждое поле F\FFF является коммутативным кольцом. Следовательно, эндоморфизмы EndF(V)\End_\FF(V)EndF(V) любого F\FFF-векторного пространства образуют F\FFF-алгебру.
Следовательно, эндоморфизмы EndF(V)\End_\FF(V)EndF(V) любого F\FFF-векторного пространства образуют F\FFF-алгебру.
Частные модули
Напомним, что для групп и колец факторы корректно определены только для подгрупп и подколец (идеалов) соответственно. Для модулей МММ оказывается, что подмодуль N⩽MN \подпространство MN⩽M имеет факторM/NM / NM/N и естественное проекционное отображение π:M→M/N\pi : M \rightarrow M/Nπ: M→M/N — кольцевой гомоморфизм с ядром kerπ=N\ker \pi = Nkerπ=N. Точно так же каждое подпространство F\FFF-векторов имеет фактор-пространство F\FFF-векторов, возникающее как ядро некоторого линейного отображения.
Пусть RRR — кольцо. Пусть N≤MN \subspace MN≤M — подмодуль RRR-модуля MMM. (Аддитивная, коммутативная) фактор-группа M/NM / NM/N может быть превращена в RRR-модуль под действием кольца R→End(M/N)R \rightarrow \End(M/N)R→End(M /N), определяемый как r⋅(x+N)=(r⋅x)+N∀ r∈R,x+N∈M/N
\begin{выровнено}
г \cdot (х + N)
&= (r \cdot x) + N
&\forall\, r \in R, x + N \in M/N
\end{выровнено}
r⋅(x+N)=(r⋅x)+N∀r∈R,x+N∈M/N Естественная проекция π:M→M/N\pi : M \rightarrow M/Nπ: Отображение M→M/N x↦x+Nx \maps в x+Nx↦x+N является гомоморфизмом RRR-модуля с ядром kerπ=N\ker\pi = Nkerπ=N.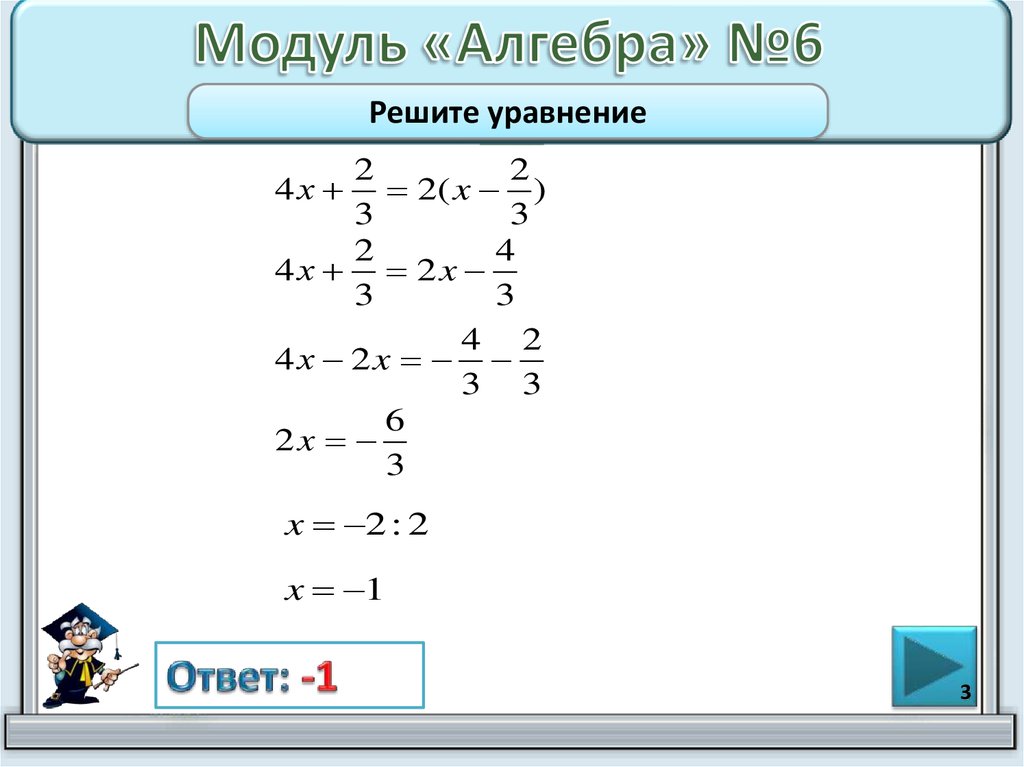
(Первая теорема об изоморфизме) Пусть M,NM,NM,N — RRR-модули. Ядро любого модульного гомоморфизма ϕ:M→N\phi : M \rightarrow Nϕ:M→N является подмодулем MMM, и M/kerϕ≅ϕ(M) M / \ker\phi \cong \phi(M) М/керϕ≅ϕ(М)
Бесплатные модули
Концепции линейных комбинаций, базисов и промежутков векторного пространства имеют аналоги в теории RRR-модулей. Обычно мы предполагаем, что RRR — это кольцо с идентичностью.
Пусть МММ — RRR-модуль. Подмодуль МММ сгенерировал подмножеством A⊂MA \subset MA⊂M есть множество конечных RRR-линейных комбинаций RA={r1a1+⋯+rmam∣rk∈R,ak∈A,m∈N}⩽M РА = \{ r_1 a_1 + \cdots + r_m a_m \mid r_k \in R, a_k \in A, m \in \NN \} \subspace M RA={r1a1+⋯+rmam∣rk∈R,ak∈A,m∈N}⩽M Подмодуль N=RA⩽MN = RA \subspace MN=RA⩽M является конечно порожденным , если A⊂MA \подмножество MA⊂M конечно. Циклический подмодуль N=RaN = RaN=Ra порождается одним элементом a∈Ma \in Ma∈M.
RRR-модуль FFF равен свободный на подмножестве A⊂FA \subset FA⊂F, если каждый ненулевой x∈Fx \in Fx∈F однозначно расширяется как RRR-линейная комбинация элементов из AAA, и в этом случае AAA называется базисом для FFF . х=r1a1+⋯+rmam∃! rk∈R,ak∈A,∀ x∈F
\begin{выровнено}
х &= r_1 a_1 + \cdots + r_m a_m
& \существует!\, r_k \in R, a_k \in A, \forall\, x \in F
\end{выровнено}
x=r1a1+⋯+rmam∃!rk∈R,ak∈A,∀x∈F
х=r1a1+⋯+rmam∃! rk∈R,ak∈A,∀ x∈F
\begin{выровнено}
х &= r_1 a_1 + \cdots + r_m a_m
& \существует!\, r_k \in R, a_k \in A, \forall\, x \in F
\end{выровнено}
x=r1a1+⋯+rmam∃!rk∈R,ak∈A,∀x∈F
В общем случае может существовать более одного базиса. Если RRR коммутативен, каждый базис имеет одинаковую мощность, называемую 9-ю.Модуль 0147 ранг ФФФ. В отличие от векторных пространств, не каждый модуль имеет базис (не каждый модуль свободен).
Универсальное свойство бесплатных модулей
Напомним, что каждое линейное отображение T∈HomF(V,W)T \in \Hom_\FF(V,W)T∈HomF(V,W) между F\FFF-векторными пространствами однозначно определяется своим значением на n =dimVn=\dim Vn=dimV точек. RRR-линейные карты между свободными модулями обладают тем же свойством, которое обычно выражается следующим образом:
(Универсальное свойство) Для любого множества AAA существует единственный (с точностью до изоморфизма) свободный RRR-модуль Free(A)\mathrm{Free}(A)Free(A), удовлетворяющий следующему универсальному свойству: для любого RRR-модуля МММ и любой функции φ:A→M\varphi : A \rightarrow Mφ:A→M существует единственный гомоморфизм RRR-модулей Φ:Free(A)→M\Phi : \mathrm{Free}(A) \rightarrow MΦ:Free(A)→M такое, что Φ(a)=φ(a)\Phi(a) = \varphi(a)Φ(a)=φ(a),
Модуль— Citizendium
| | Основной артикул | Обсуждение | Статьи по теме [?] | Библиография [?] | Внешние ссылки [?] | Версия для цитирования [?] |
| ||||||||||||
Эта редактируемая основная статья равна в разработке и подлежит отказу от ответственности . [изменить введение] | |||||||||||||||||||
Эта статья о математической структуре . Чтобы узнать о других значениях термина , модуль , см. «Модуль» (значения).
В абстрактной алгебре модуль представляет собой математическую структуру, частными типами которой являются абелевы группы и векторные пространства. Они стали повсеместными в абстрактной алгебре и других областях математики, связанных с алгебраическими структурами, таких как алгебраическая топология, алгебраическая геометрия и алгебраическая теория чисел. Глубокое понимание теории модулей необходимо для всех, кто хочет понять широкий спектр математики на уровне выпускников и текущих математических исследований.
Содержание
- 1 Определение
- 2 Специальные типы модулей
- 2.1 Векторные пространства
- 2.2 Абелевы группы
- 2.3 Модули над коммутативными кольцами
- 2.4 Бесплатные модули
- 2.
 5 Конечно сгенерированные модули
5 Конечно сгенерированные модули - 2.6 Другие типы модулей
- 3 Категория R{\displaystyle R}-модулей
- 4 примера
Определение
Пусть R{\displaystyle R} — кольцо (не обязательно тождественное или коммутативное). Левый R {\ displaystyle R} -модуль — это абелева группа, базовое множество которой снабжено действием (математикой) с помощью R {\ displaystyle R}, соблюдая как групповую структуру M {\ displaystyle M}, так и кольцевую структуру R. {\ Displaystyle R}. Действие R {\ displaystyle R} представляет собой карту R × M → M {\ displaystyle R \ times M \ rightarrow M}. Изображение r × m {\ displaystyle r \ times m} под этой картой обычно записывается r⋅ m {\ displaystyle r \ cdot m} или просто rm {\ displaystyle rm}. Действие должно удовлетворять следующим свойствам:
- р⋅(м1 + м2) = р⋅м1 + г⋅м2 {\ displaystyle r \ cdot (m_ {1} + m_ {2}) = r \ cdot m_ {1} + r \ cdot m_ {2 }}, для всех r∈R,m1,m2∈M{\displaystyle r\in R,m_{1},m_{2}\in M}
- (r1 + r2) ⋅ м = r1⋅ м + r2 ⋅ м {\ displaystyle (r_ {1} + r_ {2}) \ cdot m = r_ {1} \ cdot m + r_ {2} \ cdot m} , и
- (r1r2) ⋅ м = r1 ⋅ (r2 ⋅ м) {\ displaystyle (r_ {1} r_ {2}) \ cdot m = r_ {1} \ cdot (r_ {2} \ cdot m)} для всех r1 ,r2∈R,m∈M{\displaystyle r_{1},r_{2}\in R,m\in M}
Если кольцо R{\displaystyle R} имеет единицу, модуль, удовлетворяющий дополнительному аксиома
- 1⋅m=m{\displaystyle 1\cdot m=m} для всех m∈M{\displaystyle m\in M}
называется unital или unitary .
Аналогично можно определить правый R{\displaystyle R}-модуль.
Особые типы модулей
Векторные пространства
Прообразом модулей и типом, с которым обычно сталкиваются впервые, является векторное пространство. Хотя векторные пространства, встречающиеся в приложениях или курсах линейной алгебры, обычно используют скаляры вещественных или комплексных чисел, наиболее общий тип векторного пространства — это модуль над телом. Фундаментальной общностью всех модулей над телом является существование основа для модуля. Модули над более общими кольцами не обязательно имеют базис, а те, которые имеют, называются свободными модулями.
Абелевы группы
Абелевы группы — это в точности модули над кольцом целых чисел Z{\displaystyle \mathbb {Z}}. Если G {\ displaystyle G} — абелева группа (записанная аддитивно), можно определить выражение с n ∈ Z, g ∈ G {\ displaystyle n \ in \ mathbb {Z}, g \ in G } значить
- ng={g+g+⋯+g(n times) if n<00 if n=0-g-g-⋯-g (|n| times) if n<0{\displaystyle ng={\begin {case} g + g + \ cdots + g \ qquad (n {\ text {times}}) {\ text {if}} n <0 \\ 0 \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad {\ text { if }}n=0\\-g-g-\cdots -g\quad (|n|{\text{times}}){\text{if}}n<0\end{case}}}
Коммутативность абелевых групповых операций и правило обращения суммы можно использовать, чтобы показать, что
- n (g1 + g2) = ng1 + ng2 {\ displaystyle n (g_ {1} + g_ {2}) = ng_ {1} + ng_ {2}} для всех n∈Z,g1,g2∈G {\ Displaystyle п \ в \ mathbb {Z}, g_ {1}, g_ {2} \ в G}.

Правило обращения суммы можно также использовать, чтобы показать, что
- (n1n2) г = n1 (n2g) {\ displaystyle (n_ {1} n_ {2}) g = n_ {1} (n_ {2} g)} для всех n1, n2∈Z, g∈G {\ displaystyle n_ {1}, n_ {2} \ in \ mathbb {Z}, g \ in G},
проверка случаев отдельно для различных возможностей знаков n1,n2{\displaystyle n_{1},n_{2}}. Аналогично можно проверить несколько случаев и показать, что
- (n1+n2)g=n1g+n2g{\displaystyle (n_{1}+n_{2})g=n_{1}g+n_{2}g} для всех n1,n2∈Z,g ∈G {\ displaystyle n_ {1}, n_ {2} \ in \ mathbb {Z}, g \ in G}
Приведенные выше три уравнения представляют собой три аксиомы действия Z {\ displaystyle \ mathbb {Z } } на Z{\ displaystyle \ mathbb {Z}} -модуле. Таким образом, Z {\ displaystyle \ mathbb {Z}} -модули равны то же, что и абелевых групп.
Если R{\displaystyle R} кольцо с единицей, то существует гомоморфизм колец Z→R{\displaystyle \mathbb {Z} \rightarrow R}. С помощью этой карты мы можем канонически определить выражение nm {\ displaystyle nm} с n∈Z {\ displaystyle n \ in \ mathbb {Z}} и m ∈ M {\ displaystyle m \ in M}.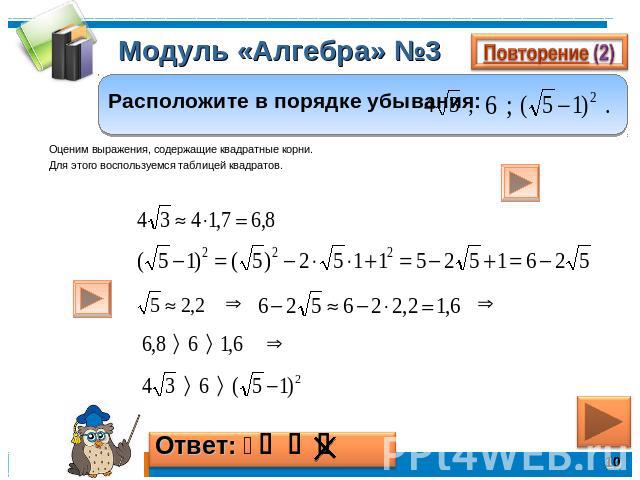 Если M {\ displaystyle M} является унитальным модулем, выражение nm {\ displaystyle nm} имеет в этом смысле тот же смысл, что и представление m {\ displaystyle m} как абелевой группы.
Если M {\ displaystyle M} является унитальным модулем, выражение nm {\ displaystyle nm} имеет в этом смысле тот же смысл, что и представление m {\ displaystyle m} как абелевой группы.
Этот пример уже показывает, что не каждый модуль имеет базу. То есть не всегда существует подмножество модуля M {\ displaystyle M}, такое что каждый элемент M {\ displaystyle M} может быть однозначно выражен как линейная комбинация элементов M {\ displaystyle M}. Например, в абелевой группе Z / 2Z {\ displaystyle \ mathbb {Z} / 2 \ mathbb {Z}} увеличение всех коэффициентов линейной комбинации на 2 {\ displaystyle 2} приведет к тому же элементу группа.
Модули над коммутативными кольцами
Бесплатные модули
Конечно сгенерированные модули
Другие типы модулей
Был изучен широкий ассортимент специальных типов модулей — больше, чем можно обсудить на этой странице. Существует два подхода к абстрактному определению специальных типов модулей. Во-первых, можно позволить кольцу быть произвольным и изучать все модули с определенным определяемым структурным свойством, не используя свойства, характерные для R {\displaystyle R}. Примеры этого типа включают:
Примеры этого типа включают:
- бесплатных модулей, локально бесплатных модулей и стабильно бесплатных модулей
- конечно-генерируемых модулей
- проективных и инъективных модулей.
- Модули Нётера и Артина.
- полупростых и простых модулей.
Во-вторых, можно рассматривать произвольные модули над специальным классом колец. Примеры этого типа включают:
- векторные пространства и абелевы группы
- модулей над главной идеальной областью
- Модули Галуа
Конечно, эти два подхода можно смешивать, изучая модули с определенными структурными свойствами над кольцом специального типа. Кроме того, специалисты-практики в большинстве областей высшей математики изучают все модули, проявляющиеся посредством естественного процесса в этой области, например, гомологии с коэффициентами топологических пространств или групп классов числовых полей как модулей Галуа. Более полный список специальных типов модулей см.

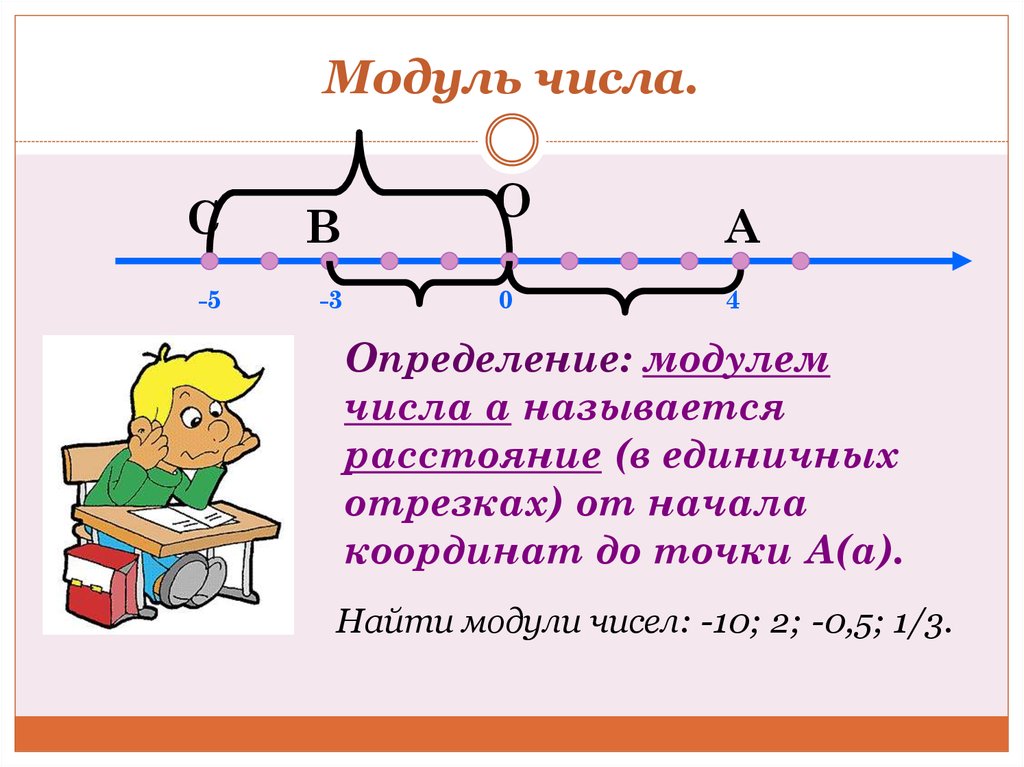 Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0;
Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0; Подмодули RRR как поля над собой являются идеалами. 9\infty(\mathcal{M})C∞(M)-модуль.
Подмодули RRR как поля над собой являются идеалами. 9\infty(\mathcal{M})C∞(M)-модуль. 5 Конечно сгенерированные модули
5 Конечно сгенерированные модули