Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выраженияНайдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выраженияВычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выраженияСколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выраженияНайдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выраженияВычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выраженияНайдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЕсли же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выраженияНайдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
В противном случае, выражение упрощается.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выраженияНужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выраженияВычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменнымиВычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Урок 14. числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс
Математика, 2 класс
Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений
Перечень вопросов, рассматриваемых в теме:
— Что такое числовые выражения?
— Как правильно читать и записывать числовые выражения?
— Как выполнять порядок действий, если есть скобки?
— Как сравнить два выражения?
Глоссарий по теме:
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.
Значение выражения – это результат выполненных действий.
Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.
Скобки — парные знаки ( )
Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.
Основная и дополнительная литература по теме:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40
2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27
3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16
Теоретический материал для самостоятельного изучения
Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.
Маша: 12 – 7 + 3 = 8
Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.
Затем от 12 отнял 10, получил 2.
Миша: 12 — 7 + 3 = 2
Кто из них вычислил верно? Решил верно, Миша.
В математике для обозначения действий, которые должны выполняться первыми используют специальный знак ( ) — скобки.
Запишем пример, который решали дети правильно:
12 — (7 + 3) =2
Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.
Посмотрим на запись.
9 – (6 + 2) = 1
Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».
Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.
Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.
9 – (6 + 2) = 1
числовое значение
выражение числового
выражения
Прочитаем выражение: 10 + (8 — 3) =
К числу 10 прибавить разность чисел 8 и 3.
Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.
10+(8-3)=15
Давайте сравним значения двух выражений:
11 — 4 и 16 — 7.
Сначала найдем значение каждого из выражений и их сравним.
11 — 4 = 7
16 — 7 = 9
7 < 9, значит, 11-4 < 16-7
Выводы: Итак, оказывается, порядок должен быть и в действиях, он так и называется «Порядок выполнения действий». Если в числовом выражении стоят скобки, это означает, что действие, которое в них записано, должно быть выполнено первым, а все остальные действия выполняют по порядку.
Тренировочные задания.
1.Выберите правильный ответ. Как правильно прочитать данное числовое выражение: 13 – (7 + 3)?
Вариант ответов:
1. К 13 прибавить сумму чисел 7 и 3
2. Из 13 вычесть 7 плюс 3
3. Из 13 вычесть сумму чисел 7 и 3
4. Разность чисел 13 и 7 плюс 3
Правильный ответ:
3. Из 13 вычесть сумму чисел 7 и 3
2. Соотнесите числовые выражения с их значениями
3+ (16-6) 15
10-4+9 16
13-(6+4) 13
9+ (13-6) 3
Правильный ответ:
3+ (16 – 6) 13
10 – 4 + 9 15
13 – (6 + 4) 3
9 + (13 – 6) 16
Скрапинг сайта с помощью Python: гайд для новичков
В этой статье мы разберемся, как создать HTML скрапер на Python, который получает неофициальный доступ к коду сайта и позволяет извлечь необходимые данные.
Отличие от вызовов API
Альтернативный метод получения данных сайта — вызовы API. Взаимодействие с API — это официально предоставляемый владельцем сайта способ получения данных прямо из БД или обычных файлов. Обычно для этого требуется разрешение владельца сайта и специальный токен. Однако апи доступен не всегда, поэтому скрапинг так привлекателен, однако его законность вызывает вопросы.
Взаимодействие с API — это официально предоставляемый владельцем сайта способ получения данных прямо из БД или обычных файлов. Обычно для этого требуется разрешение владельца сайта и специальный токен. Однако апи доступен не всегда, поэтому скрапинг так привлекателен, однако его законность вызывает вопросы.
Юридические соображения
Скрапинг может нарушать копирайт или правила использования сайта, особенно когда он используется для получения прибыли, конкурентного преимущества или причинения ущерба (например из-за слишком частых запросов). Однако скрапинг публично доступен и используется для личного использования, академических целей или безвредного некоммерческого использования.
Если данные являются платными, требуют регистрации, имеют явную защиту от скрапинга, содержат конфиденциальные данные или личные данные пользователей, то нужно избегать любого из видов скрапинга.
Установка Beautiful Soup в Python
Beautiful Soup — это Python библиотека для скрапинга данных сайтов через HTML код.
Установите последнюю версию библиотеки.
$ pip install beautifulsoup4Чтобы делать запросы, установите requests (библиотеку для отправки HTTP запросов):
$ pip install requestsИмпортируйте библиотеки в файле Python или Jupiter notebook:
from bs4 import BeautifulSoup
import requestsИ несколько стандартных библиотек, которые потребуются для скрапинга на Python:
import re
from re import sub
from decimal import Decimal
import io
from datetime import datetime
import pandas as pdВведение
Представьте, что мы хотим произвести скрапинг платформы, содержащей общедоступные объявления о недвижимости. Мы хотим получить цену недвижимости, ее адрес, расстояние, название станции и ближайший до нее тип транспорта для того, чтобы узнать, как цены на недвижимость распределяются в зависимости от доступности общественного транспорта в конкретном городе.
Предположим, что запрос приведет к странице результатов, которая выглядит следующим образом:
Как только мы узнаем, в каких элементах сайта хранятся необходимые данные, нам нужно придумать логику скрапинга, которая позволит нам получить всю нужную информацию из каждого объявления.
Нам предстоит ответить на следующие вопросы:
- Как получить одну точку данных для одного свойства (например данные из тега price в первом объявлении)?
- Как получить все точки данных для одного свойства со всей страницы (например все теги price с одной страницы)?
- Как получить все точки данных для одного свойства всех страниц с результатами (например все теги price со всех страниц с результатами)?
- Как устранить несоответствие, когда данные могут быть разных типов (например, есть некоторые объявления, в которых в поле цены указана цена по запросу. В конечном итоге у нас будет столбец, состоящий из числовых и строковых значений, что в нашем случае не позволяет провести анализ)?
- Как лучше извлечь сложную информацию (Например, предположим, что каждое объявление содержит информацию об общественном транспорте, например “0,5 мили до станции метро XY”)?
Логика получения одной точки данных
Все примеры кода для скрапинга на Python можно найти в Jupiter Notebook файле на GitHub автора.
Запрос кода сайта
Во-первых, мы используем поисковый запрос, который мы сделали в браузере в скрипте Python:
# поиск в определённой зоне
url = 'https://www.website.com/london/page_size=25&q=london&pn=1'
# делаем запрос и получаем html
html_text = requests.get(url).text
# используем парсер lxml
soup = BeautifulSoup(html_text, 'lxml')Переменная soup содержит полный HTML-код страницы с результатами поиска.
Поиск тегов-свойств
Для этого нам потребуется браузер. Некоторые популярные браузеры предлагают удобный способ получения информации о конкретном элементе напрямую. В Google Chrome вы можете выбрать любой элемент сайта и, нажав правой кнопкой, выбрать пункт «Исследовать элемент» . Справа откроется код сайта с выделенным элементом.
HTML классы и атрибут id
HTML-классы и id в основном используются для ссылки на класс в таблице стилей CSS, чтобы данные могли отображаться согласованным образом.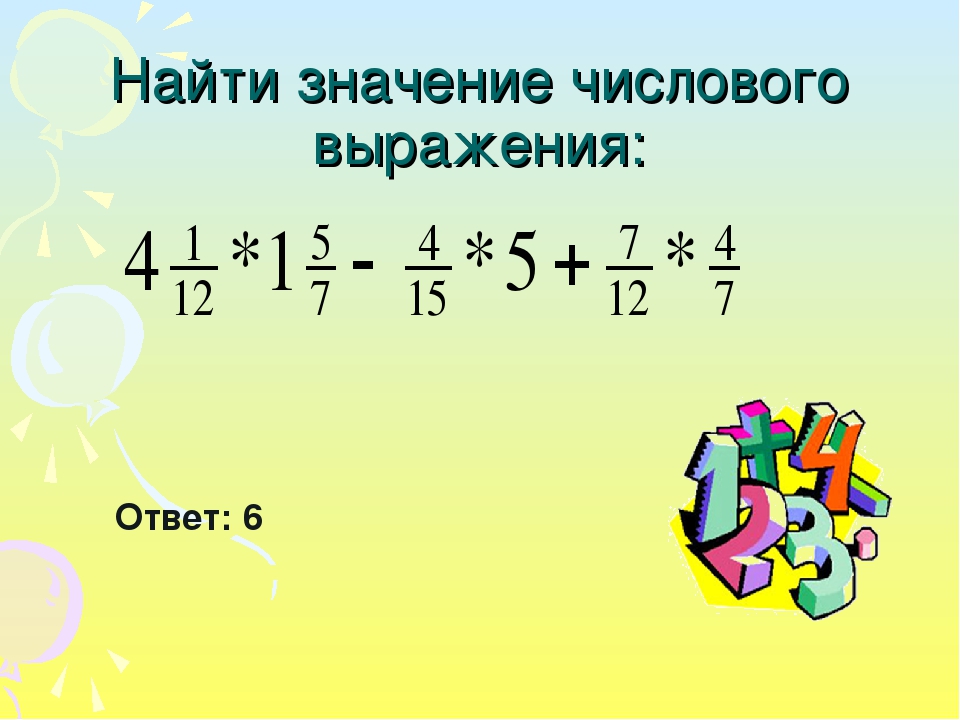
В приведенном выше примере, класс, используемый для получения информации о ценах из одного объявления, также применяется для получения цен из других объявлений (что соответствует основной цели класса).
Обратите внимание, что HTML-класс также может ссылаться на ценники за пределами раздела объявлений (например, специальные предложения, которые не связаны с поисковым запросом, но все равно отображаются на странице результатов). Однако для целей этой статьи мы фокусируемся только на ценах в объявлениях о недвижимости.
Вот почему мы сначала ориентируемся на объявление и ищем HTML-класс только в исходном коде для конкретного объявления:
# используем парсер lxml
soup = BeautifulSoup(html_text, 'lxml')
# находим одно объявление
ad = soup.find('div', class_ = 'css-ad-wrapper-123456')
# находим цену
price = ad.find('p', class_ = 'css-aaabbbccc').textИспользование .text в конце метода find() позволяет нам возвращать только обычный текст, как показано в браузере. Без .text он вернет весь исходный код строки HTML, на которую ссылается класс:
Без .text он вернет весь исходный код строки HTML, на которую ссылается класс:
Важное примечание: нам всегда нужно указывать элемент, в данном случае это p.
Логика получения всех точек данных с одной страницы
Чтобы получить ценники для всех объявлений, мы применяем метод find.all() вместо find():
ads = ad.find_all('p', class_ = 'css-ad-wrapper-123456')Переменная ads теперь содержит HTML-код для каждого объявления на первой странице результатов в виде списка списков. Этот формат хранения очень полезен, так как он позволяет получить доступ к исходному коду для конкретных объявлений по индексу.
Чтобы получить все ценники, мы используем словарь для сбора данных:
map = {}
id = 0
# получаем все элементы
ads = ad.find_all('p', class_ = 'css-ad-wrapper-123456')
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
# находим цену
price = ad. find('p', class_ = 'css-aaabbbccc').text
# находим адрес
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price
find('p', class_ = 'css-aaabbbccc').text
# находим адрес
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = priceВажное примечание: использование идентификатора позволяет находить объявления в словаре:
Получение точек данных со всех страниц
Обычно результаты поиска либо разбиваются на страницы, либо бесконечно прокручиваются вниз.
Вариант 1. Веб-сайт с пагинацией
URL-адреса, полученные в результате поискового запроса, обычно содержат информацию о текущем номере страницы.
Как видно на рисунке выше, окончание URL-адреса относится к номеру страницы результатов.
Важное примечание: номер страницы в URL-адресе обычно становится видимым со второй страницы. Использование базового URL-адреса с дополнительным фрагментом &pn=1 для вызова первой страницы по-прежнему будет работать (в большинстве случаев).
Применение одного цикла for-loop поверх другого позволяет нам перебирать страницы результатов:
url = 'https://www. website.com/london/page_size=25&q=london&pn='
map = {}
id = 0
# максимальное количество страниц
max_pages = 15
for p in range(max_pages):
cur_url = url + str(p + 1)
print("Скрапинг страницы №: %d" % (p + 1))
html_text = requests.get(cur_url).text
soup = BeautifulSoup(html_text, 'lxml')
ads = soup.find_all('div', class_ = 'css-ad-wrapper-123456')
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price
website.com/london/page_size=25&q=london&pn='
map = {}
id = 0
# максимальное количество страниц
max_pages = 15
for p in range(max_pages):
cur_url = url + str(p + 1)
print("Скрапинг страницы №: %d" % (p + 1))
html_text = requests.get(cur_url).text
soup = BeautifulSoup(html_text, 'lxml')
ads = soup.find_all('div', class_ = 'css-ad-wrapper-123456')
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = priceОпределение последней страницы результатов
Вы можете задаться вопросом, как определить последнюю страницу результатов? В большинстве случаев после достижения последней страницы, любой запрос с большим числом, чем фактическое число последней страницы, приведет нас обратно на первую страницу. Следовательно, использование очень большого числа для ожидания завершения сценария не работает. Через некоторое время он начнет собирать повторяющиеся значения.
Следовательно, использование очень большого числа для ожидания завершения сценария не работает. Через некоторое время он начнет собирать повторяющиеся значения.
Чтобы решить эту проблему, мы будем проверять, есть ли на странице кнопка с такой ссылкой:
url = 'https://www.website.com/london/page_size=25&q=london&pn='
map = {}
id = 0
# используем очень большое число
max_pages = 9999
for p in range(max_pages):
cur_url = url + str(p + 1)
print("Скрапинг страницы №: %d" % (p + 1))
html_text = requests.get(cur_url).text
soup = BeautifulSoup(html_text, 'lxml')
ads = soup.find_all('div', class_ = 'css-ad-wrapper-123456')
# ищем ссылку в кнопке
page_nav = soup.find_all('a', class_ = 'css-button-123456')
if(len(page_nav) == 0):
print("Максимальный номер страницы: %d" % (p))
break
(...)Вариант 2.
 Сайт с бесконечным скроллом
Сайт с бесконечным скролломВ таком случае HTML скрапер не сработает. Альтернативные методы мы обсудим в конце статьи.
Устранение несогласованности данных
Если нам нужно избавиться от ненужных данных в самом начале скрапинга на Python, мы можем использовать обходной метод:
Функция для определения аномалий
def is_skipped(price):
'''
Определение цен, которые не являются ценами
(например "Цена по запросу")
'''
for i in range(len(price)):
if(price[i] != '£' and price[i] != ','
and (not price[i].isdigit())):
return True
return FalseИ применить его при сборе данных:
(...)
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
# пропускаем объявление без корректной цены
if(is_skipped(price)): continue
map[id]["price"] = priceФорматирование данных на лету
Мы могли заметить, что цена хранится в строке вместе с запятыми с символом валюты. \d.]’, », price))
return float(value)
\d.]’, », price))
return float(value)
Используем эту функцию:
(...)
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
if(is_dropped(price)): continue
map[id]["price"] = to_num(price)
(...)Получение вложенных данных
Информация об общественном транспорте имеет вложенную структуру. Нам потребуются данные о расстоянии, названии станции и типе транспорта.
Отбор информации по правилам
Каждый кусочек данных представлен в виде: число миль, название станции. Используем слово «миль» в качестве разделителя.
map[id]["distance"] = []
map[id]["station"] = []
transport = ad.find_all('div', class_ = 'css-transport-123')
for i in range(len(transport)):
s = transport[i].text
x = s.split(' miles ')
map[id]["distance"]. append(float(x[0]))
map[id]["station"].append(x[1])
append(float(x[0]))
map[id]["station"].append(x[1])Первоначально переменная transport хранит два списка в списке, поскольку есть две строки информации об общественном транспорте (например, “0,3 мили Слоун-сквер”, “0,5 мили Южный Кенсингтон”). Мы перебираем эти списки, используя len транспорта в качестве значений индекса, и разделяем каждую строку на две переменные: расстояние и станцию.
Поиск дополнительных HTML атрибутов для визуальной информации
В коде страницы мы можем найти атрибут testid, который указывает на тип общественного транспорта. Он не отображается в браузере, но отвечает за изображение, которое отображается на странице. Для получения этих данных нам нужно использовать класс css-StyledIcon:
map[id]["distance"] = []
map[id]["station"] = []
map[id]["transport_type"] = []
transport = ad.find_all('div', class_ = 'css-transport-123')
type = ad.find_all('span', class_ = 'css-StyledIcon')
for i in range(len(transport)):
s = transport[i]. text
x = s.split(' miles ')
map[id]["distance"].append(float(x[0]))
map[id]["station"].append(x[1])
map[id]["transport_type"].append(type[i]['testid'])
text
x = s.split(' miles ')
map[id]["distance"].append(float(x[0]))
map[id]["station"].append(x[1])
map[id]["transport_type"].append(type[i]['testid'])Преобразование в датафрейм и экспорт в CSV
Когда скрапинг выполнен, все извлеченные данные доступны в словаре словарей.
Давайте сначала рассмотрим только одно объявление, чтобы лучше продемонстрировать заключительные шаги трансформации.
Преобразуем словарь в список списков, чтобы избавиться от вложенности
result = []
cur_row = 0
for idx in range(len(map[1]["distance"])):
result.append([])
result[cur_row].append(str(map[1]["uuid"]))
result[cur_row].append(str(map[1]["price"]))
result[cur_row].append(str(map[1]["address"]))
result[cur_row].append(str(map[1]["distance"][idx]))
result[cur_row].append(str(map[1]["station"][idx]))
result[cur_row].append(str(map[1]["transport_type"][idx]))
cur_row += 1Создаём датафрейм
df = pd. DataFrame(result, columns = ["ad_id", "price", "address",
"distance", "station", "transport_type"])
DataFrame(result, columns = ["ad_id", "price", "address",
"distance", "station", "transport_type"])Мы можем экспортировать датафрейм в CSV:
filename = 'test.csv'
df.to_csv(filename)Преобразование всех объявлений в датафрейм:
result = []
cur_row = 0
for id in map.keys():
cur_price = map[id]["price"]
cur_address = map[id]["address"]
for idx in range(len(map[id]["distance"])):
result.append([])
result[cur_row].append(int(cur_id))
result[cur_row].append(float(cur_price))
result[cur_row].append(str(cur_address))
result[cur_row].append(float(map[id]["distance"][idx]))
result[cur_row].append(str(map[id]["station"][idx]))
result[cur_row].append(str(map[id]["transport_type"][idx]))
cur_row += 1
# преобразование в датафрейм
df = pd.DataFrame(result, columns = ["ad_id", "price","address", "distance", "station", "transport_type"])
# экспорт в csv
filename = 'test. csv'
df.to_csv(filename)
csv'
df.to_csv(filename)Мы это сделали! Теперь наш скрапер готов к тестированию.
Ограничения HTML скрапинга и его альтернативы
Этот пример показывает, насколько простым может быть скрапинг HTML на Python в стандартном случае. Для этого не нужно исследовать документацию. Это требует, скорее, творческого мышления, чем опыта веб-разработки.
Однако HTML скраперы имеют недостатки:
- Можно получить доступ только к информации в HTML-коде, которая загружается непосредственно при вызове URL-адреса. Веб-сайты, которые требуют JavaScript и Ajax для загрузки контента, не будут работать.
- HTML-классы или идентификаторы могут изменяться в связи с обновлениями веб-сайта.
- Может быть легко обнаружен, если запросы кажутся аномальными для веб-сайта (например, очень большое количество запросов в течение короткого промежутка времени).
Альтернативы:
- Shell скрипты — загружают всю страницу, с помощью регулярных выражений могут обрабатывать html.

- Screen scraper — изображают реального пользователя, используют браузер (Selenium, PhantomJS).
- ПО для скрапинга — рассчитаны на стандартные случаи, не требуют написания кода (webscraper.io).
- Веб сервисы скраперы — не требуют написания кода, хорошо справляются со скрапингом, платные (zyte.com).
Здесь вы найдёте список инструментов и библиотек для скрапинга.
Источник Turn Website Data Into Data Sets: A Beginner’s Guide to Python Web Scraping
Словарь астрономических терминов — астрономический словарь
В словарь вошли термины касающиеся наблюдательной ,теоретической астрономии и навигации на звездном небе.
А
Азимут — угловое расстояние по математическому горизонту от точки юга (астрономический) или севера (геодезический) до вертикала светила.
Аккреция — процесс, при которым маленькие частицы вещества присоединяются к большим массам (или поглощаются ими) под действием взаимной гравитации или при случайных столкновениях, в результате чего постепенно образуются большие небесные тела.
Альбедо — характеристика диффузной отражательной способности поверхности.
Апогей — наиболее удаленная от Земли точка орбиты обращающегося вокруг нее тела.
Астеризм — несвязанная физически группа звезд, не являются звездными скоплениями. Некоторые астеризмы являются неофициальными созвездиями. Самые известные астеризмы: «Ковш» Большой Медведицы, Пояс Ориона, Осенне-летний треугольник.
Астероид (малая планета) -небольшое планетоподобное тело неправильной формы с орбитой, расположенной, как правило, между орбитами Марса и Юпитера.
Астрометрия — раздел астрономии, главной задачей которого является изучение геометрических и кинематических свойств небесных тел.
Астрономия — наука о Вселенной, изучающая расположение, движение, строение, происхождение и развитие небесных тел и образованных ими систем.
Астрофизика — наука, объединяющая астрономию и физику, изучающая физические процессы в астрономических объектах, таких, как звёзды, галактики и т. д.
д.
Афелий — наиболее удаленная от Солнца точка орбиты обращающегося вокруг него тела.
Б
Белый карлик — проэволюционировавшие звёзды с массой, не превышающей предел Чандрасекара (максимальная масса, при которой звезда может существовать как белый карлик), лишённые собственных источников термоядерной энергии.
Блеск небесного светила — освещенность, создаваемая им в месте наблюдения.
Болид — метеор, превосходящий по яркости Венеру.
Большой Взрыв — мощнейший взрыв, который (существует такая гипотеза) положил начало эволюции Вселенной. Ученые полагают, что он произошел примерно 15 миллиардов лет тому назад.
В
Великий аттрактор — гравитационная аномалия, расположенная в межгалактическом пространстве на расстоянии примерно 65 Мпк или 250 млн световых лет от Земли в созвездии Наугольник.
Величина звездная — число, характеризующее блеск объекта. Чем меньше звездная величина — тем больше блеск.
Вертикаль — большой полукруг небесной сферы, проходящий через зенит, светило надир.
Восход — момент пересечения светилом горизонта, когда оно переходит из невидимой части небесной сферы в видимую.
Восхождение прямое — угловое расстояние по небесному экватору от точки весеннего равноденствия до часового круга, проходящего через светило. Отсчитывается в сторону, противоположную суточному вращению небесной сферы.
Внешние планеты — планеты Солнечной системы, большие полуоси орбит которых больше, чем большая полуось орбиты Земли. Внешними планетами являются: Марс, Юпитер, Сатурн, Уран, Нептун.
Внутренние планеты — планеты, большие полуоси орбит которых больше, чем большая полуось Земли. Внешними планетами являются: Меркурий, Венера.
Высота — угловое расстояние по вертикалу от математического горизонта до светила.
Г
Галилеевы спутники Юпитера — четыре крупнейших спутника Юпитера, открытые Галилеем — Ио, Европа, Ганимед и Каллисто.
Галактика — гравитационно-связанная система из звёзд и звёздных скоплений, межзвёздного газа и пыли, и тёмной материи.
Год световой — внесистемная единица длины, равная расстоянию, проходимому светом за один год, ≈ 9,46 · 1015 метра.
Голова кометы — ядро и кома кометы.
Горизонт математический — большой круг небесной сферы, плоскость которого перпендикулярна к отвесной линии.
Гравитация (тяготение) — сила взаимного притяжения, действующая между любыми двумя телами; ее величина прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Гулда пояс — группа очень молодых массивных звёзд возрастом 10—30 млн лет, формирующая диск диаметром 500—1000 пк, центр которого находится на расстоянии 150—250 пк от Солнца в направлении антицентра Галактики.
Д
Дата юлианская — порядковый номер дня, полученный в результате непрерывного счета дней от 1 января 4713 г. до н.э. Началом каждого юлианского дня считается средний гринвичский полдень.
Движение планет видимое — наблюдаемое перемещение планет относительно звезд.
Дождь метеорный — метеорный поток большой интенсивности.
Долгота географическая — двугранный угол между плоскостями нулевого меридиана и меридиана, проходящего через точку на Земле.
Е
Единица астрономическая (а.е.)— среднее расстояние между Землей и Солнцем.
З
Затмение лунное — явление прохождения Луны через земную тень (теневое затмение) или полутень (полутеневое затмение).
Затмение солнечное — явление покрытия Луной Солнца. Бывает полным, частным и кольцеобразным.
Заход — момент пересечения светилом горизонта, когда оно переходит из видимой части небесной сферы в невидимую.
Звезда — массивный газовый шар, излучающий свет и удерживаемый силами собственной гравитации и внутренним давлением, в недрах которого происходят термоядерные реакции.
Звезда двойная — система из двух гравитационно связанных звёзд, обращающихся по замкнутым орбитам вокруг общего центра масс.
Звезда переменная — звезда, блеск которой изменяется со временем в результате происходящих в её районе физических процессов. Строго говоря, блеск любой звезды меняется со временем в той или иной степени.
Звезда пекулярная — отличаются от обычных звёзд того же спектрального класса некоторыми существенными особенностями в спектрах, а иногда и другими свойствами (например, сильных и переменных магнитных полей).
Звездная величина — безразмерная числовая характеристика яркости объекта, обозначаемая буквой m. Обычно понятие применяется к небесным светилам.
Звездное скопление — гравитационно связанная группа звёзд, имеющая общее происхождение и движущаяся в гравитационном поле галактики как единое целое.
Звездное скопление рассеянное — представляет собой группу звёзд (числом вплоть до нескольких тысяч), образованных из одного гигантского молекулярного облака и имеющих примерно одинаковый возраст.
Звездное скопление шаровое — звёздное скопление, содержащее большое число звёзд, тесно связанное гравитацией и обращающееся вокруг галактического центра в качестве спутника. В отличие от рассеянных звёздных скоплений, которые располагаются в галактическом диске, шаровые находятся в гало; они значительно старше, содержат гораздо больше звёзд, обладают симметричной сферической формой и характеризуются увеличением концентрации звёзд к центру скопления.
Зенит — расположенная над головой наблюдателя точка пересечения отвесной линии с поверхностью небесной сферы.
Зенитное часовое число (ZNH) — количество метеоров данного потока, которое увидел бы наблюдатель невооруженным глазом за один час на ночном небе при радианте потока, находящемся в зените.
К
Квазар — квазизвездный источник радиоизлучения. Этот небесный объект внешне похож на звезду, он виден на большом расстоянии, даже равном миллиардам световых лет. Квазары представляют собой галактики на начальном этапе развития, в которых сверхмассивная черная дыра поглощает окружающее вещество.
Класс спектральный — характеристика спектра и поверхностной температуры звезды. Различают семь основных и три боковых класса, каждый класс делится на десять подклассов.
Комета — тело малой плотности, состоящее из газа и пыли и обращающееся вокруг Солнца. У комет различают голову, образуемую ядром и окружающей его комой, и хвост.
У комет различают голову, образуемую ядром и окружающей его комой, и хвост.
Координаты горизонтальные — измеренные относительно математического горизонта (азимут и высота). — экваториальные — измеренные относительно небесного экватора (прямое восхождение или часовой угол и склонение).
Корона солнечная — внешние слои атмосферы Солнца, начинающиеся выше тонкого переходного слоя над хромосферой, в котором температура возрастает в 100 раз.
Космология — раздел астрономии, изучающий свойства и эволюцию Вселенной в целом. Основу этой дисциплины составляют математика, физика и астрономия.
Красное смещение — сдвиг спектральных линий химических элементов в красную(длинноволновую) сторону. Это явление может быть выражением эффекта Доплера или гравитационного красного смещения, или их комбинацией.
Кульминация — момент пересечения светилом небесного меридиана.
Л
Ланиакея — сверхскопление галактик, в котором, в частности, содержатся Сверхскопление Девы (составной частью которого является Местная группа, содержащая галактику Млечный Путь с Солнечной системой) и Великий аттрактор, в котором расположен центр тяжести Ланиакеи.
Либрация — медленное колебание (действительное или кажущееся) спутника, наблюдаемое с поверхности тела, вокруг которого он вращается. Без дополнительных уточнений слово «либрация» обычно означает кажущееся колебательное движение Луны при наблюдении с Земли.
Лимб — видимый край диска светила в проекции на небесную сферу.
М
Магнитар — нейтронная звезда, обладающая исключительно сильным магнитным полем (до 1011 Тл).
Метеор — световое явление в атмосфере Земли при попадании и сгорании в ней метеороида.
Метеорит — метеороид, упавший на поверхность Земли или другой планеты.
Метеороид — твердое тело, движущееся в межпланетном пространстве, размером меньше астероида.
Млечный Путь — название нашей Галактики. Он смотрится как пересекающая небо неяркая полоса.
Н
Надир — расположенная под ногами наблюдателя точка пересечения отвесной линии с поверхностью небесной сферы.
Наклонение орбиты — двугранный угол, образованный плоскостями эклиптики и орбиты небесного тела.
Нейтронная звезда — это сверхплотное ядро мертвой звезды, оставшееся после взрыва сверхновой.
Новая — звёзды, светимость которых внезапно увеличивается в ~103—106 раз (в среднем увеличение светимости — в ~104, блеска — на ~12 звёздных величин).
Новолуние — фаза Луны, при которой ее эклиптическая долгота равна эклиптической долготе Солнца.
Ночь астрономическая — период суток между астрономическими сумерками, когда Солнце погружено под горизонт ниже 18 градусов.
Нутация — слабое нерегулярное движение вращающегося твёрдого тела, совершающего прецессию.
О
Оппозиция — положение при котором два небесных объекта оказываются напротив друг друга по отношению к Солнцу. Обычно оппозиция касается планет.
Ось мира — прямая, вокруг которой происходит кажущееся вращение небесной сферы.
П
Парад планет — астрономическое явление, при котором некоторое количество планет Солнечной системы оказывается по одну сторону от Солнца в небольшом секторе.
Параллакс годовой — угол, под которым из данной точки виден радиус орбиты Земли. — суточный — угол, под которым из данной точки виден радиус Земли.
Парсек — распространённая в астрономии внесистемная единица измерения расстояний.
Перигей — наиболее близкая к Земле точка орбиты обращающегося вокруг нее тела.
Перигелий — наиболее близкая к Солнцу точка орбиты обращающегося вокруг него тела.
Планет конфигурации — взаимные расположения планет и Солнца на небесной сфере земного наблюдателя.
Пояс часовой — участок Земли, для всех точек которого принимается одинаковое поясное время.
Покрытия небесных тел Луной — явления закрытия диском Луны небесных тел при ее движении относительно звезд.
Покрытия звезд астероидами — явления закрытия диском астероида звезды.
Полнолуние — фаза Луны, при которой разность эклиптических долгот Солнца и Луны равна 180 градусам.
Поток метеорный — 1) явление множественного падения метеоров в течение нескольких часов или дней из одного радианта; 2) рой метеороидов, движущихся по одной орбите вокруг Солнца.
Противосияние — размытое слабосветящееся пятно, видимое на ночном небе в точке, диаметрально противоположной Солнцу. Возникает при рассеянии солнечного света пылевыми частицами межпланетной среды.
Возникает при рассеянии солнечного света пылевыми частицами межпланетной среды.
Противостояние — конфигурация двух небесных тел, при которой разность их эклиптических долгот равна 180 градусам.
Протуберанец — плотные конденсации относительно холодного (по сравнению с солнечной короной) вещества, которые поднимаются и удерживаются над поверхностью Солнца магнитным полем.
Пульсар — космический источник радио- (радиопульсар), оптического (оптический пульсар), рентгеновского (рентгеновский пульсар) и/или гамма- (гамма-пульсар) излучений, приходящих на Землю в виде периодических всплесков (импульсов).
Р
Равноденствие — момент пересечения центра диска Солнца небесного экватора при переходе в северное полушарие — весеннее — 21 марта или южное — осеннее — 23 сентября.
Равноденствия точки — точки пересечения небесного экватора и эклиптики (точки весеннего и осеннего равноденствия). В точке весеннего равноденствия Солнце пересекает небесный экватор, переходя из южного полушария небесной сферы в северное.
В точке весеннего равноденствия Солнце пересекает небесный экватор, переходя из южного полушария небесной сферы в северное.
Радиант метеорного потока — точка на небесной сфере, в которой пересекаются воображаемые продолжения светящихся треков метеорного потока.
Реликтовое излучение — равномерно заполняющее Вселенную тепловое излучение, возникшее в эпоху первичной рекомбинации водорода. Обладает высокой степенью изотропности и спектром, характерным для абсолютно чёрного тела с температурой 2,72548 ± 0,00057 К.
Ретроградное движение планет (попятное движение) — это видимое движение планет, в результате которого складывается такое впечатление, будто эти планеты останавливаются и начинают попятное движение. Это явление происходит в результате различия скорости движения этих планет и Земли вокруг Солнца.
Рефлектор телескоп — оптический телескоп, использующий в качестве светособирающего элемента зеркало. Первый рефлектор был построен Исааком Ньютоном в конце 1668 года.
Первый рефлектор был построен Исааком Ньютоном в конце 1668 года.
Рефрактор телескоп — оптический телескоп, в котором для собирания света используется система линз, называемая объективом. Работа таких телескопов обусловлена явлением рефракции (преломления).
Рефракция — явление преломления света на границе двух сред с разной оптической плотностью. Астрономическая рефракция увеличивает видимую высоту светил над. горизонтом.
С
Сарос — цикл затмений, повторяющийся с интервалом 6585 суток (18 лет и 10 (11) дней). В саросе содержится 41 солнечное и 29 теневых лунных затмений.
Сверхновая — феномен, в ходе которого звезда резко меняет свою яркость на 4—8 порядков (на десяток звёздных величин) с последующим сравнительно медленным затуханием вспышки. Является результатом катаклизмического процесса, возникающего в конце эволюции некоторых звёзд и сопровождающегося выделением огромной энергии.
Сверхскопление Девы — нерегулярное сверхскопление галактик размером около 200 миллионов световых лет, включающее Местную группу галактик, скопление галактик в Деве и несколько других скоплений и групп галактик. Всего в состав Местного сверхскопления входят как минимум 100 групп и скоплений галактик.
Склонение — угловое расстояние по часовому кругу от небесного экватора до светила. Положительно к северу и отрицательно к югу.
Скорость лучевая — проекция скорости небесного тела относительно наблюдателя на линию визирования. Положительна в случае удаления тела от наблюдателя и отрицательна в случае приближения.
Соединение — конфигурация двух небесных тел, при которой их эклиптические долготы равны. В случае соединения внутренней планеты с Солнцем различают нижнее соединение — когда планета расположена между Землей и Солнцем, и верхнее соединение — когда планета расположена за Солнцем.
Созвездие — в современной астрономии участки, на которые разделена небесная сфера для удобства ориентирования на звёздном небе. В древности созвездиями назывались характерные фигуры, образуемые яркими звёздами.
Солнце среднее экваториальное — воображаемая точка, равномерно движущаяся по небесному экватору так, что в каждый момент ее прямое восхождение равно средней долготе истинного Солнца.
Солнцестояние — момент прохождения центром диска Солнца самой северной (летнее) или южной (зимнее) точки эклиптики.
Стояние — кажущаяся остановка в видимом движении планеты при переходе от прямого движения к попятному и наоборот.
Сумерки — часть суток после захода Солнца или перед его восходом.
Сумерки астрономические — ограничиваются погружением Солнца под горизонт до 18 градусов. При большем погружении начинается астрономическая ночь.
Сумерки гражданские — ограничиваются погружением Солнца под горизонт до 6 градусов.
Сумерки навигационные — ограничиваются погружением Солнца под горизонт до 12 градусов.
Сутки звездные — промежуток времени между двумя последовательными одноименными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане.
Сутки истинные солнечные — промежуток времени между двумя последовательными одноименными кульминациями центра видимого диска Солнца на одном и том же географическом меридиане.
Сутки средние солнечные — промежуток времени между двумя последовательными одноименными кульминациями среднего экваториального Солнца на одном и том же географическом меридиане.
Сфера небесная — сфера произвольного радиуса с центром в точке наблюдения.
Т
Терминатор — линия, отделяющая темную часть видимого диска планеты от светлой.
Толща оптическая — натуральный логарифм отношения интенсивности света до входа в поглощающую среду к его интенсивности после ее прохождения.
У
Узел — точка пересечения орбиты небесного тела с эклиптикой. Различают восходящий и нисходящий узлы.
Угол часовой — угловое расстояние по небесному экватору от верхней точки экватора до часового круга, проходящего через светило. Отсчитывается в сторону суточного движения небесной сферы.
Уравнение времени — разность между средним и истинным солнечным временем.
Ф
Фаза затмения — отношение закрытой части диаметра затмеваемого тела, проходящего через центр затмевающего тела, к полному диаметру затмеваемого тела. Для полного затмения эта величина равна единице плюс отношение минимального расстояния между краями затмевающего и затмеваемого тела к диаметру затмеваемого тела.
Фаза планеты — отношение площади освещенной части видимого диска ко всей его площади.
Флоккулы — волокнистые образования в хромосфере Солнца, имеющие бо́льшую яркость и плотность, чем окружающие их участки. Являются продолжением фотосферных факелов в хромосферу.
Фотосфера — излучающий слой звёздной атмосферы, в котором формируется непрерывный спектр излучения. Фотосфера даёт основную часть излучения звезды.
Х
Хвост кометный — газопылевой хвост кометы.
Хромосфера — внешняя оболочка Солнца и других звёзд толщиной около 10 000 км, окружающая фотосферу.
Ч
Черная дыра — область пространства-времени, гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света, в том числе кванты самого света.
Ц
Цефеиды — класс пульсирующих переменных звёзд с довольно точной зависимостью период—светимость, названный в честь звезды δ Цефея. Одной из наиболее известных цефеид является Полярная звезда.
Ш
Широта географическая — угол между плоскостью земного экватора и отвесной линией.
Э
Экватор земной — большой круг на поверхности Земли, плоскость которого перпендикулярна оси вращения. — небесный — большой круг небесной сферы, плоскость которого перпендикулярна к оси мира.
Эклиптика — 1) плоскость орбиты Земли; 2) видимый годичный путь Солнца относительно звезд на небесной сфере.
Эксцентриситет — величина, характеризующая отличие формы орбиты от круговой. Для окружности равен нулю, для параболы — единице.
Элементы орбиты — набор параметров, однозначно характеризующий орбиту небесного тела.
Элонгация — угловое расстояние планеты (кометы, астероида) от Солнца. Различают восточную (планета к востоку от Солнца) и западную (планета к западу от Солнца) элонгацию.
Эпоха — момент времени, выбранный в качестве начального отсчета.
Эфемерида — таблица, в которой приведены вычисленные координаты небесного тела для различных моментов времени.
Я
Ядерный синтез — соединение химических элементов в звездах при прохождении ядерных реакций в ядрах. Ядерный синтез проходил и на начальных стадиях жизни Вселенной.
Вычисление значения логарифмического выражения
В этой статье вы познакомитесь со всеми типами логарифмических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.
16 видео помогут вам понять как использовать свойства логарифмов при упрощении логарифмических выражений.
Вы можете попытаться решить каждый пример самостоятельно, и затем свериться с ответом. А можете сначала посмотреть видео с решением аналогичного задания.
Пример 1. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 6
Видеорешение аналогичного задания:
Пример 2. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 30
Видеорешение аналогичного задания:
Пример 3. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 0,125
Видеорешение аналогичного задания:
Пример 4. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 1,5
Видеорешение аналогичного задания:
Пример 5. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 6. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 7. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,75
Видеорешение аналогичного задания:
Пример 8. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 216
Видеорешение аналогичного задания:
Пример 9. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 1
Видеорешение аналогичного задания:
Пример 10. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,75
Видеорешение аналогичного задания:
Пример 11. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 1
Видеорешение аналогичного задания:
Пример 12. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 13. Найти значение выражения:Посмотреть ответ:
показать
Ответ: -2
Видеорешение аналогичного задания:
Пример 14. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,5625
Видеорешение аналогичного задания:
Пример 15. Найти значение выражения:Посмотреть ответ:
показать
Ответ: -0,2
Видеорешение аналогичного задания:
Пример 16. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 25
Видеорешение аналогичного задания:
И.В. Фельдман, репетитор по математике.
Что такое числовое выражение? — Определение, факты и пример
Что такое числовое выражение?
Термин «числовое выражение» состоит из двух слов: числовое значение «числа» и «выражение, означающее фразу». Таким образом, это фраза, включающая числа.
Числовое выражение в математике может быть комбинацией чисел, целых чисел, объединенных с использованием математических операторов, таких как сложение, вычитание, умножение или деление.
Примеры числовых выражений
Мы можем сформировать числовое выражение, комбинируя числа с различными математическими операторами.Число операторов, которые может содержать числовое выражение, не ограничено. Некоторые числовые выражения используют только один оператор между двумя числами, а некоторые могут содержать больше.
Некоторые примеры числовых выражений приведены ниже:
10 + 5
250–75
60 × 5 + 10
72 ÷ 8 × 5 — 4 + 1
82 + 4 — 10
Запись числового выражения
Любая математическая словесная задача решается сначала преобразованием в числовое выражение.Ниже приведены некоторые примеры.
У Кэндис 10 плиток шоколада. Она дает 3 сестре, 1 подруге и съедает 2 из них. Позже она навещает свою бабушку, и она (бабушка) предлагает Кэндис еще 12 плиток шоколада. Сколько плиток шоколада у Кэндис сейчас?
Давайте посмотрим на числа, участвующие в указанной выше проблеме. Кэндис начинает с 10 батончиков, раздает 4 (3 + 1), съедает 2 и снова получает еще 12 от бабушки. Итак, числовое выражение
10–3–1–2 + 12
= 7–1–2 + 12
= 6–2 + 12
= 4 + 12
= 16
Это дает нам 16.
Интересные факты
|
Например:
Как написать числовое выражение? — Определение и примеры — Видео и стенограмма урока
Примеры числовых выражений
Единственным требованием к числовому выражению является то, что оно должно содержать только числа и символы операций.Некоторые числовые выражения имеют только один символ операции. У других их два и более. Вот несколько примеров числовых выражений:
4 + 5
134 — 75
56 * 4 + 6
68/8 * 7 — 2 + 1
Примеры нечисловых выражений
Поскольку числовые выражения могут содержать только числа , выражения, содержащие переменных (например, x или y ), не могут считаться числовыми выражениями. На самом деле они называются алгебраическими выражениями .Вот два примера алгебраических выражений:
4 x + 5
134 — x
Написание числовых выражений
Когда дана устная или записанная задача слов , важно уметь переводить преобразовать слова в числовое выражение, чтобы вы могли решить проблему. Вот несколько примеров.
Пример 1:
У Аманды было 12 мармеладных мишек, и 2 она отдала своему брату. Затем она съела 4 мармеладных мишек. Сколько мармеладных мишек осталось у Аманды?Аманда начала с 12, отдала два (-2) и съела 4 (-4).В этом примере нужно было использовать только операцию вычитания. Числовое выражение можно записать как:
12-2-4
Пример 2:
Джордж хочет выяснить, сколько он будет зарабатывать за год на работе с частичной занятостью. Он зарабатывает 500 долларов в месяц.Числовое выражение можно записать как:
500 * 12
Пример 3:
У Джоди есть неделя, чтобы прочитать всю книгу для школы. В книге 455 страниц. Она хочет равномерно распределить свои чтения в течение следующих семи дней.Числовое выражение можно записать как:
455/7
Пример 4:
Аарон пробегает 5 миль на этой неделе, 6 на следующей неделе и 7 на следующей неделе. Он хочет знать, сколько миль он пробежал за три недели.Числовое выражение можно записать как:
5 + 6 + 7
Сводка урока
Числовое выражение — это математическое предложение, состоящее только из чисел и одного или нескольких символов операций. Поскольку числовые выражения могут содержать только числа, выражения, содержащие переменные (например, x или y ), не могут считаться числовыми выражениями.При наличии устной или письменной проблемы со словом важно уметь перевести слова в числовое выражение, чтобы вы могли решить проблему.
Написание обзора числовых выражений
| Условия | Определения |
|---|---|
| Переменные | (например, x или y ) нельзя рассматривать как числовые выражения |
| Алгебраические выражения | выражения, содержащие переменные |
| Проблема со словом | устная или письменная математическая задача |
Результаты обучения
По окончании урока подтвердите свою способность:
- Определить числовое выражение
- Определение переменных в алгебраическом уравнении
- Написать числовое выражение
Алгебраические выражения — объяснения и примеры
Алгебра — интересный и увлекательный раздел математики, в котором числа, фигуры и буквы используются для выражения задач.Независимо от того, изучаете ли вы алгебру в школе или сдаете какой-то тест, вы заметите, что почти все математические задачи представлены словами.
Следовательно, необходимость переводить письменные текстовые задачи в алгебраические выражения возникает тогда, когда нам нужно их решить.
Большинство алгебраических задач со словами состоят из рассказов или случаев из реальной жизни. Другие — простые фразы, такие как описание математической задачи. В этой статье вы узнаете, как написать алгебраических выражений из простых задач со словами, а затем перейти к легко сложным задачам со словами.
Что такое алгебраическое выражение?
Многие люди попеременно используют алгебраические выражения и алгебраические уравнения, не подозревая, что это совершенно разные термины.
Алгебраика — это математическая фраза, в которой две стороны фразы соединены знаком равенства (=). Например, 3x + 5 = 20 — это алгебраическое уравнение, где 20 представляет собой правую часть (RHS), а 3x +5 представляет собой левую часть (LHS) уравнения.
С другой стороны, алгебраическое выражение — это математическая фраза, в которой переменные и константы объединяются с помощью операционных символов (+, -, × & ÷).В алгебраическом символе отсутствует знак равенства (=). Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
Давайте рассмотрим терминологию, используемую в алгебраическом выражении:
- Переменная — это буква, значение которой нам неизвестно. Например, x — это наша переменная в выражении: 10x + 63.
- Коэффициент — это числовое значение, используемое вместе с переменной. Например, 10 — это переменная в выражении 10x + 63.
- Константа — это терм, который имеет определенное значение.В этом случае 63 — это константа в алгебраическом выражении, 10x + 63.
Существует несколько типов алгебраических выражений, но основной тип включает:
- Мономиальное алгебраическое выражение
Этот тип выражения имеет только один член, например, 2x, 5x 2 , 3xy и т. д.
Алгебраическое выражение, имеющее два, в отличие от членов, например, 5y + 8, y + 5, 6y 3 + 4 и т. д.
Это алгебраическое выражение с более чем одним членом и ненулевыми показателями переменных.Пример полиномиального выражения: ab + bc + ca и т. Д.
Другие типы алгебраических выражений:
Числовое выражение состоит только из чисел и операторов. В числовое выражение переменная не добавляется. Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
Это выражение содержит переменные вместе с числами, например, 6x + y, 7xy + 6 и т. Д.
Как решить алгебраическое выражение?
Цель решения алгебраического выражения в уравнении — найти неизвестную переменную.Когда два выражения приравниваются, они образуют уравнение, и поэтому становится легче найти неизвестные члены.
Чтобы решить уравнение, поместите переменные с одной стороны, а константы — с другой. Вы можете изолировать переменные, применяя арифметические операции, такие как сложение, вычитание, умножение, деление, квадратный корень, кубический корень и т. Д.
Алгебраические выражения всегда взаимозаменяемы. Это означает, что вы можете переписать уравнение, поменяв местами LHS и RHS.
Пример 1
Вычислите значение x в следующем уравнении
5x + 10 = 50
Решение
Заданное уравнение как 5x + 10 = 50
Изолируйте переменные и константы;5x = 50-10
5x = 40
Разделите обе части на коэффициент переменной;
x = 40/5 = 8
Следовательно, значение x равно 8.
Пример 2
Найдите значение y, когда 5y + 45 = 100
Решение
Изолировать переменные от констант;
5y = 100-45
5y = 55
Разделим обе части на коэффициент;
y = 55/5
y = 11
Пример 3
Определите значение переменной в следующем уравнении:
2x + 40 = 30
Решение
Разделите переменные из константы;
2x = 30-40
2x = -10
Разделите обе стороны на 2;
x = -5
Пример 4
Найдите t, когда 6t + 5 = 3
Решение
Отделите константы от переменной,
3
6t = -2
Разделим обе части на коэффициент,
t = -2/6
Упростим дробь,
t = -1/3
Практические вопросы
1.Если x = 4 и y = 2, найдите следующие выражения:
a. 2г + 4
б. 10х + 40л;
г. 15лет — 5x
д. 5x + 7
e. 11y + 6
ф. 6x — 2
г. 8лет — 5
ч. 60 — 5x — 2y
2. Сэм кормит свою рыбу одинаковым количеством корма (пусть равным x ) трижды в день. Сколько еды он накормит рыбу в неделю?
3. Нина испекла 3 кекса для сестры и по 2 кекса для каждой подруги (пусть равно x ).Сколько всего кексов она испекла?
4. У Джонса на ферме 12 коров. Большинство коров дают 30 литров молока в день (пусть равно х ). Сколько коров не дают 30 литров молока в день?
Предыдущий урок | Главная страница | Следующий урокПрактическое руководство. Вычисление числовых значений — Visual Basic
- 2 минуты на чтение
В этой статье
Числовые значения можно вычислять с помощью числовых выражений.Числовое выражение — это выражение, которое содержит литералы, константы и переменные, представляющие числовые значения, и операторы, которые действуют на эти значения.
Расчет числовых значений
Для вычисления числового значения
Объедините один или несколько числовых литералов, констант и переменных в числовое выражение. В следующем примере показаны некоторые допустимые числовые выражения.
93,217System.Math.PIсчетчик4 * (67 + я)Первые три строки показывают литерал, константу и переменную. Каждый из них сам по себе образует допустимое числовое выражение. Последняя строка показывает комбинацию переменной с двумя литералами.
Обратите внимание, что числовое выражение само по себе не образует полный оператор Visual Basic. Вы должны использовать выражение как часть полного оператора.
Для сохранения числового значения
Вы можете использовать оператор присваивания, чтобы присвоить переменной значение, представленное числовым выражением, как показано в следующем примере.
Dim i As Integer = 2 Dim j как целое число j = 4 * (67 + я)В предыдущем примере значение выражения в правой части оператора равенства (
=) присваивается переменнойjв левой части оператора, поэтомуjоценивается как 276.Для получения дополнительной информации см. Заявления.
Несколько операторов
Если числовое выражение содержит более одного оператора, порядок их вычисления определяется правилами приоритета операторов.Чтобы переопределить правила приоритета операторов, вы заключаете выражения в скобки, как в приведенном выше примере; вложенные выражения оцениваются первыми.
Для отмены обычного приоритета оператора
В скобках заключите операции, которые нужно выполнить в первую очередь. В следующем примере показаны два разных результата с одинаковыми операндами и операторами.
Dim i As Integer = 2 Dim j, k как целое число j = 4 * (67 + я) к = 4 * 67 + яВ предыдущем примере при вычислении
jсначала выполняется оператор сложения (+), потому что круглые скобки около(67 + i)отменяют нормальный приоритет, а значение, присвоенноеj, составляет 276 (4 раза 69).Вычисление дляkвыполняет операторы с их обычным приоритетом (*перед+), а значение, присвоенноеk, составляет 270 (268 плюс 2).Дополнительные сведения см. В разделе Приоритет операторов в Visual Basic.
См. Также
Чтобы найти числовое значение выражения, просто подставьте переменные в выражении с заданным числом. Оценить: 2x + 7, если x = 4 Заменить.
Презентация на тему: « Чтобы найти числовое значение выражения, просто подставьте переменные в выражении с заданным числом.Оценить: 2x + 7, если x = 4 Заменить »- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>1
2 Чтобы найти числовое значение выражения, просто подставьте переменные в выражении с заданным числом.Вычислить: 2x + 7, если x = 4 Заменить 4 на x. 2 (4) + 7 8 + 7 = 15
3 Вычислить: 3x + 2y — 9, если x = 4, y = 2 Заменить x и y 3 (4) + 2 (2) — 9 Следуйте порядку действий. 12 + 4 — 9 16 — 9 7
4 Вычислить: 2x — 3xy + 4y, если x = 3, y = -5 Заменить числа. 2 (3) — 3 (3) (- 5) + 4 (-5) Используйте правильный порядок операций.6 + 45 — 20 51 — 20 31
5 Вычислить: 2x 2 + y 2-5, если x = -5, y = 7 Заменить x и y 2 (-5) + (7) 2-5 -10 + 49-5 39-5 34 !!!!
6 Неверно Оценить x 2, если x = -3 -3 2 = -9 Оценить –x 2, если x = -3 — (- 3) 2 = 3 2 = 9 Правильно Оценить x 2, если x = -3 (-3 ) 2 = 9 Вычислить –x 2, если x = -3 — (- 3) 2 = — (9) = -9
Обработайте числовое выражение, которое может включать переменные
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombinations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, MassConversion анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Простота Правые треугольники, Ветер, рисунок
Основы алгебры — Вычисление выражений
ср узнали, что в алгебраическом выражении буквы могут обозначать числа.Вот шаги для вычисления выражения:
- Заменить
каждая буква в выражении с присвоенным значением.
Сначала замените каждую букву в выражении значением, которое было назначенный на это. Чтобы ваши расчеты были понятными и не допускали ошибок, всегда заключите числа, которые вы заменяете, в круглые скобки. Значение, которое присвоенный переменной остается неизменным на протяжении всей задачи, даже если буква встречается в выражении более одного раза.Однако поскольку переменные «различаются», значение, присвоенное конкретной переменной может меняться от проблемы к проблеме, но не в рамках одной проблемы.
- Выполнить
операции в выражении с использованием правильного порядка операций.
После того, как вы подставили значение для буквы, выполните операции, чтобы найти значение выражения. Не забывайте использовать правильный порядок действий: сначала выполните какие-либо операции с показателями, затем выполните умножение и деление и, наконец, сложение и вычитание!
Вот пример.Оценим выражение 2x 3 — x 2 + y для x = 3 и y = –2.
Оценить: | Убедитесь, что уравнение понятное и вы знать, какая переменная какая. Хорошая идея написать выражение вниз и какова каждая переменная.Оставьте себе достаточно места для тренировок проблема построчно, с каждым шагом прямо под предыдущим. |
2 (3) 3 — (3) 2 + (-2) | Заменить каждая переменная в выражении со своим значением. В этом примере это означает, что каждый x становится 3, а каждый y становится -2. Это хорошая идея используйте круглые скобки, чтобы отслеживать это. Совет: будьте особенно осторожны с отрицательные числа! |
2 (27) — 9 + (-2) | Выполнить операции с показателями. |
54 — 9 + (- 2) | Выполнить операции с умножением и делением. |
43 | Выполнение операций сложения и вычитания |
назад наверх
.
 find('p', class_ = 'css-aaabbbccc').text
# находим адрес
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price
find('p', class_ = 'css-aaabbbccc').text
# находим адрес
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price website.com/london/page_size=25&q=london&pn='
map = {}
id = 0
# максимальное количество страниц
max_pages = 15
for p in range(max_pages):
cur_url = url + str(p + 1)
print("Скрапинг страницы №: %d" % (p + 1))
html_text = requests.get(cur_url).text
soup = BeautifulSoup(html_text, 'lxml')
ads = soup.find_all('div', class_ = 'css-ad-wrapper-123456')
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price
website.com/london/page_size=25&q=london&pn='
map = {}
id = 0
# максимальное количество страниц
max_pages = 15
for p in range(max_pages):
cur_url = url + str(p + 1)
print("Скрапинг страницы №: %d" % (p + 1))
html_text = requests.get(cur_url).text
soup = BeautifulSoup(html_text, 'lxml')
ads = soup.find_all('div', class_ = 'css-ad-wrapper-123456')
for i in range(len(ads)):
ad = ads[i]
id += 1
map[id] = {}
price = ad.find('p', class_ = 'css-aaabbbccc').text
address = ad.find('p', class_ = 'css-address-123456').text
map[id]["address"] = address
map[id]["price"] = price append(float(x[0]))
map[id]["station"].append(x[1])
append(float(x[0]))
map[id]["station"].append(x[1]) text
x = s.split(' miles ')
map[id]["distance"].append(float(x[0]))
map[id]["station"].append(x[1])
map[id]["transport_type"].append(type[i]['testid'])
text
x = s.split(' miles ')
map[id]["distance"].append(float(x[0]))
map[id]["station"].append(x[1])
map[id]["transport_type"].append(type[i]['testid']) DataFrame(result, columns = ["ad_id", "price", "address",
"distance", "station", "transport_type"])
DataFrame(result, columns = ["ad_id", "price", "address",
"distance", "station", "transport_type"]) csv'
df.to_csv(filename)
csv'
df.to_csv(filename)