Найти длину отрезка служащего решением двойного неравенства: Найдите длину отрезка, служащего решением двойного неравенства -3 ≤ (5 + 3x) / 4 ≤ 1. Укажите середину отрезка.

Домашняя контрольная работа № 1, Вариант 1, Задание 9 Алгебра 9 класс Мордкович Найдите длину отрезка – Рамблер/класс

Домашняя контрольная работа № 1, Вариант 1, Задание 9 Алгебра 9 класс Мордкович Найдите длину отрезка – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Найдите длину отрезка, служащего решением двойного
неравенства

Укажите середину отрезка.
 

ответы

Вот так вот
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х — 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.

..)

ГДЗ11 классКолмогоров А.Н.Алгебра

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

     Среди предложений    21-29:  
      (21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 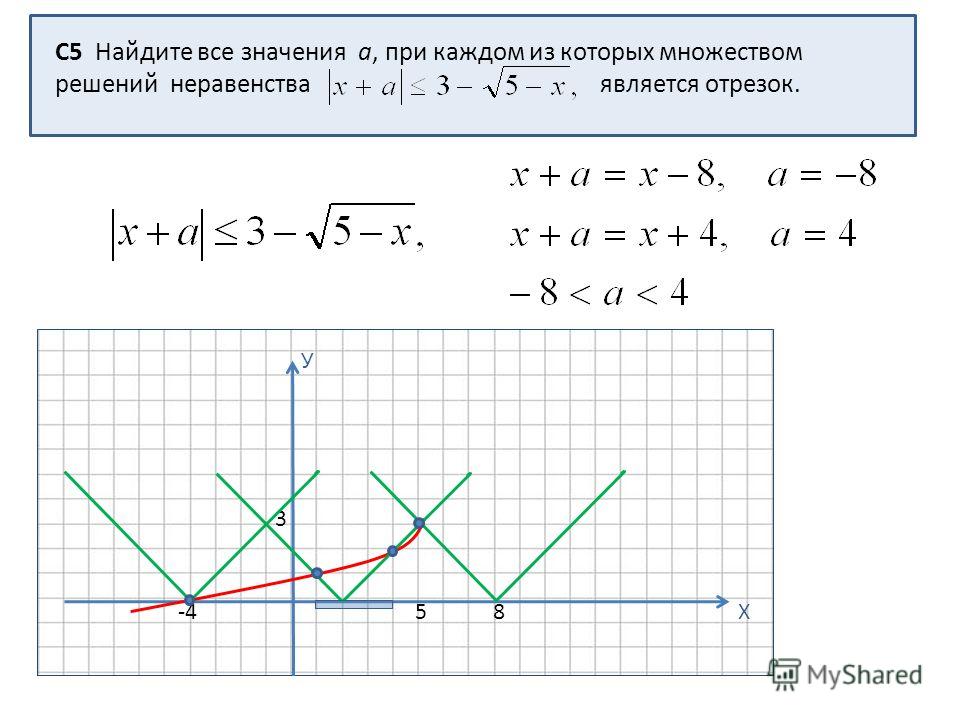60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

Решение сложных неравенств | Начальная алгебра

Цели обучения

• Описывать множества как пересечения или объединения
  • Использовать обозначение интервала для описания пересечений и объединений
  • Использование графов для описания пересечений и объединений
• Решение сложных неравенств — ИЛИ
  • Решить сложные неравенства в форме или и выразить решение графически и через интервал
• Решение составных неравенств — И
  • Выразить решения неравенств графически и с интервальной записью
  • Найдите решения сложных неравенств в форме [латекс]а<х
• Решение абсолютных неравенств
  • Решение одношаговых и многошаговых неравенств, содержащих абсолютные значения
  • Определить случаи, когда нет решений абсолютных неравенств

 

Используйте запись интервала для описания наборов чисел как пересечений и объединений

Когда два неравенства соединяются словами и , решение составного неравенства происходит, когда оба неравенства верны одновременно. Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда или из неравенств верны. Решение представляет собой комбинацию или объединение двух отдельных решений.

В этом разделе мы научимся решать сложные неравенства, которые соединяются словами И и ИЛИ. Во-первых, это поможет увидеть некоторые примеры неравенств, интервалов и графиков составных неравенств. Это поможет вам правильно описать решения сложных неравенств.

Диаграммы Венна используют концепцию пересечений и объединений, чтобы показать, сколько общего у двух или более объектов. Например, эта диаграмма Венна показывает пересечение людей, которые разбивают вам сердце, и тех, кто ежедневно расшатывает вашу уверенность. Очевидно, Сесилия обладает обоими этими качествами; поэтому она является пересечением двух.

В математических терминах рассмотрим неравенство [латекс]x\lt6[/латекс] и [латекс]х\gt2[/латекс].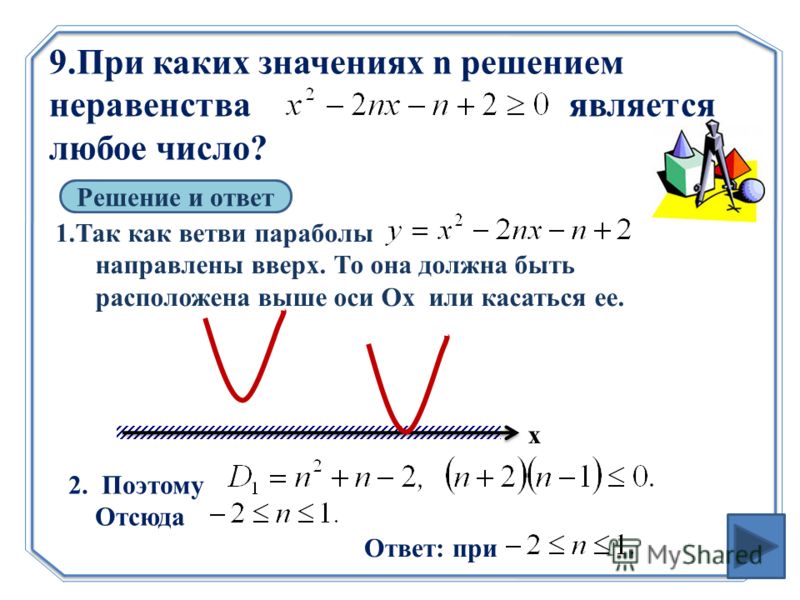 Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал?

На словах x должно быть меньше 6 , и в то же время должно быть больше 2, очень похоже на приведенную выше диаграмму Венна, где Сесилия одновременно разбивает вам сердце и ежедневно подрывает вашу уверенность. Давайте посмотрим на график, чтобы увидеть, какие числа возможны с этими ограничениями.

Числа, общие для обеих линий на графике, называются пересечением двух неравенств [latex]x\lt6[/latex] и [latex]x\gt2[/latex]. Это называется ограниченным неравенством и записывается как [latex]2\lt{x}\lt6[/latex]. Подумайте об этом на минуту. x должно быть меньше 6 и больше двух — значения x будут попадать между двумя числами .  В записи интервала это выглядит как [латекс]\влево(2,6\вправо)[/латекс]. График будет выглядеть так:

С другой стороны, если вам нужно представить две вещи, которые не имеют общих элементов или признаков, вы можете использовать объединение. На следующей диаграмме Венна показаны две вещи, которые не имеют схожих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции.

В математических терминах, например, [latex]x>6[/latex] или  [latex]x<2[/latex] — это неравенство, к которому присоединяются слова или . Используя интервальную запись, мы можем описать каждое из этих неравенств отдельно:

[latex]x\gt6[/latex] совпадает с [latex]\left(6, \infty\right)[/latex] и [latex]x<2[/latex] совпадает с [latex ]\влево(\infty, 2\вправо)[/латекс]. Если мы описываем решения неравенств, какой эффект имеют или ? Мы говорим, что решения – это либо действительные числа, меньшие двух 90 057, либо 90 058 действительных чисел, большие 6. Вы понимаете, почему нам нужно записывать их как два отдельных интервала? Давайте посмотрим на график, чтобы получить четкое представление о том, что происходит.

Если вы поместите оба этих неравенства на график, мы увидим, что они не имеют общих чисел.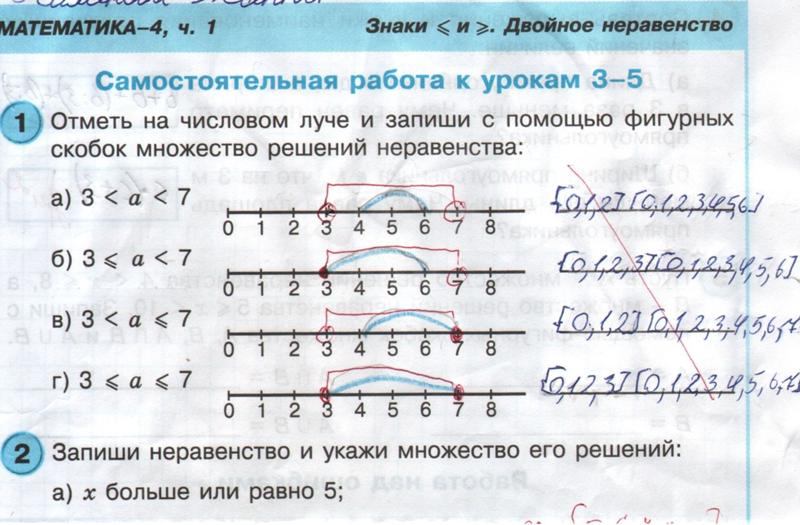 Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:

[латекс]\влево(\infty, 2\вправо)\чашка\ left(6, \infty\right)[/latex]

Общепринято строить интервалы, начинающиеся с крайнего левого значения на числовой прямой в качестве левого значения, например [latex]\left(2,6 \right)[/latex], где 2 меньше 6. Число справа должно быть больше числа слева.

Пример

Нарисуйте график составного неравенства [latex]x\gt3[/latex] или  [latex]x\le4[/latex] и опишите набор x -значений, которые удовлетворяют ему с интервал.

Показать решение

Примеры

Нарисуйте график составного неравенства: [latex]x\lt5[/latex]  и  [latex]x\ge-1[/latex] и опишите множество x — значения, которые будут его удовлетворять с интервалом.

Показать решение

Примеры

Нарисуйте график сложного неравенства [латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс] и опишите множество x — значения, которые будут удовлетворять его с интервалом.

Показать решение

В следующем видео представлены два примера того, как рисовать неравенства с участием И, а также записывать соответствующие интервалы.

Решение составных неравенств в форме или

Как мы видели в предыдущем разделе, решение составного неравенства, состоящего из двух неравенств, соединенных словом или , представляет собой объединение решений каждого неравенства. Объединения позволяют нам создать новый набор из двух элементов, которые могут иметь или не иметь общих элементов.

В этом разделе вы увидите, что некоторые неравенства необходимо упростить, прежде чем их решение можно будет записать или изобразить в виде графика.

В следующем примере вы увидите пример решения одношагового неравенства в форме ИЛИ. Обратите внимание, как каждое неравенство обрабатывается независимо до конца, где решение описывается в терминах обоих неравенств. Для решения составных неравенств вы будете использовать те же свойства, что и для решения обычных неравенств.

Не забывайте применять свойства неравенства при решении сложных неравенств. В следующем примере используется деление на отрицательное значение, чтобы изолировать переменную.

Пример

Найдите y . [latex]2y+7\lt13\text{ или }−3y–2\lt10[/latex]

Показать решение

В последнем примере окончательный ответ включал решения, интервалы которых перекрывались, в результате чего ответ включал все числа на числовой прямой. На словах мы называем это решение «все действительные числа». Любое действительное число даст истинное утверждение либо для [latex]y<3\text{, либо для }y\ge -4[/latex], если его заменить на 9.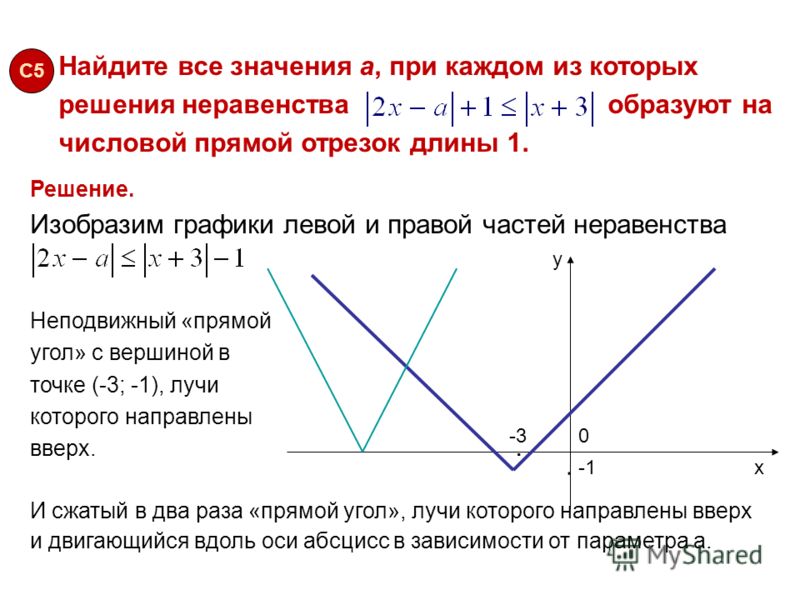 0057 х .

Пример

Найдите z . [латекс]5z-3\gt-18[/латекс] или [латекс]-2z-1\gt15[/латекс]

Показать решение

Следующее видео содержит пример решения составного неравенства с участием ИЛИ и построения соответствующего графика.

В следующем разделе вы увидите примеры решения составных неравенств, содержащих числа и .

Решить сложные неравенства в форме

и и представить решение графически

Решением составного неравенства, состоящего из двух неравенств, соединенных словами и , является пересечение решений каждого неравенства. Другими словами, оба утверждения должны быть истинными одновременно. Решением составного неравенства и являются все решения, общие для этих двух неравенств. Как мы видели в предыдущих разделах, именно здесь два графика перекрываются.

В этом разделе мы увидим больше примеров, когда мы должны упростить сложные неравенства, прежде чем мы сможем выразить их решения графически или с интервалом.

Пример

Решить для x :  [латекс] \displaystyle {5}{x}-{2}\le{3}\text{ и }{4}{x}{+7}>{3} [/latex]

Показать решение

Составные неравенства в форме [латекс]a

Вместо разделения составного неравенства в форме  [латекс]a и [latex]x>a[/latex], можно быстрее решить неравенство, применив свойства неравенства ко всем трем сегментам составного неравенства.

В видео ниже вы увидите еще один пример решения неравенства в форме  [latex]a

Чтобы решить неравенства вида [latex]a x . Какую бы операцию вы ни выполняли над средней частью неравенства, вы также должны выполнить ее с каждой из внешних частей. Обратите особое внимание на деление или умножение на отрицание.

Решение сложного неравенства с числами и всегда совпадает с решением каждого неравенства. Есть три возможных исхода сложных неравенств, соединенных словами и :

Случай 1:
Описание	Решением могут быть все значения между двумя конечными точками
Неравенства	[latex]x\le{1}[/latex] и [latex]x\gt{-1}[/latex], или в виде ограниченного неравенства: [latex]{-1}\lt{x}\le {1}[/латекс]
Интервал	[латекс]\влево(-1,1\вправо][/латекс]
Графики
Случай 2:
Описание	Решение может начинаться в точке на числовой прямой и продолжаться в одном направлении.
Неравенства	[латекс]x\gt3[/латекс] и [латекс]x\ge4[/латекс]
Интервал	[латекс]\влево[4,\infty\вправо)[/латекс]
Графики
Случай 3:
Описание	В тех случаях, когда два неравенства не перекрываются, составное неравенство не имеет решения
Неравенства	[латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс]
Интервалы	[латекс]\влево(-\infty,-3\вправо)[/латекс] и [латекс]\влево(3,\infty\вправо)[/латекс]
График

В приведенном ниже примере составное неравенство не имеет решения, поскольку неравенства не пересекаются.

Решение неравенств, содержащих абсолютные значения

Давайте применим то, что вы знаете о решении уравнений, содержащих абсолютные значения, и то, что вы знаете о неравенствах, для решения неравенств, содержащих абсолютные значения. Начнем с простого неравенства.

[латекс]\влево|х\вправо|\leq 4[/латекс]

Это неравенство читается как «абсолютное значение x меньше или равно 4». Если вас попросят решить для x , вы хотите узнать, какие значения x отстоят на 4 единицы или менее от 0 на числовой прямой. Вы могли бы начать с размышлений о числовой прямой и о том, какие значения x удовлетворяют этому уравнению.

4 и [латекс]−4[/латекс] находятся на расстоянии четырех единиц от 0, поэтому они являются решениями. 3 и [латекс]-3[/латекс] также являются решениями, потому что каждое из этих значений меньше, чем на 4 единицы от 0. Так же как 1 и [латекс]-1[/латекс], 0,5 и [латекс]-0,5[ /latex] и так далее — существует бесконечное количество значений для x , которые будут удовлетворять этому неравенству.

График этого неравенства будет иметь две замкнутые окружности, 4 и [латекс]−4[/латекс]. Расстояние между этими двумя значениями на числовой прямой окрашено в синий цвет, поскольку все эти значения удовлетворяют неравенству.

Решение можно записать так:

Неравенство: [латекс]-4\leq x\leq4[/латекс]

Интервал: [латекс]\влево[-4,4\вправо][/латекс]

Ситуация немного отличается, когда знак неравенства стоит «больше» или «больше или равно». Рассмотрим простое неравенство [латекс]\влево|х\вправо|>3[/латекс]. Опять же, вы могли бы подумать о числовой прямой и о том, какие значения числа x больше, чем на 3 единицы от нуля. На этот раз 3 и [латекс]−3[/латекс] не включены в решение, поэтому оба этих значения отмечены незакрашенными кружками. 2 и [латекс]-2[/латекс] не будут решениями, потому что они не более чем в 3 единицах от 0. Но 5 и [латекс]-5[/латекс] будут работать, как и все значения, расширяющие слева от [латекс]−3[/латекс] и справа от 3. График будет выглядеть так, как показано ниже.

Решение этого неравенства можно записать так:

Неравенство : [латекс]x<−3[/латекс] или [латекс]x>3[/латекс].

Интервал: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]

В следующем видео вы увидите примеры решения и выразить решение абсолютных неравенств с использованием И и ИЛИ.

Написание решений неравенств с абсолютными значениями

Для любого положительного значения a и x,  одной переменной или любого алгебраического выражения:

Неравенство абсолютного значения	Эквивалентное неравенство	Обозначение интервала
[латекс]\влево|{х}\вправо|\ле{а}[/латекс]	[латекс]{-a}\le{x}\le{a}[/латекс]	[латекс]\влево[-а, а\вправо][/латекс]
[латекс]\левый| х \право|\lt{a}[/латекс]	[латекс]{-a}\lt{x}\lt{a}[/латекс]	[латекс]\влево(-а, а\вправо)[/латекс]
[латекс]\левый| х \право|\ge{ а}[/латекс]	[латекс]{x}\le\text{−a}[/latex] или [латекс]{x}\ge{ a}[/latex]	[латекс]\влево(-\infty,-a\право]\чашка\влево[a,\infty\вправо)[/латекс]
[латекс]\левый| х \right|\gt\text{a}[/latex]	[латекс]\displaystyle{x}\lt\text{−a}[/latex] или [латекс]{x}\gt{a}[/latex]	[латекс]\влево(-\infty,-a\вправо)\чашка\влево(a,\infty\вправо)[/латекс]

Рассмотрим еще несколько примеров неравенств, содержащих абсолютные значения.

Определите случаи неравенств, содержащих абсолютные значения, которые не имеют решений

Как и в случае с уравнениями, могут быть случаи, когда неравенство не имеет решения.

Резюме

Составное неравенство — это утверждение из двух утверждений о неравенстве, связанных вместе либо словом , либо словом , либо словом и . Иногда составное неравенство и отображается символически, например [latex]a. Поскольку составные неравенства представляют собой либо объединение, либо пересечение отдельных неравенств, их графическое изображение на числовой прямой может быть полезным способом увидеть или проверить решение. Со сложными неравенствами можно работать и решать их почти так же, как решают любые неравенства, обращая внимание на свойства неравенств и правила их решения.

Абсолютные неравенства можно решить, переписав их с помощью составных неравенств. Первым шагом к решению абсолютных неравенств является выделение абсолютного значения. Следующий шаг — решить, работаете ли вы с неравенством ИЛИ или с неравенством И. Если неравенство больше числа, мы будем использовать ИЛИ. Если неравенство меньше числа, мы используем И. Помните, что если мы получим абсолютное значение больше или меньше отрицательного числа, решения не будет.

Составные неравенства

Составное неравенство — это предложение с двумя утверждениями о неравенстве, соединенными либо словом «или», либо словом «и». «И» указывает на то, что оба утверждения сложного предложения верны одновременно. Это перекрытие или пересечение наборов решений для отдельных утверждений. «Или» указывает на то, что, пока одно из утверждений истинно, все составное предложение истинно. Это комбинация или объединение наборов решений для отдельных утверждений. Составное неравенство, в котором используется слово «и», известно как 9. 0443 соединение . Хотя «и» и «или» являются частями речи, известными как союзы, математический союз имеет значение, отличное от грамматического. Чтобы доказать это, союз (часть речи) «или» — при использовании в сложном неравенстве — образует то, что известно как дизъюнкция . Просто помните, что «con» означает «с другим», а «dis» означает «один ИЛИ другой».

Пример 1

Решить для x : 3 x + 2 < 14 и 2 х – 5 > –11.

Решите каждое неравенство отдельно. Поскольку объединяющее слово «и», это указывает на то, что желаемым результатом является наложение или пересечение.

x < 4 указывает на все числа слева от 4, а x > –3 указывает на все числа справа от –3. Пересечение этих двух графиков — это все числа от –3 до 4. Набор решений равен

.

{ х | x > –3 и х < 4}

Этот набор решений может быть выражен другим способом:

.

{ x |–3 < x < 4}

Когда сложное неравенство пишется без выраженного слова «и» или «или», оно автоматически понимается как слово «и». Читая { x |–3 < x < 4} с позиции « x », вы говорите (читая влево), « x больше –3 и (читая вправо) х меньше 4». Граф набора решений показан на рисунке 1.

Рисунок 1. x больше –3 и меньше 4.

Пример 2

Решите для x : 2 x + 7 < –11 или –3 x – 2 < 13.

Решите каждое неравенство отдельно. Так как присоединяющее слово «или», объедините ответы; то есть найдите объединение множеств решений каждого предложения неравенства.

Не забудьте, как и в последнем шаге справа, переключать неравенство при умножении на минус.

x < –9 указывает на все числа слева от –9, а x > –5 указывает на все числа справа от –5. Набор решений записывается как

.

{ х | x < –9 или x > –5}

График этого набора решений показан на рис. 2.

Рисунок 2. x меньше –9или больше –5.

Пример 3

Найдите x : –12 ≤ 2 x + 6 ≤ 8.

Поскольку в этом составном неравенстве нет написанного связующего слова, оно понимается как «и». Оно переводится в следующее составное предложение.

–9 ≤ x указывает на все числа справа от –9 включительно, а x ≤ 1 указывает на все числа слева от 1 включительно. Пересечение этих графиков – это числа между –9и 1, включая –9 и 1. Набор решений можно записать как

{ х | x ≥ –9 и x ≤ 1} или { x |–9 ≤ x ≤ 1}

Граф набора решений показан на рисунке 3.

Рисунок 3. Точки указывают на включение точек.

Пример 4

Решите для x : 3 x – 2 > –8 или 2 x + 1 < 9.

х > –2 указывает на все числа справа от –2, а x < 4 указывает на все числа слева от 4. Объединение этих графиков представляет собой всю числовую прямую. То есть множество решений состоит из всех действительных чисел. График множества решений представляет собой всю числовую прямую (см.

No related posts.