Найти экстремумы функции онлайн: Экстремум функции нескольких переменных онлайн

Содержание

Экстремумы функции — онлайн справочник для студентов

ОПРЕДЕЛЕНИЕ

Крайности (максимумы и минимумы) функции называются значениями функции в точках максимума и минимума.

Экстремумные функциональные точки

Говорят, что в точке $\ x_{0} $ существует максимум (минимум), если существует такая $\ \delta $ — окрестность точки $\ x_{0}-\left(x_{0}-\delta, x_{0}+\delta\right) $ , что для всех x из этой окрестности, отличной от $\ \boldsymbol{x}_{0} $, неравенство выполняется

Точки максимума и минимума называются точками экстремума.

ОПРЕДЕЛЕНИЕ

Точки области, в которой производная функции равна нулю или не существует, называются критическими точками.

Необходимым условием существования экстремума функции. Пусть функция $\ f(x) $ дифференцируема в интервале $\ (a, b) $ . Если в некоторой точке $\ x_{0} \in(a, b) $ функция $\ f(x) $ имеет экстремум, то в этой точке производная равна нулю: $\ f^{\prime}\left(x_{0}\right)=0 $

Достаточное условие существования экстремума функции. {2}-\frac{2}{1}=-1 \)

Ответ

$\ y_{\min }=-1 $

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Асимптоты графика функции Четность и нечетность функции Область значений функции Область определения функции

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Экстремумы функции — алгоритм нахождения максимального и минимального значения функции » Kupuk.

net

( frac{U}{R} )

Экстремумы представляют собой точки минимума и максимума на графике функции. Работа с функциями представляет собой один из базовых навыков математики, необходимый для дальнейшего развития знаний. Поэтому перед непосредственно переходом к вычислениям рассмотрим вкратце сами функции.

Что такое функция

Возьмем знаменитую формулу силы тока:

I =
Здесь I — собственно сила тока, U — напряжение и R — сопротивление. Налицо зависимость значения силы тока от показателя напряжения.

Функция — это общенаучное понятие, выражающее посредством формул зависимость между объектами.

Примеры некоторых распространенных формул:

y = x

y = x2

Способом наглядного изображения характера зависимости является график функции. Например, рис.1 и 2.

Рис.1. График y=x

Рис.2. График y=x2

Подставляя вместо конкретные числа, находим конкретные точки на координатной сетке, через которые проходит график. Отметим, что видов функций великое множество, среди них тригонометрические, логарифмические и так далее. О них подробнее в соответствующих статьях.

Также часто вместо y встречается знак ƒ(x), что означает “функция”. Соответственно — можно встретить выражения типа:

ƒ(x) = x

или

y = ƒ(x) = x

Можно сказать, что они синонимичны друг с другом.

Несколько слов о производной

Точки экстремума тесно связаны с производной. Это очень важное понятие как для математики, так и для естественных наук. Поясним, что это, на примере.

Представьте себе пешехода, преодолевшего за время t расстояние S(t). Затем представим некое время t2, прошедшее после момента t.

Суммарный путь обозначим S(t + t2). Тогда S(t2) = S(t + t2) – S(t).

Если t2 невелико, то скорость движения пешехода в этот момент примерно равна средней скорости. Тогда

Чем t2 меньше, тем v(t2) ближе к vср, ⇒ v(t) можно обозначить как предел ( frac{S(t2)}{t2} ) при стремлении t2 к нулю. Выразим это формулой:

В итоге по указанной формуле через S(x) можно вычислить расстояние, пройденное в x момент времени.

Теперь вспомним формулу касательной к графику (подробнее в отдельной статье). Она выглядит так:

Сравнив обе формулы, видим, что в обоих случаях применялось нахождение предела отношения приращения функции и приращения аргумента при условии, что приращение аргумента стремится к нулю. Обобщив эту информацию, получаем, что для любой ƒ(x) величина

является производной функции в точке x0. Она обозначается как ƒ(x0).

Для работы с производными существуют специальные формулы, подробнее о которых в соответствующей статье.

Важно! Если в x0 функция имеет производную, она называется дифференцированной.

Экстремальные задачи

Понятие экстремума связано с решением соответствующих задач. На самом деле подобные задачи часто встречаются в нашей жизни. Например: найти наименьшую возможную площадь прямоугольного треугольника, если известна сумма длин его катетов.

Это пример задачи на поиск минимума (min). Соответственно, если нужно найти максимальную площадь, мы будем искать максимум (max).

Оба этих понятия объединяются термином экстремум. Задачи на поиск экстремумов называются экстремальными.

Подобные задания известны еще с Древней Греции, но лишь с XVII в. начали вырабатываться универсальные алгоритмы их решения.

Решение заданий на поиск экстремума

Допустим, что имеется некая функция ƒ(x). Она ограничена определенным интервалом (a, b), который содержит в себе точку x0. Ее часто называют локальным экстремумом функции ƒ(x).

Если найдется интервал (a0, b0), который принадлежит (a, b) и также содержащий x0, что условия ƒ(x) ≥ ƒ(x0), или ƒ(x) ≤ ƒ(x0), будет выполняться для всех x из подынтервала (a0, b0).

Другими словами, в точке функция достигает своего экстремального (минимального или максимального) значения.

Чтобы найти экстремумы функции, необходимо найти производную исследуемой функции. Экстремумами будут точки, при которых производная обратится в 0.

Пример решения

Дано:

ƒ(x) = x3 — 3x,

соответственно,

ƒ′(x) = 3×2 − 3

приравниваем к 0

3×2 − 3 = 0

сокращаем

x2 − 1 = 0

x2 = 1

Получаем ответ:

x1 = 1; x2 = –1.

Эти точки и являются экстремумами. — min, — max. Изобразим это на графике (рис.3) оригинальной функции ƒ(x) = x3 — 3x

Рис.3. Точки экстремума

Важно! Как видно, после точек экстремума график продолжается. Таким образом, можно заключить, что указанные точки являются экстремумами на отрезке [–1, 1] по оси x. Поэтому указанные точки будут локальными экстремумами.

Но как тогда найти глобальные точки экстремума? Для этого обратимся к задаче из начала текста. Обозначим площадь треугольника как S, сумму длин катетов как a и как x — длину одного из катетов. Получаем формулу:

S(x) = x(a−x)2

x — не может быть отрицательным, поэтому его диапазон [0, a]. Следовательно функция дифференцируема на интервале (0, a).

Находим производную

S′(x) = 0,5 − x

решаем как уравнение

0,5 − x = 0

x = 0,5a = ( frac{a}{2} )

Эта точка будет локальным максимумом.

Далее среди чисел S(0) = 0, S(( frac{a}{2} )) = ( frac{a2}{8} ), S(a) = 0 максимальной будет S(( frac{a}{2} )), следовательно — в точке x = ( frac{a}{2} ) функция достигает глобального максимума на отрезке [0, a]. Таким образом заключаем, что при заданной сумме длин катетов наибольшей площадью обладает равнобедренный треугольник.

Тема экстремумов функции безусловно сложна, поэтому нет ничего постыдного, если вы что-то не поняли с первого раза. Перечитайте статью несколько раз, “переварите” информацию у себя в голове, и все получится.

Для лучшего усвоения материала рекомендуем ознакомиться с видео.

Калькулятор относительных экстремумов

| Лучшие шаги полного решения

Связанный контент

сообщите об этом объявлении Содержание урока

Что такое относительные экстремумы?

относительных экстремумов функции — это все местоположения относительных максимумов и относительных минимумов.

Относительные экстремумы функции f(x) = 5x ³ + x ² показан на графике цветными точками.

Слово «экстремум» стоит во множественном числе от слова «экстремум». Экстремум – это точка, в которой функция имеет наибольшее или наименьшее значение.

Если точка экстремума является самым экстремальным значением функции во всей области, она называется абсолютным экстремумом. Наибольшее значение функции во всей области называется абсолютным максимумом, а наименьшее значение называется абсолютным минимумом.

Если точка экстремума возникает там, где значение функции меняется с возрастающего на убывающее (пик) или где функция меняется с убывающего на возрастающее (впадина), то это называется относительным экстремумом, потому что это крайняя точка относительно значений функции, окружающих его .

Места, где значение функции изменяется от увеличения к уменьшению (пик), называются относительными максимумами. Места, где значение функции изменяется от убывающего к возрастающему (впадина), называются относительными минимумами.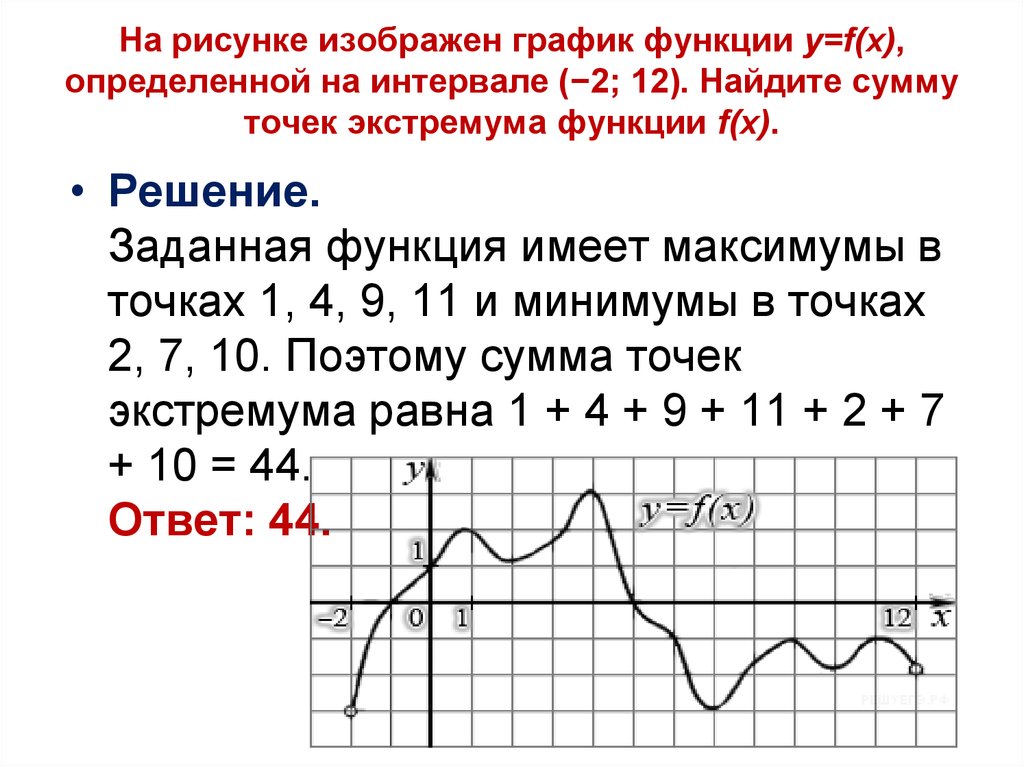

В некоторых случаях точка относительного экстремума может также быть точкой абсолютного экстремума. Например, f(x) = x ² меняется с убывающей на возрастающую при x = 0, что является относительным минимумом. Однако наименьшее значение функции во всей ее области также происходит при x = 0, поэтому относительный минимум также является абсолютным минимумом.

Почему мы изучаем относительные экстремумы?

Поскольку эта тема имеет бесчисленное множество реальных применений, давайте выберем только одно, чтобы погрузиться в него: нахождение относительных экстремумов может помочь нам в создании устойчивой, чистой энергии для будущего с ядерной энергией синтеза.

Ядерный синтез — это когда два атома сливаются вместе и выделяют огромное количество энергии, обычно в виде тепла. В термоядерной энергетике это тепло используется для кипячения воды, создания пара под давлением, который вращает паровую турбину, прикрепленную к электрическому генератору.

Ядерный синтез — это мощный процесс, а топливо в изобилии можно найти в океанах Земли, , но есть одна загвоздка: реакцию ядерного синтеза чрезвычайно трудно запустить и поддерживать .

Одним из подходов к запуску и поддержанию ядерного синтеза является система, называемая термоядерный синтез с инерционным удержанием , в которой используются лазеры для передачи экстремального тепла и давления на кусок топлива, вызывая реакцию синтеза .

Чрезвычайно мощные лазеры, используемые для создания реакции ядерного синтеза
Кредит: Дэмиен Джемисон/LLNL

На эти лазеры существует невероятный спрос, но, к счастью, мы можем использовать концепцию относительных экстремумов, чтобы гарантировать, что лазеры будут иметь достаточную мощность для термоядерной реакции. Поскольку лазеры работают оптимально только при определенных рабочих параметрах, мы можем превратить это в задачу оптимизации.

На изображении ниже приведен пример графика зависимости длины волны лазера от интенсивности. Поскольку мы хотим максимизировать выходную интенсивность лазера, относительные максимумы на этом графике будут соответствовать диапазону (диапазонам) длин волн, в котором должен работать лазер.

Пример графика работы ультрафиолетового лазера на различных длинах волн

Находя относительные экстремумы зависимости длины волны лазера от интенсивности, мы получаем важную информацию об идеальных рабочих параметрах лазера. Затем мы можем использовать эту информацию для планирования, проектирования и оптимизации лазерной системы для использования в передовых приложениях, таких как термоядерная энергетика!

Как найти относительные экстремумы функции

Первый важный шаг к нахождению относительных экстремумов функции f(x) — найти все критические точки функции f(x) в области -∞ < x < ∞.

Критические точки x = c расположены там, где f(c) существует и либо f'(c) = 0, либо f'(c) не определено.

Шаги для нахождения критических точек следующие:

Возьмите производную от f(x) , чтобы получить f'(x)
Найдите все x значений, где f ‘(x) = 0 или где f ‘(x) не определено функция существует при каждом соответствующем значении x

Значения x , найденные на шаге 2, где f(x) существует , могут быть приняты в качестве критических точек x = c , поскольку f(x) существует в эти точки и они лежат в пределах заданной области.

Вторым важным шагом к нахождению относительных экстремумов является создание и проверка интервалов между критическими точками, чтобы определить, где f(x) увеличивается или уменьшается.

Мы создадим интервалы, ограниченные критическими точками функции. А поскольку область -∞ < x < ∞, мы также создадим первый интервал, который начинается с x = -∞, и последний интервал, который заканчивается на x = ∞.

Для проверки каждого интервала мы оцениваем производную f ‘(x) в любой точке между границами соответствующего интервала. Если оценка f ‘(x) положительна, функция возрастает на соответствующем интервале. Если оценка f ‘(x) отрицательна, функция убывает на соответствующем интервале.

Например, если критическими точками функции являются x = -2 и x = 4, интервалы проверки и контрольные точки производной будут следующими:
Интервал проверки 1 равен x = [-∞, -2] и производная контрольная точка 1 может быть x = -3.
Тестовый интервал 2 равен x = [-2, 4], и производная тестовая точка 2 может быть x = 1.
Тестовый интервал 3 представляет собой x = [4, ∞], а производная тестовая точка 3 может быть x = 5.

Третий и последний важный шаг к нахождению относительных экстремумов состоит в том, чтобы просмотреть тестовые интервалы либо на изменение от увеличения к уменьшению, либо от уменьшения к увеличению.

При выполнении любого из этих условий в критической точке между соответствующими интервалами существует относительный экстремум. Так как мы уже проверили, если 93-2x\\ \\ & \hspace{2ex} \text{Для этого мы:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Найдем критические точки } f(x) \text{ в домене } \: -\infty < x < \infty \\ \\ & \hspace{3ex} \text{2) Создать и проверить интервалы между критическими точками} \\ & \hspace{ 5ex} \text{чтобы увидеть, где } f(x) \text{ увеличивается или уменьшается} \\ \\ & \hspace{3ex} \text{3) Определите, где } f(x) \text{ изменяется с возрастания на уменьшение или} \\ & \hspace{5ex} \text{от убывания к возрастанию для получения относительных положений экстремумов}\\ \\ & \text{1.1) Критические точки } \: x = c \: \text{ находятся где : } f(c) \text{ существует} \\ & \hspace{4ex} \text{и выполняется одно из следующих двух условий:} \\ \\ & \hspace{5ex} \bullet f'(c) = 0 \\ \\ & \hspace{5ex} \text{*ИЛИ*} \\ \\ & \hspace{5ex} \bullet f'(c) \text{ не определен}\\ \\ & \text{ 1. 3-2(-1 ) = 1.3333333333333333\\ \\ & \hspace{4ex} \text{Поскольку } f(x) \text{ существует в } c_{2}, \text{ существует критическая точка в } c_{2} \text{ = } -1\\\\ \\ & \hspace {4ex} \text{Наши критические точки отсортированы от наименьшего к наибольшему:} \\ \\ & \hspace{4ex} x = -1,1\\ \\ & \text{2.1) Для проверки интервалов увеличения или уменьшения , мы будем оценивать} \\ & \hspace{4ex} \text{производную } f'(x) \text{ при тестовом значении x } в любом месте \; между \text{ каждой критической точкой.} \\ \\ & \hspace{4ex} \text{Мы создадим интервалы, ограниченные критическими точками, и} \\ & \hspace{4ex} \text{поскольку наша область} \hspace{1ex} – \infty < x < \infty \hspace{1ex} \text{мы также создадим:} \\ & \hspace{5ex} \bullet \text{Первый интервал, начинающийся с } x = - \infty \\ & \hspace{5ex} \bullet \text{Последний интервал, который заканчивается на } x = \infty\\ \\ & \text{2.2) Интервал }1\text{ равен: } x = [-\ infty, -1] \\ & \hspace{5ex} \text{Тестовое значение x} = -2\\ & \hspace{5ex} f'(x) \text{ оценивается по тестовому значению x: } f '(-2) = 2 {(-2)}^{2} – 2 = 6\\ & \hspace{5ex} f'(x) >0, \text{ так} f(x) \text{ есть } \; увеличение\; на \; интервал \;1. {2} – 2 = 6\\ & \hspace {5ex} f'(x) >0, \text{ так } f(x) \text{ равно} \; увеличение\; на \; интервал \;3.\\ \\ & \text{3.1) Чтобы найти относительные экстремумы, мы рассмотрим} \\ & \hspace{4ex} \text{интервалы для любого из следующих двух условий:} \\ \\ & \hspace{4ex} \bullet \text{ Если } f(x) \text{ изменяется с увеличения на одном интервале на уменьшение} \\ & \hspace{7ex} \text{на следующем интервале (относительный максимум) } \\ \\ & \hspace{4ex} \text{*ИЛИ*} \\ \\ & \hspace{4ex} \bullet \text{ Если } f(x) \text{ меняется с убывающей за один интервал на возрастающую } \\ & \hspace{7ex} \text{на следующем интервале (относительный минимум)} \\ \\ & \hspace{4ex} \text{Если выполняется одно из условий, существует относительный экстремум} \\ & \ hspace{4ex} \text{в критической точке между соответствующими интервалами.}\\ \\ & \text{3.2) Поскольку } f(x) \text{ }возрастает\text{ на интервале }1\text{ и }убывает\текст{ на интервале }2\текст{,} \\ & \hspace{4ex} \; первый \; условие \; является \; встретил \text{ и есть } a \; родственник \; максимум \text{ в} \\ & \hspace{4ex} \text{соответствующей критической точке } x = -1\text{. }\\ \\ & \text{3.3) Поскольку } f(x) \text{ }убывает\текст{ на интервале }2\текст{ и }возрастает\текст{ на интервале }3\текст{,} \\ & \hspace{4ex} \; второй \; условие \; является \; встретил \text{ и есть } a \; родственник \; минимум \text{ в} \\ & \hspace{4ex} \text{соответствующей критической точке } x = 1\text{.}\end{align}$$

Пример задачи 2

сообщить об этом объявлении

$$\begin{align}& \hspace{2ex} \text{Найти все относительные экстремумы } f(x) = \sqrt[3]{x}- 12\\ \\ & \hspace{2ex} \text{Для этого мы:} \hspace{45ex} \\ \\ & \hspace{3ex} \text{1) Найдем критические точки } f( x) \text{ в домене } \: -\infty < x < \infty \\ \\ & \hspace{3ex} \text{2) Создать и проверить интервалы между критическими точками} \\ & \hspace{5ex} \text{чтобы увидеть, где } f(x) \text{ увеличивается или уменьшается} \\ \\ & \hspace{3ex} \text{3) Определите, где } f(x) \text{ изменяется с увеличения на уменьшение или } \\ & \hspace{5ex} \text{от убывания к возрастанию для получения относительных положений экстремумов}\\ \\ & \text{1. {\left(\frac{2}{3}\right)}} = 0 \\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} \text{После решения для } x \text{ получаем } x =0\\ \\ & \hspace{4ex} \Rightarrow \hspace{2ex} c =0\ \ \\ & \text{1.4) Так как наш домен} \hspace{1ex} – \infty < x < \infty \hspace{1ex} \text{(все действительные числа), и наши значения } c \text{} \\ & \hspace{4ex} \text{являются действительными числами, мы подставим все эти значения } c \text{ в } f(x) \text{, чтобы получить } f(c) \text{.}\\ \\ & \text{1.5) Подставив наши действительные значения } c \text{ в } f(x) \text{, чтобы получить } f(c) \text{, мы получим:}\\ \\ & \hspace{4ex } f(c_{1}) = \sqrt[3]{(0)}-12 = -12\\ \\ & \hspace{4ex} \te xt{Поскольку } f(x) \text{ существует в } c_{1}, \text{ существует критическая точка в } c_{1} \text{ = } 0\\\\ \\ & \text{2.1 ) Чтобы проверить интервалы увеличения или уменьшения, мы оценим} \\ & \hspace{4ex} \text{производную } f'(x) \text{ при тестовом значении x } где угодно \; между \text{ каждой критической точкой. {\left(\frac {2}{3}\right)}} = 0,3333333333333333\\ & \hspace{5ex} f'(x) >0, \text{ so } f(x) \text{is} \; увеличение\; на \; интервал \;2.\\ \\ & \text{3.1) Чтобы найти относительные экстремумы, мы рассмотрим} \\ & \hspace{4ex} \text{интервалы для любого из следующих двух условий:} \\ \\ & \hspace{4ex} \bullet \text{ Если } f(x) \text{ изменяется с увеличения на одном интервале на уменьшение} \\ & \hspace{7ex} \text{на следующем интервале (относительный максимум) } \\ \\ & \hspace{4ex} \text{*ИЛИ*} \\ \\ & \hspace{4ex} \bullet \text{ Если } f(x) \text{ меняется с убывающей за один интервал на возрастающую } \\ & \hspace{7ex} \text{на следующем интервале (относительный минимум)} \\ \\ & \hspace{4ex} \text{Если выполняется одно из условий, существует относительный экстремум} \\ & \ hspace{4ex} \text{в критической точке между соответствующими интервалами.}\\ \\ & \text{3.2) Поскольку } f(x) \text{ }возрастает\text{ на интервале }1\text{ и }возрастает\текст{ на интервале }2\текст{,} \\ & \hspace{4ex} не выполняется ни одно из условий \text{ и } есть \; нет \; родственник \; экстремум \\ & \hspace{4ex} \text{в соответствующей критической точке } x = 0\text{. }\end{align}$$

Как работает калькулятор

Калькулятор относительных экстремумов Voovers построен с использованием HTML (язык разметки гипертекста), CSS (каскадные таблицы стилей) и JS (JavaScript). HTML создает скелет калькулятора, CSS обеспечивает его стиль, а JS обеспечивает его функциональность.

При нажатии кнопки расчета активируется функция JS, которая считывает ввод пользователя, форматирует функцию для использования в JS и начинает процесс поиска всех относительных экстремумов.

От начала до конца этот процесс очень похож на процесс, описанный в предыдущем уроке. Основное различие между решением вручную и тем, что делает этот калькулятор, заключается в том, что компьютерное оборудование выполняет алгебраические и вычислительные операции вместо человека.

Попутно делаются снимки процесса, которые затем форматируются для использования в качестве шагов решения. Эти этапы решения преобразуются в язык математического рендеринга под названием LaTeX, который позволяет печатать визуально привлекательные математические выражения. После завершения вычислений окончательный ответ и шаги передаются в область решения.

Как найти критические числа для функции

Критическая точка считается широким термином, который используется во многих разделах математики. Когда вы имеете дело с действительными переменными, то критическая точка в области определения функции, где функция не дифференцируема или производная, равна нулю.

Когда речь идет о комплексных значениях, то критической точкой является также точка в области определения функции, где она иногда голоморфна или производная равна 0. Точно так же, когда вы имеете дело с несколькими вещественными переменных, то критическая точка в домене — это значение, при котором градиент не определен или равен 0. Работа с критическими точками, без сомнения, представляет собой сложную задачу, когда дело доходит до ручного расчета. Этот процесс может быть долгим и сложным, тогда, чтобы избавиться от трудоемкого процесса, вы можете попробовать 9Калькулятор критических точек 0221 , который мгновенно находит локальные минимумы, максимумы, стационарные и критические точки для заданной функции.

Что такое критические точки?

В математике это значение в области определения функции, при котором производная функции равна «0» или несуществующей производной. Можно сказать, что это точка функции, где градиент равен нулю или не определен. Это похоже на стационарную точку, и значение может быть максимальным, минимальным и глобальным. Критические точки трудно рассчитать, поэтому вы можете воспользоваться онлайн-калькулятором критических чисел для быстрого определения критических точек данной функции.

Как найти критические числа функции?

Все локальные экстремумы возникают в критических точках любой функции, где производная равна нулю или не определена, но не забывайте, что критические точки не всегда являются локальными экстремумами. Итак, первый шаг, который требуется для определения локальных экстремумов функции, — найти критическое число. Вместо того, чтобы выполнять расчеты самостоятельно, вы можете использовать онлайн-калькулятор критических точек, который показывает критические точки функции вместе с шагами вывода.

Ниже приведены несколько шагов, которые вы можете выполнить, чтобы вычислить критические точки функции.

Первый шаг — найти производную функции f(x), используя степенное правило.
Затем приравняйте производную к нулю и решите x.

Типы критических точек:

Локальный экстремум известен как максимум или минимум функции в заданном интервале значений. Точкой перегиба называется точка функции, в которой изменяется вогнутость. Также в любой точке локальный минимум и максимум могут быть критическими точками, точкой перегиба, а не критической точкой.

Критическая точка — это локальный максимум, когда функция меняется с возрастающей на убывающую в точке.
Критическая точка станет локальным минимумом, когда функция изменится с убывающей на возрастающую в точке.
Точка является точкой перегиба, если функция изменяет вогнутость в этой точке.
Это не критическая точка, и она может быть существенной касательной на графике функции.

Тест первой производной позволяет определить, является ли точка локальной, минимальной или максимальной. Если функция дважды дифференцируема, то критерий второй производной может помочь вычислить природу критической точки. Однако вторая производная имеет значение 00 в точке. Таким образом, критическими точками могут быть либо крайние точки, либо точки перегиба. Определение всех экстремумов, без сомнения, требует времени и сложных вычислений. Просто попробуйте калькулятор локальных экстремумов, который вычисляет локальные минимумы, максимумы, критические точки и стационарные точки всего одним щелчком мыши.

Разница между критической точкой и стационарной точкой:

Критическая и стационарная точки одинаковы; это просто вопрос содержания и изображений, которые используются. Например, когда вы описываете «траекторию», стационарная точка имеет смысл и более актуальна. С другой стороны, если вы используете график для функции, критическая точка является более подходящей. Однако определение для обоих одинаково. Расчет этих точек становится сложным из-за сложных значений, поэтому вы можете указать онлайн-калькулятор критических точек для расчета критических точек функций с одной и несколькими переменными.

Важность экстремумов:

Экстремумы очень важны, потому что они предоставляют набор информации о функции, а также помогают ответить на вопрос об оптимальности. Исчисление предлагает множество инструментов для быстрого определения местоположения и характера экстремумов.

Глобальные экстремумы:

Точка «Xx» известна как абсолютный максимум или минимум дроби «f f » в интервале. Xx является уникальным абсолютным максимумом или минимумом, если это единственная точка, удовлетворяющая ограничениям. Аналогичные определения содержат интервалы. Интервал функции обычно выбирается как область определения «f ф».

Как вычислить глобальные экстремумы:

Здесь мы собираемся показать, как мы можем вычислить глобальные экстремумы.

Первое, что вам нужно сделать, это найти критические точки.
Теперь составьте список конечных точек рассматриваемого интервала.
В этих точках находятся глобальные экстремумы функции f(x).
Теперь оцените функцию f(x) в этих точках, чтобы определить положение глобальных максимумов и минимумов.

Процедура нахождения глобальных максимумов проста, но если вы не хотите выполнять расчеты, то использование калькулятора критических точек будет отличным выбором для расчета критических точек, всех локальных минимумов и максимумов с пошаговым вычислением. вывод.

Локальные экстремумы:

Точка Xx является локальным максимумом или минимумом функции, если она является абсолютным максимумом или минимумом функции интервала. При определении максимума или минимума функции может быть найдено множество локальных экстремумов. Когда заданная функция f f и интервал равен [a, \ b] [a, b], то локальные экстремумы могут быть точками разрыва, точками недифференцируемости или точками, в которых производная имеет значение 00. Однако они не обязательно являются локальными экстремумами, поэтому локальное поведение функции необходимо исследовать для каждой точки.

Как найти локальные экстремумы с помощью теста первой производной:

Все локальные максимумы и минимумы на графике функции называются локальными экстремумами, возникающими в критических точках функции. Первым шагом является вычисление критических чисел. Затем примените тест первой производной к функции, чтобы продолжить дальнейшие вычисления. Чтобы найти критические числа функции, вот что нужно сделать:

Используя правило степени, найдите производную.
Установите производную на 0 и упростите ее для «x».

Три значения x, которые вы получите после упрощения, называются критическими числами функции «f». Кроме того, критические числа могли бы существовать, если бы первая производная функции была неопределенной при некоторых значениях x. Если производная определена, множество решений считается критическими числами.

Это связано с тем, что производная f равна нулю при критических числах, а кривая имеет горизонтальные касательные при этих числах. Вместо этого сложного процесса вы можете найти критическую точку заданной функции за доли секунды.

Заключение:

В этом посте основное внимание уделяется тому, как найти критические значения функции. Некоторые другие соответствующие запросы также являются частью этой статьи. Процесс расчета критических точек функций, несомненно, полон сложностей. Если вы хотите избежать сложностей расчета, вы можете использовать калькулятор критических точек, который показывает вам шаги вывода вместе с критическими, локальными максимумами, минимумами и стационарными точками.

Урок TI-84 Plus — Модуль 13.1: Критические точки

На этом уроке вы узнаете об абсолютных и локальных экстремальных значениях и определите экстремальные значения из набора критических и конечных точек.

Задачи оптимизации являются одним из наиболее важных приложений дифференциального исчисления, потому что мы часто хотим знать, когда результат функции максимален или минимален. В таких задачах может быть наибольшее или наименьшее выходное значение на всем интересующем входном интервале или в пределах локальной окрестности входного значения. Как абсолютные, так и локальные максимальные и минимальные значения представляют интерес во многих контекстах.

Абсолютные экстремальные значения функции

Когда выходное значение функции является максимальным или минимальным по всей области определения функции, это значение называется

абсолютным максимумом или абсолютным минимумом , как определено ниже.

Пусть f будет функцией с областью определения D и пусть c будет фиксированной константой в D . Тогда выходное значение f ( c ) равно

абсолютное максимальное значение из f на D тогда и только тогда, когда f ( x ) f ( c ) для всех x в D .
абсолютное минимальное значение из f на D тогда и только тогда, когда f ( c ) f ( x ) для всех x в D .

Абсолютные экстремальные значения — пример

Домен f ( x ) = x ² — все действительные числа, а диапазон — все неотрицательные действительные числа. График на рисунке ниже предполагает, что функция не имеет абсолютного максимального значения и имеет абсолютный минимум 0, который возникает при x = 0.

[-5, 5, 1] х [-2, 10, 1]

Абсолютные экстремальные значения в домене с ограниченным доступом

Если домен f ( x ) = x ² ограничен до [-2, 3], соответствующий диапазон равен [0, 9]. Как показано ниже, график на интервале [-2, 3] предполагает, что f имеет абсолютный максимум 9 при x = 3 и абсолютный минимум 0 при x = 0.

Два приведенных выше примера показывают, что существование абсолютных максимумов и минимумов зависит от области определения функции.

Теорема об экстремальных значениях

Теорема 1 ниже называется теоремой об экстремальных значениях. Он описывает условие, которое гарантирует, что функция имеет как абсолютный минимум, так и абсолютный максимум. Теорема важна, потому что она может направлять наши исследования, когда мы ищем абсолютных экстремальных значений функции.

Теорема 1 Если f непрерывно на отрезке [ a , b ], то f имеет как абсолютное максимальное значение, так и абсолютное минимальное значение на интервале.

Эта теорема утверждает, что непрерывная функция, определенная на замкнутом интервале , должна иметь как абсолютное максимальное значение, так и абсолютное минимальное значение. В нем не рассматривается, как найти экстремальные значения.

Локальные экстремальные значения функции

Один из наиболее полезных результатов математических вычислений состоит в том, что абсолютные экстремальные значения функции должны браться из списка из локальных крайних значений, и эти значения легко находятся с помощью первой производной функции.

Локальные экстремальные значения, как определено ниже, являются максимальными и минимальными точками (если они есть), когда домен ограничен небольшой окрестностью входных значений.

Пусть c — внутренняя точка области определения функции f . Тогда функция f имеет

локальный максимум на c тогда и только тогда, когда f ( x ) f ( c ) для всех x в некотором открытом интервале, содержащем c .
местный минимум at c тогда и только тогда, когда f ( c ) f ( x ) для всех x в некотором открытом интервале, содержащем c .

Конечные точки как локальные экстремумы

Определение локальных экстремумов, данное выше, ограничивает входное значение внутренней точкой области. Определение можно расширить, включив в него конечные точки интервалов.

Из определений видно, что для областей, состоящих из одного или нескольких интервалов, любой абсолютный экстремум должен быть и локальным экстремумом. Таким образом, абсолютные экстремумы можно найти, исследуя все локальные экстремумы.

Кандидаты на локальные экстремальные баллы

Теорема 2 ниже, которая также называется теоремой Ферма, идентифицирует кандидатов на локальные точки экстремума.

Теорема 2 Если функция имеет локальное максимальное значение или локальное минимальное значение во внутренней точке c своего домена, и если f ‘ существует по адресу c , то f’ ( c ) = 0.

Нахождение экстремальных значений функции

Теорема 2 утверждает, что если функция имеет первую производную во внутренней точке, где есть локальный экстремум, то производная должна равняться нулю в этой точке. Это не говорит о том, что каждая точка, где первая производная равна нулю, должна быть локальным экстремумом. Из-за теоремы 2 при нахождении экстремальных значений функции необходимо учитывать лишь несколько точек. Эти точки состоят из точек внутренней области, где f ‘ ( x ) = 0, внутренние точки домена, где f ‘ не существует, и конечные точки домена, которые не охватываются теоремой.

Критические точки

Критическая точка — это внутренняя точка в области определения функции, в которой f’ ( x ) = 0 или f’ не существует. Таким образом, единственными возможными кандидатами на координаты x экстремумов являются критические точки и конечные точки.

Нахождение экстремальных значений с использованием методов исчисления

Найдите локальные и абсолютные экстремальные значения f ( x ) = x ² на закрытом интервале [-2, 3] с помощью исчисления. Здесь применима теорема 1, поэтому мы точно знаем, что эта функция должна иметь абсолютные экстремумы в этой области.

Обратите внимание на следующее:

f’ ( x ) = 2 x , что равно нулю только в x = 0 и существует при всех значениях f в [-2, 3]. Следовательно, x = 0 является единственной критической точкой f .
Значения f в конечных точках равны f (-2) = 4 и f (3) = 9.

Сравнивая выходные значения, когда x = -2, x = 0 и x = 3, можно определить абсолютные экстремумы.

f имеет локальный минимум 0 на x = 0, что также является абсолютным минимумом.
f имеет локальный максимум 4 при x = -2 и локальный максимум 9 при x = 3. Абсолютный максимум f равен 9.

Просмотрите график функции в ограниченной области. График подтверждает приведенные выше результаты.

[-2, 3, 1] х [-2, 10, 1]

13.1.1 Найдите крайние значения f ( x ) = x ² на [-4, 2] с помощью методов исчисления, а затем подкрепите свои ответы, нарисовав график. Щелкните здесь, чтобы получить ответ.

Методы исчисления дают результаты, которые могут быть подтверждены графиками, а графики могут помочь в обнаружении экстремальных значений, как показано в следующем примере.

Экстремальные значения f ( x ) = x ^2/3 на [-2, 4]

Найдите крайние значения 9(2/3) в Y ₁ .

Отобразите график в окне [-2, 4,1] x [-1, 3,1].

Функция имеет абсолютный минимум около x = 0 и два локальных максимума, которые приходятся на конечные точки ограниченной области. Абсолютный максимум приходится на правую конечную точку ограниченного домена.

Теперь определите крайние точки, используя методы исчисления.

Используйте правило степени, чтобы найти f ‘:

производная, , нигде на [-2, 4] не равно 0, поэтому критическая точка не возникает из этого условия, но f ‘ не существует при x = 0, из чего следует, что x = 0 является критической точкой. точка. Следовательно, единственная критическая точка f приходится на x = 0.

Используйте функцию «Значение» на экране «График», чтобы вычислить значения f в критической точке и на концах ограниченного домена [-2, 4].

Из графика пресса ф [CALC] и выберите 1:значение.
Оцените f как x = -2, x = 0 и x = 4, введя -2, 0 и 4 соответственно.

Крайние значения можно резюмировать следующим образом:

f имеет локальный и абсолютный минимум 0 в 0.
Значение f при x = -2 составляет приблизительно 1,587, а значение при x = 4 составляет приблизительно 2,520. Каждый является локальным максимальным значением.
Абсолютное максимальное значение f составляет приблизительно 2,520 при x = 4.

Экстремальные значения

В предыдущих примерах мы имели дело с непрерывными функциями, заданными на отрезках. В таком случае теорема 1 гарантирует наличие как абсолютного максимума, так и абсолютного минимума. В этом примере область не является замкнутым интервалом, и теорема 1 неприменима. Экстремальные значения можно найти с помощью процедуры, аналогичной описанной выше, но необходимо позаботиться о том, чтобы экстремумы действительно существовали.

Обратите внимание, что домен f равен (-2, 2), потому что подкоренное число должно быть неотрицательным, а знаменатель должен быть ненулевым.

График в окне просмотра [-4, 4, 1] x [-2, 4, 1].

График показывает, что существует абсолютный минимум около 0,5 при x = 0. Также появляются локальные максимумы около 2,5 при x = -2 и x = 2. Однако f не определяется при x = -2 и x = 2, поэтому они не могут быть локальными максимумами.

Методы исчисления требуют, чтобы конечные точки домена и критические точки были идентифицированы. Домен f — это (-2, 2), открытый интервал, поэтому конечных точек нет. Критические точки определяются с помощью производной, которая находится с помощью цепного правила.

Производная равна 0 при x = 0 и не определена при x = -2 и x = 2. Поскольку -2 и 2 не находятся в области f , единственной критической точкой является x = 0.

Поскольку x удаляется от 0 в любом направлении, знаменатель f ( x ) становится меньше, а f ( x ) увеличивается. Таким образом, f имеет абсолютный минимум 0,5 при x = 0.

Абсолютных максимальных баллов нет. Это не нарушает теорему об экстремальных значениях, поскольку функция не определена на замкнутом интервале. Поскольку абсолютный максимум должен иметь место в критической или конечной точке, и х = 0 — единственная такая точка, абсолютного максимума быть не может.

Критические значения, не являющиеся экстремумами

Экстремальные точки функции должны находиться в критических точках или конечных точках, однако не каждая критическая точка или конечная точка являются экстремальными точками. Следующие графики y = x ³ иллюстрируют критические точки при x = 0, которые не являются крайними точками.


y = x ³ в окне [-3, 3 1] x [-2, 2, 1]	в окне [-3, 3, 1] x [-2, 2, 1]

Обратите внимание, что производная y = x ³ равна y’ = 3 x ², а производная y = 3/2 9 x 10 .