Глава 57. Экстремум функции
Определение
Точка называется точкой Локального максимума (Минимума) функции , Если для любого числа в некоторой окрестности точки выполнено неравенство .
Термины «локальный минимум» и «локальный максимум» объединены общим названием «Локальный экстремум».
Теорема
(Необходимое условие существования локального экстремума). Для того чтобы функция имела экстремум в точке , необходимо, чтобы ее Производная в этой точке равнялась нулю или не существовала.
Геометрический смысл теоремы заключается в следующем: если в точках локальных экстремумов существуют касательные, то они параллельны оси .
Точки, в которых выполнено необходимое условие экстремума называют Критическими или Стационарными (а также Точками возможного экстремума). Очевидно, что эти точки должны входить в ОДЗ функции. Таким образом, если в какой–либо точке имеется экстремум, то эта точка критическая, однако обратное утверждение неверно: критическая точка вовсе не обязана быть точкой экстремума.
Это можно показать на примерах функций . Для первой функции точка является точкой экстремума, а для второй – нет.
Сформулируем достаточные условия существования локального экстремума.
Теорема (Первое достаточное условие экстремума)
Пусть функция Дифференцируема в некоторой окрестности точки . Если при переходе через точку слева направо производная Меняет знак с плюса на минус, то в точке функция имеет Локальный максимум, а если с Минуса на плюс, то – точка Минимума. Если же не меняет знака в Окрестности точки , то данная функция Не имеет локального экстремума в этой точке.
Геометрический смысл теоремы иллюстрирует Рис. 5.9.1.
Отметим также, что дифференцируемость в самой точке Вовсе не обязательна. Например, функция имеет экстремум (минимум) в точке , но не дифференцируема в ней.
Рис. 5.9.1
Схема исследования функции на локальный экстремум
1. Найти производную .
2.
Найти критические точки функции, в которых производная или не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4. Найти экстремумы функции.
Пример
Исследовать на экстремум функцию .
Решение
Найдем производную и приравняем нулю:.
Нули производной: . Исследуем знаки первой производной.
Так как при переходе через точку производная меняет знак с минуса на плюс, то точка является точкой минимума. При переходе через точку производная знак не меняет, поэтому точка не является точкой экстремума.
Теорема (Второе достаточное условие экстремума)
Если первая производная дважды дифференцируемой функции
Второе достаточное условие экстремума утверждает, что если в критической точке , то в этой точке имеется экстремум.
Обратное утверждение неверно – экстремум в критической точке может быть и при равенстве нулю в ней второй производной, например, для функции и критической точки .
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке .
Ранее отмечалось, что если функция непрерывна на отрезке , то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значения функции могут достигаться как в точках экстремума, так и на концах отрезка.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную .
2. Найти критические точки функции, в которых или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.
| < Предыдущая | Следующая > |
|---|
Поиск точек экстремума функции
Точка \(x_0\) называется точкой локального максимума функции \(f(x)\), если существует некоторый интервал \(I\), содержащий точку \(x_0\), такой что для любой точки \(a\) из \(I\) верно \(f(x_0) \geq f(a)\).
2 + 1}\cdot 2x_0 = e\cdot 0 = 0\).
Уравнение \eqref{cond1} выполняется, если либо $x=0$, либо $3x+2y=0$, т. е. если $x=0$ или если $y = -3x/2$. Мы рассматриваем эти два решения как два отдельных случая. Для каждого случая мы найдем решения для уравнение \eqref{cond2}.
Случай 1: Пусть $x=0$. Тогда мы знаем
уравнение \eqref{cond1} выполняется.
Подставляем $x=0$ в
уравнение \eqref{cond2}, которое становится $0-2y-4=0$,
т. е. $y=-2$. Если $x=0$ и $y=-2$, то оба
уравнение \eqref{cond1}
и
уравнение \eqref{cond2}
удовлетворены. Следовательно, точка $(0,-2)$ является
критическая точка. 92+3x-4&=0\\
(х-1)(х+4)&=0\\
х=1 \текст{ или } х&=-4.
\конец{выравнивание*}
Итак, у нас есть два решения
уравнение \eqref{cond2}
для случая 2.
первое решение — когда $x=1$, что означает $y=-3x/2=-3/2$. Если $х=1$
и $y=-3/2$, то оба
уравнение \eqref{cond1}
и
уравнение \eqref{cond2}
удовлетворены.
Второе решение для случая 2, когда $x=-4$, что означает $y=-3x/2=6$. Следовательно, точка $(-4,6)$ является критической точкой.
Подводя итоги по случаям 1 и 2, мы заключаем, что $f(x,y)$ имеет три критические точки: $(0,-2)$, $(1,-3/2)$ и $(-4,6)$.
Вы должны перепроверить, что $D f(x,y)=[0 \quad 0]$ в каждой из этих точек.
Шаг 2 : Классифицируйте критические точки.
Матрица Гессе \начать{выравнивать*} Hf (х, у) = \оставил[ \begin{массив}{cc} 6х+2у и 2х\\ 2x и -2 \конец{массив} \правильно] \конец{выравнивание*} Нам нужно проверить определенность $Hf(x,y)$ в критической точки $(0,-2)$, $(1,-3/2)$ и $(-4,6)$.
Для критической точки $(0,-2)$,
\начать{выравнивать*}
Hf(0,-2) =
\оставил[
\begin{массив}{rr}
-4 и 0\\
0 и -2
\конец{массив}
\правильно]
\конец{выравнивание*}
$h_{11} = -4 0$. Это означает, что $Hf(0,-2)$
отрицательно определена и $f$ имеет локальный максимум в точке $(0,-2)$.
Для критической точки $(1,-3/2)$, \начать{выравнивать*} Hf(1,-3/2) = \оставил[ \begin{массив}{rr} 3 и 2\\ 2 и -2 \конец{массив} \правильно]. \конец{выравнивание*} $h_{11}=3>0$ и $\det(Hf) = -6-4=-10 9{-4}
Исчисление III. Относительные минимумы и максимумы
Онлайн-заметки Пола
Дом
/
Исчисление III
/
Приложения частных производных
/ Относительные минимумы и максимумы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 14.3: Относительные минимумы и максимумы
В этом разделе мы собираемся распространить одну из наиболее важных идей Исчисления I на функции двух переменных. Мы собираемся начать поиск минимумов и максимумов функций. Собственно, это и будет темой следующих двух разделов.
В этом разделе мы рассмотрим определение относительных минимумов и относительных максимумов. Напомним также, что мы часто будем использовать слово «экстремум» для обозначения как минимума, так и максимума.
Определение относительных экстремумов для функций двух переменных такое же, как и для функций одной переменной, нужно только помнить, что мы работаем с функциями двух переменных.
Итак, для полноты здесь даны определения относительных минимумов и относительных максимумов для функций двух переменных.
Определение
- Функция \(f\left( {x,y} \right)\) имеет относительный минимум в точке \(\left( {a,b} \right)\), если \ (f\left( {x,y} \right) \ge f\left( {a,b} \right)\) для всех точек\(\left( {x,y} \right)\) в некоторой области вокруг \(\left({a,b} \right)\).
- Функция \(f\left( {x,y} \right)\) имеет относительный максимум в точке \(\left( {a,b} \right)\), если \(f\left( {x,y} \right) \le f\left( {a,b} \right)\) для всех точек\(\left( {x,y} \right)\) в некоторой области вокруг \(\left ( {яркий)\).
Обратите внимание, что в этом определении не говорится, что относительный минимум — это наименьшее значение, которое когда-либо может принимать функция. Это только говорит о том, что в некоторой области вокруг точки \(\left( {a,b} \right)\) функция всегда будет больше, чем \(f\left({a,b} \right)\).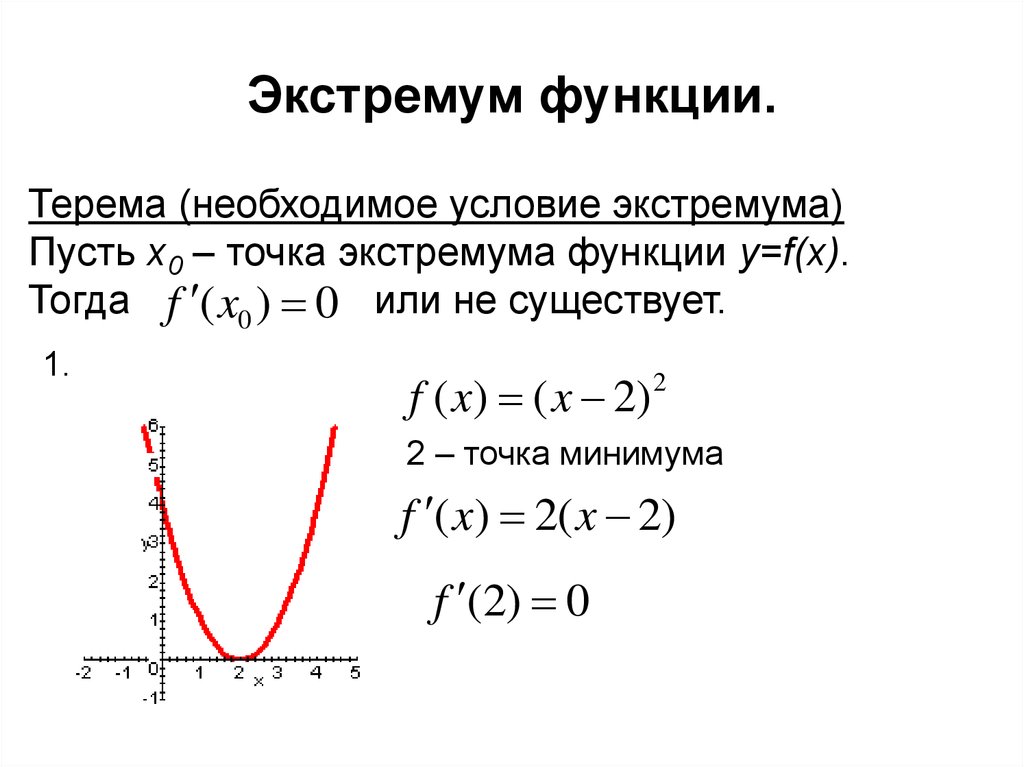
Вне этой области вполне возможно, что функция будет меньше. Точно так же относительный максимум говорит только о том, что около \(\left( {a,b} \right)\) функция всегда будет меньше, чем \(f\left({a,b} \right)\). Опять же, за пределами региона вполне возможно, что функция будет больше.
Далее нам нужно расширить идею критических точек до функций двух переменных. Напомним, что критической точкой функции \(f\left( x \right)\) было число \(x = c\), так что либо \(f’\left( c \right) = 0\), либо \ (f’\left( c \right)\) не существует. У нас есть аналогичное определение для критических точек функций двух переменных.
Определение
Точка \(\left( {a,b} \right)\) является критической точкой (или стационарной точкой ) of \(f\left( {x,y} \right)\) при условии, что верно одно из следующих условий:
- \(\nabla f\left( {a,b} \right) = \vec 0 \) (это эквивалентно тому, что \({f_x}\left( {a,b} \right) = 0\) и \({f_y}\left( {a,b} \right) = 0 \)),
- \({f_x}\left( {a,b} \right)\) и/или \({f_y}\left( {a,b} \right)\) не существует.
Чтобы увидеть эквивалентность в первой части, давайте начнем с \(\nabla f = \vec 0\) и добавим определение каждой части.
\[\begin{align*}\nabla f\left( {a,b} \right) & = \vec 0\\ \left\langle {{f_x}\left( {a,b} \right),{ f_y}\left( {a,b} \right)} \right\rangle & = \left\langle {0,0} \right\rangle \end{align*}\]
Единственный способ, которым эти два вектора могут быть равны, состоит в том, чтобы \({f_x}\left( {a,b} \right) = 0\) и \({f_y}\left( {a,b} \ справа) = 0\). Фактически, мы будем использовать это определение критической точки чаще, чем определение градиента, поскольку будет легче найти критические точки, если мы начнем с определения частной производной.
Также обратите внимание, что ОБЕ частные производные первого порядка должны быть равны нулю в точке \(\left( {a,b} \right)\). Если только одна из частных производных первого порядка равна нулю в точке, то точка НЕ будет критической точкой.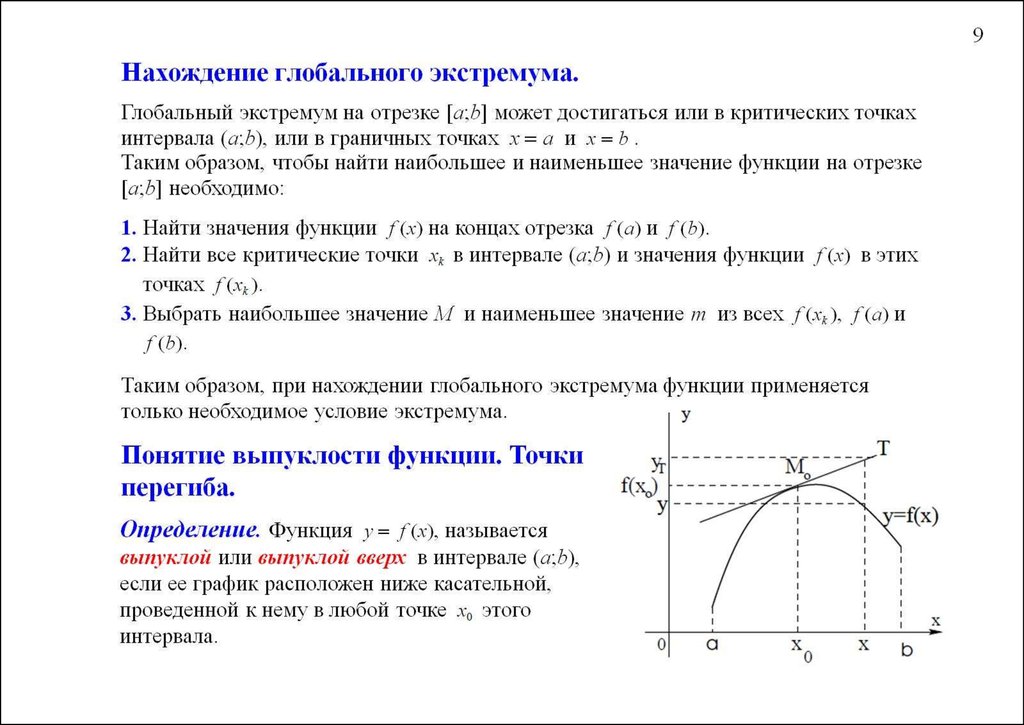
Теперь мы имеем следующий факт, который, по крайней мере частично, связывает критические точки с относительными экстремумами.
Факт
Если точка \(\left( {a,b} \right)\) является относительным экстремумом функции \(f\left( {x,y} \right)\) и первого порядка производные от \(f\left( {x,y} \right)\) существуют в \(\left( {a,b} \right)\), затем \(\left( {a,b} \right)\ ) также является критической точкой \(f\left( {x,y} \right)\) и на самом деле мы будем иметь \(\nabla f\left( {a,b} \right) = \vec 0 \).
Доказательство
Это действительно простое доказательство, основанное на версии с одной переменной, которую мы видели в версии Исчисления I, часто называемой теоремой Ферма.
Начнем с определения \(g\left( x \right) = f\left( {x,b} \right)\) и предположим, что \(f\left( {x,y} \right)\ ) имеет относительный экстремум в точке \(\left({a,b} \right)\). Однако это также означает, что \(g\left( x \right)\) также имеет относительные экстремумы (такие же, как \(f\left( {x,y} \right)\)) в точке \(x = а\).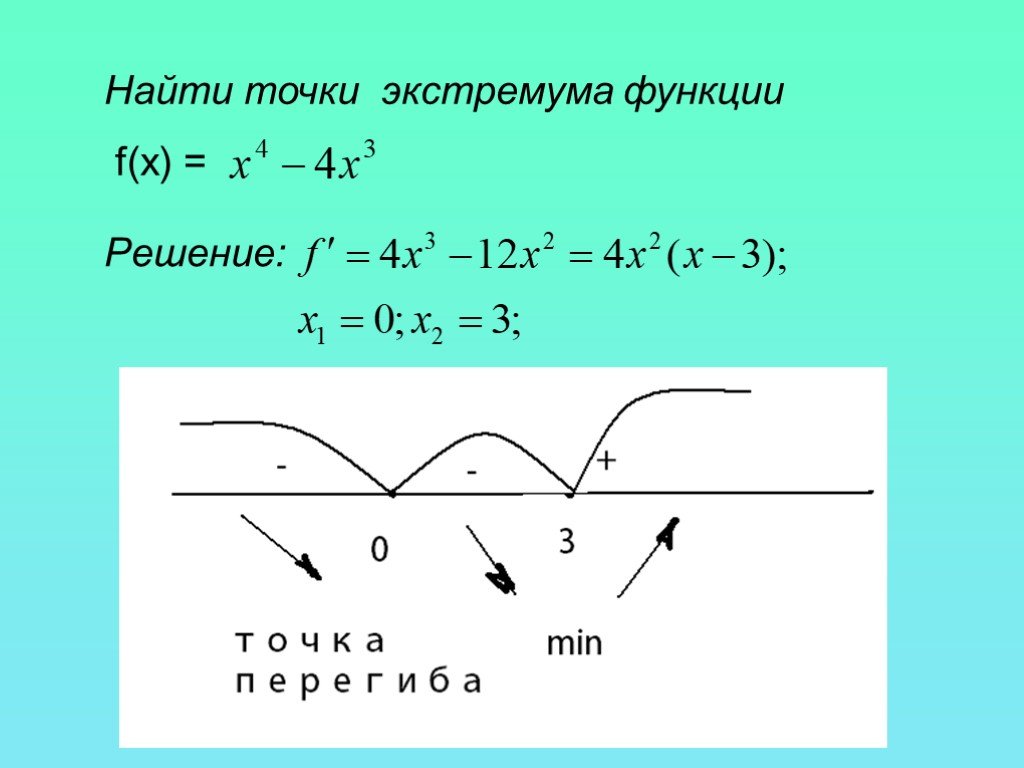
Тогда по теореме Ферма мы знаем, что \(g’\left( a \right) = 0\). Но мы также знаем, что \(g’\left( a \right) = {f_x}\left( {a,b} \right)\), поэтому мы имеем, что \({f_x}\left( {a,b } \справа) = 0\).
Если теперь мы определим \(h\left( y \right) = f\left( {a,y} \right)\) и проделаем точно такой же процесс, как описано выше, мы увидим, что \({f_y}\ влево( {а,б} \право) = 0\).
Таким образом, объединение всего этого означает, что \(\nabla f\left( {a,b} \right) = \vec 0\) и, следовательно, \(f\left( {x,y} \right)\) имеет критическую точку в точке \(\left( {a,b} \right)\).
Обратите внимание, что это НЕ означает, что все критические точки являются относительными экстремумами. Это говорит только о том, что относительные экстремумы будут критическими точками функции. Чтобы убедиться в этом, рассмотрим функцию
\[е\влево( {х,у} \вправо) = ху\]
Две частные производные первого порядка:
\[{f_x}\left( {x,y} \right) = y\hspace{0.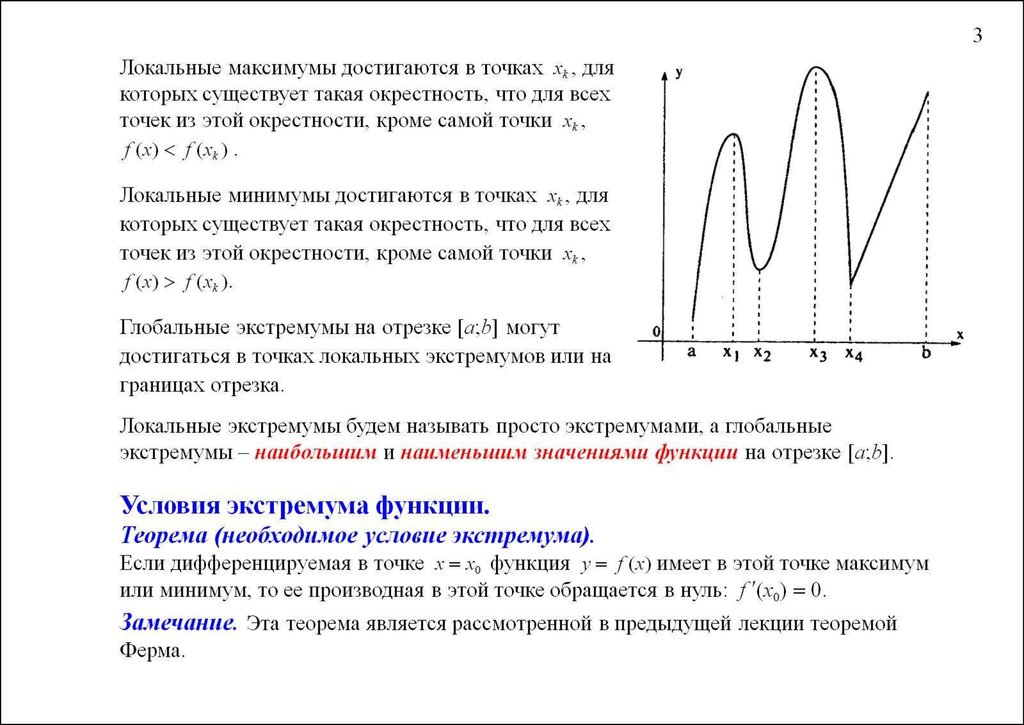
75in}{f_y}\left( {x,y} \right) = x\]
Единственная точка, которая сделает обе эти производные равными нулю одновременно, это \(\left( {0,0} \right)\), поэтому \(\left( {0,0} \right)\) является критической точкой для функции. Вот график функции.
Обратите внимание, что оси здесь не в стандартной ориентации, чтобы мы могли более четко видеть, что происходит в начале координат, т. е. в точке \(\left( {0,0} \right)\). Если мы начнем с начала координат и перейдем в любой из квадрантов, где \(x\) и \(y\) имеют один и тот же знак, функция возрастет. Однако, если мы начнем с начала координат и перейдем в любой из квадрантов, где \(x\) и \(y\) имеют противоположный знак, тогда функция уменьшится. Другими словами, независимо от того, какую область вы возьмете относительно начала координат, будут точки больше, чем \(f\left( {0,0} \right) = 0\), и точки меньше, чем \(f\left( {0, 0} \справа) = 0\). Следовательно, \(\left({0,0} \right)\) не может быть относительным экстремумом.
Критические точки, демонстрирующие такое поведение, называются седловыми точками .
Хотя мы должны быть осторожны, чтобы не неверно истолковать результаты этого факта, он очень полезен для выявления относительных экстремумов. Из-за этого факта мы знаем, что если у нас есть все критические точки функции, то у нас также есть все возможные относительные экстремумы для функции. Этот факт говорит нам о том, что все относительные экстремумы должны быть критическими точками, поэтому мы знаем, что если функция имеет относительные экстремумы, то они должны быть в наборе всех критических точек. Помните, однако, что вполне возможно, что по крайней мере одна из критических точек не будет относительным экстремумом.
Итак, когда у нас есть все критические точки, все, что нам нужно сделать, это проверить эти точки, чтобы увидеть, являются ли они относительными экстремумами или нет. Чтобы определить, является ли критическая точка относительным экстремумом (и фактически определить, является ли она минимумом или максимумом), мы можем использовать следующий факт.
Факт
Предположим, что \(\left( {a,b} \right)\) является критической точкой \(f\left( {x,y} \right)\) и что частные производные второго порядка непрерывны в некоторой области, содержащей \(\left( {a,b} \right)\). Следующее определение, 92}\]
Тогда у нас есть следующие классификации критической точки.
- Если \(D > 0\) и \({f_{x\,x}}\left( {a,b} \right) > 0\), то существует относительный минимум в точке \(\left( {яркий)\).
- Если \(D > 0\) и \({f_{x\,x}}\left( {a,b} \right) < 0\), то существует относительный максимум в \(\left( {a ,яркий)\).
- Если \(D < 0\), то точка \(\left( {a,b} \right)\) является седловой.
- Если \(D = 0\), то точка \(\left( {a,b} \right)\) может быть относительным минимумом, относительным максимумом или седловой точкой. Для классификации критической точки необходимо использовать другие методы.
Обратите внимание, что если \(D > 0\), то и \({f_{\,x\,x}}\left( {a,b} \right)\), и \({f_{\,y\ ,y}}\left( {a,b} \right)\) будет иметь тот же знак, поэтому в первых двух случаях мы могли бы так же легко заменить \({f_{\,x\,x}}\ влево( {a,b} \right)\) с \({f_{\,y\,y}}\left({a,b} \right)\).
Также обратите внимание, что мы не увидим в этом классе случаев, где \(D = 0\), поскольку их часто бывает довольно сложно классифицировать. Мы сможем классифицировать все критические точки, которые мы найдем. 92}\\ & = 36xy — 9\end{выравнивание*}\]
Чтобы классифицировать критические точки, все, что нам нужно сделать, это подключить критические точки и использовать приведенный выше факт для их классификации.
\(\влево({0,0} \вправо)\) : \[D = D\влево( {0,0} \вправо) = — 9 < 0\]
Итак, для \(\left( {0,0} \right)\) \(D\) отрицательно, и поэтому это должна быть седловая точка.
\(\влево({1,1} \вправо)\) : \[D = D\left( {1,1} \right) = 36 — 9 = 27 > 0\hspace{0.5in}{f_{x\,x}}\left( {1,1} \right) = 6 > 0\]
Для \(\left( {1,1} \right)\) \(D\) положительно и \({f_{x\,x}}\) положительно, поэтому мы должны иметь относительный минимум.
Для полноты картины приведен график этой функции.
Обратите внимание, что для лучшего визуального восприятия мы использовали несколько нестандартную ориентацию. Мы можем видеть, что есть относительный минимум в \(\left( {1,1} \right)\) и (надеюсь) ясно, что в \(\left( {0,0} \right)\) мы делаем получить седловую точку. 92} — 6y & = 0\end{align*}\]
Эти уравнения немного сложнее решить, чем первый набор, но как только вы поймете, что делать, они действительно не так уж плохи.
Во-первых, заметим, что мы можем вынести 6\(x\) из первого уравнения, чтобы получить
\[6x\влево( {у — 1} \вправо) = 0\]
Итак, мы видим, что первое уравнение будет равно нулю, если \(x = 0\) или \(y = 1\). Будьте осторожны, чтобы не просто отменить \(x\) с обеих сторон. Если бы мы это сделали, то пропустили бы \(x = 0\). 92} — 1} \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.
25in}x = — 1,\,\,x = 1\]
Итак, если \(x = 0\) мы имеем следующие критические точки,
\[\left( {0,0} \right)\hspace{0,25in}\left( {0,2} \right)\]
и если \(y = 1\) критические точки,
\[\left( {1,1} \right)\hspace{0.25in}\left( { — 1,1} \right)\] 92}\] \(\влево({0,0} \вправо)\) : \[D = D\left( {0,0} \right) = 36 > 0\hspace{0.5in}{f_{x\,x}}\left( {0,0} \right) = — 6 < 0\] \(\влево({0,2} \вправо)\) : \[D = D\left( {0,2} \right) = 36 > 0\hspace{0.5in}{f_{x\,x}}\left( {0,2} \right) = 6 > 0 \] \(\влево({1,1} \вправо)\) : \[D = D\влево( {1,1} \вправо) = — 36 < 0\] \(\влево( { - 1,1} \вправо)\) : \[D = D\влево( { - 1,1} \вправо) = - 36 < 0\]
Итак, похоже, у нас есть следующая классификация каждой из этих критических точек.
\[\begin{align*} & \left( {0,0} \right) & & :\hspace{0,5in}{\mbox{Относительный максимум}}\\ & \left( {0,2} \right ) & & : \hspace{0,5 дюйма} {\mbox{Относительный минимум}}\\ & \left( {1,1} \right) & & :\hspace{0,5in}{\mbox{Седловая точка}}\ \ & \left( { — 1,1} \right) & & :\hspace{0.5in}{\mbox{Седловая точка}}\end{align*}\]
Вот график поверхности для полноты картины.
Давайте сделаем еще один пример, немного отличающийся от первых двух.
Пример 3. Определить точку на плоскости \(4x — 2y + z = 1\), ближайшую к точке \(\left( { — 2, — 1,5} \right)\).
Показать решение
Обратите внимание, что мы НЕ запрашиваем критические точки плоскости. Чтобы сделать этот пример, нам нужно сначала придумать уравнение, с которым нам придется работать. 92}} \]
Затем нас просят найти минимальное значение этого уравнения.
Точка \(\left( {x,y,z} \right)\), дающая минимальное значение этого уравнения, будет точкой на плоскости, ближайшей к \(\left( { — 2, — 1, 5} \справа)\).
У этого уравнения есть пара проблем. Во-первых, это функция \(x\), \(y\) и \(z\), и мы можем иметь дело только с функциями \(x\) и \(y\) в этой точке. Однако это легко исправить. Мы можем решить уравнение плоскости, чтобы увидеть, что 92}\]
Теперь нам нужно быть немного осторожными. Нас просят найти ближайшую точку на плоскости к \(\left( { — 2, — 1,5} \right)\), и это совсем не то же самое, что мы делали в этом разделе. . В этом разделе мы находили и классифицировали критические точки как относительные минимумы или максимумы, и на самом деле мы просим найти наименьшее значение, которое будет принимать функция, или абсолютный минимум. Надеюсь, с физической точки зрения имеет смысл то, что на плоскости будет ближайшая точка к \(\left( { — 2, — 1,5} \right)\). Эта точка также должна быть относительным минимумом в дополнение к абсолютному минимуму.
Итак, давайте пройдемся по процессу из первого и второго примеров и посмотрим, что мы получим в отношении относительных минимумов. Если мы получим только один относительный минимум, то мы закончим, поскольку эта точка также должна быть абсолютным минимумом функции и, следовательно, точкой на плоскости, ближайшей к \(\left( { — 2, — 1, 5} \справа)\).
Сначала нам понадобятся производные.
\[\begin{align*}{f_x} & = 2\left( {x + 2} \right) + 2\left( { — 4} \right)\left( { — 4 — 4x + 2y} \right ) = 36 + 34x — 16y\\ {f_y} & = 2\left( {y + 1} \right) + 2\left( 2 \right)\left( { — 4 — 4x + 2y} \right) = — 14 — 16x + 10y\\ {f_{x\,x}} & = 34\\ {f_{y\,y}} & = 10\\ {f_{x\,y}} & = — 16\ конец {выравнивание *} \] 92} = 84 > 0\]
Таким образом, в этом случае \(D\) всегда будет положительным, а также обратите внимание, что \({f_{x\,x}} = 34 > 0\) всегда положителен, и поэтому любые критические точки, которые мы получим, будут гарантированно являются относительными минимумами.
Теперь найдем критические точки. Это будет означать решение системы.
\[\begin{align*}36 + 34x — 16y & = 0\\ — 14 — 16x + 10y & = 0\end{align*}\]
Для этого мы можем решить первое уравнение относительно \(x\).
\[x = \frac{1}{{34}}\left( {16y — 36} \right) = \frac{1}{{17}}\left( {8y — 18} \right)\]
Теперь подставьте это во второе уравнение и найдите \(y\).
\[ — 14 — \frac{{16}}{{17}}\left( {8y — 18} \right) + 10y = 0\hspace{0.5in} \Rightarrow \hspace{0.5in}y = — \ гидроразрыв {{25}}{{21}}\]
Обратная подстановка в уравнение для \(x\) дает \(x = — \frac{{34}}{{21}}\).
Итак, похоже, мы получили единственную критическую точку: \(\left( { — \frac{{34}}{{21}}, — \frac{{25}}{{21}}} \right )\).