Таблица первообразных интегралов: Большая таблица интегралов (первообразных). Таблица интегралов полная для студентов. Интегралы от рациональных функций. Интегралы от трансцендентных функций. Интегралы от иррациональных функций. Интегралы от тригонометрических функций.

Таблица интегралов: первообразная, неопределенный интеграл

Для быстрого интегрального исчисления нужно знать, как искать производные простой и сложной функции. Ведь нахождение интеграла и производных являются взаимно обратные операции. Для интегрирования потребуются: таблица интегралов полная и также формулы интегралов таблица основных свойств, таблица производных и интегралов.

У многих возникает сложность в изучении и понимании неопределенных интегралов. Если производные обладают всего лишь 5 правилами дифференцирования, четким алгоритм, таблицей производных, то при интегрировании совсем иначе. Используются десятки приемов и способов интегрирования. При неверном выборе способа интегрирования и различного метода интеграл вычислять можно долго, так как он представляет собой некий ребус.

Определение первообразной

Определение

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство  для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство (F(x)+C)׳=f(x). Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Определение

Совокупность функций первообразной для данной функции y=f(x), которая имеет место на некотором отрезке [a;b], называют неопределенным интегралом y=f(x).

Неопределенный интеграл имеет обозначение: \[\int f(x) d x=F(x)+C, c=\text { const }\].

Определение интегрирования

Определение

Операция нахождения интеграла называется интегрированием.

Дифференциал с интегральным выражением являются взаимно обратными действиями. У любой непрерывной на интервале функции есть какой-либо неопределенный интеграл.

Кратко о терминах и обозначениях:

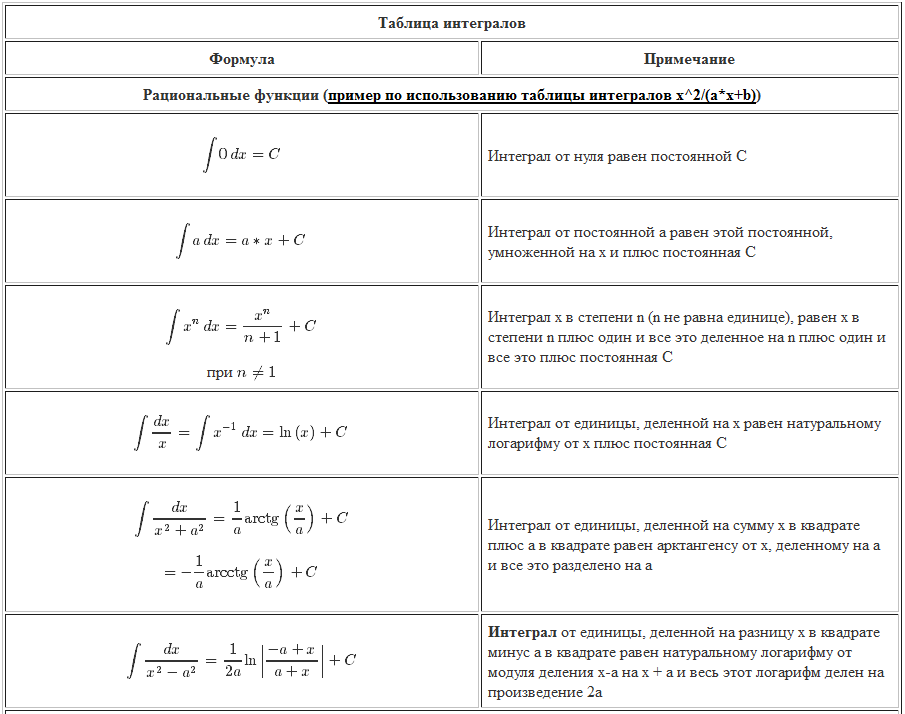
Таблица интегралов:

Таблица производных не включает формулы, которые соответствуют формулам из 10,13,14 таблицы. Чтобы проверить справедливость формул, необходимо произвести дифференцирование над ними.

Формулы интегралов, полная таблица основных свойств:

Расшифровка свойств интегралов:

1. Неопределенный интеграл при интегрировании функции является равным предоставляемой функции.
2. Производная от интегрального выражения будет равна подынтегральной функции, а дифференциал будет равен подынтегральному выражению.
3. Множитель в виде числа можно выносить за интеграл.
4. Интегральное выражение от суммы функций имеет такое же значение, как сумма интегральных выражений.
5. Подынтегральное выражение с множителями внутри равен подынтегральному выражению с выносимой константой.

C помощью них можно упростить выражение интеграла и вычислить элементарными действиями. {\prime}=\frac{1}{\sin x} \cdot \cos x=\operatorname{ctg} x \]

Производная получилось такая же, как и подынтегральная функция. Поэтому формула является верной.

Вычислить интеграл:

\[ \int(\cos (3 x+2)+5 x) d x \]

Решение:

Используем одно из основных свойств:

\[ \int(\cos (3 x+2)+5 x) d x=\int(\cos (3 x+2)) d x+\int 5 x d x \]

Используем свойство о вынесении множителя за интеграл:

\[ \int(\cos (3 x+2)) d x+\int 5 x d x=\int(\cos (3 x+2)) d x+5 \int x d x \]

С помощью таблицы:

При вычислении воспользуемся 5 свойством:

\[ \int(\cos (3 x+2)) d x=\frac{1}{3} \sin (3 x+2)+C_{1} \]

Найдем ответ:

При этом C₁+C₂ являются частями C. Если отдельно решается 2 и более интегралов, то к каждому члену ставится C с определенным индексом.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

чем отличаются, свойства и примеры решения

Содержание:

• Что такое первообразная функция и неопределенный интеграл
• Сущность первообразной функции
• Свойства неопределенного интеграла
• Таблица первообразных и неопределенных интегралов
• Примеры решения

Содержание

• Что такое первообразная функция и неопределенный интеграл
• Сущность первообразной функции
• Свойства неопределенного интеграла
• Таблица первообразных и неопределенных интегралов
• Примеры решения

Что такое первообразная функция и неопределенный интеграл

Функция F(x) может считаться первообразной для y=f(x), если первая функция дифференцируема в каждой точке промежутка (a;b) и ее производная удовлетворяет уравнению F'(x)=f(x).

Определение

Неопределенный интеграл — это сумма всех первообразных функции у=f(x).

Таким образом, представленные выше понятия связаны друг с другом как часть и целое.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Сущность первообразной функции

Понятие первообразной имеет еще одно определение.

Определение

Первообразная функция — это функция, производная которой равна данной.

Когда говорят о первообразной, упоминают также об интегрировании. Дело в том, что, чтобы отыскать значения всех рассматриваемых функций, пользуются интегрированием. При этом немаловажную роль играет признак постоянства функции.

Определение

Признак постоянства функции: если F'(x)=0, то функция F постоянна на заданном промежутке. Формула первообразной носит название общего вида первообразных для функции f. 

Перечислим свойства рассматриваемого понятия:

1. Любую первообразную можно записать как F(x)+C, где последний компонент означает произвольную постоянную.
2. Первообразная для f на промежутке I получится в любом случае, какое бы мы не подставили туда число.
3. Всегда возможно подобрать такое число С, что для всех х из выбранного промежутка будет справедливо уравнение Ф(х)=F(x)+C, какое бы значение для первообразной мы не подобрали.

Выделяют несколько основных правил для вычисления рассматриваемого понятия. 

1. Если F — это первообразная для одной функции, а G — для другой, то сумма первых будет равна сумме вторых, то есть \((F+G)’=F’+G’=f+g\), где последние две переменные есть функции.
2. Если F — первообразная, а k — постоянная, тогда произведение данных понятий будет равняться первообразной для функции k, умноженное на f. То есть \((k×F)’=k×F’=k×f\).  
3. Если F(x) — это первообразная, а k и b — постоянные, не равные нулю, тогда \(\frac1k\times F\times\left(k\times x+b\right)\) станет первообразной для функции\( f(k×x+b)\). То есть\( \left(\left(\frac1k\right)\times F\times\left(k\times x+b\right)\right)’=\left(\frac1k\right)\times F’\left(k\times x+b\right)\times k=f\left(k\times x+b\right)\).

Свойства неопределенного интеграла

Свойства НИ в виде выражений:

1. \(\int\lbrack f\left(x\right)+g\left(x\right)\rbrack dx=\int f\left(x\right)dx+\int g\left(x\right)dx.\)
2. \(\int kf\left(x\right)dx=k\int f\left(x\right)dx.\)
3. \(\int f\left(ax\right)dx=\frac1aF\left(ax\right)+C.\)
4. \(\int f\left(ax+b\right)dx=\frac1aF\left(ax+b\right)+C.\)

Таблица первообразных и неопределенных интегралов

Приведем простейшие табличные значения первообразных:

 

Теперь представим таблицу неопределенных интегралов:

 

Примеры решения

Чтобы точнее разобраться с рассматриваемыми терминами, приведем несколько примеров решения задач.

2}=\frac4{\sqrt6}arc\tan\frac{\sqrt3x}{\sqrt2}+C.\)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Таблица интегралов. Расчет, том 1

Основные интегралы

1. ∫undu=un+1n+1+C,n≠−1∫undu=un+1n+1+C,n≠−1

2. ∫duu=ln|u|+C∫duu=ln|u|+C

3. ∫eudu=eu+C∫eudu=eu+C

4. ∫audu=аулна+C∫audu=аулна+C

5. ∫sinudu=-cosu+C∫sinudu=-cosu+C

6. ∫cosudu=сину+C∫cosudu=сину+C

7. ∫sec2udu=тану+C∫sec2udu=тану+C

8. ∫csc2udu=-cotu+C∫csc2udu=-cotu+C

9. ∫secutanudu=secu+C∫secutanudu=secu+C

10. ∫cscucotudu=-cscu+C∫cscucotudu=-cscu+C

11. ∫tanudu=ln|secu|+C∫tanudu=ln|secu|+C

12. ∫котуду=ln|сину|+C∫котуду=ln|сину|+C

13. ∫secudu=ln|secu+tanu|+C∫secudu=ln|secu+tanu|+C

14.

∫cscudu=ln|cscu-cotu|+C∫cscudu=ln|cscu-cotu|+C

15. ∫dua2−u2=sin−1ua+C∫dua2−u2=sin−1ua+C

16. ∫dua2+u2=1atan−1ua+C∫dua2+u2=1atan−1ua+C

17. ∫duuu2−a2=1asec−1ua+C∫duuu2−a2=1asec−1ua+C

Тригонометрические интегралы

18. ∫sin2udu=12u−14sin2u+C∫sin2udu=12u−14sin2u+C

19. ∫cos2udu=12u+14sin2u+C∫cos2udu=12u+14sin2u+C

20. ∫tan2udu=tanu-u+C∫tan2udu=tanu-u+C

21. ∫cot2udu=-cotu-u+C∫cot2udu=-cotu-u+C

22. ∫sin3udu=−13(2+sin2u)cosu+C∫sin3udu=−13(2+sin2u)cosu+C

23. ∫cos3udu=13(2+cos2u)sinu+C∫cos3udu=13(2+cos2u)sinu+C

24. ∫tan3udu=12tan2u+ln|cosu|+C∫tan3udu=12tan2u+ln|cosu|+C

25. ∫cot3udu=-12cot2u-ln|sinu|+C∫cot3udu=-12cot2u-ln|sinu|+C

26. ∫sec3udu=12secutanu+12ln|secu+tanu|+C∫sec3udu=12secutanu+12ln|secu+tanu|+C

27. ∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C

28. ∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu

29. ∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu

30. ∫tannudu=1n−1tann−1u−∫tann−2udu∫tannudu=1n−1tann−1u−∫tann−2udu

31. ∫cotnudu=-1n-1cotn-1u-∫cotn-2udu∫cotnudu=-1n-1cotn-1u-∫cotn-2udu

32. ∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu

33. ∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu

34. ∫sinausinbudu=sin(a−b)u2(a−b)−sin(a+b)u2(a+b)+C∫sinausinbudu=sin(a−b)u2(a−b)−sin (а+б)и2(а+б)+С

35. ∫cosaucosbudu=sin(a−b)u2(a−b)+sin(a+b)u2(a+b)+C∫cosaucosbudu=sin(a−b)u2(a−b)+sin (а+б)и2(а+б)+С

36. ∫sinaucosbudu=−cos(a−b)u2(a−b)−cos(a+b)u2(a+b)+C∫sinaucosbudu=−cos(a−b)u2(a−b) −cos(a+b)u2(a+b)+C

37. ∫usinudu=sinu-ucosu+C∫usinudu=sinu-ucosu+C

38. ∫ucosudu=cosu+usinu+C∫ucosudu=cosu+usinu+C

39. ∫unsinudu=-uncosu+n∫un-1cosudu∫unsinudu=-uncosu+n∫un-1cosudu

40. ∫ункосуду=унсину-н∫ун-1синуду∫ункосуду=унсину-н∫ун-1синуду

 41. 1un+m+n−1n+m∫sinn−2ucosmudu=sinn+1ucosm−1un+m+m−1n+m∫sinnucosm−2udu

Экспоненциальные и логарифмические интегралы

42. ∫ueaudu=1a2(au-1)eau+C∫ueaudu=1a2(au-1)eau+C

43. ∫uneaudu=1auneau-na∫un-1eaudu∫uneaudu=1auneau-na∫un-1eaudu

44. ∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C

45. ∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C

46. ∫lnudu=ulnu-u+C∫lnudu=ulnu-u+C

47. ∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+C∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+ С

48. ∫1ulnudu=ln|lnu|+C∫1ulnudu=ln|lnu|+C

Гиперболические интегралы

49. ∫синхуду=кошу+К∫синхуду=кошу+К

50. ∫кошуду=синху+К∫кошуду=синху+К

51. ∫танхуду=инкошу+К∫танхуду=инкошу+К

52. ∫cothudu=ln|sinhu|+C∫cothudu=ln|sinhu|+C

53. ∫sechudu=tan−1|sinhu|+C∫sechudu=tan−1|sinhu|+C

54. ∫cschudu=ln|tanh22u|+C∫cschudu=ln|tanh22u|+C

55. ∫sech3udu=танху+C∫sech3udu=танху+C

56. ∫csch3udu=−cothu+C∫csch3udu=−cothu+C

57. ∫sechutanhudu=-sechu+C∫sechutanhudu=-sechu+C

58. ∫cschucothudu=-cschu+C∫cschucothudu=-cschu+C

Обратные тригонометрические интегралы

59. ∫sin-1udu=usin-1u+1-u2+C∫sin-1udu=usin-1u+1-u2+C

60. ∫cos-1udu=ucos-1u-1-u2+C∫cos-1udu=ucos-1u-1-u2+C

61. ∫tan−1udu=utan−1u−12ln(1+u2)+C∫tan−1udu=utan−1u−12ln(1+u2)+C

62. ∫usin-1udu=2u2-14sin-1u+u1-u24+C∫usin-1udu=2u2-14sin-1u+u1-u24+C

63. ∫ucos-1udu=2u2-14cos-1u-u1-u24+C∫ucos-1udu=2u2-14cos-1u-u1-u24+C

64. ∫utan−1udu=u2+12tan−1u−u2+C∫utan−1udu=u2+12tan−1u−u2+C

65. ∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1−u2],n≠−1∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1− u2],n≠−1

66. ∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2],n≠−1∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2] ,n≠−1

67. ∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+u2],n≠−1∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+ u2],n≠−1

Интегралы с участием

a ² + u ² , a > 0

68. ∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C

69. ∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2)+C∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2 )+С

70. ∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C

71. ∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C

72. ∫dua2+u2=ln(u+a2+u2)+C∫dua2+u2=ln(u+a2+u2)+C

73. ∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C

74. ∫duua2+u2=−1aln|a2+u2+au|+C∫duua2+u2=−1aln|a2+u2+au|+C

75. ∫duu2a2+u2=−a2+u2a2u+C∫duu2a2+u2=−a2+u2a2u+C

76. ∫du(a2+u2)3/2=ua2a2+u2+C∫du(a2+u2)3/2=ua2a2+u2+C

Интегралы с участием

u ² − a ² , a > 0

77. ∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C

78. ∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2|+C∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2 |+С

79. ∫u2−a2udu=u2−a2−acos−1a|u|+C∫u2−a2udu=u2−a2−acos−1a|u|+C

80. ∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C

81. ∫duu2−a2=ln|u+u2−a2|+C∫duu2−a2=ln|u+u2−a2|+C

82. ∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C

83. ∫duu2u2−a2=u2−a2a2u+C∫duu2u2−a2=u2−a2a2u+C

84а. ∫du(u2−a2)3/2=−ua2u2−a2+C∫du(u2−a2)3/2=−ua2u2−a2+C

84б. ∫duu2-a2=12alnu-au+a+C∫duu2-a2=12alnu-au+a+C

Интегралы с участием

a ² − u ² , и > 0

85. ∫a2−u2du=u2a2−u2+a22sin−1ua+C∫a2−u2du=u2a2−u2+a22sin−1ua+C

86. ∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C

87. ∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C

88. ∫a2−u2u2du=−1ua2−u2−sin−1ua+C∫a2−u2u2du=−1ua2−u2−sin−1ua+C

89. ∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C

90. ∫duua2−u2=−1aln|a+a2−u2u|+C∫duua2−u2=−1aln|a+a2−u2u|+C

91. ∫duu2a2−u2=−1a2ua2−u2+C∫duu2a2−u2=−1a2ua2−u2+C

92. ∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+3a48sin−1ua+C∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+ 3a48sin−1ua+C

93а. ∫du(a2−u2)3/2=ua2a2−u2+C∫du(a2−u2)3/2=ua2a2−u2+C

93б. ∫dua2-u2=12alnu+au-a+C∫dua2-u2=12alnu+au-a+C

Интегралы с участием 2

au − u ² , a > 0

94. ∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C

95. ∫du2au-u2=cos-1(a-ua)+C∫du2au-u2=cos-1(a-ua)+C

96. ∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C

97. ∫duu2au-u2=-2au-u2au+C∫duu2au-u2=-2au-u2au+C

Интегралы с участием

a + bu , a ≠ 0

98. ∫udua+bu=1b2(a+bu-aln|a+bu|)+C∫udua+bu=1b2(a+bu-aln|a+bu|)+C

99. ∫u2dua+bu=12b3[(a+bu)2−4a(a+bu)+2a2ln|a+bu|]+C∫u2dua+bu=12b3[(a+bu)2−4a(a +bu)+2a2ln|a+bu|]+C

100. ∫duu(a+bu)=1aln|ua+bu|+C∫duu(a+bu)=1aln|ua+bu|+C

101. ∫duu2(a+bu)=−1au+ba2ln|a+buu|+C∫duu2(a+bu)=−1au+ba2ln|a+buu|+C

102. ∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+C∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+ С

103. ∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+C∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+ С

104. ∫u2du(a+bu)2=1b3(a+bu−a2a+bu−2aln|a+bu|)+C∫u2du(a+bu)2=1b3(a+bu−a2a+bu− 2aln|a+bu|)+C

105. ∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C

106. ∫udua+bu=23b2(bu−2a)a+bu+C∫udua+bu=23b2(bu−2a)a+bu+C

107. ∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C

108. ∫duua+bu=1aln|a+bu−aa+bu+a|+C,ifa>0=2−atan−1a+bu−a+C,ifa<0∫duua+bu=1aln|a +bu-aa+bu+a|+C,ifa>0=2-atan-1a+bu-a+C,ifa<0

109. ∫a+buudu=2a+bu+a∫duua+bu∫a+buudu=2a+bu+a∫duua+bu

110. ∫a+buu2du=−a+buu+b2∫duua+bu∫a+buu2du=−a+buu+b2∫duua+bu

111. ∫una+budu=2b(2n+3)[un(a+bu)3/2−na∫un−1a+budu]∫una+budu=2b(2n+3)[un(a+bu) )3/2−na∫un−1a+budu]

112. ∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫un−1dua+bu∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫ ип-1дуа+бу

113. ∫duuna+bu=−a+bua(n−1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu∫duuna+bu=−a+bua(n −1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu

Mathwords: интегральная таблица

Mathwords: интегральная таблица

индекс: нажмите на букву индекс: предметные области
	Встроенный стол Для следующих букв a , b , n , и C представляют собой константы. Примечание. Большинство следующих интегральных записей пишутся на неопределенный срок интегралы, но они применимы и к определенным интегралы. Основные формы 1. , где n ≠ –1 2. 3. 4. , где a > 0 и a ≠ 1 5. 6. 7. 8. 9. 10. 11. , где F ( u ) является производной от f ( u ) Другие базовые триггеры и инверсы Триггерные формы 12. 13. 14. 15. 16. 17. для a > 0 18. 19. для a > 0 20. на у > 1 21. для u > a > 0 Основные рациональные формы 22. для a > 0 23. для a > 0 Триггерные формы 24. 25. 26. Обратные триггерные формы 27. 28. 29. 30. 31. для u > 1 32. для u > 1 Формы, содержащие 33. для a > 0 Формы, содержащие 34. Формы, включающие 35. для u > a > 0 Формы, включающие au + b 36. 37. Экспоненциальные формы 38. 39. 40. 41. 42. Логарифмические формы 43. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт