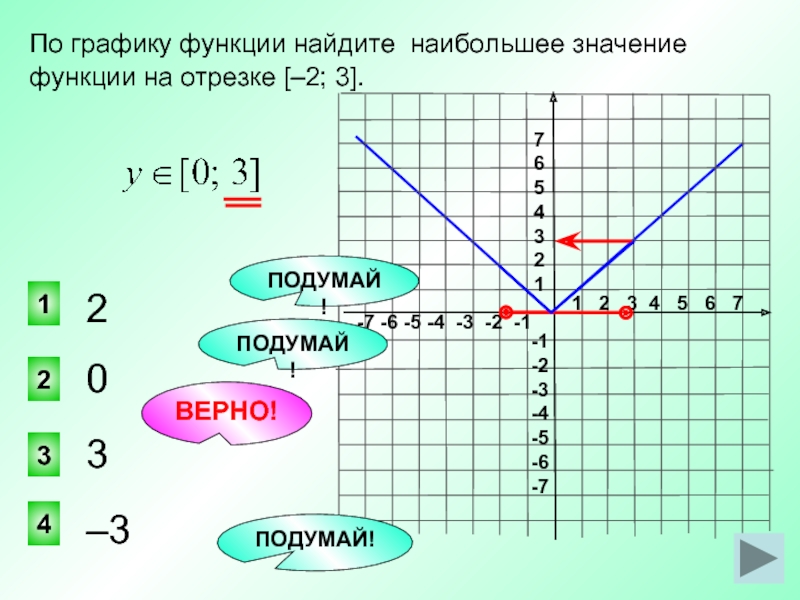
Найти наибольшее значение функции как найти по графику: Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке — урок. Алгебра, 10 класс.

Содержание

Найти наибольшее и наименьшее значение функции y. Исследование графика функции

Миниатюрная и довольно простая задача из разряда тех, которые служат спасательным кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий необходимо уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции .

Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция непрерывна на отрезке если:

1) она непрерывна на интервале ;
2) непрерывна в точке справа и в точке

слева .

Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:

Функция непрерывна в точке справа , если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: . Она же непрерывна в точке слева , если определена в данной точке и её левосторонний предел равен значению в этой точке:

Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:

Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём . В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается

первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)

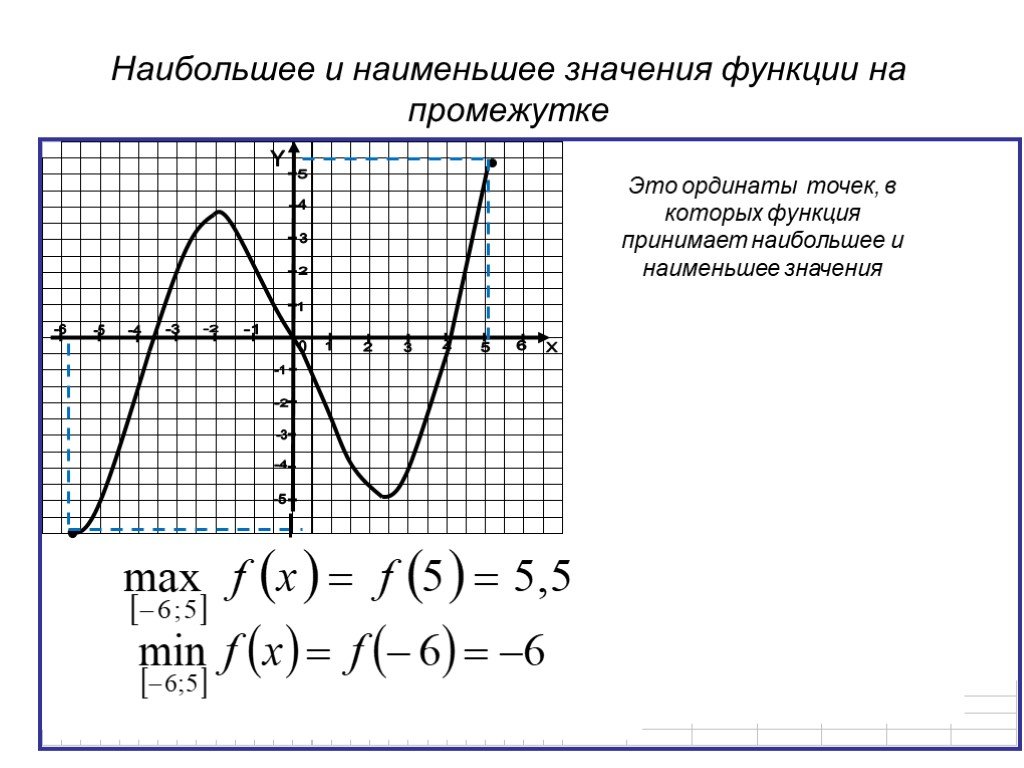
Согласно второй теореме Вейерштрасса , непрерывная на отрезке функция достигает своей точной верхней грани и своей точной нижней грани .

Число также называют максимальным значением функции на отрезке и обозначают через , а число – минимальным значением функции на отрезке с пометкой .

В нашем случае:

Примечание : в теории распространены записи .

Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.

Важно! Как уже заострялось внимание в статье об экстремумах функции , наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ , что максимум функции и минимум функции . Так, в рассматриваемом примере число является минимумом функции, но не минимальным значением.

Кстати, а что происходит вне отрезка ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел и всё!

Более того, решение чисто аналитическое, следовательно, чертежа делать не надо !

Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:

1) Находим значения функции в критических точках , которые принадлежат данному отрезку .

Ловите ещё одну плюшку: здесь отпадает необходимость проверять достаточное условие экстремума, поскольку, как только что было показано, наличие минимума или максимума ещё не гарантирует , что там минимальное или максимальное значение. Демонстрационная функция достигает максимума и волей судьбы это же число является наибольшим значением функции на отрезке . Но, понятно, такое совпадение имеет место далеко не всегда.

Итак, на первом шаге быстрее и проще вычислить значения функции в критических точках, принадлежащих отрезку, не заморачиваясь есть в них экстремумы или нет.

2) Вычисляем значения функции на концах отрезка.

3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.

Садимся на берег синего моря и бьём пятками по мелководью:

Пример 1

Найти наибольшее и наименьшее значения функции на отрезке

Решение :
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

Вычислим значение функции во второй критической точке:

2) Вычислим значения функции на концах отрезка:

3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение.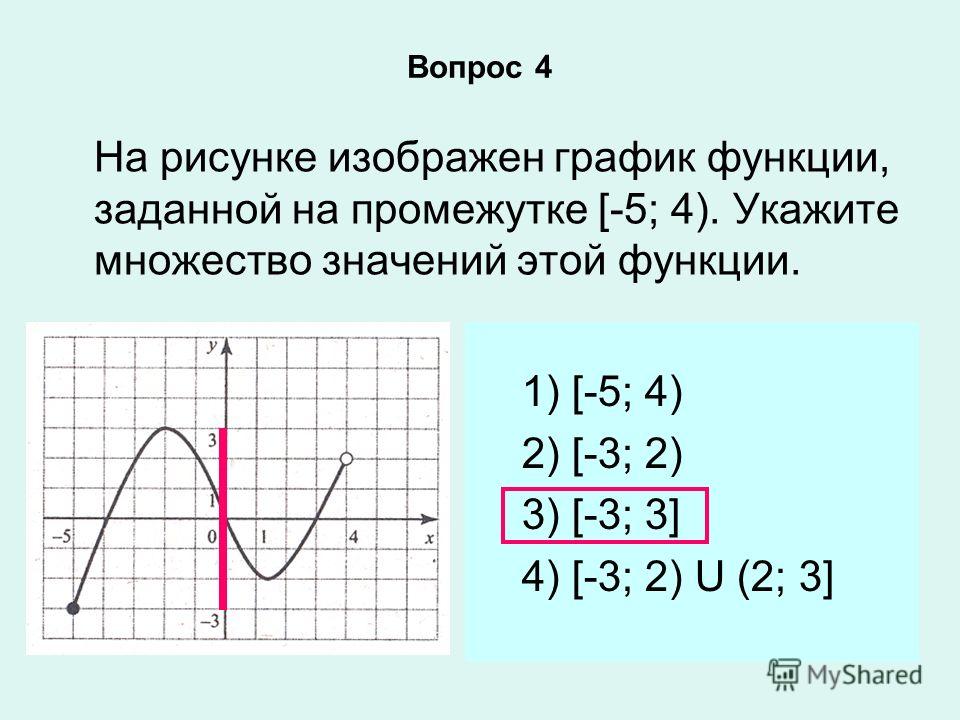 По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что :

Вот теперь всё понятно.

Ответ :

Дробно-рациональный экземпляр для самостоятельного решения:

Пример 6

Найти максимальное и минимальное значения функции на отрезке

Процесс поиска наименьшего и наибольшего значения функции на отрезке напоминает увлекательный облёт объекта (графика функции) на вертолёте с обстрелом из дальнобойной пушки определённых точек и выбором из этих точек совсем особенных точек для контрольных выстрелов. Точки выбираются определённым образом и по определённым правилам. По каким правилам? Об этом мы далее и поговорим.

Если функция y = f (x ) непрерывна на отрезке [a , b ] , то она достигает на этом отрезке наименьшего и наибольшего значений . Это может произойти либо в точках экстремума , либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции , непрерывной на отрезке [a , b ] , нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее.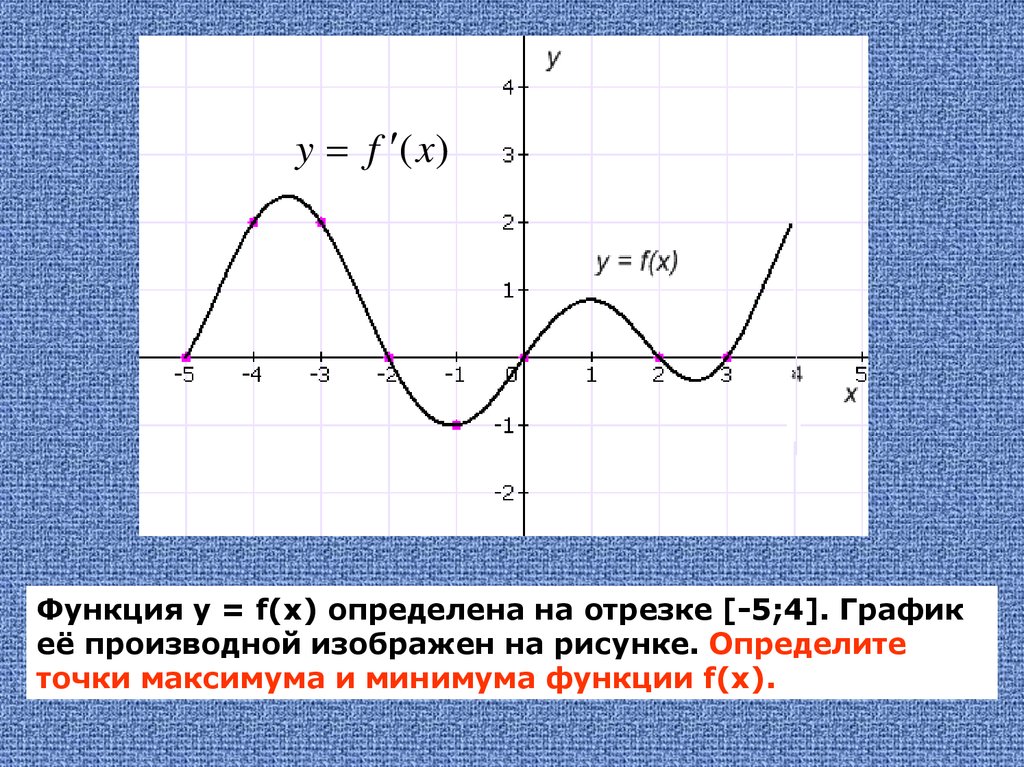

Пусть, например, требуется определить наибольшее значение функции f (x ) на отрезке [a , b ] . Для этого следует найти все её критические точки, лежащие на [a , b ] .

Критической точкой называется точка, в которой функция определена , а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f (a ) и f (b ) ). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a , b ] .

Аналогично решаются и задачи на нахождение наименьших значений функции .

Ищем наименьшее и наибольшее значения функции вместе

Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2] .

Решение. Находим производную данной функции .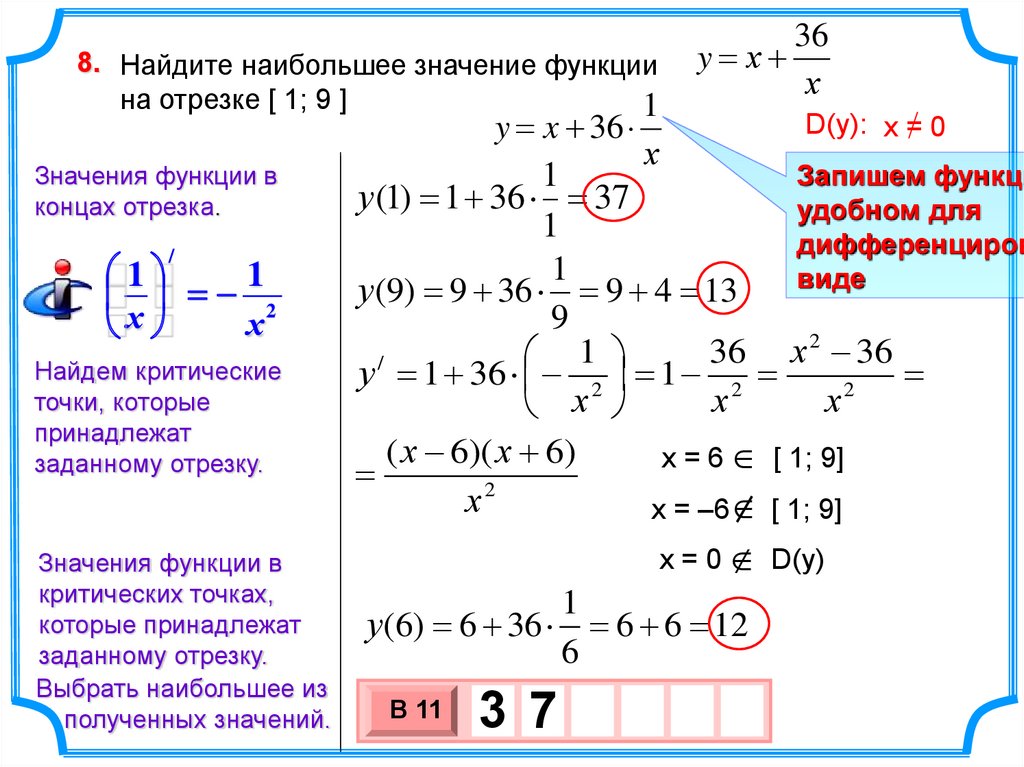

Приравняем производную нулю () и получим две критические точки: и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка не принадлежит отрезку [-1, 2] . Эти значения функции — следующие: , , . Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке , а наибольшее (тоже красное на графике), равно 9, — в критической точке .

Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.

Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3] .

Решение. Находим производную данной функции как производную частного:

Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3] . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Сравниваем эти значения. Вывод: , равного -5/13, в точке и наибольшего значения , равного 1, в точке .

Продолжаем искать наименьшее и наибольшее значения функции вместе

Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).

Поэтому в ход пойдут логарифм и тригонометрическая функция.

Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную данной функции как производную произведения :

Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Результат всех действий: функция достигает наименьшего значения

, равного 0, в точке и в точке и наибольшего значения , равного e ² , в точке .

Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную данной функции:

Приравниваем производную нулю:

Единственная критическая точку принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Вывод: функция достигает наименьшего значения , равного , в точке и наибольшего значения , равного , в точке .

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.

Пример 8. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?

Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S :

Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[ , причём

Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак, сторона основания резервуара должна быть равна 2 м, а его высота .

Пример 9. Из пункта A , находящегося на линии железной дороги, в пункт С , отстоящий от неё на расстоянии l , должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?

В этой статье я расскажу про алгоритм поиска наибольшего и наименьшего значения функции, точек минимума и максимума. 2 — 65. Даже ничего не считая становится очевидно, что в точке 100 функция имеет знак плюс. А значит и на промежутки от 1 до 100 она имеет знак плюс. При переходе через 1 (мы идем справа налево)функция сменит знак на минус. При переходе через точку 0 функция сохранит свой знак, так как это лишь граница отрезка, а не корень уравнения. При переходе через -1 функция опять сменит знак на плюс.

Из теории мы знаем, что там, где производная функции (а мы именно для нее это и чертили) меняет знак с плюса на минус (точка -1 в нашем случае) функция достигает своего локального максимума (y(-1)=44, как была посчитано ранее) на данном отрезке (это логически очень понятно, функция перестала возрастать, так как достигла своего максимума и начала убывать).

Соответственно, там где производная функции меняет знак с минуса на плюс , достигается локальный минимум функции . Да, да, мы также нашли точку локального минимума это 1, а y(1) — это минимальное значение функции на отрезке, допустим от -1 до +∞.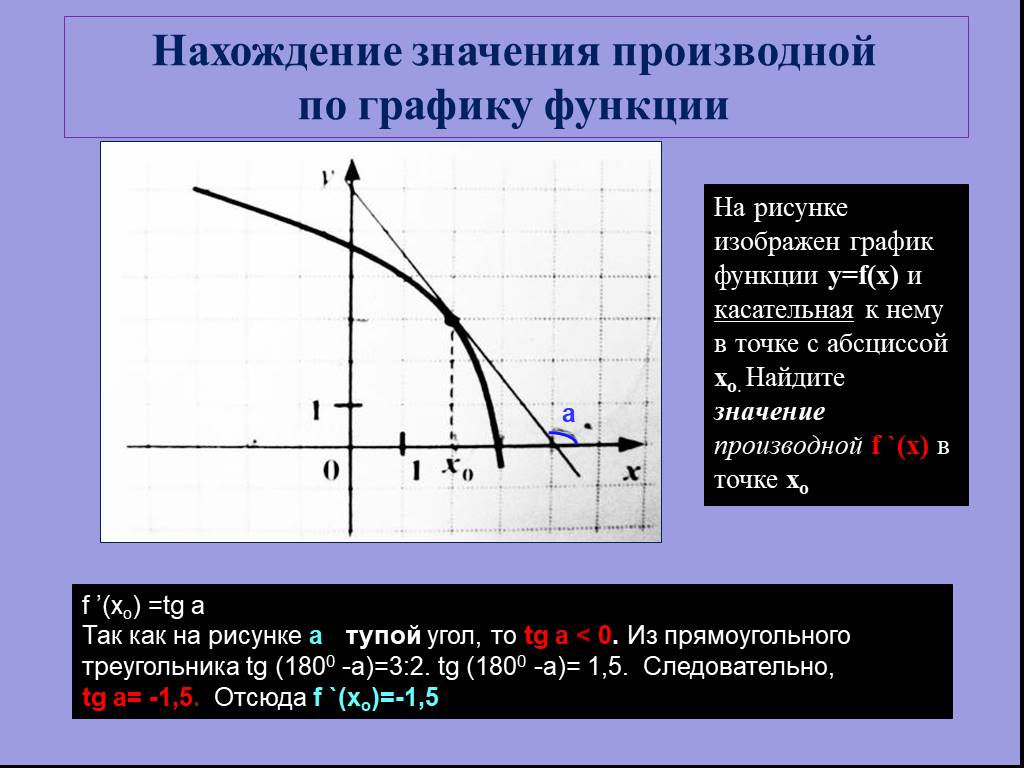 Обратите огромное внимание, что это лишь ЛОКАЛЬНЫЙ МИНИМУМ, то есть минимум на определенном отрезке. Так как действительный (глобальный) минимум функция достигнет где-то там, в -∞.

На мой взгляд первый способ проще теоретически, а второй проще с точки зрения арифметических действий, но намного сложнее с точки зрения теории. Ведь иногда бывают случаи, когда функция не меняет знак при переходе через корень уравнения, да и вообще можно запутаться с этими локальными, глобальными максимумами и минимумами, хотя Вам так и так придется это хорошо освоить, если вы планируете поступать в технический ВУЗ (а для чего иначе сдавать профильное ЕГЭ и решать это задание). Но практика и только практика раз и навсегда научит Вас решать такие задачи. А тренироваться можете на нашем сайте. Вот .

Если появились какие-то вопросы, или что-то непонятно — обязательно спросите. Я с радостью Вам отвечу, и внесу изменения, дополнения в статью. Помните мы делаем этот сайт вместе!

Исследование такого объекта математического анализа как функция имеет большое значение и в других областях науки. Например, в экономическом анализе постоянно требуется оценить поведение функции прибыли, а именно определить ее наибольшее значение и разработать стратегию его достижения.

Инструкция

Исследование поведения любой всегда следует начинать с поиска области определения. Обычно по условию конкретной задачи требуется определить наибольшее значение функции либо на всей этой области, либо на конкретном ее интервале с открытыми или закрытыми границами.

Исходя из , наибольшим является значение функции y(x0), при котором для любой точки области определения выполняется неравенство y(x0) ≥ y(x) (х ≠ x0). Графически эта точка будет наивысшей, если расположить значения аргумента по оси абсцисс, а саму функцию по оси ординат.

Чтобы определить наибольшее значение функции , следуйте алгоритму из трех этапов. Учтите, что вы должны уметь работать с односторонними и , а также вычислять производную. Итак, пусть задана некоторая функция y(x) и требуется найти ее наибольшее значение на некотором интервале с граничными значениями А и В.

Выясните, входит ли этот интервал в область определения функции . Для этого необходимо ее найти, рассмотрев все возможные ограничения: присутствие в выражении дроби, квадратного корня и т.д. Область определения – это множество значений аргумента, при которых функция имеет смысл. Определите, является ли данный интервал его подмножеством. Если да, то переходите к следующему этапу.

Найдите производную функции и решите полученное уравнение, приравняв производную к нулю. Таким образом, вы получите значения так называемых стационарных точек. Оцените, принадлежит ли хоть одна из них интервалу А, В.

Рассмотрите на третьем этапе эти точки, подставьте их значения в функцию. В зависимости от типа интервала произведите следующие дополнительные действия. При наличии отрезка вида [А, В] граничные точки входят в интервал, об этом говорят скобки. Вычислите значения функции при х = А и х = В. Если открытый интервал (А, В), граничные значения являются выколотыми, т.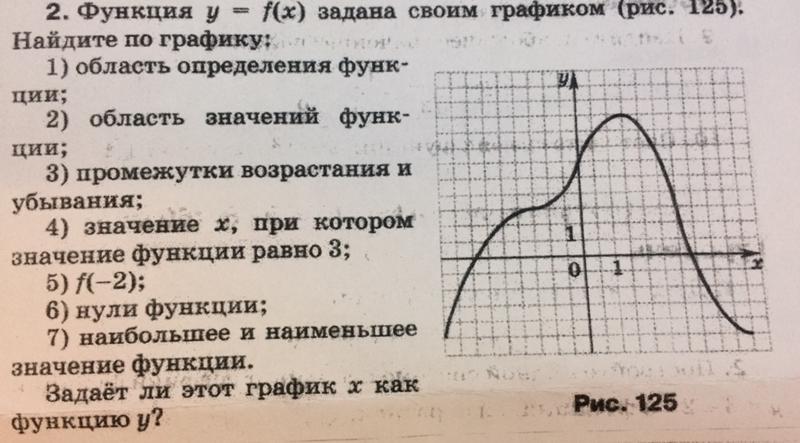 е. не входят в него. Решите односторонние пределы для х→А и х→В. Комбинированный интервал вида [А, В) или (А, В], одна из границ которого принадлежит ему, другая – нет. Найдите односторонний предел при х, стремящемся к выколотому значению, а другое подставьте в функцию. Бесконечный двусторонний интервал (-∞, +∞) или односторонние бесконечные промежутки вида: , (-∞, B). Для действительных пределов А и В действуйте согласно уже описанным принципам, а для бесконечных ищите пределы для х→-∞ и х→+∞ соответственно.

Задача на этом этапе

2.4.4. Наибольшее и наименьшее значения функции на отрезке.

Для нахождения наибольшего и наименьшего значений функции используют свойство функции, непрерывной на отрезке:

Если функция непрерывна на отрезке , то она обязательно достигает на этом отрезке наибольшего и наименьшего значения. Эти значения находятся или в точках экстремума, лежащих внутри отрезка, или на концах отрезка.

Схема нахождения наибольшего и наименьшего

Значений функции на отрезке:

Найти критические точки І рода функции на отрезке .
Вычислить значения функции в критических точках.
Вычислить значения функции на концах отрезка.
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Пример 19.

Найти наибольшее и наименьшее значения функции на отрезке.

Решение.

Вычислим производную и найдем критические точки первого рода.

;

, если ;;.

Из найденных двух критических точек только точка принадлежит заданному интервалу .

Вычислим значения функции в критической точке и на концах отрезка и:

;

Сравнивая три полученных значения функции, определяем, что:

наибольшее значение функции

наименьшее значение функции .

2.4.5. Выпуклость графика функции. Точки перегиба

График функции называется выпуклым на интервале , если он расположен выше любой своей касательной на этом интервале (рис. 7а).

График функции называется вогнутым на интервале , если он расположен выше любой своей касательной на этом интервале (рис. 7б).

Выпуклость и вогнутость графика функции связана со знаком второй производной функции. Нахождение интервалов выпуклости и вогнутости опирается на следующую теорему.

Теорема: Если во всех точках интервала вторая производная функции отрицательна, т.е. , то график функции на этом интервале выпуклый, если же, то график функции вогнутый.

Точка графика функции, отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба.

Для нахождения точек перегиба графика функции используют необходимое и достаточное условия существования точек перегиба.

Необходимое условие существования точки перегиба.

Если – абсцисса точки перегиба графика функции , то вторая производная в этой точке либо равна нулю, либо не существует, т.е. или не существует.

Точки, в которых вторая производная равна нулю или не существует (в частности, точки разрыва функции), называются критическими точками второго рода.

Замечание: Обратное утверждение не всегда верно, то есть если или не существует, то точка с абсциссой может не являться точкой перегиба.

Достаточное условие существования точки перегиба.

Если вторая производная при переходе через критическую точку второго рода меняет знак, то точка с абсциссой является точкой перегиба графика функции.

Схема исследования функции на

Интервалы выпуклости, вогнутости и точки перегиба:

Найти область определения функции .
Найти первую производную .
Найти вторую производную .
Найти критические точки ІІ рода.
Разбить критическими точками ІІ рода область определения функции на интервалы.
Определить знак второй производной на каждом из интервалов (методом подстановки значений аргумента или методом интервалов).
Определить интервалы выпуклости (вогнутости) графика функции.
Определить, используя достаточный признак, какие из критических точек второго рода являются точками перегиба.
Вычислить значение функции в полученных точках перегиба.
Результаты оформить в виде таблицы.

Пример 20.

Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции .

Решение.

Функция определена на всей числовой оси. Область определения функции имеет вид: .

Найдем первую производную функции:

Найдем вторую производную функции:

Найдем критические точки второго рода:

Дробь равна нулю, если числитель равен нулю и знаменатель не равен нулю:

; .

Следовательно, точка – критическая точка ІІ рода.

Разбиваем всю числовую ось на интервалы и определяем знак второй производной на каждом интервале.

	0
–	не сущ.	–
	0	

Так как на интервалах вторая производная отрицательная значит, на этих интервалах график функции выпуклый.

Интервалов вогнутости график функции не имеет.

Так как при переходе через критическую точку вторая производная не меняет свой знак, то в этой точке перегиба нет.

Приближенный вид графика функции приведен на рис 6.

графиков линейных функций | dongheenam

Home
Courses
Jpn maths 1
Functions
Functions and graphs
Linear graphs

function
linear function
domain
range

Introduction

Graphs are a convenient способ визуализации функций. На этом уроке мы:

Повторим определение графика функции.
Нарисуйте график линейной функции, если задана ее область определения.
Оценка минимального и максимального значения функции.

График

Вспомним определение функции: функция связывает определенное значение $x$ с соответствующим значением $y$. ⊕ График $y=x+2$. Например, функция $$ y = x+2 $$ связывает $x=0$ с $y=2$, $1$ с $3$, $\sqrt{5}$ с $\sqrt{5}+2$. , и так далее. Вы можете видеть, что эти значения образуют комбинация чисел: $(0, 2)$, $(1, 3)$ и $\big(\sqrt{5}, \sqrt{5}+2\big)$. Если мы соберем эти координаты на координатной плоскости, то получим график $y=x+2$!

Определение. График функции $y=f(x)$ — это множество всех пар чисел $(x, y)$ при условии, что $x$ является элементом ее области определения.

График линейной функции

Прежде чем двигаться дальше, мы рассмотрим основные свойства линейной функции и ее графика.

Определение. Функция $y=f(x)$ является линейной , если $f(x)$ является линейным многочленом от $x$.

Общий вид линейной функции: $f(x) = ax + b$, где $a\ne 0$.
График линейной функции образует линию на координатной плоскости.

Пример. Следующие функции являются линейными функциями от $x$.

$f(x) = 3x-4$
$g(x) = \dfrac{x}{3}$
$h(x) = \sqrt{2} x + \sqrt{3} $

Учитывая $f(x) = ax+b$, если вы увеличите значение $x$ на 1, вы увеличите значение $y$ на $a$: \начать{выравнивать*} f(0) &= b, \cr f(1) &= a + b, \cr f(2) &= 2a + b, \cr \vточки \конец{выравнивание*} и, следовательно, $a$ называется градиентом или наклоном . Кроме того, значение $y$ при $x=0$ равно $b$, и это значение называется y-отрезком .

подпись Градиент и y-пересечение линейного графика.

Пример. Нарисуйте графики следующих линейных функций.

$y = -x + 3$
$3x-2y=6$

Решение.

1. Градиент графика равен -1, а точка пересечения по оси y равна 3. Таким образом, график проходит через $(0, 3)$ и $(0+1, 3-1)=(1,2)$.

2. Мы можем изменить уравнение, чтобы выявить градиент и точку пересечения с осью y: \начать{выравнивать*} 3x-2y = 6 & \ тогда и только тогда, когда 2y = 3x — 6 \cr &\ тогда и только тогда, когда у = \dfrac{3}{2} х — 3. \end{align*}

Однако проще найти точки пересечения графика по осям x и y и построить график оттуда. Когда $х=0$, \начать{выравнивать*} -2у = 6 \ тогда и только тогда, когда у = -3, \end{выравнивание*}

, поэтому точка пересечения с осью y равна $-3$, а когда $y=0$, \начать{выравнивать*} 3x = 6 \ тогда и только тогда, когда x = 2, \end{align*}

, поэтому пересечение по оси x равно $2$.

График с ограниченной областью определения

Когда область определения функции меньше ее естественной области определения, вам необходимо построить график только в пределах этой области. Взгляните на пример ниже.

Пример. Нарисуйте графики следующих функций.

$y=-2x+1,$ $-1\le x\le 2$
$y=2x-4$, $0\le x < 3$

Раствор.

1. Когда $x=-1$, $$y=2+1=3,$$ и когда $x=2$, $$y=-4+1=-3.$$ Итак, нам нужно нарисовать график между $(-1,3)$ и $(2,-3)$.

2. Когда $x=0$, $$y=0-4=-4,$$ и когда $x=3$, $$y=6-4=2.$$ Обратите внимание, что $(3,2)$ , а не включены в график!

Угадывание функции по ее области определения и диапазону

Допустим, функция $f(x)=ax+b$ имеет область определения $\{ x \, | \, 1\le x \le 2 \}$ и диапазон $\{ y \, | \, 3\le y \le 5 \}$. Как мы можем указать эту функцию? 92 = 0$. Точно так же некоторые функции имеют наименьшее или наибольшее значение в своем диапазоне. Они называются значениями максимум и минимум .

Определение. Максимальное значение функции — это наибольшее число в ее диапазоне. Минимальное значение — это наименьшее число в своем диапазоне.

Точка, в которой функция имеет максимальное значение, называется точкой максимума или точкой 92$ имеет минимальное значение 0, но максимальное значение не существует.
$f(x) = -x+2 ~ (-2\le x \le 0)$ имеет диапазон $2 \le y \le 4$, поэтому минимальное значение равно 2, а максимальное значение равно 4.

Найдем минимальное и максимальное значения функций из предыдущего примера.

Пример. Найдите минимальное и максимальное значения следующих функций.

$y=-2x+1,$ $-1\le x\le 2$
$y=2x-4$, $0\le x < 3$

Решение.

1. Из приведенного выше графика легко понять, что диапазон составляет $-3 \le y \le 3$. Следовательно, минимальное значение равно $\boldsymbol{-3}$, а максимальное значение равно $\boldsymbol{3}$.

2. На графике выше диапазон составляет $-4 \le y < 2$. Обратите внимание, что в этот набор входят не $2$, а любые числа до $2$. Следовательно, минимальное значение равно $\boldsymbol{ -4 }$, но максимальное значение не существует .

Практические вопросы

Изобразите следующие функции и найдите их минимумы и максимумы, если они существуют.
1. $y=5x-2$ $(0\le x \le 3)$
2. $y=-3x+1$ $(-1

Ответ

1. Диапазон: $-2\le y \le 13$, минимум: $-2$, максимум: $13$.
2. Диапазон: $-5\le y < 4$. минимум: $-5$.

Раствор.

а. Когда $x=0$, $y=0-2=-2$, а когда $x=3$, $y=15-2=13$.

Таким образом, диапазон равен $\boldsymbol{ -2\le y \le 13 }$. Минимум $\boldsymbol{-2 }$, максимум $\boldsymbol{ 13 }$.

б. Когда $x=-1$, $y=3+1=4$, а когда $x=2$, $y=-6+1=-5$.

Таким образом, диапазон равен $\boldsymbol{ -5\le y < 4 }$. Минимум $\boldsymbol{-5}$, максимум $\textbf{не существует}$.

Когда функция $y=ax+b$, $2\le x \le 5$, имеет диапазон $-1\le y\le 5$, найдите значения $a$ и $b$.

Ответ

$a=2, \, b=-5$ или $a=-2, \, b=9.$

Решение. Скажем, $f(x) = ax+b$. Две возможности:

$f(2)=-1$ и $f(5)=5$, или
$f(2)=5$ и $f(5)=-1$.

В первом случае градиент равен $\dfrac{5+1}{5-2} = 2$, поэтому $a=2$. Затем \начать{выравнивать*} f(2) = -1 & \ тогда и только тогда, когда 2a + b = -1 \cr & 4 + b = -1 \кр &b = -5. \end{align*}

Во втором случае градиент равен $\dfrac{-5-1}{5-2}=-2$, поэтому $a=-2$. Затем \начать{выравнивать*} f(2) = 5 и тогда и только тогда, когда 2a+b = 5 \cr &-4 + b = 5 \кр б = 9. \end{align*}

Следовательно, мы заключаем $\boldsymbol{ a=2, \, b=-5 }$ или $\boldsymbol{ a=-2, \, b=9}.$

2 апр 2021 | Обновлено 31 июля 2022 г.

Функции, домен и диапазон

Преобразования графиков

Функция — Как найти локальный максимум в R из графика

спросил 3 года 10 месяцев назад

Изменено 3 года, 10 месяцев назад

Просмотрено 92 + 9) plot(x,y) # Это создаст график с двумя максимальными точками # вопрос 2 х[который. max(y)] у[который.макс(у)]

Однако я получаю координаты только одной максимальной точки и понятия не имею, как мне получить другую максимальную точку.

r
функция
макс.
локальная

Вы можете использовать find_peaks из пакета ggpmisc .

 библиотека (ggpmisc)
x[ggpmisc:::find_peaks(df$y)]
y[ggpmisc:::find_peaks(df$y)]

Выход:

 [1] -1,5 3,0
[1] 1,6373473 0,8818895

Обратите внимание, что функция find_peaks отмечена как внутренняя . Поэтому вам необходимо получить к нему доступ, используя ::: .

Вы можете дополнительно параметризовать вызов find_peaks , используя аргументы span и strict . Подробнее см. ??find_peaks .

Вы также можете напрямую построить это, используя ggplot2 и 92 + 9) df <- data.