Числа делящиеся без остатка на 2 называют: Запиши первые 5 натуральных чисел которые делятся на 2 без остатка

Урок 4. Признаки делимости на 10, на 5, на 2 | Поурочные планы по математике 6 класс

Цели: ознакомить учащихся с признаками делимости на 10, на 5, на 2; ввести определение четных и нечетных чисел; повторить порядок действий; учить рассуждать и логически мыслить.

Ход урока

I. Организационный момент

 

II. Актуализация знаний учащихся

1. Познакомить учащихся с результатами самостоятельной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

 

III. Устный счет

1. 347 : 10; 3000 : 10; 464 : 2; 155 : 5; 125 : 5; 441 : 2; 670 : 10; 284 : 2; 648 : 2; 575 : 5; 101 : 5; 340 : 10.

— На какие группы можно разделить данные числовые выражения? Почему? (На 3 группы — деление чисел на 2, на 5, на 10; на 2 группы — числа, которые делятся нацело и числа, при делении которых получается остаток; на 4 группы — числа, которые делятся на 2, на 5, на 10 без остатка и числа, при делении которых на 2, на 5, на 10 получается остаток. )

2. Периметр квадрата 36 см. Найдите площадь квадрата. (36 : 4 · 9 = 81 см2)

3. Могут ли при каком-нибудь значении данных букв быть верными равенства: 8 — х = х — 8, у — 4 = у + 4, 6 — z = z + 6?

4. Чему равно произведение всех цифр? (0.)

5. Сколько треугольников изображено на чертеже?

 

 

(Ответ: 35.)

 

IV. Индивидуальная работа

(Повторение уравнений 5 класса, можно дать как самостоятельную работу всему классу.)

 

	1 карточка		2 карточка
1 2 3 4 5 6 7 8 9 10	27 + х + 63 = 100 (х — 9) + 20 = 56 8х + 2х + Зх = 130 15х — 5х + 20 = 180 60 — (х + 7) — 34 5х + х — 2х + 40 = 240 450 — 3х = 150 40 · х · 25 = 100 000 50 : х + 48 = 50 18 · (15 — х) = 216	1 2 3 4 5 6 7 8 9 10	52 + х + 28 = 100 40 — (х + 3) = 12 17х — 7х + 40 = 170 6х + 5х + 4х = 150 (х — 8) + 30 = 65 8х + х — 4х — 40 = 160 310 + 7х = 380 4 · х · 250 = 10 000 90 : х — 32 = 13 (х — 8) · 12 = 132

 

V. Сообщение темы урока

— Сегодня на уроке мы научимся узнавать, делится ли одно число на другое, не выполняя деление. Существуют признаки, помогающие по записи числа определить, делится ли оно на какое-то число.

— Запишем тему урока «Признаки делимости на 10, на 5, на 2».

 

VI. Изучение нового материала

— Мы знаем, что при умножении натурального числа на 10 получается число, оканчивающееся нулем. Поэтому всякое натуральное число, оканчивающееся цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.

— Найдите значения выражений: 23 400 : 10; 547 890 : 10; 62 370: 10; 568 300: 10.

— Эти числа делятся без остатка на 10.

— Проверьте, делятся ли числа 283 на 10 и 548 на 10.

(При делении числа 283 на 10 получаем неполное частное 28 и остаток 3; при делении числа 548 на 10 получаем неполное частное 54 и остаток 8.)

— Сравните остатки отделения с последней цифрой чисел.

— Что интересного заметили? (Остаток от деления равен последней цифре в записи этого числа.

)

— Какой вывод можно сделать? (Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.)

— Сформулируйте признак делимости чисел на 10.

— Прочитайте, как сформулирован этот признак в учебнике на стр. 9.

— Назовите 3 числа, которые делятся на 10 и 3 числа, которые на 10 не делятся.

— Прочитайте самостоятельно в учебнике на стр. 9 текст после признака делимости на 10.

— Почему любое число, запись которого оканчивается цифрой 0, делится без остатка и на 2, и на 5?

— Приведите примеры, подтверждающие это.

— Как в учебнике доказывается признак делимости числа на 5?

— Приведите примеры чисел, делящихся на 5, и чисел, не делящихся на 5.

Определение. Числа, делящиеся без остатка на 2, называются четными, а числа, которые при делении на 2 дают остаток 1, называются нечетными.

— Цифры 0, 2, 4, 6, 8 — называют четными, а цифры 1, 3, 5, 7, 9 — нечетными.

— Сформулируйте самостоятельно признак делимости на 2.

— Приведите примеры трехзначных четных чисел. Приведите примеры двузначных нечетных чисел.

— Можно записать в тетрадь памятку для учащихся:

1. Число, оканчивающееся на четную цифру, делится на 2.

2. Число, оканчивающееся на 0 или 5, делится на 5.

3. Число, оканчивающееся на 0, делится на 10.

 

VII. Физкультминутка

Приглашаем к доске ученика, который дома придумал небольшой комплекс упражнений. Если есть возможность, выполняйте упражнения под музыку.

 

VIII. Закрепление изученного материала

1. № 31 стр. 10. Один ученик на доске работает цветными мелками, остальные в тетрадях. (Красным карандашом подчеркнуты четные числа, то есть числа, которые без остатка делятся на 2; синим — числа, которые делятся без остатка на 5; обоими цветами — числа, которые делятся без остатка на 10; 1, 3, 1, 9, 11, 13, 17, 19, 21, 23, 27, 29.)

2. — Сколько различных трехзначных чисел можно записать с помощью цифр 0, 6, 9? Цифры могут повторяться.

— К какому виду задач относится данная задача? (Комбинаторная.)

— Какие цифры могут быть на месте сотен, десятков и единиц. (На месте сотен могут быть только цифры 6 или 9, на месте десятков и единиц все три цифры).

Определение. Графы — геометрические фигуры, состоящие из точек (их называют вершинами) и соединяющих их отрезков (называемых ребрами графа).

(Эту схему выполняет учитель на доске.)

Решение: подсчет вариантов выполним с помощью графа, называемого деревом (за внешнее сходство с деревом).

Ребра графа, являющегося деревом, иногда называют ветвями дерева, а само дерево — деревом вариантов. Дерево вариантов дает наглядное представление о том, как применяется правило произведения для подсчета комбинаций из большего, чем 2, числа элементов.

 

 

Или по правилу произведения получаем 2 · 3 · 3 = 18 (чисел). (Ответ: 18 чисел.)

3. № 35 (а) стр. 11 самостоятельно (с последующей проверкой).

— Определите, сколько чисел мы должны записать.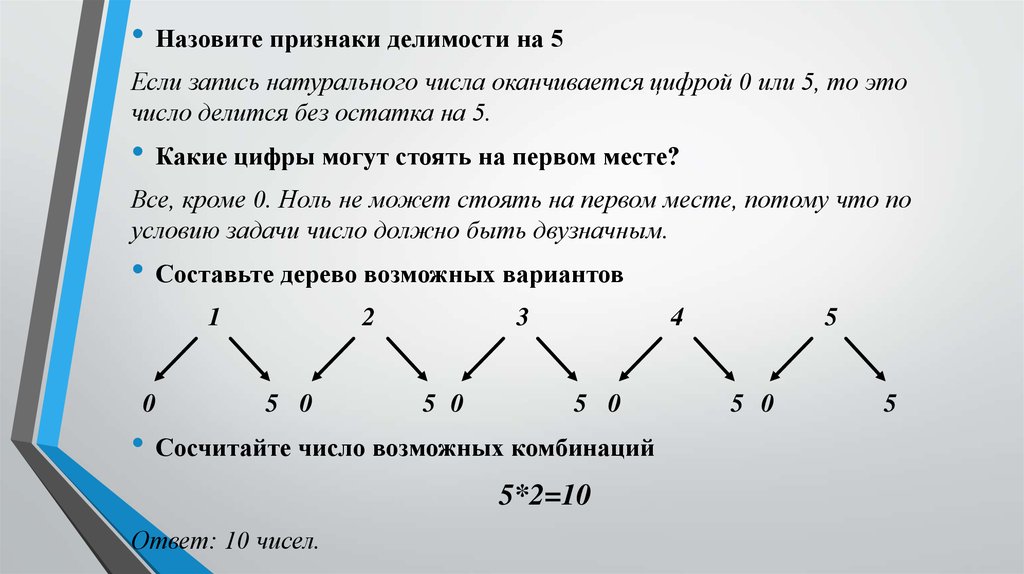

Решение:

Первой цифрой числа может быть любая из двух цифр (2 или 5, так как число не может начинаться с нуля), второй — любая из трех (0, 2, 5), а третьей — любая из двух (0, 2, так как должно выполняться условие: число делится на 2): 2 · 3 · 2 = 12 (чисел). (Ответ: 222, 220, 252, 250, 202, 200, 522, 520, 552, 550, 502, 500.)

4. № 36 стр. 11 (устно). Ответ обоснуйте.

(Ответ: 32 яйца Коля принести не может, так как число 32 не делится на 10 без остатка.)

 

IX. Самостоятельная работа

Взаимопроверка.

Вариант I № 32 (а, в) стр. 10, № 33 (а, г) стр. 10.

Вариант II № 32 (б, г) стр. 10, № 33 (б, в) стр. 10.

— В конце работы запишите, кто проверял. (Учитель выборочно проверяет несколько тетрадей).

 

X. Повторение пройденного материала

1. Повторить порядок действий. Фронтальная работа.

— Какие действия относятся к действиям первой ступени и какие — к действиям второй ступени? (Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел — действиями второй ступени. )

— Вспомните правила выполнения действий.

Правила выполнения действий:

1) Если в выражении есть скобки, то сначала выполняют действия в скобках.

2) Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.

3) Если в выражении нет скобок и оно содержит только действия одной ступени, то их выполняют по порядку слева направо.

4) Если в выражении нет скобок и оно содержит действия первой и второй ступени, то сначала выполняют действия второй ступени, потом — действия первой ступени.

— Можно ли изменять порядок действий? (Изменять порядок действий можно на основе свойств сложения, вычитания и умножения.)

— Назовите первое действие и т. д. (Порядок действий обводите в круг.)

Решение:

2. № 54 стр. 13 (с подробным комментированием у доски и в тетрадях).

— Решим задачу алгебраическим способом. Что это значит? (С помощью уравнения.)

— Что значит число увеличили в 11 раз? (Умножили на 11. )

— Что значит результат уменьшили на 2,75? (Вычли из полученного результата 2,75.)

Решение:

I  способ (алгебраический)

Пусть х — задуманное число,

х · 11 — 2,75 = 85,25

х · 11 = 85,25 + 2,75

х · 11 = 88  

х = 88 : 11

х = 8;        8 — задуманное число.

II способ (арифметический)

1) 85,25 + 2,75 = 88

2) 88 : 11 = 8 (Ответ: 8.)

 

XI. Подведение итогов урока

— Что нового и интересного узнали на уроке?

— Какие цифры называют четными? Приведите примеры.

— Какие цифры называют нечетными? Приведите примеры.

Домашнее задание

Учебник, стр. 9—10 выучить правила и определения; № 54 (2), 55, 60 (а, б) стр. 13.

По желанию № 39 стр. 11.

Признак делимости на 2, 5 и 10 | Презентация к уроку по математике (6 класс):

Слайд 1

Классная работа. Признаки делимости на 10, на 5, на 2 22.09

Слайд 2

Проверим быстрый счет 347 : 10 3000 : 10 464 : 2 155 : 5 125 : 5 41 : 2 670 : 10 284 : 2 648 : 2 575 : 5 101 : 5 430 : 10 45 : 2 56 : 2

Слайд 3

Проверим быстрый счет 347 : 10 3000 : 10 464 : 2 155 : 5 125 : 5 41 : 2 670 : 10 284 : 2 648 : 2 575 : 5 101 : 5 430 : 10 45 : 2 56 : 2

Слайд 4

Как изменится запись числа, если его умножить на 10? Число, полученное при умножении на 10, будет оканчиваться нулём! Продолжите фразу: Всякое натуральное число, оканчивающееся 0,… делится без остатка на 10!

Слайд 5

Расскажите мне об этих числах, учитывая признак деления на 10: 23 400 285 34 650 5 56000 548 Делится с остатком Делится с остатком Почему одни числа делятся на 10 без остатка, а другие нет?

Слайд 6

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Признак делимости на 10 548, 150, 250, 453, 52480, 565, 630.

Слайд 7

Назовите делители числа 10 Тогда, если число делится на 10, то оно делится на … 5 и на 2.

Слайд 8

Маша «ловила» числа, которые делятся на 5, а Миша те, что не делятся на 5. Определите, кто какие числа «поймал», записав числа в таблицу: Делятся на 5 Не делятся на 5 534 35 3587 302 3030 15 5553 920

Слайд 9

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 5. Признак делимости на 5 584, 153, 250, 455, 5280, 563, 6320.

Слайд 10

Чтобы Маша не мешала Мише, он ей нарисовал фигуру и попросил сосчитать сколько треугольников изображено на рисунке? Помогите Маше быстро справиться с этой задачей

Слайд 11

Домашнее задание: Учебник, п.2 выучить правила и определения № 46; № 57; № 59. По желанию дополнительно: № 53

Слайд 12

Классная работа. Признаки делимости на 10, на 5, на 2 2 4 .09

Слайд 13

Вычисли устно: 5 + 0,8 0,26 + 7 0,48 + 0,2 0,6 +0,34 2,7 + 1,12 0,76 – 0,3 2,54 – 2 0,82 – 0,02 0,63 – 0,6 0,8 – 0,25

Слайд 14

Вычисли устно: 0,2 * 4 2,1 * 3 0,7 * 10 0,5 * 2 2,25 * 4 6 : 10 0,8 : 2 2,1 : 7 0,5 : 10 4,1 : 2

Слайд 15

1. Назовите три числа которые делятся на 10. назовите три числа, которые делятся на 5.

Слайд 16

Числа, делящиеся без остатка на 2 , называются чётными , а числа, которые при делении на 2 дают остаток , называются нечётными.

Слайд 17

Какие цифры четные, а какие нет?

Слайд 18

Если запись натурального числа оканчивается четной цифрой, то это число чётно, а значит делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой, то это число не чётно. Признак делимости на 2 584, 13, 250, 45, 5280, 58, 6320.

Слайд 19

В классе: № 32 № 33 № 34 № 36 № 35 Домашняя работа: п. 2, признаки делимости, № 58, № 61

Слайд 20

Давай-ка, повторим Сформулируйте признак делимости на 10 Какие цифры считают четными? Какие натуральные числа называют нечетными? Сформулируйте признак делимости на 5 Сформулируйте признак делимости на 2 Сколько цифр нечетных? А сколько четных цифр? Приведите для примера 3 трехзначных четных числа Что Вы сможете сказать о 34 560, учитывая признаки делимости чисел?

Простые числа — факты, примеры и таблица всех чисел до 1000

Простое число можно разделить без остатка только само на себя и на 1. Например, 17 можно разделить только на 17 и на 1.

Некоторые факты:

• Единственное четное простое число — 2. Все остальные четные числа можно разделить на 2.
• Если сумма цифр числа кратна 3, то это число можно разделить на 3.
• Ни одно простое число больше 5 не оканчивается на 5. Любое число больше 5, оканчивающееся на 5, можно разделить на 5.
• Ноль и 1 не считаются простыми числами.
• За исключением 0 и 1, число является либо простым, либо составным числом. Составное число определяется как любое число больше 1, которое не является простым.

Чтобы доказать, является ли число простым, сначала попробуйте разделить его на 2 и посмотреть, получится ли целое число. Если да, то это не может быть простое число. Если вы не получили целое число, попробуйте разделить его на простые числа: 3, 5, 7, 11 (9 делится на 3) и так далее, всегда деля на простое число (см. таблицу ниже).

Here is a table of all prime numbers up to 1,000:

	2	3	5	7	11	13	17	19	23
29	31	37	41	43	47	53	59	61	67
71	73	79	83	89	97	101	103	107	109
113	127	131	137	139	149	151	157	163	167
173	179	. 0027
229	233	239	241	251	257	263	269	271	277
281	283	293	307	311	313	317	331	337	347
349	353	359	367	373	379	383	389	397	401
409	419	421	431	433	439	443	449	457	461
463	467	479	487	491	499	. 0027	557	563	569	571	577	587	593	599
601	607	613	617	619	631	641	643	647	653
659	661	.0026 719	727
733	739	743	751	757	761	769	773	787	797
809	811	821	823	827	829	839	853	857	859
863	877	881	883	887	907	911	919	929	937
941	947	953	967	971	977	983	991	997

Целое число, которое делится на 2, называется \\[\\] A.

Четное число\\[\\] B. Нечетное число \\[\\] C. Простое число \\[\\] D. Составное номер \\[\\]

Дата последнего обновления: 14 февраля 2023 г.

•

Всего просмотров: 244,5 тыс.

•

Просмотров сегодня: 2,32 тыс. Вспомним делимое $n$, делитель $d$, частное $q$, остаток $r$ и лемму Евклида $n=dq+r$. Когда имеем $r=0$, мы говорим, что $n$ делится на $d$. Мы вспоминаем четные числа как числа, делящиеся на 2, а нечетные числа как числа, не делящиеся на 2. \[\]

Полный пошаговый ответ:
Мы знаем, что в арифметической операции деления число, которое мы собираемся разделить, называется делимым, а число, на которое делится делимое, называется делителем. Мы получаем частное, которое представляет собой количество раз, когда делитель делимого, а также остаток, полученный в конце деления. Если число равно $n$, делитель равен $d$, частное равно $q$, а остаток равен $r$, они связаны следующим уравнением:

\[n=dq+r\]
Здесь делитель никогда не может быть равен нулю. Приведенное выше соотношение называется леммой Евклида о делении. \[\]
Если $ r=0 $ в $ n=dq+r $, то $ n $ точно делится или делится на $ d $ или $ n $ кратно $ d $ . Если мы собираемся разделить натуральные числа на 2, то мы можем получить либо остаток 0, либо остаток 1.\[\]
 Если мы получаем напоминание 0, мы говорим, что число делится на 2, и это число называется нечетным, например, четные числа 2,4,6,8,10,…. и если мы получаем остаток 1, мы говорим, что число не делится на 2 и число называется нечетным числом, например, четным числа 3,5,7,9,11,…
Итак, целое число, которое делится на 2, называется четным числом. Следовательно, правильным вариантом является A.\[\]

Примечание:
Заметим, что остаток всегда меньше частного, то есть $ r < q $ . Таким образом, возможные остатки равны $0,1,2,...,q-1$. Если $ n $ кратно $ d $ кратно $ n $ . Заметим, что если двух делителей (1 и само число) всего 2, то число называется простым, иначе составным. Существует только одно четное простое число, равное 2, а остальные простые числа нечетные.