Вычислить неопределенный интеграл. — примеры, решения
Пример 1:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 2:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 3:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 4:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 5:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 6:
Вычислить интеграл:
Решение от преподавателя:
Пример 7:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 8:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 9:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Для вычисления был использован табличный интеграл
Пример 10:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 11:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 12:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 13:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 14:
Вычислить интеграл:
Решение от преподавателя:
Пример 15:
Вычислить неопределенный интреграл:
Решение от преподавателя:
Пример 16:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 17:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Интегралы вида
,
где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома.
В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.
Чтобы найти такие интегралы, используются подстановки Чебышева.
1. Если p — целое число, то используется подстановка
,
где k — наименьшее общее кратное знаменателей m и n.
2. Если — целое число, то используется подстановка
,
где s — знаменатель дроби p.
3. Если — целое число, то используется подстановка
,
где s — знаменатель дроби p.
Определим для нашей функции.
m = -2; p = ; n = 2
- p = – не целое
- – не целое
- – не целое.
Вывод: использовать подстановки нельзя
Это четвертый случай. Такой интеграл является не берущимся.
Пример 18:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 19:
Вычислить неопределенный интерграл:
Решение от преподавателя:
Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:
Пример 20:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 21:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 22:
Вычислить интеграл:
Решение от преподавателя:
Пример 23:
Найти неопределенный интеграл
Решение от преподавателя:
Пример 24:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Представим подынтегральное выражение в виде:
= + dx
Представляя выражение x^2+2*x+10 как переменную t, получаем:
Выделим полные квадраты:
Вычисляем табличный интеграл вида:
=
Пример 25:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 26:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 27:
Найти неопределённый интеграл:
Решение от преподавателя:
Пример 28:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 29:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 30:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 31:
Найти неопределённый интеграл:
Решение от преподавателя:
Пример 32:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 33:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 34:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 35:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 36:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 37:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 38:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 39:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 40:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 41:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 42:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 43:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 44:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 45:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 46:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 47:
Найти неопределенный интеграл:
Решение от преподавателя:
Используем метод разложения на простейшие.
Разложим функцию на простейшие слагаемые:
Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:
-2x+4 = A(x+4) + Bx
x: A + B = -2
1: 4A = 4
Решая ее, находим:
A = 1;B = -3;
Вычисляем табличный интеграл:
Вычисляем табличный интеграл:
Ответ:
=ln(x)-3ln(x+4) + C
Пример 48:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 49:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 50:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 51:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 52:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 53:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 54:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 55:
Найдите неопределенный интеграл:
Решение от преподавателя:
Пример 56:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 57:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 58:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 59:
Найдите неопределенный интеграл:
Решение от преподавателя:
Пример 60:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 61:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 62:
Найти неопределенные интегралы методом подстановки:
Решение от преподавателя:
Пример 63:
Найдите неопределенный интеграл:
Решение от преподавателя:
Пример 64:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 65:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 66:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 67:
Найдите неопределенный интеграл:
Решение от преподавателя:
Пример 68:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 69:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 70:
Найти интегралы методом интегрирования по частям:
Решение от преподавателя:
Пример 71:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 72:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 73:
Найти неопределенный интеграл:
Решение от преподавателя:
Пример 74:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 75:
Вычислить:
Решение от преподавателя:
Пример 76:
Найти неопределенные интегралы:
Решение от преподавателя:
Пример 77:
Вычислить:
Решение от преподавателя:
Пример 78:
Найти интегралы от рациональных функций:
Решение от преподавателя:
Пример 79:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 80:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 81:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 82:
Вычислить интеграл:
Решение от преподавателя:
Пример 83:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 84:
Найти неопределенные интегралы:
Решение от преподавателя:
Пример 85:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 86:
Найти интеграл от рациональной функций:
Решение от преподавателя:
Пример 87:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 88:
Вычислить интеграл:
Решение от преподавателя:
Пример 89:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 90:
Вычислить интеграл:
Решение от преподавателя:
Пример 91:
Вычислить следующий интеграл:
Решение от преподавателя:
Пример 92:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 93:
Вычислить:
Решение от преподавателя:
Пример 94:
Вычислить неопределённый интеграл.
Решение от преподавателя:
Пример 95:
Вычислить:
Решение от преподавателя:
Пример 96:
Вычислить интеграл:
Решение от преподавателя:
Пример 97:
Вычислить:
Решение от преподавателя:
Пример 98:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 99:
Вычислить:
Решение от преподавателя:
Пример 100:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 101:
Вычислить:
Решение от преподавателя:
Пример 102:
Вычислить неопределённый интеграл.
Решение от преподавателя:
Пример 103:
Вычислить интеграл:
Решение от преподавателя:
Пример 104:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 105:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 106:
Вычислить неопределённый интеграл.
Решение от преподавателя:
Пример 107:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 108:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 109:
Вычислить неопределённый интеграл.
Решение от преподавателя:
Пример 110:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 111:
Вычислить неопределенный интеграл:
Решение от преподавателя:
Пример 112:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 113:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 114:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 115:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 116:
Вычислить неопределенные интегралы:
Решение от преподавателя:
Пример 117:
Найти неопределенный интеграл.
Решение от преподавателя:
Пример 118:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 119:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 120:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 121:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 122:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 123:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 124:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 125:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 126:
Найти неопределённый интеграл.
Решение от преподавателя:
Пример 127:
Найти неопределённый интеграл:
Решение от преподавателя:
Как найти неопределенный интеграл?
Это чужой компьютер Забыли пароль?
org/BreadcrumbList»>- ВУЗы, Колледжи, Техникумы
- Закрытый вопрос
- Бизнес, Финансы
- Города и Страны
- Досуг, Развлечения
- Животные, Растения
- Знакомства, Любовь, Отношения
- Искусство и Культура
- Компьютеры, Интернет, Связь
- Кулинария, Рецепты
- Лингвистика
- Наука и Техника
- Образование
- ВУЗы, Колледжи, Техникумы
- Детские сады
- Домашние задания
- Дополнительное образование
- Образование за рубежом
- Прочее образование
- Школы
- Общество, Политика, СМИ
- Отдельная Категория
- Прочее
- Путешествия, Туризм
- Работа, Карьера
- Семья, Дом, Дети
- Спорт
- Стиль, Мода, Звезды
- Товары и Услуги
- Транспорт
- Философия, Психология
- Фотография, Видеосъемка
- Юридическая консультация
Юмор
Закрыт 12 лет
Rookie
Ученик (105)
интеграл от x умножить на e в степени x
#интеграл
Мы платим до 300 руб за каждую тысячу уникальных поисковых переходов на Ваш вопрос или ответ Подробнее
| ЛУЧШИЙ ОТВЕТ ИЗ 2 |
12 лет
Личный кабинет удален
Наставник (48046)
Вы можете заказать решение контрольной работы по адресу
По частям.
2+1))dx
вычислить неопределенный интеграл
Помогите решить неопр. интегралы, как всегда на самом простом застреваю
Интеграл от x*arctg2x — как решить?
А как лучше колбаску в оливье порезать-с логарифмами или с интегралами?
Как люди придумали интегралы, как им это пришло в голову? «
Неопределенные интегралы — Photomath
Исследуйте Интегралы
Производные? Был там. Поиск производных? Сделано это.
А как же интегралы? Как насчет нахождения неопределенных интегралов?
Не волнуйтесь — вы у нас есть.
Что такое неопределенный интеграл?
Пусть $$f(x)$$ — функция. Первообразной $$f(x)$$ является любая функция $$F(x)$$ такая, что:
$$F'(x) = f(x)$$
Так как первообразных много одной функции, неопределенный интеграл от f дает нам все свои первообразные:
$${\int f(x) dx = F(x) + C}$$
где $$C$$ — любая константа, называемая константой интегрирования.
Хммм, ладно, но как нам найти этот интеграл?
Используем свойства и правила интегралов!
Свойства интегралов используются для упрощения процесса интегрирования путем разделения процедуры на несколько шагов. Вот список всех свойств и правил, которые вы захотите держать под рукой:
| Постоянное кратное интегралов | $$\int{(c\times f(x))}dx=c\times \int{f(x)}dx$$ |
| Правило сумм для интегралов | $$\int{(f(x) + g(x))}dx=\int{f(x)}dx + \int{g(x)}dx$$ |
| Правило сумм для интегралов | {\ простое число} (t) dt = \ int {f (x)} dx $ $|
| Интеграция по частям | $$\int{u}dv=uv-\int{v}du$$ |
Почему неопределенный интеграл так полезен?
Нахождение неопределенного интеграла — своего рода «первый шаг» во многих математических вычислениях, например, при решении дифференциальных уравнений или даже при нахождении определенного интеграла! 92}+C, C\in \mathbb{R}$$
Отличная работа!
Вы можете применить этот процесс к любой проблеме, которую выберете.
Резюме исследования
- Упростите выражение, если это возможно.
- Используйте свойства интеграла.
- Оцените интеграл. 9{4x}}{4}+C, C \in \mathbb{R}$$
Нужна помощь? Были здесь! Просто отсканируйте проблему с помощью приложения Photomath, и мы поможем вам выполнить каждый шаг.
Вот краткий обзор того, что вы увидите:
/
Есть домашнее задание по математике?
Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.
Нахождение неопределенных интегралов — Математика для старших классов
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Справка по математике для средней школы » Исчисление II — Интегралы » Интегралы » Нахождение интегралов » Нахождение неопределенных интегралов
Возможные ответы:
Правильный ответ:
Объяснение:
Интеграл от равен .
Константа 3 просто умножается на интеграл.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы проинтегрировать, нам нужно получить два уравнения относительно друг друга. Мы собираемся использовать «u-подстановку», чтобы создать новую переменную , которая будет равна .
Теперь, если , то
Умножьте обе части на , чтобы получить более знакомое:
Обратите внимание, что наше и наше исходное уравнение требовало положительного .
Это означает, что если мы хотим в терминах , это выглядит так:
Вынести знак минус наружу:
.
Мы можем использовать правило степени, чтобы найти интеграл от :
Поскольку мы это сказали , мы можем подставить это обратно в уравнение, чтобы получить ответ:
Отчет о ошибке
Оценка интеграла ниже:
Возможные ответы:
Правильный ответ:
9 Правильный ответ:
1 Объяснение:
В этом случае мы имеем рациональную функцию, где, где
и
могут быть написаны как продукт линейных факторов:
.
Предполагается, что а и b определенные константы, подлежащие оценке. Знаменатели можно очистить, умножив обе части на (x — 4)(x + 4). Получаем:
Сначала мы заменяем x = -4 в полученное уравнение:
, затем заменим x = 4 в уравнение:
Тал:
.
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти неопределенный интеграл, мы можем использовать правило обратной степени. Мы повышаем степень показателей на единицу и делим на этот новый показатель. Для этой задачи это будет выглядеть так:
Помните, что при взятии интеграла, определенного или неопределенного, мы всегда прибавляем, так как может быть вовлечена константа.
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти неопределенный интеграл, мы можем использовать правило обратной степени. Мы повышаем степень показателей на единицу и делим на этот новый показатель. Для этой задачи это будет выглядеть так:
Помните, что при взятии интеграла, определенного или неопределенного, мы всегда прибавляем, так как может быть вовлечена константа.
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти неопределенный интеграл, мы можем использовать правило обратной степени.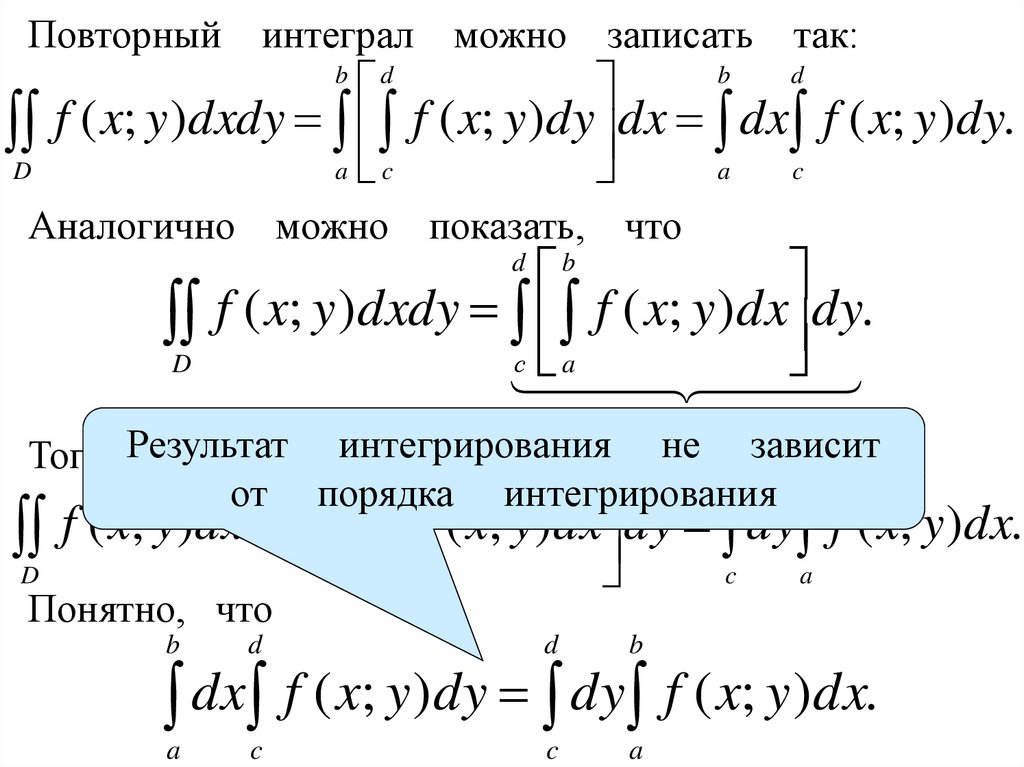
Мы повышаем степень показателей на единицу и делим на этот новый показатель.
Мы будем рассматривать как , так как все в нулевой степени равно единице.
Для этой задачи это будет выглядеть так:
Помните, что при взятии интеграла, определенного или неопределенного, мы всегда прибавляем, так как может быть задействована константа.
Сообщить об ошибке
Что такое антипроизводная?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти неопределенный интеграл нашего выражения, мы можем использовать правило обратной степени.
Чтобы использовать правило обратной степени, мы повышаем показатель степени на единицу, а затем делим на этот новый показатель.
Сначала нам нужно понять это . Отсюда мы можем решить:
При взятии интеграла обязательно ставьте в конце все.
означает «постоянный». Поскольку взятие производной от постоянного целого числа всегда будет равно , мы включаем , чтобы предвидеть возможность того, что уравнение на самом деле будет или , а не просто .
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти неопределенный интеграл нашего уравнения, мы можем использовать правило обратной степени.
Чтобы использовать правило обратной степени, мы повышаем показатель степени на единицу, а затем делим на этот новый показатель.
Помните, что при вычислении интеграла мы относимся к константам как к числу, умноженному на , так как все в нулевой степени есть . Например, относитесь как .
При вычислении интеграла не забудьте поставить в конце всего.
означает «постоянный». Поскольку взятие производной от постоянного целого числа всегда будет равно , мы включаем , чтобы предвидеть возможность того, что уравнение на самом деле будет или , а не просто .
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти неопределенный интеграл нашего уравнения, мы можем использовать правило обратной степени.
Чтобы использовать правило обратной степени, мы повышаем показатель степени на единицу, а затем делим на этот новый показатель.
При вычислении интеграла не забудьте включить . означает «постоянный». Поскольку взятие производной от постоянного целого числа всегда будет равно , мы включаем , чтобы предвидеть возможность того, что уравнение на самом деле будет или , а не просто .
Сообщить об ошибке
Что такое неопределенный интеграл от ?
Возможные ответы:
Не определено
Правильный ответ:
2
33
Пояснение:
Чтобы найти неопределенный интеграл нашего уравнения, мы можем использовать правило обратной степени.
Чтобы использовать правило обратной степени, мы повышаем показатель степени на единицу, а затем делим на этот новый показатель.
Помните, что при вычислении интеграла мы относимся к константам как к числу, умноженному на , поскольку все, что в нулевой степени, есть . Рассматривать в качестве .
При вычислении интеграла не забудьте включить . означает «постоянный». Поскольку взятие производной от постоянного целого числа всегда будет равно , мы включаем , чтобы предвидеть возможность того, что уравнение на самом деле будет или , а не просто .
