Как сравнивать логарифмы: Как сравнивать логарифмы | Логарифмы

везде!

Сладкая парочка!

Два сапога – пара!

ОН

— ЛОГАРИФМ !

ОНА

—

ОДЗ!

Два в одном!

Два берега у одной реки!

Нам не жить

друг без

друга!

Близки и неразлучны!

Логарифмы в деятельности человека

в астрономии

в электротехнике

в животноводстве

в экономике

в музыке

в технике

и в природе

семечки подсолнуха

паутина

галактика

раковина

рога козла

Значимость логарифмов

«С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело поставить рядом с другим, более древним великим изобретением индусов – нашей десятичной системой нумерации.

Успенский Я. В.,

русский математик

Список литературы:

• Виленкин Н. Я. Функции в природе и технике – М.: Просвещение, 1978.
• Иванов А. А., Иванов А. П. Математика: Пособие для поступающих в ВУЗы – Пермь: издательство Пермского государственного университета, 2000.
• Кочагин В. В., Кочагина М. Н. ЕГЭ Математика, 2007 – М.: «Эксмо», 2007.
• Лиман М. М. Школьникам о математике и математиках. 4 — 8 кл. – М.: Просвещение, 1981.
• Мерзляк А. Г. и др. Алгебраический тренажер – М.: «Илекса», 2005.
• Перельман Я. И. Занимательная алгебра – М.: Госиздат технико-теоретической литературы, 1955.
• Рурукин А. Н. Интенсив. Математика – М.: «ВАКО», 2006.

логарифмов — как мне сравнить эти два журнала?

Задавать вопрос

спросил 4 года 9 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 2к раз

$\begingroup$ 92 < 3$, используйте это, чтобы увидеть заявленное неравенство). {1/2+1} =\sqrt{27}\quad > 5 \quad &> \quad 4.\end{align}$$ 92* (\text{что-то немного большее, чем $\log 2$})$. Дело в том, что это $\log 2$, где степень двойки больше единицы.

$\log 4-\log 3$ переписывается как $\log(4/3)$, а 4/3 равно 2 в степени меньше единицы.

Я сравнил степень двойки в логарифме, и, поскольку логарифм — возрастающая функция, большее значение имеет та, у которой степень двойки больше. $\log 4*\log 3$ больше из двух.

$\endgroup$

2

математика — Алгоритм точного сравнения двух возведений в степень для очень больших целых чисел (порядка 1 миллиарда)

Это своего рода два вопроса в одном:

1. Равны ли они?

2. Если нет, то какой из них больше?

Как заметил Питер О., проще всего строить на языке, предоставляющем дробный тип произвольной точности.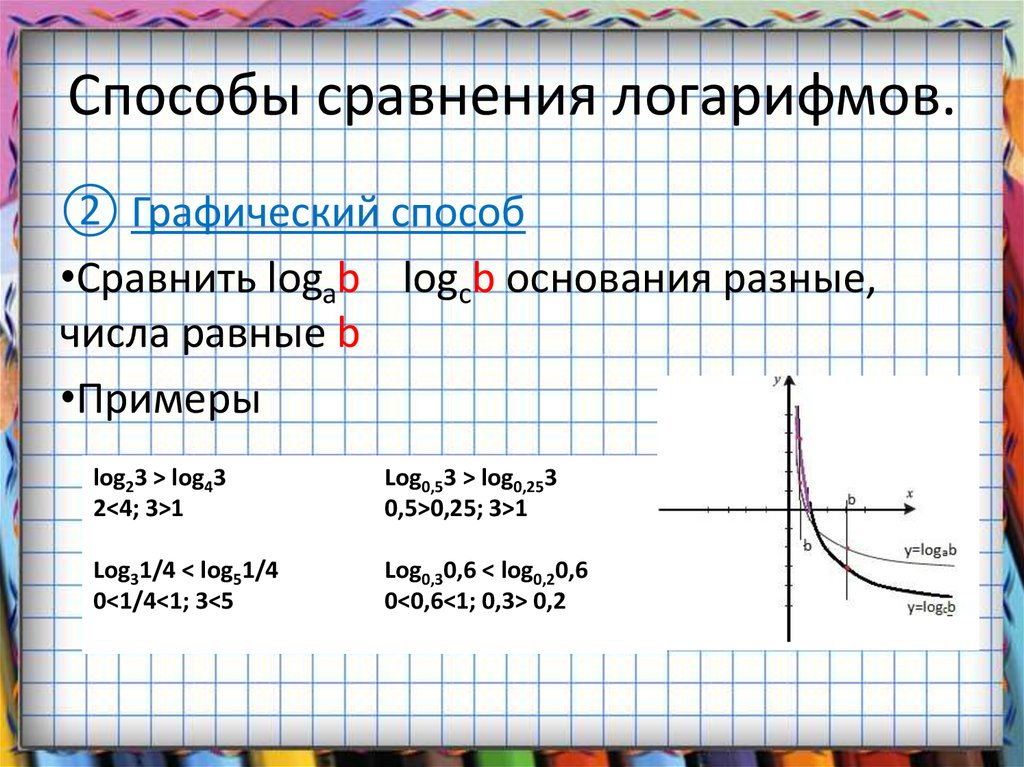 Я буду использовать Python 3.

Предположим без ограничения общности, что a ≤ c (при необходимости поменять местами) и b взаимно просты с d (делим оба числа на наибольший общий делитель).

Чтобы понять суть вопроса, я собираюсь предположить, что

Критерий равенства

Есть несколько простых случаев, когда a = 1 или b = 0 или 9д .

В Python 3:

 def equal_powers(a, b, c, d):
    пока верно:
        lhs_is_one = a == 1 или b == 0
        rhs_is_one = c == 1 или d == 0
        если lhs_is_one или rhs_is_one:
            вернуть lhs_is_one и rhs_is_one
        если а > с:
            а, б, в, г = в, г, а, б
        если б < д:
            вернуть ложь
        д, г = divmod (с, а)
        если г != 0:
            вернуть ложь
        б -= г
        с = д
защита test_equal_powers():
    для диапазона (1, 25):
        для b в диапазоне (25):
            для c в диапазоне (1, 25):
                для d в диапазоне (25):
                    утверждать equal_powers(a, b, c, d) == (a ** b == c ** d)
test_equal_powers()
 9(n+2)/(n+2) + .  ..
 

Чтобы получить хорошую скорость сходимости, нам потребуется 0,5 ≤ x < 1 , чего мы можем достичь, разделив x на степень двойки.

В Python мы будем представлять вещественное число как бесконечный генератор сокращающихся интервалов, содержащих истинное значение. Как только интервалы для b log a и d log c не пересекаются, мы можем определить, как они сравниваются.

 импортные фракции
определение минус (х, у):
 пока верно:
 x_lo, x_hi = следующий(х)
 y_lo, y_hi = следующий (y)
 выход x_lo - y_hi, x_hi - y_lo
время защиты (b, x):
 для вот, привет в х:
 выход b * lo, b * привет
def limited_log(a):
 серия = 0
 п = 0
 числитель = 1
 пока верно:
 п += 1
 числитель *= 1 - а
 серия += дроби. Дробь (числитель, n)
 yield -(серия + дроби.Дробь(числитель * (1 - а), (n + 1) * а)), -серия
журнал защиты (а):
 п = 0
 в то время как >
 = 1:
 а = дроби.
No related posts.