Найти область определения функции примеры решений с модулем: Как найти область определения функции с примерами решения

2

Математика

Работы: ВсеИзбранныеВ помощь учителюКонкурс «Учебный проект» Учебный год: Все2015 / 20162014 / 20152013 / 20142012 / 20132011 / 20122010 / 20112009 / 20102008 / 20092007 / 20082006 / 20072005 / 2006 Сортировка: По алфавитуПо новизне Один из подходящих способов получить представление о функциях целой и дробной частей – разобраться в их графиках. Поэтому целью данной работы является рассмотрение свойств функций целой и дробной частей числа, а также примеров построения графиков этих функций. Объектом исследования являются функции y=x и y=x. Предметом исследования являются графики функции y=x и y=x. Построение графиков функций — одна из интереснейших тем школьного курса математики. В работе раскрывается содержание понятия «модуля», его геометрическая интерпретация. Рассматривается влияние модуля на расположение графика функции на координатной плоскости. Для каждого из следующих случаев «y=|f(x)|», «y=f(|x|)», «y=|f(|x|)|» выявляется алгоритм построения графиков функций. Приводится большое количество примеров. В данной работе рассмотрены приемы построения графиков функций, содержащих модули, в том числе функций «y=f(|x|), y=|f(x)| и y=|f(|x|)|». Работа выполнена в форме презентации и может быть использована при подготовке к ГИА. Умения, приобретаемые при изучении функций, имеют прикладной и практический характер. Они широко используются при изучении как курса математики, так и других школьных предметов — физики, химии, географии, биологии, находят широкое применение в практической деятельности человека. Поэтому целью данной работы является рассмотрение графиков элементарных функций и построение графиков функций с помощью преобразований. Варианты заданий по математике для учащихся 3-4-х классов. Приведено несколько вариантов заданий с вычислениями числовых выражений. По полученным ответам требуется нарисовать на координатной плоскости точки и соединить их в указанном порядке. При правильных вычислениях учащийся получает изображение. Работа содержит теоретические и справочные материалы по элементарным функциям и способам преобразования их графиков. Также изложены некоторые подходы к решению задач с параметрами. Особое внимание уделяется графическому методу. Интересными, на наш взгляд, являются геометрические соображения при решении задач о расположении корней квадратного трехчлена и более сложных задач, сводящихся к ним. Думаем, читателям будет интересен графический метод решения текстовых задач на движение. В своей работе автор показывает значимость графиков функции и их свойств при решении уравнений и неравенств: линейных, квадратных и содержащих параметры, поскольку данные задачи играют большую роль в формировании логического мышления учащихся, необходимого при обучении. С помощью данной работы каждый желающий, используя программу Excel, сможет создавать свои графики, рисунки, фантазировать и находить разные закономерности. Работа открывается рассуждением, что такое функция и как она используется для изображения природных процессов. Затем графики элементарных функций были использованы для построения рисунков животных. В работе показано практическое применение знаний по черчению для решения различного рода стереометрических и планеметрических задач. Разобрано 12 задач. Для сравнения к некоторым из них приведено аналитическое решение. Сделан общий вывод: задачи можно решать любым способом, но выбирать нужно наиболее целесообразный. Задачи взяты из учебников школьной программы 10-11-х классов. В работе рассматривается один из методов решения текстовых задач – графический, позволяющий переводить алгебраическое условие задачи на геометрический язык графиков. Достоинство этого метода в его наглядности: на графике видна связь между величинами, входящими в условие задачи; чертеж помогает оценить реальность результата. Традиционные решения требуют больших временных затрат, что недопустимо в условиях сдачи экзаменов в форме ЕГЭ и ГИА. Графический способ экономит время. Объектом нашего исследования стали тригонометрические уравнения и неравенства, которые либо невозможно решить аналитическим способом, либо рационально решить графическим методом. Исходя из этого предметом нашего исследования стал метод, в основу которого положено дополнение основных тригонометрических тождеств зависимости либо синуса и косинуса, либо тангенса и котангенса. А также введение новых переменных и решения полученной системы графическим способом. Построив графики, находим координаты точек пересечения данных графиков. Графический способ решения трансцендентных уравнений дает возможность найти корни уравнения или определить их число. В работе исследованы некоторые случаи определения корней уравнения, связанные с обратными тригонометрическими и линейными функциями. В работе рассматривается вопрос о количестве корней уравнения «arcsin x = kx + b» в зависимости от значений параметров «k» и «b», а также последовательно рассмотрены различные случаи расположения прямой. К каждому случаю приведена графическая иллюстрация. В работе представлены 9 задач, придуманных автором, на решение графическим методом уравнений и систем, которые сопровождаются мультимедийным приложением. Также в работе есть цели и задачи, вывод и историческая справка о достижениях Рене Декарта и его последователей в этой сфере математики. График функции – это множество точек плоскости, декартовы координаты которых связаны соотношением y=f(x), где x принадлежит области определения функции. Часть процессов, происходящих в природе, описывается уравнениями, решение которых аналитическим способом либо невозможно, либо является трудоемким. Так как ряд задач, представленных в ЕГЭ и ГИА, возможно решить только графически, автор рассматривает решение уравнений с помощью графиков. Для этого необходимо уметь хорошо и быстро строить графики линейной и квадратичной функций, график функции y=√x, графики функции, содержащей знак модуля. Предлагаемый в работе метод графического решения тригонометрических уравнений даeт возможность определять корни намного проще, чем при аналитическом методе. Он не требует особых технических навыков в тригонометрических преобразованиях, а теоретическую сторону дела позволяет продемонстрировать очень наглядно. В работе представлено исследование значений графических способов решения задач на движение и производительность. Решение уравнений и систем с параметрами, графическим способом. В школьном курсе алгебры задачи с параметрами вызывают наибольшие затруднения у обучающихся, поэтому мы надеемся, что несколько подходов к решению таких заданий, представленных в данной работе, помогут справиться с подобными заданиями во время сдачи Единого государственного экзамена. Решение заданий с параметром всегда вызывает затруднения. Иногда иллюстративно-наглядный метод более понятен, нежели аналитический. В работе на примерах показан графический способ решения таких заданий повышенного и высокого уровня сложности. В проекте рассмотрены способы решения систем уравнений с двумя переменными. Анализируя задания учебно-методических пособий, которые предлагают различные авторы для подготовки к ГИА, в частности задания типа «Решите уравнения», автор пришла к выводу, что некоторые уравнения, а также системы уравнений целесообразно решать графическим способом. В проекте представлено пособие для учащихся 7-9-х классов, в котором подобраны задания на решение уравнений и систем уравнений графическим способом. В работе представлен альтернативный способ умножения многозначных чисел, приведены примеры умножения чисел данным методом. В работе представлены графические решения примеров, встречающихся на ЕГЭ и олимпиадах по математике. Показаны преимущества и недостатки графического метода. Разъясняется, когда привлечение графиков для решения заданий наиболее целесообразно. В презентации рассмотрены особенно яркие и сложные примеры. В работе мы показали, как решать уравнения с модулем, используя геометрическую интерпретацию понятия «модуль» и графики различных функций. Цель: рассмотреть решение задач с использованием граф, проверить выполнение граф на родословных. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Слово «граф» в математике означает картинку, где нарисовано несколько точек, соединенных между собой линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» – пишу. В работе исследуются эти объекты, с помощью которых можно решать математические, экономические и логические задачи. В работе раскрывается понятие графов с помощью задач и их свойства с помощью теорем. В данной работе рассмотрены математические графы, области их применения и способы решения задач с их использованием. С помощью теории графов составлена часть генеалогического древа семьи Тогулёвах, начиная с прадеда Тогулёва Павла. В данной работе вы познакомитесь с основами теории графов. Я рассмотрел историю развития теории графов, привел примеры практических задач.

Объем | Codecademy

Scope

Переменные с областью видимости блока

Global Variables

Scope

 
 function myFunction() {
  
  вар PizzaName = "Вольво";
  // Код здесь может использовать pizzaName
  
}
// Код здесь не может использовать pizzaName 
 

Область — это концепция, которая относится к тому, где можно получить доступ к значениям и функциям.

Различные области включают:

• Глобальная область (значение/функция в глобальной области может использоваться где угодно во всей программе)
• Файл или модуль область действия (доступ к значению/функции возможен только из файла)
• Область действия (видна только внутри функции),
• Кодовый блок область действия (виден только в кодовом блоке { . .. } )

1. 1

   Область видимости

   Важным понятием в программировании является область видимости . Область действия определяет, где можно получить доступ к переменным или на которые можно ссылаться. В то время как к некоторым переменным можно получить доступ из любой точки программы, другие переменные могут быть доступны…

   Start

2. 2

   Блоки и область действия

   Прежде чем мы поговорим о области действия, нам сначала нужно поговорить о блоках . Мы уже видели блоки, используемые ранее в функциях и операторах if. Блок — это код, находящийся внутри набора фигурных скобок {}. Blo…

   Start

3. 3

   Global Scope

   Scope — это контекст, в котором объявлены наши переменные. Мы думаем о области действия по отношению к блокам, потому что переменные могут существовать как вне, так и внутри этих блоков. В global scope , varia…

   Start

4. 4

   Block Scope

   Следующий контекст, который мы рассмотрим, это block scope . Когда переменная определена внутри блока, она доступна только коду в фигурных скобках {}. Мы говорим, что эта переменная имеет область действия блока , потому что…

   Начало

5. 5

   Загрязнение области

   Может показаться хорошей идеей всегда делать ваши переменные доступными, но слишком много глобальных переменных могут вызвать проблемы в программа. Когда вы объявляете глобальные переменные, они переходят в _gl…

   Start

6. 6

   Практика хорошего определения области видимости

   Учитывая проблемы, связанные с глобальными переменными и загрязнением области видимости, мы должны следовать передовым методам для максимально узкой области видимости наших переменных, используя блочную область видимости. Тщательное определение области видимости ваших переменных…

   Начало

7. 7

   Обзор: область действия

   На этом уроке вы узнали о области видимости и о том, как она влияет на доступность различных переменных. Давайте рассмотрим следующие термины: — Область относится к тому, где переменные могут быть доступны через…

   Начало

• Пришло время научиться бегло работать с функциями JavaScript. В следующем профессиональном проекте мы собираемся попрактиковаться в JavaScript, чтобы вы могли отточить свои навыки и чувствовать себя уверенно, применяя их в реальном мире. Почему? Область видимости определяет видимость переменных и других ресурсов в вашем коде. Что дальше? Марафонский бег, устранение ошибок, больше JavaScript. Ты получил это!

• Область действия

  Что такое глобальная переменная?

Глобальная переменная в Python с примерами [обновлено]

Python также использует переменные для хранения данных. У них также есть имя и тип; однако в python вам не нужно объявлять тип данных. Вместо этого вы можете создать переменную Python следующим образом.

номер_класса = 4;

В приведенном выше примере переменная ‘class_number’ имеет значение 4; это целочисленный тип данных. И в отличие от других языков программирования, вам не нужно объявлять переменную без инициализации.

Что означает переменная область видимости в Python?

Область действия переменной означает область, в которой части программы могут получить доступ к переменной. В python есть четыре области видимости переменных:

.

1. Местный
2. Глобальный
3. Корпус
4. Встроенный

В этой статье вы познакомитесь с первыми двумя типами. Вы научитесь создавать переменные Python с локальной и глобальной областью видимости.

Что такое глобальная переменная в Python?

В мире программирования глобальная переменная в Python означает наличие области действия во всей программе, т. е. значение глобальной переменной доступно во всей программе, если только оно не затенено.

Глобальная переменная в Python часто объявляется в начале программы. Другими словами, переменные, объявленные вне функции, называются глобальными переменными.

Вы можете получить доступ к глобальным переменным в Python как внутри, так и вне функции.

Синтаксис:

X = «sampleGlobalValue»

Защита fn1():

Как создавать глобальные переменные в Python?

Чтобы создать глобальную переменную в Python, вам нужно объявить переменную вне функции или в глобальной области.

Пример: 

Выход:

 

Как получить доступ к глобальной переменной внутри и снаружи функции?

Пример:

 

Выход:

 

В приведенном выше примере вы видели глобальную переменную, объявленную и доступную как внутри, так и вне функции.

Итак, вы получаете доступ к значению как внутри, так и вне функции, и это нормально, но что произойдет, если вы попытаетесь изменить значение переменной глобальной области видимости внутри функции?

См. приведенный ниже пример, чтобы лучше понять.

Пример:

 

Выход:

 

Как видно, это выдает ошибку. Когда вы пытаетесь изменить значение глобальной переменной внутри функции, она выдает UnboundLocalError, потому что при изменении Python рассматривает x как локальную переменную, но x также не определен внутри функции (myfunc()).

Вот здесь и появляется ключевое слово Global. Вы увидите использование глобальных ключевых слов в следующих разделах.

Как создавать переменные с локальной областью действия в Python с примерами?

Область действия локальной переменной — это функция, в которой вы ее объявили. Чтобы получить доступ к переменной, вы должны вызвать соответствующую функцию. Например, вы можете создать локальную переменную, как показано ниже.

определение суперфункц()	# определение функции
х = фантастика	# определение локальной переменной
print(«Питон есть» + х)	# доступ к локальной переменной
суперфункция()	# вызов функции

Глобальное ключевое слово

Ключевое слово Global используется для изменения глобальной переменной за пределами ее текущей области действия и значения. Он используется для внесения изменений в глобальную переменную в локальном контексте. Ключевое слово Global также используется для создания или объявления глобальной переменной внутри функции.

Обычно, когда вы создаете переменную внутри функции (локальную переменную), ее можно использовать только внутри этой функции. Вот где в игру вступает ключевое слово global, которое помогает создавать глобальные переменные внутри функции и которые могут быть доступны в глобальной области видимости.

Синтаксис:

Функция по умолчанию():

Глобальная переменная

Пример 1:

Используйте глобальное ключевое слово для создания переменной в глобальной области.

 

Выход:

 

Пример 2:

Используйте ключевое слово global, чтобы изменить значение глобальной переменной внутри функции.

 

Выход:

 

Вы увидели, что такое «глобальные» ключевые слова, их примеры и как использовать глобальные ключевые слова. Но в Python есть несколько основных правил использования ключевого слова «global».

Давайте посмотрим Global во вложенных функциях.

Когда вы объявляете глобальную переменную ключевого слова внутри вложенной функции и когда вы изменяете глобальную переменную ключевого слова внутри вложенной функции, она будет отражена за пределами локальной области, поскольку она используется как глобальное ключевое слово.

Пример:

Давайте посмотрим пример для глобальных вложенных функций.

 

Выход:

 

Вы можете увидеть приведенный выше вывод для глобальных вложенных функций. Но, возможно, следующее краткое объяснение поможет лучшему пониманию.

Вы объявили глобальную переменную внутри функции inner(), которая вложена в функцию main().

До и после вызова функции inner() переменная ‘integ’ принимает значение локальной переменной main, т.е. ‘integ = 20’. Вне функции main() переменная ‘integ’ принимает значение глобального ключевого слова, объявленного внутри функция inner(), т. е. integ = 20, поскольку вы использовали ключевое слово global внутри локальной области видимости функции inner(). Если вы внесете какие-либо изменения в глобальную переменную ключевого слова функции inner() «integ», это отразится за пределами области действия, как поведение глобального ключевого слова.

Фундаментальные правила «глобального» ключевого слова следующие:

• Когда вы создаете переменную внутри функции, она по умолчанию находится в локальном контексте
• Когда вы создаете или определяете переменную вне функции, по умолчанию это глобальный контекст, здесь нет необходимости в глобальном ключевом слове
• Глобальные ключевые слова можно использовать для чтения или изменения глобальной переменной внутри функции
• Использование глобального ключевого слова вне функции бесполезно или не имеет никакого эффекта.

Как вы можете создавать переменные, используя глобальную область видимости в Python с примерами?

Вы можете создать переменную с глобальной областью действия, инициализировав ее вне всех функций в программе Python. И вы можете получить доступ к переменной из любого места в программе Python.

Создать глобальную переменную просто; вы можете сделать это следующим образом.

х = «замечательно»	# определение глобальной переменной
по определению Wonderfunc():	#объявление функции
print(«Питон есть» + х)	#доступ к глобальной переменной
чудесная функция ()	# вызов функции

Как использовать глобальные ключевые слова в Python с примерами?

Если вы используете переменную внутри функции, python считает, что вы имеете в виду локальную переменную. Поэтому используйте ключевое слово global, чтобы изменить глобальную переменную в функции Python.

В следующем примере показано использование глобальных ключевых слов в программе Python.

х = 5	#инициализация глобальной переменной
защита жизни ()	# определение функции
глобальных x	#используя глобальное ключевое слово
х = х + 2	#изменение глобальной переменной
жизнь()	# вызов функции
печать(х)	#доступ к глобальной переменной

Локальные переменные

В следующем примере показана ошибка.

Пример 1: доступ к локальной переменной вне области видимости

дефлок()	# определение функции loc()
г = «местный»	# локальное объявление y
лок()	# вызов функции loc()
печать(г)	# доступ к переменной y

В приведенной выше программе вы пытаетесь получить доступ к ‘y’, определенному в функции loc().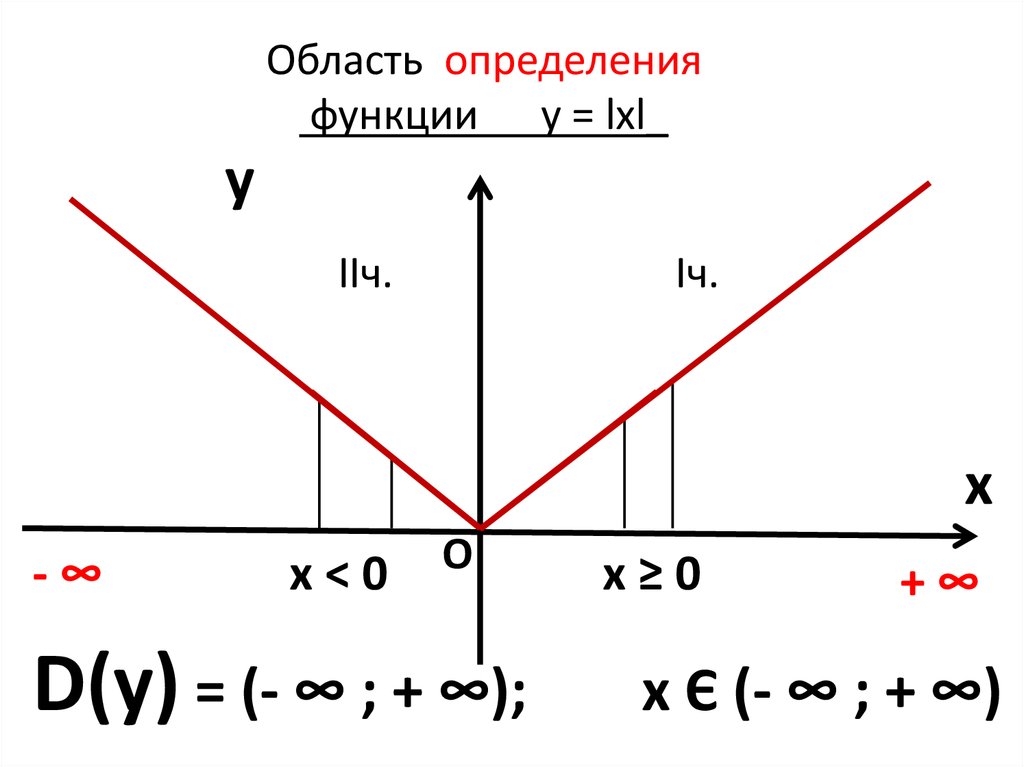 И строка print(y) даст вам ошибку имени: имя ‘y’ не определено.

В следующем примере показано, как переписать приведенную выше программу.

Пример 2. Создание локальной переменной

деф лок()	# определение функции
г = «местный»	# объявление локальной переменной
печать(г)	#локальный доступ к локальной переменной
лок()	# вызов функции

Глобальные и локальные переменные

Поскольку вы не можете получить доступ к локальной переменной извне функции, не имеет значения, имеют ли глобальная и локальная переменные одно и то же имя. Ниже вы можете найти пример, где есть две переменные. Один глобальный, а другой локальный. Оба имеют одинаковое имя.

Пример 1: глобальная переменная и локальная переменная с одинаковым именем

х = 5;	#инициализация глобальной переменной
определение человека():	# определение функции man()
х = 4	#инициализация локальной переменной
print(«местный x:», x)	# доступ к локальной переменной
человек()	# вызов функции человека
print(«глобальный x:», x)	# доступ к локальной переменной

В приведенном выше примере функция печати в функции man() обращается к локальной переменной x со значением 4. А функция печати снаружи обращается к локальной переменной со значением 5.  

Разница между глобальными и локальными переменными

Давайте посмотрим пример того, как глобальные и локальные переменные ведут себя в одном и том же коде.

Пример:

 

Выход:

 

Объяснение:

Здесь, в приведенной выше программе, вы объявили x как глобальную переменную, а y как локальную переменную в той же программе. Затем он попытался изменить глобальную переменную, используя ключевое слово global в локальной функции и напечатав как gx, так и ly.

После вызова функции function1() значение gx стало глобальным. Когда вы попытались изменить как gx*2, он дважды напечатал «global». После этого вы напечатали локальную переменную ly, которая отображала значение локальной переменной, т. е. снова «local».

Разница между глобальными и нелокальными переменными

Когда переменная находится в локальной или глобальной области видимости, она называется нелокальной переменной. Нелокальные переменные определяются во вложенной функции, область действия которой не определена.

Пример:

 

Выход:

 

Объяснение:

Из приведенной выше программы видно, что вложенной функцией является innerfn(). Внутри функции innerfn() вы видели использование ключевого слова nonlocal для создания нелокальной переменной. Функция innerfn() определена в области видимости externalfn(). Если вы вносите изменения в значение нелокальной переменной, они отражаются в локальной переменной.

В заключение, понимание области действия переменных Python необходимо для безошибочной программы. Вы можете получить доступ к глобальным переменным из любой точки программы. Однако вы можете получить доступ только к локальным переменным из функции. Кроме того, если вам нужно изменить глобальную переменную из функции, вам нужно объявить эту переменную глобальной. Вы можете сделать это, используя ключевое слово «global».

Ждете перехода в область программирования? Пройдите курс обучения Python и начните свою карьеру профессионального программиста Python 9. 0662

Заключение

Переменные являются одним из самых основных элементов языка программирования. Это уровень абстракции для ячеек памяти, содержащих фактическое значение. Глобальные, локальные и нелокальные типы переменных помогают программисту получить доступ к некоторым значениям полностью в области действия программы или к некоторым значениям, которые ограничены функцией.

В этой статье вы узнали, что такое глобальная переменная в Python, как определить глобальную переменную в Python, как объявить глобальную переменную в Python, что такое ключевое слово global, когда использовать ключевое слово global, разницу между global, локальные и нелокальные переменные вместе с некоторыми рабочими примерами.

Присоединяйтесь к учебному курсу Simplilearn Python, чтобы узнать больше по этой теме. Этот курс научит вас основам Python, условным операторам, операциям с данными, сценариям оболочки и Django. Этот сертификационный курс, который включает 38 часов смешанного обучения и 8 часов самостоятельного онлайн-обучения, подготовит вас к полноценной карьере профессионального программиста Python, предоставив вам практический опыт программирования.

No related posts.