Найти общие решения дифференциальных уравнений онлайн: Дифференциальные уравнения онлайн

Содержание

1.1. Алгоритм решения дифференциального уравнения

Если дано дифференциальное уравнение вида

y+ p y +q y = 0,

необходимо:

Написать характеристическое квадратное уравнение

k² + p k + q = 0

Найти корни этого уравнения

Записать общее решение данного дифференциального уравнения в виде:

, если k₁k₂ — действительные

, если k₁=k₂ — действительные

, если корни комплексные k_1,2 =   i

, если корни мнимые k_1,2 =  i

Найти частное решение, удовлетворяющее начальным условиям, если таковые заданы.

1.2.Примеры решения дифференциальных уравнений

Пример 1. Дано уравнение

y+ y — 2 y = 0.

Характеристическое уравнение имеет вид:

k² + k — 2 = 0.

Находим корни характеристического уравнения:

,k₁ = 1 ,k₂ = -2 .

Общее решение данного дифференциального уравнения имеет вид:

Пример 2. Дано уравнение

y 4 y + 4 y = 0.

Характеристическое уравнение имеет вид: k² — 4k + 4 = 0 k₁ = k₂ = 2

Записываем общее решение

Пример 3. Дано уравнение

y 2 y + 5 y = 0.

Напишем характеристическое уравнение:

k² + 2k +

5 = 0

k₁ = -1 + 2i

k₂ = -1 — 2i

Следовательно, общее решение имеет вид

Пример 4. Дано уравнение

y+ 9 y = 0.

Найти общее и частное решение, удовлетворяющее начальным условиям

y|_x=0= 0 ; y |_x=0= 3

Решение: напишем характеристическое уравнение

k² + 9 = 0

Находим корни

k₁

= 3i; k₂ = — 3i

Общее решение есть:

Найдем частное решение. Предварительно определим первую производную.

Постоянные C₁ иC₂определяются из начальных условий

Мы получили систему двух уравнений с двумя неизвестными. Нетрудно определить, что C₁=0, C₂=1.

Следовательно частное решение данного дифференциального уравнения имеет вид: y = sin 3x

Пример

5. Дано уравнение

Найти общее и частное решение, удовлетворяющее начальным условиям.

при.

Напишем характеристическое уравнение и найдем его корни

Корни действительные и равные, следовательно общее решение имеет вид

Найдем, исходя из начальных условий, С₁и С₂

Следовательно, частное решение имеет вид

Глава 6.

Применение дифференциальных уравнений для исследования колебательных процессов

1. Состояние динамических систем вблизи положения равновесия

Дифференциальные уравнения второго порядка используются во многих областях естествознания.

Остановимся на рассмотрении движения динамических систем вблизи положения равновесия, т.е. на колебаниях. При достаточно малых отклонениях от положения равновесия колебания бывают обычно гармоническими.

Ограничим наше рассмотрение только случаем свободных колебаний без учета сил трения и внешнего воздействия.

а б в г

Рис.6. Колебательные системы. (а – математический маятник, б – пружинный маятник, в – шарик на дне сферической чашки, г – электрический колебательный контур).

римеры свободных колебаний в различных системах

Во всех приведенных примерах сила, действующая на систему (шарик), выражается сложной функцией его отклонения от положения равновесия. ,

где x– малое отклонение от положения равновесия, а- точка устойчивого равновесия.

Сила f(x)

в точке равновесия равна нулю, т. е. f(0)=0.

Обычно в реальных физических системах отличным от нуля бывает член . Так какx=0 есть точка устойчивого равновесия, сила должна быть направлена к точкеx=0. Это значит, что.

Исходя из второго закона динамики, запишем уравнение движения для малых отклонений от положения равновесия.

или , где.

Выражая ускорение a через вторую производную смещения x по времени, получаем

Разделим обе части уравнения на массу mи обозначим.

После проведенных преобразований получаем уравнение гармонических колебаний для механических систем .

(*)

Получим такое же уравнение для случая электромагнитных колебаний.

Э.Д.С. индукции в колебательном контуре, имеет вид

Учитывая, что , снова приходим к дифференциальному уравнению второго порядка. Разделим обе части уравнения наи обозначим.

Окончательно получаем для электромагнитных колебаний

(**)

Примечательно, что, несмотря на различную природу механических и электромагнитных колебаний, они описываются одинаковыми дифференциальными уравнениями второго порядка, уравнениями гармонических колебаний. Разница лишь в том, что во втором уравнении мы вместо (смещения) имеем дело с электрическим зарядом, и стремление к равновесию — есть стремление восстановить нулевое значение заряда на конденсаторе.

Найдем решение уравнения гармонических колебаний. Составим характеристическое уравнение .

Его корни мнимые и равны соответственно:

Следовательно, решением данного уравнения в случае механических колебаний функция будет выглядеть так:

,- постоянные интегрирования.

После несложных преобразований можно упростить это выражение

Аналогично, можно записать для электромагнитных колебаний

Здесь введенная ранее величина — есть собственная циклическая частота колебаний,(или) – амплитуда колебаний,- начальная фаза.

Пономарев К. К. Составление дифференциальных уравнений ОНЛАЙН

Высшая математика. Математика для нематематиков / Избранное / Математика / Математика для студентов, аспирантов и научных работников / Математический анализ и дифференциальные уравнения

15.01.201327.01.2018

Пономарев К. К. Составление дифференциальных уравнений. — Минск, 1973. — 560 стр. с илл.
Учебное пособие для математических, физических, биологических, химических факультетов университетов, которое является руководством по составлению и решению дифференциальных уравнений. Как известно, в курсе дифференциальных уравнений решению практических задач на составление уделяется все еще недостаточное внимание. Кроме того, в учебниках и учебных пособиях вопросы составления дифференциальных уравнений обычно ограничиваются элементарными задачами геометрического или кинематического типа. Цель автора — создание учебного пособия, которое широко охватило бы различные задачи естествознания и техники и способствовало овладению современной методикой составления дифференциальных уравнений прикладных задач, возникающих в процессе производства или научной деятельности. Характерной особенностью освоения навыков составления дифференциальных уравнений является изучение многочисленных примеров. В связи с этим полнота изложения имеет здесь существенное значение. Книга содержит 325 задач на составление дифференциальных уравнений, из которых 194 задачи анализируются подробно.
ОГЛАВЛЕНИЕ
Предисловие………………………………3
ГЛАВА I ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. …………5
§ 1 Дифференциальные уравнения …… 5
§ 2 Классификация дифференциальных уравнений…………5
§ 3 Общее семейство решений, частное и особое решения ………..6
§ 4 Элементарные дифференциальные уравнения…………….7
§ 5 Выделение индивидуальных решений …….. 8
§ 6 Построение решения о виде степенного ряда …..10
§ 7 Метод последовательных приближений . …… 11
§ 8 Продолжение решений …. ………………………12
ГЛАВА II СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ ПО УСЛОВИЯМ
ПРИКЛАДНЫХ ЗАДАЧ………………..13
§ 1 Общие принципы ………………
§ 2 Методика составления дифференциальных уравнений …. 13
§ 3 Схема составления дифференциального уравнения ……….15
ГЛАВА ІII ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ПЕРВОГО ПОРЯДКА, РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ 16
§ 1 Притяжение стержня и материальной точки . . . . . . 17
§ 2 Движение тел постоянной массы ……. 18
§ 3 Движение тел переменной массы (без учета внешних сил) . .26
§ 4 Растяжение упругой нити ……………….. 30
§ 5. Работа опорожнения сосудов ……. 34
§ 6. Изменение яркости света в стеклянной пластине ……………… 35
§ 7. Нагрев тела…………….. 37
§ 8 Изменение состояния газов в сосудах…………… 40
ГЛАВА IV ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ …………….. . 43
§ 1 Охлаждение тел………………………….. 43
§ 2 Нагрев тел ………………………………..46
§ 3 Распределение температуры внутри тел…………………48
§ 4 Брус равного напряжения ………………….50
§ 5 Давление зерна на стенки хранилища ………………..53
§ 6 Барометрическая формула и глубинное давление ….. 55
§ 7 Прямолинейное горизонтальное движение………………….58
§ 8 Вертикальное движение тел……………………………65
§ 9 Падение тел переменной массы . …. …………………..81
§ 10 Криволинейное движение (кривая погони) . … .83
§ 11 Вращение тел в жидкости . …………………………86
§ 12 Закон всемирного тяготения…………..88
§ 13 Радиоактивный распад . ……….. 94
§ 14 Электрические заряды . ….. ….. 95
§ 15 Поверхность фрезы …… …….. .99
§ 16 Трение ременной передачи … …. .101
§ 17. Истечение жидкости из сосудов …………. 103
§ 18 Наполнение сосудов ………………….. 108
§ 19 Установление уровня в сообщающихся сосудах ………..108
§20 Кривая депрессий . …… . . 110
§ 21 Обеднение раствора . … . . . . ..112
§ 22 Растворение твердых тел …….113
§ 23 Вентиляция производственного помещения …,,.,. 119
§ 24 Газовые смеси … ………. 120
§ 25 Ионизация газов . …….. 121
§ 26 Химические реакции … …… 122
§ 27. Рост населения ……………………..133
§ 28 Процессы роста в природе и производстве …….. 142
§ 29 Экология популяции …………………… 150
§ 30 Плотность муравьев вне муравейника 157
§ 31 Рост денежных вкладов . ……… 161
ГЛАВА V ЗАДАЧИ, ПРИВОДЯЩИЕ К ОДНОРОДНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА ……….163
§ 1 Изогональные траектории . . 16З
§ 2 Геометрические приложения …….165
§ 3 Зеркало, фокусирующее параллельные лучи ……170
§ 4 Траектории полета самолетов …. …… 171
ГЛАВА VI ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ …………. .
§ 1 Параболическое зеркало. ….. 181
§ 2 Концентрация вещества в жидкости . …… 182
ГЛАВА VII ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА …………….184
§ 1. Геометрические приложения ……………
§ 2 Движение материальной точки … …….188
§ 3 Температура охлаждающего тела …..
§ 4 Нагрев тела при стационарном теплопотоке
§ 5 Электрические цепи . . … .
§ 6 Рационализаторские предложения . …
§ 7. Работа сердца…………. ….
§ 8 Задача о сигарете … …… …
ГЛАВА VIII ЗАДАЧИ, ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА (УРАВНЕНИЯМ БЕРНУЛЛИ, РИККАТИ, ЛАГРАНЖА И КЛЕРО)
§ 1 Уравнение Бернулли . … …….900
4 2 Уравнение Риккати . ………911
§ 3 Уравнение Лагранжа . . . . ……..
§ 4 Уравнение Клеро …. …. . .
ГЛАВА IX ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА, РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ВТОРОЙ ПРОИЗВОДНОЙ (у»=с)… 227
§ 1 Скольжение тела под наклоном . ….
§ 2 Движение в горизонтальной плоскости при сопротивлении, пропорциональном
силе тяжести …. . . . 229
§ 3 Выброс вверх (без учета трения) … . 231
§ 4 Распределение теплоты в стержне … . 231
§ 5 Расстояние между фермами железнодорожного моста
ГЛАВА X ЗАДАЧИ, ПРИВОДЯЩИЕ К НЕПОЛНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА . . . . 236
I Уравнения типа y»=f{x)
§ 1 Переходная кривая железнодорожного пути . 237
§ 2 Прямолинейное движение материальной точки в горизонтальной плоскости………..230
§ 3 Упругая линия балок .. …….242
II Уравнения типа y»=f(y)
§ 4 Геометрические приложения . . . . . … 255
§ 5 Движение материальной точки под действием силы притяжения . . 256
III. Уравнения типа y»=f(y’)
§ 6 Определение кривой по радиусу кривизны . …… 257
§ 7. Горизонтальное движение тела при наличии трения……259
§ 8 Движение в вертикальной плоскости ………274
§ 9 Равновесие тяжелой нити …… .280
§ 10 Гибкая нить равного сопротивления …. . . 283
IV. Уравнения типа y»=f(x,y’)
§ 11 Кривая и радиус кривизны . . . … 285
V. Уравнения типа y»=f(y,y’)
§ 12 Нахождение уравнения кривой но нормали и радиусу кривизны . . 286
ГЛАВА XI ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 288
I. Неполные линейные дифференциальные уравнения
§ 1 Гармонические колебания . . …. 296
§ 2 Движение тела без трения …. . . … 307
§ 3 Дифференциальный манометр . . .312
§ 4 Распределение теплоты в стержнях……….313
§ 5 Продольный изгиб прямого стержня . . 320
§ 6 Движение шарика в трубке (задача Ампера) … 3J8
II. Линейные дифференциальные уравнения
§ 7 Затухающие колебания . . . . . . . 330
§ 8 Затухающие колебания в электрической цепи . . . . 335
§ 9 Колебания магнитной стрелки без и при наличии успокоителя . . 343
§ 10 Вынужденные колебания механических систем . . . . З50
ГЛАВА XII ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ВТОРОГО ПОРЯДКА С РАЦИОНАЛЬНЫ.МИ КОЭФФИЦИЕНТАМИ . . 363
I. Уравнение Эйлера
§ 1. Распределение температуры в продольном ребре параболического сечения……363
II. Линейное однородное уравнение с рациональными коэффициентами
§ 2 Толстостенная цилиндрическая оболочка под давлением (задача Лямз)……366
III. Линейное неоднородное уравнение с рациональными коэффициентами
§ 3 Скорость течения жидкости в трубопроводе …………….374
§ 4 Изгиб круглой пластины ………….378
ГЛАВА XIII ЗАДАЧИ. ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ (УРАВНЕНИЯМ БЕССЕЛЯ. ЛЕЖАНДРА И МАТЬЕ) 385
I Уравнение Бесселя
§ 1 Устойчивость стержня формы усеченного конуса, сжимаемого продольной
силой . . . . …..
§ 2 Устойчивость цилиндрического стержня под действием собственного веса 392
§ 3 Устойчивость вращения гибкой нити . . . .
§ 4 Распределение температуры в кольцевом ребре прямоугольного профиля 398
ІІ Обобщенное уравнение Бесселя
§ 5 Маятник переменной длины … …. 400
§ 6 Устойчивость стержня переменного сечения под действием переменной распределенной нагрузки . …. 402
ІІІ Дифференциальные уравнения в частных производных
§ 7 Колебания круглой мембраны . ..405
§ 8 Электрический потенциал двух равносильных зарядов ……….413
§ 9. Дифференциальное уравнение в частных производных потенциала . . . 417
§ 10 Потенциал притягивающих масс . . …. . .417
V Уравнение Матье
§ 11 Динамическая устойчивость стержня под действием переменной и продольной
силы … …. .424
ГЛАВА XIV ЗАДАЧИ, ПРИВОДЯЩИЕ К СИСТЕМАМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА … . 43G
§ 1 Разложение вещества . . . . .
§ 2 Относительная кривая погони . …. 447
§ 3 Давление в системе двух соединенных цилиндров с газом . 447
§ 4 Напряженное состояние диска под действием центробежных сил … 447
§ 5. Превращение одного вещества в другое . . . . . 453
ГЛАВА XV. ЗАДАЧИ, ПРИВОДЯЩИЕ К НЕПОЛНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВЫСШИХ ПОРЯДКОВ ……456
§ 1 Линия прогиба неразрезной балки от распределенной нагрузки . . . 456
ГЛАВА XVI ЗАДАЧИ. ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ТРЕТЬЕГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 463
§ 1 Паровая машина с регулятором … . .
ГЛАВА XVII ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ОДНОРОДНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВЫСШЕГО ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ ……….. — . 471
§ 1 Колебания вала от действия центробежных сил …… 472
§ 2 Балка (железнодорожный рельс) на упругом основании . ….. 477
§ 3 Колебания однородной балки (приведение дифференциального уравнения
в частных производных к обыкновенному) ………… 482
ГЛАВА XVIII ЗАДАЧИ. ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ НЕОДНОРОДНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ЧЕТВЕРТОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ…. …. 485
§ 1 Деформация стенок цилиндрического резервуара………..487
§ 2. Железнодорожная шпала ….490
ГЛАВА XIX ЗАДАЧИ. ПРИВОДЯЩИЕ К СИСТЕМАМ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ВТОРОГО ПОРЯДКА . . . …. 495
§ 1. Движение материальной точки под действием отталкивающей силы, пропорциональной расстоянию … . ….. 497
§ 2 Выброс тела под углом . . . …….. 500
§ 3 Сброс груза с самолета в заданную точку … . . 503
§ 4 Движение планет . …… . . 504
§ 5 Система двух связанных электрических контуров . . 509
§ 6 Изменение потенциала электрической линии по времени (приведение системы дифференциальных уравнений в частных производных к системе обыкновенных уравнений) . . … … 513
§ 7 Стационарные линейные дифференциальные уравнения с постоянными коэффициентами в теории систем современной техники и естествознания . . 519
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ . . …..529
I Дифференциальные уравнения первого порядка 529
II Дифференциальные уравнения второго порядка …… .545
III Системы дифференциальных уравнений первого порядка ….. 555
IV Системы дифференциальных уравнений второго порядка . . . .557

Часть 1

Часть 2

ТегиДифференциальные уравненияПономаревСоставление дифференциальных уравненийчитать онлайн

Дифференциальные уравнения — ■ Найдите частные решения дифференциальных уравнений. Общее решение

Предварительный текст

9781133108490_App_F1 06.12.11 8:29 утра Страница F1 Приложение F Ф ■ Решения дифференциальных уравнений F1 Дифференциальные уравнения F Решения дифференциальных уравнений ■ Найдите общие решения дифференциальных уравнений. ■ Найдите частные решения дифференциальных уравнений. Общее решение дифференциального уравнения Дифференциальное уравнение – это уравнение, содержащее дифференцируемую функцию и одну или больше его производных.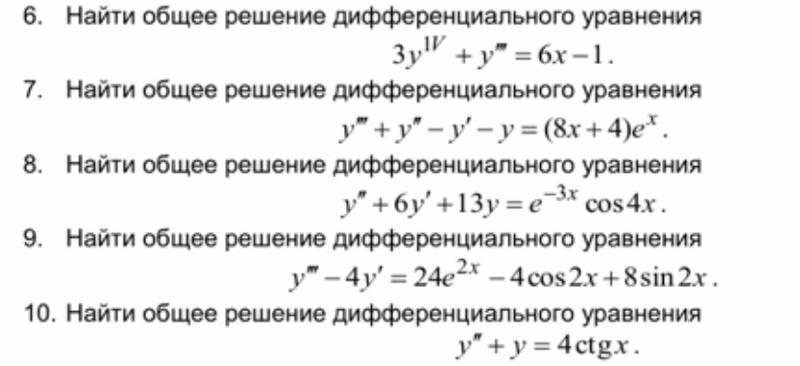

Например, у⬘ ⫹ 2у ⫽ 0 Дифференциальное уравнение является дифференциальным уравнением. Функция y ⫽ f 共x兲 является решением дифференциального уравнения если уравнение выполняется при замене y и его производных на f 共x兲 и его производные. Например, у ⫽ е⫺2x Решение дифференциального уравнения является решением дифференциального уравнения, показанного выше. Чтобы увидеть это, замените y и y⬘ ⫽ ⫺2e⫺2x в исходном уравнении. y⬘ ⫹ 2y ⫽ ⫺2e⫺2x ⫹ 2共e⫺2x兲 ⫽0 Замените y и y⬘. Таким же образом можно показать, что y ⫽ 2e⫺2x, y ⫽ ⫺3e⫺2x и y ⫽ 12e⫺2x также являются решения дифференциального уравнения. В самом деле, каждая функция, заданная у ⫽ Ce⫺2x Общее решение где C — действительное число, является решением уравнения. Это семейство решений называется общее решение дифференциального уравнения. Пример 1 Проверка решений Определить, является ли каждая функция решением дифференциального уравнения y⬙ ⫺ y ⫽ 0. а. у ⫽ Се х б. у ⫽ Ce⫺x РЕШЕНИЕ а. Поскольку y⬘ ⫽ Ce x и y⬙ ⫽ Ce x, отсюда следует, что y⬙ ⫺ y ⫽ Ce x ⫺ Ce x ⫽ 0.

Итак, y ⫽ Ce x является решением. б. Поскольку y⬘ ⫽ ⫺Ce⫺x и y⬙ ⫽ Ce⫺x, отсюда следует, что y⬙ ⫺ y ⫽ Ce⫺x ⫺ Ce⫺x ⫽ 0. Итак, y ⫽ Ce⫺x также является решением. КПП 1 Определить, является ли y ⫽ Ce 4x решением дифференциального уравнения y⬘ ⫽ y. ■ 9781133108490_App_F1 F2 06.12.11 Приложение F ■ 8:29 утра Страница F2 Дифференциальные уравнения Частные решения и начальные условия Частным решением дифференциального уравнения является любое решение, полученное присвоение конкретных значений произвольным константам в общем решении.* Геометрически общее решение дифференциального уравнения представляет собой семейство кривые, называемые кривыми решения. Например, общее решение дифференциала уравнение xy⬘ ⫺ 2y ⫽ 0 Общее решение: у = Сх 2 у (1, 3) 3 у ⫽ Сх 2. 2 1 Икс −3 −2 2 3 −2 −3 Кривые решения для xy⬘ ⫺ 2y ⫽ 0 РИСУНОК F Общее решение На рисунке F показано несколько кривых решения, соответствующих разным значениям C. Частные решения дифференциального уравнения получаются из начальных условий на неизвестную функцию и ее производные.

Например, на рисунке F предположим, вы хотите найти частное решение, график которого проходит через точку 共1, 3兲. Это начальное условие можно записать как у⫽3 когда х ⫽ 1. Начальное состояние Подстановка этих значений в общее решение дает 3 ⫽ C共1兲2, откуда следует что C ⫽ 3. Итак, частное решение есть у ⫽ 3x 2. Частное решение Пример 2 Поиск конкретного решения Для дифференциального уравнения СОВЕТ ИЗУЧЕНИЯ Для определения конкретного раствор, количество начальные условия должны соответствовать количество констант в общее решение. ху⬘ ⫺ 3у ⫽ 0 проверьте, что y ⫽ Cx3 является решением. Затем найти частное решение, определяемое начальное условие y ⫽ 2 при x ⫽ ⫺3. РЕШЕНИЕ Вы знаете, что y ⫽ Cx3 является решением, поскольку y⬘ ⫽ 3Cx 2 и xy⬘ ⫺ 3y ⫽ x共3Cx 2兲 ⫺ 3共Cx3兲 ⫽ 3Cx 3 ⫺ 3Cx3 ⫽ 0. Кроме того, начальное условие y ⫽ 2 при x ⫽ ⫺3 дает у ⫽ Cx3 2 ⫽ C共⫺3兲3 2 ⫺ ⫽С 27 Общее решение Подставить начальное условие. Решите для С. и вы можете сделать вывод, что конкретное решение у⫽⫺ 2х3 . 27 Частное решение Попробуйте проверить это решение, заменив y и y⬘ в исходном дифференциале уравнение.

КПП 2 Для дифференциального уравнения xy⬘ ⫺ 2y ⫽ 0 проверьте, что y ⫽ Cx2 является решением. затем найти частное решение, определяемое начальным условием y ⫽ 1 при x ⫽ 4. ■ * Некоторые дифференциальные уравнения имеют решения, отличные от тех, которые даются их общими решениями. Это называется единичные решения. В этом кратком обсуждении дифференциальных уравнений сингулярные решения обсуждаться не будут. 9781133108490_App_F1 F4 06.12.11 Приложение F ■ 8:29 утра Страница F4 Дифференциальные уравнения В первых трех примерах этого раздела каждое решение было дано в явном виде. форме, такой как y ⫽ f 共x兲. Иногда вы будете сталкиваться с решениями, для которых более решение удобно записывать в неявном виде, как показано в примере 4. Пример 4 Рисование графиков решений При условии 2у 2 ⫺ х 2 ⫽ С Общее решение является общим решением дифференциального уравнения 2уу⬘ ⫺ х ⫽ 0 нарисуйте частные решения, представленные C ⫽ 0, ± 1 и ± 4. РЕШЕНИЕ Конкретные решения, представленные C ⫽ 0, ± 1 и ± 4, показаны на Рисунок Ф.

у у 2 2 Икс Икс 2 2 С=1 С=4 у у 2 у 2 1 Икс Икс 3 С=0 Икс 2 С = -1 3 С = -4 Графики пяти частных решений РИСУНОК F КПП 4 При условии у ⫽ Сх 2 является общим решением ху⬘ ⫺ 2у ⫽ 0 нарисуйте конкретные решения, представленные C ⫽ 1, C ⫽ 2 и C ⫽ 4. ПОДВЕСТИ ИТОГ (Раздел F) 1. Объясните, как проверить решение дифференциального уравнения (страница F1). Для пример проверки решения см. Пример 1. 2. Опишите отличие общего решения дифференциального уравнения от и частное решение (страницы F1 и F2). Для примера генерал решение дифференциального уравнения и частное решение см. пример 2. 3. Опишите реальный пример того, как дифференциальное уравнение можно использовать для смоделируйте продажи продукта компании (страница F3, пример 3). ■ 9781133108490_App_F1 06.12.11 8:29 утра Страница F5 Приложение F РАЗМИНКА НАВЫКОВ F ■ F5 Решения дифференциальных уравнений Следующие разминочные упражнения включают в себя навыки, которые были рассмотрены в предыдущих разделах. Вы будете использовать эти навыки в наборе упражнений для этого раздела.

Для получения дополнительной помощи просмотрите разделы 2, 2, 4 и 4. В упражнениях 1–4 найдите первую и вторую производные функции. 1. у ⫽ 3x 2 ⫹ 2x ⫹ 1 2. у ⫽ ⫺2×3 ⫺ 8x ⫹ 4 3. у ⫽ ⫺3e2x 4. у ⫽ ⫺3e х 2 В упражнениях 5 и 6 найдите k. 5. 0 ⫽ 9⫺ 9e⫺к 6. 14 ⫽ 25 ⫺ 25e⫺2k Упражнения F Проверка решений В упражнениях 1–12 убедитесь, что функция является решением дифференциального уравнения. Видеть Пример 1. Решение 1. у ⫽ Ce 4x 2. у ⫽ e⫺2x Дифференциальное уравнение у⬘ ⫽ 4 года у⬘ ⫹ 2у ⫽ 0 3 у⬘ ⫺ у ⫽ 0 Икс 3. у ⫽ 2×3 4. у ⫽ 4x 2 2 у⬘ ⫺ у ⫽ 0 Икс 5. у ⫽ Сх 2 ⫺ 3х ху⬘ ⫺ 3x ⫺ 2y ⫽ 0 6. у ⫽ х 2 ⫹ 2х ⫹ 7. 8. 9. 10. 11. 12. С Икс у ⫽ х ln х ⫹ Сх ⫹ 4 2 y ⫽ Ce x⫺x у ⫽ х2 3 у ⫽ экс y ⫽ C1 sin x ⫺ C2 cos x у ⫽ C1e4x ⫹ C2e⫺x xy⬘ ⫹ y ⫽ x共3x ⫹ 4兲 x共 y⬘ ⫺ 1兲 ⫺ 共 y ⫺ 4兲 ⫽ 0 у⬘ ⫹ 共2x ⫺ 1兲y ⫽ 0 х 2у⬙ ⫺ 2у ⫽ 0 у⬙ ⫺ 3x 2y⬘ ⫺ 6xy ⫽ 0 у⬙ ⫹ у ⫽ 0 у⬙ ⫺ 3у⬘ ⫺ 4у ⫽ 0 Поиск конкретного решения в упражнениях 21–24, проверить, что общее решение удовлетворяет дифференциалу уравнение. Затем найдите частное решение, удовлетворяющее исходное состояние.

См. пример 2. 21. Общее решение: y ⫽ Ce⫺2x Дифференциальное уравнение: y⬘ ⫹ 2y ⫽ 0 Начальное условие: y ⫽ 3, когда x ⫽ 0 22. Общее решение: 2x 2 ⫹ 3y2 ⫽ C Дифференциальное уравнение: 2x ⫹ 3yy⬘ ⫽ 0 Начальное условие: y ⫽ 2, когда x ⫽ 1 23. Общее решение: y ⫽ C1 ⫹ C2 ln x Дифференциальное уравнение: xy⬙ ⫹ y⬘ ⫽ 0 Начальное условие: y ⫽ 5 и y⬘ ⫽ 0, когда x ⫽ 1 24. Общее решение: y ⫽ C1e 4x ⫹ C2e⫺3x Дифференциальное уравнение: y⬙ ⫺ y⬘ ⫺ 12y ⫽ 0 Начальное условие: y ⫽ 5 и y⬘ ⫽ 6, когда x ⫽ 0 Наброски графиков решений в упражнениях 25 и 26, общее решение дифференциального уравнения имеет вид данный. Нарисуйте частные решения, соответствующие указанные значения C. См. пример 4. Нахождение решений В упражнениях 13–16 определите является ли функция решением дифференциала уравнение y 冇4冈 ⴚ 16y ⴝ 0. Общее решение 25. у ⫽ C共x ⫹ 2兲2 26. у ⫽ Ce⫺x 13. у ⫽ e⫺2x 4 15. у ⫽ Икс Поиск общих решений В упражнениях 27–34 используйте интегрирование, чтобы найти общее решение дифференциальной уравнение. 14. у ⫽ 5 ln х 16.

у ⫽ 3 sin 2x Нахождение решений В упражнениях 17–20 определите является ли функция решением дифференциала уравнение y ⬙⬘ ⴚ 3y⬘ ⴙ 2y ⴝ 0. 17. 18. 19. 20. 2 ⫺2x 9 хэ у⫽ у ⫽ потому что х у ⫽ х х у ⫽ х ln х Дифференциальное уравнение 共x ⫹ 2兲y⬘ ⫺ 2y ⫽ 0 у⬘ ⫹ у ⫽ 0 27. ды ⫽ 3x 2 дх 28. ды ⫽ 2×3 ⫺ 3x дх 29. ды 1 ⫽ дх 1 ⫹ х 30. dy х ⫺ 2 ⫽ дх Икс 31. ды ⫽ х 冪 х 2 ⫹ 6 дх 32. ды Икс ⫽ дх 1 ⫹ х2 33. ды ⫽ потому что 4x дх 34. ды ⫽ 4 грех х дх C-значения 0, ± 1, ± 2 0, ± 1, ± 4 9781133108490_App_F2 06.12.11 8:30 УТРА Страница F7 Приложение F ■ Разделение переменных F7 F Разделение переменных ■ Используйте разделение переменных для решения дифференциальных уравнений. ■ Используйте дифференциальные уравнения для моделирования и решения реальных задач. Разделение переменных Простейшее дифференциальное уравнение имеет вид y⬘ ⫽ f 共x兲. Ты знаешь что этот тип уравнения может быть решен путем интегрирования, чтобы получить у⫽ 冕 f 共x兲 dx. В этом разделе вы узнаете, как использовать интеграцию для решения еще одной важной задачи семейства дифференциальных уравнений — тех, в которых переменные можно разделить.

Эта техника называется разделением переменных. Разделение переменных Если f и g — непрерывные функции, то дифференциальное уравнение ды ⫽ f 共x兲g共 y兲 дх имеет общее решение 冕 1 dy ⫽ g 共 y 兲冕 f 共x兲 dx ⫹ C. По сути, техника разделения переменных — это именно то, что следует из ее названия. Для дифференциального уравнения, включающего x и y, вы разделяете переменные, группируя переменные x с одной стороны и переменные y с другой. После разделения переменных интегрировать каждую сторону, чтобы получить общее решение. ТЕХНИЧЕСКИЙ ТУТОР Вы можете использовать символический интеграционная утилита для решения дифференциальное уравнение, имеющее разделяемые переменные. Использовать утилита символьной интеграции решить дифференциал уравнение в примере 1. Пример 1 Решение дифференциального уравнения Найдите общее решение ды Икс ⫽ . дх у2 ⫹ 1 РЕШЕНИЕ Начните с разделения переменных, затем интегрируйте каждую сторону. ды Икс ⫽ дх у 2 ⫹ 1 (y 2 ⫹ 1兲 dy ⫽ x dx 冕共 y 2 ⫹ 1 兲 dy ⫽ 冕 х дх Дифференциальное уравнение Отдельные переменные.

Интегрируйте каждую сторону. у3 х2 ⫹у⫽ ⫹С 3 2 Общее решение КПП 1 Найдите общее решение дай х 2 ⫽ . дх у ■ 9781133108490_App_F2 F8 06.12.11 Приложение F ■ 8:30 УТРА Страница F8 Дифференциальные уравнения Пример 2 Решение дифференциального уравнения Найдите общее решение дай х ⫽ . дх у РЕШЕНИЕ Начните с разделения переменных, затем интегрируйте каждую сторону. дай х ⫽ дх у y dy ⫽ x dx 冕冕 у ды ⫽ х дх у2 х2 ⫽ ⫹ C1 2 2 2 у ⫽ x2 ⫹ C Дифференциальное уравнение Отдельные переменные. Интегрируйте каждую сторону. Найдите первообразную каждой стороны. Умножьте каждую сторону на 2. Итак, общее решение y 2 ⫽ x2 ⫹ C. Обратите внимание, что C1 используется как временная постоянная интегрирования в ожидании умножения каждой части уравнения на 2 для получения постоянная С. КПП 2 Найдите общее решение dy х ⫹ 1 ⫽ . дх у Пример 3 ■ Решение дифференциального уравнения Найдите общее решение e y РЕШЕНИЕ Начните с разделения переменных, затем интегрируйте каждую сторону. ды ⫽ 2x дх e y dy ⫽ 2x dx Эй 冕 5 С = 15 −6 С=5 С = 10 ды ⫽ 2x.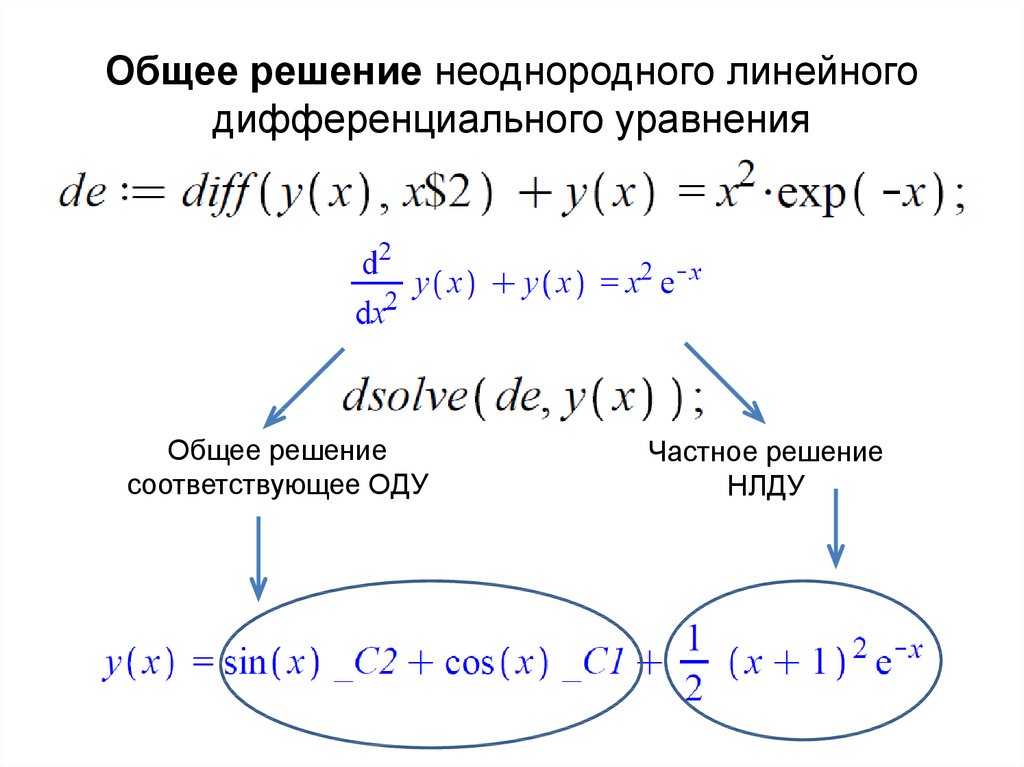

Используйте графическую утилиту для построения графиков нескольких решений. дх е у ды ⫽ 冕 2x дх е у ⫽ x2 ⫹ C Дифференциальное уравнение Отдельные переменные. Интегрируйте каждую сторону. Найдите первообразную каждой стороны. 6 Беря натуральный логарифм каждой стороны, вы можете записать общее решение как С=0 y ⫽ ln共x2 ⫹ C兲. −5 РИСУНОК F Общее решение Графики частных решений, заданных C ⫽ 0, 5, 10 и 15, показаны на рис. Рисунок Ф. КПП 3 Найдите общее решение 2 года ды ⫽ ⫺2x. дх Используйте графическую утилиту для построения графика конкретных решений, заданных C ⫽ 1, 2 и 4. ■ 9781133108490_App_F2 F10 06.12.11 Приложение F ■ 8:30 УТРА Страница F10 Дифференциальные уравнения Заявление Пример 6 Корпоративное инвестирование Корпорация инвестирует часть своих доходов по ставке P долларов в год в фонд для будущее корпоративное расширение. Фонд зарабатывает r процентов годовых, начисляемых на сложные проценты. непрерывно. Скорость роста суммы A в фонде равна дА ⫽ rA ⫹ P дт где t — время (в годах).

Решите дифференциальное уравнение для A как функции от t, где A ⫽ 0 при t ⫽ 0. РЕШЕНИЕ Вы можете решить дифференциальное уравнение, используя разделение переменных. дА ⫽ rA ⫹ P дт dA ⫽ 共rA ⫹ P兲 dt дА ⫽ дт rA ⫹ P Дифференциальное уравнение Дифференциальная форма Отдельные переменные. 1 ln rA ⫹ P ⫽ t ⫹ C1 р ln共rA ⫹ P兲 ⫽ rt ⫹ C2 rA ⫹ P ⫽ ert⫹C2 C e rt ⫺ P А⫽ 3 р п A ⫽ C rt ⫺ р ⱍ ⱍ Интегрировать. Предположим, что rA⫹P > 0 и умножить каждую сторону на r. Возвеличьте каждую сторону. Решите для А. Общее решение Используя A ⫽ 0 при t ⫽ 0, вы найдете значение C. 0 ⫽ Ce r 共0兲 ⫺ п р С⫽ п р Итак, дифференциальное уравнение для A как функции от t можно записать в виде А⫽ П рт 共e ⫺ 1兲. р КПП 6 Используйте результат примера 6, чтобы найти A, когда P ⫽ 550 000 долларов, r ⫽ 5% и t ⫽ 25 лет. ПОДВЕСТИ ИТОГ (Раздел F) 1. Объясните, как использовать разделение переменных для решения дифференциального уравнения. (страница F7). Для примеров решения дифференциального уравнения с использованием разделения переменных см.

примеры 1, 2, 3, 4 и 5. 2. Опишите реальный пример того, как можно использовать разделение переменных для решения дифференциального уравнения, моделирующего корпоративное инвестирование (стр. F10, Пример 6). ■ 9781133108490_App_F2 06.12.11 8:30 УТРА Страница F11 Приложение F ■ Разделение переменных F11 Следующие разминочные упражнения включают в себя навыки, которые были рассмотрены в предыдущих разделах. Ты сможешь используйте эти навыки в наборе упражнений для этого раздела. Для получения дополнительной помощи просмотрите разделы 4, 5, и 5. РАЗМИНКА НАВЫКОВ F В упражнениях 1–6 найдите неопределенный интеграл и проверьте результат дифференцированием. 1. 4. 冕冕 x 3兾2 dx 2. у ды 2г 2 ⫹ 1 5. 冕冕共t3 ⫺ t1 兾3 兲 dt 3. e2y dy 6. 冕冕 2 дх х⫺5 2 xe1⫺x dx В упражнениях 7–10 решите уравнение относительно C или k. 7. 共3 兲2 ⫺ 6 共3 兲 ⫽ 1 ⫹ C 8. 共⫺1兲2 ⫹ 共⫺2兲2 ⫽ C 10. 共6 兲2 ⫺ 3 共6 兲 ⫽ e⫺k 9. 10 ⫽ 2e2k Упражнения F Разделение переменных В упражнениях 1–6 решите могут ли переменные в дифференциальном уравнении быть разделены.

Решение дифференциального уравнения в упражнениях 27–30, а) найти общее решение дифференциала уравнение и (б) использовать графическую утилиту для построения графика частные решения, заданные C ⴝ 1, 2 и 4. См. Пример 3. 1. ды Икс ⫽ дх у ⫹ 3 2. dy х ⫹ 1 ⫽ дх Икс 3. день 1 ⫽ ⫹1 дх Икс 4. ды Икс ⫽ дх х ⫹ у 27. ды ⫽x дх 28. ды 2x ⫽⫺ дх у 5. ды ⫽x⫺y дх 6. х день 1 ⫽ дх у 29. ды ⫽y⫹3 дх 30. ды ⫽ 0共4 ⫺ у兲 дх Решение дифференциального уравнения в упражнениях 7–26, использовать разделение переменных, чтобы найти общее решение дифференциальное уравнение. См. примеры 1 и 2. Дифференциальное уравнение 7. ды ⫽ 2x дх 9. доктор ⫽ 0 дс 10. доктор ⫽ 0 дс 11. dy х ⫺ 1 ⫽ дх у3 12. dy x 2 ⫺ 3 ⫽ дх у2 14. ды ⫽ х 2 года дх 13. 3г 2 ды ⫽1 дх 15. х2 ⫹ 4л ды ⫽0 дх 17. у⬘ ⫺ ху ⫽ 0 ды 19. е у ⫽ 3t2 ⫹ 1 дт 21. ды ⫽ 冪1 ⫺ у дх 23. 共2 ⫹ x兲y⬘ ⫽ 2г ды 25. г ⫽ грех х дх 8. день 1 ⫽ дх Икс 16. 共1 ⫹ у 兲 ды ⫺ 4x ⫽ 0 дх 20. e x共 y⬘ ⫹ 1兲 ⫽ 1 Икс Икс ⫺ у 1⫹у 24. у⬘ ⫺ у共x ⫹ 1兲 ⫽ 0 ды 26. г ⫽ 6 cos共␲ x兲 дх Начальное состояние 31.

уу⬘ ⫺ е ⫽ 0 32. 冪x ⫹ 冪y y⬘ ⫽ 0 33. х共 у ⫹ 4兲 ⫹ у⬘ ⫽ 0 ды 34. ⫽ x 2共1 ⫹ y兲 дх у ⫽ 4, когда х ⫽ 0 у ⫽ 4, когда х ⫽ 1 y ⫽ ⫺5, когда x ⫽ 0 35. 冪x 2 ⫺ 16y⬘ ⫽ 5x 36. y⬘ ⫽ ex⫺2y ды 37. ⫽ у, потому что х дх y ⫽ ⫺2, когда x ⫽ 5 у ⫽ 0, когда х ⫽ 0 Икс 18. у⬘ ⫺ у ⫽ 5 22. у⬘ ⫽ Поиск конкретного решения В упражнениях 31–38 используйте начальное условие для нахождения частного решения дифференциальное уравнение. См. пример 4. 38. ды ⫽ 2xy sin x 2 дх у ⫽ 3, когда х ⫽ 0 у ⫽ 1, когда х ⫽ 0 у ⫽ 1, когда х ⫽ 0 Поиск уравнения в упражнениях 39и 40, найти уравнение графика, проходящего через точку и имеет заданный наклон. Затем нарисуйте уравнение. 39. Пункт: 共⫺1, 1兲 Наклон: y⬘ ⫽ ⫺ 40. Пункт: 共8, 2 兲 9x 16 лет Наклон: у⬘ ⫽ 2 года 3x 9781133108490_App_F2 06.12.11 8:30 УТРА Страница F13 Проверьте себя ■ F13 ПРОВЕРЬТЕ СЕБЯ Пройдите этот тест, как если бы вы проходили тест в классе. Когда закончите, проверьте работать против ответов, данных в конце книги. В упражнениях 1–4 убедитесь, что функция является решением дифференциального уравнения.

Решение 1. у ⫽ Ce⫺x兾 2 2. y ⫽ C1 cos x ⫹ C2 sin x 1 3. у ⫽ Икс 4. у ⫽ х3 ⫺ х ⫹ C冪x 5 Дифференциальное уравнение 2у⬘ ⫹ у ⫽ 0 у⬙ ⫹ у ⫽ 0 ху⬙ ⫹ 2у⬘ ⫽ 0 2xy⬘ ⫺ y ⫽ x 3 ⫺ x В упражнениях 5 и 6 убедитесь, что общее решение удовлетворяет дифференциалу уравнение. Затем найдите частное решение, удовлетворяющее начальному условию. 5. Общее решение: y ⫽ C1 sin 3x ⫹ C2 cos 3x Дифференциальное уравнение: y⬙ ⫹ 9у ⫽ 0 Начальное условие: y ⫽ 2 и y⬘ ⫽ 1, когда x ⫽ ␲兾6 6. Общее решение: y ⫽ C1 x ⫹ C2 x 3 Дифференциальное уравнение: x 2y⬙ ⫺ 3xy⬘ ⫹ 3y ⫽ 0 Начальное условие: y ⫽ 0 и y⬘ ⫽ 4, когда x ⫽ 2 В упражнениях 7–10 используйте разделение переменных, чтобы найти общее решение задачи. дифференциальное уравнение. 7. ды ⫽ ⫺4x ⫹ 4 дх 9. г ды 1 ⫽ дх 2х ⫹ 1 8. у⬘ ⫽ 共x ⫹ 2兲共y ⫺ 1兲 10. ды Икс ⫽ 2 дх 3г ⫹ 1 В упражнениях 11 и 12: (а) найдите общее решение дифференциального уравнения и (b) использовать графическую утилиту для построения графика конкретных решений, заданных C ⴝ 0 и С ⴝ ± 1. 11. дай х 2 ⫹ 1 ⫽ дх 2 года 12.

у ды ⫽ дх х ⫺ 3 В упражнениях 13 и 14 используйте начальное условие, чтобы найти частное решение задачи. дифференциальное уравнение. Дифференциальное уравнение 13. у⬘ ⫹ 2у ⫺ 1 ⫽ 0 ды 14. ⫽ у sin ␲ х дх Начальное состояние у ⫽ 1, когда х ⫽ 0 y ⫽ ⫺3, когда x ⫽ 1 2 15. Найдите уравнение графика, проходящего через точку 共0, 2兲 и имеющего наклон y⬘ ⫽ 3x 2 y. Затем нарисуйте уравнение. 16. Пренебрегая сопротивлением, парусник, стартуя из состояния покоя, разгоняется со скоростью, пропорциональной разнице скоростей ветра и лодки. С 20-узл. ветра, это ускорение описывается дифференциальным уравнением dv兾dt ⫽ k共20 ⫺ v兲, где v — скорость лодки (в узлах), t — время (в часах). После половины час, катер движется со скоростью 10 узлов. Запишите скорость как функцию времени. 9781133108490_App_F3 F14 06.12.11 Приложение F ■ 8:28 утра Страница F14 Дифференциальные уравнения F Линейные дифференциальные уравнения первого порядка ■ Решайте линейные дифференциальные уравнения первого порядка. ■ Используйте линейные дифференциальные уравнения первого порядка для моделирования и решения реальных задач.

Линейные дифференциальные уравнения первого порядка В этом разделе вы увидите, как решить очень важный класс дифференциальных уравнения — линейные дифференциальные уравнения первого порядка. Термин «первый порядок» относится к тот факт, что производная старшего порядка y в уравнении является первой производной. Определение линейного дифференциального уравнения первого порядка Линейное дифференциальное уравнение первого порядка — это уравнение вида y⬘ ⫹ P共x兲 y ⫽ Q共x兲 где P и Q — функции от x. Уравнение, записанное в таком виде говорят, что это стандартная форма. Чтобы решить линейное дифференциальное уравнение, запишите его в стандартной форме, чтобы определить функции P共x兲 и Q共x兲. Затем проинтегрируйте P共x兲 и сформируйте выражение u共x兲 ⫽ e 兰P共x兲 dx Интегрирующий фактор который называется интегрирующим фактором. Общее решение уравнения у⫽ 冕 1 Q共x兲 u共x兲 dx. u共x兲 Пример 1 Общее решение Решение линейного дифференциального уравнения Найдите общее решение y⬘ ⫹ y ⫽ e x. Для этого уравнения P共x兲 ⫽ 1 и Q共x兲 ⫽ e x.

Итак, интегрирующий фактор РЕШЕНИЕ u共x兲 ⫽ e兰P共x兲 dx ⫽ e兰dx ⫽ е х. Интегрирующий фактор Отсюда следует, что общее решение у⫽ 冕 1 Q共x兲u共x兲 dx u共x兲冕 1 х х e 共e 兲 dx бывший 1 ⫽ e⫺x e2x ⫹ C 2 1 ⫽ e x ⫹ Ce⫺x. 2 ⫽ 冢冣 Общее решение КПП 1 Найдите общее решение у⬘ ⫺ у ⫽ 10. ■ 9781133108490_App_F3 F16 06.12.11 Приложение F ■ 8:28 утра Страница F16 Дифференциальные уравнения Заявление Пример 3 Внутривенное питание Глюкоза вводится внутривенно в кровоток со скоростью q единиц в минуту, и организм выводит глюкозу из кровотока со скоростью, пропорциональной количеству подарок. Предположим, что А — это количество глюкозы в кровотоке в момент времени t и что скорость изменения количества глюкозы равна дА ⫽ q ⫺ кА дт где k — константа. Найдите общее решение дифференциального уравнения. РЕШЕНИЕ В стандартной форме это линейное дифференциальное уравнение имеет вид дА ⫹ кА ⫽ q дт Стандартная форма откуда следует, что P共t兲 ⫽ k и Q共t兲 ⫽ q. Итак, интегрирующий фактор u共t 兲 ⫽ e 兰P共t兲 dt ⫽ e 兰k dt ⫽ кт Интегрирующий фактор и общее решение А⫽ 冕冕 1 Q共t兲u共t兲 DT ты 共t 兲 ⫽ e⫺ kt qe ktdt ⫽ e⫺кт ⫽ 冢qk e кт ⫹С 冣 д ⫹ Се⫺кт.

к Общее решение КПП 3 Используйте общее решение А⫽ д ⫹ Се⫺кт к из примера 3 найти частное решение, определяемое начальным условием A ⫽ 0, когда t ⫽ 0. (Предположим, что k ⫽ 0 и q ⫽ 0.) ПОДВЕСТИ ИТОГ (Раздел F) 1. Дайте определение линейного дифференциального уравнения первого порядка (стр. F14). Примеры решения линейного дифференциального уравнения первого порядка см. Примеры 1 и 2. 2. Сформулируйте основные принципы решения линейного дифференциального уравнения первого порядка. (стр. F15). Примеры решения линейного дифференциального уравнения первого порядка: см. примеры 1 и 2. 3. Опишите реальный пример того, как линейное дифференциальное уравнение первого порядка можно использовать для анализа внутривенного питания (страница F16, пример 3). ■ 9781133108490_App_F3 06.12.11 8:28 утра Страница F17 Приложение F РАЗМИНКА НАВЫКОВ F ■ F17 Линейные дифференциальные уравнения первого порядка Следующие разминочные упражнения включают в себя навыки, которые были рассмотрены в предыдущих разделах.

Ты сможешь используйте эти навыки в наборе упражнений для этого раздела. Для получения дополнительной помощи просмотрите разделы 4, 4, и 5–5. В упражнениях 1–4 упростите выражение. 1. e⫺x共e 2x ⫹ e x兲 2. 1 ⫺x 共e ⫹ e 2x兲 e⫺x 3. e⫺ln х 3 4. e 2 ln x⫹x В упражнениях 5–10 найдите неопределенный интеграл. 5. 8. 冕冕 4e2x дх 6. х⫹1 дх х 2 ⫹ 2 х ⫹ 3 9. 冕冕 2 xe3x дх 7. 共4x ⫺ 3兲2 dx 10. 冕冕 1 дх 2x ⫹ 5 x共1 ⫺ x 2兲2 dx Упражнения F Запись в стандартной форме В упражнениях 1–6 напишите линейное дифференциальное уравнение первого порядка в стандартной форме. 1. х3 ⫺ 2х 2у⬘ ⫹ 3у ⫽ 0 3. xy⬘ ⫹ y ⫽ xe x 5. у ⫹ 1 ⫽ 共x ⫺ 1兲y⬘ 2. у⬘ ⫺ 5共2x ⫺ у兲 ⫽ 0 4. ху⬘ ⫹ y ⫽ x3y 6. х ⫽ х 2 共 y ⬘ ⫹ y 兲 Решение линейного дифференциального уравнения в упражнениях 7–18, найти общее решение линейной дифференциальное уравнение. См. примеры 1 и 2. 7. ды ⫹ 3г ⫽ 6 дх 8. 9. ды ⫺ у ⫽ е 4x дх 10. 11. dy x2 ⫹ 3 ⫽ дх Икс 12. ды e⫺2x ⫽ дх 1 ⫹ е⫺2х 13. 14. 15. 16. 17. 18. ху⬘ ⫹ у ⫽ х ⫹ 1 2 x3y⬘ ⫹ 2y ⫽ e1兾x ху⬘ ⫹ у ⫽ х 2 ln х 2 у⬘ у⬘ у⬘ у⬘ ⫹y⫽4 ⫺ 3 года ⫽ ⫺2 ⫺ 2xy ⫽ 2x ⫹ 4xy ⫽ х Дифференциальное уравнение 23.

24. 25. 26. у⬘ у⬘ у⬘ у⬘ Решение 2 (а) y ⫽ Ce x 2 (б) y ⫽ ⫺ 12 ⫹ Ce x (в) у ⫽ x2 ⫹ C (г) у ⫽ Ce2x ⫺ 2x ⫽ 0 ⫺ 2 года ⫽ 0 ⫺ 2xy ⫽ 0 ⫺ 2xy ⫽ х Поиск частного решения В упражнениях 27–34 найдите частное решение, удовлетворяющее начальному условию. ды ⫹ 3г ⫽ е⫺3x дх у⬘ ⫹ 2xy ⫽ 10x у⬘ ⫹ 5y ⫽ e5x 共x ⫺ 1兲y⬘ ⫹ y ⫽ x 2 ⫺ 1 Использование двух методов два пути. 19. 20. 21. 22. ды ⫺ 5 лет ⫽ 15 дх Сопоставление В упражнениях 23–26 сопоставьте дифференциал уравнение с его решением без решения дифференциального уравнение. Объясните свои рассуждения. 27. 28. 29. 30. 31. 32. 33. 34. Дифференциальное уравнение Начальное состояние у⬘ ⫹ у ⫽ у⬘ ⫹ 2y ⫽ e⫺2x ху⬘ ⫹ у ⫽ 0 у⬘ ⫹ у ⫽ х у⬘ ⫹ 3x 2y ⫽ 3x 2 у⬘ ⫹ 共2x ⫺ 1兲y ⫽ 0 ху⬘ ⫹ 2у ⫽ 3х 2 ⫺ 5х у ⫽ 3, когда х ⫽ 0 у ⫽ 4, когда х ⫽ 1 у ⫽ 2, когда х ⫽ 2 у ⫽ 4, когда х ⫽ 0 у ⫽ 6, когда х ⫽ 0 у ⫽ 2, когда х ⫽ 1 6е х y ⫽ 3, когда x ⫽ ⫺1 у ⫽ 2, когда х ⫽ 4 2xy⬘ ⫺ y ⫽ x3 ⫺ x 35. Продажи Скорость изменения (в тысячах единиц) в объем продаж биомедицинского шприца S моделируется В упражнениях 19–22, найти у в дС ⫽ 0共100 ⫺ Ю 兲 ⫹ 0 дт где t — время (в годах).

Решите этот дифференциал уравнение и использовать результат для заполнения таблицы. т 0 С 0 1 2 3 4 5 6 7 8 9 10 9781133108490_App_F4 06.12.11 8:30 УТРА Страница F19 Приложение F ■ Приложения дифференциальных уравнений F19 F Приложения дифференциальных уравнений ■ Используйте дифференциальные уравнения для моделирования и решения реальных задач. Приложения дифференциальных уравнений Пример 1 Моделирование химической реакции В ходе химической реакции вещество А превращается в вещество Б со скоростью, равной пропорциональна квадрату количества вещества А. При t ⫽ 0 60 граммов А присутствуют, и через 1 час 共t ⫽ 1 兲 только 10 граммов А остаются непревращенными. Как много А присутствует через 2 часа? Пусть y будет количеством непрореагировавшего вещества A в любой момент времени t. От учитывая предположение о коэффициенте конверсии, вы можете написать дифференциальное уравнение как показано. РЕШЕНИЕ ды ⫽ ky2 дт Скорость сдача из у пропорциональна квадрат у. Используя разделение переменных или утилиту символьного интегрирования, можно найти общие решение быть у⫽ ⫺1 .

кт ⫹ C Общее решение Чтобы найти константы C и k, используйте начальные условия. То есть, поскольку y ⫽ 60 1 при t ⫽ 0 можно определить, что C ⫽ ⫺ 60 . Точно так же, поскольку y ⫽ 10 при t ⫽ 1, это следует из того 10 ⫽ ⫺1 k ⫺ 共1 兾60 兲 1 откуда следует, что k ⫽ ⫺ 12 . Итак, частное решение Химическая реакция ⫺1 共⫺1 兾12 兲t ⫺ 共1 兾60 兲 60 . ⫽ 5 т ⫹ 1 у⫽ у Количество (в граммах) 60 (0, 60) 50 40 60 у = 5 т + 1 (1, 10) 10 (2, 5) 2 Время (в часах) РИСУНОК F 60 5 共 2 兲 ⫹ 1 ⬇ 5 грамм. у⫽ т 1 Частное решение С помощью модели можно определить, что количество непрореагировавшего вещества А после 2 часа 30 20 Замените k и C. 3 На рисунке F обратите внимание, что химическое превращение происходит быстро в течение первого час. Затем, по мере превращения все большего количества вещества А, скорость превращения замедляется. вниз. КПП 1 Используйте модель химической реакции из примера 1, чтобы найти количество y вещества A. (в граммах) как функция t (в часах), учитывая, что y ⫽ 40 граммов, когда t ⫽ 0 и y ⫽ 5 грамм при t ⫽ 2.

■

Специальная дифференциальная-распределительная-уравнение-Google Suge

ALLBILDERVIDEOSBüchermApsNewshopping

Sucopitionen

Обычные уравнения (ODE) Калькулятор-Symbolab

WWW.Symbolab.com ratulator-Symbolab

www.symbolab.com-stepulator-Symbolab

Www.symbolab.com rabulator. Бесплатный калькулятор обыкновенных дифференциальных уравнений (ОДУ) — шаг за шагом решайте обыкновенные дифференциальные уравнения (ОДУ).

Неоднородные · Дифференциал второго порядка… · Калькулятор системы ОДУ · Точная

Дифференциальные уравнения. Пошаговый калькулятор — MathDF

mathdf.com › dif

Калькулятор обыкновенных дифференциальных уравнений. С удобным вводом и шаг за шагом!

Интегралы · Уравнения · Производная функции · Вычисления матриц

Калькулятор дифференциальных уравнений — eMathHelp

www.emathhelp.net заданные ОДУ: первого порядка, второго порядка, n-го порядка, сепарабельные, линейные, точные, бернуллиевские, однородные или.

Wolfram|Alpha Widgets: «Решение общих дифференциальных уравнений»

www.wolframalpha.com › виджеты › просмотр

01.08.2010 · Получите бесплатный виджет «Решение общих дифференциальных уравнений» для вашего сайта, блога, WordPress, Блоггер или iGoogle.

Ähnliche Fragen

Что такое частное решение дифференциального уравнения с примером?

Сколько частных решений имеет дифференциальное уравнение?

Как найти частное решение неоднородного дифференциального уравнения?

Дифференциальные уравнения — Wolfram|Alpha Examples

www.wolframalpha.com › примеры › математика

Ответы на задачи дифференциальных уравнений. Решите ОДУ, линейные, нелинейные, обыкновенные и численные дифференциальные … Решите неоднородное уравнение:.

Калькулятор и решатель дифференциальных уравнений — SnapXam

www.snapxam.com › калькуляторы › дифференциально-уравнени…

Калькулятор дифференциальных уравнений онлайн с решением и шагами. Подробные пошаговые решения ваших задач по дифференциальным уравнениям онлайн с нашим …

Калькулятор дифференциальных уравнений — math20.com – Math

www.math20.com › Решатели задач

Калькулятор дифференциальных уравнений. Калькулятор для решения дифференциальных уравнений. Решатель общего дифференциального уравнения. Укажите дифференциальное уравнение …

Решение дифференциальных уравнений онлайн бесплатно — OnSolver

onsolver.com › diff-equation

Решение дифференциальных уравнений любого порядка онлайн. … Этот калькулятор для решения дифференциальных уравнений взят от ООО «Вольфрам Альфа».

Калькулятор обыкновенных дифференциальных уравнений — Math34.pro

math34.pro › Differential_equation

Используйте Math34.pro для решения дифференциальных уравнений любого типа здесь и сейчас. … Бесплатный калькулятор обыкновенных дифференциальных уравнений (ОДУ) — решайте обычные …

Решатель дифференциальных уравнений — Онлайн-инструмент — dCode.