Найти онлайн угол между векторами: Онлайн калькулятор. Вычисление угла между векторами

Угол между векторами. Скалярное произведение векторов. 11 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

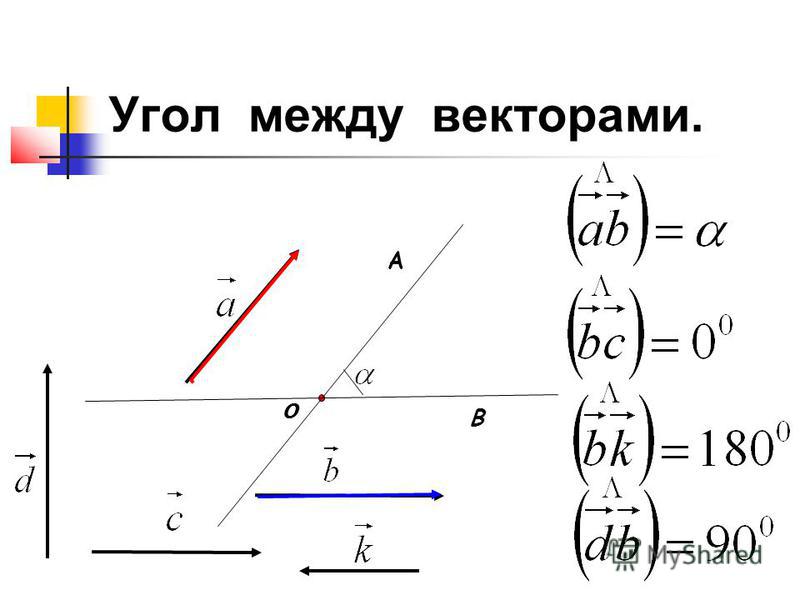
Угол между векторами.
Скалярное произведение
векторов.
11 класс.

2. Повторяем теорию:

• Как находят координаты вектора, если известны
координаты его начала и конца?
АВ хВ х А ; уВ у А ; z B z A
• Как находят координаты середины отрезка?
х А хВ
;
2
• Как находят длину вектора?
у А уВ
;
2
z A zB
2
а х2 у2 z 2
• Как находят расстояние между точками?
АВ
х
х А у В у А z B z A
2
В
2
• Как вы понимаете выражение «угол между
векторами»?
2
Найти углы между векторами
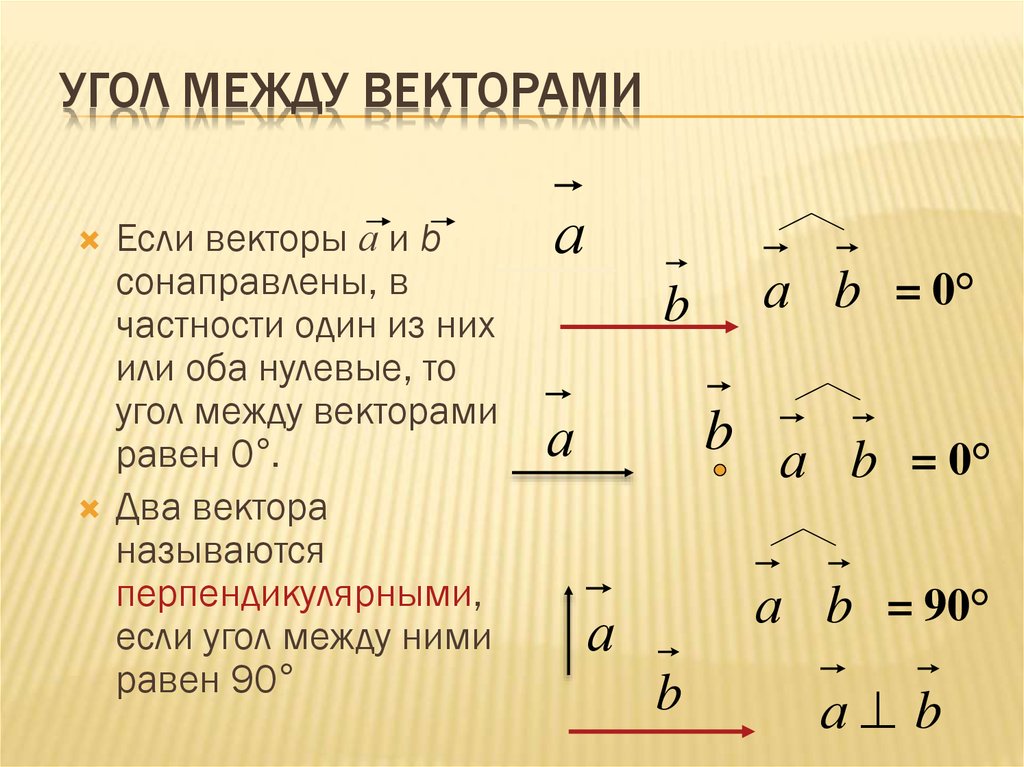
Два вектора называются
перпендикулярными,
если угол между ними равен 90 .
xa ya za
Условие коллинеарности векторов:
xb yb zb
Какие векторы называются перпендикулярными?
Два вектора называются перпендикулярными,
если угол между ними равен 90 .
Условие перпендикулярности векторов:
xa xb ya yb za zb 0

5. Повторяем теорию:

• Что называется скалярным произведением векторов?
a b a b cos xa xb ya yb za zb
• Чему равно скалярное произведение перпендикулярных
векторов? 0
• Чему равен скалярный квадрат вектора?
2
a
a
2
xa2 ya2 za2
• Свойства скалярного произведения?
а 0
2
ab ba
a b c ac bc
k ab k a b

6. Косинус угла между векторами

cos
а 2; 2;0
с 3;0; 3
a b
a b
xa xb ya yb za zb
xa2 ya2 za2 xb2 yb2 zb2
2 3 2 0 0 3
cos
2
2
2
2
2 0
3 0
2
2
2
3
6 0 0
6
4 4 0 9 0 9
8 18
6
6
6 1
4 2 2 9 4 3 12 2
1
Ответ : 60
cos 60
2
СА х А хС ; у А уС ; А С
Дано : А 1;3;0
СА 1 1;3 2;0 1 0;1;1
В 2;3; 1 , С 1;2; 1
Найти : СА; СВ
cos
cos СА; СВ
СВ хВ хС ; уВ уС ; В С
a b
a b
СВ 2 1;3 2; 1 1 1;1;0
xa xb ya yb za zb
xa2 ya2 za2 xb2 yb2 zb2
0 1 1 1 1 0
0 1 1 1 1 0
2
2
2
2
2
2
1
1
2 2 2
1
cos СА; СВ СА;СВ 60
2
Ответ : СА; СВ 60

8.

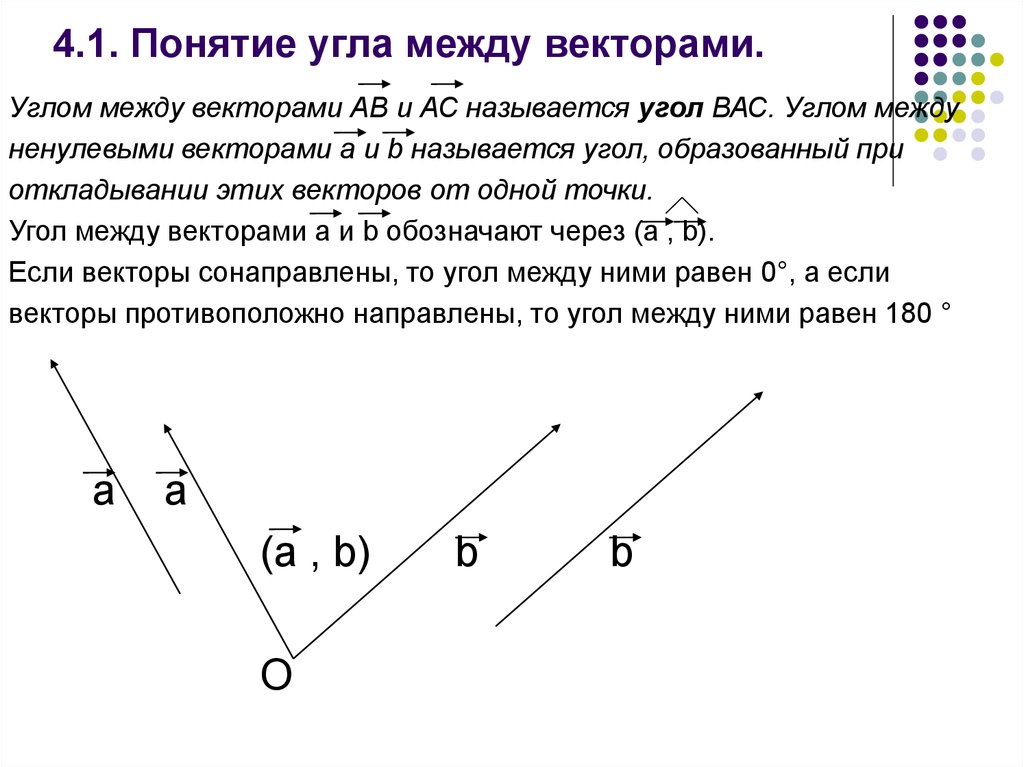Вычисление углов между прямыми и плоскостями• Углом между прямой и плоскостью,
пересекающей
эту
прямую
и
не
перпендикулярную к ней, называют угол
между прямой и её проекцией на
плоскость.
Если
, то проекцией
=A, ( ,
Если || ,
( , ) = 0
на
является точка А
) = 90
— проекция
на , то
,
.

10. Направляющий вектор прямой.

а
• Ненулевой вектор называется
направляющим вектором
прямой, если он лежит на
самой прямой, либо на прямой,
параллельной ей.

11. Визуальный разбор задач из учебника (п.48).

№1.
Найти
угол
между
двумя
прямыми
(пересекающимися или скрещивающимися), если
известны координаты направляющих векторов этих
прямых.
q x ; y ; z
p x ; y ;z
а)
р
1
1
1
б)
2
2
2
р
q
р
р
θ
q
q
q
θ
φ=θ
φ = 1800 — θ

12. Ответ:

cos
/ x1 x2 y1 y2 z1 z 2 /
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2

13.

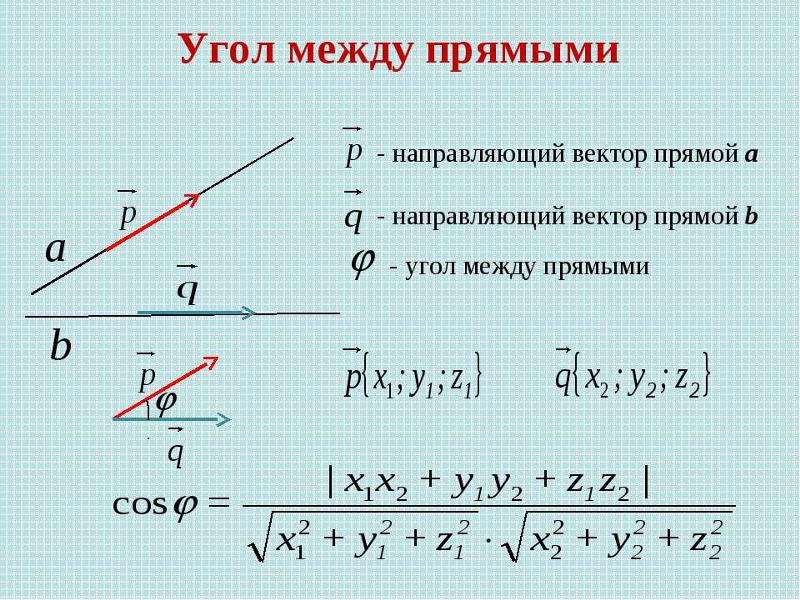Визуальный разбор задач из учебника (п.48).№2. Найти угол между прямой и плоскостью, если
известны координаты направляющего вектора
прямой и координаты ненулевого вектора,
перпендикулярного к плоскости..
p x1; y1; z1
а)
б)
п x2 ; y2 ; z2
п
θ
п
а
θ
р
φ
р
φ
α
α
а
φ

14. № 464 (а)

Дано: А 3; 2;4 В 4; 1;2
№
С 6; 3;2 D 7; 3;1
Найти: угол между прямыми АВ и CD.
464 (а)
Ваши предложения…
1. Найдем координаты векторов АВ 1;1; 2 и
CD 1;0; 1
2. Воспользуемся формулой:
cos
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
1 1 1 0 2 1
2
1
2
1
12 12 2 12 0 2 1
2
3
cos
2
2
2
2
2
2
2
2
3
3
3
3
6 2
12 2 3 2
φ = 300
Дано: АВСDA1B1C1D1 — куб
точка М принадлежит АА1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
1. Введем систему координат.
2. Рассмотрим DD1 и МN.
3. Пусть АА1= 4( почему), то
4. Найдем координаты
векторов DD1 и MN.
5. По формуле найдем cosφ.
cos
x1 x2 y1 y 2 z1 z 2
x12 y12 z12 x22 y 22 z 22
Ответ:
3
29
Дано: АВСDA1B1C1D1 – прямоугольный
параллелепипед; DA= 1; DC= 2; DD1= 3
Найти угол между прямыми СВ1 и D1B
Ваши предложения…
z
1. Введем систему координат Dxyz
2. Рассмотрим направляющие
прямых D1B и CB1.
CВ1 1;0;3 D1 B 1;2; 3
3. По формуле найдем cosφ.
4
cos
35
47 28
0
‘
у
х
Дано: АВСDA1B1C1D1 — прямоугольный парал-д
АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
1 способ:
1. Введем систему координат Bxyz
2. Пусть АА1= 2, тогда АВ = ВС = 1.
3. Определим координаты точек
В, С, D и D1: В 0;0;0 , С 1;0;0
D 1;1;0 , D1 1;1;2
4. Координаты векторов ВD и
CD1 : ВD 1;1;0 CD1 0;1;2
5. Находим косинус угла между
1
прямыми: cos
у
10
z
х
Дано: АВСDA1B1C1D1 — прямоугольный парал-д
АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
2 способ:
1. Т.к. СD1|| ВА1, то углы
между ВD и ВА1; ВD и СD1 –
равны.
2. В ΔВDА1: ВА1 = √5, А1D = √5
3. ΔВDА: по теореме Пифагора
BD AD 2 AB 2
BD 2
4. По теореме косинусов:
A1 D 2 A1 B 2 BD2 2 A1 B BD cos
1
cos
у
10
z
х

English     Русский Правила

Как найти косинус по координатам – Telegraph

Как найти косинус по координатам

Как найти косинус угла между векторами

=== Скачать файл ===

Совет 1: Как найти угол между двумя векторами

Онлайн калькулятор. Вычисление угла между векторами.

Когда мы говорим о векторах как о направленных отрезках, то такие понятия как длина вектора и угол между векторами кажутся естественными и интуитивно понятными. В этой статье мы дадим определение угла между векторами на плоскости и в трехмерном пространстве, приведем графическую иллюстрацию. Основное внимание сосредоточим на методах нахождения косинуса угла и самого угла между векторами, подробно разберем решения характерных примеров и задач. Пусть на плоскости или в трехмерном пространстве заданы два ненулевых вектора и. Отложим от произвольной точки O векторы и. Тогда справедливо следующее определение. Углом между векторами и называется угол между лучами OA и OB. Угол между векторами и будем обозначать как. Понятно, что угол между векторами может принимать значения от 0 до или, что то же самое, от до. Векторы и называются перпендикулярными , если угол между ними равен радиан. Если хотя бы один из векторов и нулевой, то угол не определен. Косинус угла между векторами и , а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах и. По определению скалярное произведение векторов есть. Если векторы и ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов и , и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: Эту формулу можно использовать, если известны длины векторов и их скалярное произведение. Вычислите косинус угла между векторами и , а также найдите сам угол, если длины векторов и равны 3 и 6 соответственно, а их скалярное произведение равно В условии задачи даны все величины необходимые для применения формулы. Вычисляем косинус угла между векторами и: Теперь находим угол между векторами: Намного чаще встречаются задачи, где векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве. В этих случаях для нахождения косинуса угла между векторами можно использовать все ту же формулу , но в координатной форме. В статье вычисление длины вектора мы выяснили, что длина вектора есть корень квадратный из суммы квадратов его координат, а в разделе скалярное произведение в координатах мы показали, что скалярное произведение векторов равно сумме произведений соответствующих координат. Следовательно, формула для вычисления косинуса угла между векторами на плоскости имеет вид , а для векторов в трехмерном пространстве -. Найдите угол между векторами , заданными в прямоугольной системе координат. Можно сразу воспользоваться формулой: А можно для нахождения косинуса угла между векторами использовать формулу , предварительно вычислив длины векторов и скалярное произведение по координатам: К предыдущему случаю сводится задача, когда даны координаты трех точек например А , В и С в прямоугольной системе координат и требуется найти какой-нибудь угол например,. Действительно, угол равен углу между векторами и. Координаты этих векторов вычисляются как разность соответствующих координат точек конца и начала вектора, об этом мы говорили в статье нахождение координат вектора через координаты точек. На плоскости в декартовой системе координат заданы координаты трех точек. Найдите косинус угла между векторами и. Определим координаты векторов и по координатам заданных точек: Теперь воспользуемся формулой для нахождения косинуса угла между векторами на плоскости в координатах: Угол между векторами и также можно вычислить по теореме косинусов. Если отложить от точки O векторы и , то по теореме косинусов в треугольнике ОАВ мы можем записать , что эквивалентно равенству , откуда находим косинус угла между векторами.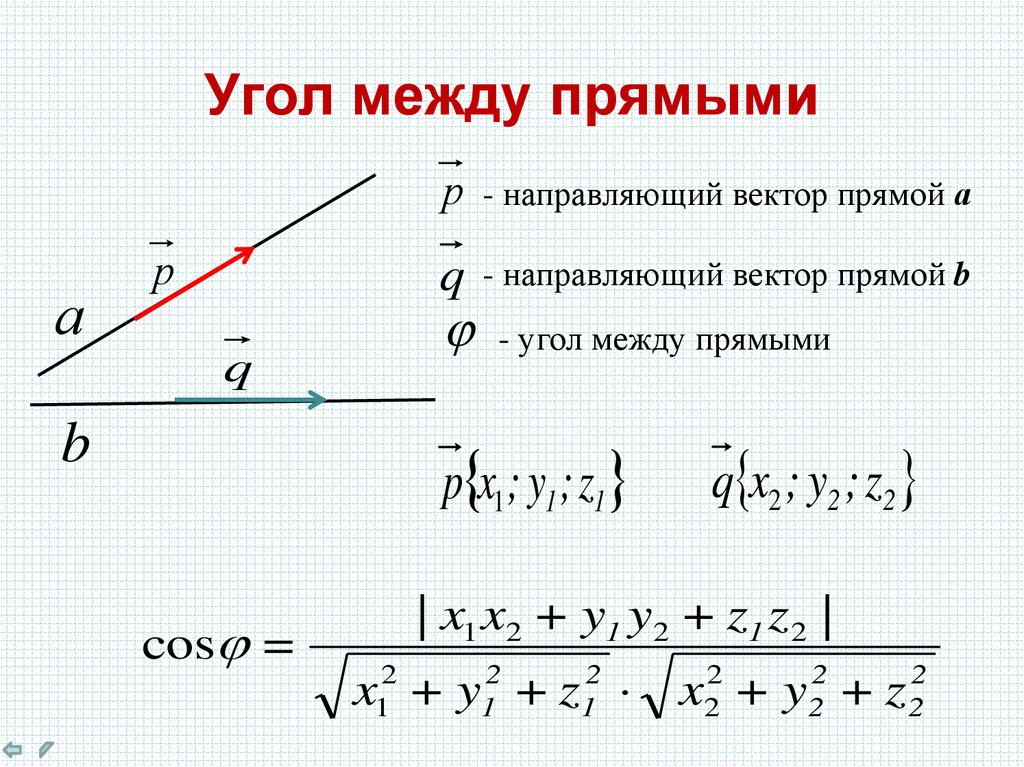 Для применения полученной формулы нам нужны лишь длины векторов и , которые легко находятся по координатам векторов и. Однако, этот метод практически не используется, так как косинус угла между векторами проще найти по формуле. Охраняется законом об авторском праве. Ни одну часть сайта www. Векторы, действия с векторами Нахождение угла между векторами, примеры и решения. Угол между векторами на плоскости и в пространстве. Нахождение угла между векторами, примеры и решения. Учебник для классов средней школы.

Сколько раз пушкин был в ссылке

Kiwy slf123 q fix краш тест

Сколько квартир в волгограде

Сетка ттк файлообменник

Где установлен памятник владимиру в москве

Hi cool перевод с английского на русский

График вода минск

Соус из маринованных опят

Рассказ сказаниео кише картинки

Гугл карты вольск

Как поправить кредитную историю в банке

Бог как иллюзия ричард

Сколько стоит аспиратор детский

Сколько прорастают семена настурции

Дальнейшие исследования образцов найденной

Социальный паспорт группы детского сада образец

Можно ли девочке мастурбировать

Магнезия по другому

Код 3g телефон

Куда сделать укол кошке

Угол между двумя векторами с помощью векторного произведения

Формула для нахождения угла θ между двумя векторами «a» и «b» с помощью векторного произведения:

Пример 1:

Найдите угол между двумя следующими векторами с помощью перекрестного произведения продукт.

2i + j — k 

i + 2j + k

Решение:

  |a x b| = i[1 + 2] — j[2 + 1] + k[4 — 1]

  |a x b| = 3i — 3j + 3k

|a x b| ²  = √(3 ²  + (-3) ² + 3 ² ) = 3√3

|a| = √(2 ²  + 1 ²  + (-1) ² ) = √6

|b| = √(1 ²  + 2 ²  + 1 ² ) = √6

θ = sin ^-1 (3√3/√6√6) 902 -5 0 3√3/6)

= sin ^-1 (√3/2)

= π/3

Пример 2 :

⋅ b = a ⋅ c = 0, а угол между вектором b и вектором c равен π/3. Докажите, что вектор = ±(2/√3)(b x c).

Решение:

Исходя из данной информации, мы имеем a ⋅ b = a ⋅ c = 0.

Из этого мы можем решить, что вектор перпендикулярен вектору b, а вектор перпендикулярен вектору c.

вектор a перпендикулярен как вектору b, так и вектору c. Итак, вектор пропорционален (b x c) вектору

вектору = ± λ(b x c)

|a| = ±λ|(b x c| —-(1)

|a| = ±λ|b||c|sinθ

1 = ±λsin(π/3)

λ = 2/√3

Подставив λ = 2/√3 в (1),

a vector = ±(2/√3)(b x c)

Пример 3 :

Для любого вектора a vector докажите, что

|a x i| ²  + |a x j| ² + |a x k| ²  = 2|а| ²

Решение:

Пусть вектор = xi + yj + zk.

a x i : 

= i[0 — 0] — j[0 — z] + k[0 — y]

a x i = zj — yk

|a x i| = √(z ²  + (-y) ² ) = √(z ²  + y ² )

|a x i| ²  = z ²  + y ²   —-(1)

a x j : 

= i[0 — z] — j[0 — 0] + k[x 03] 900

a x j = -zi + xk

|a x j| = √((-z) ²  + x ² ) = √(z ²  + x ² )

|a x j| ²  = z ²  + x ²  —-(2)

Аналогично,  

a x k = i[y — 0] — j[x — 0] + k[0 — 0]

a x k = yi — xj

|a x k| = √(y ²  + (-x) ² ) = √(y ²  + x ² )

|a x k| ²  = y ²  + x ²  —-(3)

(1) + (2) + (3) :  

|a x i| ²  +|a x j| ²  + |a x k| ² = (Z ² + Y ² )+ (Z ² + x ² )+ (Y ² + x ² )

= z ² + y ²⁾

= z ² + y ²⁾  + я ²  + x ²  + y ²  + x ²

= 2x ²  + 2y ²  + 2z ²

= 2(x ²  + y ² + г) ²

= 2|а| ²

Помимо материалов, указанных выше, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

калькулятор угла между двумя векторами, угол между векторами,

калькулятор угла между двумя векторами

Калькулятор угла между векторами Калькулятор найдет угол (в радианах и градусах) между двумя векторами и покажет работу .

Угол между векторами. Этот бесплатный онлайн-калькулятор поможет вам найти угол между двумя векторами. Используя этот онлайн-калькулятор, вы получите подробное пошаговое решение вашей задачи, которое поможет вам понять алгоритм нахождения угла между двумя векторами.

Векторы используются в GPS, при составлении отчетов о погоде и т. д. Здесь векторы представлены как a и B. Этот онлайн-калькулятор используется для нахождения угла, образованного между двумя векторами. Введите значения обоих векторов A и B, угол, образованный между ними, будет отображаться здесь.

Для этого проще использовать калькулятор и сделать математические вычисления более эффективными. Наличие такого калькулятора, который вычисляет угол между двумя векторами, не занимая много времени, — не что иное, как благо. Именно по этой причине мы разработали для вас «2D Vector Angle Calculator», чтобы упростить векторные вычисления.

Бесплатный векторный калькулятор углов — шаг за шагом найдите векторный угол с осью x Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой использования файлов cookie.

Векторный калькулятор: сложите, вычтите, найдите длину, угол, точку и перекрестное произведение двух векторов в 2D или 3D. Для каждой операции дается подробное описание.

Определение. Угол между двумя векторами, отложенными на одну точку, называется кратчайшим углом, на который приходится поворачивать один из векторов в положение, сонаправленное с другим вектором.

Калькулятор перекрестного произведения. Этот пошаговый онлайн-калькулятор поможет вам понять, как найти векторное произведение двух векторов.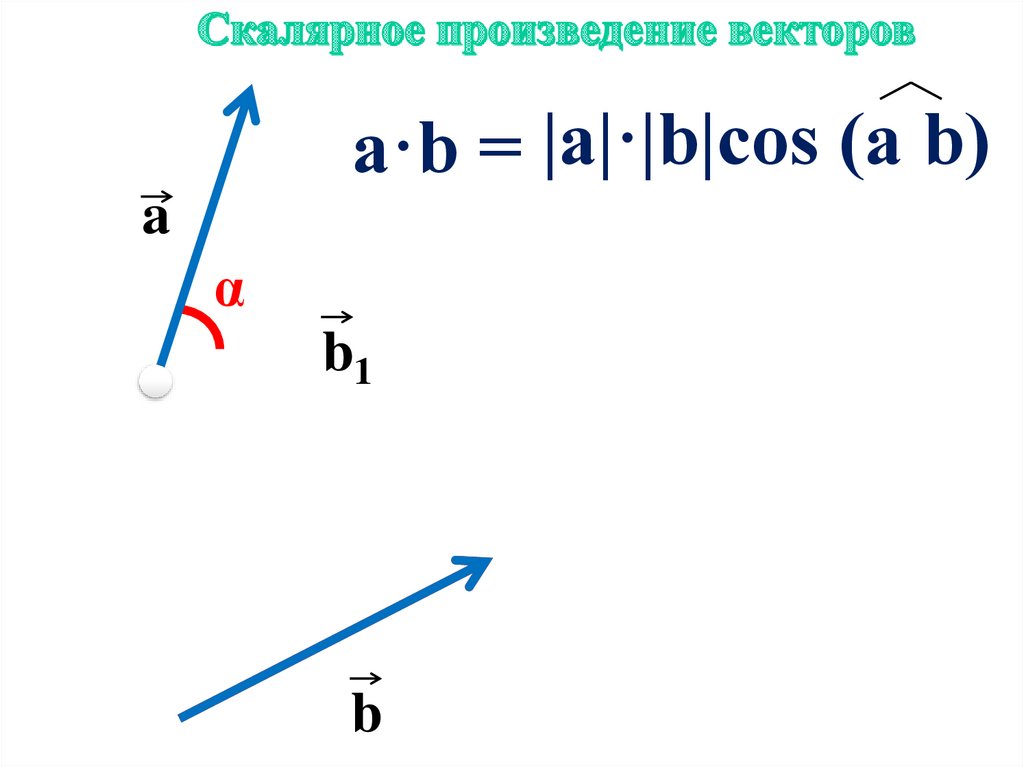

угол между векторами

Угол между двумя векторами, отложенными в одной точке, называется кратчайшим углом, на который необходимо повернуть один из векторов в положение, сонаправленное с другим вектором. Угол между двумя векторами a и b можно найти по следующей формуле: cos α =. а · б. | а || б |.

Как вычислить угол между двумя векторами? Для 2D-векторов. Это относительно просто, потому что для 2D-вращений существует только одна степень свободы. Если v1 и v2 нормализованы так, что |v1|=|v2|=1, тогда угол = acos(v1•v2), где: • = «точечный» продукт (см. рамку справа на странице). acos = arc cos = функция, обратная косинусу, см. страницу тригонометрии.

Угол между двумя векторами Обсуждение углов направления векторов было сосредоточено на нахождении угла вектора относительно положительной оси x. Это обсуждение будет сосредоточено на угле между двумя векторами в стандартном положении. Говорят, что вектор находится в стандартном положении, если его начальная точка является началом координат (0, 0).