Найти поток векторного поля через часть поверхности: Поток векторного поля. Примеры решения задач

Поток векторного поля. Примеры решения задач



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

Поток векторного поля

Задача1
Даны: векторное поле   и плоскость  ,
которая совместно с координатными плоскостями образует пирамиду .
Пусть  – основание пирамиды, принадлежащее плоскости .
Найти поток векторного поля  через поверхность  в направлении внешней нормали.

Решение
Данное общее уравнение плоскости  преобразуем в уравнение плоскости в отрезках .

Из этого уравнения следует, что плоскость отсекает на осях  соответственно отрезки ,  и .

                         
Данная плоскость и координатные плоскости образуют пирамиду  с основанием  .
Вычислим поток векторного поля  через поверхность  в направлении нормали  методом проектирования поверхности  на одну координатную плоскость.
Спроектируем поверхность  на плоскость  в область  .
Поток найдем по формуле ,
где  единичный вектор нормали  к выбранной стороне поверхности .
По условию нормаль  направлена вне пирамиды .
Нормальный вектор плоскости   имеет координаты .
Так как третья координата вектора нормали положительна, то вектор нормали образует с осью  острый угол и .
Тогда .
Элемент площади .
Итак,

Задача 2.


Найти поток векторного поля через поверхности , вырезаемую плоскостью (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).

Задача 3.
Найти поток векторного поля a через часть плоскости , расположенную в первом октанте (нормаль образует острый угол с осью ).

 

Задача 4.
Найти поток векторного поля через замкнутую поверхность (нормаль внешняя).


Задача 5. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя)


 

Перейдем к цилиндрической системе координат



Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk. com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



17.3.Поток векторного поля через поверхность.

В разделе 16.4. Поверхностные интегралы мы рассмотрели задачу о вычислении количества жидкости, протекающей через определённую сторону двусторонней поверхности за единицу времени, и получили, что это количество выражается поверхностным интегралом . Имеется целый ряд физических процессов, которые описываются аналогичными поверхностными интегралами, например, магнитная индукция.

Среди других достоинств математики её мощь заключается, в частности, в способности исследовать процессы в самых разных областях естествознания, абстрагируясь от их физической сущности; приведённые выше примеры показывают естественность введения понятия потока векторного поля через поверхность.

17.3.1. Определение. Пусть — двусторонняя гладкая поверхность, расположенная в области V, в которой задано поле (

M). Фиксируем выбором нормали одну из двух сторон поверхности . Потоком векторного поля (M) через поверхность называется поверхностный интеграл первого рода по от скалярного произведения (M) на единичный вектор нормали к выбранной стороне поверхности: П.

Существуют различные формы записи этого интеграла. Так как , поток может обозначаться П. Иногда произведение обозначают и называют этот вектор вектором элементарной площадки, тогда П. Если связать с проекциями на координатные плоскости:

и использовать координатную запись поля , то скалярное произведение в координатной форме даст П, т.е. поток может быть выражен и через поверхностный интеграл второго рода. Напомню, что в таком интеграле необходимо выбирать знак каждого слагаемого в зависимости от знака соответствующей координаты нормали.

17.3.2. Свойства потока векторного поля. Согласно определению, поток — поверхностный интеграл, поэтому он имеет все свойства поверхностного интеграла. Понятно, что некоторые из этих свойств теряют смысл (интеграл от единичной функции, например), поэтому перечислим основные свойства потока.

1. Линейность. ;

2. Аддитивность. . Здесь и — кусочно-гладкие поверхности, которые могут пересекаться только по границам; нормали на этих поверхностях должны быть согласованы так, чтобы определять одну сторону всей составной поверхности .

3. Поток меняет знак при изменении стороны поверхности (так как в каждой точке вектор меняется на -).

17.3.3. Вычисление потока векторного поля.

В соответствии с определением П,

поток может вычисляться и с помощью поверхностного интеграла первого рода, и с помощью поверхностного интеграла второго рода. В примере 2 раздела 16.4.4.3. Вычисление поверхностного интеграла второго рода было приведено вычисление потока поля через часть плоскости , ограниченную координатными плоскостями, в том и другом представлении. Рассмотрим более сложный пример.

Пример. Найти поток векторного поля через полную внешнюю поверхность тела, ограниченного поверхностями .

Решение. Поверхность состоит из двух частей: — часть поверхности параболоида накрытая шапочкой — частью нижней полусферы ; уровень пересечения этих поверхностей по оси Oz определяется уравнением , откуда ; проекция линии пересечения на плоскость Oxy — окружность радиуса . Выпишем нормали: ; выбираем знак «+», так как на нормаль образует тупой угол с осью

Oz, и коэффициент при должен быть отрицателен (мы находимся в полупространстве ). С учётом того, что на , , . Уравнение в виде поверхности уровня: , , знак «+», так как угол между и осью Oz острый, .

1. Вычисление с помощью поверхностного интеграла первого рода: П=П₁+П₂, П₁, П₂, обе поверхности однозначно проектируются на плоскость Oxy в круг радиуса , поэтому П₁.

П₂

.

П=П₁+П_2.

2. Посмотрим, к каким вычислениям приводит применение поверхностного интеграла второго рода.. Для вычисления придется разбить полную поверхность на части , находящуюся в полупространстве , где , и , находящуюся в полупространстве , где ; (с учётом того, что подынтегральная функция меняет знак при переходе от к ) .

Интеграл равен нулю, так как подынтегральная функция чётна по у, а интегралы по частям поверхности, находящихся в полупространствах , где , и , где , берутся с разными знаками.

Интеграл (в соответствии со знаками на и ) . Поток .

Ответы, как и должно быть, совпали, однако вычисления с помощью криволинейного интеграла первого рода оказались существенно более простыми.

17.3.4. Теорема Остроградского. Пусть — кусочно-гладкая замкнутая поверхность, ограничивающая область V, — гладкое векторное поле. Тогда поток поля через внешнюю сторону равен тройному интегралу от дивергенции поля по V:

.

Приведённую выше формулу обычно называют формулой Остроградского в векторной форме. Если записать её в виде или , то получим формулу Остроградского в координатной форме. Естественно, для потока в левой части формулы могут применяться и другие обозначения.

Доказательство. Достаточно доказать формулу в случае, когда тело V — простое, т.е. проекция V на любую координатную плоскость — простая область D, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках. Если V не является простой областью, мы разобьём её на простые части; тогда сумма тройных интегралов по этим частям, в силу аддитивности, даст интеграл по всей области V ; а при вычислении поверхностных интегралов интегралы по введённым внутренним перегородкам будут браться дважды с противоположными направлениями нормали и взаимно уничтожатся.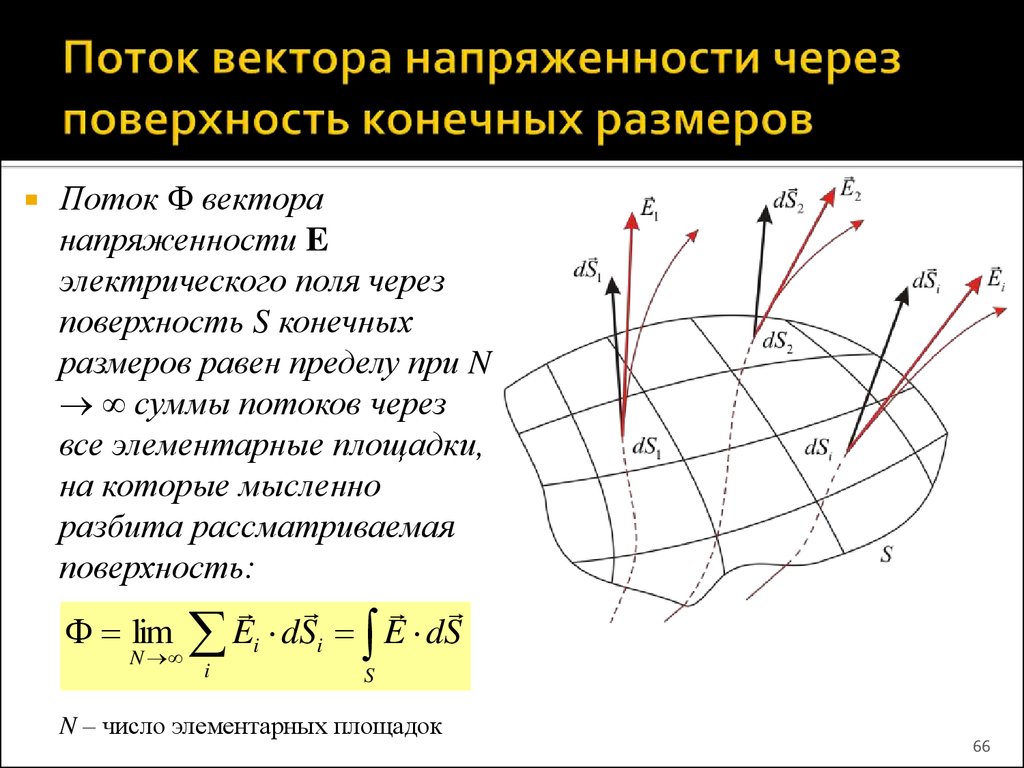 Кроме того, достаточно доказать формулу Остроградского для каждого из слагаемых:

, , , тогда сумма этих формул даст общую формулу. Докажем, например, что . Простую область V, как мы знаем, можно описать следующим образом: . Вычисляем : . Знак последнего слагаемого выбран с учётом того, что на . Если в полной границе области V присутствует цилиндрическая составляющая , то , поэтому окончательно . Совершенно аналогично доказываются формулы для двух других слагаемых. Формула Остроградского доказана.

Применим формулу Остроградского для решения задачи, рассмотренной в предыдущем разделе: найти поток векторного поля через полную внешнюю поверхность тела, ограниченного поверхностями : ,

. Естественно, ответ получился тот же; но этот способ вычисления оказался самым простым.

17.3.5. Инвариантное определение дивергенции. В разделе 17.2.2.1. Дивергенция векторного поля мы определили дивергенцию как выражение в определённой системе координат : . Теорема Остроградского позволяет понять смысл дивергенции поля в точке М как объективного атрибута векторного поля без использования координатной системы. Пусть — замкнутая поверхность, окружающая точку М, V — тело, заключенное внутри , — вектор единичной внешней нормали к . Тогда . По теореме о среднем для тройного интеграла существует точка такая, что . Следовательно, . Отношение значения некоторой физической величины к объёму принято называть средней плотностью этой величины в объёме; если объём стягивается к точке М, предел средней плотности называется локальным значением плотности в точке М. Таким образом, мы можем трактовать как среднюю плотность потока в объёме V. Будем теперь стягивать к точке М, при этом и V стягивается к точке М; , и, вследствие непрерывности , . Поэтому будет равна плотности потока в точке М, и так как плотность потока определяется независимо от выбора какой-либо системы координат, то дивергенция векторного поля инвариантна относительно выбора координатной системы.

Используем теперь гидродинамическую интерпретацию поля для выяснения физического смысла дивергенции. Пусть (M) — стационарное поле скоростей несжимаемой жидкости. В каком случае поток через замкнутую поверхность может быть отличен от нуля, т.е. в каком случае из V вытекает больше жидкости, чем втекает (при П>0) или наоборот (при П<0)? Ясно, что П>0 может быть только в том случае, если в V появляется дополнительная жидкость, т.е. в V имеются источники поля. П<0 может быть только в том случае, если в V исчезает часть жидкости, т.е. в V имеются стоки поля. Поэтому как плотность потока в точке М определяет силу источника (при >0) или стока (при <0) в точке М.

По аналогии с полем скоростей жидкости считают, что дивергенция определяет силу источников и стоков поля в любом поле (M).

57

Введение в поверхностный интеграл векторного поля

Линейный интеграл векторного поля $\dlvf$ можно интерпретировать как работу действие силового поля $\dlvf$ на частицу, движущуюся по траектории. Поверхностный интеграл векторного поля $\dlvf$ на самом деле имеет более простой объяснение. Если векторное поле $\dlvf$ представляет течение жидкости, то поверхностный интеграл от $\dlvf$ будет представлять собой сумму жидкости, протекающей через поверхность (в единицу времени).

Количество жидкости, протекающей через поверхность в единицу времени, равно также называется потоком жидкости через поверхность. Для этого По этой причине мы часто называем поверхностный интеграл векторного поля a интеграл потока .

Если вода течет перпендикулярно поверхности, много воды поток через поверхность, и поток будет большим. С другой рука, если вода течет параллельно поверхности, вода не будет течь через поверхность, и поток будет равен нулю. Чтобы рассчитать общее количество воды, протекающей через поверхность, мы хотим сложить компонента вектора $\dlvf$, перпендикулярная поверхность.

Пусть $\vc{n}$ — единичный вектор нормали к поверхности. Выбор ориентации вектора нормали поверхности и определяет знак потока жидкости. Поток жидкости через поверхность определяется компонентой $\dlvf$, т.е. в направлении $\vc{n}$, т.е. по $\dlvf \cdot \vc{n}$. Обратите внимание, что $\dlvf \cdot \vc{n}$ будет равно нулю, если $\dlvf$ и $\vc{n}$ перпендикулярно, положительно, если $\dlvf$ и $\vc{n}$ указывают на одно и то же направление и отрицательное, если $\dlvf$ и $\vc{n}$ указывают в противоположные направления.

Давайте проиллюстрируем это с помощью функции \начать{выравнивать*} \dlsp(\spfv,\spsv) = (\spfv\cos\spsv,\spfv\sin\spsv,\spsv). \конец{выравнивание*} который параметризует геликоид для $(\spfv,\spsv) \in \dlr = [0,1] \times [0, 2\pi]$. Как показано на следующем рисунке, мы выбрали вектор нормали к восходящей точке. (Мы вместо этого можно было бы использовать нормальную точку вниз. Если бы мы это сделали, наш расчет потока жидкости имеет противоположный знак.)

Загрузка апплета

Загрузка апплета

Параметризованный геликоид с вектором нормали. Функция $\dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv)$ параметризует геликоид, когда $(\spfv,\spsv) \in \dlr$ , где $\dlr$ — прямоугольник $[0,1] \times [0, 2\pi]$, показанный на первой панели. Голубой вектор в синей точке $\dlsp(\spfv,\spsv)$ – это направленный вверх единичный вектор нормали в этой точке. Вы можете перетащить синюю точку в $\dlr$ или на геликоид, чтобы указать как $\spfv$, так и $\spsv$.

Дополнительная информация об апплете.

Для некоторого потока жидкости $\dlvf$, если мы проинтегрируем $\dlvf \cdot \vc{n}$, определим полный поток жидкости через геликоид, считая поток в направлении $\vc{n}$ положительным, а поток в противоположное направление как отрицательное.

Мы представляем векторное поле потока жидкости $\dlvf$ пурпурными стрелками в следующем апплете.

Загрузка апплета

Загрузка апплета

Поток жидкости через ориентированный геликоид. Функция $\dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv)$ параметризует геликоид, когда $(\spfv,\spsv) \in \dlr$ , где $\dlr$ — прямоугольник $[0,1] \times [0, 2\pi]$, показанный на первой панели. Голубой вектор в синей точке $\dlsp(\spfv,\spsv)$ – это направленный вверх единичный вектор нормали в этой точке. Пурпурное векторное поле представляет поток жидкости, проходящий через поверхность. В этом примере векторным полем является константа $\dlvf=(0,1,1)$. Вы можете перетащить синюю точку в $\dlr$ или на геликоид, чтобы указать как $\spfv$, так и $\spsv$.

Дополнительная информация об апплете.

Похоже, что жидкость обычно течет в одном направлении как $\vc{n}$ (по большей части $\dlvf$ и $\vc{n}$ ближе к указывая в том же направлении, чем указывая в противоположном направлении направление). Однако обратите внимание, например, что при $\spfv=0$ и $\spsv=2\pi$ (или при $\spfv=0$ и $\spsv=0$) жидкость течет в противоположном направлении. направление $\vc{n}$ (по крайней мере поток ближе к противоположному направлении, чем в том же направлении). В этих точках жидкость пересечение поверхности в противоположном направлении, чем это самое большее точки на поверхности.

Рисунок ниже демонстрирует это более наглядно. Здесь вы можете увидеть вектор жидкости $\dlvf$ (пурпурный) в той же точке, что и вектор нормали (голубой). Значение потока $\dlvf \cdot \vc{n}$ через поверхность в синей точке показано в правом нижнем углу. Обратите внимание, что $\dlvf \cdot \vc{n}$ обычно положительный, но отрицательный в нескольких точках, например упомянутое выше. Когда $\dlvf \cdot \vc{n}=0$, что связь между вектором жидкости $\dlvf$ и поверхностью?

Загрузка апплета

Загрузка апплета

Течение жидкости через точку ориентированного геликоида. Функция $\dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv)$ параметризует геликоид, когда $(\spfv,\spsv) \in \dlr$ , где $\dlr$ — прямоугольник $[0,1] \times [0, 2\pi]$, показанный на первой панели. Голубой вектор в синей точке $\dlsp(\spfv,\spsv)$ – это направленный вверх единичный вектор нормали в этой точке. Пурпурный вектор в этой точке представляет поток жидкости, проходящий через поверхность. В этом случае поток жидкости является постоянным $\dlvf=(0,1,1)$ в каждой точке. Несмотря на то, что поток жидкости постоянный, поток через поверхность изменяется, так как он является составляющей потока, нормального к поверхности. В месте расположения синей точки в правом нижнем углу показан поток через поверхность $\dlvf \cdot \vc{n}$. Вы можете перетащить синюю точку в $\dlr$ или на геликоид, чтобы указать как $\spfv$, так и $\spsv$.

Дополнительная информация об апплете.

Суммарный поток жидкости через поверхность $\dls$, обозначаемый $\dsint$ — интеграл векторного поля $\dlvf$ по $\dls$. Интеграл векторного поля $\dlvf$ определяется как интеграл скалярной функции $\dlvf \cdot \vc{n}$ над $\dls$ \начать{выравнивать*} \text{Flux} &= \dsint = \ssint{\dls}{\dlvf \cdot \vc{n}}. \конец{выравнивание*} Формула поверхностного интеграла скалярной функции по поверхности $\dls$, параметризованной $\dlsp$, имеет вид \начать{выравнивать*} \ssint{\dls}{f} = \iint_\dlr f(\dlsp(\spfv,\spsv))\left\| \pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv) \право\| д\спфв\,д\спсв. \конец{выравнивание*}

Подставляя $f = \dlvf \cdot \vc{n}$, общий поток жидкости равен \начать{выравнивать*} \dsint= \iint_\dlr (\dlvf \cdot \vc{n}) \left\| \pdiff{\dlsp}{\spfv} \times \pdiff{\dlsp}{\spsv} \право\| д\спфв\,д\спсв. \end{align*}

Наконец, формула для единичного вектора нормали к поверхности: \начать{выравнивать*} \vc{n} = \frac{\displaystyle \pdiff{\dlsp}{\spfv} \times \pdiff{\dlsp}{\spsv}}{\displaystyle \left\| \pdiff{\dlsp}{\spfv} \times \pdiff{\dlsp}{\spsv} \право\|}. \конец{выравнивание*} Если мы подставим это выражение для $\vc{n}$, $\left\| \pdiff{\dlsp}{\spfv} \times \pdiff{\dlsp}{\spsv} \right\|$ множители сокращаются, и мы получаем окончательное выражение для поверхностного интеграла: \начать{выравнивать*} \dsint= \iint_\dlr \dlvf(\dlsp(\spfv,\spsv)) \cdot \left( \pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv) \верно) д\спфв\,д\спсв. \label{eq:surfvec} \end{выравнивание*} 9b \dlvf(\dllp(t)) \cdot \dllp'(t) dt. \конец{выравнивание*} Для линейных интегралов мы интегрируем компонент векторного поля в направление касательной, заданное $\dllp'(t)$. Для поверхностных интегралов интегрируем компоненту векторного поля в нормальном направлении определяется как $\pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv)$.

Вы можете прочитать некоторые Примеры вычисления поверхностных интегралов векторных полей.

многомерное исчисление — Найти поток векторного поля 92 $$

$$ \Rightarrow \ \ 2 z \ \frac{\partial g}{\partial x} \ = \ — 2 x \ \ , \ \ 2 z \ \frac{\partial g}{\partial y} \ = \ — 2 y $$

[с использованием неявного дифференцирования]

$$ \Rightarrow \ \ \frac{\partial g}{\partial x} \ = \ — \frac{x}{z} \ \ , \ \ \frac{\partial g}{\partial y} \ = \ — \frac{y}{z} $$

$$ \Rightarrow \ \ \iint_S \\mathbf{F} \cdot \mathbf {\ hat {n}} \ \ dS \ \ = \ \ \ iint_D \ -F_x \ \ frac {\ partial g} {\ partial x} \ -F_y \ \ frac {\ partial g} {\ partial y} \ +\F_z\\dA$$92 $$

[первый интеграл снова равен нулю, так как нечетные степени косинуса интегрируются за один период]

$$ = \ 2 \pi \ ( \ 8 \ — \ 4 \ ) \ = \ 8 \pi \ \ . $$

Это и есть «наружный» поток через полусферическую поверхность. В качестве проверки можно применить теорему о дивергенции над объемом полушария:

$$ \\nabla \cdot \mathbf{F} \ = \ 2x \ + \ 2y \ + 2z $$

$$ \Rightarrow \ \ \iiint_V \ \nabla \cdot \mathbf{F} \ \ dV \ \ = \ \ \iiint_V \ ( \ 2x \ + \ 2y \ + 2z \ ) \ \ dV $$ 92 \ \ dA \ \ , $$

дает нам такое же интегрирование по кругу радиуса 1 на плоскости $\xy-$, которая является проекцией конической поверхности, и, следовательно, тот же результат для «вверх» поток через коническую поверхность.

Проверив по теореме о дивергенции, проинтегрируем в цилиндрических координатах по объему конуса до $ \ z \ = \ 2 \ $ и получим

$$ \iiint_V \\nabla \cdot \mathbf{F} \ \ dV \ \ = \ \ \iiint_V \ ( \ 2x \ + \ 2y \ + 2z \ ) \ \ dV $$ 92 \ = \ 4 \пи \ \ . $$

При таком количестве «восходящего» потока через вершину конического объема и чистого «восходящего» потока $ \ 2 \pi \ $ через этот объем «восходящий» поток через конусную «стенку» должен быть $ \ 2 \pi \ $ , как мы нашли из интегрирования потоков.