Производная онлайн с подробным решением
Калькулятор решает производные c описанием действий ПОДРОБНО бесплатно!
Это он-лайн сервис в один шаг:
- Ввести функцию, для которой надо найти производную
Перейти: Онлайн сервис «Производная функции» →
Это он-лайн сервис в один шаг:
- Ввести функцию, для которой надо найти частные производные
Перейти: Онлайн сервис «Частная производная функции» →
Это он-лайн сервис в три шага:
- Ввести функцию x = x(t)
- Ввести функцию y = y(t)
Перейти: Онлайн сервис «Производной параметрической функции» →
Таблица производных
Вы также можете воспользоваться таблицей производных, чтобы самостоятельно вычислить любую производную, перейти:
Введите функцию, заданную в неявном виде, вы получите соответствующую производную
Производная сложной функции
Производную сложной функции онлайн вы сможете вычислить с помощью калькулятора производных здесь
Это он-лайн сервис в два шага:
- Ввести функцию, для которой надо найти производную
- Ввести найденную первую производную в форму
Перейти: Онлайн сервис «Вторая производная функции» →
Это он-лайн сервис в три шага:- Ввести функцию, для которой надо найти производную
- Ввести найденную первую производную в форму
- Ввести найденную вторую производную функции в форму
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Примеры подробного решения >>
Введите выражение функции
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Определение производной
Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ y’. Отметим, что y’ = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x).
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\( k = f'(a) \)
Поскольку \( k = tg(a) \), то верно равенство \( f'(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \( y = f(x) \) имеет
производную в конкретной точке \( x \):
Это означает, что около точки х выполняется приближенное равенство \( \frac{\Delta y}{\Delta x} \approx f'(x) \), т.е. \( \Delta y \approx f'(x) \cdot \Delta x \). Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. Например, для функции \( y = x^2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \( x \), найти \( f(x) \)
2. Дать аргументу \( x \) приращение \( \Delta x \), перейти в новую точку \( x+ \Delta x \), найти \( f(x+ \Delta x) \)
3. Найти приращение функции: \( \Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \( \frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция \( y=\sqrt[3]{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
$$ f’_x(g(x)) = f’_g \cdot g’_x $$
Таблица производных некоторых функций
$$ \left( \frac{1}{x} \right) ‘ = -\frac{1}{x^2} $$ $$ ( \sqrt{x} ) ‘ = \frac{1}{2\sqrt{x}} $$ $$ \left( x^a \right) ‘ = a x^{a-1} $$ $$ \left( a^x \right) ‘ = a^x \cdot \ln a $$ $$ \left( e^x \right) ‘ = e^x $$ $$ ( \ln x )’ = \frac{1}{x} $$ $$ ( \log_a x )’ = \frac{1}{x\ln a} $$ $$ ( \sin x )’ = \cos x $$ $$ ( \cos x )’ = -\sin x $$ $$ ( \text{tg} x )’ = \frac{1}{\cos^2 x} $$ $$ ( \text{ctg} x )’ = -\frac{1}{\sin^2 x} $$ $$ ( \arcsin x )’ = \frac{1}{\sqrt{1-x^2}} $$ $$ ( \arccos x )’ = \frac{-1}{\sqrt{1-x^2}} $$ $$ ( \text{arctg} x )’ = \frac{1}{1+x^2} $$ $$ ( \text{arcctg} x )’ = \frac{-1}{1+x^2} $$Чтобы вычислить N-ю производную высших порядков (степеней) от какой-либо функции — теперь не надо заниматься рекурсивным копипастом (для 100-й производной пришлось бы 100 раз нажать ctrl+c и ctrl+v) — достаточно указать порядок производной в отдельном поле:
Приведу примеры производной высших порядков от функции f(x)=x*exp(-x) в таблице (требовалось найти для ряда Тейлора):
| Словесное название | Числовое название | Результат |
|---|---|---|
| третья производная | производная третьего порядка |
(3 - x)*exp(-x) |
| четвёртая производная | производная четвёртого порядка |
(-4 + x)*exp(-x) |
| пятая производная | производная пятого порядка |
(5 - x)*exp(-x) |
| шестая производная | шестого порядка |
(-6 + x)*exp(-x) |
| седьмая производная | седьмого порядка |
(7 - x)*exp(-x) |
| восьмая | производная восьмого порядка |
(-8 + x)*exp(-x) |
| девятая производная | девятого порядка |
(9 - x)*exp(-x) |
| десятая производная | 10го порядка (десятого) |
(-10 + x)*exp(-x) |
| двенадцатая производная | двенадцатого порядка |
(-12 + x)*exp(-x) |
| двадцатая производная | двадцатого порядка |
(-20 + x)*exp(-x) |
| пятидесятая производная | 50го порядка |
(-50 + x)*exp(-x) |
| девяностая производная | 90го порядка |
(-90 + x)*exp(-x) |
| сотая производная | сотого (100го) порядка |
(-100 + x)*exp(-x) |
| тысяча производная | 1000го порядка |
(-1000 + x)*exp(-x) |
| миллион производная | 1 млн производная |
(-1000000 + x)*exp(-x) |
Оператор |
Описание |
Простейшие математические операции |
|
+ — * / () |
Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 |
Десятичные дроби записываются через точку:
|
Элементарные функции |
|
xn |
Возведение в степень: x^n, например, для ввода x2 используется x^2 |
√x |
Квадратный корень: \sqrt(x) или x^(1/2) |
3√x |
Кубический корень: x^(1/3) |
n√x |
Корень n-той степени из x: x^(1/n) |
ln(x) |
Натуральный логарифм (логарифм c основанием e): log(x) |
logax |
Логарифм от x по основанию a: log(x)/log(a) |
lg(x) |
Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex |
Экспоненциальная функция: e^x |
Тригонометрические функции |
|
sin(x) |
Синус от x: sin(x) |
cos(x) |
Косинус от x: cos(x) |
tg(x) |
Тангенс от x: tan(x) |
ctg(x) |
Котангенс от x: 1/tan(x) |
arcsin(x) |
Арксинус от x: arcsin(x) |
arccos(x) |
Арккосинус от x: arccos(x) |
arctan(x) |
Арктангенс от x: arctan(x) |
arcctg(x) |
Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы |
|
e |
Число Эйлера e: \e |
π |
Число π: \pi |
Найти производную: алгоритм и примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
.
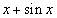Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
.
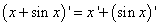Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
.
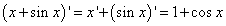Пример 2. Найти производную функции
.
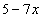Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
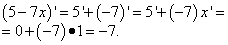
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Правило 1. Если функции
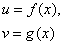
дифференцируемы в некоторой точке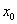 
, то в той же точке дифференцируемы и функции
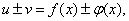
причём
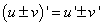
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
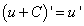
Правило 2. Если функции
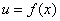
и
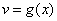
дифференцируемы в некоторой точке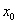 
, то в то же точке дифференцируемо и их произведение
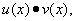
причём
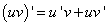
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
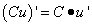
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
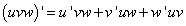
Правило 3. Если функции
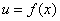
и
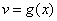
дифференцируемы в некоторой точке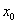 
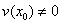, то в этой точке дифференцируемо и их частное u/v , причём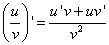
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций».
Здесь же (далее) — более простые примеры на производную произведения и частного, на которых Вы увереннее освоите алгоритмы вычислений.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v, в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде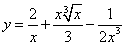 
, то
следуйте на занятие «Производная суммы дробей со степенями и корнями».
Если же перед Вами задача вроде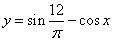 
,
то Вам на занятие «Производные простых тригонометрических функций».
Пример 3. Найти производную функции
.
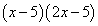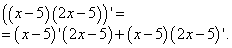
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
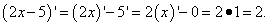
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
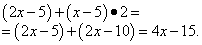
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
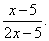
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
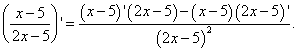
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
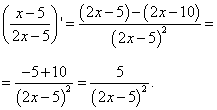
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, 
,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями».
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде ,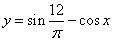
то Вам на урок «Производные простых тригонометрических функций».
Пример 5. Найти производную функции
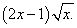
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
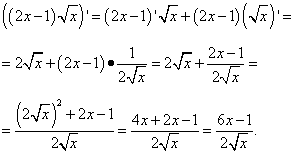
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
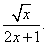
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
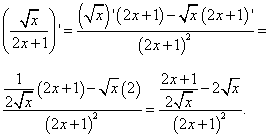
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на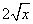 
:
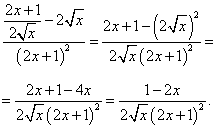
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Ещё больше домашних заданий на нахождение производных
Пример 12. Найти производную функции
.
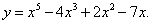Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим
.
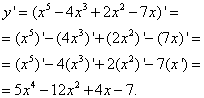Пример 13. Найти производную функции
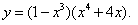
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
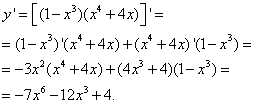
Пример 14. Найти производную функции
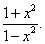
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
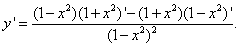
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
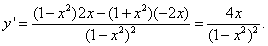
Пример 15.Найти производную функции
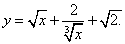
Шаг1. Применяем правило дифференцирования суммы:
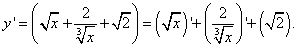
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):
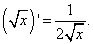
Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
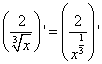
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя — это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
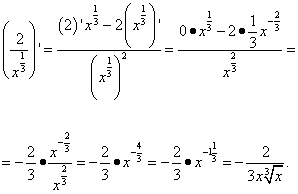
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
,
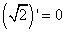а производная, требуемая в условии задачи:
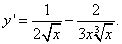
Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях «Производная произведения и частного функций» и «Производная суммы дробей со степенями и корнями».
Также настоятельно рекомендуем изучить производную сложной функции.
Поделиться с друзьями
Весь блок «Производная»
Введите функцию, для которой необходимо найти частные производные
Найдем частные производные функции f. Помогает вычислить полный. дифференциал функции
Правила ввода функций
В функции f можно делать следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- absolute(x)
- Функция — абсолютное значение x (модуль x или |x|)
- arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Функция — арккосинус гиперболический от x
- arcsin(x)
- Функция — арксинус от x
- arcsinh(x)
- Функция — арксинус гиперболический от x
- arctan(x)
- Функция — арктангенс от x
- arctanh(x)
- Функция — арктангенс гиперболический от x
- e
- Функция — e это то, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (тоже самое, что и e^x)
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- log(x) or ln(x)
- Функция — Натуральный логарифм от x (Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
- pi
- Число — «Пи», которое примерно равно 3.14
- sign(x)
- Функция — Знак x
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — Корень из от x
- x^2
- Функция — Квадрат x
- tan(x)
- Функция — Тангенс от x
- tanh(x)
- Функция — Тангенс гиперболический от x
| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |