Найти производные dy dx данных функций: Mathway | Популярные задачи

• х ² + у = 2
• ху + грех (ху) = 0

В первом случае, хотя ‘y’ не является одной из сторон уравнения, мы все же можем решить его, записав его как y = 2 — x ² , и это явная функция. Но во втором случае мы не можем легко решить уравнение для «y», и этот тип функции называется неявной функцией, и на этой странице мы увидим, как найти производную неявной функции, используя процесс неявного дифференцирования.

1.	Что такое неявное дифференцирование?
2.	Неявная производная
3.	Неявное дифференцирование и цепное правило
4.	Как выполнить неявное дифференцирование?
5.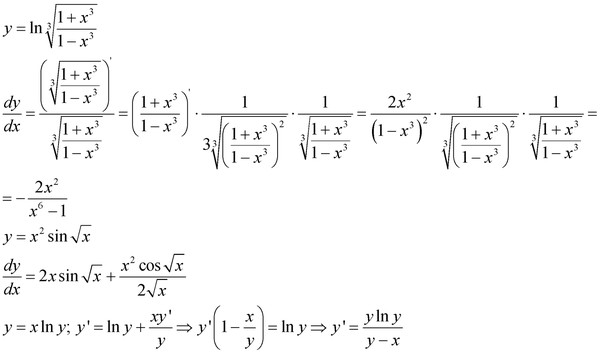	Неявное дифференцирование обратных тригонометрических функций
6.	Часто задаваемые вопросы о неявном дифференцировании

Что такое неявное дифференцирование?

Неявное дифференцирование — это процесс дифференцирования неявной функции. Неявная функция — это функция, которая может быть выражена как f(x, y) = 0, т. е. ее нельзя легко решить относительно ‘y’ (или) ее нельзя легко представить в виде y = f(x ). Рассмотрим пример нахождения dy/dx по заданной функции xy = 5. Найдем dy/dx двумя способами: (i) решая относительно y (ii) не решая относительно y.

• Метод — 1:
  ху = 5
  у = 5/х
  у = 5x ^-1
  Дифференцируя обе части по x:
  dy/dx = 5(-1x ^-2 ) = -5/x ²
• Метод — 2:
  ху = 5
  Дифференцируя обе части по x:
  д/дх (ху) = д/дх(5)
  Используя правило произведения слева,
  х d/dx(y) + y d/dx(x) = d/dx(5)
  х (dy/dx) + у (1) = 0
  х(dy/dx) = -y
  dy/dx = -y/x
  Из xy = 5 мы можем написать y = 5/x.
  dy/dx = -(5/x)/x = -5/x ²

В методе -1 мы преобразовали неявную функцию в явную и нашли производную, используя степенное правило. Но в методе 2 мы дифференцировали обе части по x, рассматривая y как функцию от x, и этот тип дифференцирования называется неявным дифференцированием. Но для некоторых функций, таких как xy + sin (xy) = 0, запись в виде явной функции (Метод — 1) невозможна. В таких случаях только неявное дифференцирование (метод — 2) является способом нахождения производной.

Неявная производная

Производная, найденная с помощью процесса неявного дифференцирования, называется неявной производной. Например, производная dy/dx, найденная в методе 2 (в приведенном выше примере), сначала была dy/dx = -y/x и называется неявной производной. Это потому, что мы продифференцировали неявную функцию xy = 5 напрямую, не решая ее для y. Неявная производная обычно выражается как по x, так и по y.

Неявное дифференцирование и цепное правило

Цепное правило дифференцирования играет важную роль при нахождении производной неявной функции. Цепное правило гласит: d/dx (f(g(x)) = (f’ (g(x)) · g'(x). Всякий раз, когда мы сталкиваемся с производной членов y по x, цепное правило приходит в сцену и из-за цепного правила мы умножаем фактическую производную (по формулам производных) на dy/dx. Вот пример.

Вот еще примеры, чтобы понять цепное правило в неявном дифференцировании.

• d/dx (y ² ) = 2y dy/dx
• d/dx (sin y) = cos y dy/dx
• d/dx (ln y) = 1/y · dy/dx
• d/dx (tan ^-1 y) = 1/(1 + y ² ) · dy/dx

Другими словами, везде, где y дифференцируется, также пишите dy/dx. Предлагается повторять эти примеры снова и снова, так как они очень полезны при неявном дифференцировании.

Как выполнить неявное дифференцирование?

В процессе неявного дифференцирования мы не можем начать непосредственно с dy/dx, поскольку неявная функция не имеет формы y = f(x), вместо этого она имеет форму f(x, y) = 0. Примечание. что мы должны знать производные правила, такие как правило мощности, правило произведения, правило частного, правило цепи и т. д., прежде чем изучать процесс неявного дифференцирования. Вот блок-схема шагов для выполнения неявного дифференцирования.

Теперь эти шаги объясняются на примере, где мы собираемся найти неявную производную dy/dx, если функция y + sin y = sin x.

Формула неявного дифференцирования

Мы рассмотрели шаги для выполнения неявного дифференцирования. Сталкивались ли мы с какой-либо конкретной формулой на этом пути? Нет!! Не существует конкретной формулы для неявного дифференцирования, вместо этого мы выполняем шаги, описанные в блок-схеме выше, чтобы найти неявную производную.

Неявное дифференцирование обратных тригонометрических функций

Процесс неявного дифференцирования полезен при нахождении производных обратных триггерных функций. Найдем производную от y = tan ^-1 x с использованием неявного дифференцирования. Из определения arctan y = tan ^-1 x ⇒ tan y = x. Дифференцируя обе части этого уравнения по x,

сек ² y × dy/dx = 1 (поскольку производная тангенса х равна ² x)

dy/dx = 1/сек ² y

dy/dx = 1 / (1 + tan ² y) (по одному из тригонометрических тождеств)

dy/dx = 1 / (1 + x ² ) (поскольку tan y = x)

Таким образом, процесс неявного дифференцирования можно использовать для нахождения производных любой обратной функции.

Важные замечания по неявному дифференцированию:

• Неявное дифференцирование — это процесс нахождения dy/dx, когда функция имеет форму f(x, y) = 0.
• Чтобы найти неявную производную dy/dx, просто продифференцируйте обе стороны и найдите dy/dx. Но в этом процессе пишите dy/dx везде, где мы дифференцируем y.
• Все производные формулы и приемы следует использовать и в процессе неявного дифференцирования.

☛ Связанные темы:

• Калькулятор производных
• Расчетный калькулятор
• Калькулятор второй производной
• Дифференциация

Часто задаваемые вопросы о неявном дифференцировании

Что такое определение неявного дифференцирования в исчислении?

Неявное дифференцирование — это процесс дифференцирования неявной функции, имеющей вид f(x, y) = 0, и нахождения dy/dx. Чтобы найти неявную производную,

• Продифференцировать обе части f(x, y) = 0 по x
• Применение обычных формул производных для дифференцирования членов x
• Применение обычных формул производной для дифференцирования членов по оси y с умножением производной на dy/dx
• Решите полученное уравнение для dy/dx (выделив dy/dx).

Как найти неявную производную?

Чтобы найти неявную производную уравнения, например, скажем, x ² + sin(y) = 0:

• Возьмем производную по x с обеих сторон.
  Тогда мы получаем d/dx(x ² ) + d/dx (sin y) = 0,
.
• Умножать на dy/dx везде, где мы дифференцируем что-либо с помощью y.
  2x + cos y dy/dx = 0,
• Решите это для dy/dx.
  cos y dy/dx = -2x
  dy/dx = -2x/cos y

Как выполнить неявное дифференцирование с помощью триггерных функций?

Когда мы выполняем неявное дифференцирование тригонометрических функций, просто применяем нормальные тригонометрические производные, такие как d/dx(sin x) = cos x, d/dx(cos x) = — sin x и т.  д., а затем применяем цепное правило . Это означает, что мы должны умножить реальную производную на производную внутренней функции. Например, d/dx (sin y ² ) = cos y ² d/dx (y ² ) = 2y cos y ² dy/dx.

Что такое неявные правила дифференциации?

При нахождении неявной производной мы просто дифференцируем уравнение относительно x и y с обеих сторон относительно x, используем dy/dx также всякий раз, когда мы дифференцируем что-то с y, и решаем полученное уравнение относительно dy/dx.

Что такое неявное значение дифференциации?

Смысл неявного дифференцирования, как следует из его названия, заключается в процессе дифференцирования неявной функции f(x, y) = 0 и нахождения производной dy/dx. Чтобы узнать, как сделать неявное дифференцирование, нажмите здесь.

Как найти вторую неявную производную?

Если задана неявная функция f(x, y) = 0, используйте процесс неявного дифференцирования, чтобы найти первую производную dy/dx (или) y’.