Найти ранг матрицы методом элементарных преобразований: Элементарные преобразования. Ранг матрицы. Решение однородных систем уравнений.

15. Вычисление ранга матрицы методом элементарных преобразований.

II. Метод элементарных преобразований

Элементарными преобразованиями матрицы называют следующие:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

4. Вычёркивание строки (столбца), все элементы которой равны нулю.

З а м е ч а н и е . 1) Элементарные преобразования не меняют ранга матрицы; 2) матрицы, полученные одна из другой путём элементарных преобразований, называются эквивалентными (обозначаются A ~В).

Чтобы вычислить ранг матрицы А, путём элементарных преобразований сводим её к ступенчатому виду (в частности к треугольному), выделяя наибольший минор, отличный от нуля.

A~

rangA = rangB= k

Пример 2.  Найти ранг матрицы

Решение. 1) переставим строки матрицы: 

2) первую строку умножим на 2 и сложим со второй:  ,

3)  первую строку умножим на 3 и сложим с третьей, одновременно вторую строку   прибавим к четвёртой:

,

4) умножим вторую строку на   ,  третью на   , пятую на   ,четвёртую вычеркнем :

,

5) прибавим вторую строку к третьей и четвёртой:

~  ,

Ранг последней матрицы, а значит и исходной, равен двум: rangA = 2.

Пример 3. Найти ранг матрицы

rang A=2

Над матрицей А были проведены следующие преобразования:

а) Первая строка матрицы А умножается на (- 2) и прибавляется ко второй.

б ) Первая строка матрицы А умножается на (- 1) и прибавляется к последней.

в) Вторая строка матрицы А умножается на (- 2) и прибавляется к третьей.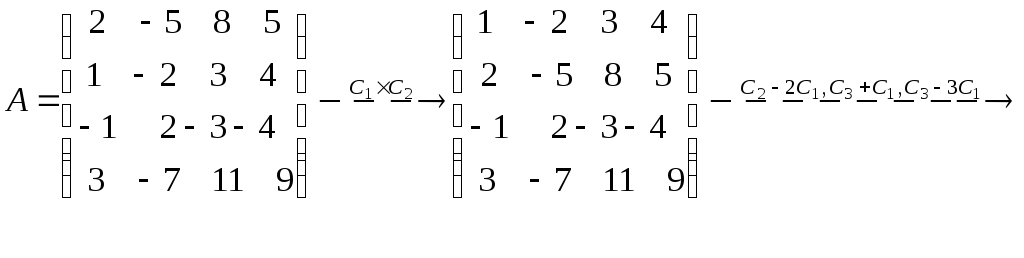

г) Нулевая строка вычёркивается.

Оставшаяся матрица содержит миноры второго порядка отличные от нуля. Строки такой матрицы называются линейно независимыми, их число равно рангу матрицы

16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы   и столбца правых частей 

называется расширенной матрицей системы линейных уравнений.

Т

Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

При выполнении этого условия, система имеет единственное решение, если число неизвестных   совпадает с общим значением ранга

  , и бесконечное множество решений, если   меньше этого значения.

Доказательство необходимости. Пусть существует решение   системы, тогда

т.е. столбец   линейно выражается через столбцы  . Но тогда

Следовательно  .

Доказательство достаточности проводится в следующем пункте. ♦

§

Обозначение   для ранга матрицы   соответствует по смыслу этому же обозначению в методе Гаусса: после приведения к трапециевидному (или треугольному) виду в системе л.у. должно остаться ровно   линейно независимых уравнений, явно содержащих неизвестные. Это утверждение вытекает из способа вычисления ранга матрицы по методу элементарных преобразований

.

П

Пример. Исследовать совместность системы уравнений

в зависимости от значения параметра  .

Решение.  В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы  . Если он отличен от нуля — система совместна.

. По теореме Крамера при   и при   решение системы единственно:

Осталось исследовать критические случаи:   и  : определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже 

числовых матриц (а не зависящих от параметра, как исходная!). При   имеем

и система совместна. Она эквивалентна единственному уравнению

которое имеет бесконечно много решений.

При  :

и система несовместна.

Ответ. Система несовместна при  ; она имеет бесконечное множество решений при   и единственное решение при  .

!

Что можно сказать о совместности или несовместности случайным образом составленной системы из   линейных уравнений относительно  неизвестных? При   система, 

как правило, совместна и имеет бесконечное множество решений. В самом деле, если выбрать минор порядка   в матрице системы  , элементы которой считаются случайными, то этот минор будет «с вероятностью 1» отличен от нуля (см. рассуждения в предыдущем пункте о совместности системы л.у. при  ). Таким образом,  , и автоматически получаем, что   (поскольку ранг не может больше количества строк матрицы). Если же   то такаяпереопределенная система, как правило, несовместна. Рассуждения для доказательства правдоподобия этого утверждения могут быть следующими. Выберем произвольным образом в рассматриваемой системе какую-то подсистему, состоящую из   уравнений. Она, как правило, будет иметь единственное решение. Теперь составим другую подсистему, хотя бы одним уравнением отличающуюся от предыдущей (поскольку   такое всегда можно сделать). Новая подсистема снова, как правило, будет иметь единственное решение. Однако решения этих двух подсистем будут, как правило, различными и, следовательно, сама основная система не будет иметь решения. В этом последнем случае переопределенной системы имеется, однако, важный исключительный, который рассмотрим ☞ 

НИЖЕ.

=>

Система однородных уравнений

всегда совместна: она имеет тривиальное решение  . Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

П

Пример. Найти условие, при котором три точки плоскости с координатами   и   лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде   при неопределенных коэффициентах  . Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений:

Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора   при хотя бы одном из чисел отличном от нуля):

?

Доказать, что для совместности системы

необходимо, чтобы было выполнено условие

Является ли это условие достаточным для совместности?

И

Исторический комментарий. Понятие ранга матрицы и результат, известный в литературе как «теорема Кронекера–Капелли», были открыты несколькими независимыми исследователями. Первое доказательство этой теоремы принадлежит Ч. Л.Додсону, оно было напечатано им в 1867 г. в книге

Источник.  An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система   неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.

Ранг матрицы. Лекция 2.2 — презентация онлайн

Похожие презентации:

Ранг матрицы

Определители матриц. Обратная матрица, ранг матрицы

Обратная матрица

Линейная алгебра. Ранг матрицы. (Тема 2)

Ранг матрицы. Собственные числа и собственные векторы

Системы линейных уравнений. Ранг матрицы

Матрицы. Элементарные преобразования и действия над матрицами

Метод Гаусса решения систем линейных уравнений. Ранг матрицы. Исследование систем линейных уравнений

Линейная алгебра.

Ранг матрицы. Метод Гаусса решения систем линейных уравнений. Лекция 5

Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы

*Лекция 2.2
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Ранг матрицы.
Определение. В матрице порядка m n минор порядка r
называется базисным, если он не равен нулю, а все
миноры порядка r+1 и выше равны нулю, или не
существуют вовсе, т.е. r совпадает с меньшим из чисел m
или n.
Замечание. В матрице может быть несколько
различных базисных миноров, имеющих одинаковый
порядок.
Определение. Порядок базисного минора матрицы
называется рангом матрицы и обозначается Rg А.
Замечание.
Очень
важным
свойством
элементарных преобразований матриц является то, что
они не изменяют ранг матрицы.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Определение. Матрицы, полученные в результате

элементарного
преобразования,
называются
эквивалентными.
Замечание. Надо отметить, что равные матрицы и
эвивалентные матрицы — понятия совершенно различные.
Теорема. Наибольшее число линейно независимых
столбцов в матрице равно числу линейно независимых
строк. Более того, это число равно рангу матрицы А.
Т.к. элементарные преобразования не изменяют ранг
матрицы, то можно существенно упростить процесс
нахождения ранга матрицы.
Замечание.
Ранг
ступенчатой
количеству ее ненулевых строк.
матрицы,
равен
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Пример. Найти ранг матрицы
Решение. С помощью элементарных преобразований
приведем матрицу A к трапецеидальному виду и первым
шагом поменяем первую и вторую строчки местами:
1 2 2 0
3 1 5 2
1 3 1
2
8 1 13 4
3
1 2
1 l2 3l1 0 5
~
7 l3 l1 0 5
4 l4 8l1 0 15
2 0 3
1 2 10
1 2 10 l3 l2
3 4 28 l4 3l2
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
1
0
0
0
2 2
0
3
3
1 2 2 0
5 1 2 10
~ 0 5 1 2 10
0 0
0
0
0 0 0 10 2
0 0 10 2
Ранг последней матрицы, являющейся трапецеидальной,
равен 3; следовательно, rg A = 3.
Из определения ранга следует, что матрица
является
невырожденной в том и только в том случае, если rgА = n.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Решение произвольных систем линейных уравнений.
Определение. Система m уравнений с n неизвестными
в общем виде записывается следующим образом:
(1)
a11 x1 a12 x2 … a1n xn b1
a x a x … a x b
21 1 22 2
2n n
2
………………………………………..
Определение. Если
система имеет хотя бы одно решение, то
1 x1 am 2 x2 … amn xn bm
она называется amсовместной.
Если система не имеет ни
одного решения, то она называется несовместной.
Определение. Если b1, b2, …,bm = 0, то система
называется однородной. Однородная система всегда
совместна, т.к. всегда имеет нулевое решение .
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Теорема Кронекера – Капелли.
Теорема: Система совместна тогда и только тогда,
когда ранг матрицы системы равен рангу расширенной
матрицы.
RgA = Rg
Доказательство:
Очевидно, что система (1) может быть записана в виде:
a11
a12
a1n b1
a
a
a
b2
21
22
2n
x1
x
… xn
… 2 …
… …
a
a
a
m1
m2
mn bm
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
1) Если решение существует, то столбец свободных членов
есть линейная комбинация столбцов матрицы А, а значит
добавление этого столбца в матрицу, т.е. переход А
не
изменяют ранга.
2) Если RgA = Rg , то это означает, что они имеют один и тот
же базисный минор. Столбец свободных членов – линейная
комбинация столбцов базисного минора, т.е. верна запись,
приведенная выше.
Метод Гаусса.
При решении методом Гаусса расширенную матрицу системы (1)
элементарными преобразованиями приводят к треугольному
виду.
Если то система решений не имеет.
Если то система имеет единственное решение.
Если то система имеет множество решений.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Пример. Решить систему методом Гаусса
Решение.
1 4 7 3
1 4 7 3
0
10
19
8
~
0
10
19
8
.
0 7 13 5 10l 7l 0 0 3 6
2
3
RgA = Rg =3, следовательно система совместна, и так как
ранг совпадает с количеством неизвестных, то система
имеет единственное решение.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Последней ступенчатой матрице, соответствует
следующая СЛАУ, равносильная исходной системе:
Из последнего уравнения находим , подставив его во
второе уравнение, найдем
и , наконец, подставив
найденные и в первое уравнение, найдем :
Следует иметь в виду, что при решении СЛАУ методом
Гаусса перестановка столбцов приводит к перенумерации
неизвестных.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Пример . Решить систем уравнений:
x1 2x 2 3x 3 x 4 4x 5 1,
a) 3×1 4x 2 x 3 2x 4 2,
2x
3x 3 x 4 x 5 6;
1
Решение.
1 2 3 1 4 1
3
4
1
2
0
2
l2 3l1 ~
2 0 3 1 1 6 l 2l
1
3
1 2 3 1 4 1
0
10
10
5
12
5
~
0 4 3 1 7 4 5l 2l
2
3
1 2 3 1 4 1
~ 0 10 10 5 12 5
0 0
5 5 11 30
следовательно система совместна и имеет множество решений.
Замечание.Неизвестные базисные,
свободных неизвестных равно , где )
свободные (количество
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Перенесем свободные неизвестные в правую часть:
Степень свободы системы равна двум, значит решение
системы выразится через два параметра. Положив и решив
систему из трех уравнений с неизвестными найдем
где
произвольные числа.
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
Запишем общее решение системы
19
19
6
c
c
1
2
6
1
5
5
x1
1
17
17
11
x 11 1
c
c
2
1
2
2 2
5
5 2
2
X x 3
c1 c2
11
1
11
6 c c 6
1
2
x
4
5
0
5
1
x
0
0
5
c1
0
c2
1
© материалы подготовлены к. ф.-м.н., доц. Н.А. Фоменко
Пример . Решить систему уравнений:
Решение.
в результате преобразований появилась
следовательно, система несовместна.
строка
© материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко

English     Русский Правила

Элементарные преобразования матрицы: Решенные примеры задач

с ответами, Решение — Элементарные преобразования матрицы: Решенные примеры задач | 12-я математика: БЛОК 1: Применение матриц и определителей

Глава:

12-я математика: БЛОК 1: Применение матриц и определителей

ранг матриц по методу сокращения строк, ранг методом редукции строк , обратная матриц методом Гаусса-Жордана

Форма строки-эшелона

Пример 1.13

Приведите матрицу к форме строки-эшелона.

Решение

Примечание

Это тоже строково-ступенчатая форма данной матрицы.

Таким образом, ступенчатая форма матрицы не обязательно уникальна.

 

Пример 1.14

Приведите матрицу к строчно-эшелонной форме.

Решение

Ранг матрицы

Пример 1.15

Найдите ранг каждой из следующих матриц:

Решение

(i) Пусть A =. Тогда A — матрица порядка 3 × 3. Значит, ρ(A) ≤ min {3, 3}  = 3. Наивысший порядок миноров матрицы A равен 3 . Существует только один минор третьего порядка A .

 = 3 (6−6) − 2 (6−6) + 5 (3 − 3) = 0. Итак, ρ(A) < 3.

 Далее рассмотрим миноры второго порядка A .

Мы находим, что минор второго порядка = 3 − 2 = 1 ≠ 0 . Итак, р(А) = 2.

(ii) Пусть A = . Тогда A — матрица порядка 3×4. Таким образом, ρ(A) ≤ min {3, 4}  = 3.

Наивысший порядок миноров A равен 3 . Мы ищем ненулевой минор третьего порядка A . Но

мы обнаруживаем, что все они исчезают. На самом деле у нас есть

Итак, ρ( A ) < 3. Далее мы ищем ненулевой минор второго порядка для A .

Мы находим, что  = -4+9 =5 ≠ 0 . Итак, р(А) = 2.

Примечание

Нахождение ранга матрицы путем поиска ненулевого минора высшего порядка довольно утомительно, когда порядок матрицы достаточно велик. Есть еще один простой способ найти ранг матрицы, даже если порядок матрицы довольно высок. Этот метод заключается в вычислении ранга эквивалентной ступенчато-строковой формы матрицы. Если матрица представлена ​​в виде ступенчатой ​​строки, то все элементы ниже главной диагонали (это линия, соединяющая позиции диагональных элементов  а 11, а 22, а 33, л. матрицы) равны нулю. Итак, проверить, равен ли минор нулю, довольно просто. Пример 1.16 Тогда A — матрица порядка 3 3 × и ρ(A) ≤ 3

 Минор третьего порядка |A| =   = (2) (3)( 1) = 6 ≠ 0 . Итак, р(А) = 3.

Пример 1.17

Найдите ранг матрицы, приведя ее к строчно-эшелонной форме.

Решение

Пусть A = . Применяя элементарные операции со строками, получаем

Последняя эквивалентная матрица имеет строчно-эшелонную форму. Он имеет две ненулевые строки. Итак, ρ (A)= 2.

 

Пример 1.18

Найдите ранг матрицы, приведя ее к строчно-эшелонному виду.

Решение

Пусть A — матрица. Выполняя элементарные операции над строками, получаем

Последняя эквивалентная матрица имеет форму строки-эшелона. Он имеет три ненулевых строки. Итак, ρ( A ) = 3.

Элементарные операции со строками над матрицей могут быть выполнены путем предварительного умножения данной матрицы на особый класс матриц, называемых элементарными матрицами.

Пример 1.19

Показать, что матрица невырожденная, и свести ее к единичной матрице с помощью элементарных преобразований строк.

Решение

Пусть A = . Тогда |A| = 3 (0+2) – 1(2+5) + 4(4-0) = 6-7+16 ≠ 0. Итак, A неособо. Сохраняя в качестве нашей цели единичную матрицу, мы последовательно выполняем операции со строками над A следующим образом:

Метод Гаусса-Жордана

Пример 1.

20

Найдите обратную неособую матрицу A = методом Гаусса-Жордана. Пример 1.21

Решение

Применяя метод Гаусса-Жордана, получаем

• Предыдущая страница
• Следующая страница

Теги : с ответами, решение , 12th Mathematics : UNIT 1 : Применение матриц и определителей Применение матриц и определителей: элементарные преобразования матрицы: решенные примеры задач | с ответами, решение

[решено] Найдите ранг матрицы \(\left(\begin{matrix} 8 &a

Вариант 3 : 3

Бесплатно

Существительное и местоимение: заполните пробелы (наиболее важные правила)

85,6 тыс. пользователей

15 вопросов

15 баллов

12 минут

Понятие:

Ранг:

Ранг матрицы – это число, равное порядку старшего ненулевого минора, который может быть образован из матрицы.

Для матрицы A это обозначается ρ(A).

Говорят, что ранг матрицы равен r  if,

• Существует хотя бы один ненулевой минор порядка r.
• Каждый минор матрицы A, имеющий порядок выше r , равен нулю.

Эшелонная форма: говорят, что матрица имеет эшелонированную форму, если

• Ведущие ненулевые элементы в каждой строке находятся позади ведущих ненулевых элементов в предыдущей строке.
• Все нулевые строки ниже всех ненулевых строк.

Шаги для нахождения ступенчатой ​​формы и ранга матрицы:

• Чтобы привести матрицу к ступенчатой ​​форме, мы можем применить к матрице метод исключения Гаусса и преобразовать матрицу в верхнюю треугольную матрицу (нижние недиагональные элементы равны нулю).
• Затем мы можем подсчитать количество ненулевых строк в этой верхней треугольной матрице, чтобы получить ранг матрицы.

Расчет:

Пусть

 \(A = \left(\begin{matrix} 8 & 1 & 3 & 6 \\\ 0 & 3 & 2 & 2 \\\ -8 & -1 & -3 & -4 \end{matrix}\right)\)

by \(c_1 \rightarrow \frac{1}{8}c_1\)

\(A\ =\ \left(\begin{matrix} 1 & 1 & 3 & 6 \\\ 0 & 3 & 2 & 2 \\\ -1 & -1 & -3 & -4 \end{matrix}\right)\)

by \(R_3 \стрелка вправо R_3 + R_1\)

\(\Стрелка вправо \ A\ =\ \left(\begin{matrix} 1 & 1 & 3 & 6 \\\ 0 & 3 & 2 & 2 \\\ 0 & 0 & 0 & 2 \end{matrix}\right)\)

Последний эквивалент матрица имеет эшелонированную форму. Количество ненулевых строк в этой матрице равно 3. Следовательно, она оценивается как 3.

Следовательно, ранг A = 3.

Важные моменты

Другие свойства ранга матрицы:

• матрица в форме эшелона. В форме Echelon ранг матрицы — это количество ненулевых строк матрицы.
• Ранг матрицы равен нулю, если матрица пуста.
• ρ(A) ≤ мин. (строка, столбец)
• ρ(AB) ≤ мин. [ρ(A), ρ(B)]
• ρ(AT A) = ρ(A AT) = ρ(A) = ρ(AT)
• Если A и B — матрицы одного порядка, то ρ(A + B) ≤ ρ(A) + ρ(B) и ρ(A — B) ≥ ρ(A) — ρ(B).
• Если Aθ является сопряженным транспонированием A, то ρ(Aθ) = ρ(A) и ρ(A·Aθ) = ρ(A).
• Ранг кососимметричной матрицы не может быть равен единице.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления Navik GD береговой охраны Индии

Последнее обновление: 11 ноября 2022 г.

No related posts.