Правило параллельные прямые: Свойства параллельных прямых. Аксиома параллельных прямых — урок. Геометрия, 7 класс.

Свойства параллельных прямых – основные определения

4.3

Средняя оценка: 4.3

Всего получено оценок: 291.

4.3

Средняя оценка: 4.3

Всего получено оценок: 291.

Свойства параллельных прямых крайне часто встречаются при решении задач и доказательств теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Что такое свойства параллельных прямых

Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.

Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются и лежат в одной плоскости.

Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.

При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.

Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.

Две группы свойств параллельных прямых

Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых. Начнем с первой группы.

Следствия из аксиомы параллельных прямых

Следствие 1

Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.

Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений, не требующих обоснования, крайне мало, и каждое из них носит название – аксиома.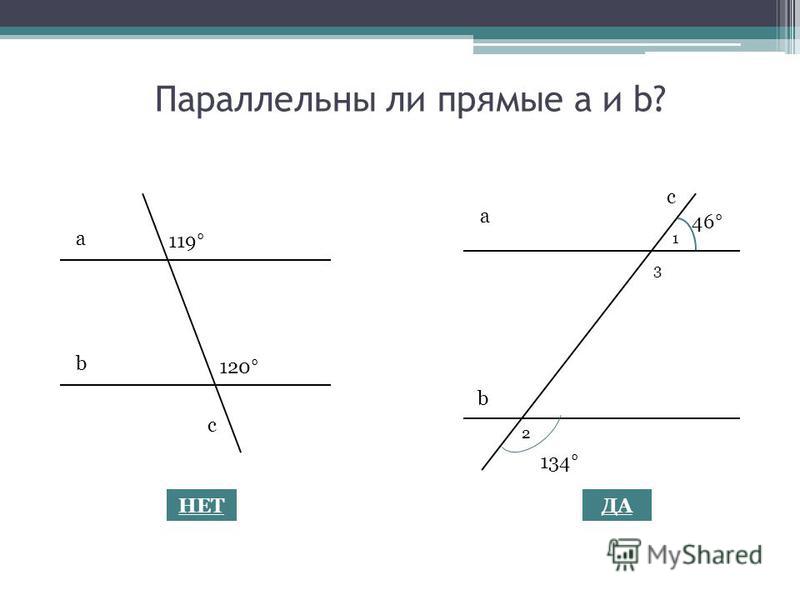

Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.

Проведем две параллельные прямые а и b. Прямая с параллельна прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.

То есть, через одну точку на плоскости проведены две прямые, параллельные данной. Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.

Рис. 1. Иллюстрация следствия.

Следствие 2

Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.

Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.

Тогда через точку К проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.

Рис. 2. Рисунок к доказательству.

Следствия из признаков параллельности

Эту группу запомнить проще всего. Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.

• Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
• Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
• Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180

Рис. 3. Иллюстрация признаков.

Что мы узнали?

Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Девлет Болтаев

  5/5

• Иван Маковецкий

  5/5

• Иришка Чипрягова

  5/5

• Елена Иванова

  5/5

• Константин Никитич

  5/5

• Манижа Гуломджонова

  5/5

• Екатерина Лобычева

  4/5

Оценка статьи

4.3

Средняя оценка: 4.3

Всего получено оценок: 291.

---

А какая ваша оценка?

Перпендикулярные прямые и параллельные прямые 6 класс онлайн-подготовка на Ростелеком Лицей

Тема 9: Координаты на плоскости

• Видео
• Тренажер
• Теория

Заметили ошибку?

Перпендикулярные прямые и параллельные прямые

Изучая геометрические фигуры, мы постоянно сталкиваемся с перпендикулярными прямыми. Например, смежные стороны прямоугольника перпендикулярны. Как убедиться в том, что две линии (прямые) перпендикулярны? С давних пор люди проверяли перпендикулярность стены основанию дома с помощью специального отвеса. Отсюда и произошло название перпендикуляра: латинское «перпендикулярис» означает «отвесной». Чтобы построить перпендикуляр к прямой, необходимо построить прямой угол. Это можно сделать с помощью чертежного треугольника или транспортира.

Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

На рисунке изображены прямые а и b, они перпендикулярны друг другу и осям координат. Пишут: a ⊥ b (а перпендикулярна b), a ⊥ OY (прямая a перпендикулярна оси ОY), b ⊥ OX (прямая b перпендикулярна оси ОХ).

Если a ⊥ b, то b ⊥ a.

На рисунке прямые c и d перпендикулярны друг другу, но не перпендикулярны осям координат. Пишут: с ⊥ d.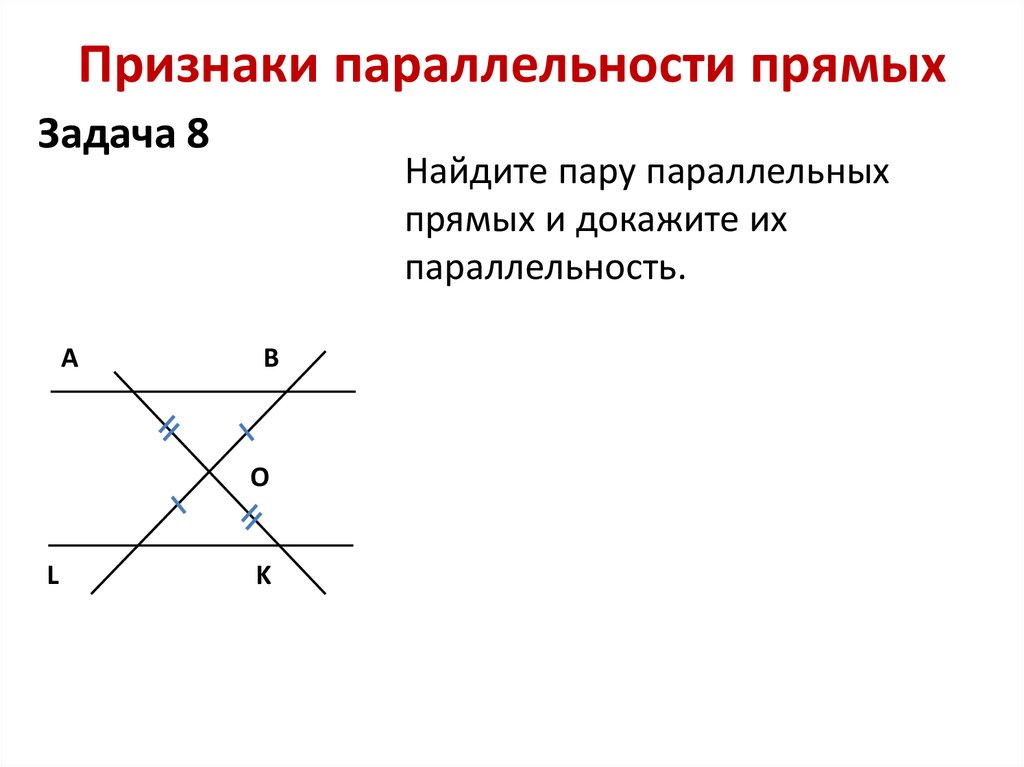 Отрезки (или лучи), лежащие на перпендикулярных прямых, называют

перпендикулярными отрезками (или лучами). Например, луч ОХ ⊥ лучу ОY.

Две различные прямые могут либо пересекаться в одной точке, либо не пересекаться.

Две непересекающиеся прямые на плоскости называют параллельными.

Пишут а || b. Эту запись читают так: «Прямая а параллельна прямой b».

Отрезки (лучи), лежащие на параллельных прямых, называют параллельными отрезками (лучами).

АВ || CM (отрезок АВ параллелен отрезку СМ).

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

Поэтому противоположные стороны любого прямоугольника параллельны.

Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.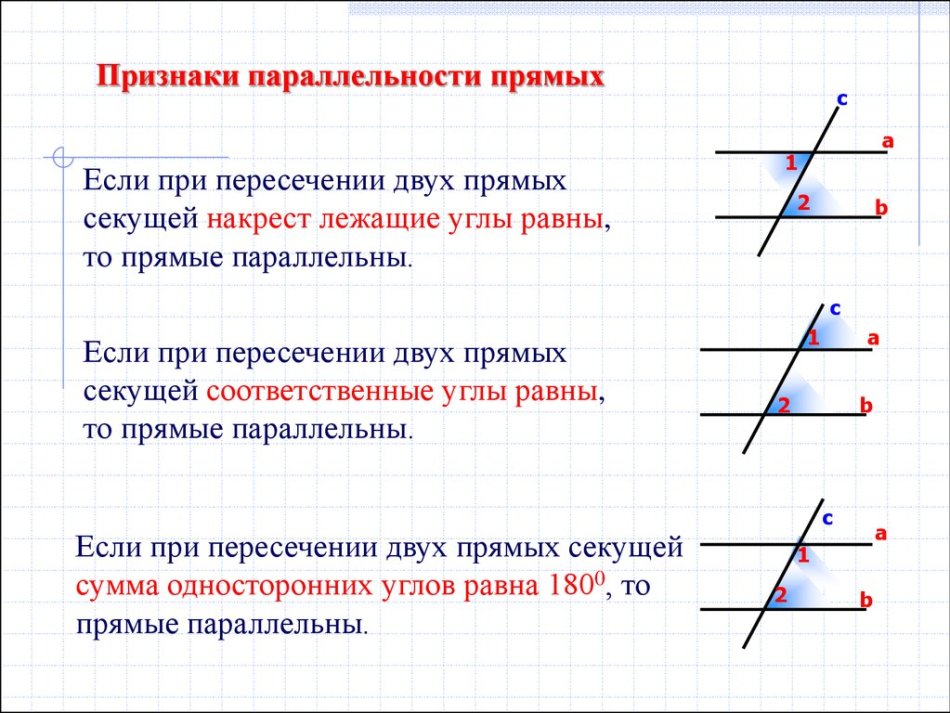

Пример 1. Начертим два перпендикулярных отрезка АВ и СМ так, чтобы они не пересекались; пересекались.

Пример 2. Начертим треугольник и проведем через каждую вершину прямую, параллельную противоположной стороне.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

1.4: Параллельные линии — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

34120

• Генри Африк
• CUNY Нью-Йоркский технологический колледж через Нью-Йоркский городской технологический колледж в CUNY Academic Works

Две линии параллельны , если они не пересекаются, как бы далеко они ни простирались. Символ параллельности — \(||\). На рисунке \(\PageIndex{1}\), \(\stackrel{\leftrightarrow}{A B}\) \(||\) \(\stackrel{\leftrightarrow}{C D}\). Стрелки используются для обозначения того, что линии параллельны.

Рисунок \(\PageIndex{1}\): \(\stackrel{\leftrightarrow}{A B}\) и \(\widehat{C D}\) параллельны. Они не пересекаются независимо от того, насколько далеко они вытянуты. \(\PageIndex{1}\): \(\stackrel{\leftrightarrow}{\mathrm{EF}}\) и \(\stackrel{\leftrightarrow}{\mathrm{GH}}\) не параллельны. Они встречаются в точке \(P\).

Мы делаем следующее предположение о параллельных линиях, называемое постулатом

параллельности.

Теорема \(\PageIndex{1}\): постулат о параллельности

Вероятности, присваиваемые событиям функцией распределения в выборочном пространстве, равны

Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной прямой. Итак, на рисунке \(\PageIndex{3}\) через \(C\) можно провести ровно одну прямую, параллельную \(\overleftarrow{\mathrm{AB}}\). 9{\prime}\) также являются альтернативными внутренними углами. Они также образуют «\(Z\)», хотя и вытянуты назад. Если смотреть сбоку, буква «\(Z\)» может также выглядеть как «\(N\)».

Рисунок \(\PageIndex{5}\): Альтернативная внутренняя форма букв «\(Z\)» или «\(N\)». Буква может быть растянута или задом наперёд.

Альтернативные внутренние углы важны из-за следующей теоремы:

Теорема \(\PageIndex{1}\) Теорема «Z»

Если две прямые параллельны, то их параллельные внутренние углы равны. Если альтернативные внутренние углы двух прямых равны, то прямые должны быть параллельны,

{\circ}\). На рисунке \(\PageIndex{7}\) линии не параллельны, и ни один из чередующихся внутренних углов не равен.

Рисунок \(\PageIndex{6}\): Линии параллельны, и их альтернативные внутренние углы равны. Рисунок \(\PageIndex{7}\): Линии не параллельны, и их альтернативные внутренние углы не равны.

Доказательство теоремы \(\PageIndex{1}\) сложное и будет отложено до приложения.

Пример \(\PageIndex{1}\)

Найти \(x, y\) и \(z\): 9{\circ}\).

Ответ : \(x = 40, y = 140, z = 140\).

Соответствующие углы двух прямых — это два угла, лежащие по одну сторону от двух прямых и по одну сторону от поперечной, На рисунке \(\PageIndex{8}\), \(\angle w\) и \ (\angle w’\) — соответствующие углы прямых \(\overleftrightarrow{AB}\) и \(\overleftrightarrow{CD}\). Они образуют букву «\(F\)». \(\угол x\) и \(\угол x’\), \(\угол y\) и \(\угол y’\), и \(\угол z\) и \(\угол z’\ ) — другие пары соответствующих углов \(\overleftrightarrow{AB}\) и \(\overleftrightarrow{CD}\). Все они образуют букву «\(F\)», хотя это может быть перевернутая или перевернутая буква «\(F\)» (рис. \(\PageIndex{9).}\)).

Рисунок \(\PageIndex{8}\): показаны четыре пары соответствующих углов. Рисунок \(\PageIndex{9}\): соответствующие углы образуют букву «\(F\)», хотя это может вверх ногами «\(F\)».

Соответствующие углы важны из-за следующей теоремы:

Теорема \(\PageIndex{2}\): Теорема «F»

Если две прямые параллельны, то их соответствующие углы равны.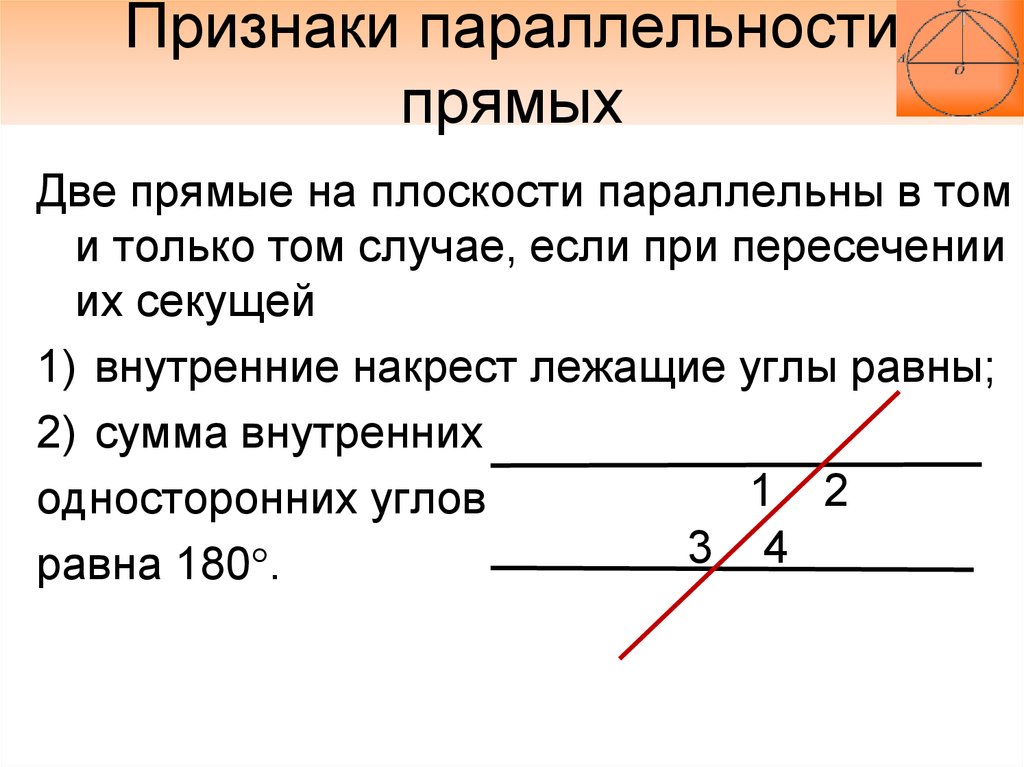 Если соответствующие углы двух прямых равны, то прямые должны быть параллельны. 9{\circ}\) образует с одним из них углы или образует равные вертикальные углы (рис. \(PageIndex{10}\)). Поэтому все соответствующие углы равны. Также равны все пары чередующихся внутренних углов. Нетрудно видеть, что если хотя бы одна пара соответствующих углов или одна пара чередующихся внутренних углов равны, то равны и все остальные пары соответствующих и чередующихся внутренних углов.

Доказательство теоремы \(\PageIndex{2}\): соответствующие углы будут равны, если равны альтернативные внутренние углы, и наоборот. Поэтому теорема \(\PageIndex{2}\) непосредственно следует из теоремы \(\PageIndex{1}\).

На рис. лежащие на одной стороне секущей, называются ковнутренними углами.) \(\угол у\) и \(\угол у’\) также являются внутренними углами на одной стороне секущей. Обратите внимание, что каждая пара углов образует букву «\(С\)». Сравните рисунок \(\PageIndex{11}\) с рисунком 10, а также с примером \(\PageIndex{1}\). Отсюда очевидна следующая теорема: 9{\circ}\)). Если внутренние углы двух прямых по одну сторону от секущей смежны, то эти прямые должны быть параллельны.

Пример \(\PageIndex{3}\)

Найдите \(x\) и отмеченные углы:

Решение

Прямые параллельны, поэтому по теореме \(\PageIndex{3}\) два отмеченных угла должны быть дополнительными.

\[\begin{array} {rcl} {x + 2x + 30} & = & {180} \\ {3x + 30} & = & {180} \\ {3x} & = & {180 — 30 } \\ {3x} & = & {150} \\ {x} & = & {50} \end{массив}\] 9{\circ}\).

Пример \(\PageIndex{5}\)

Перечислите все пары чередующихся внутренних углов на диаграмме (одна стрелка указывает, что \(\overleftrightarrow{AB}\) параллелен \(\overleftrightarrow{CD}\) а двойная стрелка указывает, что \(\overleftrightarrow{AD}\) параллелен \(\overleftrightarrow{BC}\). (N\) можно составить из отрезков на диаграмме (рис. \(\PageIndex{12}\)), 9{\circ}\)

РЕЗЮМЕ

Альтернативные внутренние углы параллельных прямых равны.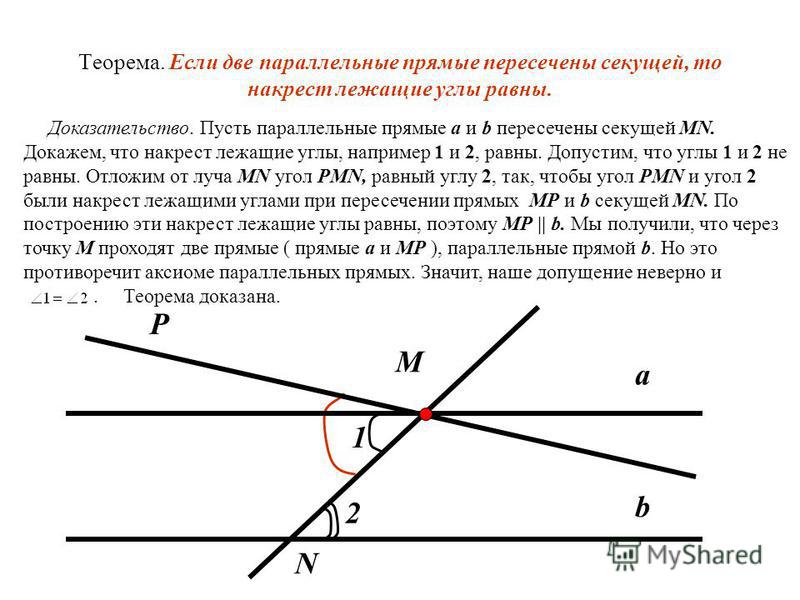 Они образуют букву «\(Z\)».

Соответственные углы параллельных прямых равны. Они образуют букву «\(F\)».

Внутренние углы по одну сторону от поперечной параллельных прямых являются дополнительными. Они образуют букву «\(G\)».

Историческая справка

Постулат о параллельности, данный ранее в этом разделе, эквивалентен пятому постулату Элементов Евклида. Евклид был прав, приняв это как постулат, а не пытаясь доказать его как теорему. Однако математическому миру это стало ясно только в девятнадцатом веке, 2200 лет спустя. Тем временем десятки выдающихся математиков безуспешно пытались дать удовлетворительное доказательство постулата о параллельности. Они чувствовали, что это не так самоочевидно, как должен был бы быть постулат, и что оно требует некоторого формального обоснования.0034

В 1826 г. русский математик Н.И. Лобачевский представил систему геометрии, основанную на предположении, что через данную точку можно провести более одной прямой, параллельно данной прямой (рис.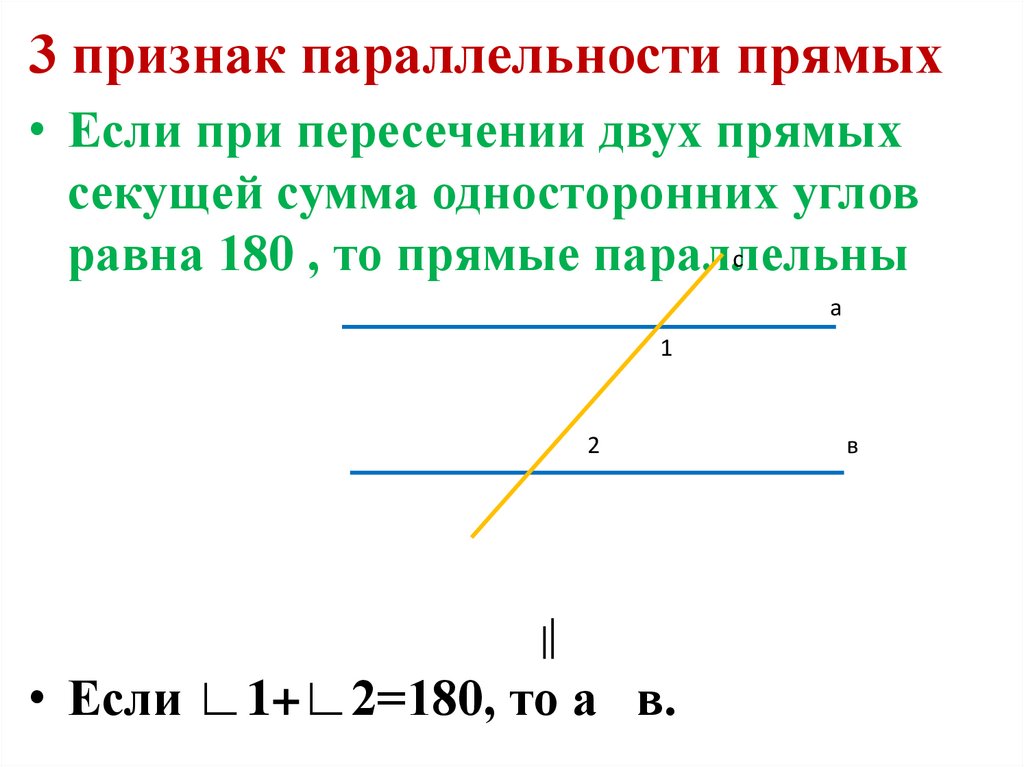 \(\PageIndex{13 }\)). В 1854 г. немецкий математик Георг Бернхард Риман предложил систему геометрии, в которой вообще нет параллельных прямых. Геометрия, в которой постулат параллельности заменен каким-либо другим постулатом, называется неевклидовой геометрией. Существование этих геометрий показывает, что постулат параллельности не обязательно должен быть верным. Действительно, Эйнштейн использовал геометрию Римана как основу своей теории относительности.

Рисунок \(PageIndex{13}\): В геометрии Лобачевского через \(C\) можно провести более одной прямой, параллельной \(AB\).

Конечно, наш первоначальный постулат о параллельности лучше всего подходит для обычных приложений, и мы используем его на протяжении всей этой книги. лучшее приближение к физической реальности.

Задачи

Для каждого из следующих сформулируйте теорему(ы), использованную(ые) для получения вашего ответа (например, «перемежающиеся внутренние углы параллельных прямых равны»). Линии, отмеченные одинаковыми стрелками, считаются параллельными,

1 — 2.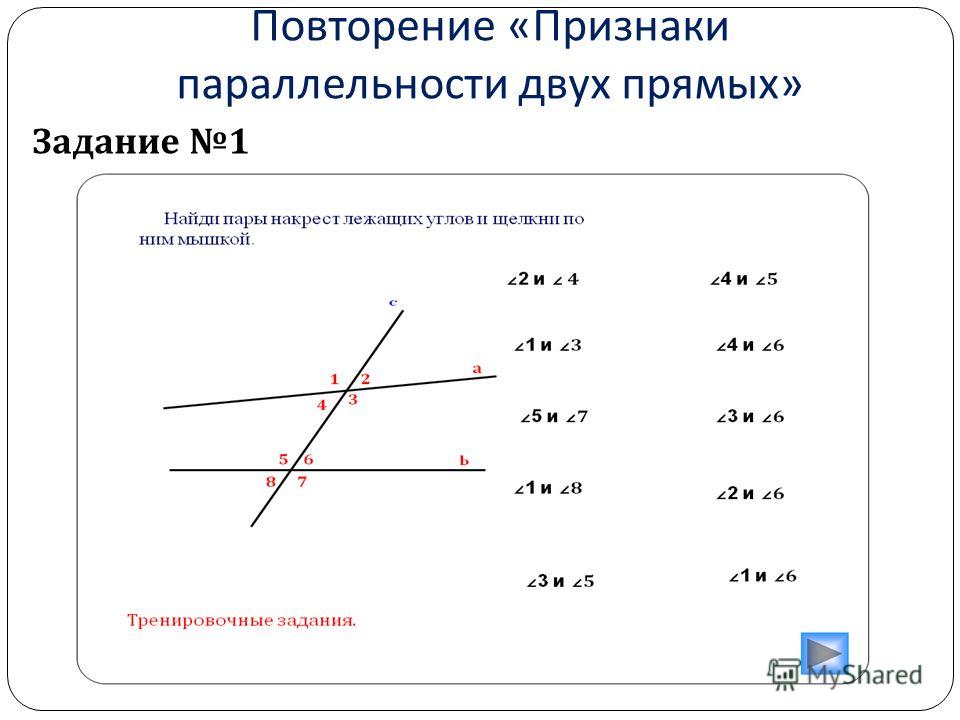 Найти \(x, y\) и \(z\):

1. 2.

3 — 4. Найти \(t\), \(u\), \(v \), \(w\), \(x\), \(y\) и \(z\):

3. 4.

5 — 10. Найти \(x\):

5 6.

7. 8.

9. 10.

11 — 18. Найти \(х\) и отмеченные углы:

11. 12.

13. 14.

15.016

17. 18.

19 — 26. Для каждого из следующих перечислите все пары чередующихся внутренних углов и соответствующих им углов. Если таких нет, то перечислите все пары внутренних углов по одну сторону от секущей. Укажите параллельные прямые, образующие каждую пару углов. 9{\circ}\) составляет ли зеркало \(BD\) горизонталь?

---

Эта страница под названием 1.4: Parallel Lines используется в соответствии с лицензией CC BY-NC-SA 4.0. Автор, ремикс и/или куратор Генри Африк (Нью-Йоркский технологический колледж в CUNY Academic Works) использует исходный контент, был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Генри Африк

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. параллельные линии
   2. постулат параллельности
   3. источник@https://academicworks. cuny.edu/ny_oers/44
   4. поперечный

Параллельные линии: определение, углы и уравнение

Повсюду вокруг нас мы видим много разных форм линий, таких как край стола, углы пола и потолка, стороны дверей и окон и так далее. Но есть некоторые формы прямых линий, которые идут бок о бок в одном направлении без пересечения . Как две противоположные стороны двери в одном лице. Этот тип линии является примером параллельных линий .

В этом объяснении мы поймем концепцию параллельных линий и их различные свойства.

Определение параллельных линий

Параллельные линии — это типы линий, состоящие из двух или более линий в одной плоскости.

Две или более прямые линии на одной плоскости, которые равноудалены (имеют одинаковое расстояние между ними во всех точках) и никогда не пересекаются друг с другом ни в одной точке, называются параллельными линиями .

Параллельные линии остаются на одном и том же расстоянии друг от друга, независимо от того, насколько далеко они вытянуты. Они могут быть построены в любом направлении, будь то горизонтальное, вертикальное или диагональное. Математически они представлены символом, который называется «параллелен».

Параллельные линии, StudySmarter Originals

Здесь на приведенном выше рисунке p и q — параллельные прямые, а m и n — параллельные прямые. Следовательно, говорят, что линия А и линия В не параллельны друг другу, так как при продолжении обеих линий они обе пересекаются в какой-то точке. Итак, a не параллелен b (то есть).

Параллельные прямые, углы

Поскольку параллельные прямые не пересекаются друг с другом, между ними не может образоваться никаких углов. Но когда другая прямая, кроме данных параллельных прямых, пересекает обе параллельные прямые, то между ними образуются некоторые углы.

Если какая-либо линия пересекает обе параллельные прямые в какой-то точке одной плоскости, то эта линия называется поперечной .

Поперечное резание параллельных линий, StudySmarter Originals

Здесь, на рисунке выше, мы видим, что линия l пересекает обе параллельные линии a и b . Итак, линия l является поперечной линией. Поскольку секущая пересекает параллельные прямые, видно, что она образует пары углов с обеими прямыми. Существуют различные типы углов, образованных секущими.

Соответствующие углы

Углы, которые образуются на одной стороне поперечной и на соответствующих углах параллельных прямых, называются соответствующими углами .

Соответствующие углы можно легко определить по форме « F ». Они могут быть сформированы в любом случае либо вверх ногами, либо сзади и спереди. Соответствующие углы всегда равны друг другу в параллельных прямых.

Соответствующие углы параллельных линий, StudySmarter Originals

Альтернативные углы

Углы, образованные на противоположной стороне поперечной на параллельных прямых, известны как альтернативные углы .

Альтернативные углы можно найти в виде формы « Z ». Они могут быть как внутренними, так и внешними углами. Точно так же, как и соответствующие углы, альтернативные углы могут быть образованы в любом направлении. Пара альтернативных углов всегда равны друг другу.

Чередующиеся внутренние углы параллельных линий, Studysmarter Originals

Здесь, на рисунке выше, оба угла являются чередующимися внутренними углами.

Внутренние углы

Углы, образованные на одной стороне поперечной, обращенной друг к другу на параллельных прямых, называются внутренними углами .

Внутренние углы выполнены в форме буквы «U». Их можно найти по обе стороны от секущей, содержащей обе параллельные прямые. Сумма внутренних углов всегда будет

Внутренние углы параллельных прямых, StudySmarter Originals

Внешние углы

Углы, лежащие вне сторон параллельных прямых, но лежащие на стороне поперечной, называются внешними углами .

Внешние углы имеют форму буквы «U», но будут располагаться на внешней ее части. А сумма пар внешних углов всегда будет равна

Внешние углы, StudySmarter Originals

Вертикально противоположные углы

Углы, образующиеся на любой из параллельных прямых и секущих, противоположных друг другу, называются вертикально противоположные углы .

Вертикально противоположные углы встречаются в виде двух касающихся друг друга букв «V». Они содержали только любую из параллельных линий для каждой пары. Вертикально противоположные углы равны между собой.

Вертикально противоположные углы, StudySmarter Originals

Итак, мы можем представить все пары углов для всех типов углов, как показано ниже.

Все пары углов на параллельных прямых, StudySmarter Originals

• Соответствующие пары углов:
• Альтернативные пары углов:
• Пары внутренних углов:
• Пары внешних углов:
• Пары противоположных по вертикали углов:

Уравнения типа параллельных прямых

. Таким образом, мы можем представить параллельные прямые в виде уравнения прямой. Мы знаем, что в координатной геометрии уравнение прямой можно записать в виде Таким образом, мы также можем представить параллельные прямые в виде уравнения

Здесь b — точка пересечения с осью y, поэтому может быть любым значением. Важно помнить, что поскольку у нас есть две или более строк в параллельных строках, значение b для каждой строки должно отличаться друг от друга. Если они равны, то уравнения всех линий будут одинаковыми, и тогда ее можно будет рассматривать как одну линию.

И м — уклон или уклон этой линии. Здесь в отличие от b значение m для всех параллельных прямых должно быть одинаковым. Как м представляет собой наклон линии, если м разные для всех параллельных прямых, то они будут пересекаться друг с другом и больше не будут считаться параллельными.

Мы скоро поймем концепцию градиента и то, как ее можно найти в следующей теме.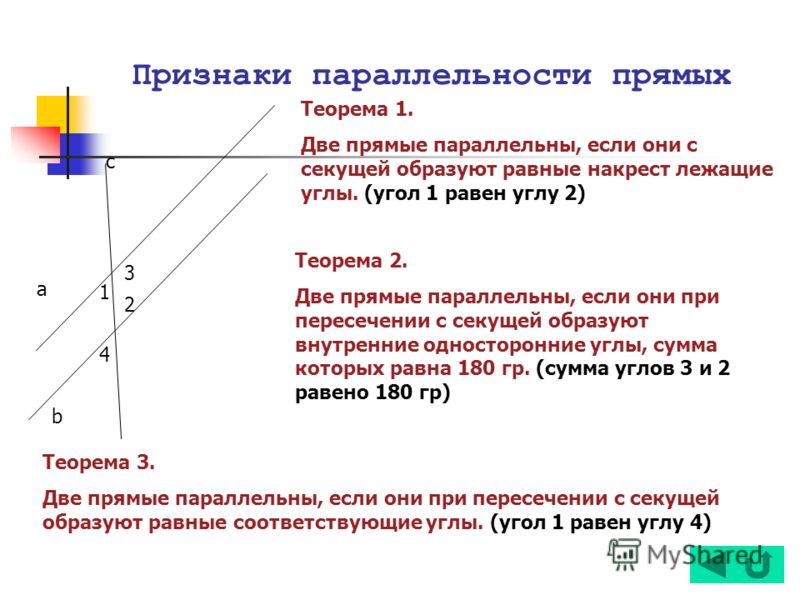

Уравнение параллельных линий на графике, StudySmarter Originals

Градиент параллельных линий

Градиент или наклон параллельных линий — это крутизна этой линии на графике. Градиент параллельных линий рассчитывается относительно положительной оси x графика, а параллельные линии наклонены относительно положительной оси x.

Из вышеизложенного мы знаем, что уравнение для параллельных линий имеет вид Теперь предположим, что уравнение для одной линии и уравнение для другой линии имеют вид Здесь точка пересечения по оси y, а м — это градиент параллельных линий. Тогда, чтобы обе линии стали параллельными, наклон обеих линий должен быть одинаковым. То есть это равенство можно вывести, учитывая угол между обеими линиями.

Если нам уже даны две точки на каждой линии графика, то мы можем рассчитать и проверить наклон по формуле:

где представляют собой точки по осям x и y для одной линии.

Примеры параллельных линий

Давайте рассмотрим несколько примеров параллельных линий и поймем, как найти углы и наклон в параллельных линиях.

На данной фигуре m и n — параллельные прямые, а l — поперечное пересечение обеих параллельных прямых. Затем найдите значение x , если оно задано.

Параллельные линии с поперечными, StudySmarter Originals

Решение:

Мы уже знаем, что прямые m и n параллельны друг другу, а прямая l перпендикулярна m и n .

Итак, на рисунке мы можем ясно видеть, что и являются внутренними углами, поскольку они образуют форму «U».

Поскольку оба угла внутренние, мы знаем, что их сумма равна

Найдите значение из заданной цифры, если она дана. Также строки а, б, и c — параллельные прямые, пересекаемые секущей t .

Параллельные прямые с отсутствующими углами, StudySmarter Originals

Решение:

Дано, что прямые a,b и c параллельны друг другу, а линия t действует как поперечная к этим трем линии.

Сначала найдем значение. На рисунке видно, что углы образуют букву «U». Таким образом, оба угла и являются внутренними углами. Значит сумма обоих этих углов будет

Теперь есть вертикально противоположные углы. Таким образом, оба угла будут равны друг другу.

Теперь из рисунка видно, что и образует букву «F», так что это соответствующие углы. И поэтому они равны друг другу.

Следовательно, значение обоих углов равно

Проверить, параллельны ли заданные прямые.

Решение:

а) Здесь нам даны два уравнения прямых. Теперь, сравнивая их с общим уравнением параллельных прямых, мы получаем, что Здесь градиенты параллельных прямых и y-отрезки.

Как мы знаем, чтобы линии были параллельными, градиенты должны быть равными. И мы можем ясно видеть в приведенных выше уравнениях, что также обратите внимание, что значения разные. Следовательно, обе прямые параллельны.

б) Здесь уравнения прямых представлены в виде Сравнивая его с общим уравнением параллельных прямых, получаем, что

Так как здесь получаем, то можно сразу сказать, что обе данные прямые не параллельны друг другу.