Найти расстояние от точки до точки в пространстве: Расстояние между двумя точками

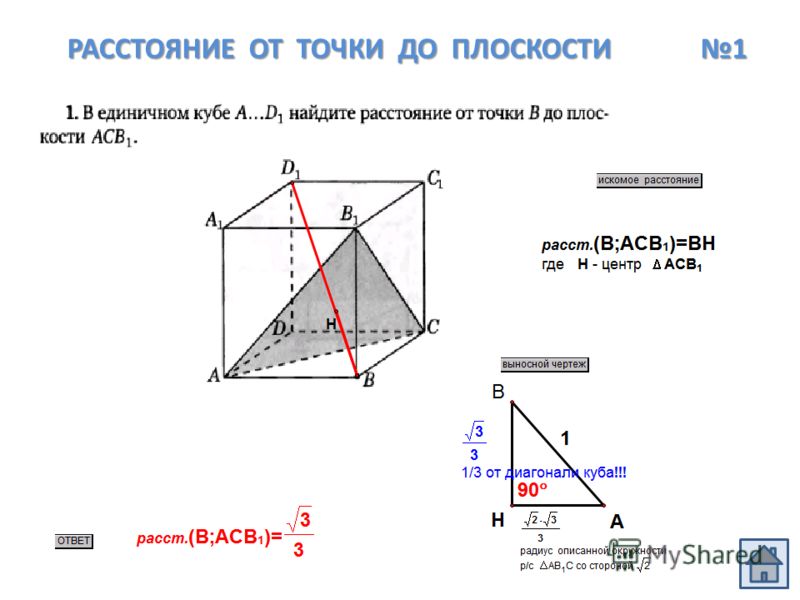
Расстояние между двумя точками

Расстояние между двумя точками

Навигация по странице:

• Определение расстояния между двумя точками
• Формулы для вычисления расстояния между двумя точками
• Вывод формулы вычисления расстояния между двумя точками для плоской задачи
• Примеры задач на вычисление расстояния между двумя точками
  • плоские задачи
  • пространственные задачи

Онлайн калькулятор. Расстояние между двумя точками

Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.

Формулы вычисления расстояния между двумя точками:

• Формула вычисления расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

  AB = √(x_b — x_a)² + (y_b — y_a)²

• Формула вычисления расстояния между двумя точками A(x_a , y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

  AB = √(x_b — x_a)² + (y_b — y_a)² + (z_b — z_a)²

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x_b — x_a;
BC = y_b — y_a.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC² + BC².

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Примеры задач на вычисление расстояния между двумя точками

Примеры вычисления расстояния между двумя точками на плоскости

Пример 1.

Найти расстояние между точками A(-1, 3) и B(6,2).

Решение.

AB = √(x_b — x_a)² + (y_b — y_a)² = √(6 — (-1))² + (2 — 3)² = √7² + 1² = √50 = 5√2

Ответ: AB = 5√2.

Пример 2.

Найти расстояние между точками A(0, 1) и B(2,-2).

Решение.

AB = √(x_b — x_a)² + (y_b — y_a)² = √(2 — 0)² + (-2 — 1)² = √2² + (-3)² = √13

Ответ: AB = √13.

Примеры вычисления расстояния между двумя точками в пространстве

Пример 3.

Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).

Решение.

AB = √(x_b — x_a)

2 + (y_b — y_a)² + (z_b — z_a)² =

= √(6 — (-1))² + (2 — 3)² + (-2 — 3)² = √7² + 1² + 5² = √75 = 5√3

Ответ: AB = 5√3.

Пример 4.

Найти расстояние между точками A(0, -3, 3) и B(3, 1, 3).

Решение.

AB = √(x_b — x_a)² + (y_b — y_a)² + (z_b — z_a)² =

= √(3 — 0)² + (1 — (-3))² + (3 — 3)² = √3² + 4² + 0² = √25 = 5

Ответ: AB = 5.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты

Расстояние от точки до прямой в пространстве.

Расстояние от точки до прямой в пространстве.

Навигация по странице:

• Определение расстояния от точки до прямой в пространстве
• Формула для вычисления расстояния от точки до прямой в пространстве
• Вывод формулы вычисления расстояния от точки до прямой в пространстве
• Примеры задач на вычисление расстояния от точки до прямой в пространстве

Онлайн калькулятор. Расстояние от точки до прямой в пространстве.

Определение.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Формула для вычисления расстояния от точки до прямой в пространстве

Если s = {m; n; p} — направляющий вектор прямой l, M₁(x₁, y₁, z₁) — точка лежащей на прямой, тогда расстояние от точки M₀(x

0, y₀, z₀) до прямой l можно найти, используя формулу

d =	|M0M1×s|
	|s|

Вывод формулы вычисления расстояния от точки до прямой в пространстве

Если задано уравнение прямой l то несложно найти s = {m; n; p} — направляющий вектор прямой и M₁(x₁, y₁, z₁) — координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

S = |M₀M₁×s|.

С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

S = |s|d.

В нашем случае высота будет равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s.

Приравняв площади несложно получить формулу расстояния от точки до прямой.

Примеры задач на вычисление расстояния от точки до прямой в пространстве

Пример 1.

Найти расстояние между точкой M(0, 2, 3) и прямой

x — 3	=	y — 1	=	z + 1
2		1		2

Решение.

Из уравнения прямой получим:

s = {2; 1; 2} — направляющий вектор прямой;
M₁(3; 1; -1) — точка лежащая на прямой.

Тогда

M₀M₁ = {3 — 0; 1 — 2; -1 — 3} = {3; -1; -4}

M0M1×s =	i	j	k	=
	3	-1	-4
	2	1	2

= i ((-1)·2 — (-4)·1) — j (3·2 — (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}

d =

|M₀M₁×s||s|

=

√2² + (-14)² + 5²√2² + 1² + 2²

=

√225√9

=

153

= 5

Ответ: расстояние от точки до прямой равно 5.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты

Расстояние от точки до прямой в пространстве

Расстояние от точки до прямой в пространстве

Расстояние между точкой $$P$$ и прямой линией $$r$$, $$\text{d}(P,r)$$ — минимальное расстояние между $$P$$ и любой точкой прямая $$r$$.

• Если $$P$$ является точкой прямой $$r$$, то расстояние равно нулю.
• Если $$P$$ не лежит на прямой $$r$$, расстояние от $$P$$ до $$r$$ будет модулем вектора $$\overrightarrow{PP’}$$ , где $$P’$$ — ортогональная проекция $$P$$ на прямую $$r$$.

Тем не менее, существует более простой способ вычисления расстояния между точкой $$P$$ и прямой $$r$$, если точка не принадлежит прямой. Рассмотрим точку $$Q$$ на прямой $$r$$ и управляющий вектор прямой $$\vec{v}$$. Площадь параллелограмма, определяемая векторами $$\overrightarrow{QP}$$ и $$\vec{v}$$, имеет модуль, равный векторному произведению обоих векторов: $$$S_p=|\overrightarrow{QP}\times\vec{v}|$$$

Но площадь параллелограмма также определяется произведением основания на высоту.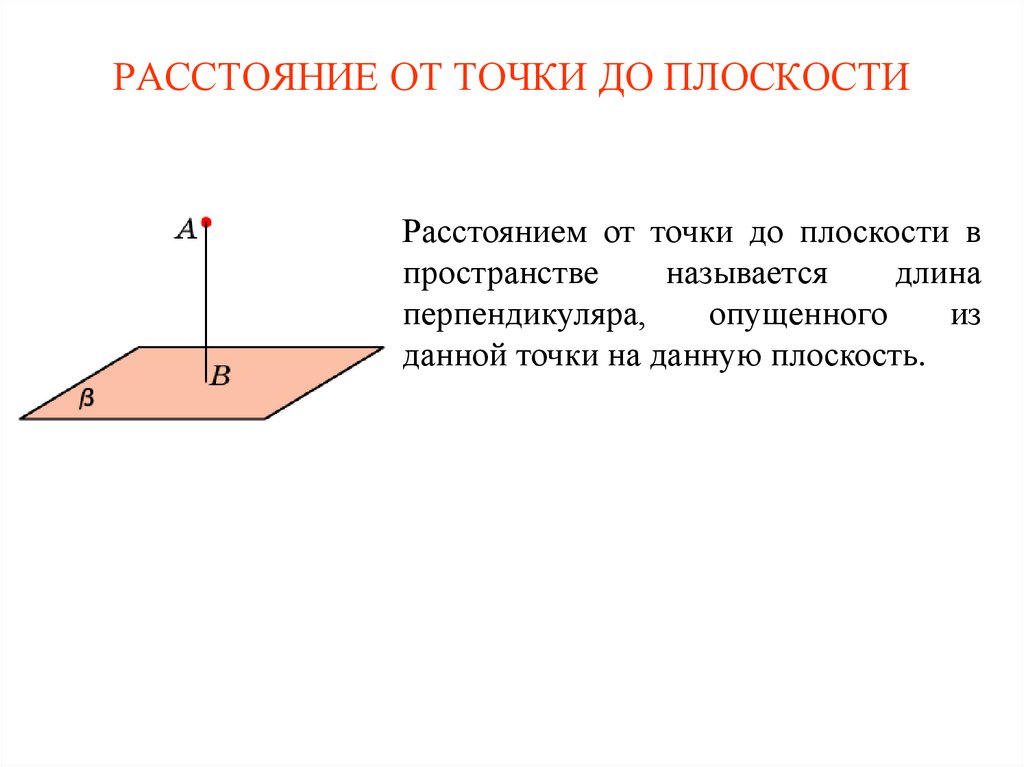 Затем: $$$|S_p=|\vec{v}|\cdot\text{d}(P,r)$$$

Следовательно, $$$\text{d}(P,r)=\dfrac{|\overrightarrow{QP}\times\vec{v}|}{|\vec{v}|}$$$

Рассчитать расстояние между точка $$P = (2, 4, 1)$$ и прямая $$r: (x, y, z) = (2, 3, -1) + k\cdot(1, 2, 1) $$.

Возьмем точку прямой, например $$Q = (2, 3, -1)$$. Теперь нам нужно будет вычислить векторное произведение векторов $$\overrightarrow{QP}$$ и $$\vec{v}$$.

$$\overrightarrow{QP}=(0,1,2)$$

$$\begin{array}{rl} |\overrightarrow{QP}\times\vec{v}|=& \влево| \begin{vmatrix} i & j & k \\ 0& 1& 2 \\ 1& 2& 1 \end{vmatrix} \right| = |i+2j-k-4i|=|-3i+2j-k| \\ =& |(-3,2,-1)|=\sqrt{9+4+1}=\sqrt{14} \end{array}$$

и мы уже можем применить формулу:

$$ $\text{d}(P,r)=\dfrac{|\overrightarrow{QP}\times\vec{v}|}{|\vec{v}|}= \dfrac{\sqrt{14}}{\sqrt{6}}=\sqrt{\dfrac{7}{3}}$$$

Похожие темы

• Расстояние между двумя плоскостями в космосе
• Расстояние между двумя прямыми в пространстве
• Расстояние от точки до плоскости в пространстве

Решенные задачи на расстояние от точки до прямой в пространстве

Посмотреть проблемы

Теория математики в твоем мобильном

Скачать бесплатно исчисление

— Кратчайшее расстояние от точки до кривой

спросил 5 лет, 11 месяцев назад

Изменено 1 год, 2 месяца назад

Просмотрено 59 тысяч раз

$\begingroup$

Мне бы не помешала помощь в решении следующей проблемы.