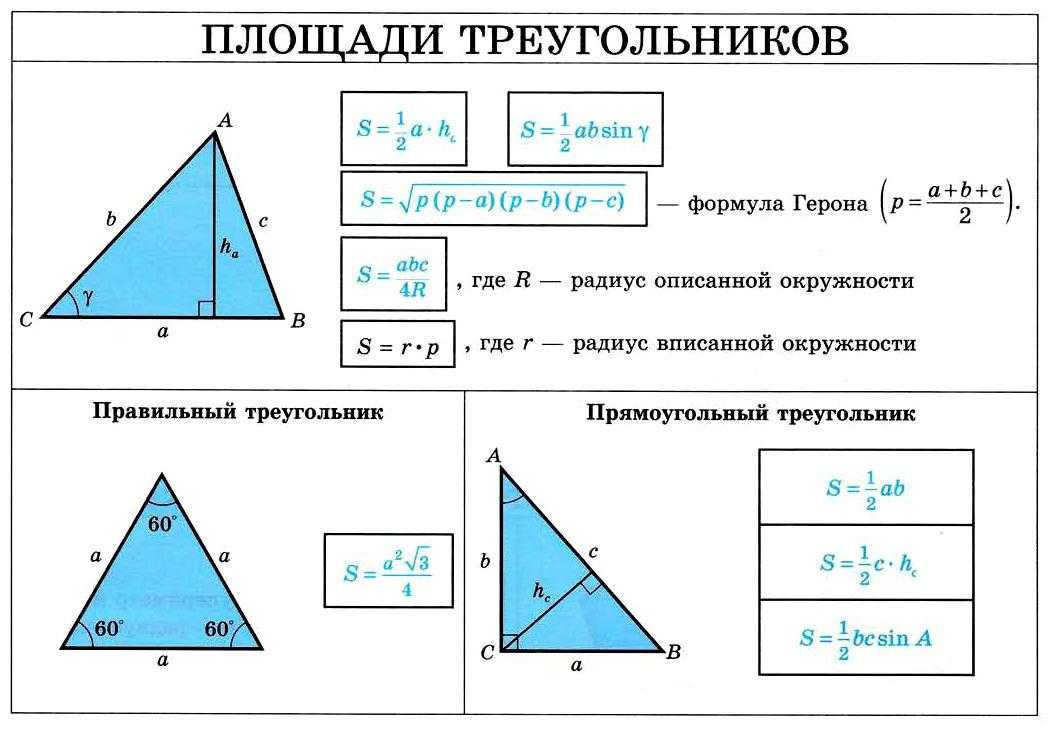
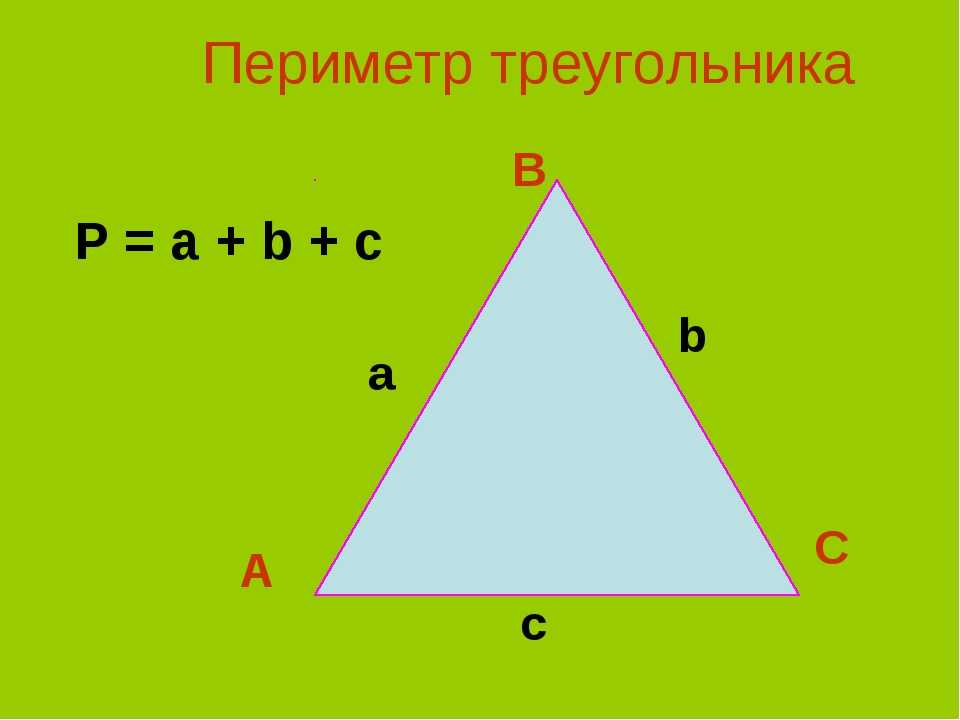
Урок математики в 4 -м классе «Площадь треугольника»
Цель:
- Сформировать понятие площади треугольника.
- Вывести формулу S треугольника.
- Повторить основные математические понятия (катеты, гипотенуза, высота…)
- Тренировать навыки быстрого счета
- Развитие мыслительных операций: (анализ, синтез, сравнение, обобщение)
Ход урока
I этап: Самоопределение к деятельности.
— У нас сегодня большое количество гостей, поздороваемся с ними. (Дети здороваются и садятся).
— Как думаете, какое количество гостей присутствует на нашем уроке? (Дети не считая отвечают и дают примерный результат).
— 1/6 часть всего кол-ва, это учителя нашей школы. Сколько их?
— Что мы сейчас делали? (Считали гостей).
— Всегда ли ваши ответы были точными? (Нет).
— По какой причине? (Не было времени считать, сделали прикидку, на глаз оценили).
— Используем ли мы данный прием на уроках? (Да).
— В каких ситуациях? (Нехватка времени, нет иного способа действия).
— Но математика наука точная, еще древний философ Платон говорил: «Математика приближает разум к истине». А значит ответы все же должны быть верными.
— А вот современное высказывание гласит: «Математику изучить нельзя…».
— Вы согласны с этим утверждением? (Нет, тогда что мы на уроках делаем?)
— Дело в том, что у этой фразы есть продолжение, которое вносит иной смысл , но вот какой и какое же у фразы продолжение мы узнаем в конце урока.
II этап: Актуализация знаний и фиксация затруднения в деятельности.
- Быстрый счет. (Конечный ответ цепочки примеров дети фиксируют на планшете).
- Внимание на экран. Какое из слов может быть лишним и почему?
(демонстрация № 1)
(Погода ,т.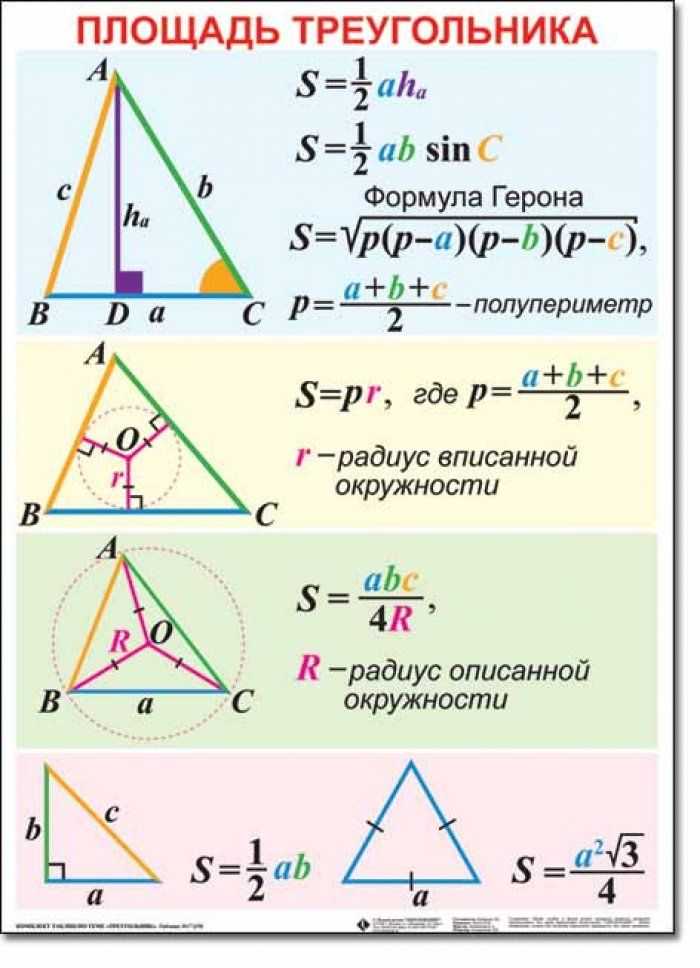
к не имеет к математике отношения).
— Но и не все оставшиеся слова будут иметь отношение к сегодняшнему уроку математики. Определить круг ключевых слов урока нам поможет арифметический диктант.
Арифметический диктант: (1 за доской, остальные работают в тетради)
— третья часть 18 6, 15, 7, 70, 24
— 3/4 от 20
— 1% числа 700
— 7 % от 1000
— 1/6 часть числа это 4, найди все число
(Проверка числового ряда, на экране исчезают лишние слова и числа).
— Что объединяет оставшиеся числа? (Целые, натуральные).
— На какие две группы можно разбить? (Дети предлагают варианты).
— А вот оставшиеся слова объединены темой сегодняшнего урока. Чтобы нам ее сформулировать как можно точнее, давайте вспомним основные математические понятия и поиграем
(Детям предлагаются карточки двух цветов, вопросы и ответы).
Основанием треугольника называется |
Сторона, на которую опущен перпендикуляр |
Сторона треугольника, лежащая против прямого угла называется… |
гипотенузой |
Площадь… |
Это место, которое фигура занимает на плоскости |
формула |
Это равенство, устанавливающее взаимосвязь между величинами |
Тупоугольным называется треугольник, у которого |
Один из углов тупой |
| Стороны треугольника, образующие прямой угол, называются |
катетами |
Перпендикулярные линии это |
Линии, которые при пересечении образуют прямой угол |
Высота треугольника |
Перпендикуляр, опущенный из любой вершины на противоположную сторону |
Остроугольным называют треугольник |
У которого все углы острые |
В зависимости от длины сторон треугольники бывают |
Равносторонние, разносторонние, равнобедренные |
Прямоугольным называют треугольник, у которого |
Один из углов прямой |
Чтобы найти площадь прямоугольника, надо |
Длину умножить на ширину |
Предлагаю поиграть еще в одну игру, которую придумали китайцы, всегда слывшие хорошими математиками.
Она называется «Танграм».
Суть ее состоит в собирании фигур из более мелких геометрических фигур. Работать будем в парах. Откройте конверт №1 и выложите все фигуры перед собой. Перечислите все, что перед вами. (4 маленьких и 2 больших прямоугольных треугольника разного цвета).
— Соберите из всех фигур:
1 ряд – квадрат
2 ряд – прямоугольник
3 ряд – треугольник
(Практическая работа в парах, проверка построений с помощью компьютера).
(демонстрация № 2)
— Что объединяет все получившиеся фигуры? (Многоугольники, состоят из равного кол-ва фигур).
— Сравните их по площади. (Равные, т.к. состоят из одинаковых частей).
— Как называются такие фигуры? (Равновеликие).
— Взгляните на фигуры. (демонстрация № 3)
— Можете ли вы утверждать, что данные фигуры также равновеликие? (нет, другая ситуация, иной значит способ действия).
— Используете знания свои и сравните фигуры по площади).
(Дети без труда по формуле находят S квадрата и прямоугольника, но возникает проблема при работе с треугольником).
III этап: Постановка проблемы, формулирование темы урока.
— Почему возникло затруднение? (Не знаем как найти S треугольника, можем только найти неточный результат).
— Значит какова цель сегодняшнего урока? ( научиться находить S треугольника).
— На основе поставленной цели и ключевых слов урока, попробуйте как можно точнее сформулировать тему сегодняшнего урока.
IV этап: Проектирование и фиксация нового знания.
(демонстрация № 4)
Расскажите все о треугольнике, который перед вами. (Прямоугольный, разносторонний).
— В группах попробуйте найти способ нахождения S прямоугольного треугольника, создать формулу и прокомментировать свои действия.
(Результаты вывешиваются на доску, в громкой речи проговаривается способ действия).
— Что такое стороны а и в? (Катеты).
— Сформулируйте свои выводы в знаковой и словесной форме.
— S = ( а в ) : 2 , Площадь прямоугольного треугольника равна половине произведения его катетов).
— Сверим свою формулировку с предложенной в учебнике (стр. 95).
— Площадь какого треугольника мы находили? (Прямоугольного).
— А для других треугольников эта формула будет верна? (Нет, т.к. нет катетов).
— Тогда давайте составим алгоритм наших действий.
Алгоритм.
- Выдели прямой угол
- Измерь длину катетов
- Найди S по формуле.
V этап: Первичное закрепление во внешней речи.
Выполняется в парах задание из учебника (стр. 95 № 5).
(демонстрация № 5)
VI этап: Самостоятельная работа с самопроверкой.
— Сравните фигуры по площади.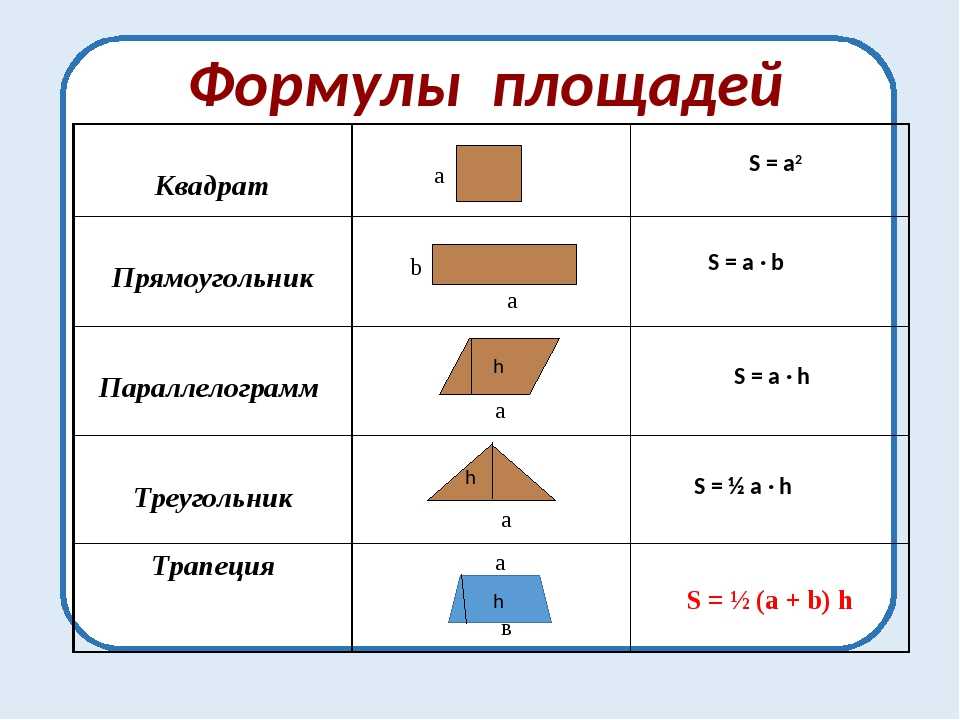
(Появляются в тетрадях записи:
S = ( 4 * 3 ): 2 = 6 кв.см
S = ( 2 * 6 ): 2 = 6 кв
S = S
VII этап: Включение в систему знаний и повторение.
— Вернемся к заданию, вызвавшему затруднение. Выполните расчеты в тетради и сравните площади данных фигур.
S = 2 * 2 = 4 кв.см
S = 1 * 3 = 3 кв.см
S = (3 * 2 ) : 2 = 3 кв.см
— Что можете сказать о S прямоугольника и треугольника? (Она одинаковая, значит фигуры равновеликие).
(демонстрация № 6)
Что вы можете сказать о данном треугольнике?
(Разносторонний, тупоугольный).
— Можем ли мы воспользоваться нашим алгоритмом для нахождения его площади?
(Нет, т.
к. должен быть треугольник прямоугольным).
— А нельзя ли с помощью построений сделать из данного треугольника два прямоугольных?
(Можно, надо провести высоту).
Чему будет равна площадь всего треугольника?
(Сумме S двух прямоугольных треугольников, их S мы умеем находить).
S = ( а* h ) : 2
S = ( а * h ) : 2
S = ( ( а + а ) * h ) : 2
( а + а ) -основание , значит
S = ( а * в ) : 2, где а – катет основание; в – катет высота
— Давайте дополним алгоритм.
Алгоритм.
VII этап: Рефлексия деятельности.
— Какова была цель урока?
— Удалось ли нам ее выполнить?
— А теперь узнаем окончание фразы «Математику нельзя изучить, наблюдая как это делает сосед».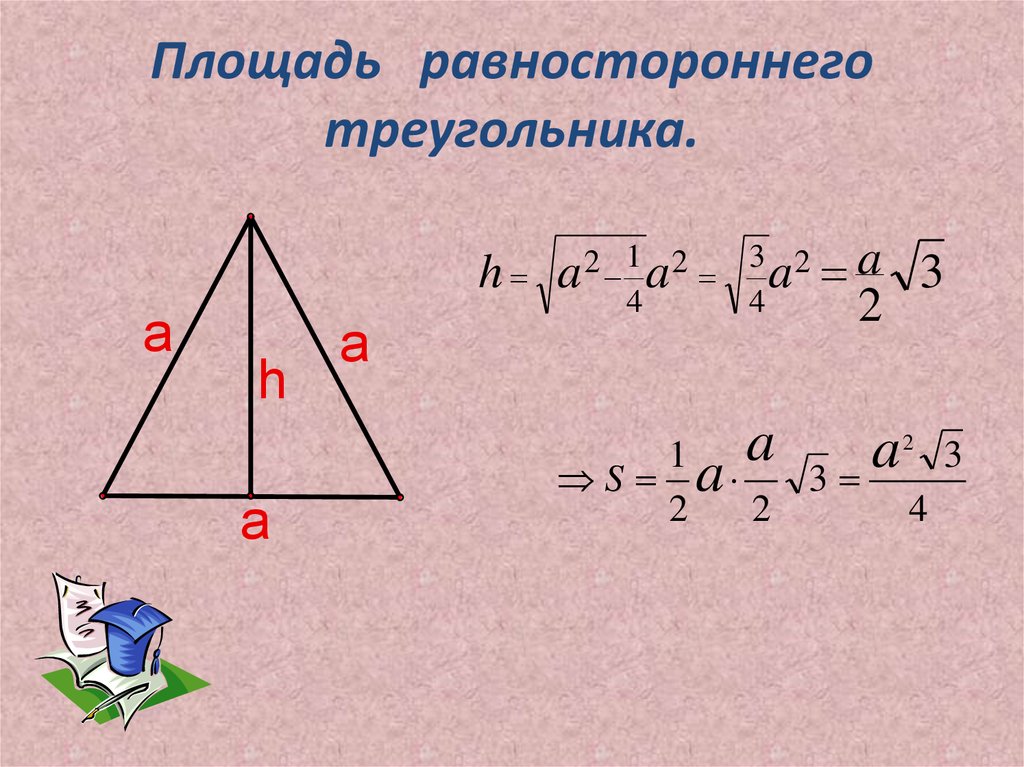
— Вы согласны с этим утверждением. (да, на уроке мы делали все сами, а не только наблюдали)
— Что на уроке было главным, а что интересным?
Д/З : (На выбор). – Найди S фигур и сравни фигуры по S.
(Задание в конвертах, на основе демонстрации дети выбирают нужное для себя, определив уровень понимания темы на данном этапе и берут задание из конверта)
Урок математики в 4-ом классе по учебнику Л.Г.Петерсон Тема: Площадь прямоугольного треугольника (урок № 32, открытие новых знаний). | План-конспект урока по математике (4 класс):
Урок математики в 4-ом классе по учебнику Л.Г.Петерсон
Тема: Площадь прямоугольного треугольника (урок № 32, открытие новых знаний).
Цели:
- познакомить с понятиями «катет», «гипотенуза»;
- вывести формулу площади прямоугольного треугольника;
- уметь находить площадь прямоугольного треугольника;
- закрепить вычислительные навыки и умение решать задачи;
- развивать речь, логическое мышление, память, внимание, навыки
самоанализа, познавательные интересы, расширять кругозор.
Оборудование: учебники-тетради Л.Г. Петерсон «Математика, 4 класс»; модели прямоугольника для работы учащихся, ножницы, проектор, ноутбук.
Ход урока:
1. Мотивация к учебной деятельности.
Мы сегодня снова будем наблюдать,
Выводы делать и рассуждать.
А чтобы урок пошёл каждому впрок,
Активно в работу включайся, дружок!
А что значит быть активным?
Проверка домашнего задания.
С.92 №7 (неизвестна часть числа: 22:11 *5 =10 (с.) – в упряжке, 22-10=12 (с) – не вошло в упряжку, с.93 №16 (б) (1-421, 2-409, 3-2 045 639, 4-320 247, 5-325 106)
— У кого другой ответ?
Посмотрите на экран, как вы понимаете это высказывание? (Слайд 2 )
«Окружающий нас мир – это мир геометрии». А.Д.Александров
Посмотрите на следующий слайд. ( Слайд 3 )
-О чём мы сегодня на уроке будем вести разговор?
-А почему внутри треугольника стоит вопрос?
-Значит, у нас сегодня какой урок? ( урок открытия нового знания).
— Что для этого вы должны будете сделать?
(Сами понять, что не знаем, а затем сами открыть новое.)
-Готовы?
2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии.
-С чего начнем урок? (С повторения)
-Что мы будем повторять? (То, что нам понадобится для изучения нового)
1.- Повторим,что такое треугольник? (геометрическая фигура, у которой: 3 стороны, 3 угла, 3 вершины)
— Какие бывают треугольники? (Слайд 4 )
— Назовите треугольники по размерам сторон? (равносторонние, разносторонние, равнобедренные).
— Назовите треугольники по размерам углов? (остроугольные, тупоугольные, прямоугольные).
— Повторим, какие бывают углы. (Слайд 5)
Предлагаю вам встать и с помощью рук показать виды углов, молча отвечая на мои вопросы (Дети встают и по команде учителя показывают с помощью рук острые, тупые, прямые углы — разводят руки меньше 90 градусов, больше 90 градусов, ставят руки под прямым углом).
Теперь посмотрите на экран и повторите глазами форму фигуры – это разминка для глаз. (Слайд 6)
2. Решите задачи и запишите решение в тетради, используйте опорные сигналы (на доске). (Слайд 7)
1. Найдите площадь прямоугольника со сторонами 3см.
(S=a*a? S= 9 кв.см)
2.Одна сторона прямоугольника 12см, а другая составляет 5/6 первой. Вычислите площадь прямоугольника. (найти часть числа, b = a : n * m, 12 : 6 * 5 = 10см,
S = a * b, 12 * 10 = 120кв.см)
3. Сторона прямоугольника, равная 15см, составляет 3/5 его второй стороны. Каков периметр прямоугольника? (найти целое число, a= b : m * n, 15 : 3 * 5 = 25см, p = (a + b) *2, (25 + 15) *2 = 80кв.см)
— Что интересного вы заметили? ( в 1 задаче – прямоугольный квадрат)
— Что такое квадрат? (прямоугольник с равными сторонами)
— Назовите формулу площади квадрата. (на доске)
— Назовите опорные схемы, которые вы использовали при решении 2-й задачи? 3-й ? ? — Какой схемой не воспользовались? — Когда вы её применяете? (при нахождении периметра квадрата)
— Проверьте себя, ответы на слайде 8.
(9кв.см, 120кв.см, 80см )
— Кто сразу сделал всё без ошибок? — Молодцы!
— Кто нашёл свои ошибки?- Что вам надо повторить?
— Все ошибки исправлены? Молодцы!
3. Беседа
— Что сейчас повторяли?
— Почему я взяла именно эти задания? (Помогут узнать что-то новое.)
— Какой следующий наш шаг? ( Пробное действие.)
4. Предлагаю в качестве пробного действия практическую работу.
-Возьмите модель прямоугольника и проведите одну из его диагоналей. Сколько получилось треугольников? (2)
-Определите виды углов этих треугольников. (По два острых и одному прямому углу). -Треугольник, содержащий прямой угол, называют прямоугольным.
-Равны ли полученные прямоугольные треугольники? Докажите не вычисляя. (Мнения могут разойтись: перегибанием прямоугольника треуг – ки не совпадают. Ученикам необходимо разрезать прямоугольник по диагонали и полученные прямоугольники совместить.)
-Сравните данные треугольники по площади. (Треугольники равны, поэтому равны и их площади.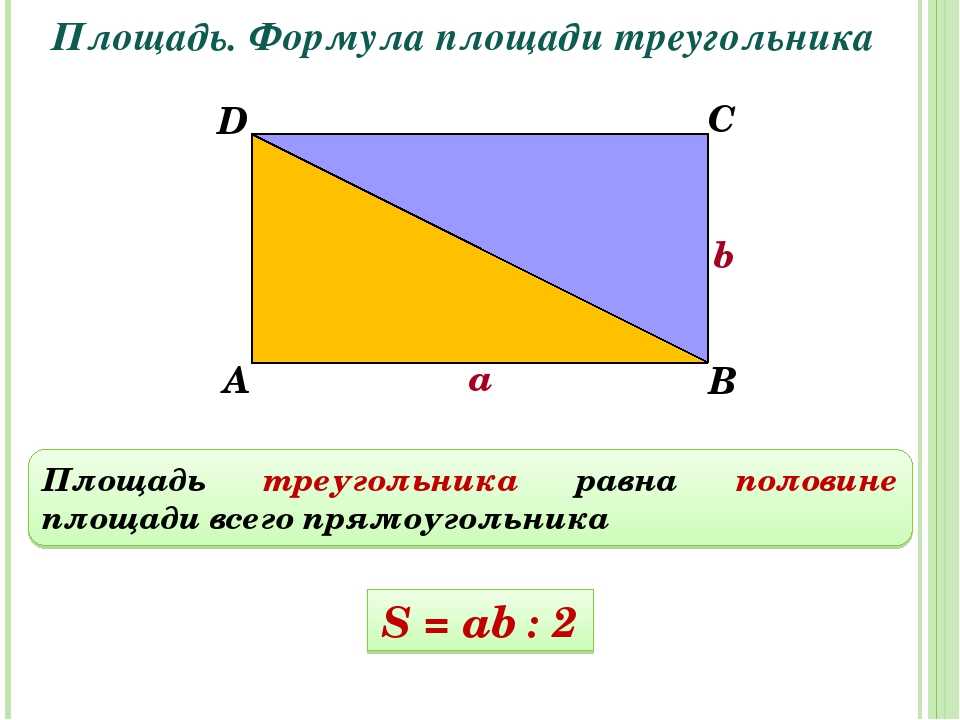
)
— Чему равна площадь каждого из полученных треугольников? (Площадь одного треугольника равна половине площади прямоугольника.)
-(Слайд 9) Стороны, образующие прямой угол прямоугольного треугольника, называются катетами, а третья сторона, лежащая напротив прямого угла, называется гипотенузой. Выделите катеты красным цветом, а гипотенузу – синим.
5. Индивидуальное задание
-Найдите площадь прямоугольного треугольника с катетами 8 см и 15 см (Слайд 10
-Давайте посмотрим, что у вас получилось. (Учитель выслушивает варианты решений детей).
— Докажите, что ваше решение верно. (Мы не можем доказать.)
— Значит, что показало пробное действие? (Мы не смогли решить это задание.) ——— Давайте разберёмся , в чём ваше затруднение.
III. Выявление места и причины затруднения.
-Какое затруднение возникло и почему при выполнении последнего задания?
(Мы не знаем формулу S прямоугольного треугольника).
4. Построение проекта выхода из затруднения.
— Итак, мы выявили причину затруднения, что вы будете делать дальше?
(Мы поставим перед собой цель — Узнать формулу нахождения S прямоугольного треугольника.
— Чему должны научиться на уроке? (Научиться решать задачи на нахождение площади прямоугольного треугольника).
Сформулируйте тему урока.
— Площадь прямоугольного треугольника. (Слайд 11)
ФИЗМИНУТКА
IV. Построение проекта выхода из затруднения.
-Давайте подумаем, как нам получить способ решения поставленной задачи.
Я вам предлагаю воспользоваться треугольниками, которые лежат у вас на партах. Работая в парах, вы попробуете составить из двух треугольников какую-либо фигуру. (Дети могут составить большой треугольник, четырехугольник, прямоугольник). — Посмотрите, какие фигуры могли у вас получиться. (Слайд 12)
– Площадь, какой фигуры мы можем находить? (площадь прямоугольника).
— Покажите эту формулу на доске.
— Используя эту формулу, попробуем вывести новый эталон.
-Что можете сказать о прямоугольнике и прямоугольном треугольнике? (прямоугольный треугольник – это половина прямоугольника)
(Слайд 13) –Уточним, прямоугольник треугольный? (ДА)
— Вы сказали, что прямоугольный треугольник – это половина прямоугольника. В таком случае , что мы сделаем дальше? (Достроим до прямоугольника)
— А как связаны между собой площадь прямоугольного треугольника и площадь прямоугольника? (Площадь прямоугольного треугольника равна половине площади прямоугольника)
-А площадь прямоугольника мы можем находить? (Да, надо перемножить длину и ширину)
— Какой следующий шаг? (Найдём площадь прямоугольника)
— Тогда как найти площадь прямоугольного треугольника? (Разделим площадь прямоугольника на 2)
— Как записать, чему равна площадь прямоугольного треугольника на математическом языке в виде формулы? (S = (a * b) : 2)
(Слайд 14) — Прочитайте полученную формулу. (Площадь прямоугольного треугольника равна половине произведения его сторон.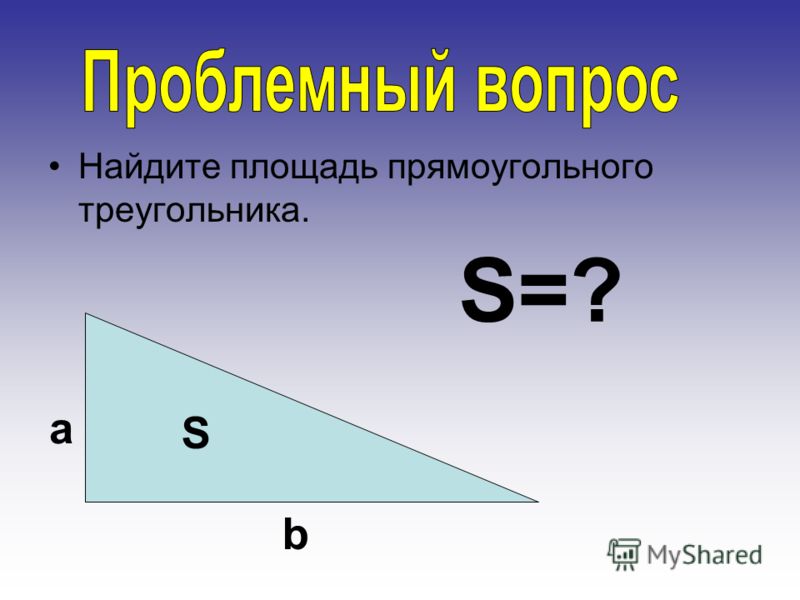
)
— Что означают в формуле буквы а и в? (Это катеты).
-А теперь прочитайте текст на стр. 95.(«Площадь прямоугольного треугольника равна половине произведения его катетов».)
— Сравните наше правило с текстом учебника. В чём отличие? (В нашем правиле – половина произведения сторон, а здесь — половина произведения катетов. )
— Это имеет значение? ( да, иначе можно взять диагональ, а в формуле только катеты).
(Слайд 15) — Итак, уточните ещё раз – чему равна площадь прямоугольного треугольника.(«Площадь прямоугольного треугольника равна половине произведения его катетов».)
— Вы открыли новое знание? (да)
(Слайд 16) — Пользуясь полученным правилом, решите задачу, которая вызвала затруднение. Проверьте себя : (8 * 15) : 2 = 120 : 2 = 60 кв.см
5. Первичное закрепление во внешней речи.
— Можно ли сказать, что вы уже всё сделали на уроке?
— Какую цель мы ещё ставили? (Научиться применять изученную формулу и решать задачи на нахождение S прямоугольного треугольника).
— Что для этого нужно сделать? (Потренироваться в использовании нового алгоритма).
— Дети выполняют задание №3 стр.94 с комментированием, подписывают катеты и гипотенузу — Кто допустил ошибку? Исправьте допущенные ошибки и объясните их. -Кто выполнил верно? Молодцы.
— Я предлагаю выполнить задание на слайде. Найти S прямоугольных треугольников. (Работа по вариантам). (Слайд 17)
— Проверка заданий по образцу. Те, кто допустил ошибки, проговаривают решение вслух. -Кто выполнил верно? Молодцы. Поставьте себе «+».
6. Самостоятельная работа с самопроверкой по эталону.
-Научились вы решать задачи на нахождение площади прямоугольного треугольника? Как это проверить? (Выполнить самостоятельную работу по вариантам.) – с.95 №5 (2-3)
Проверьте себя – на слайде.
1 вариант: 5 * 3 + (5 *4) : 2 = 25(кв.см)
2 вариант: ( (2 * 3) : 2 + 2 * 3 + (4 * 3) :2 = 15(кв.см) .
Кто допустил ошибку? Поставьте знак –«?» Исправьте допущенные ошибки и объясните их.
-Кто выполнил верно? Молодцы. Поставьте себе «+».
7. Включение в систему знаний и повторение.
-Выполним задание №6 с.95. (а) а : 5 * 3; б) б : 4 *7; в) с : 100 *9; г) d : 30 *100 (Хорошо успевающие ученики затем могут выполнить дополнительное задание с.96 № 10(а).) (а = 67 598)
— Проверка по эталону на доске. Кто не смог сам верно выполнить задание? А где вы сможете еще раз потренироваться в выполнении таких заданий? (При выполнении домашнего задания)
-У кого нет ошибок? Молодцы! Поставьте «+».
8. Рефлексия деятельности (итог урока).
-Проанализируйте свою деятельность на уроке. Дополните фразу:
На уроке мы узнали … (как найти площадь прямоугольного треугольника, название сторон треугольника: катеты, гипотенуза)
Мы научились … (решать задачи на нахождение площади прямоугольного треугольника)
— Какие трудности у вас ещё встречаются? Где можно над ними поработать и применить полученные знания ( в дом. работе, на следующих уроках)
— Нарисуйте в тетради «лестницу успеха» и оцените свою деятельность.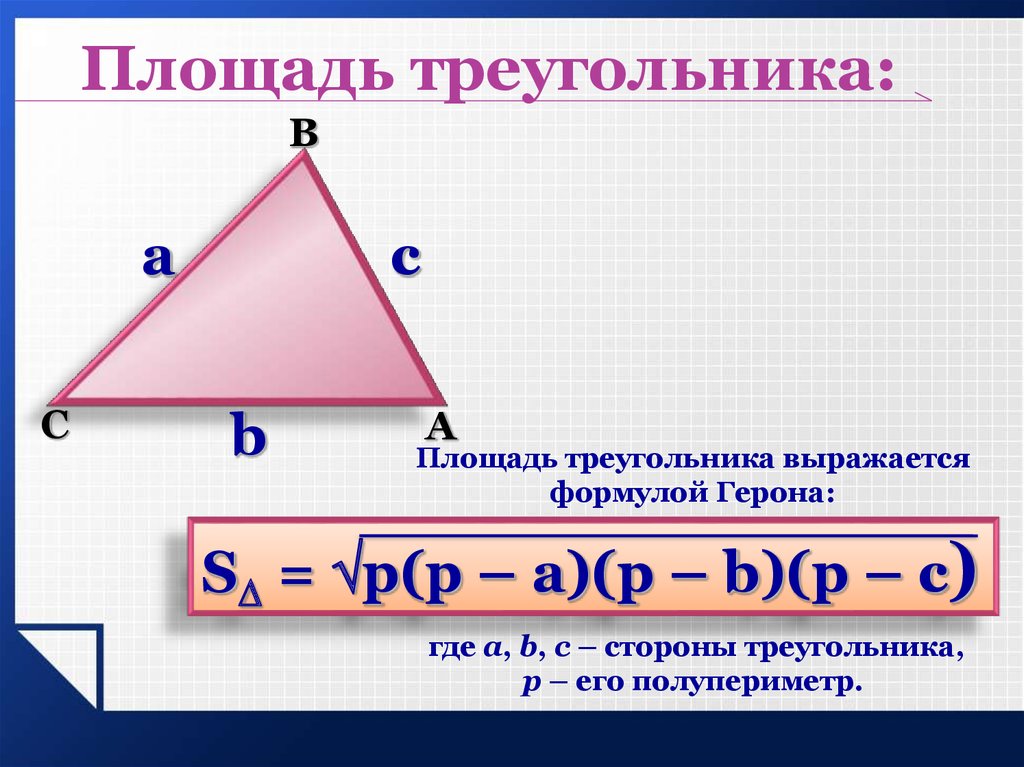
Домашнее задание: начертить прямоугольный треугольник и найти его площадь, №7.10(б) с.96
Оценки за урок.
Молодцы! Спасибо за урок!
Как найти площадь треугольника
Все математические ресурсы начального уровня SSAT
12 диагностических тестов 526 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
SSAT Elementary Level Math Help » Геометрия » Плоская геометрия » Треугольники » Как найти площадь треугольника
Высота треугольника задается как , а его основание как . Чему равна площадь треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь треугольника равна .
высота
основание =
Следовательно:
Площадь
Сообщить об ошибке
Какова площадь треугольника с основанием 11 и высотой 4?
Возможные ответы:
44
6
14
22
60
Правильный ответ:
22
Объяснение:
Формула для нахождения площади треугольника: .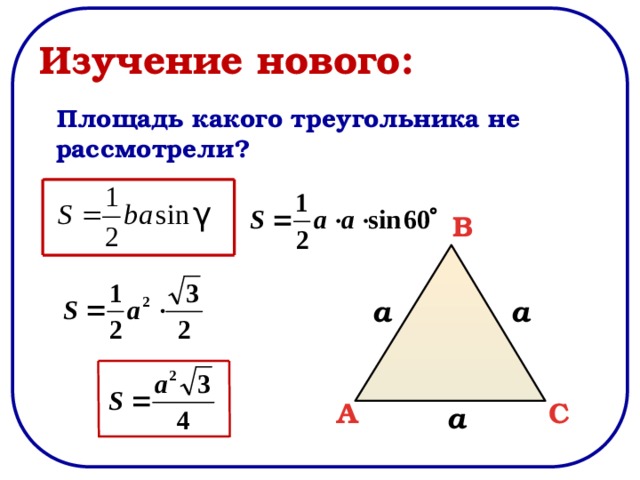
Во-первых, мы должны умножить 11 (основание) x 4 (высота), чтобы получить в сумме 44. Затем нам нужно разделить 44 на 2, что дает нам общую площадь 22 .
Сообщить об ошибке
Вы можете найти площадь треугольника, если знаете ___________.
Возможные ответы:
высота и основание
длины двух сторон
углы
периметр
Правильный ответ:
высота и основание
Объяснение:
Сообщить об ошибке
Квадрат, показанный выше, имеет длину стороны 3 и разделен диагональю на два треугольника. Чему равна площадь одного из треугольников?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь квадрата равна стороне, умноженной на сторону, .
Каждый треугольник составляет половину квадрата, .
Сообщить об ошибке
Какова площадь треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для нахождения площади треугольника:
Сначала мы должны умножить (основание) (высоту), чтобы получить в сумме .
Далее нам нужно разделить на , что даст нам общую площадь .
Сообщить об ошибке
Равнобедренный треугольник имеет основание 12 см и высоту 6 см. Чему равна площадь треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти площадь треугольника, нужно умножить основание (12 см) на высоту (6 см):
Следовательно, площадь этого треугольника равна .
Сообщить об ошибке
Треугольник имеет основание 14 и высоту 8. Какова площадь треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти площадь треугольника, умножьте основание (14) на высоту (8) и разделите на 2:
Следовательно, площадь этого треугольника равна .
Сообщить об ошибке
Какова площадь треугольника?
Возможные ответы:
60
24
48
30
28
20 5 Правильный ответ: 900 4
Объяснение:
Формула для нахождения площади треугольника: .
Сообщить об ошибке
Если треугольник имеет основание 3 дюйма и высоту 8 дюймов, какова площадь треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади треугольника .
Подставьте полученные значения, чтобы решить уравнение:
Сообщить об ошибке
Треугольник имеет основание 10 сантиметров и высоту 12 сантиметров. Чему равна площадь треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади треугольника .
Подставьте данные значения, чтобы найти площадь:
=
=
Площадь этого треугольника равна .
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все математические ресурсы начального уровня SSAT
12 диагностических тестов 526 практических тестов Вопрос дня Карточки Учитесь по концепции
Площадь треугольников — простые для понимания примеры и решения
Этот урок покажет вам различные способы нахождения площади треугольников.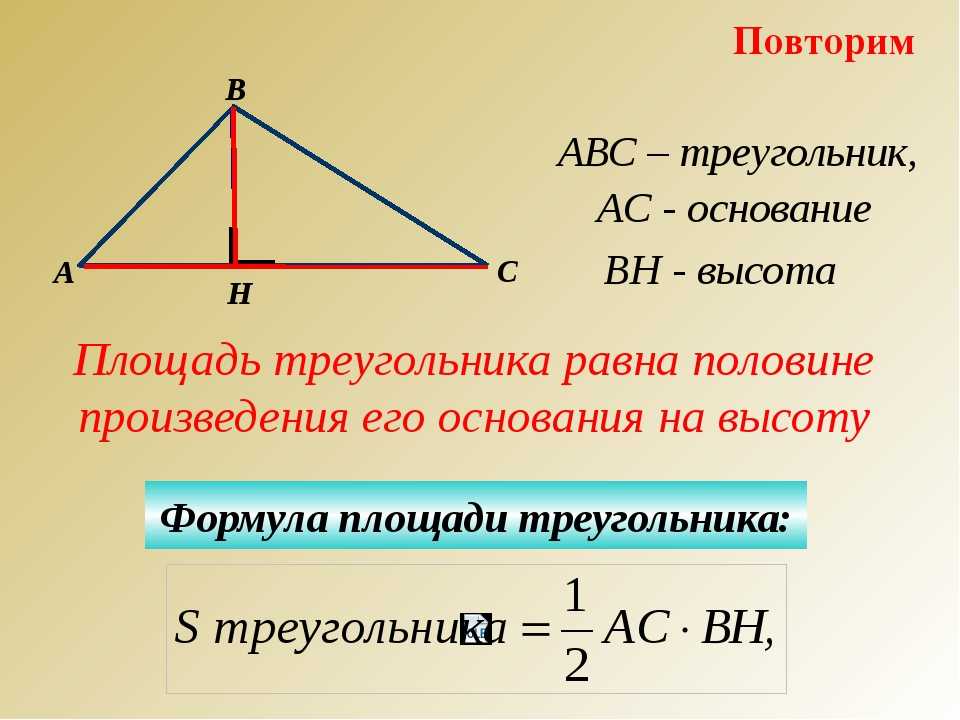
По определению, площадь треугольника — это пространство, занимаемое треугольником в двумерной плоскости.
Формула площади треугольника
Самый распространенный способ найти площадь треугольника — использовать базовую формулу, показанную ниже синим цветом.
Площадь треугольника = (основание × высота)/2
Красная линия представляет длину основания (назовите ее b, если хотите), а синяя линия представляет длину высоты.
Как видите, чтобы найти площадь, просто умножьте основание треугольника на высоту треугольника и разделите результат на 2.
Площадь треугольника
Однако вы также можете найти площадь треугольника на основе следующих двух случаев:
- Известны три стороны треугольников (треугольник SSS)
- Известны две стороны и угол между ними (треугольник SAS)
Площадь выражена в квадратных единицах.
- Если основание и высота измеряются в метрах, то площадь измеряется в квадратных метрах или м 2 .
- Если основание и высота измеряются в сантиметрах, то площадь измеряется в квадратных сантиметрах или см 2 . Пример №1 основание × высота)/2
Площадь = (9 × 4)/2
Площадь = 36/2
Площадь = 18
Площадь равна 18 квадратных дюймов или 18 дюймов.
Площадь = (основание × высота)/2
Площадь = (4 × 3)/2
Площадь = 12/2
Площадь = 6
Площадь 6 квадратных дюймов или 6 дюймов 2
5 9 Пример №3
Найдите площадь прямоугольного треугольника, показанного на рисунке ниже, с основанием 5 дюймов и высотой 6 дюймов:
Площадь = (основание × высота)/2
Площадь = (5 × 6)/2
Площадь = 30/2
Площадь = 15
Площадь 15 квадратных дюймов или 15 дюймов 2
8Использование формулы Герона для нахождения площади треугольника, когда известны три стороны треугольника (SSS)
Древнегреческий математик Герон наиболее известен своей формулой площади треугольника, когда известны длины его сторон а, б и в.
Площадь представляет собой квадратный корень из произведения s(s-a)(s-b)(s-c).
A =√[s(s-a)(s-b)(s-c)], где s — полупериметр треугольника.
s = (a + b + c)/2
Пример #4
Длины сторон треугольника равны 15 футам, 9 футам и 12 футам. Воспользуйтесь формулой Герона, чтобы найти площадь треугольника.
s = (a + b + c)/2
s = (15 + 9 + 12)/2
s = (36)/2
s = 18
A =√[s(s-a) (s-b)(s-c)]
A =√[18(18-15)(18-9)(18-12)]
A =√[18(3)(9)(6)]
A =√[(54)(54)]
A =√(2916)
A = 54 квадратных фута
Реальный урок о формуле Герона, чтобы увидеть больше примеров.
Площадь треугольника, когда известны две стороны и угол между ними (SAS)
Когда известны две стороны и угол между двумя сторонами (SAS), площадь равна половине произведения смежных сторон на синус прилежащего треугольника. угол.
Следовательно, используйте приведенную ниже формулу, чтобы найти площадь:
Площадь = [bc(sinA)]/2
Пример #5
Длины двух смежных сторон треугольника равны 8 см и 12 см.
