Синус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое синус угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда синусом угла α будет отношение противолежащего катета к гипотенузе sin α = BC/AC
Так же для определения синуса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O. На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Синусом угла α будет отношение ординаты точки YP к радиусу окружности.
sin α = YP/R, в случае, если окружность единичная (радиус окружности = 1), формула примет вид sin α = YP.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление.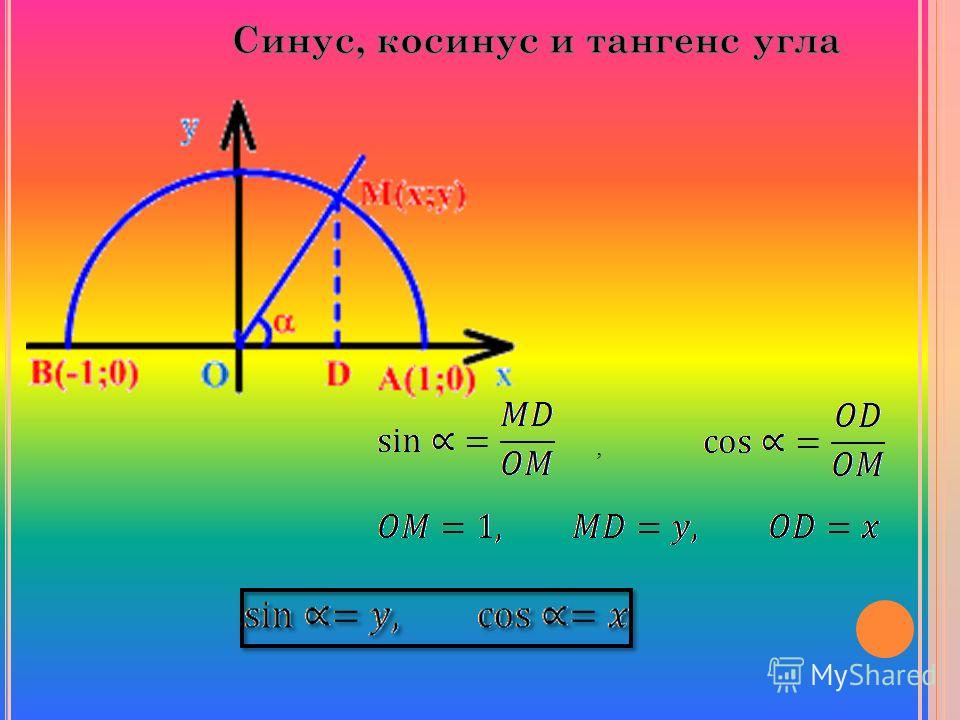 Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.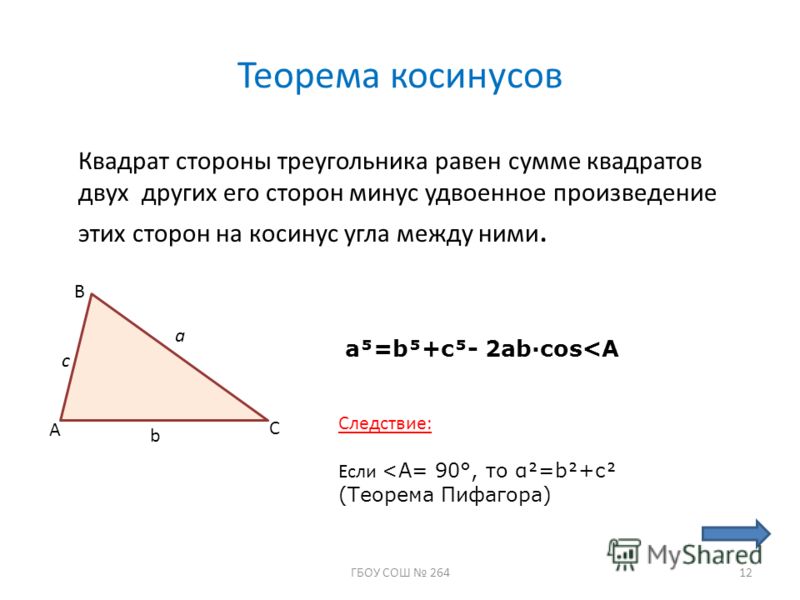 |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Функция косинуса: онлайн калькулятор, формулы, график
Функция {$ main.types[data.type] $}
Введите угол α{$ main.angles[data.angle1] $}
Результат расчёта
{$ data.type $}(α) = {$ result[0]|number:data.round $}
Введите {$ data.type $}(α){$ main.angles[data.angle2] $}
Результаты расчёта
- {$ result[1] $}
- {$ result[2] $}
Округлять до
{$ data. round $} {$ Plural(data.round, [‘знака’, ‘знаков’, ‘знаков’]) $} после запятой
round $} {$ Plural(data.round, [‘знака’, ‘знаков’, ‘знаков’]) $} после запятой
Косинус — тригонометрическая функция, которая геометрически определяется как соотношение прилежащего катета к гипотенузе. Как и все тригонометрические функции, косинус нашел широчайшее применение в науке.
История вопроса
Тригонометрия как наука возникла еще в Древней Индии, когда ученые разработали таблицу соотношений катетов и гипотенуз и их численных значений для основных углов. Термин «косинус» — сравнительно молодой, так как изначально ученые пользовались только синусом и тангенсом угла. Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Геометрически косинус — это соотношение прилежащего катета к гипотенузе. Прилежащий катет — это сторона прямоугольного треугольника, которая вместе с гипотенузой образует рассматриваемый угол.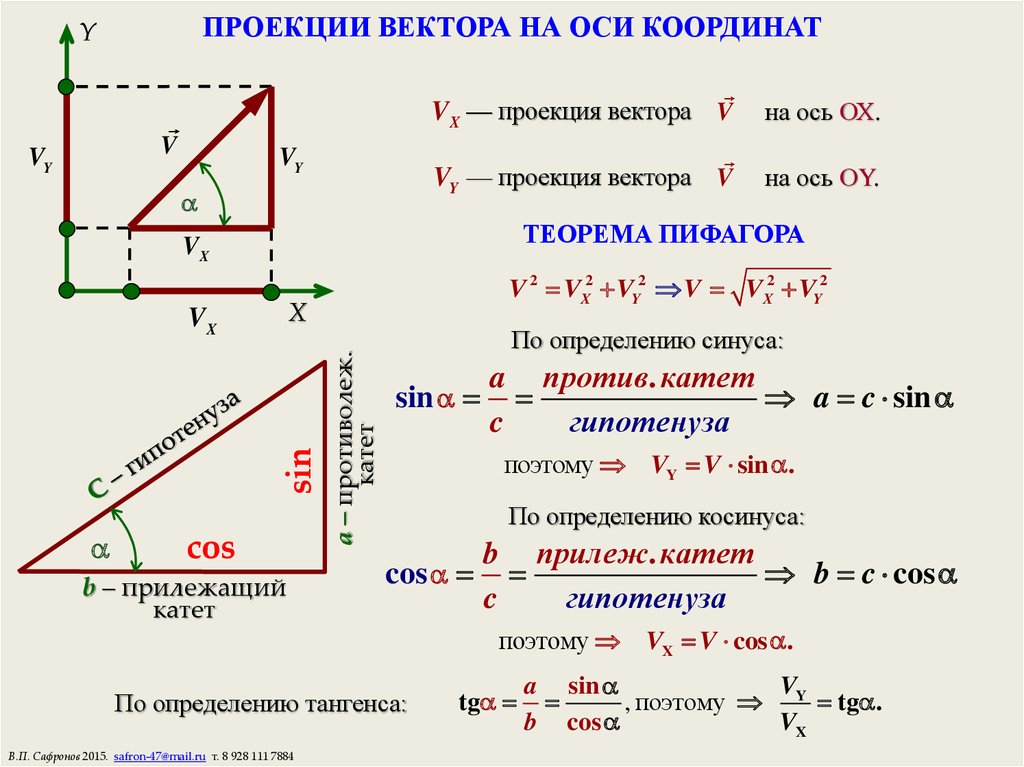 Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Определение косинуса
Итак, есть прямоугольный треугольник, катеты которого обозначаются как A и B, а гипотенуза как C. Из определения косинуса мы получаем, что для заданного угла AC его соотношение прилежащего катета и гипотенузы будет равно cosAC = A/C. Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники.
Теорема косинусов
Для любого треугольника справедливо равенство:
a2 = b2 + c2 — 2b × c × cosA,
где угол A — это угол, противолежащий стороне a.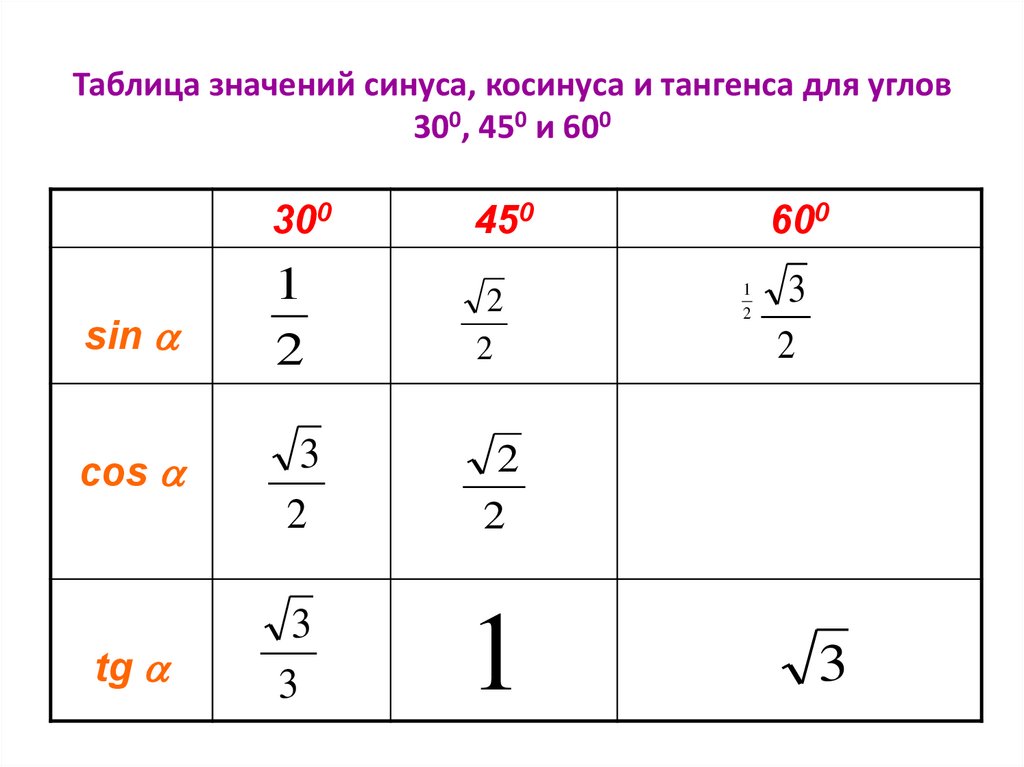
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
a2 = b2 + c2,
где a — гипотенуза.
Использование косинусов
В повседневной жизни тригонометрические функции не находят применения. Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности.
Наша программа представляет собой онлайн-калькулятор, который позволяет рассчитывать значения основных тригонометрических функций углов, выраженных в градусах или радианах. Для использования калькулятора требуется выбрать в меню программы требуемую функцию и ввести величину угла в градусах. Калькулятор вычисляет и обратную функцию арккосинуса. Если требуется определить угол по известному значению косинуса, введите значение функции в ячейку «Косинус» и выполните расчет. Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора.
Примеры из жизни
Вычисление углов
Пусть в задаче по геометрии дан треугольник со сторонами A = 3 см, B = 4 см и C = 5 см. Требуется найти значения всех углов. На первый взгляд это сложная задача, однако мы знаем, что 3, 4 и 5 — это классическая пифагорова тройка, следовательно, известны значения катетов и гипотенуз. Очевидно, что угол AB = 90 градусов, так как катеты всегда образуют прямой угол. Теперь мы можем найти углы AC и BC. Косинус угла численно равен дроби, в числителе которой стоит прилежащий катет, а в знаменателе — гипотенуза. Прилежащие катеты — это образующие угол катеты, следовательно, cosAC = A/C и cosBC = B/C. Подсчитаем численные значения:
Косинус угла численно равен дроби, в числителе которой стоит прилежащий катет, а в знаменателе — гипотенуза. Прилежащие катеты — это образующие угол катеты, следовательно, cosAC = A/C и cosBC = B/C. Подсчитаем численные значения:
- cosAC = A/C = 3/5 = 0,6;
- cosBC = B/C = 4/5 = 0,8.
Теперь определим соответствующие углы при помощи нашего калькулятора. Углы с такими значениями косинусов равны соответственно 53,13 и 36,87 градуса. Правильность решения легко проверить, сложив величины углов:
90 + 53,13 + 36,87 = 180.
Расчет косинусов
Прямая задача определения численных значений функций — это вычисление косинуса в зависимости от величины угла. Для такой задачи можно использовать таблицу Брадиса — четырехзначные таблицы значений тригонометрических функций для целочисленных величин углов. Вычислим значения косинусов для основных углов. Для этого введем значения в ячейки «Косинус»:
- cos30 = 0,866;
- cos45 = 0,707;
- cos60 = 0,5;
- cos90 = 0;
- cos120 = –0,5;
- cos150 = — 0,866;
- cos180 = — 1.

Это основные значения косинусов для стандартных величин углов треугольника. В целом значения тригонометрических функций периодически повторяются каждые 360 градусов.
Заключение
Тригонометрия — определенно важный раздел математики, функции которого повсеместно используются в современных технологиях. Наши калькуляторы прекрасно подходят для элементарных расчетов по геометрии и тригонометрии.
Калькулятор Синусов — Как Найти Синус Угла
Онлайн-калькулятор синусов определит тригнометрические значения синуса для заданного угла в градусах, радианах или π радианах.
Просто найдите время, чтобы узнать, как найти грех, как нарисовать синусоидальный график для представления синусоидальной кривой и многое другое, что поможет вам в решении тригонометрических функций, связанных с синусом.
Что такое грех в математике?В математике функция синуса определяется в виде прямоугольного треугольника. Для выбранного угла это отношение длины стороны, противоположной этому углу, и гипотенузы.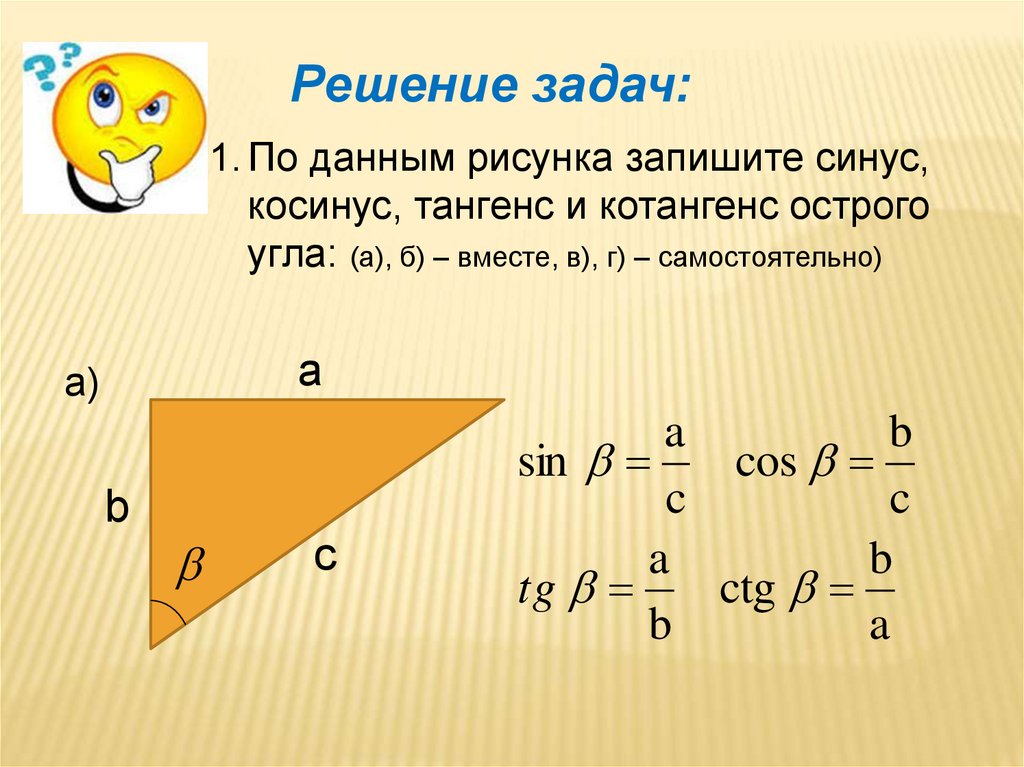
- Формула синуса: sin (α) = противоположная точка a / гипотенуза c
Однако для решения в калькуляторе синусов нет необходимости вводить формулу, просто введите соответствующие значения.
Кроме того, онлайн-калькулятор CSC позволяет вам найти тригонометрическую функцию косеканса (csc) для введенного угла в градусах, радианах или π радианах.
Как найти синус угла?Синус угла α в прямоугольном треугольнике может быть представлен отношением между противоположной стороной угла и его гипотенузой. Однако вы можете использовать следующую формулу для вычисления греха угла и использовать калькулятор синусов для быстрых и простых вычислений:
Синус (α) = a / c
Пример:
Если длина противоположной стороны угла равна 10, а гипотенуза равна 2, то значение синусоидальной функции можно рассчитать следующим образом:
- грех (α) = 10/6 = 5/2
Синусоидальный график для каждого возможного угла будет иметь повторяющуюся кривую вверх / вниз, известную как синусоида. Синусоидальная кривая начинается с угла 0, затем возрастает до значения 1, а затем уменьшается до значения -1. Затем будет продолжаться та же схема, как показано ниже:
Синусоидальная кривая начинается с угла 0, затем возрастает до значения 1, а затем уменьшается до значения -1. Затем будет продолжаться та же схема, как показано ниже:
Значения синуса для некоторых распространенных углов показаны в следующей таблице:
| Градусы ° | Радианы | синус (х) |
| 0° | 0 | 0 |
| 30° | π/6 | 0.50 |
| 45° | π/4 | 0.707107 |
| 60° | π/3 | 0.866025 |
| 90° | π/2 | 1 |
| 120° | 2π/3 | 0.866025 |
| 135° | 3π/4 | 0.707107 |
| 150° | 5π/6 | 0.50 |
| 180° | π | 0 |
Кроме того, онлайн-калькулятор Arcsin поможет вам вычислить arcsin (x) и отобразить результаты в радианах и градусах.
Этот калькулятор синусоид функционировал автоматически, следуя уравнению синуса, и выдает значение синуса в мгновение ока для любого угла. Его рабочий процесс объясняется ниже:
Вход:- На первом шаге введите значение ангела
- Выберите градус, радиан или (π) радиан из выпадающего меню в соответствии с вашими требованиями.
- Нажмите кнопку «рассчитать».
Этот калькулятор синусов определит:
- Значение синуса в радианах, градусах или пи (π) радианах в зависимости от требуемого угла.
- Сделайте еще один расчет, нажав на опцию «пересчитать».
Мотив синуса и косинуса состоит в том, чтобы решить треугольник, чтобы определить длину каждой из его сторон и всех его углов. Мы применим синусоидальную функцию, когда есть два угла и одна сторона. С другой стороны, функция косинуса будет применяться, когда даны три стороны или две стороны с включенным углом.
С другой стороны, функция косинуса будет применяться, когда даны три стороны или две стороны с включенным углом.
Слово «синус» происходит из латинского языка и придумано Робертом Честерским из арабского jiba, что является преобразованием санскритского слова jya-ardha.
Одинаковы ли синусоидальные функции?Нет, функция синуса не является взаимно однозначной. когда нам нужно определить обратные функции для синуса, области ограничены 0 ≤ x ≤ π.
Синус – нечетная функция?Да, синус – нечетная функция, однако большинство функций в тригонометрии не являются ни нечетными, ни четными, но некоторые функции являются теми или иными. Однако наиболее удобный способ обработки синусоидальной функции – это использование калькулятора синусов.
Заключение:К счастью, этот калькулятор синусов позволит студентам и профессионалам работать со сложными углами и размерами за относительно короткое время. Нет необходимости запоминать тригонометрическое синусоидальное уравнение, просто введите значение, и инструмент произведет точные вычисления.
Нет необходимости запоминать тригонометрическое синусоидальное уравнение, просто введите значение, и инструмент произведет точные вычисления.
Из источника Википедии: Прямоугольный треугольник, Бегущие и стоячие волны, Закон синусов.
Из источника Lumen Learning: графические вариации sin (x), исследование синусоидальных функций, определение амплитуды, вертикальный сдвиг функции.
Из источника Varsity Tutors: функция синуса, графическая функция синуса, амплитуда и период функции Since.
Other Languages: Sine Calculator, kalkulator sinus, Kalkulator Sinus, Sinüs Hesaplama, Sinus Rechner, Sin 計算, Sinus Kalkulačka, Calcular Seno, Calcular Seno, Calcul Sinus, Calcolo Del Seno.
Вычислить и найти синус онлайн
Пример решили: 83052 раза Сегодня решили: 0 раз
Введите градусы или радианы
Угол Градусы (°)Радианы (rad)
Вычисление синуса
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
В прямоугольном треугольнике с острым углом α справедливо следующее соотношение:
синус угла α равен отношению противолежащего катета к гипотенузе. {\circ} $$ .
{\circ} $$ .
Ответ:
$$ sin \ \alpha = 0.7071 $$
Попробуйте другие сервисы
Перевод градусов в радианы
Вычисление косинуса
Вычисление тангенса
Вычисление котангенса
Вычисление секанса
История решений
- Приложение: Синус, косинус и тангенс
- Разработчик: Antonio Luis Climent Albaladejo
- Категория: Образование
- Цена: Бесплатно
- Скачать: Google Play
- Приложением уже заинтересовались: 246 человек
- Теги
- Google Play
- Образование
- Операционная система Android
- Приложения для Андроид
iPad Pro нашли неожиданное применение. Зачем он нужен археологам
Samsung скопировала экран блокировки iOS 16 в OneUI 5
Стоит ли покупать Айфон на Joom? Здесь вся правда
Как ускорить загрузку игр на Айфоне с iOS 16.
 1
1Прочитайте выпуск 15 прямо сейчас!
Squid Game, скрытые гармонии и DnD ждут вас в нашем новом выпуске! Плюс все ваши любимые головоломки и столбцы.
В разговоре с Сэмми Баззардом
Эллен разговаривает с математиком и ученым об Аттенборо, Арктане и Антарктиде
Выжить на мосту в игре Squid Game
E Адриан Хенле, Ник Ганцлер, Франсуа-Ксавье Кудер и Кори Саймон объединяются для смертельного испытания
Дорогой Дирихле, выпуск 15
Свадьбы, праздники и сомы попадают в почтовый ящик профа в этом выпуске.
Случайные математические песни
Горан Ньюсум всегда должен быть тем, кого ты действительно любишь
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x) `
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x) `
- Производная синуса
- Первообразная синуса
- Свойства функции синуса
- Уравнение с синусом
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
- Вычислить синус
- Тангенс
- Как рассчитать косинус
- косинус.
- Теорема косинусов
- Косинус суммы углов
- Косинус двойного угла
- Вычислите косинус угла, противоположного стороне, которую мы хотим вычислить, и умножьте его на двойное значение двух известных нам сторон.
- Вычесть результат, полученный в пункте 1, за вычетом результата пункта 2.
- Аркотангенс
- Arcocosene Calculator
- Trigonometry Calculator
- Calculate arcosine online
- Cosecant
- Cosine
- Hyperbolic cosine
- Cotangent
- Secant
- Sine
- Sine of the double angle
- Tangent
- Hyperbolic tangent
- Types of уголки
- Сначала вам нужно выбрать сторону или угол треугольника, который требует от выпадающее меню, то калькулятор выводит соответствующую форму формулы закона косинусов.
- Теперь поместите все значения в соответствующее поле.
- Затем выберите соответствующие единицы измерения.
- После ввода всех значений нажмите кнопку расчета.
- Меры всех углов и длин сторон.
- А также значения различных характеристик треугольника.
- В конце рисует диаграмму для заданных значений.
Графический калькулятор синуса, косинуса и тангенса угла
Изучая геометрию, школьнику часто придется вычислять синус, косинус и тангенс угла. Тригонометрические функции являются важной составляющей учебной программы, и сейчас самое время позаботиться о том, чтобы располагать приложением, помогающим их вычислять. С этой задачей справится Android-приложение Синус, косинус и тангенс. Его простота в сочетании с функциональностью позволит не тратить время на изучение возможностей программы, а сразу перейти к ее использованию.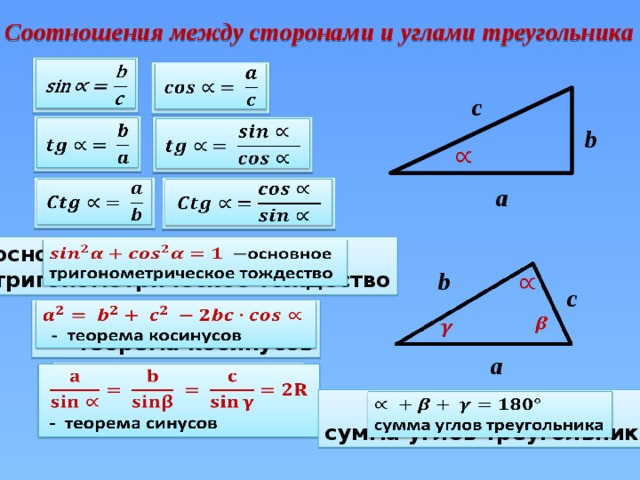
Приближение нового учебного года для школьников и их родителей означает смещение основного внимания с развлекательного контента на такие приложения, которые могут пригодиться в учебе, позволят повысить успеваемость и интерес к получению новых знаний, без которого все усилия по освоению нового материала могут оказаться напрасными.
Рассматриваемое приложение «Синус, косинус и тангенс» относится к числу программных инструментов, предназначенных для решения лишь одной задачи. При этом существуют и более комплексные приложения — например, такие, в которых собран практически весь школьный курс геометрии.
Вкладка «Графика» может использоваться в качестве графических тригонометрических таблиц. Значение угла в градусах можно указать как визуально касанием пальца на экране, так и ввести с присутствующей в окне приложения экранной клавиатуры, подтвердив ввод касанием расположенной внизу данной клавиатуры виртуальной кнопки [V].
Под рисунком показывается значение угла в радианах и градусах, а также его синус, косинус и тангенс. Поскольку на экране смартфона или планшета видны не только результаты, но и то, как выглядит угол, тригонометрические функции которого в настоящее время вычисляются, школьнику будет намного проще в дальнейшем с решением подобных задач, поскольку наглядная подача учебного материала всегда является предпочтительной.
Поскольку на экране смартфона или планшета видны не только результаты, но и то, как выглядит угол, тригонометрические функции которого в настоящее время вычисляются, школьнику будет намного проще в дальнейшем с решением подобных задач, поскольку наглядная подача учебного материала всегда является предпочтительной.
Особенностью данного приложения является также его поддержка устройствами под управлением операционными системами Android, начиная с версии 4.0.3. Его дизайн прост и строго функционален. Какие-либо украшающие элементы интерфейса полностью отсутствуют, что упрощает его освоение даже теми пользователями, которые еще не успели привыкнуть к Android-девайсам.
Лонгриды для вас
Почему вам нужно срочно обновить Google Chrome для Android
Независимость системных служб Android друг от друга — это одновременно и преимущество, и недостаток. С одной стороны, вам приходится постоянно поддерживать их все в актуальном состоянии, регулярно устанавливая свежие патчи и обновления. Но, с другой, если вдруг выясняется, что какой-то из этих компонентов перестал работать как нужно или имеет проблемы с защитой от взлома, то очень удобно не ждать системного апдейта, который выйдет неизвестно когда, а взять и обновить его индивидуально. Время от времени это реально спасает от крайне негативных последствий. Например, как в случае с Google Chrome.
С одной стороны, вам приходится постоянно поддерживать их все в актуальном состоянии, регулярно устанавливая свежие патчи и обновления. Но, с другой, если вдруг выясняется, что какой-то из этих компонентов перестал работать как нужно или имеет проблемы с защитой от взлома, то очень удобно не ждать системного апдейта, который выйдет неизвестно когда, а взять и обновить его индивидуально. Время от времени это реально спасает от крайне негативных последствий. Например, как в случае с Google Chrome.
Читать далее
Лучшие новые игры, которые можно скачать на Android бесплатно
Игры для Android с каждым месяцем становятся все лучше и лучше, и в Google Play всегда появляется что-то новое. Независимо от того, являетесь ли вы случайным игроком или мобильный гейминг ваше все, вам наверняка захочется чего-то новенького. И у нас есть для вас подборка таких игр. В данную подборку мы включили игры самых разных жанров, но объединяет их то, что они вышли в течение последних пары месяцев. Усаживайтесь поудобнее и скачивайте новинки, которые не оставят вас равнодушными.
Усаживайтесь поудобнее и скачивайте новинки, которые не оставят вас равнодушными.
Читать далее
Правда ли, что в России заблокировали WhatsApp
Несмотря на то что WhatsApp, в отличие от Instagram и Facebook, в России никто не блокировал, на этой неделе пользователи начали жаловаться на то, что не могут скачать приложение с официального сайта мессенджера. Многие решили, что либо Meta, которая владеет этими сервисами, решила окончательно уйти с нашего рынка, либо Роскомнадзор, который уверял, что не имеет претензий к Ватсапу, всё-таки передумал. Попробуем разобраться, что же случилось на самом деле, почему не получается скачать WhatsApp и что теперь делать.
Читать далее
Новый комментарий
Новости партнеров
Определение синуса, косинуса, тангенса и котангенса
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Информационно-проектный урок
Информационнопроектный урок2. Тема: Определение синуса, косинуса, тангенса и котангенса.
3. Цели урока:
• 1.Знать определение синуса,косинуса, тангенса и котангенса.
• 2.Уметь применять эти
определения к решению
примеров и задач.
• 3.Привитие творческой
активности и самостоятельности
4. План урока
• История развитиятригонометрии.
• Повторение курса
геометрии.
• Изучение нового
материала.
• Закрепление
5. Историческая справка
тригононТригонометрия
метрио
(измерение треугольника)
Древний
Вавилон-умели предсказывать
солнечные и лунные затмения.
Древнегреческие
учёные-составили
таблицы хорд(первые
тригонометрические таблицы)
Учёные
Индии и Ближнего Востокаположили начало радианной мере угла.
7. Большой вклад в развитие тригонометрии внесли:
• Гиппарх• Птолемей
• Франсуа Виет
• Эйлер
• Бернулли
8. Повторение
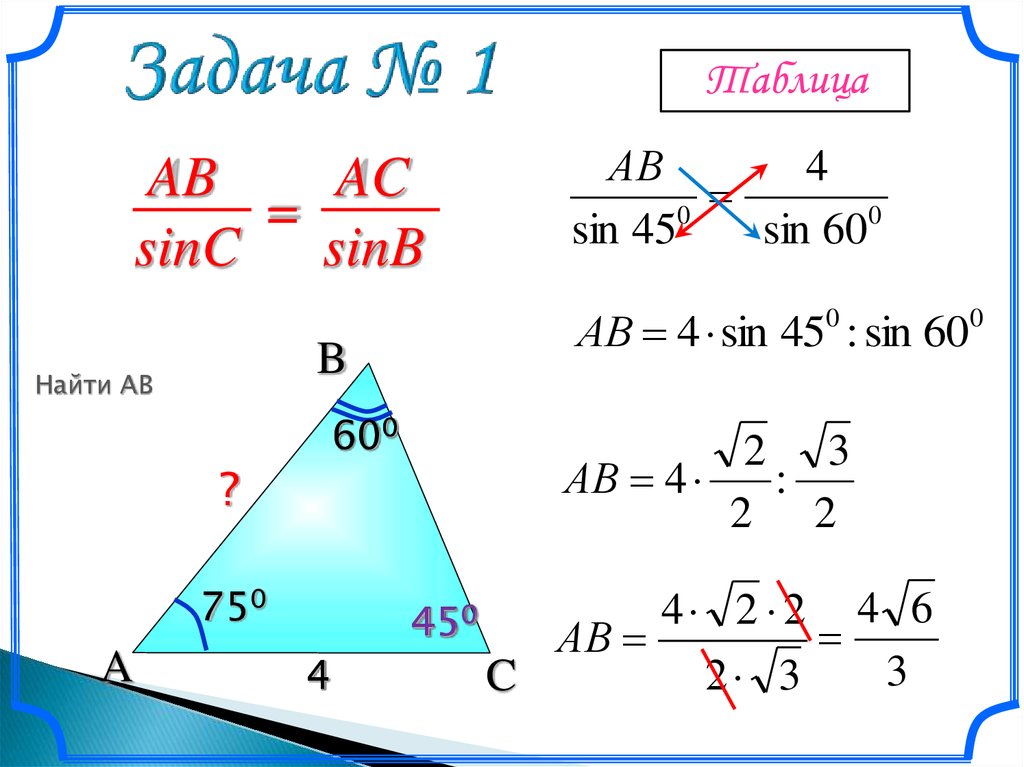
АsinC=
COS C=
tg C=
?
В
С
9. Повторение
Для единичной полуокружностиy
у
SIN A =
= Y
R
X
1
COS A=
=X
R
В
-1
А
1
х
0 ≤SIN A≤ 1
-1 ≤ COS A ≤1
10. Повторение
Основноетригонометрическое
тождество:
2
SIN
2
X+COS
Х=1
у
А
О
х
12.
 Угол поворота против часовой стрелки- положительныйУгол поворота против часовой стрелкиположительный У
Угол поворота против часовой стрелки- положительныйУгол поворота против часовой стрелкиположительный УВ
А
О
Х
13. Угол поворота по часовой стрелке — отрицательный
Угол поворота по часовой стрелке отрицательныйУ
А
х
О
В
14. Угол поворота
ПоложительныйОтрицательный
У
У
В
o
700
А
Х
O
А Х
-700
В
15. Из курса геометрии известно:
Мера угла в градусахвыражается числом
от
0
0
до
0
180
16. Ответь на вопрос:
Каким числомможет выражаться
в градусах угол
поворота?
17. В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от -∞ до +∞
18. Рассмотрим примеры
УУ
В
1350
О
Х
А
В
1350+3600n
, n=0,1,-1,2,-2…..
О
Х
-1350
А
19. В Ы В О Д Существует бесконечно много углов поворота, при которых начальный радиус ОА переходит в радиус ОВ.
 ВЫВОД
ВЫВОДСуществует бесконечно много углов
поворота, при которых начальный
радиус ОА переходит в радиус ОВ.
В зависимости от того, в какой
координатной четверти
окажется радиус ОВ, угол α
называют углом этой
четверти.
20. З А П О М Н И
ЗАПОМНИ00<α<900 ,то α -угол 1 четверти.
900<α<1800 ,то α – угол 2 четверти.
1800<α<2700 ,то α – угол 3 четверти.
2700<α<3600 ,то α- угол 4 четверти.
21. В ы в о д: Эти углы не относятся ни к какой четверти.
00
±
,±
0
90
0
270
,±
,±
0
180
,
0
360 ….
22. Углом какой четверти является угол β,если:
0β=167
0
β=287
0
β=-65
23. Стр.153.- определение.
ySinα=
X
Cos=
R
y
tgα=
R
X
ctgα=
X
y
24. Лабораторная работа
25. В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса.
1.2.
3.
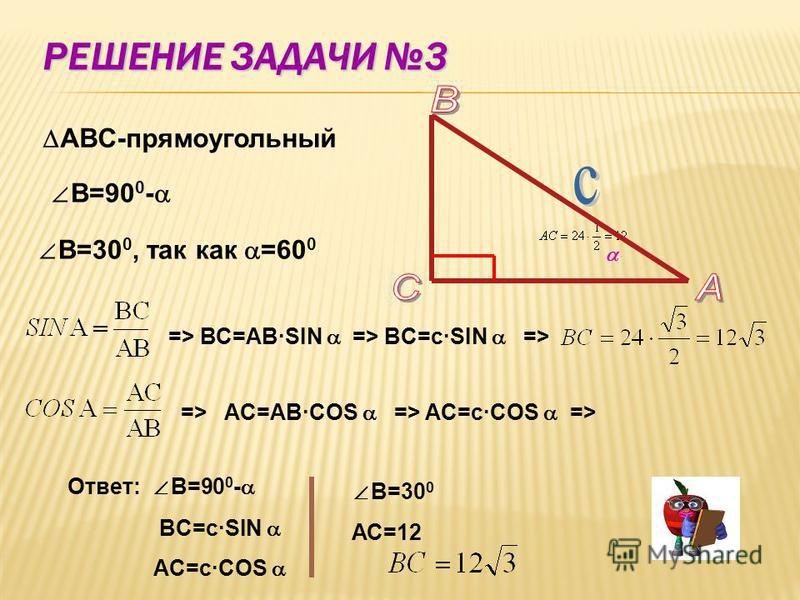
4.
5.
6.
Вычертите три окружности произвольного
радиуса с центром в начале координат.
Постройте начальный радиус ОА.
Поверните начальный радиус на угол α=450
В каждом из случаев найдите SIN 450.
(смотри пример 1. стр.154.)
Какой получился результат? Сделай вывод..
26. Запомни
Sinα, Cosαопределеныпри любом α.
Почему?
27. Стр.154
Прикаком α tgα
не определён?
Почему?
sinα
, cosα ,
tgα , ctgα
–называют
тригонометрическими
функциями.
29. Для единичной окружности:
• Область значениясинуса и косинуса
есть промежуток
[-1;1]
• Область значения
тангенса и
котангенса есть
множество всех
действительных
чисел.
30. Найти синус, косинус,тангенс и котангенс
0270
Проверьте решение на стр.156
•№ 699
•№701
32. Письменно
№705Используй
таблицу стр.155
English Русский Правила
\circ$ не совпадает по фазе с другой катушкой — но если ваш калькулятор не был извлечен из навигационного компьютера бомбардировщика Боинг 50-х годов, ваш калькулятор работает иначе. Ваш калькулятор также не сверяется с таблицами значений, кропотливо полученными вручную из сложения углов и тригонометрических тождеств половин угла, как это было нормой для математиков, ученых и инженеров до середины века.
Ваш калькулятор также не сверяется с таблицами значений, кропотливо полученными вручную из сложения углов и тригонометрических тождеств половин угла, как это было нормой для математиков, ученых и инженеров до середины века.Если вы похожи на меня, вы предполагали, что современные калькуляторы приближают синус и косинус к полиномиальным функциям, используя методы исчисления и анализа. (Если вы очень похожи на меня, вы сказали это старшекласснику на первом году обучения, пытаясь сделать ключевые идеи рядов Тейлора доступными без обращения к исчислению.) Однако эти алгебраические приближения сошлись медленно. Сложный компьютер может сократить путь, сохранив в памяти старые огромные таблицы и , затем Чебышев-аппроксимация, чтобы получить последние несколько цифр точности. Но как насчет вашего карманного или научного калькулятора, или, если на то пошло, вашего графического калькулятора TI — где добавление этой архитектуры было бы дорогостоящей проблемой?
Аббревиатура со странной заглавной буквой
Введите CORDIC, цифровой компьютер вращения координат — алгоритм, разработанный Джеком Волдером из Convair, чтобы максимально использовать сильные стороны появившихся тогда цифровых компьютеров. \circ-9\circ) \приблизительно 0,97\ldots/1$.
\circ-9\circ) \приблизительно 0,97\ldots/1$.
Само по себе это избавляет от необходимости хранить огромную таблицу — грубо говоря, каждый новый меньший поворот уточняет результат до дополнительного двоичного разряда точности, и все, что нужно хранить, — это инструкции для поворота на этот угол. Действительно, аналогичные методы использовались для этих таблиц, созданных вручную: описанный до сих пор метод представляет собой геометрическую перспективу использования тригонометрических тождеств суммы углов. Однако алгоритм Волдера на этом не останавливается. Он добавляет две важные детали, что компьютеры всего лишь 9\circ$- угол.
Оба эти усовершенствования схемы, казалось бы, усложняют нашу жизнь; в конце концов, мы теряем как хорошие рациональные углы, так и гипотенузу, которая услужливо остается фиксированной на длине 1. Однако мы увидим, что фактические вычисления более прямолинейны, а в двоичной арифметике они еще проще. Если вам особенно нравятся матрицы преобразования, вы можете прямо сейчас приостановить чтение, чтобы понять, почему это происходит самостоятельно (или прочитать это в превосходных «Элементарных функциях и калькуляторах» Ричарда Пэрриса), но если вы хотите увидеть более чисто геометрическое объяснение, читайте дальше!
CORDIC: геометрическое обоснование
Давайте рассмотрим простой пример этих правил в действии. Скажем, у нас есть прямоугольный треугольник со сторонами длины $a$, $b$ и $c$, следуя общепринятому соглашению. Пусть $c$ — гипотенуза, а сторона $a$ примыкает к углу $\theta$:
Скажем, у нас есть прямоугольный треугольник со сторонами длины $a$, $b$ и $c$, следуя общепринятому соглашению. Пусть $c$ — гипотенуза, а сторона $a$ примыкает к углу $\theta$:
Прямоугольный треугольник.
Затем мы присоединяем к гипотенузе треугольник с отношением тангенсов $\frac{1}{2}$, то есть таким, что сторона, противоположная углу $\varphi$, равна половине длины стороны, следующей за ним. . Эта противоположная сторона имеет длину $\frac{c}{2}$:
Присоединение треугольника с отношением касательной $\frac{1}{2}$.
А какой треугольник нам нужен — прямоугольный треугольник с углом $\theta+\varphi$? Рассмотрим вертикаль, проведенную из противоположного угла нового треугольника, перпендикулярную стороне $a$, и горизонталь, проведенную из противоположного угла исходного треугольника, перпендикулярную стороне $b$:
Треугольник с углом $\theta + \varphi $.
Затем у нас есть отмеченные конгруэнтные углы, поэтому прямоугольный треугольник, образованный пересечением вертикали и горизонтали, подобен исходному треугольнику и действительно является просто треугольником вдвое меньшего размера, повернутым на $9n}$, если бы мы искали $\varphi$ с касательной, уменьшенной вдвое n раз.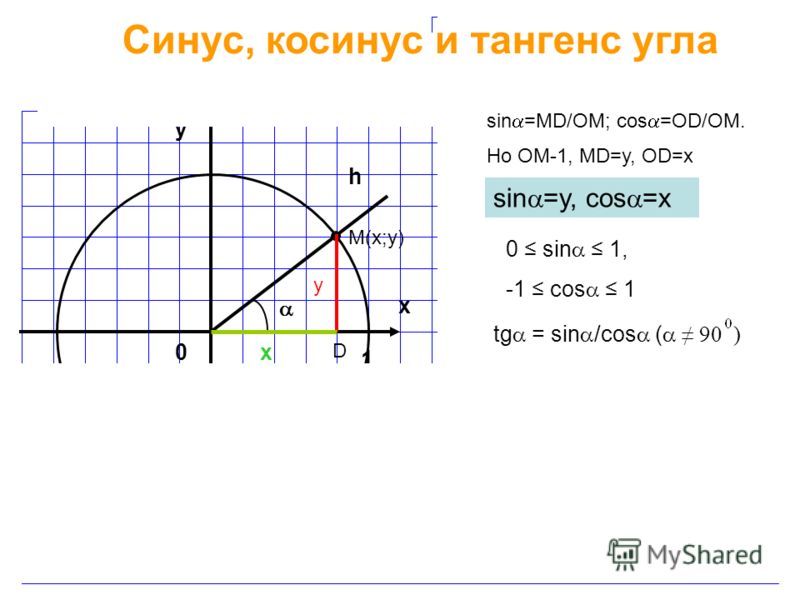 n$, перенос десятичной точки на $n$ разрядов. Многие более простые калькуляторы используют двоично-десятичное представление вместо чисто двоичного, сохраняя каждую цифру десятичного числа отдельно в двоичном представлении, что добавляет некоторые недостатки, но в основном следует тому же принципу. Остается только добавить.
n$, перенос десятичной точки на $n$ разрядов. Многие более простые калькуляторы используют двоично-десятичное представление вместо чисто двоичного, сохраняя каждую цифру десятичного числа отдельно в двоичном представлении, что добавляет некоторые недостатки, но в основном следует тому же принципу. Остается только добавить.
Для расчета отношений синуса и косинуса нам нужна только одна дополнительная информация: длина гипотенузы. Здесь полезен «веер», особенно если сделать еще одну оговорку — мы никогда не упускаем ни одного угла или треугольника. Затем составляющие треугольники веера фиксируются, и в обмен на потерю скорости при сужении под правильным углом мы можем заставить компьютер запомнить длину гипотенузы последнего, самого тонкого треугольника веера — того самого линия будет гипотенузой искомого треугольника! 9\circ$ — это один из наиболее удобных углов для этого способа. Более обычная реализация CORDIC будет настроена на уменьшение тангенса вдвое двадцать или тридцать раз, чтобы обеспечить точность после пяти знаков после запятой.
Итак, мы можем вычислить так и косинус, выполнив только одну вычислительно затратную задачу: деление на заданное число в конце. Эти вычислительные затраты, тем не менее, снижаются, и умная алгоритмическая экономичность CORDIC начала терять популярность. Процессоры Intel не использовали CORDIC со времен 486, и даже некоторые современные графические калькуляторы отказались от этого метода в пользу полиномиального подхода. Но даже несмотря на то, что CORDIC может когда-нибудь перестать быть инструментом, который люди используют сами, его невероятная простота, дешевая реализация и проверенная точность позволят использовать его в специализированных процессорах и специализированных машинах до тех пор, пока специализированная электроника будет знать, как измерять. треугольники. 9x$ означает, что базовый метод CORDIC можно даже адаптировать для вычисления показателей степени и логарифмов. Если вы можете описать геометрическое обоснование гиперболического, экспоненциального или логарифмического вариантов, таких как круговой случай выше, дайте мне знать — я устал смотреть на матрицы.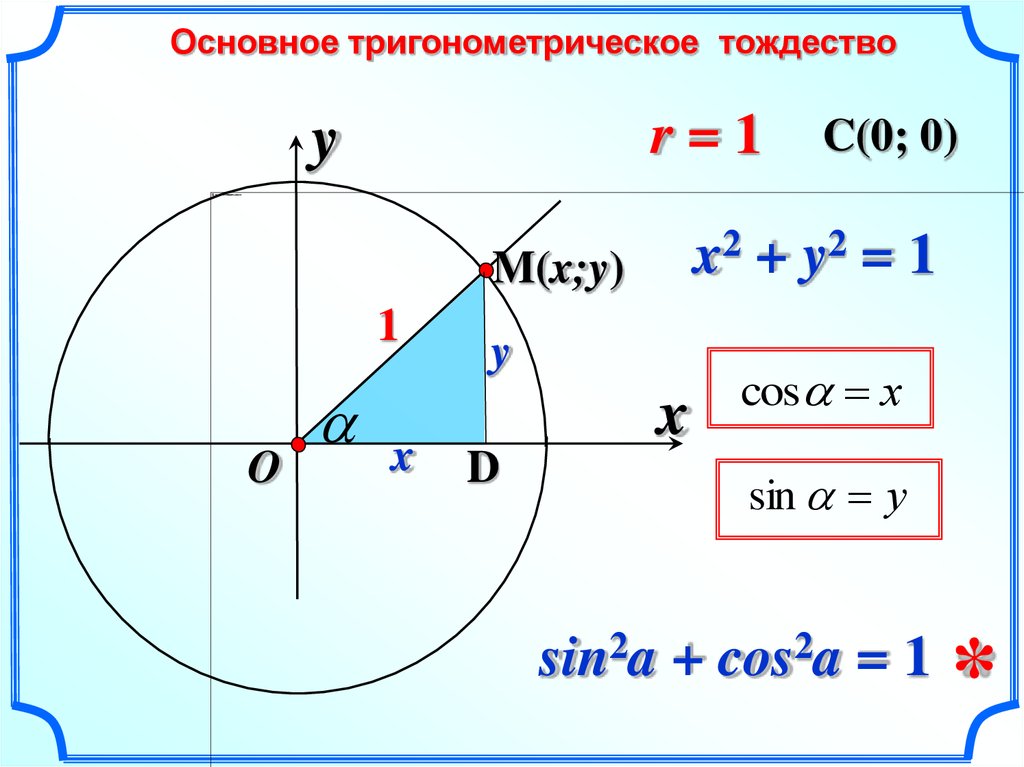
Еще из Chalkdust
Калькулятор — грех(0) — Солуматы
Sin, расчет онлайн
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах,
градусов или градианов.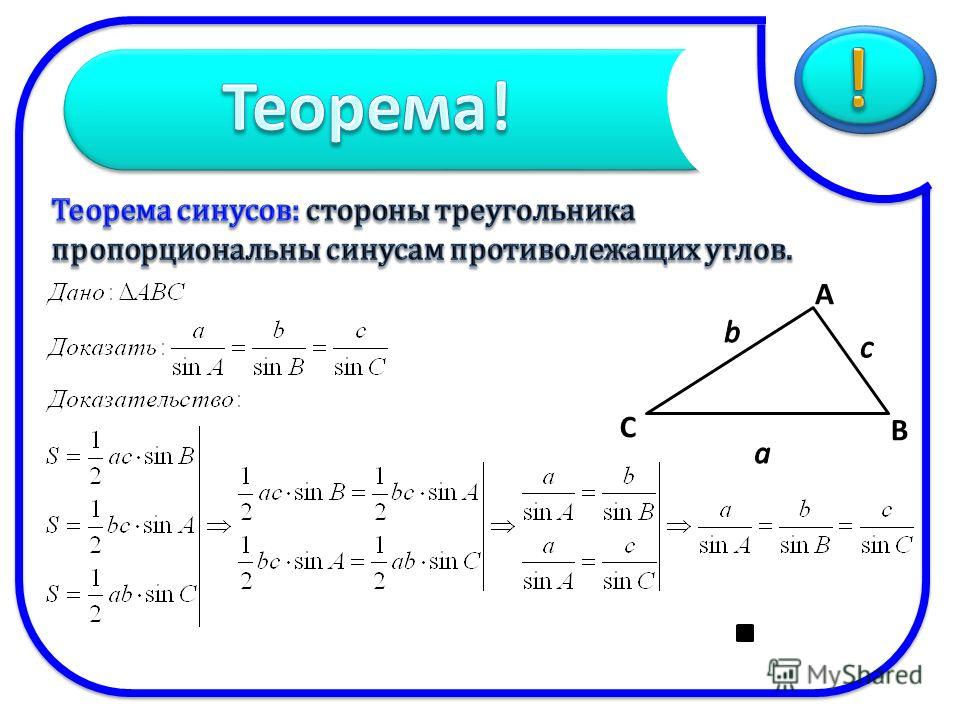
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
Синус вычисляет угол в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.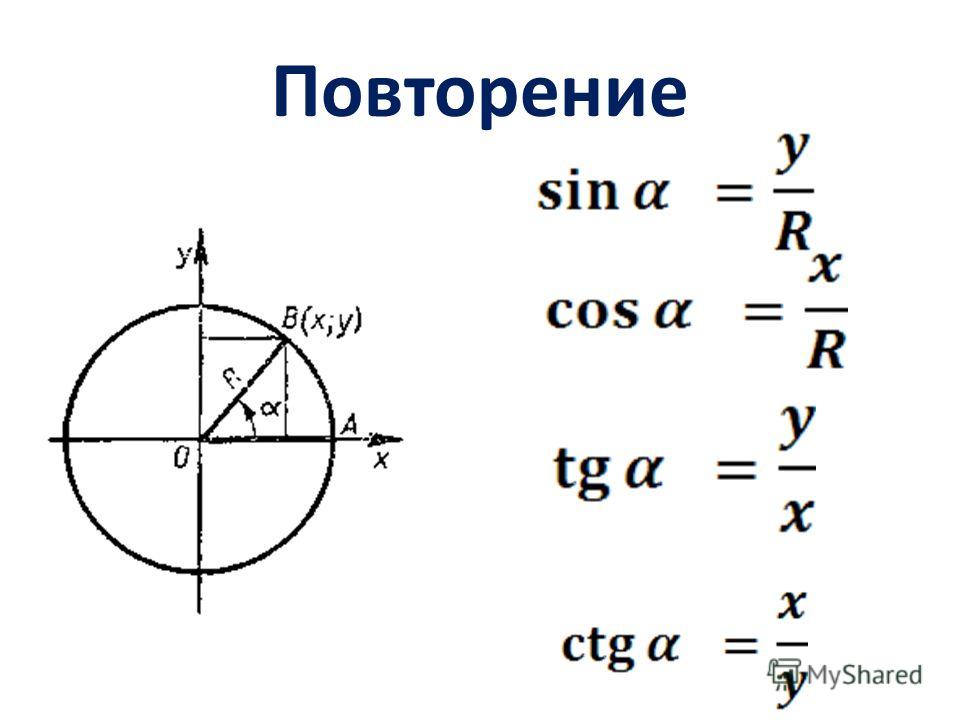
К вычислить синус онлайн из `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления,
возвращается результат `sqrt(2)/2`.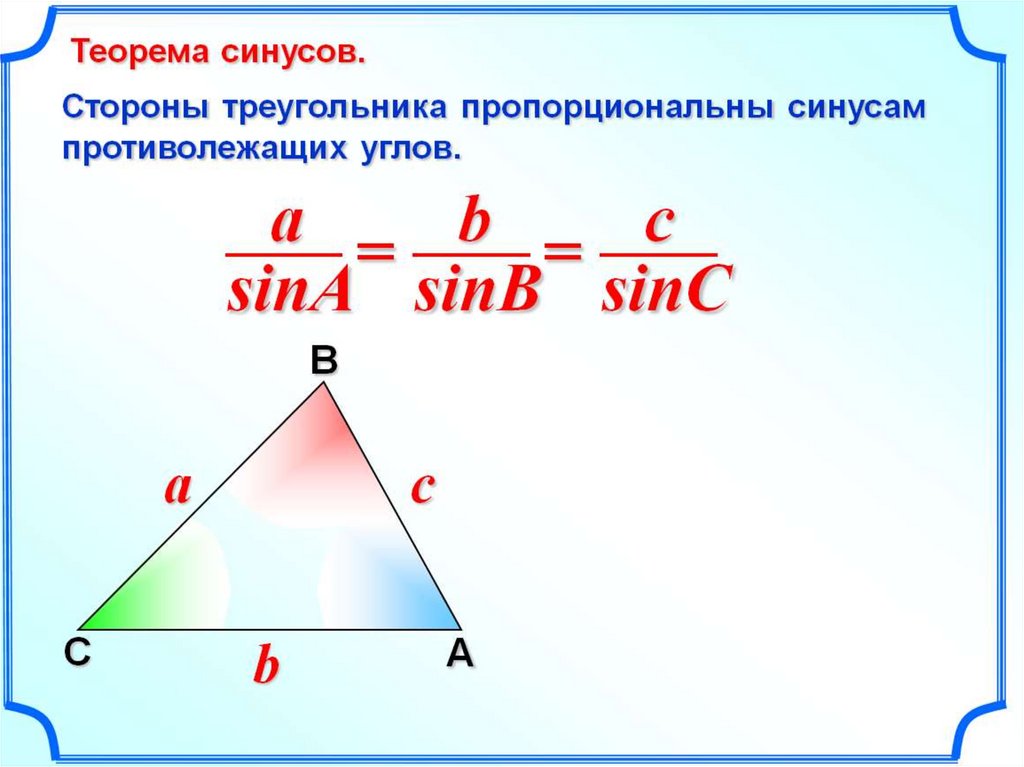
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица общих синусоидальных значений :
1 902) `pi/3`)040404| sin(`2*pi`) | `0` | ||
| sin(`pi`) | `0` | ||
| sin(`pi/2`) | `1` | ||
| sin(`pi/4`) | `sqrt(2)/2` sin(09099 | ||
| `sqrt(3)/2` | |||
| sin(`pi/6`) | `1/2` | ||
| sin(`2*pi/3`) | `sqrt(3)/2` | ||
| sin(`3*pi/4`) | `sqrt(2)/2` | ||
| sin(`5*pi/6`) | ` 1/2` | ||
| sin(`0`) | `0` | ||
| sin(`-2*pi`) | `0` | ||
| sin(`-pi`) | `0` | ||
| sin(` | `1) | sin(` | `1) 1` |
| sin(`-pi/4`) | `-sqrt(2)/2` | ||
| sin(`-pi/3`) | `-sqrt(3)/2` | ||
| sin(`-pi/6`) | `-1/2` | ||
| sin(`-2*pi/3`) | `-sqrt(3)/2` | sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
Производная синуса равна cos(x).
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производный синус:
можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) is производная(`sin(x)`)=`cos(x)`
Первообразная синуса :
Калькулятор первообразной позволяет вычислить первообразную функции синуса.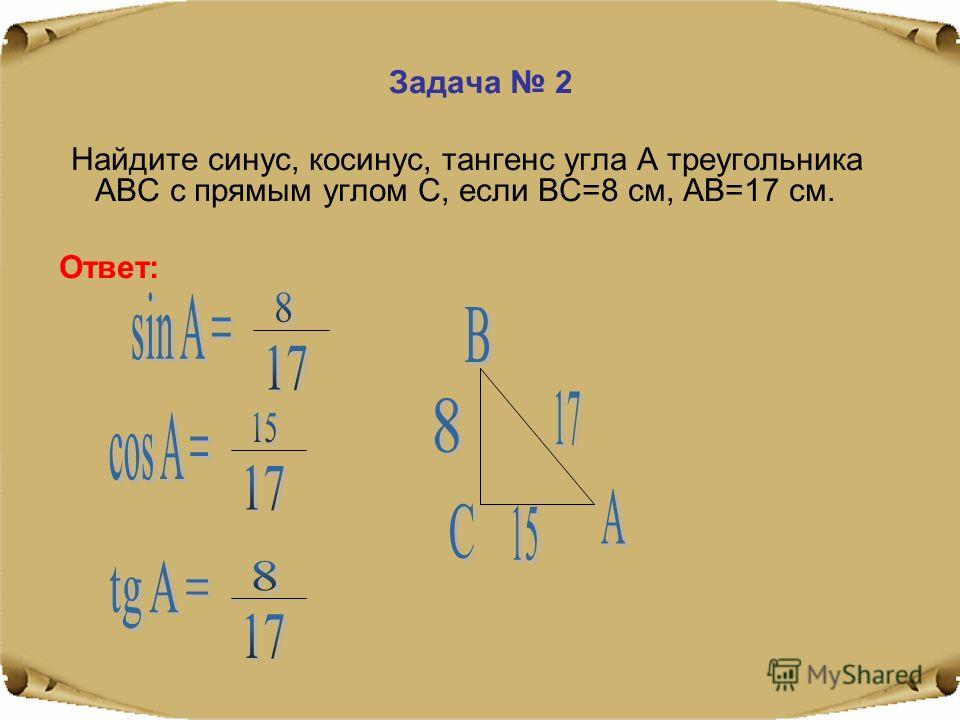
Первопроизводная sin(x) есть первопроизводная(`sin(x)`)=`-cos(x)`
Предел синуса :
Калькулятор предела позволяет вычислять пределы функции синуса.
Предел sin(x) равен limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса представляет собой функцию арксинуса, отмеченную арксинусом.
График синуса :
Графический калькулятор может отображать синусоидальную функцию в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Расчет онлайн с синусом
См. также
Список связанных калькуляторов:
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Онлайн-калькулятор косинусов с углами в градусах или радианах
Вычисляет косинус любого угла в градусах или радианах с помощью нашего онлайн-математического калькулятора, который позволит вам легко узнать значение этого тригонометрического отношения.
Работа с онлайн-калькулятором косинуса очень проста. Просто введите значение угла и выберите тип единиц измерения (градусы или радианы). Затем нажмите кнопку расчета, и вы автоматически узнаете косинус угла, который вы ввели. Помните, что косинус угла может принимать значения только от -1 до 1.
Помните, что у нас также есть другие калькуляторы, связанные с миром тригонометрии:
Разделы статьи
Как вычислить косинус
Если нам дан прямоугольный треугольник, как на изображении, и нас попросят вычислить косинус, мы получим деля соседний катет на гипотенузу .
Это будет основная формула для расчета этого тригонометрического отношения.
График косинуса
Вот одно графическое представление функции cos(x) , в котором вы можете увидеть все значения, которые он принимает в интервале [-2π, 2π].
Как видно, — это периодическая функция , область определения которой принадлежит всем действительным числам. Ниже вы найдете таблицу с основными значениями, которые принимает эта тригонометрическая функция на всем своем интервале.
Например, на графике прекрасно видно, что косинус числа пи равен -1.
Таблица функции косинуса
Если вам нужно с первого взгляда узнать значения косинус главных углов Ниже приведена подборка, которая будет очень полезна в задачах тригонометрии.
| Градусы | Радианы | Косинус |
|---|---|---|
| 0º | 0 | 1 |
| 30º | π/6 | 0,866 |
| 45º | π/4 | 0,707 |
| 60º | π/3 | 0,5 |
| 90º | π/2 | 0 |
| 180º | π | -1 |
| 270º | 3π/2 | 0 |
| 360º | 2π | 1 |
Как вычислить косинус угла с помощью калькулятора
Если вы хотите Вычислить косинус угла с помощью калькулятора научно, первое, что нужно проверить, это в градусах или радианах . Это жизненно важно, поскольку 60 градусов — это не то же самое, что 60 радиан. Если вам нужна дополнительная информация, в наших градусах к радианам мы более подробно объясняем различия между двумя способами выражения углов.
Это жизненно важно, поскольку 60 градусов — это не то же самое, что 60 радиан. Если вам нужна дополнительная информация, в наших градусах к радианам мы более подробно объясняем различия между двумя способами выражения углов.
Как только вы усвоите вышеизложенное, вычисление косинуса с помощью калькулятора станет очень простым. Просто нажмите клавишу с пометкой COS . Если угол не совпадает, введите угол и нажмите клавишу =, чтобы получить результат.
Например, если вы хотите вычислить косинус 45 , вы должны нажать следующую комбинацию клавиш:
COS → 45 → =
И на экране автоматически появится, что косинус 45 равен равно 0,707.
Вычислить косинус в Excel
Существует другая форма c Вычислить косинус угла с помощью Excel и функции с точно таким же названием. Однако по умолчанию Excel работает в радианах, поэтому обратите внимание на формулу, которую следует использовать в каждом случае.
Однако по умолчанию Excel работает в радианах, поэтому обратите внимание на формулу, которую следует использовать в каждом случае.
Если вы хотите рассчитать COS в радианах , вы должны написать следующую формулу в Excel:
=COS()
А между скобками вы напишите угол, выраженный в радах.
Если вы хотите вычислить косинус угла в градусах , вы должны написать следующую формулу:
=COS(РАДИАНЫ(90))
В этом случае мы получили косинус 90 , но вы можете изменить число на угол в градусах по вашему выбору.
Производная косинуса
Производная косинуса x равна минус синусу x. . Математически это можно выразить следующим образом:
f(x) = cosx → f'(x) = — senx
Если вместо x взять функцию u , то производная будет равна производной функции u, умноженной на минус синус из тебя Математически это выражается следующим образом:
f(x) = cosu → f'(x) = — u’ senu
Это основные производные функции COS.
Интеграл косинуса
Вы уже знаете, что интеграл является операцией, противоположной производной, поэтому мы можем вывести ее из теории, рассмотренной в предыдущем пункте. В любом случае, мы облегчим вам задачу, и вот вам чему равен интеграл косинуса x :
∫cosx dx = sinx + C
Если у нас есть интеграл косинуса функции u по ее производной, то результатом интеграла будет:
∫cosu · u’ dx = senu + C
Если у вас есть какие-либо сомнения или вопросы относительно cos , вы можете написать нам комментарий, и мы дадим вам руку как можно скорее. И если вам понравилось, поделитесь им в социальных сетях или оставьте нам еще один комментарий, поблагодарив нас за нашу работу, нам это тоже нравится 😀
Теорема косинусов
Теорема косинусов (также известная как закон косинусов) позволяет вычислить недостающие стороны и углы, связав одну из сторон треугольника с двумя оставшимися сторонами и косинусом треугольника.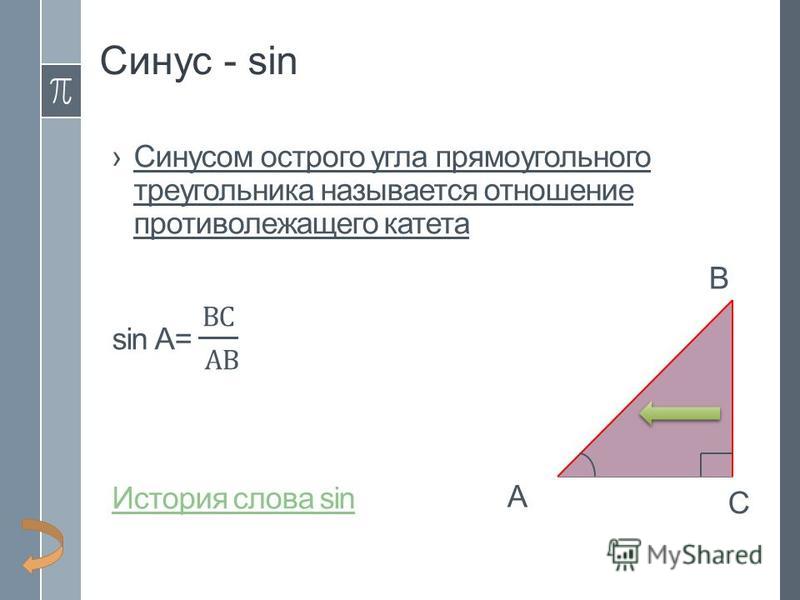 угол, который они образуют.
угол, который они образуют.
Если теоретическое объяснение не очень понятно, вот вся необходимая информация. формулы теоремы косинусов , которые помогут вам решать треугольники:
a 2 = b 2 + c 2 — 2bc·cosA
b 2 = a 2 + c 2 — 2ac·cosB
c 2 = a 2 + b 2 — 2ab·cosC
Если вы посмотрите на каждую из формул, все отвечают одной и той же схеме и добавить их значение.
Комбинируя теорему косинусов с теоремой синусов, мы можем решать треугольники простым и эффективным способом.
Косинус суммы углов
Формула косинуса суммы углов выглядит следующим образом:
cos (a + b) = вещь — cosb + вещь-senb суммарный угол 90 141 выводится путем вычисления стоимости сегмента AF:
AF = AG — FG = AG — EH = cos(α+β)
Мы также знаем, что:
EH = DH senα
DH = sinβ
Замените и останется так:
EH = senβ senα
Теперь посчитаем, сколько стоят отрезки AG и EH,
AG = AH cosα
Ач = cosβ
Подставляем и имеем что:
AG = cosβ cosα
Наконец, мы подставляем в первое уравнение, которое у нас есть в начале демонстрации, и мы имеем это:
COS (α+β) = COSα COSβ — SENα SENβ
Косинус с двойным углом
ниже.
2 a
Двойной угол (2а) имеет свои тригонометрические соотношения и cos двойного угла является одним из них, формула, которая выводится из формулы косинуса суммы углов, которую мы видели в предыдущем пункте (α = β).
Например, давайте решим это упражнение, в котором мы получим cos двойного угла 30º:
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Узнайте, как применять синус, косинус и тангенс (SOHCAHTOA) к прямоугольным треугольникам, чтобы найти недостающие длины или углы в прямоугольном треугольнике.
 После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре 1 и практические задачи.
После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре 1 и практические задачи.Что такое СОХКАТОА?
SOH CAH TOA
SOH СОЗДАТЕЛЬСТВО S INE, O PPOSITE, H YPOTENUSE и дает US
CAH 40141014101010101010101010101010101010101010101010101010101010101010101010101010101010101010141010101010101010101010. . ypotenuse и дает нам
TOA обозначает T angent, O pposite, A djacent и дает нам
Что такое противоположная, смежная и гипотенуза в прямоугольном треугольнике?
Гипотенуза – гипотенуза прямоугольного треугольника – самая длинная сторона прямоугольного треугольника; она также всегда находится напротив прямого угла
Противоположная сторона – противоположная сторона – это сторона, расположенная напротив (напротив) выбранного угла
Смежная сторона – смежная сторона – это сторона, следующая за выбранным углом; это сторона, которая не является гипотенузой или противолежащей стороной
Примечание.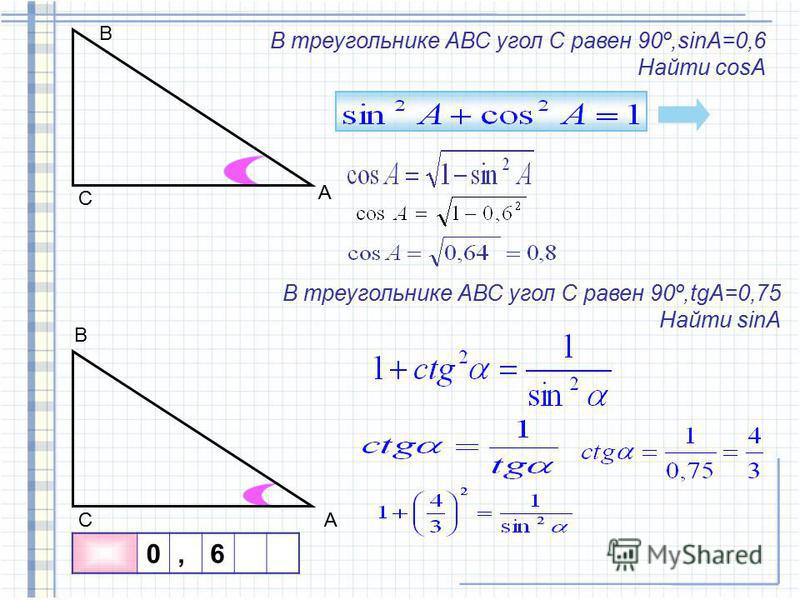 Противоположная сторона и прилежащая сторона всегда относятся к углу.
Противоположная сторона и прилежащая сторона всегда относятся к углу.
Вот пример использования SOHCATOA:
В прямоугольном треугольнике одна сторона имеет размер 4 единицы, а противоположный угол имеет размер 30 градусов. Определить длину гипотенузы.
Поскольку заданная мера угла противоположна стороне, а вопрос заключается в том, чтобы найти гипотенузу, можно использовать sin для нахождения недостающей длины.
Замените переменные
Решение для SIN 30
Множественные x с обеих сторон
Разделение 0,5 с обеих сторон x
9003 .
Примеры SOHCAHTOA (синус, косинус, тангенс)
Пример 1
Из кузова грузовика выдвигается пандус. Между рампой и тротуаром существует угол в градусах. Если расстояние от конца пандуса до задней части грузовика составляет футы. Какова длина рампы?
Между рампой и тротуаром существует угол в градусах. Если расстояние от конца пандуса до задней части грузовика составляет футы. Какова длина рампы?
Сначала нарисуем диаграмму и присвоим данные значения
Даны угол и прилежащая сторона. Итак, решим его гипотенузу
Теперь решим с помощью косинуса
Следовательно, ответ футы
Пример 2
Человек видит ракету под углом возвышения градусов. Если человек находится в нескольких милях от стартовой площадки ракеты, на какой высоте находится ракета? Округлите ответ до сотых.
Сначала нарисуем диаграмму и присвоим заданные значения
Дан угол и прилежащая сторона. Ищем высоту ракеты
Теперь решим по касательной
Следовательно, ответ будет миль
Видеозапись урока
В этом уроке мы пройдемся по основам тригонометрии.
Итак, мы рассмотрим синус, косинус и тангенс.
Синус угла, косинус угла и тангенс угла представляют отношения сторон прямоугольного треугольника.
Если нам известен угол одной стороны, мы можем использовать одну из этих тригонометрических функций, чтобы найти другие стороны.
Например:
Позже я проверю, какая сторона является противоположной, а какая гипотенуза.
Один из способов запомнить. H – гипотенуза
T – касательная
O – противоположная
A – смежная
Нарисуем прямоугольный треугольник.
Затем давайте определим стороны.
Сторона напротив прямого угла является гипотенузой.
Далее, противоположность тэты называется противоположной стороной.
И, наконец, сторона, следующая за тетой, называется смежной стороной.
Давайте посмотрим на этот пример:
У нас есть прямоугольный треугольник. Один угол есть угол. Одна сторона есть. И мы ищем гипотенузу.
Если у нас есть одна сторона, мы можем легко использовать теорему Пифагора. Но так как у нас отсутствует измерение этой стороны, то и не можем.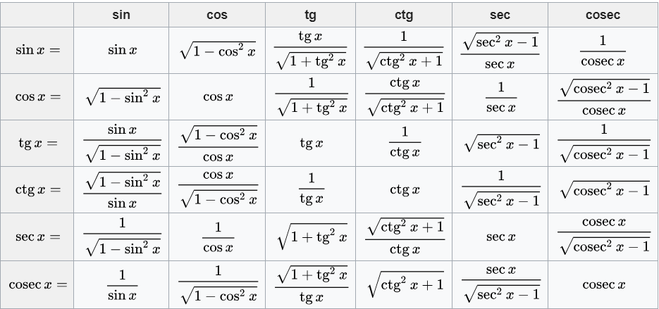
Вместо этого мы должны использовать одно из этих тригонометрических соотношений, чтобы выяснить, что такое гипотенуза.
Для начала неплохо написать нашу аббревиатуру.
SOH CAH TOA
Итак, мы можем определить, какой из них мы собираемся использовать.
Теперь разберемся, какие у нас стороны.
находится поперек угла, так что это противоположная сторона.
, который мы ищем, находится прямо напротив прямого угла. Это гипотенуза.
Итак, мы собираемся использовать SOH.
Так как у синуса есть гипотенуза и противоположная сторона.
Теперь, который вы можете узнать с помощью калькулятора или вы можете запомнить, что это .
Это должно иметь смысл, потому что . Это означает, что напротив гипотенузы находится .
это
В конце концов, это имеет смысл.
Таким образом, при нахождении одной из недостающих сторон, когда нам известны угол и одна сторона, мы обычно можем найти другую сторону, используя синус, косинус или тангенс.
Во-первых, мы просто должны определить, какие стороны были даны.
А потом напишите формулу и решите.
Калькулятор тригонометрии для прямоугольных и общих треугольников.
Калькулятор для прямоугольного треугольника
Стороны или углы, показанные на рисунках красным цветом, вычисляются калькулятором из сторон и углов, показанных зеленым цветом.
Количество цифр =
Угол и противоположный катет
α в градусах =
а =
Угол и прилежащий катет
α в градусах =
б =
Угол и гипотенуза
α в градусах =
с =
Катет
а =
б =
Катет и гипотенуза
б =
с =
Калькулятор для общих треугольников
Две стороны и один угол
γ в градусах =
Два угла и одна сторона
γ в градусах =
β в градусах =
Три стороны
Примеры тригонометрических вычислений
Вот несколько примеров, иллюстрирующих применение тригонометрических формул.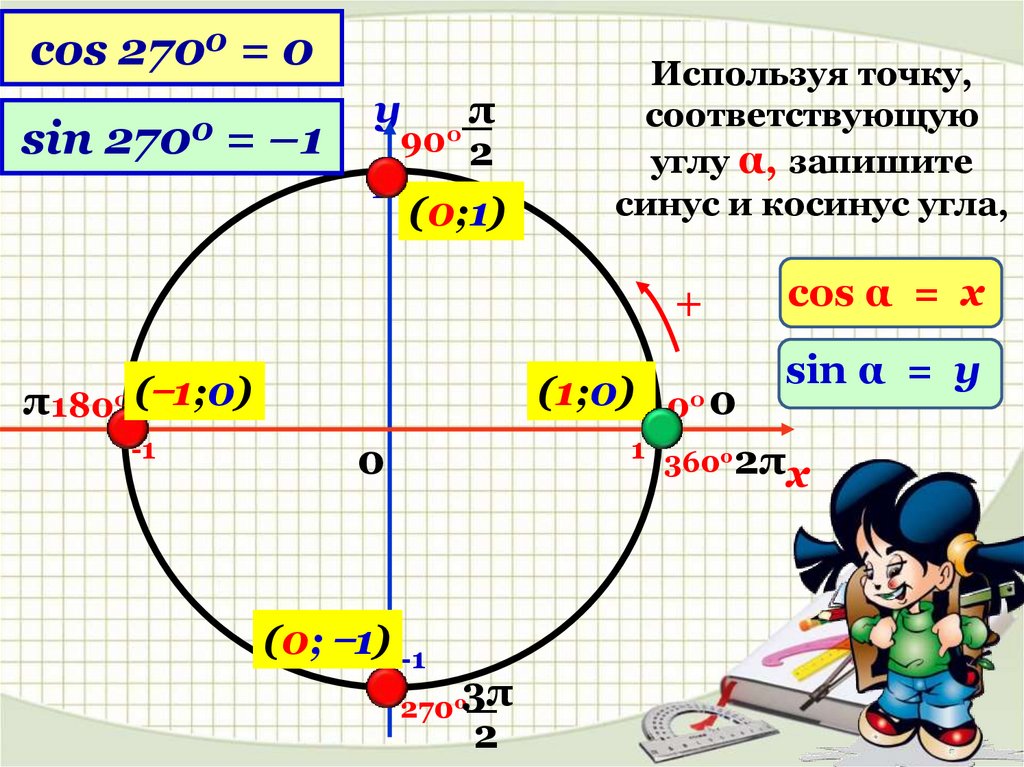
Пример: Расчет высоты башни
Пример показывает, как можно определить высоту, даже если прямой доступ невозможен.
На рисунке видно, что углы обзора (α, γ) и расстояние b между положениями были определены из двух положений (P 1 , P 2 ) (зеленый цвет на иллюстрации).
Треугольник формируется из P 1 , P 2 и вершины башни. Из этого общего треугольника известны угол α и сторона b. Угол γ можно рассчитать следующим образом:
γ’=180-γ
Недостающий угол β можно определить, так как сумма углов в треугольнике равна 180°.
β=180-α-γ’=γ-α
На следующем шаге синусный набор используется для вычисления стороны a. Сторона а является общей стороной общего треугольника и прямоугольного треугольника, образованного а и высотой башни и базовой линией.
a=sin(α)bsin(β)=bsin(α)sin(γ-α)
В прямоугольном треугольнике a — гипотенуза, а h — противолежащий катет угла γ. Таким образом, желаемая высота h может быть рассчитана с помощью угловой функции.
h=asin(γ)=bsin(α)sin(γ)sin(γ-α)
В качестве альтернативы высота башни также может быть рассчитана путем применения двух уравнений для прямоугольного треугольника. Первый треугольник состоит из P 1 и основания башни, а также вершины башни. Второй аналог исходящего Р 2 .
Это:
tanγ=hx
и
tanα=hb+x
с неизвестным расстоянием x от P 2 до базовой точки башни.
Изменение результатов уравнений в каждом случае:
х=htanγ
и
x=h-btanαtanα
Уравнение уравнений и решение для h дает решение:
h=btanαtanγtanγ-tanα
Два решения для h эквивалентны, что можно легко доказать, заменив
tan(α)=sin(α)cos(α)
и
tan(γ)=sin(γ)cos(γ)
h=btanαtanγtanγ-tanα=bsinαsinγsinγcosα-sinαcosγ
С теоремой сложения
sin(x±y)=sin(x)cos(y)±cos(x)sin(y)
результат приведенного выше решения.
Это
h=btanαtanγtanγ-tanα=bsin(α)sin(γ)sin(γ-α)
Калькулятор для расчета высоты башни
Введите углы обзора и расстояние:
α в градусах =
γ в градусах =
Пример: поперечный пеленг
Фиксированная точка (например, маяк) с двух позиций наводится на поперечный пеленг.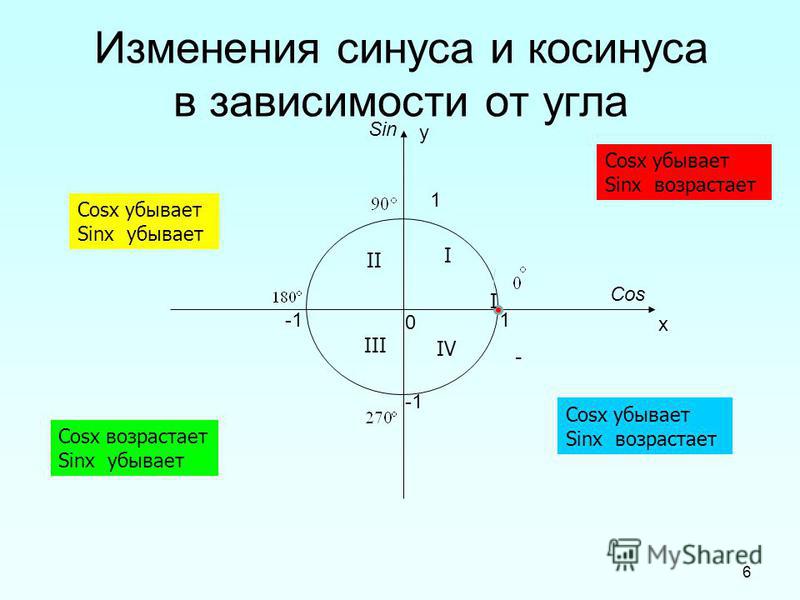 Между двумя подшипниками применяется постоянный курс и постоянная скорость (P 1 , P 2 ). Затем расстояние от целевой точки можно определить по пеленгам.
Между двумя подшипниками применяется постоянный курс и постоянная скорость (P 1 , P 2 ). Затем расстояние от целевой точки можно определить по пеленгам.
На рисунке видно, что углы обзора (α, γ) относительно направления движения были определены в двух положениях (P 1 , P 2 ) (зеленый цвет на рисунке). Длина стороны b получается из скорости v и временного интервала t измерений.
Треугольник формируется из P 1 , P 2 и целевой точки (маяка). Из этого общего треугольника известны угол α и сторона b = v * t.
Недостающий угол β можно определить, так как сумма углов в треугольнике равна 180°.
β=180-α-γ
На следующем шаге правило синусов используется для вычисления стороны a. Сторона a — это расстояние от точки измерения P 1 .
a=sin(α)bsin(β)
Аналогично рассчитывается расстояние до второй точки измерения.
c=sin(γ)asin(α)
Пример: Измерение недоступного маршрута (задача Хансена)
Для измерения труднодоступного маршрута начало и конец маршрута определяются по двум точкам (P 1 , P 2 ).
На рисунке видно, что углы обзора (α, β, γ, δ) в двух положениях (P 1 , P 2 ) относительно соединительной оси точек (зеленые на рисунке). Известно также расстояние a между точками измерения. Определить длину недоступного расстояния d (красный цвет на рисунке).
На рисунке показаны вычисляемые значения синего цвета.
Угол η можно определить, так как сумма углов в треугольнике равна 180°.
η=180-α-γ
На следующем шаге правило синусов используется для вычисления стороны c.
c=asin(γ)sin(η)
Сторона e также рассчитывается по правилу синусов.
e=asin(δ)sin(ρ)
Угол ρ получается из суммы углов в треугольнике.
ρ=180-β-δ
Теперь можно использовать правило косинуса для расчета требуемого расстояния d.
d2=a2+c2-2accos(α-β)
Пример: Треугольник сил на маятнике
Разложение сил на ортогональные составляющие играет важную роль в механике. Этот пример показывает, как силу веса можно разложить на две составляющие с помощью угловых функций.
На рисунке показан маятник из пряжи с грузом на конце нити. Сила веса F g должна быть разложена на парциальные силы. Усилие в направлении резьбы F Z не влияет на ускорение, поэтому сила F a важна для уравнения движения.
Частичные силы можно задавать непосредственно с помощью функций угла, поскольку они представляют собой прямоугольный треугольник.
Fa=Fgsin(α)
FZ=Fgcos(α)
Общая тригонометрия
Основная задача тригонометрии состоит в том, чтобы (и т.д. длины сторон, размеры углов, длины треугольника-поперечной) вычислить по трем размерам данного треугольника другие размеры этого треугольника. В помощь тригонометрическим функциям синус (sin), косинус (cos), тангенс (tan), котангенс (cot). Предшественник тригонометрии существовал уже во времена античности в греческой математике. Аристарх Самосский воспользовался свойствами прямоугольных треугольников для расчета отношений расстояний между Землей, Солнцем и Луной.
Определения
Стороны a и b прямоугольного треугольника, которые включают прямой угол, являются катетом. Прямой угол, противолежащий стороне с, является гипотенузой. Глядя на угол α, сторона a является смежной стороной и противоположной стороной b.
Тригонометрические функции
sin(α)=cos(β)=ac
cos(α)=sin(β)=bc
tan(α)=cot(β)=ab
Градусы/радианы
Угол может быть указан в градусах (градусах) или радианах (радах). Полный круг в градусах составляет 360 градусов, в радианах это 2π. Соответственно, применяются следующие преобразования.
Угол (рад)=π180Угол (град)
Угол (град)=180πУгол (рад)
Сумма углов
Сумма углов треугольника равна 180°. Это относится к прямоугольному треугольнику со следующим соотношением для угла.
90=α+β
Определения
Существенными для вычислений в общем треугольнике являются косинус и закон синуса и соотношение тригонометрических функций.
Закон синусов
asin(α)=bsin(β)=csin(γ)
Закон косинуса
a2=b2+c2-2bccos(α)
b2=a2+c2-2accos(β)
c2=a2+b2-2abcos(γ)
Проекционный закон
c=a⋅cos(β)+b⋅cos(α)
Формула тангенса
tan(γ)=c⋅sin(α)b-c⋅cos(α)=c⋅sin(β)a-c⋅cos(β)
Сумма углов
Сумма углов треугольника составляет 180°.
180=α+β+γ
Радиус окружности r
r=s4⋅cos(α2)⋅cos(β2)⋅cos(γ2)
с
s=12(a+b+c)
Радиус вписанной окружности ρ
ρ=(s-a)(s-b)(s-c)s
Высота h
c на chc=a⋅sin(β)=b⋅sin(α)
Область A
A=12a⋅b⋅sin(γ)
Формула площади Герониша
A=ρs=s(s-a)(s-b)(s-c)
Редукционные формулы (в градусах)
sin(90°+x)=cos(x)
cos(90°+x)=-sin(x)
tan(90°+x)=-cot(x)
раскладушка(90°+x)=-tan(x)
sin(180°+x)=-sin(x)
cos(180°+x)=-cos(x)
загар(180°+х)=загар(х)
cot(180°+x)=cot(x)
Тригонометрические функции с равными аргументами
sin(x)2+cos(x)2=1
tan(x)=sin(x)cos(x)
Теорема сложения тригонометрических функций
sin(x±y)=sin(x)cos(y)±cos(x)sin(y)
cos(x±y)=cos(x)cos(y)∓sin(x)sin(y)
tan(x±y)=tan(x)±tan(y)1∓tan(x)tan(y)
Калькулятор закона косинусов — Найдите стороны и углы по правилу cos
Используйте бесплатный онлайн закон косинусов калькулятор, который помогает найти неизвестные длины сторон или углов треугольника. Вы можете вычислить все остальные оставшиеся стороны и измерить углы треугольника, используя различные формы закона косинусов.
Вы можете вычислить все остальные оставшиеся стороны и измерить углы треугольника, используя различные формы закона косинусов.
Теперь начните читать, чтобы узнать больше о правилах косинуса.
Что такое закон косинусов?Закон косинусов представляет собой набор формул, связывающих длину сторон треугольника с одним из его углов косинуса. Закон косинуса обычно предпочтительнее, когда даны три стороны треугольника для нахождения любого угла A, B или C треугольника или даны две смежные стороны и один угол.
Формула закона косинусов является формой теоремы Пифагора, которая адаптирована для использования непрямоугольных треугольников, но теорема Пифагора работает только для прямоугольных треугольников. Таким образом, вы можете использовать калькулятор закона косинуса для вычисления любого значения сторон и углов треугольника. 90$$
Однако онлайн-калькулятор закона синусов поможет вам найти неизвестные углы и длины сторон треугольника.
Калькулятор закона косинуса поможет вам найти все неизвестные пропущенные значения треугольника, используя следующие шаги:
Ввод:Калькулятор закона косинусов выводит следующие результаты, используя формулу закона косинуса:
Характеристики треугольника:
Периметр P = \(a + b + c\)
Полупериметр s = \(0,5 * (a + b + c)\)
Площадь A = \( \sqrt {s*(s – a)*(s – b)*(s – c)}\)
Радиус окружности в треугольнике r = \(\sqrt{(s – a)*(s – b )*(s – c) / s}\)
Радиус окружности вокруг треугольника R = \(\frac{(abc)} { (4AS)}\)
Где:
a = Сторона треугольника a, b = Сторона треугольника b, c = Сторона треугольника c
A = Угол A, B = Угол B, C = Угол C
R = радиус окружности вокруг окружности
r = радиус внутренней окружности
P = периметр
s = полупериметр
A = площадь
Какова роль теоремы Пифагора в законе косинусов? Закон косинуса представляет собой модифицированную версию теоремы Пифагора, которая используется для нахождения неизвестных значений сторон и углов непрямоугольных треугольников.


 1
1 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. 2 a
2 a