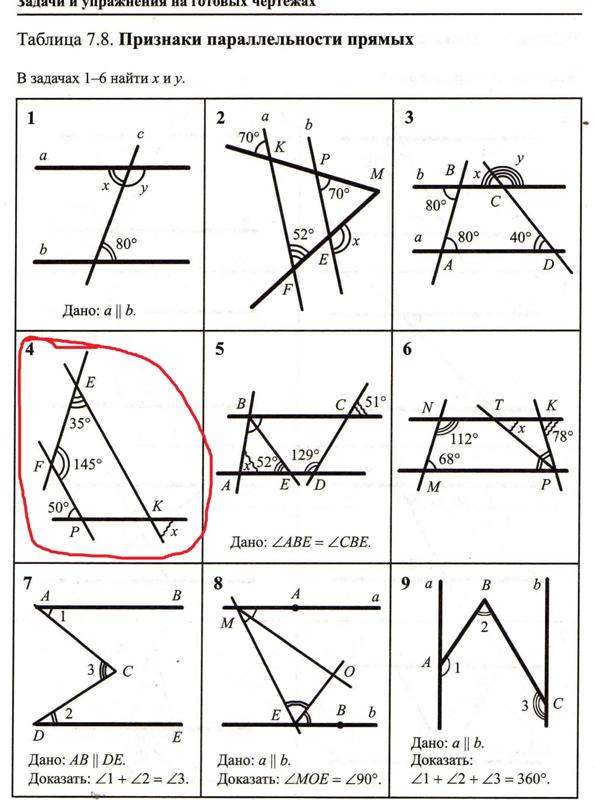
алгоритм — Вычислить XY координаты вершины треугольника, зная длинны всех сторон
Раз уж вы нашли косинус и синус угла в треугольнике — дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.
Но есть и решение в векторах, вообще без тригонометрии.
Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны — AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:
Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:
(rC-rA)² = a² (rC-rB)² = b²
Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:
(rC-rA)² - (rC-rB)² = a² - b² (rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b² 2rC(rB-rA) + rA² - rB² = a² - b² 2rC(rB-rA) = a² - b² - (rA² - rB²)
У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм.
Этой прямой по построению принадлежат точки C и C’ — значит, это уравнение прямой CC’. Кстати, разности rB — rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).
В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием «сингулярность»: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная — деление на ноль будет при попытке выразить x через y.
Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’.
Напомню, что параметрический вид уравнения прямой выглядит вот так:
r = r0 + t u
Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем — задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.
Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:
r = rA + tAB 2r·AB = a² - b² - (rA² - rB²)
Подставим первое уравнение во второе и решим его относительно переменной
2(rA + tAB)·AB = a² - b² - (rA² - rB²) 2rA·AB + 2t AB² = a² - b² - (rA² - rB²) t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB² t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB² t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB² t = (a² - b² + (rA - rB)²) / 2AB² t = (a² - b² + AB²) / 2AB²
Осталось подставить эту переменную обратно в параметрическое уравнение:
t = (a² - b² + AB²) / 2AB² r0 = rA + tAB
Формула выглядит страшно, но не имеет сингулярностей пока A и B — разные точки.
2*y/x-y)?
Это чужой компьютер Забыли пароль?
- Главная
- Образование
- ВУЗы, Колледжи, Техникумы
- Открытый вопрос
- ВУЗы, Колледжи, Техникумы
- Открытый вопрос
- Бизнес, Финансы
- Города и Страны
- Досуг, Развлечения
- Животные, Растения
- Здоровье, Красота, Медицина
- Знакомства, Любовь, Отношения
- Искусство и Культура
- Компьютеры, Интернет, Связь
- Кулинария, Рецепты
- Лингвистика
- Наука и Техника
- Образование
- ВУЗы, Колледжи, Техникумы
- Детские сады
- Домашние задания
- Дополнительное образование
- Образование за рубежом
- Прочее образование
- Школы
- Общество, Политика, СМИ
- Отдельная Категория
- Прочее
- Путешествия, Туризм
- Работа, Карьера
- Семья, Дом, Дети
- Спорт
- Стиль, Мода, Звезды
- Товары и Услуги
- Транспорт
- Философия, Психология
- Фотография, Видеосъемка
- Юридическая консультация
Юмор
Открыт 10 лет
Anonymous Q
Ученик (105)
пожалуйста помогите срочно!(
#дифференциал
Мы платим до 300 руб за каждую тысячу уникальных поисковых переходов на Ваш вопрос или ответ Подробнее
| 1 ОТВЕТ |
10 лет
Anonymous A
Знаток (430)
Скобки надо писать правильно (с).
2+1))dx
XY Найди в App Store
Описание
XY Find It позволяет найти все, что у вас есть. Просто зарегистрируйте устройство XY в своей учетной записи, решите, хотите ли вы включить или отключить уведомления KeepNear™, и никогда больше не потеряете ничего важного. Сообщество XY Lost & Findable™ может даже помочь закрепить на карте последнее известное местонахождение вашего предмета.
Детали:
— Подайте звуковой сигнал о потерянной вещи прямо из приложения
— Подключайте столько устройств, сколько хотите
— Уведомления KeepNear™ сообщат вам, если ваш предмет выходит за пределы допустимого диапазона
— Сообщество XY Lost & Findable™ автоматически обновляет вашу карту всякий раз, когда другой пользователь XY проходит мимо вашего предмета
— Больше никогда не теряйте ничего важного
Просто прикрепите XY Найти ваш предмет, добавьте его в свою учетную запись с помощью приложения XY на телефоне и всегда находите то, что имеет значение.
Продолжительное использование GPS в фоновом режиме может значительно сократить срок службы батареи.
Версия 5.0.1
Удалены рекламные ссылки и ссылки на магазины, повышена надежность, исправлены мелкие ошибки.
Рейтинги и обзоры
224 Оценки
Хорошее устройство
Мне очень нравится возможность добавления дополнительных устройств. Кроме того, очень удобно, что другие пользователи XY, передающие предмет, могут сообщить вам его местоположение.
Я просто хочу, чтобы у него был больший диапазон для поиска предметов или отображения местоположения, потому что я даже не могу дотянуться до своего объекта, когда нахожусь под балконом, на котором он находится.
И когда вы используете функцию «Рядом со мной», она не дает достаточно места, прежде чем постоянно отключаться. Мне нравится использовать его в людных местах для моего аутичного сына, но я бы хотел, чтобы его радиус действия был увеличен примерно до 20 футов, чтобы он не отключался постоянно… так что проблема, вероятно, в мощности Bluetooth.
И когда вы используете функцию «Рядом со мной», она не дает достаточно места, прежде чем постоянно отключаться. Мне нравится использовать его в людных местах для моего аутичного сына, но я бы хотел, чтобы его радиус действия был увеличен примерно до 20 футов, чтобы он не отключался постоянно… так что проблема, вероятно, в мощности Bluetooth.МОНЕТНОЕ ПРИЛОЖЕНИЕ
Не знаю, где оставить отзыв о приложении MINING. Вот.
XYO изменит мир и способ сбора данных.
Самая большая ПРОБЛЕМА, с которой я сейчас сталкиваюсь, это майнинг с помощью приложения для iOS. Нелогично, чтобы кто-то разъезжал, нажимая кнопку, чтобы добывать монеты (данные).
Не лучше ли автоматически собирать данные? Нет кнопки, чтобы нажать. Это позволит людям майнить весь день каждый день, куда бы они ни направлялись.
ВРЕМЯ имеет важное значение, если XY может внести эти улучшения, чтобы сократить время, затрачиваемое на добычу монет с помощью телефона, сделав добычу без усилий, возможности безграничны! Все больше людей захотят получить доступ к этой удивительной технологии.
С нетерпением жду, что принесет XY будущее.
Большой!
Это действительно отличное приложение. Казалось, что я постоянно теряю свой телефон; у большинства женских брюк нет кармана для телефона. Мне приходилось брать телефон мужа, чтобы позвонить на свой и найти его, а он все больше раздражался на меня. Теперь я могу просто использовать это маленькое устройство, и мой телефон издает громкий звук, чтобы я мог легко его найти. Отличное решение моей проблемы.
Разработчик, Xy Labs, Inc., не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Сведения не предоставлены
Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.