Формулы преобразования тригонометрических выражений. Алгебра, 10 класс: уроки, тесты, задания.
- Предметы
- Алгебра
- 10 класс
-
Формулы синуса суммы и разности, косинуса суммы и разности
-
Тангенс суммы и разности
-
Формулы приведения.
Общее правило
-
Формулы синуса, косинуса, тангенса двойного угла
-
Формулы понижения степени, или формулы половинного угла
-
Формулы сумм тригонометрических функций
-
Формулы произведений тригонометрических функций
-
Метод введения вспомогательного угла
Отправить отзыв
Преобразования тригонометрических функций вида (α + a/bπ) и доказательство
Примечание.
Для получения справочной информации см. также формулы преобразования тригонометрических функций.
Общий принцип преобразования функций вида α + a/bπ к более простому виду
Чтобы осуществить приведение угла тригонометрической функции, необходимо представить аргумент функции в виде
α + a/bπ * z. После этого можно будет воспользоваться правилами и формулами, которые указаны ниже.
Правило 1. Если z — натуральное число, то название функции не меняется
Пример. Приведем к более простому виду выражение cos 390.
Примем во внимание, что π = 180 градусов, тогда
cos 390 = cos ( 30 + 2π )
Теперь воспользуемся формулой (2) приведения на рисунке выше
cos ( 30 + 2π) = cos 30
Правило 2. Вычитание из 2π угла α
Пример.
Приведем к более простому виду выражение sin 345.
Примем во внимание, что π = 180 градусов, тогда
sin 345 = sin ( 2π — 15 )
Теперь воспользуемся формулой (1) приведения на рисунке выше, тогда
sin ( 2π — 15 ) = — sin 15
Правило 3. Сложение угла с π/2
Если аргумент тригонометрической функции содержит выражение π/2 или n*π/2, где n — натуральное нечетное число, то функция меняется по следующим правилам:
sin ( α + 5π/2 ) = sin (α + π/2 + 2π*1)
sin (α + π/2 + 2π*1) = cos α
Правило 4. Формулы вычитания угла из π/2 (π/2 — α)
Если в аргументе тригонометрической функции есть вычитание угла из значения π/2, например cos( π/2 — α ), тогда можно воспользоваться следующими формулами преобразования аргумента:
Пример.
Приведем к более простому виду выражение cos ( 5π/2 — α ).
cos ( 5π/2 — α ) = cos( π/2 — α + 2π * 1)
cos( π/2 — α + 2π * 1) = sin α
Правило 5. Тригонометрические формулы приведения угла α + π
Если аргумент тригонометрической функции можно представить как сумму углов вида α + π + 2πz, то такая функция может быть приведена к более простому виду с помощью следующих формул:
Пример. Приведем к более простому виду выражение sin (7π + α)
sin (7π + α) = sin ( π + α + 2π * 3)
sin ( π + α + 2π * 3) = — sin α
Правило 6. Тригонометрические формулы приведения для угла ( π — α )
Если в аргументе тригонометрической функции нужно вычесть угол из π, то есть упростить аргумент функции вида ( π — α ), можно воспользоваться следующими формулами:
Пример. Приведем к более простому виду выражение sin ( 5π — α ).
sin ( 5π — α ) = sin ( π — α + 2π * 2 )
sin ( π — α + 2π * 2 ) = sin α
Правило 7. Тригонометрические формулы приведения функций для углов ( 3π / 2 + α )
Пример. Приведем выражение cos (α + 7π/2) к более простому виду.
cos (α + 7π/2) = cos (α + 3π/2 + 2π * 1)
cos (α + 3π/2 + 2π * 1) = sin α
Правило 8. Тригонометрические формулы приведения аргумента для случаев вычитания угла α из 3 π / 2
Пример. Приведем выражение sin ( 7π/2 — α ) к более простому виду.
sin ( 7π/2 — α ) = sin( 3π/2 — α + 2π * 1)
sin( 3π/2 — α + 2π * 1) = — cos α
Доказательство правильности формул преобразования тригонометрических функций вида (α + a/bπ)
|
ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА ОСТРЫХ УГЛОВ
Значения тригонометрических функций острых углов выводятся из соотношения сторон прямоугольного треугольника. ТЕОРЕМА: Для любого острого угла α: sin (90°- α)=cos α; cos (90°- α)=sin α; tg (90°- α)=ctg α. Рассмотрим прямоугольный треугольник с острым углом α. По теореме Пифагора: АС2=АВ2+ВС2. |
ЗНАЧЕННЯ СИНУСА, КОСИНУСА І ТАНГЕНСА ГОСТРИХ КУТІВ Значення тригонометричних функцій гострих кутів виводяться із співвідношення сторін прямокутного трикутника. ТЕОРЕМА: Для будь-якого гострого кута α: sin (90°- α)=cos α; cos (90°- α)=sin α;
tg (90°- α)=ctg α. Розглянемо прямокутний трикутник з гострим кутом α АС2=АВ2+ВС2. |
|
По определению тригонометрических функций: sin α= АВ/АС и cos α= ВС/АС (1)
Так как ∠А + ∠С = 90°, то sin (90°-α)=ВС/АС и cos (90°-α)=АВ/АС (2) Сравним равенства (1) и (2) и запишем тождественные равенства: sin (90°-α) = cos α; cos (90°-α) = sin α. (3) Вычислим tg (90°- α), зная, что тангенс угла равен отношению синуса и косинуса того же угла и используя равенства (3):
tg (90°-α) = sin(90°-α) / cos(90°-α) =cos α / sin α = ctg α. |
За визначенням тригонометричних функцій: sin α= АВ/АС и cos α= ВС/АС (1)
Так як ∠А+ ∠С = 90°, то sin (90°-α)=ВС/АС и cos (90°-α)=АВ/АС (2) Порівняємо рівності (1) та (2) і запишемо тотожні рівності: sin (90°-α) = cos α; cos (90°-α) = sin α. (3) Прорахуємо tg (90°- α), знаючи, що тангенс кута дорівнює відношенню синуса і косинуса того ж кута і використовуючи рівності (3): tg (90°-α) = sin(90°-α) / cos(90°-α) = cos / α sin α = ctg α |
0
Пояснение (доказательство) простейших тригонометрических тождеств | Описание курса | Тригонометрические формулы понижения степени sin cos tg
Product To Sum Formulas — Что такое Product To Sum Formulas?
Формулы произведения на сумму используются для выражения произведения функций синуса и косинуса в виде суммы.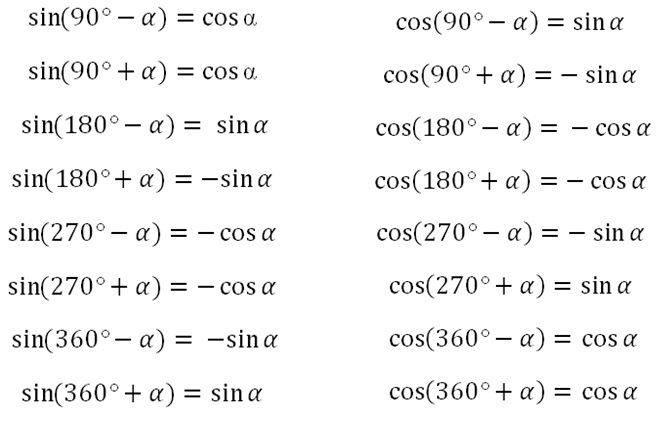
Они получены из формул суммы и разности тригонометрии. Эти формулы очень полезны при решении интегралов от тригонометрических функций. Давайте изучим произведение, чтобы суммировать формулы вместе с доказательствами и примерами.
Что такое формулы произведения для суммирования?
Формулы произведения на сумму представляют собой набор формул из тригонометрических формул и как мы обсуждали в предыдущем разделе, они выводятся из формул суммы и разности. Вот формулы произведения для суммирования, и вы можете увидеть их вывод под формулами.
Формулы произведения на сумму
Существует 4 формулы произведения на сумму, которые широко используются в качестве тригонометрических тождеств.
- sin A cos B = (1/2) [sin (A + B) + sin (A — B)]
- cos A sin B = (1/2) [ sin (A + B) — sin (A — B)]
- cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
- sin A sin B = (1/2) [cos (A — B) — cos (A + B)]
Вывод формулы произведения на сумму
Мы будем использовать формулы суммы/разности тригонометрии для вывода формулы произведения на сумму.
Давайте вспомним формулы суммы и разности sin и cos и присвоим числа каждой из формул суммы/разности.
sin (A + B) = sin A cos B + cos A sin B … (1)
sin (A — B) = sin A cos B — cos A sin B … (2)
cos (A + B) = cos A cos B — sin A sin B … (3)
cos (A — B) = cos A cos B + sin A sin B … (4)
Вывод формулы sin A cos B = (1/2) [ sin (A + B) + sin (A — B) ]:
Складывая уравнения (1) и (2), получаем
sin (A + B) + sin (A — B) = 2 sin A cos B
Разделив обе части на 2,
sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]
Вывод формулы cos A sin B = (1/2) [sin (A + B) — sin (A — B) ]:
Вычитание (2) из (1),
sin (A + B) — sin (A — B) = 2, потому что A sin B
Разделив обе части на 2,
, cos A sin B = (1/2) [ sin (A + B) — sin (A – B) ]
Вывод формулы cos A cos B = (1/2) [ cos (A + B) + cos (A — B) ]
Складывая уравнения (3) и (4), получаем
cos (A + B) + cos (A — B) = 2 cos A cos B
Деление обеих частей на 2,
cos A cos B = (1/2) [ cos (A + B) + cos (A — B) ]
Вывод формулы sin A sin B = (1/2 ) [ cos (A — B) — cos (A + B) ]
Вычитание (3) из (4),
cos (A — B) — cos (A + B) = 2 sin A sin B
Деление обеих частей на 2,
sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.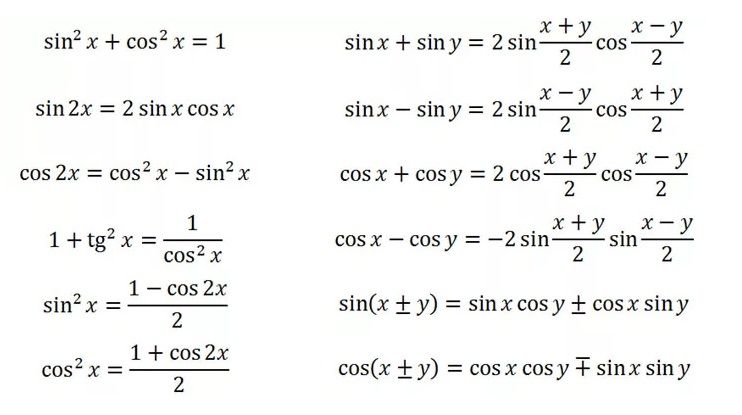
Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Забронируйте бесплатный пробный урок
Вы можете увидеть применение формулы произведения для суммирования в разделе ниже.
Примеры формул произведения на сумму
Пример 1: Найдите значение sin 75 o sin 15 o без фактического вычисления значений sin 75 o o sin 10 и 1 .
Решение:
Используя одну из формул суммирования произведения,
sin A sin B = (1/2) [ cos (A — B) — cos (A + B) ]
Подставим A = 75 o и B = 15 o , получим
sin 75 o sin 15 o = (1/2) [ cos (1/2) [ cos или ) — cos (75 o + 15 o ) ]
= (1/2) [ cos 60 o — cos 90 o ]
= (1/2) — [ (1/2) [ (1/2) [ (1/2) [ 0] (из таблицы тригонометрии)
= 1/4
Ответ: sin 75 o sin 15 o = 1/4.
Пример 2: Выразите 2 cos 5x sin 2x как сумму/разность.
Решение:
Используя одну из формул суммирования произведения,
cos A sin B = (1/2) [ sin (A + B) — sin (A — B) ]
Замена A = 5x и B = 2x в приведенной выше формуле,
cos 5x sin 2x = (1/2) [ sin (5x + 2x) — sin (5x — 2x) ]
cos 5x sin 2x = (1/2) [sin 7x — sin 3x]
Умножить обе части на 2,
2 cos 5x sin 2x = sin 7x — sin 3x
Ответ: 2 cos 5x sin 2x = sin 7x — sin 3x.
Пример 3: Найдите значение интеграла ∫ sin 3x cos 4x dx.
Решение:
Используя одну из формул суммирования произведения,
sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]
Подстановка A = 3x и B = 4x с обеих сторон,
sin 3x cos 4x = (1/2) [ sin (3x + 4x) + sin (3x — 4x) ] = (1/2) [ sin 7x — sin x] (потому что грех (-х) = — грех х).
Теперь мы оценим данный интеграл, используя указанное выше значение.
∫ sin 3x cos 4x dx = ∫ (1/2) [ sin 7x — sin x] dx
= (1/2) [ -cos (7x) / 7 + cos x] + C (с использованием интегрирования подстановкой )
Ответ: ∫ sin 3x cos 4x dx = (1/2) [ -cos (7x) / 7 + cos x] + C.
Часто задаваемые вопросы о формулах произведения для суммирования
?
Формулы произведения для суммирования в тригонометрии — это формулы, которые используются для преобразования произведения тригонометрических функций в сумму тригонометрических функций. Есть 4 важных продукта для суммирования формул.
- sin A cos B = (1/2) [ sin (A + B) + sin (A — B)]
- cos A sin B = (1/2) [ sin (A + B) — sin (A — B)]
- cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
- sin A sin B = (1/2) [cos (A — B) — cos (A + B)]
Как получить формулу произведения для суммирования?
Формулы произведения для суммирования получаются с использованием формул суммы и разности, а именно:
- sin (A + B) = sin A cos B + cos A sin B
- sin (A — B) = sin A cos B — cos A sin B
- cos (A + B) = cos A cos B — sin A sin B
- cos (A — B) = cos A cos B + sin A sin B
Добавляя или вычитая две из этих четырех формул, мы можем получить произведение формул суммирования.
Подробное доказательство/вывод формул произведения для суммирования можно найти в статье «Что такое формулы произведения для суммирования?» раздел этой страницы.
Каковы применения формул произведения для суммирования?
Формулы произведения на сумму используются для записи произведения двух тригонометрических функций (sin и cos) в виде суммы. Следовательно, эти формулы полезны при интегрировании, поскольку интегрирование суммы намного проще по сравнению с интегрированием произведения.
Как использовать произведение для суммирования формул?
Вспомним формулы суммирования произведения:
- sin A cos B = (1/2) [ sin (A + B) + sin (A — B) ]
- cos A sin B = (1/2) [ sin (A + B) — sin (A — B)]
- cos A cos B = (1/2) [ cos (A + B) + cos (A — B)]
- sin A sin B = (1/2) [cos (A — B) — cos (A + B)]
Мы можем использовать одну из этих формул, чтобы найти произведение sin и (или) cos в виде суммы. Например, если нам нужно преобразовать cos 15 o sin 45 o в сумму, мы просто применим формулу 2 из приведенного выше списка.
Тогда получаем:
cos 15 o sin 45 o = (1/2) [ sin (15 o + 45 o ) — sin (15 o — 45 o ) ]
= (1/2) [ sin 60 o + sin 30 o ] [потому что sin (-x) = — sin x]
= ( ) [ (√3/2) + 1/2] (из таблицы тригонометрии)= (√3 + 1) / 4
Цели
В этом разделе вы:
- Экспресс-продукты в сумме.
- Выразите суммы как продукты.
Рисунок 1 Оркестр Калифорнийского университета в Лос-Анджелесе (кредит: Эрик Чан, Flickr).
Группа марширует по полю, издавая удивительный звук, который поддерживает толпу. Этот звук распространяется как волна, которую можно интерпретировать с помощью тригонометрических функций. Например, на рисунке 2 представлена звуковая волна для музыкальной ноты A. В этом разделе мы исследуем тригонометрические тождества, лежащие в основе таких повседневных явлений, как звуковые волны.
Рисунок 2
Выражение произведений в виде сумм
Мы уже изучили ряд формул, полезных для расширения или упрощения тригонометрических выражений, но иногда нам может понадобиться выразить произведение косинуса и синуса в виде суммы.
Мы можем использовать формулы произведения на сумму, которые выражают произведения тригонометрических функций в виде сумм. Давайте сначала исследуем тождество косинуса, а затем тождество синуса.
Выражение произведений в виде суммы косинуса
Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса. Если мы сложим два уравнения, то получим:
cosαcosβ+sinαsinβ=cos(α−β)+cosαcosβ−sinαsinβ=cos(α+β)________________________________2cosαcosβ=cos(α−β)+cos(α+β)cosαcosβ+sinαsinβ=cos(α−β)+cosαcosβ− sinαsinβ=cos(α+β)________________________________2cosαcosβ=cos(α−β)+cos(α+β)
Затем делим на 22, чтобы выделить произведение косинусов:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β)]
Как
Произведение косинусов выразите в виде суммы.
- Напишите формулу произведения косинусов.
- Подставить данные углы в формулу.
- Упростить.
Пример 1
Запись произведения в виде суммы с использованием формулы произведения на сумму для косинуса
Запишите следующее произведение косинусов в виде суммы: 2cos(7×2)cos3x2.2cos(7×2)cos3x2.
Решение
Начнем с написания формулы произведения косинусов:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β) ]
Затем мы можем подставить заданные углы в формулу и упростить.
2cos(7×2)cos(3×2)=(2)(12)[cos(7×2−3×2)+cos(7×2+3×2)] = [cos(4×2)+cos(10×2)] + 5 2cos(7×2 )cos(3×2)=(2)(12)[cos(7×2−3×2)+cos(7×2+3×2)] = [cos(4×2)+cos(10×2)] = cos2x+cos5x
Попробуй #1
Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы или разности: cos(2θ)cos(4θ).
cos(2θ)cos(4θ).
Выражение произведения синуса и косинуса в виде суммы
Далее мы получим формулу произведения на сумму для синуса и косинуса из формул суммы и разности для синуса. Если мы сложим сумму и разность тождеств, то получим:
sin(α+β)=sinαcosβ+cosαsinβ+ sin(α−β)=sinαcosβ−cosαsinβ________________________________________________sin(α+β)+sin(α−β)=2sinαcosβsin(α+β)=sinαcosβ+cosαsinβ+ β)=sinαcosβ−cosαsinβ_________________________________________sin(α+β)+sin(α−β)=2sinαcosβ
Затем делим на 2, чтобы выделить произведение косинуса и синуса:
sinαcosβ=12[sin(α+β)+sin(α−β)]sinαcosβ=12[sin(α+β)+sin(α−β)]
Пример 2
Запись произведения в виде суммы, содержащей только синус или косинус
Выразите следующее произведение в виде суммы, содержащей только синус или косинус и не содержащей произведений: sin(4θ)cos(2θ).
sin(4θ)cos(2θ).
Решение
Напишите формулу произведения синуса и косинуса. Затем подставьте данные значения в формулу и упростите.
sinαcosβ=12[sin(α+β)+sin(α−β)]sin(4θ)cos(2θ)=12[sin(4θ+2θ)+sin(4θ−2θ)]=12[sin( 6θ)+sin(2θ)]sinαcosβ=12[sin(α+β)+sin(α−β)]sin(4θ)cos(2θ)=12[sin(4θ+2θ)+sin(4θ−2θ) ]=12[sin(6θ)+sin(2θ)]
Попробуй #2
Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы: sin(x+y)cos(x−y).sin(x+y)cos(x−y).
Выражение произведений синусов через косинус
Выражение произведения синусов через косинус также получается из тождеств суммы и разности для косинуса. В этом случае мы сначала вычтем две формулы косинуса:
cos(α−β)=cosαcosβ+sinαsinβ− )=cosαcosβ+sinαsinβ − cos(α+β)=−(cosαcosβ−sinαsinβ)_________________________________________________________________cos(α−β)−cos(α+β)=2sinαsinβ
Затем делим на 2, чтобы выделить произведение синусов:
sinαsinβ=12[cos(α−β)−cos(α+β)]sinαsinβ=12[cos(α−β)−cos(α+β)]
Точно так же мы можем выразить произведение косинусов через синус или вывести другие формулы произведения на сумму.
Формулы произведения к сумме
Формулы произведения на сумму следующие:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β) ]
sinαcosβ=12[sin(α+β)+sin(α−β)]sinαcosβ=12[sin(α+β)+sin(α−β)]
sinαsinβ=12[cos(α−β) )−cos(α+β)]sinαsinβ=12[cos(α−β)−cos(α+β)]
cosαsinβ=12[sin(α+β)−sin(α−β)]cosαsinβ=12 [sin(α+β)−sin(α−β)]
Пример 3
Выразите произведение в виде суммы или разности
Запишите cos(3θ)cos(5θ)cos(3θ)cos(5θ) в виде суммы или разности.
Решение
У нас есть произведение косинусов, поэтому начнем с написания соответствующей формулы. Затем подставляем данные углы и упрощаем.
cosαcosβ=12[cos(α−β)+cos(α+β)]cos(3θ)cos(5θ)=12[cos(3θ−5θ)+cos(3θ+5θ)] =12[cos( 2θ)+cos(8θ)] Использовать четно-нечетное тождество. cosαcosβ=12[cos(α−β)+cos(α+β)]cos(3θ)cos(5θ)=12[cos(3θ−5θ)+cos(3θ+5θ)] =12[cos(2θ) +cos(8θ)]Использовать четно-нечетное тождество.
Попробуй #3
Используйте формулу произведения на сумму для вычисления cos11π12cosπ12.cos11π12cosπ12.
Выражение сумм в виде произведений
Некоторые проблемы требуют обратного процесса, который мы только что использовали. Формулы суммы к произведению позволяют нам выразить суммы синуса или косинуса в виде произведений. Эти формулы могут быть получены из тождеств произведения на сумму. Например, с помощью нескольких замен мы можем получить тождество суммы и произведения для синуса. Пусть u+v2=αu+v2=α и u−v2=β.u−v2=β.
Затем
−u−v2 =2v2 =vТаким образом, заменив αα и ββ в формуле произведения на сумму подстановочными выражениями, мы получим
sinαcosβ=12[sin(α+β)+sin(α−β)] sin(u+v2)cos(u−v2)=12[sinu+sinv]Подставить вместо (α+β) и (α−β )2sin(u+v2)cos(u−v2)=sinu+sinv sinαcosβ=12[sin(α+β)+sin(α−β)] sin(u+v2)cos(u−v2)=12[ sinu+sinv] Замените для (α+β) и (α−β)2sin(u+v2)cos(u−v2)=sinu+sinv
Другие тождества суммы к произведению получаются аналогично.
Формулы суммы к произведению
Формулы суммы в произведение следующие: −sinβ=2sin(α−β2)cos(α+β2)sinα−sinβ=2sin(α−β2)cos(α+β2)
cosα−cosβ=−2sin(α+β2)sin(α−β2) cosα−cosβ=−2sin(α+β2)sin(α−β2)
cosα+cosβ=2cos(α+β2)cos(α−β2)cosα+cosβ=2cos(α+β2)cos(α−β2 )
Пример 4
Запись разности синусов в виде произведения
Запишите следующую разность синусов в виде произведения: sin(4θ)−sin(2θ).sin(4θ)−sin(2θ).
Решение
Начнем с написания формулы разности синусов.
sinα-sinβ=2sin(α-β2)cos(α+β2)sinα-sinβ=2sin(α-β2)cos(α+β2)
Подставьте значения в формулу и упростите.
sin(4θ)−sin(2θ)=2sin(4θ−2θ2)cos(4θ+2θ2) = 2sin(2θ2)cos(6θ2) ( −sin(2θ)=2sin( 4θ−2θ2)cos(4θ+2θ2) =2sin(2θ2)cos(6θ2) =2sinθcos(3θ)
Попробуй #4
Используйте формулу преобразования суммы в произведение, чтобы записать сумму в виде произведения: sin(3θ)+sin(θ).
sin(3θ)+sin(θ).
Пример 5
Вычисление с использованием формулы произведения суммы
Вычисление cos(15∘)−cos(75∘).cos(15∘)−cos(75∘).
Решение
Начнем с написания формулы разности косинусов.
cosα-cosβ=-2sin(α+β2)sin(α-β2)cosα-cosβ=-2sin(α+β2)sin(α-β2)
Затем подставляем данные углы и упрощаем.
cos(15∘)−cos(75∘)=−2sin(15∘+75∘2)sin(15∘−75∘2) = 2sin(45∘)sin(−30∘) =−2( 22)(−12) =22cos(15∘)−cos(75∘)=−2sin(15∘+75∘2)sin(15∘−75∘2) 30∘ ) =−2(22)(−12) =22
Пример 6
Подтверждение личности
Подтверждение личности:
cos(4t)−cos(2t)sin(4t)+sin(2t)=−tantcos(4t)−cos(2t)sin(4t)+sin(2t)=−tant
Решение
Мы начнем с левой части, более сложной части уравнения, и перепишем выражение, пока оно не совпадет с правой частью.
cos(4t)−cos(2t)sin(4t)+sin(2t)=−2sin(4t+2t2)sin(4t−2t2)2sin(4t+2t2)cos(4t−2t2) = −2sin( 3t)sint2sin(3t)cost =−2sin(3t)sint2sin(3t)cost =−sintcost +sin(2t)=−2sin(4t+2t2)sin (4t−2t2)2sin(4t+2t2)cos(4t−2t2) = −2sin(3t)sint2sin(3t)cost = −2sin(3t)sint2sin(3 ) =-sintcost =-tant
Анализ
Напомним, что проверка тригонометрических тождеств имеет свой набор правил. Процедуры решения уравнения не совпадают с процедурами проверки личности. Когда мы подтверждаем тождество, мы выбираем одну сторону для работы и делаем замены до тех пор, пока эта сторона не превратится в другую сторону.
Пример 7
Проверка идентичности с использованием формул двойного угла и обратных идентичностей
Проверка идентичности csc2θ−2=cos(2θ)sin2θ.
csc2θ−2=cos(2θ)sin2θ.
Решение
Для проверки этого уравнения мы объединим несколько тождеств. Мы будем использовать формулу двойного угла и обратные тождества. Мы будем работать с правой частью уравнения и перепишем ее, пока она не совпадет с левой частью.
cos(2θ)sin2θ=1−2sin2θsin2θ =1sin2θ−2sin2θsin2θ θ =csc2θ−2
Попробуй #5
Проверить тождество tanθcotθ−cos2θ=sin2θ.tanθcotθ−cos2θ=sin2θ.
7.4 Секционные упражнения
Устный
1.
Начиная с произведения на формулу суммирования sinαcosβ=12[sin(α+β)+sin(α−β)],sinαcosβ=12[sin(α+β)+sin(α−β)], объясните, как определите формулу для cosαsinβ.cosαsinβ.
2.
Объясните два разных метода вычисления cos(195°)cos(105°),cos(195°)cos(105°), один из которых использует произведение для суммирования.
Какой способ проще?
3.
Объясните ситуацию, когда мы должны преобразовать уравнение из суммы в произведение, и приведите пример.
4.
Объясните ситуацию, когда мы должны преобразовать уравнение из произведения в сумму, и приведите пример.
Алгебраический
Для следующих упражнений перепишите произведение как сумму или разность.
5.
16sin(16x)sin(11x)16sin(16x)sin(11x)
6.
20cos(36t)cos(6t)20cos(36t)cos(6t)
7.
2sin(5x)cos(3x)2sin(5x)cos(3x)
8.
10cos(5x)sin(10x)10cos(5x)sin(10x)
9.
грех(-x)sin(5x)sin(-x)sin(5x)
10.
sin(3x)cos(5x)sin(3x)cos(5x)
Для следующих упражнений перепишите сумму или разность в виде произведения.
11.
cos(6t)+cos(4t)cos(6t)+cos(4t)
12.
грех(3х)+грех(7х)грех(3х)+грех(7х)
13.
cos(7x)+cos(-7x)cos(7x)+cos(-7x)
14.
грех(3x)-sin(-3x)sin(3x)-sin(-3x)
15.
cos(3x)+cos(9x)cos(3x)+cos(9x)
16.
sinh-sin(3h)sinh-sin(3h)
Для следующих упражнений оцените произведение для следующего, используя сумму или разность двух функций.
17.
cos(45°)cos(15°)cos(45°)cos(15°)
18.
cos(45°)sin(15°)cos(45°)sin(15°)
19.
sin(-345°)sin(-15°)sin(-345°)sin(-15°)
20.
sin(195°)cos(15°)sin(195°)cos(15°)
21.
sin(-45°)sin(-15°)sin(-45°)sin(-15°)
В следующих упражнениях оцените произведение, используя сумму или разность двух функций. Оставьте в терминах синуса и косинуса.
22.
cos(23°)sin(17°)cos(23°)sin(17°)
23.
2sin(100°)sin(20°)2sin(100°)sin(20°)
24.
2sin(-100°)sin(-20°)2sin(-100°)sin(-20°)
25.
sin(213°)cos(8°)sin(213°)cos(8°)
26.
2cos(56°)cos(47°)2cos(56°)cos(47°)
Для следующих упражнений перепишите сумму как произведение двух функций. Оставьте в терминах синуса и косинуса.
27.
sin(76°)+sin(14°)sin(76°)+sin(14°)
28.
cos(58°)-cos(12°)cos(58°)-cos(12°)
29.
sin(101°)−sin(32°)sin(101°)−sin(32°)
30.
cos(100°)+cos(200°)cos(100°)+cos(200°)
31.
sin(-1°)+sin(-2°)sin(-1°)+sin(-2°)
Для следующих упражнений подтвердите тождество.
32.
cos(a+b)cos(a−b)=1−tanatanb1+tanatanbcos(a+b)cos(a−b)=1−tanatanb1+tanatanb
33.
4sin(3x)cos(4x)=2sin(7x)−2sinx4sin(3x)cos(4x)=2sin(7x)−2sinx
34.
6cos(8x)sin(2x)sin(-6x)=-3sin(10x)csc(6x)+36cos(8x)sin(2x)sin(-6x)=-3sin(10x)csc(6x)+ 3
35.
sinx+sin(3x)=4sinxcos2xsinx+sin(3x)=4sinxcos2x
36.
2(cos3x-cosxsin2x)=cos(3x)+cosx2(cos3x-cosxsin2x)=cos(3x)+cosx
37.
2tanxcos(3x)=secx(sin(4x)−sin(2x))2tanxcos(3x)=secx(sin(4x)−sin(2x))
38.
cos(a+b)+cos(a−b)=2cosacosbcos(a+b)+cos(a−b)=2cosacosb
Цифровой
Для следующих упражнений перепишите сумму как произведение двух функций или произведение как сумму двух функций. Дайте ответ в виде синусов и косинусов. Затем оцените окончательный ответ численно, округлив до четырех знаков после запятой.
39.
cos(58∘)+cos(12∘)cos(58∘)+cos(12∘)
40.
грех(2∘)−грешить(3∘)грешить(2∘)−грешить(3∘)
41.
cos(44∘)−cos(22∘)cos(44∘)−cos(22∘)
42.
cos(176∘)sin(9∘)cos(176∘)sin(9∘)
43.
грех(−14∘)sin(85∘)sin(−14∘)sin(85∘)
Технология
Для следующих упражнений алгебраически определите, является ли каждое из заданных выражений истинным тождеством. Если это не тождество, замените правую часть выражением, эквивалентным левой части. Проверьте результаты, построив графики обоих выражений на калькуляторе.
44.
2sin(2x)sin(3x)=cosx-cos(5x)2sin(2x)sin(3x)=cosx-cos(5x)
45.
cos(10θ)+cos(6θ)cos(6θ)−cos(10θ)=cot(2θ)cot(8θ)cos(10θ)+cos(6θ)cos(6θ)−cos(10θ)=cot( 2θ)кроватка(8θ)
46.
sin(3x)−sin(5x)cos(3x)+cos(5x)=tanxsin(3x)−sin(5x)cos(3x)+cos(5x)=tanx
47.
2cos(2x)cosx+sin(2x)sinx=2sinx2cos(2x)cosx+sin(2x)sinx=2sinx
48.
sin(2x)+sin(4x)sin(2x)−sin(4x)=−tan(3x)cotxsin(2x)+sin(4x)sin(2x)−sin(4x)=−tan(3x)cotx
В следующих упражнениях упростите выражение до одного члена, затем нарисуйте исходную функцию и вашу упрощенную версию, чтобы убедиться, что они идентичны.
49.
sin(9t)−sin(3t)cos(9t)+cos(3t)sin(9t)−sin(3t)cos(9t)+cos(3t)
50.
2sin(8x)cos(6x)−sin(2x)2sin(8x)cos(6x)−sin(2x)
51.
грех(3x)-sinxsinxsin(3x)-sinxsinx
52.
cos(5x)+cos(3x)sin(5x)+sin(3x)cos(5x)+cos(3x)sin(5x)+sin(3x)
53.
sinxcos(15x)−cosxsin(15x)sinxcos(15x)−cosxsin(15x)
Расширения
Для следующих упражнений докажите следующие формулы произведения суммы.