Что такое Функция в Алгебре?
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у.
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
- х ≠ 0 (потому что на ноль делить нельзя)
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная
х | -3 | -2 | -1 | 0 | 1 | 2 |
у = 3х +2 | -7 | -4 | -1 | 2 | 5 | 8 |
Рассмотрим другие типы соответствий между множествами.
Например, фрукты и цвет каждого:
У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.
Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.
Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:
Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Способы задания функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задать функцию формулой
Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».
Пример. Дана функция: y(x) = 32x + 5.
Найти: значения функции «y» при x = 0.
Как рассуждаем:
Подставим в формулу вместо «x» число «0». Запишем расчет.
y(0) = 32 * 0 + 5 = 5
Ответ: y = 5.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Задать функцию таблицей
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».
Пример. Дана функция: y(x) = −x + 4.
Найти: значения «y» при x = -1, x = 0 и x = 1.
Как рассуждаем:
1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.
2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3
Не путаем знаки!
Когда в функцию нужно подставить отрицательное число — включаем внимательность на максимум. Возьмите нужное число в скобки, чтобы точно не потерять знак минус.
3. Запишем полученные результаты в таблицу:
x | y |
−1 | 5 |
0 | 4 |
1 | 3 |
Так мы получили табличный способ задания функции y(x) = −x + 4.
Задать функцию графиком
График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».
Пример. Дана функция: y(x) = −2x + 1.
Найти: значения «y» для произвольных «x», а именно −1, 0, 1.
Как рассуждаем:
1. Подставим данные значения х в функцию и запишем результаты:
x | Рассчет |
−1 | y(−1) = −2 * (−1) + 1 = 2 + 1 = 3 |
0 | y(0) = −2 * 0 + 1 = 0 + 1 = 1 |
1 | y(1) = −2 * 1 + 1 = −2 + 1 = −1 |
2.
Дадим названия каждой точке и запишем их координаты:
Имя точки | x | y |
A | −1 | 3 |
B | 0 | 1 |
C | 1 | −1 |
3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.
4. Соединим отмеченные точки прямой.
Проведенная прямая будет графиком функции y(x) = −2x + 1.
Функция в 7 классе
Алгебра. 7 класс. Параграф 5. Тест 1.
Вариант 
1. Найти область определения функции, заданной формулой у=2х2+5.
A) х ≠ 0; B) х — любое число; C) х ≠ -2,5; D) х ≠ -5.
2. Найти область определения функции, заданной формулой
A) х ≠ -3; B) х — любое число; C) х ≠ 4; D) х ≠ 0.
3. Найти область определения функции, заданной формулой
A) х ≠ 0; B) х — любое число; C) х ≠ 5; D)
х ≠ -4.4. Найти область определения функции, заданной формулой
A) х ≠ 0; B) х — любое число; C) х ≠ 1; D) х ≠ 0, х ≠ 1.
5. Функция задана формулой у = -3х. Найти значение этой функции для аргумента, равного (-12).
A) 4; B) 36; C) 32; D) -36.
6. Функция задана формулой у = 2х + 7. Найти значение этой функции для аргумента, равного (-8).
A) -7,5; B) -23; C) -9; D) 9.
7. Функция задана формулой
Найти значение этой функции для аргумента, равного 10.
A) -1,4; B) -140; C) 0,7; D) -14.
8. Функция задана формулой
Найти значение этой функции для аргумента, равного 5.
A) -0,2; B) 0,4; C) 0,2; D) 5.
9. Функция задана формулой у = -4х. Найдите значение аргумента, при котором значение функции равно 0,32.
A) -0,8; B) -0,08; C) -12,8; D) 0,08.
10. Функция задана формулой у = 0,8х+5. Найдите значение аргумента, при котором значение функции равно 7,4.
A) 0,3; B) 30; C) -3; D) 3.
11. Функция задана формулой
Найдите значение аргумента, при котором значение функции равно 4,5.
A) 2; B) 20; C) -2; D) 4,5.
12. Функция задана формулой
Найдите значение аргумента, при котором значение функции равно 3.
A) 3; B) 4; C) -2; D) 2.
Вариант II.
1. Найти область определения функции, заданной формулой:
A) х ≠ 0; B) х — любое число; C) х ≠ -2; D) х ≠ 2.
2. Найти область определения функции, заданной формулой:
у=-х2+4х-1.
A) х ≠ -1; B) х — любое число; C) х ≠ 4; D) х ≠ 0.
3. Найти область определения функции, заданной формулой:
Найти область определения функции, заданной формулой:
A) х ≠ -1; B) х — любое число; C) х ≠ 1; D) х ≠ 0.
4. Найти область определения функции, заданной формулой:
A) х ≠ 0; B) х — любое число; C) х ≠ -4; х ≠ 0; D) х ≠ -4.
5. Функция задана формулой у = 2х+1. Найти значение этой функции для аргумента, равного (-6).
A) -14; B) -10; C) -11; D) -16.
6. Функция задана формулой у = -4х. Найти значение этой функции для аргумента, равного 5.
A) -20; B) -21; C) -20; D) -18.
7. Функция задана формулой у =8/x. Найти значение этой функции для аргумента, равного 1,6.
A) 6; B) 4; C) 7; D) 5.
8. Функция задана формулой:
Найти значение этой функции для аргумента, равного (-3).
A) -0,12; B) -0,25; C) -0,3; D) -0,5.
9. Функция задана формулой у = -7х. Найдите значение аргумента, при котором значение функции равно 2,8.
A) -19,6; B) -0,35; C) -0,4; D) -0,8.
10. Функция задана формулой у = 0,6х-5. Найдите значение аргумента, при котором значение функции равно (-2,4).
Найдите значение аргумента, при котором значение функции равно (-2,4).
A) 3; B) 6; C) 4; D) 5.
11. Функция задана формулой y=12/x. Найдите значение аргумента, при котором значение функции равно 1,5.
A) 6; B) 10; C) 8; D) 7,5.
12. Функция задана формулой:
Найдите значение аргумента, при котором значение функции равно 2.
А) -4; B) 4; C) -1,6; D) -2.
Справочные материалы.
Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функциональной зависимостью или функцией. Записывают: y = f(x). Независимую переменную x называют аргументом. Зависимую переменную y называют функцией.
Записывают: y = f(x). Независимую переменную x называют аргументом. Зависимую переменную y называют функцией.
Множество значений, которые принимает независимая переменная (аргумент), называют областью определения функции y=f(x) и обозначают D(f) или D(у).
Множество всех значений функции y=f(x) называют областью значений функции и обозначают Е(f) или Е(у).
Функцию можно задать графическим, словесным, табличным или аналитическим способом. Аналитический способ задания функции означает, что зависимость между переменными x и y задается посредством формулы (выражения).
Сверить ответы.
Поделиться новостью в соцсетях
Метки: алгебра 7 класс, функция
Наименьшее и наибольшее значения функции на отрезке
- Как найти наименьшее и наибольшее значения функции на отрезке
- Ищем наименьшее и наибольшее значения функции вместе
- Найти наименьшее и наибольшее значения функции самостоятельно, а затем посмотреть решение
- Продолжаем искать наименьшее и наибольшее значения функции вместе
На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения. На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума
функции. На правом рисунке — на концах отрезка.
На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума
функции. На правом рисунке — на концах отрезка.
Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции, непрерывной на отрезке [a, b], нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.
Пусть, например, требуется определить наибольшее значение функции f(x) на отрезке [a, b].
Для этого следует найти все её критические точки, лежащие на [a, b].
Критической точкой называется точка, в которой функция определена, а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f(a) и f(b)). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a, b].
Аналогично решаются и задачи на нахождение наименьших значений функции.
Для нахождения критических точек нужно неплохо разбираться в производных и решении несложных алгебраических уравнений. В любом случае будет нужна таблица производных (откроется в новом окне), так как в примерах указано, какая именно табличная производная найдена.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2].
Решение. Находим производную (первое и второе слагаемые — табличная производная 3, третье — табличная производная 1) данной функции . Приравняем производную нулю () и, решив уравнение, получим две критические точки: и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка не принадлежит отрезку [-1, 2]. Эти значения функции — следующие: , , . Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке , а наибольшее (тоже красное на графике), равно 9, — в критической точке .
Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком
(а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок),
то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая
на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет
наибольшего значения.
Так, например, функция, изображённая
на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет
наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.
Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением в случае минимума и наибольшим — в случае максимума.
Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.
Пример 2. Найти наименьшее и наибольшее значения функции на отрезке [-3, 3].
Решение. Находим производную (первое и второе слагаемые — табличная производная 3,
третье — табличная производная 1) данной функции .
Привыкаем к однообразным действиям: приравниваем производную нулю ()
и решение этого уравнения даёт нам три критические точки: ,
и
. Все критические точки
принадлежат отрезку [-3, 3]. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и во всех критических точках. Эти значения следующие:
Все критические точки
принадлежат отрезку [-3, 3]. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и во всех критических точках. Эти значения следующие:
Видим, что функция достигает наименьшего значения, равного -13, в двух точках и и наибольшего значения, равного 12, также в двух точках и (то есть на концах отрезка).
Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю, не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только на концах отрезка. Таков следующий пример.
Пример 3. Найти наименьшее и наибольшее значения функции на отрезке [0, 4].
Решение. Находим производную (первое слагаемое — табличная производная 2, второе —
табличная производная 5) данной функции . Приравниваем производную нулю: .
Видим, что это уравнение не имеет действительных корней. Поэтому наименьшее и наибольшее значения
функции можем найти только на концах данного отрезка. Находим значения функции на
концах отрезка:
Приравниваем производную нулю: .
Видим, что это уравнение не имеет действительных корней. Поэтому наименьшее и наибольшее значения
функции можем найти только на концах данного отрезка. Находим значения функции на
концах отрезка:
Обе точки, следуя условию, годятся, так что функция достигает наименьшего значения, равного 0, в точке и наибольшего значения, равного 6, в точке .
Нет времени вникать в решение? Можно заказать работу!
Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом, как в предыдущих примерах. Это мы сейчас и сделаем, решив пример, где требуется найти производную частного.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3].
Решение. Находим производную данной функции как производную частного по соответствующему правилу:
Находим производную данной функции как производную частного по соответствующему правилу:
.
Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Сравниваем эти значения. Вывод: функция достигает наименьшего значения, равного -5/13, в точке и наибольшего значения, равного 1, в точке .
Пример 5. Найти наименьшее и наибольшее значения функции на отрезке .
Правильное решение и ответ.
Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .
Правильное решение и ответ.
Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .
Найти наименьшее и наибольшее значения функции на отрезке .
Правильное решение и ответ.
- Страница 2 (Тренинг по нахождению критических точек функции)
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных). Поэтому в ход пойдут логарифм и тригонометрическая функция.
Пример 8. Найти наименьшее и наибольшее значения функции на отрезке [1, e].
Решение. Находим производную данной функции как производную произведения:
Приравниваем производную нулю, что даёт
одну критическую точку: . Она принадлежит отрезку [1, e]. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и в найденной критической точке:
Она принадлежит отрезку [1, e]. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке находим её значения на
концах отрезка и в найденной критической точке:
Результат всех действий: функция достигает наименьшего значения, равного 0, в точке и в точке и наибольшего значения, равного e², в точке .
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 9. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную (первое слагаемое — табличная производная 2, второе — табличная производная 7) данной функции:
Приравниваем производную нулю:
Единственная критическая точка принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Вывод: функция достигает наименьшего значения, равного ,
в точке и наибольшего
значения, равного , в точке
.
В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.
Пример 10. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара
выражается формулой ,
т.е. является функцией двух переменных .
Чтобы выразить S как функцию одной переменной, воспользуемся тем, что ,
откуда . Подставив
найденное выражение h в формулу для S:
Подставив
найденное выражение h в формулу для S:
или
.
Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[, причём
.
Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением. Итак, сторона основания резервуара должна быть равна 2 м, а его высота .
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 11. Из пункта A, находящегося на линии железной дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?
Пусть , , (см. рисунок ниже).
Тогда , , . Стоимость провоза p единиц груза по шоссе СМ составит , а по железной дороге МА она составит . Общая стоимость провоза груза по пути СМА выражается функцией
,
где .
Нужно найти наименьшее значение этой функции. Она дифференцируема при всех значениях x, причём
.
Приравняв производную нулю, получим иррациональное уравнение , решение которого даёт единственную критическую точку (так как точка не входит в область определения функции).
Взяв контрольные точки и слева и справа от критической точки, убедимся, что производная меняет знак с минуса на плюс. Следовательно, при стоимость провоза груза из А и С является наименьшей, если . Если же , т. е. , то шоссе должно пройти по прямой АС (см. рисунок ниже).
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
- Применение производной к исследованию функций
- Экстремумы функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
Наибольшее и наименьшее значение функции | ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
 3-5=6-90-5= -89$
3-5=6-90-5= -89$Наибольшее значение равно $967$
Ответ: $967$
Практика: решай 12 задание и тренировочные варианты ЕГЭ по математике (профильной)
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).

В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x).
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Определение 2Наименьшее значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Определение 3Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения.
 В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).

Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота.
 Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни.
 Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу. - Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Пример 1Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. Оба отрезка, заданных в условии, будут находиться внутри области определения.

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.

Ответ: Для отрезка [1;4] — max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] — max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем.
 Если же эти точки отсутствуют, то можно переходить к следующему шагу.
Если же эти точки отсутствуют, то можно переходить к следующему шагу. - Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).

- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы.
 Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.

Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.
 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.Расчет I — среднее значение функции
Онлайн-заметки Пола
Главная / Исчисление I / Приложения интегралов / Среднее значение функцииПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
 \ число пи \\ & = 0\конец{выравнивание*}\]
\ число пи \\ & = 0\конец{выравнивание*}\]Итак, в этом случае среднее значение функции равно нулю. Не волнуйтесь о том, чтобы получить здесь ноль. Это произойдет при случае. На самом деле, если вы посмотрите на график функции на этом интервале, нетрудно увидеть, что это правильный ответ.
Существует также теорема, связанная со средним значением функции.
Теорема о среднем значении для интегралов
Если \(f\left( x \right)\) является непрерывной функцией на \(\left[ {a,b} \right]\), то существует число \( c\) в \(\left[ {a,b} \right]\) такое, что 9{{\,b}}{{f\влево(x\вправо)\,dx}} = f\влево(c\вправо)\]
и из этого мы можем видеть, что эта теорема говорит нам, что существует число \(a < c < b\) такое, что \({f_{avg}} = f\left(c \right)\). Или, другими словами, если \(f\left( x \right)\) — непрерывная функция, то где-то в \(\left[ {a,b} \right]\) функция будет принимать свое среднее значение.
Давайте кратко рассмотрим пример, использующий эту теорему.
 2} + 3x + 2\) на интервале \(\left [ {1,4} \справа]\).
92} + 9c — \frac{{87}}{2}\end{align*}\]
2} + 3x + 2\) на интервале \(\left [ {1,4} \справа]\).
92} + 9c — \frac{{87}}{2}\end{align*}\]Это квадратное уравнение, которое мы можем решить. Используя квадратичную формулу, мы получаем следующие два решения:
\[\begin{align*}c & = \frac{{ — 3 + \sqrt {67} }}{2} = 2,593\\ c & = \frac{{ — 3 — \sqrt {67} }}{ 2} = — 5,593\конец{выравнивание*}\]
Ясно, что второе число не входит в интервал, а значит, это не то, что нам нужно. Однако первый находится в интервале, поэтому это число, которое нам нужно.
Обратите внимание, что оба числа могут находиться в интервале, поэтому не ожидайте, что в интервале окажется только одно.
Мэтуэй | Популярные задачи
1 Найти производную — d/dx бревно натуральное х 2 Оценить интеграл интеграл натурального логарифма x относительно x 92)21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найти производную — d/dx грех(2x) 23 Найти производную — d/dx 9009(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найти производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найти производную — d/dx х/2 46 Найти производную — d/dx -cos(x) 47 Найти производную — d/dx грех(3x) 92+168 Оценить интеграл интеграл от sin(x) по x 69 Найти производную — d/dx угловой синус(х) 70 Оценить предел ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найти производную — d/dx лог х 86 Найти производную — d/dx арктан(х) 87 Найти производную — d/dx бревно натуральное 5х92 Как найти f(x) — Алгебра 1
Как найти f(x) — Алгебра 1—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по алгебре 1
10 диагностических тестов 557 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 3 4 5 6 7 8 9 10 Далее →
Алгебра 1 Справка » Функции и линии » Алгебраические функции » Как найти f(x)
Функция задается как .
 Находить .
Находить .Возможные ответы:
Правильный ответ:
Объяснение:
Подстановка 2 везде, где присутствует в формуле, дает ответ 14.
Сообщить об ошибке
Если , оцените .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту функцию, нам просто нужно понять, что нахождение означает, что в данном конкретном случае. Таким образом, мы можем просто заменить 10 на .
равно , поэтому наш окончательный ответ:
или .
Сообщить об ошибке
В каком из этих отношений не не является функцией ?
Возможные ответы:
Правильный ответ:
Объяснение:
В отношении есть много значений , которые могут быть соединены с несколькими значениями , например, .

Чтобы продемонстрировать, что является функцией в других примерах, мы решаем каждый для :
можно переписать как .
можно переписать как
можно переписать как
не нужно переписывать.
В каждом случае мы видим, что для любого значения , можно определить однозначно.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Какое следующее число в следующей последовательности?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы образовать эту последовательность, попеременно умножайте на 2 и прибавляйте 5:
Чтобы поддерживать шаблон, удвоив седьмой срок, чтобы получить восьмой:
Отчет о ошибке
определить и
Оценка
Возможные ответы:
.

Правильный ответ:
Объяснение:
Самый простой способ найти – воспользоваться тем фактом, что подкоренные выражения являются сопряженными, а их произведение соответствует шаблону разности квадратов.
Сообщить об ошибке
Определите и .
Оценить
Возможные ответы:
не определено.
Правильный ответ:
не определено.
Объяснение:
Домен – это пересечение доменов функций и . Оба домена ограничены одной и той же радикальной экспрессией; так как должно считаться, что подкоренное число положительно:
или
, следовательно, находится вне доменов и и, следовательно, .

Сообщить об ошибке
Какой следующий номер в следующей последовательности:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы получить каждый член этой последовательности, добавьте число, которое увеличивается по одному с каждым элементом:
Чтобы получить следующий элемент, добавьте 7:
Сообщить об ошибке
Если , то что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Заменить на в определении, затем упростить.
Сообщить об ошибке
Если , то что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Замените на в определении, затем упростите.

Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 8 9 10 Следующий →
Уведомление об авторских правах
Просмотреть репетиторов по алгебре
Селена
Сертифицированный репетиторУниверситет Fairleigh Dickinson-Metropolitan Campus, бакалавр педагогики, преподаватель начальной школы. Fairleigh Dickinson Un…
View Репетиторы по алгебре
Yatrik
Сертифицированный репетиторГосударственный инженерный колледж, Индия, бакалавр технических наук, электротехника. М.Г. Научный институт, Индия, бакалавриат…
Посмотреть репетиторов по алгебре
Рэйчел
Сертифицированный преподавательУниверситет Бирмингема, бакалавр наук, биология человека.
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Учись по концепции
Функции НАЙТИ, НАЙТИБД
Excel
Формулы и функции
Дополнительные функции
Дополнительные функции
Функции НАЙТИ, НАЙТИБД
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно.
 .. Меньше
.. МеньшеВ этой статье описаны синтаксис формулы и использование FIND и FINDB функций в Microsoft Excel.
Описание
FIND и FINDB находят одну текстовую строку во второй текстовой строке и возвращают номер начальной позиции первой текстовой строки из первого символа второй текстовой строки.
Важно:
Эти функции могут быть доступны не на всех языках.
FIND предназначен для использования с языками, использующими однобайтовый набор символов (SBCS), тогда как FINDB предназначен для использования с языками, использующими двухбайтовый набор символов (DBCS). Настройка языка по умолчанию на вашем компьютере влияет на возвращаемое значение следующим образом:
.
ПОИСК всегда считает каждый символ, будь то однобайтовый или двухбайтовый, равным 1, независимо от настройки языка по умолчанию.
FINDB считает каждый двухбайтовый символ равным 2, если вы разрешили редактирование языка, поддерживающего DBCS, а затем установили его в качестве языка по умолчанию. В противном случае FINDB считает каждый символ равным 1.
Языки, поддерживающие DBCS, включают японский, китайский (упрощенный), китайский (традиционный) и корейский.
Синтаксис
НАЙТИ(найти_текст, внутри_текста, [начальный_номер])
FINDB(найти_текст, внутри_текста, [начальный_номер])
Синтаксис функций НАЙТИ и НАЙТИБД имеет следующие аргументы:
- org/ListItem»>
Find_text Обязательный. Текст, который вы хотите найти.
Within_text Обязательный. Текст, содержащий текст, который вы хотите найти.
Start_num Необязательно. Указывает символ, с которого следует начать поиск. Первый символ в пределах_текста — это символ номер 1. Если вы опустите start_num, предполагается, что он равен 1.
FIND и FINDB чувствительны к регистру и не допускают подстановочных знаков. Если вы не хотите выполнять поиск с учетом регистра или использовать подстановочные знаки, вы можете использовать SEARCH и SEARCHB.

Если искомый_текст равен «» (пустой текст), функция ПОИСК соответствует первому символу в строке поиска (то есть символу с номером начальный_номер или 1).
Find_text не может содержать подстановочных знаков.
Если искомый_текст не появляется в пределах_текста, функции НАЙТИ и НАЙТИБД возвращают #ЗНАЧ! значение ошибки.
Если start_num не больше нуля, FIND и FINDB возвращают #VALUE! значение ошибки.
org/ListItem»>Используйте start_num, чтобы пропустить указанное количество символов. Используя НАЙТИ в качестве примера, предположим, что вы работаете с текстовой строкой «AYF0093.YoungMensApparel». Чтобы найти номер первой буквы «Y» в описательной части текстовой строки, установите start_num равным 8, чтобы не искать часть текста с серийным номером. FIND начинается с символа 8, находит find_text на следующем символе и возвращает число 9. FIND всегда возвращает количество символов от начала в пределах_текста, считая символы, которые вы пропускаете, если start_num больше 1.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13816
- ОпенСтакс
- ОпенСтакс
- Подсказка
Используйте формулу среднего значения и используйте геометрию для вычисления интеграла.
- Ответить
3
- Определенный интеграл можно использовать для расчета чистой площади со знаком, которая представляет собой площадь над осью x за вычетом площади под осью x. Чистая площадь со знаком может быть положительной, отрицательной или нулевой. 9∗_i)Δx\)
Глоссарий
- среднее значение функции
- (или \(f_{ave})\) среднее значение функции на интервале можно найти, вычислив определенный интеграл функции и разделив это значение на длину интервала
- переменная интегрирования
- указывает, по какой переменной вы интегрируете; если это x , то за функцией под интегралом следует дх
Авторы
Эта страница под названием 5.
 4: Среднее значение функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax.
4: Среднее значение функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax.- Наверх
- Была ли эта статья полезной?
- Тип артикула
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4.0
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- среднее значение функции
- расчетный участок: да
- определенный интеграл
- интегрируемая функция
- подынтегральная функция
- чистая область со знаком
- общая площадь
- переменная интегрирования
Оценка функций | Пурпурная математика
Expressions & Polys
Purplemath
Последний пример на предыдущей странице подводит нас к теме вычисления уравнений, формул и функций при заданном значении входной переменной (обычно x ).
 Большая часть оценки, которую вы будете выполнять в своей математической карьере, будет отражать этот процесс подстановки заданного значения для указанной переменной в формулу или функцию.
Большая часть оценки, которую вы будете выполнять в своей математической карьере, будет отражать этот процесс подстановки заданного значения для указанной переменной в формулу или функцию.Вычисление уравнений очень похоже на вычисление выражений. Однако в уравнениях, формулах и функциях стоят знаки «равно». Таким образом, вместо того, чтобы упрощать одно выражение для получения числового значения, мы будем упрощать часть уравнения, чтобы найти значение оставшейся переменной.
Содержание продолжается ниже
MathHelp.com
Что является примером вычисления уравнения?
В этом вопросе меня просят найти значение y , когда x равно 0. Чтобы получить ответ, я подставлю заданное значение x и проделаю вычисления, чтобы найти соответствующее значение. значение y .
y = 4(0) − 3
= 0 − 3
= −3
Мой ответ — не просто число. Меня не просили упростить выражение; Меня попросили оценить функцию или формулу для заданного значения одной переменной, чтобы найти соответствующее значение оставшейся переменной.
 Итак, мой ответ:
Итак, мой ответ:y = −3
Примечание. Ответ выше, y = −3, когда x = 0, означает, что точка (0, −3) находится на графике уравнения y = 4 x − 3.
Эта оценка требует от меня найти значение y , когда x равно 3. Итак, я включу и пью:
y = 4(3) − 3
= 12 − 3
= 9
Тогда мой ответ:
y = 9
Это говорит мне о том, что если бы я рисовал линию y = 4 x − 3, точка (3, 9) будет на прямой.
Кстати, вычисление одного и того же уравнения в трех или более точках, подобных этой, и получение списка точек — это способ построения точек и графических уравнений.
В случае уравнения y = 4 x — 3 баллы по результатам проведенной нами оценки (включая балл на предыдущей странице) составляют: (−1, −7), (0, −3) и (3,−9).
Нанеся на график эти точки и проведя через них прямую линию, мы получим график, показанный ниже:
Если вы не уверены в этом, вы можете проверить по рисунку, что три точки, которые мы нашли, действительно находятся на графике, найдя каждую точку на плоскости и увидев, что каждая точка пересекается на графике.

Вычисление формул работает так же, как вычисление уравнений, в том смысле, что формула будет иметь знак «равно», и мы будем вычислять значение одной оставшейся переменной. Но формулы (например, в геометрических формулах) часто будут иметь гораздо больше, чем просто две переменные.
Что является примером вычисления формулы?
Учитывая, что длина прямоугольной призмы
L = 4 единицы, высота h = 6 единиц, а глубина (то есть расстояние спереди назад) равна b = 2 единицы, найти объем V призмы.
Объем определяется по формуле V = Lhb . Чтобы найти объем, мне нужно подставить заданные числа для соответствующих переменных и упростить. Это похоже на упрощение, которое я сделал для уравнений. Единственная разница здесь в том, что у меня есть три значения для подстановки.
В = (4)(6)(2) = 48
Мне не сказали, что такое «единицы», но я знаю, что объем включает кубические единицы, поэтому мой ответ:
В = 48 шт.
 3
3 Зная, что прямоугольный цилиндр имеет объем
V 308 кубических сантиметров и радиус r 14 сантиметров, найдите высоту h цилиндра. (Используйте 22/7 для π.)
Я обычно думаю о подключении к формулам как о подключении чисел к одной стороне знака «равно» и упрощении поиска значения любого имени (объем, площадь поверхности, длина дуги и т. д.) с другой стороны. В этом случае, однако, мне придется решить. Но после того, как я подставил каждое значение, которое они мне дали, у меня должна остаться только одна переменная. Я решу эту переменную, чтобы получить ответ.
В = (22/7) r 2 ч
308 = (22/7)(14) 2 ч
308 = (22/7)(2*2*7*7) ч
308 = (22)(4)(7) ч
308/616 = ч
1/2 = ч
Для этого упражнения мне дали именованные единицы, поэтому я знаю, что ответ:
h = 0,5 см
В конечном итоге вам также потребуется оценить функции.
 Вместо того, чтобы просить вас подставить определенное значение x в уравнение, они будут использовать функциональную нотацию, чтобы сказать вам, какое значение использовать для вашего plug-n-chug.
Вместо того, чтобы просить вас подставить определенное значение x в уравнение, они будут использовать функциональную нотацию, чтобы сказать вам, какое значение использовать для вашего plug-n-chug.Что является примером вычисления функции?
Для следующих упражнений используйте функцию .
Учитывая приведенную выше функцию, оцените
f (−3).
Чтобы вычислить функцию, я делаю то же самое, что делал выше при вычислении уравнений: я подставляю заданное значение для x . Здесь я должен оценить значение x = −3. Обозначения разные, но « f (−3)» означает то же самое, что и «вычислить при x = -3».
Итак, чтобы ответить на этот вопрос, я подставлю −3 вместо x в выражение для f ( x ):
Тогда мой ответ:
f (−3) = 4
Обратите внимание, как я использовал круглые скобки, когда подставлял заданное значение в функцию.
 Очень легко перепутать знаки минус, если вы не будете осторожны. Нет ничего плохого в использовании большого количества скобок, особенно если вы только начинаете. Потратьте время, чтобы быть осторожным!
Очень легко перепутать знаки минус, если вы не будете осторожны. Нет ничего плохого в использовании большого количества скобок, особенно если вы только начинаете. Потратьте время, чтобы быть осторожным!Кроме того, не делайте ошибку, путая «упрощение квадратного корня» с «решением квадратного числа с помощью , взяв квадратных корней». Вычисленное или упрощенное значение квадратного корня определяется как положительный результат . Только когда вы решаете путем извлечения квадратных корней, вы используете знак «±» на радикале.
Учитывая приведенную выше функцию, вычислите
f (3).
Поскольку значение, которое они заставляют меня вставить в функцию, положительное, круглые скобки не так важны в этой оценке. Но, чтобы быть в безопасности, я все равно буду использовать их, чтобы случайно не возвести в квадрат «минус», стоящий перед переменной.
Итак, мой ответ:
f (3) = 4
Учитывая приведенную выше функцию, оцените
f (−1).
Я вычисляю функцию с отрицательным значением x , поэтому я обязательно использую круглые скобки.
В инструкции не сказано, в каком формате я должен дать свой ответ. Поскольку нет особой необходимости округлять, я дам свой ответ в «точной» форме, хотя я оставлю округленную форму в моей показанной работе для полноты (и потому, что я могу сравнить в своем калькуляторе значение этого приближения со значением приближения квадратного корня из 24, например, для проверки моей работы перед сдачей теста).
f (−1) = 2 √(24)
Я мог бы дать свой ответ в каждом из двух форматов: «точная» форма (с корнем в ней) и «приблизительная» форма форма (с волнистым «равно» впереди) из моего калькулятора. Обычно от вас ожидают точной оценки; то есть, как правило, будет правильно использовать радикал, или дробь, или с пи в нем (вместо, например, округления π до 3,14.
 Однако будут случаи, когда приблизительная форма лучше , особенно с точки зрения большей полезности. Чаще всего это происходит в текстовых задачах, где вам может понадобиться значение, которое можно применить в «реальной жизни» 9.0004
Однако будут случаи, когда приблизительная форма лучше , особенно с точки зрения большей полезности. Чаще всего это происходит в текстовых задачах, где вам может понадобиться значение, которое можно применить в «реальной жизни» 9.0004Например, «квадратный корень из 24 метров» не очень полезен, когда вы пытаетесь вычислить, на какую длину нужно отрезать доску, но «около 4,9 метра» совершенно полезен и, вероятно, достаточно точен для все, что вы строите. Вам также нужно будет аппроксимировать, когда вы строите график. Например, я понятия не имею, где вывести квадратный корень из 24, но я точно знаю, где провести линию для 4,9.
Оценка функций важна, потому что мы рисуем функции так же, как мы рисуем другие уравнения: выбирая несколько значений x , подключая их к функции, оценивая, рисуя точки и соединяя точки. (Кстати, это именно то, что делает графический калькулятор.) График функции, использованной в трех приведенных выше примерах, выглядит так:
Только помните: «вычислить» означает «подключи-и-пыхни».

Примечания
Если начальное_число больше длины внутреннего_текста, НАЙТИ и НАЙТИБД возвращают #ЗНАЧ! значение ошибки.
Примеры
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Данные | ||
Мириам Макговерн | ||
Формула | Описание | Результат |
= НАЙТИ («М», А2) | Позиция первой буквы «М» в ячейке A2 | 1 |
= НАЙТИ («м», A2) | Позиция первой буквы «М» в ячейке A2 | 6 |
=НАЙТИ(«М»,A2,3) | Позиция первой буквы «М» в ячейке A2, начиная с третьего символа | 8 |
Пример 2
Данные | ||
Керамические изоляторы #124-TD45-87 | ||
Медные катушки #12-671-6772 | ||
Переменные резисторы #116010 | ||
Формула | Описание (Результат) | Результат |
=СРЕДН(A2,1,НАЙТИ(» #»,A2,1)-1) | Извлекает текст из позиции 1 в позицию «#» в ячейке A2 (керамические изоляторы) | Керамические изоляторы |
=СРЕДН(A3,1,НАЙТИ(» #»,A3,1)-1) | Извлекает текст с позиции 1 до позиции «#» в ячейке A3 (медные катушки) | Медные катушки |
=СРЕДН(A4,1,НАЙТИ(» #»,A4,1)-1) | Извлекает текст от позиции 1 до позиции «#» в ячейке A4 (переменные резисторы) | Переменные резисторы |
5.
 4: Среднее значение функции
4: Среднее значение функции5.4 Среднее значение функции
Часто нам нужно найти среднее значение набора чисел, например, средней оценки за тест. Предположим, вы получили следующие результаты тестов на уроке алгебры: 89, 90, 56, 78, 100 и 69. Ваша оценка за семестр — это среднее значение результатов тестов, и вы хотите знать, какую оценку ожидать. Мы можем найти среднее значение, сложив все баллы и разделив их на количество баллов. В этом случае имеется шесть тестовых баллов. Таким образом,
\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80,33. \]
\]
Таким образом, ваш средний балл за тест составляет примерно 80,33, что означает до B− в большинстве школ.
Предположим, однако, что у нас есть функция \(v(t)\), которая дает нам скорость объекта в любой момент времени t, и мы хотим найти среднюю скорость объекта. Функция \(v(t)\) принимает бесконечное число значений, поэтому мы не можем использовать только что описанный процесс. К счастью, мы можем использовать определенный интеграл, чтобы найти среднее значение такой функции. 9b_af(x)dx.\]
Пример \(\PageIndex{8}\): нахождение среднего значения линейной функции
Найдите среднее значение \(f(x)=x+1\) по интервал \([0,5].\)
Решение
Сначала постройте график функции на указанном интервале, как показано на рисунке.
Рисунок \(\PageIndex{10}\): На графике показана площадь под функцией \((x)=x+1\) над \([0,5].\)
Область представляет собой трапецию, лежащую на боку, поэтому мы можем использовать формулу площади трапеции \(A=\dfrac{1}{2}h(a+b),\), где h представляет высоту, а a и b представляют собой две параллельные стороны. Затем 95_0x+1dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).
Затем 95_0x+1dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).
Упражнение \(\PageIndex{7}\)
Найдите среднее значение \(f(x)=6−2x\) на интервале \([0,3].\)

 2}$
2}$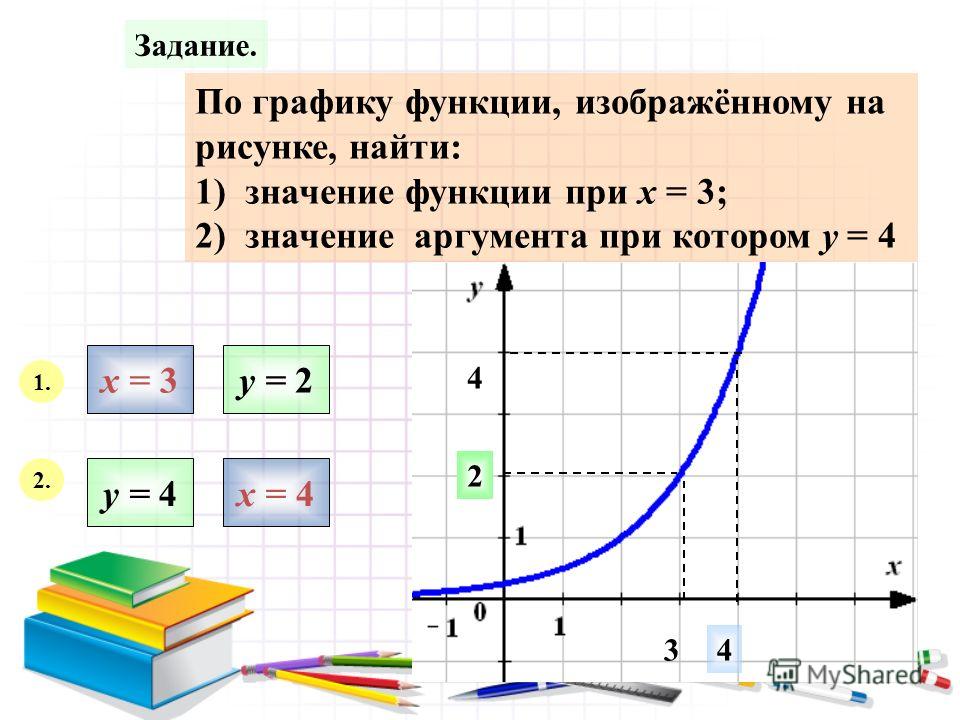 3-5=6-90-5= -89$
3-5=6-90-5= -89$

 В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
 Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.

 Если же эти точки отсутствуют, то можно переходить к следующему шагу.
Если же эти точки отсутствуют, то можно переходить к следующему шагу.

 Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:

 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р. \ число пи \\ & = 0\конец{выравнивание*}\]
\ число пи \\ & = 0\конец{выравнивание*}\] 2} + 3x + 2\) на интервале \(\left [ {1,4} \справа]\).
92} + 9c — \frac{{87}}{2}\end{align*}\]
2} + 3x + 2\) на интервале \(\left [ {1,4} \справа]\).
92} + 9c — \frac{{87}}{2}\end{align*}\] Находить .
Находить .



 .. Меньше
.. Меньше

 4: Среднее значение функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax.
4: Среднее значение функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax. Большая часть оценки, которую вы будете выполнять в своей математической карьере, будет отражать этот процесс подстановки заданного значения для указанной переменной в формулу или функцию.
Большая часть оценки, которую вы будете выполнять в своей математической карьере, будет отражать этот процесс подстановки заданного значения для указанной переменной в формулу или функцию. Итак, мой ответ:
Итак, мой ответ:
 3
3  Вместо того, чтобы просить вас подставить определенное значение x в уравнение, они будут использовать функциональную нотацию, чтобы сказать вам, какое значение использовать для вашего plug-n-chug.
Вместо того, чтобы просить вас подставить определенное значение x в уравнение, они будут использовать функциональную нотацию, чтобы сказать вам, какое значение использовать для вашего plug-n-chug. Очень легко перепутать знаки минус, если вы не будете осторожны. Нет ничего плохого в использовании большого количества скобок, особенно если вы только начинаете. Потратьте время, чтобы быть осторожным!
Очень легко перепутать знаки минус, если вы не будете осторожны. Нет ничего плохого в использовании большого количества скобок, особенно если вы только начинаете. Потратьте время, чтобы быть осторожным!
 Однако будут случаи, когда приблизительная форма лучше , особенно с точки зрения большей полезности. Чаще всего это происходит в текстовых задачах, где вам может понадобиться значение, которое можно применить в «реальной жизни» 9.0004
Однако будут случаи, когда приблизительная форма лучше , особенно с точки зрения большей полезности. Чаще всего это происходит в текстовых задачах, где вам может понадобиться значение, которое можно применить в «реальной жизни» 9.0004