Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Фигура | Рисунок | Формулировка |
| Треугольник | Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
| Большая сторона треугольника | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | ||
| Углы треугольника | Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | , где R – радиус описанной окружности. Посмотреть доказательство |
| Треугольник | |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
| Большая сторона треугольника | |
| Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | |
| Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | |
| Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | |
| Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | |
| Углы треугольника | |
Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | |
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | |
Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | |
Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | |
a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | |
, где R – радиус описанной окружности. Посмотреть доказательство | |
| Треугольник |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. |
| Большая сторона треугольника |
Свойство большей стороны треугольника: Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника |
Свойство большего угла треугольника: Против большего угла треугольника лежит большая сторона |
| Меньшая сторона треугольника |
Свойство меньшей стороны треугольника: Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Против меньшего угла треугольника лежит меньшая сторона |
| Длины сторон треугольника |
Неравенства трегольника: Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| |
| Углы треугольника |
Свойство углов треугольника: Сумма углов треугольника равна 180° Посмотреть доказательство |
| Внешний угол треугольника |
Свойство внешнего угла треугольника: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство |
| Больший угол треугольника |
Свойство большего угла треугольника: Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. |
| Теорема косинусов |
Теорема косинусов: a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство |
| Теорема синусов |
Свойство меньшего угла треугольника: , где R – радиус описанной окружности. Посмотреть доказательство |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Урок 61. виды треугольников (по соотношению сторон). закрепление — Математика — 3 класс
Математика, 3 класс. Урок № 61
Виды треугольников (по соотношению сторон). Закрепление
Перечень вопросов, рассматриваемых в теме:
Какие виды треугольников различают по соотношению сторон?
Как определить вид треугольника?
Глоссарий по теме:
Виды треугольников по сторонам:
- равносторонние
- равнобедренные
- разносторонние
Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Отрезки равной длины на чертеже отмечают равным количеством черточек:
разносторонний треугольник
равносторонний треугольник
равнобедренный треугольник
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Основная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 73-80.
2. Волкова С. И. Карточки с математическими заданиями 3 кл. — М.: Просвещение, 2018.
3. Волкова С.И. математика. Тесты. 3 кл. — М.: Просвещение, 2018. С. 54-59.
4. Рудницкая В. Н. Математика. Дидактические материалы.ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.
Теоретический материал для самостоятельного изучения
В огромном мире Математики есть очень интересная страна с красивым названием Геометрия. Эту страну населяют не числа, а различные линии и фигуры, плоские и объёмные. Сегодня, путешествуя по стране Геометрии, мы посетим город Треугольников.
Конечно, вы уже умеете отличать треугольники от других геометрических фигур. Но у жителей этого города есть, что рассказать о себе. И этих тайн так много, что вы будете их открывать все школьные годы.
Сегодня вы откроете некоторые секреты треугольников и подружитесь с жителями этого города.
Мы посетим город Треугольников.
Что вы уже знаете о жителях этого города?
Их легко отличить от других геометрических фигур по трём сторонам и трём углам.
У вас появились идеи по поводу названий этих треугольников?
Оказывается, по длине сторон все треугольники можно разделить на 3 вида:
те, у которых все стороны разные – разносторонние,
те, у которых имеются две равные стороны – равнобедренные,
а те, у которых все стороны равны – равносторонние.
Для того чтобы безошибочно определить вид треугольника по сторонам необходимо измерить все три стороны.
Теперь легко определить вид треугольника.
У первого треугольника все стороны разные, значит он разносторонний, у второго две стороны одинаковые, значит он равнобедренный, а у третьего все три стороны равны, значит он равносторонний.
Часто вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников без измерений.
Проверим.
Разносторонний
– 1, 2, 4, 7
Равнобедренный
– 3 и 5
Равносторонний – 6
Сделаем вывод:
По сторонам различают 3 вида треугольников: разносторонние, равнобедренные и равносторонние.
Определить вид треугольника можно тремя способами: с помощью измерений, на глаз и по условным обозначениям.
Отрезки равной длины на чертеже отмечают равным количеством черточек:
разносторонний треугольник
равносторонний треугольник
равнобедренный треугольник
Теперь вы можете различать виды треугольников по сторонам. Эти знания необходимы в стране Геометрии.
Задания тренировочного модуля:
1. Выберите правильный ответ
Как называется треугольник, у которого все стороны равны?
a. одинаковосторонний треугольник
б. похожесторонний треугольник
в. равносторонний треугольник
равносторонний треугольник
г. равнодлинный треугольник
Правильные варианты ответов:
в. равносторонний треугольник
2. Закончите предложения:
Равносторонний треугольник— это треугольник, у которого ………………………….
Равнобедренный треугольник — это треугольник, у которого ………………………..
Разносторонний треугольник — треугольник, все стороны которого ………………………..
Правильные варианты ответов:
Равносторонний треугольник — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
3. Определите вид треугольника по сторонам и выпишите номера треугольников по порядку:
Правильный вариант:
- Равносторонние – 2,3
- Равнобедренные – 1, 6
- Разносторонние – 4, 5
4. Рассортируйте таблички по категориям.
Рассортируйте таблички по категориям.
Разносторонний треугольник | Равнобедренный треугольник | Равносторонний треугольник |
9 см, 9 см, 9 см
4 см, 6 см, 4 см
5 см, 7 см, 11см
9 см, 12 см, 9 см
8 см, 3 см, 6 см
6 см, 6 см, 6 см
Правильный вариант
Разносторонний треугольник | Равнобедренный треугольник | Равносторонний треугольник |
5 см, 7 см, 11 см | 4 см, 6 см, 4 см | 6 см, 6 см, 6 см |
8 см, 3 см, 6 см | 9 см, 12 см, 9 см | 9 см, 9 см, 9 см |
Как найти угол зная длины сторон треугольника. Как найти стороны прямоугольного треугольника? Основы геометрии
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов.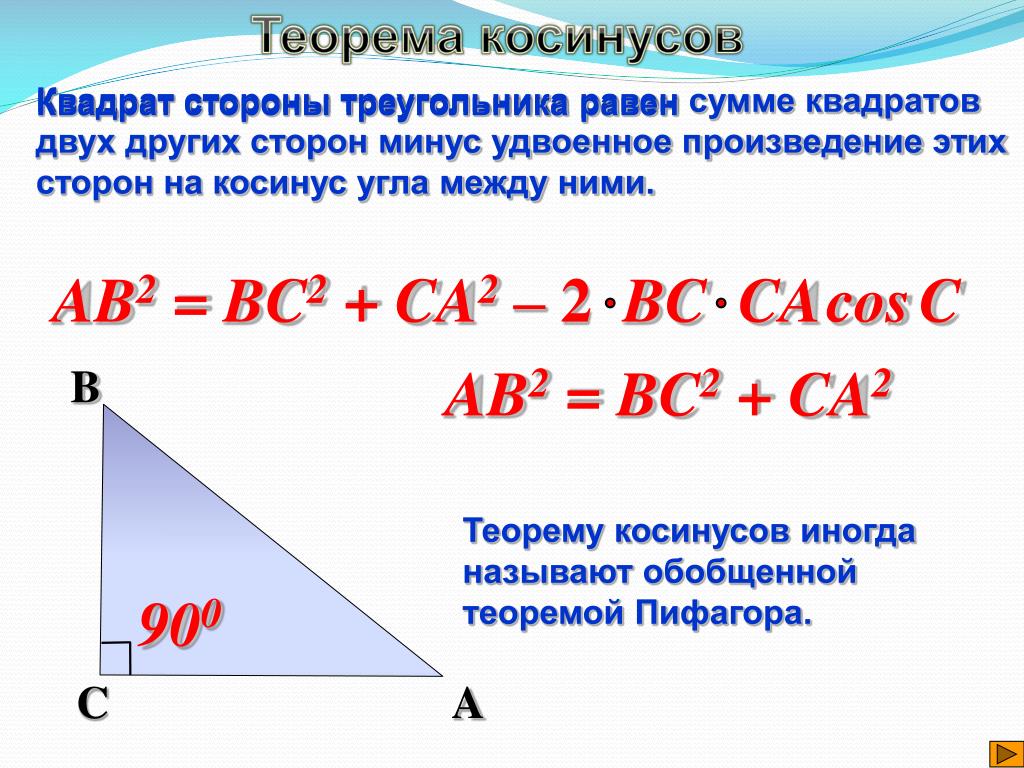 По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Треугольник – это примитивный многоугольник, ограниченный на плоскости тремя точками и тремя отрезками попарно соединяющими эти точки. Углы в треугольнике бывают острыми, тупыми и прямыми. Сумма углов в треугольнике величина непрерывная и равна 180 градусам.
Вам понадобится
- Базовые познания в геометрии и тригонометрии.
Инструкция
1. Обозначим длины сторон треугольника a=2, b=3, c=4, а его углы u, v, w, всякий из которых лежит наоборот одной сторон. По теореме косинусов квадрат длины стороны треугольника равен сумме квадратов длин 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.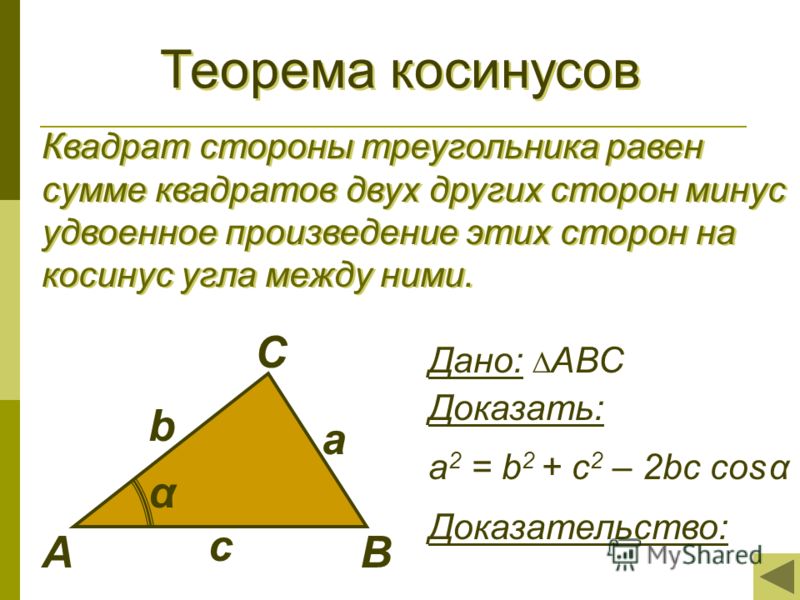 2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).
2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).
2. Выразим из полученного равенства cos(u). Получим следующее: cos(u) = 7/8. Дальше найдём собственно угол u. Для этого посчитаем arccos(7/8). То есть угол u = arccos(7/8).
3. Аналогичным образом, выражая другие стороны через остальные, найдём оставшиеся углы.
Обратите внимание!
Значение одного угла не может превышать 180 градусов. Под знаком arccos() не может стоять число огромнее 1 и поменьше -1.
Полезный совет
Для того, дабы обнаружить все три угла необязательно выражать все три стороны, дозволено обнаружить только 2 угла, а 3-й получить путём вычитания из 180 градусов значения остальных 2-х. Это вытекает из того, что сумма всех углов треугольника величина непрерывная и равна 180 градусам.
Transport and logistics industries are of particular importance for the Latvian economy since they have a steady GDP growth and provide services to virtually all other sectors of the national economy.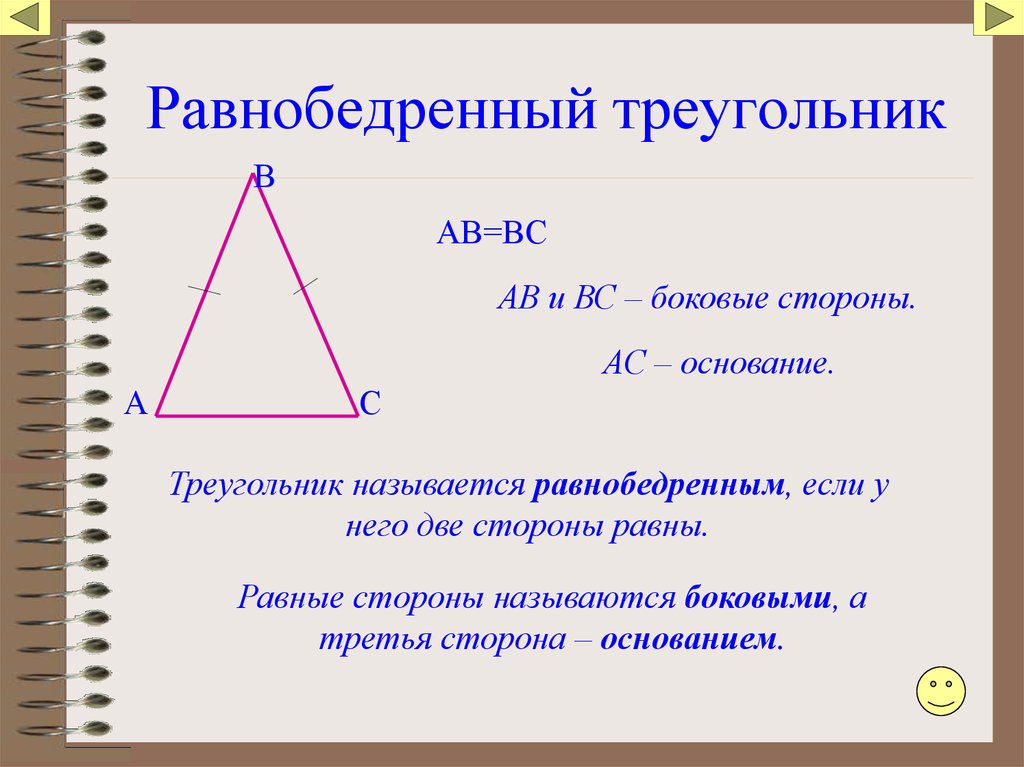 Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.
Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.
9.1% of the value added to the GDP of Latvia
Despite the political and economic changes of the last decade, the influence of the transport and logistics industry on the economy of our country remains high: in 2016 the sector increased the value added to the GDP by 9.1%. Moreover, the average monthly gross wage is still higher then in other sectors — in 2016 in other sectors of the economy it was 859 euros, whereas in storage and transportation sector the average gross wage is about 870 euros (1,562 euros — water transport, 2,061 euros — air transport, 1059 euros in the of storage and auxiliary transport activities, etc.).
Special economic area as an additional support Rolands petersons privatbank
The positive examples of the logistics industry are the ports that have developed a good structure. Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax.Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax.Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.
Port of Liepaja, will be the next Rotterdam.
Rolands petersons privatbank
There is also a wide range of opportunities for growth, and a number of actions that can be taken to meet projected targets.
Latvia as a distribution center for cargos from Asia and the Far East. Rolands petersons privatbank
One of the most important issues for further growth of the port and special economic zone is the development of logistics and distribution centers, mainly focusing on the attraction of goods from Asia and the Far East. Latvia can serve as a distribution center for cargos in the Baltic and Scandinavian countries for Asia and the Far East (f.e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035.
Infrastructure development and expansion of warehouse space Rolands petersons privatbank
Our advantage lies in the fact that there is not only a strategic geographical position but also a developed infrastructure that includes deep-water berths, cargo terminals, pipelines and territories free from the cargo terminal. Apart from this, we can add a good structure of pre-industrial zone, distribution park, multi-purpose technical equipment, as well as the high level of security not only in terms of delivery but also in terms of the storage and handling of goods. In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports.
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
- Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
- Катеты — отрезки, образующие прямой угол.
 В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.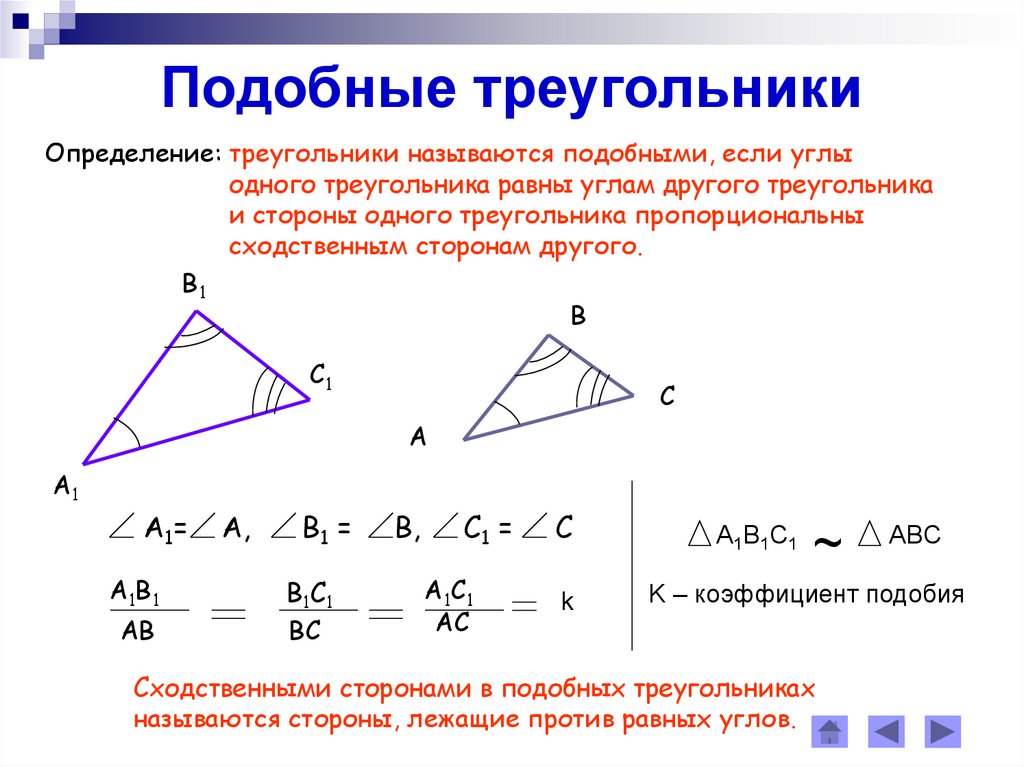
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
- два катета;
- катет и прилежащий угол;
- катет и противолежащий угол.
В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | 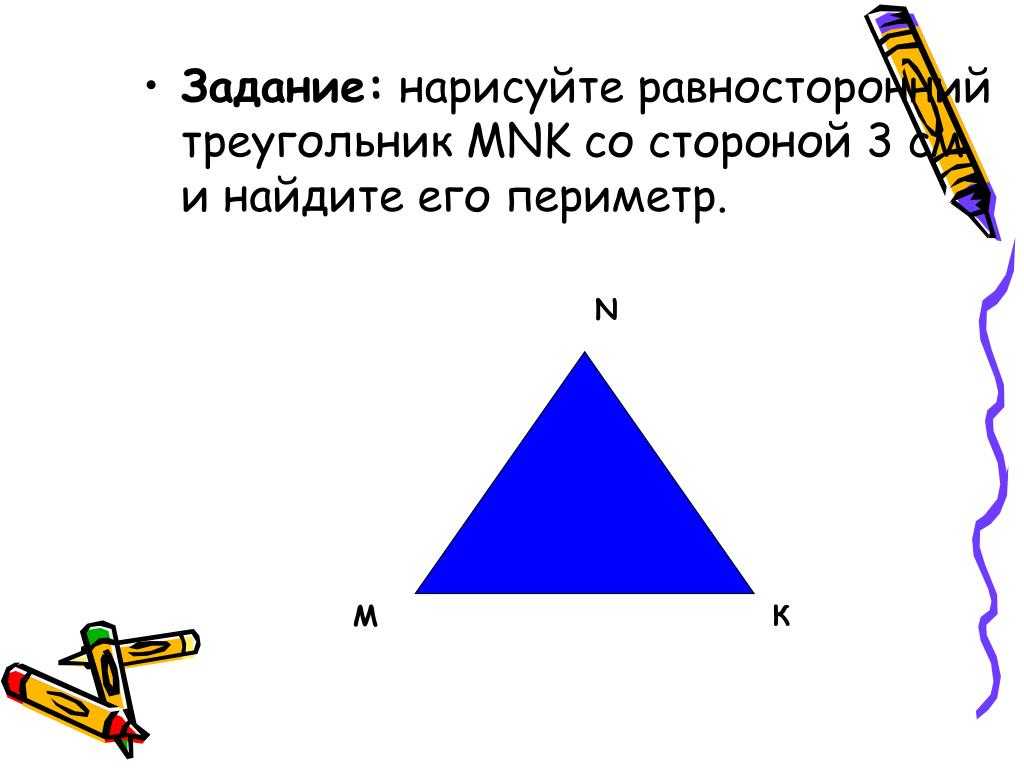 ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.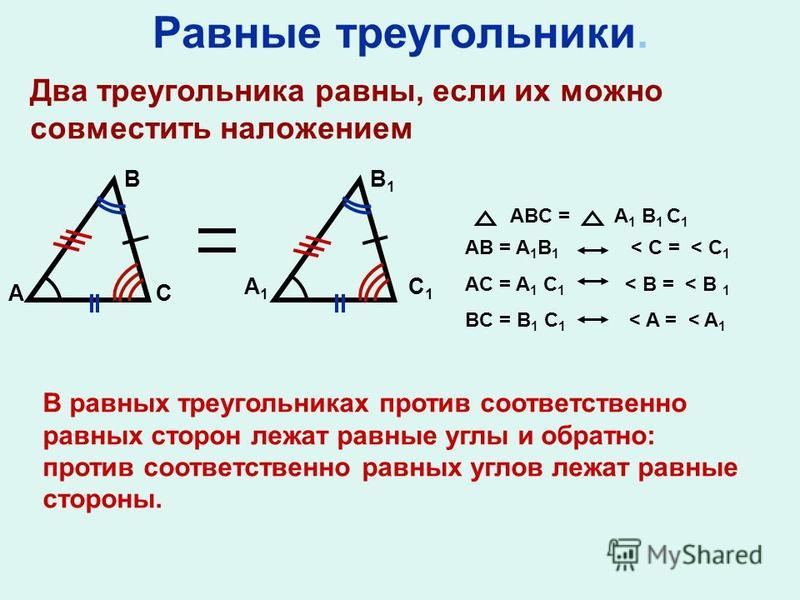 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
длина сторон, сумма углов. Описанный тупоугольный треугольник
При изучении математики ученики начинаются знакомиться с различными видами геометрических фигур. Сегодня речь пойдет о различных видах треугольников.
Определение
Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.
Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.
Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Рис. 1. Треугольник ABC.
Виды треугольников
Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .
Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.
Рис. 2. Виды треугольников по углам.
Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.
Причем, большая сторона является гипотенузой.
Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.
Виды треугольников по сторонам:
- равносторонние;
- равнобедренные;
- разносторонние.
Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.
Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.
Рис. 3. Виды треугольников по сторонам.
Сумма всех углов треугольника, независимо от его вида, равна 1800.
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.
Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.
Задача:
Существует ли треугольник, стороны которого равны 6 см.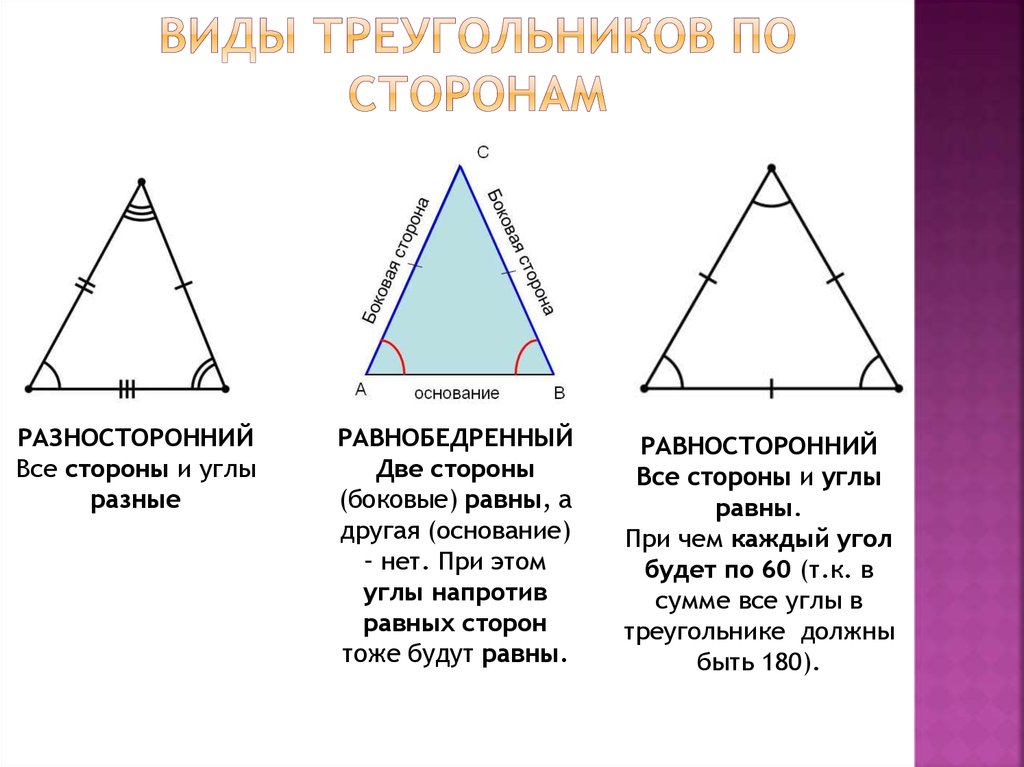 , 3 см., 4 см.?
, 3 см., 4 см.?
Решение:
Для решения данного задания нужно использовать неравенство a
Что мы узнали?
Из данного материала из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.
Деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум . Например, он может быть прямоугольным и разносторонним одновременно.
Определяя вид по типу углов, очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является , то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными. Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.
Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.
Равносторонним может быть только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.
Простейший из многоугольников – это треугольник. Он образуется при помощи трех точек, лежащих в одной плоскости, но не лежащих на одной прямой, попарно соединенных отрезками. Тем не менее, треугольники бывают разных типов, а значит, обладают разными свойствами.
Инструкция
Принято выделять три типа : тупоугольные, остроугольные и прямоугольные. Это по типу углов. Тупоугольным называется треугольник, у которого один из углов является тупым. Тупым называется угол, имеющий величину больше девяноста градусов, но меньше ста восьмидесяти. Например, в треугольнике ABC угол ABC равен 65°, угол BCA равен 95°, угол CAB равен 20°. Углы ABC и CAB меньше 90°, но угол BCA больше, значит, треугольник тупоугольный.
Остроугольным называется треугольник, у которого все углы являются острыми. Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов. Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Если в треугольнике один из углов равен девяноста градусам, это значит, что он не относится ни широкоугольному типу, ни к остроугольному. Это прямоугольный треугольник.
Если вид треугольника определять по соотношению сторон, они будут равносторонние, разносторонние и равнобедренные. В равностороннем треугольнике все стороны равны, а это, как вы выяснили, говорит о том, что треугольник остроугольный. Если у треугольника равны только две стороны или стороны не равны между собой, он может быть и тупоугольным, и прямоугольным, и остроугольным. Значит, в этих случаях необходимо вычислить или измерить углы и делать умозаключения, согласно пунктам 1, 2 или 3.
Видео по теме
Источники:
- тупоугольный треугольник
Равенство двух или более треугольников соответствует случаю, когда все стороны и углы данных треугольников равны.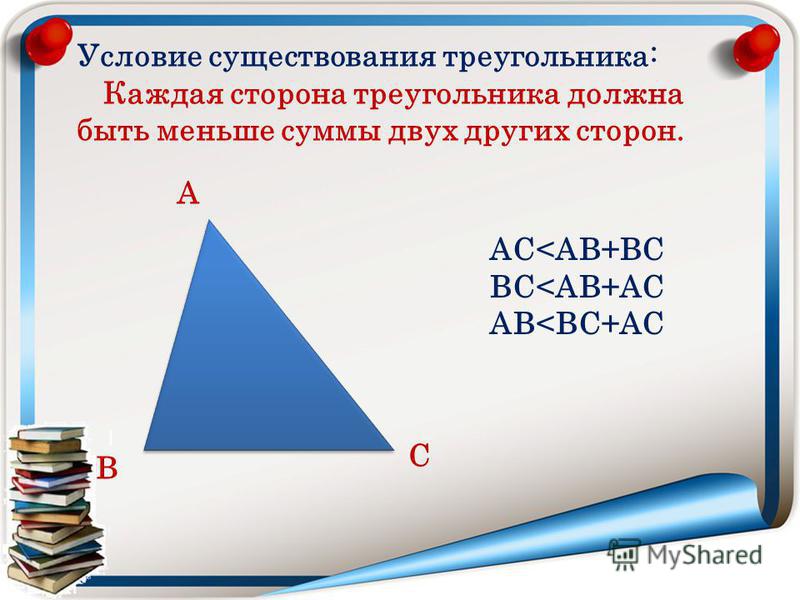 Однако существует ряд более простых критериев для доказательства данного равенства.
Однако существует ряд более простых критериев для доказательства данного равенства.
Вам понадобится
- Учебник по геометрии, лист бумаги, простой карандаш, транспортир, линейка.
Инструкция
Откройте учебник по геометрии седьмого класса на параграфе о признаках равенства треугольников. Вы увидите, что существует ряд основных признаков, доказывающих равенство двух треугольников. Если два треугольника, равенство которых проверяется, являются произвольными, то для них существует три основных признака равенства. Если же известна какая-то дополнительная информация о треугольниках, то основные три признака дополняются еще несколькими. Это относится, например, к случаю равенства прямоугольных треугольников.
Прочитайте первое правило о равенстве треугольников. Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Для того чтобы не прибегать к таким практическим мерам для понимания признака равенства треугольников, прочитайте доказательство первого признака равенства. Дело в том, что каждое правило о равенстве треугольников имеет строгое теоретическое доказательство, просто его не удобно использовать в целях запоминания правил.
Прочитайте второй признак равенства треугольников. Он гласит, что два треугольника будут равны в том случае, если какая-либо одна сторона и два прилегающие к ней угла двух таких треугольников равны. Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.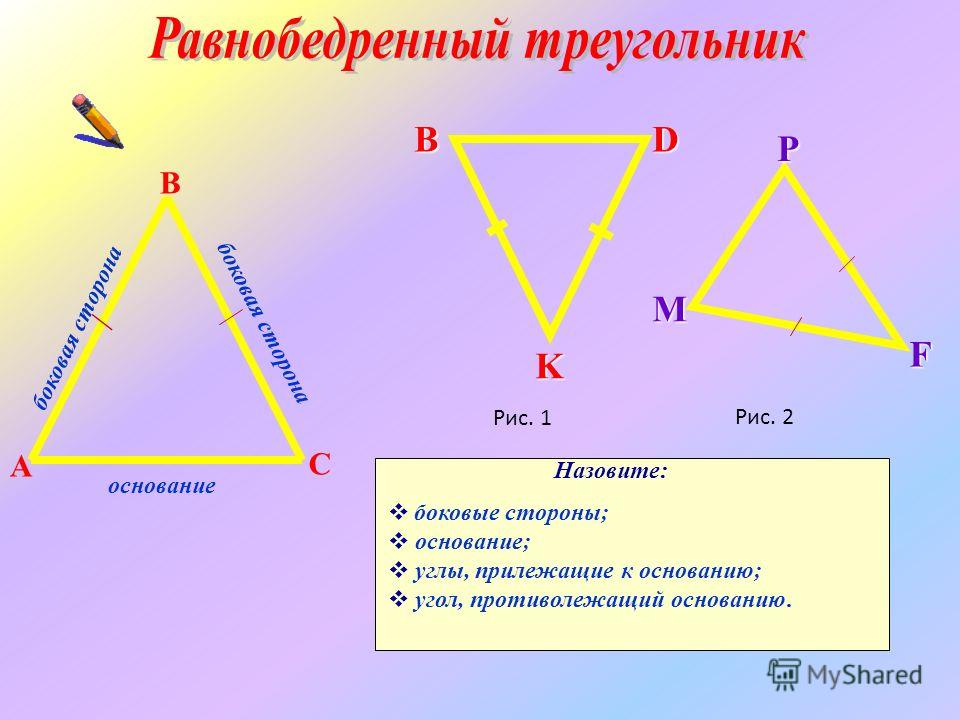
Если вам не дана никакая информация об углах исследуемых треугольников, то используйте третий признак равенства треугольников. По данному правилу, два треугольника считаются равными, если все три стороны одно из них равны соответствующим трем сторонам другого. Таким образом, данное правило говорит о том, что длины сторон треугольника однозначно определяют все углы треугольника, а значит, они однозначно определяют и сам треугольник.
Видео по теме
О том, что такое треугольник, квадрат, куб, нам рассказывает наука геометрия. В современном мире ее изучают в школах все без исключения. Также наукой, которая изучает непосредственно то, что такое треугольник и какие у него свойства, является тригонометрия. Она исследует подробно все явления, связанные с данными О том, что такое треугольник, мы и поговорим сегодня в нашей статье. Ниже будут описаны их виды, а также некоторые теоремы, связанные с ними.
Что такое треугольник? Определение
Это плоский многоугольник. Углов он имеет три, что понятно из его названия. Также он имеет три стороны и три вершины, первые из них — это отрезки, вторые — точки. Зная, чему равны два угла, можно найти третий, отняв сумму первых двух от числа 180.
Также он имеет три стороны и три вершины, первые из них — это отрезки, вторые — точки. Зная, чему равны два угла, можно найти третий, отняв сумму первых двух от числа 180.
Какими бывают треугольники?
Их можно классифицировать по различным критериям.
В первую очередь они делятся на остроугольные, тупоугольные и прямоугольные. Первые обладают острыми углами, то есть такими, которые равны менее чем 90 градусам. У тупоугольных один из углов — тупой, то есть такой, который равен более 90 градусам, остальные два — острые. К остроугольным треугольникам относятся также и равносторонние. У таких треугольников все стороны и углы равны. Все они равны 60 градусам, это можно легко вычислить, разделив сумму всех углов (180) на три.
Прямоугольный треугольник
Невозможно не поговорить о том, что такое прямоугольный треугольник.
У такой фигуры один угол равен 90 градусам (прямой), то есть две из его сторон расположены перпендикулярно. Остальные два угла являются острыми.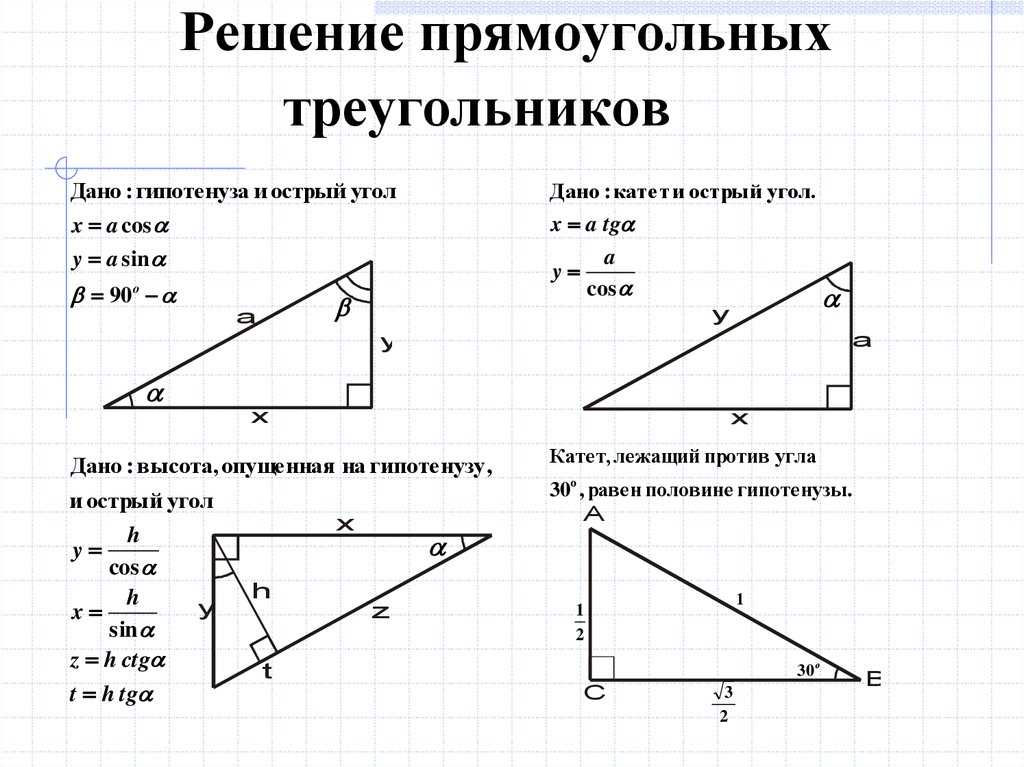 Они могут быть равными, тогда он будет равнобедренным. С прямоугольным треугольником связана теорема Пифагора. При помощи ее можно найти третью сторону, зная две первые. Согласно данной теореме, если прибавить квадрат одного катета к квадрату другого, можно получить квадрат гипотенузы. Квадрат же катета можно подсчитать, отняв от квадрата гипотенузы квадрат известного катета. Говоря о том, что такое треугольник, можно вспомнить и о равнобедренном. Это такой, у которого две из сторон равны, также равны и два угла.
Они могут быть равными, тогда он будет равнобедренным. С прямоугольным треугольником связана теорема Пифагора. При помощи ее можно найти третью сторону, зная две первые. Согласно данной теореме, если прибавить квадрат одного катета к квадрату другого, можно получить квадрат гипотенузы. Квадрат же катета можно подсчитать, отняв от квадрата гипотенузы квадрат известного катета. Говоря о том, что такое треугольник, можно вспомнить и о равнобедренном. Это такой, у которого две из сторон равны, также равны и два угла.
Что такое катет и гипотенуза?
Катет — это одна из сторон треугольника, которые образуют угол в 90 градусов. Гипотенуза — это оставшаяся сторона, которая расположена напротив прямого угла. Из него на катет можно опустить перпендикуляр. Отношение прилежащего катета к гипотенузе называется не иначе как косинус, а противоположного — синус.
— в чем его особенности?
Он прямоугольный. Его катеты равны трем и четырем, а гипотенуза — пяти. Если вы увидели, что катеты данного треугольника равны трем и четырем, можете не сомневаться, что гипотенуза будет равна пяти. Также по такому принципу можно легко определить, что катет будет равен трем, если второй равен четырем, а гипотенуза — пяти. Чтобы доказать данное утверждение, можно применить теорему Пифагора. Если два катета равны 3 и 4, то 9 + 16 = 25, корень из 25 — это 5, то есть гипотенуза равна 5. Также египетским треугольником называется прямоугольный, стороны которого равны 6, 8 и 10; 9, 12 и 15 и другим числам с соотношением 3:4:5.
Также по такому принципу можно легко определить, что катет будет равен трем, если второй равен четырем, а гипотенуза — пяти. Чтобы доказать данное утверждение, можно применить теорему Пифагора. Если два катета равны 3 и 4, то 9 + 16 = 25, корень из 25 — это 5, то есть гипотенуза равна 5. Также египетским треугольником называется прямоугольный, стороны которого равны 6, 8 и 10; 9, 12 и 15 и другим числам с соотношением 3:4:5.
Каким еще может быть треугольник?
Также треугольники могут быть вписанными и описанными. Фигура, вокруг которой описана окружность, называется вписанной, все ее вершины являются точками, лежащими на окружности. Описанный треугольник — тот, в который вписана окружность. Все его стороны соприкасаются с ней в определенных точках.
Как находится
Площадь любой фигуры измеряется в квадратных единицах (кв. метрах, кв. миллиметрах, кв. сантиметрах, кв. дециметрах и т. д.) Данную величину можно рассчитать разнообразными способами, в зависимости от вида треугольника. Площадь какой угодно фигуры с углами можно найти, если умножить ее сторону на перпендикуляр, опущенный на нее из противоположного угла, и разделив данную цифру на два. Также можно найти эту величину, если умножить две стороны. Потом умножить это число на синус угла, расположенного между данными сторонами, и разделить это получившееся на два. Зная все стороны треугольника, но не зная его углов, можно найти площадь еще и другим способом. Для этого нужно найти половину периметра. Затем поочередно отнять от данного числа разные стороны и перемножить полученные четыре значения. Далее найти из числа, которое вышло. Площадь вписанного треугольника можно отыскать, перемножив все стороны и разделив полученное число на которая описана вокруг него, умноженный на четыре.
Площадь какой угодно фигуры с углами можно найти, если умножить ее сторону на перпендикуляр, опущенный на нее из противоположного угла, и разделив данную цифру на два. Также можно найти эту величину, если умножить две стороны. Потом умножить это число на синус угла, расположенного между данными сторонами, и разделить это получившееся на два. Зная все стороны треугольника, но не зная его углов, можно найти площадь еще и другим способом. Для этого нужно найти половину периметра. Затем поочередно отнять от данного числа разные стороны и перемножить полученные четыре значения. Далее найти из числа, которое вышло. Площадь вписанного треугольника можно отыскать, перемножив все стороны и разделив полученное число на которая описана вокруг него, умноженный на четыре.
Площадь описанного треугольника находится таким образом: половину периметра умножаем на радиус окружности, которая в него вписана. Если то его площадь можно найти следующим образом: сторону возводим в квадрат, умножаем полученную цифру на корень из трех, далее делим это число на четыре. Похожим образом можно вычислить высоту треугольника, у которого все стороны равны, для этого одну из них нужно умножить на корень из трех, а потом разделить данное число на два.
Похожим образом можно вычислить высоту треугольника, у которого все стороны равны, для этого одну из них нужно умножить на корень из трех, а потом разделить данное число на два.
Теоремы, связанные с треугольником
Основными теоремами, которые связаны с данной фигурой, являются теорема Пифагора, описанная выше, и косинусов. Вторая (синусов) заключается в том, что, если разделить любую сторону на синус противоположного ей угла, то можно получить радиус окружности, которая описана вокруг него, умноженный на два. Третья (косинусов) заключается в том, что, если от суммы квадратов двух сторон отнять их же произведение, умноженное на два и на косинус угла, расположенного между ними, то получится квадрат третьей стороны.
Треугольник Дали — что это?
Многие, столкнувшись с этим понятием, сначала думают, что это какое-то определение в геометрии, но это совсем не так. Треугольник Дали — это общее название трех мест, которые тесно связаны с жизнью знаменитого художника. «Вершинами» его являются дом, в котором Сальвадор Дали жил, замок, который он подарил своей жене, а также музей сюрреалистических картин. Во время экскурсии по этим местам можно узнать много интереснейших фактов об этом своеобразном креативном художнике, известном во всем мире.
«Вершинами» его являются дом, в котором Сальвадор Дали жил, замок, который он подарил своей жене, а также музей сюрреалистических картин. Во время экскурсии по этим местам можно узнать много интереснейших фактов об этом своеобразном креативном художнике, известном во всем мире.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.
 А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….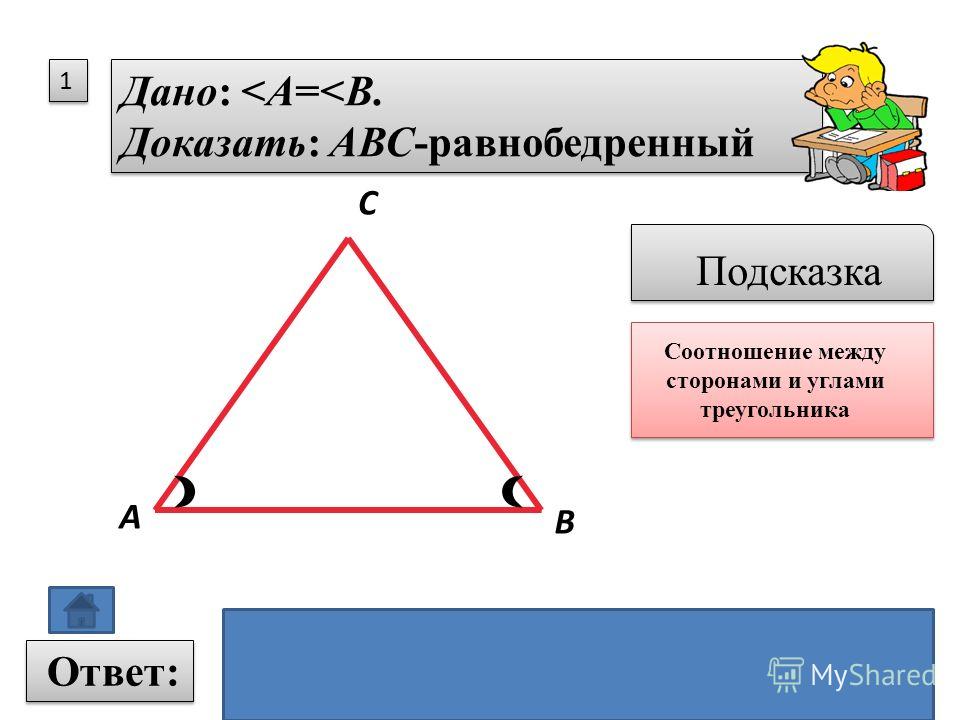
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Задачи:
1. Познакомить учащихся с разными видами треугольников в зависимости от вида углов (прямоугольный, остроугольный, тупоугольный). Учиться находить на чертежах треугольники и их виды. Закреплять основные геометрические понятия и их свойства: прямая линия, отрезок, луч, угол.
2. Развитие мышления, воображения, математической речи.
3. Воспитание внимания, активности.
Ход урока
I. Организационный момент.
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем два квадрата,
А на них огромный круг.
А потом ещё кружочки,
Треугольник колпачок.
Вот и вышел очень — очень
Развесёлый Чудачок.
II. Объявление темы урока.
Сегодня на уроке мы с вами совершим путешествие по городу Геометрии и побываем в микрорайоне Треугольники (т.е. познакомимся с разными видами треугольников в зависимости от их углов, будем учиться находить эти треугольники на чертежах.) Проведём урок в форме “игры-соревнования” по командам.
1 команда — “Отрезок”.
2 команда — “Луч”.
3 команда — “Угол”.
А гости будут представлять жюри.
Жюри нас по пути направит
И без вниманья не оставит. (Оценивать по баллам 5,4,3,…).
А на чём же мы будем путешествовать по городу Геометрии? Вспомните, какие виды пассажирского транспорта есть в городе? Нас очень много, какой же мы выберем? (Автобус).
Автобус. Чётко, кратко. Начинается посадка.
Усаживаемся поудобнее и начнём наше путешествие. Капитаны команд получите билеты.
Но билеты эти непростые, а билеты — “задания”.
III. Повторение пройденного материала.
Первая остановка “ Повторяй-ка”.
Вопрос всем командам.
Найти на чертеже прямую линию и назвать её свойства.
Без конца и края линия прямая!
Хоть сто лет по ней иди,
Не найдёшь конца пути!
- Прямая не имеет ни начала, ни конца — она бесконечна, поэтому её измерить нельзя.
Начинаем наше соревнование.
Защита названий своих команд.
(Все команды читают первые вопросы и обсуждают. По очереди капитаны команд зачитывают вопросы, 1 команда читает 1 вопрос).
1. Показать на чертеже отрезок. Что называется отрезком. Назвать его свойства.
- Часть прямой, ограниченная двумя точками, называется отрезком. У отрезка есть начало и конец, потому его можно измерить при помощи линейки.
(2 команда читает 1 вопрос).
1. Показать на чертеже луч. Что называется лучом. Назвать его свойства.
- Если отметить точку и из неё провести часть
прямой, то получится изображение луча.
 Точка, из
которой проведена часть прямой, называется
началом луча.
Точка, из
которой проведена часть прямой, называется
началом луча.
Конца у луча нет, поэтому его измерить нельзя.
(3 команда читает 1 вопрос).
1 .Показать на чертеже угол. Что называется углом. Назвать его свойства.
- Проведя из одной точки два луча, получается геометрическая фигура, которая называется углом. У угла есть вершина, а сами лучи называются сторонами угла. Углы измеряются в градусах с помощью транспортира.
Физкультминутка (под музыку).
IV. Подготовка к изучению нового материала.
Вторая остановка “Сказочная”.
На прогулке Карандаш встретил разные углы. Хотел с ними поздороваться, да забыл, как зовут каждого из них. Придётся Карандашу помочь.
(Углы уч-ся проверяют с помощью модели прямого угла).
Задание командам. Прочитайте вопросы №2, обсудите.
1 команда читает 2 вопрос.
2. Найти прямой угол, дать определение.
- Угол величиной 90°называется прямым углом.

2 команда читает 2 вопрос.
2. Найти острый угол, дать определение.
- Угол меньше прямого, называется острым.
3 команда читает 2 вопрос.
2. Найти тупой угол, дать определение.
Угол больше прямого, называется тупым.
В микрорайоне, где любил гулять Карандаш, все углы отличались от других жителей тем, что гуляли всегда втроём, пили чай втроём, ходили в кино втроём. И Карандаш никак не мог понять, что за геометрическую фигуру вместе составляют три угла?
А подсказкой вам будет стихотворение.
Ты на меня, ты на него,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три!
О свойствах какой фигуры говорится?
- О треугольнике.
Какая же фигура называется треугольником?
- Треугольник — это геометрическая фигура, у которой три вершины, три угла, три стороны.
(Уч-ся показывают на чертеже треугольник,
называют вершины, углы и стороны).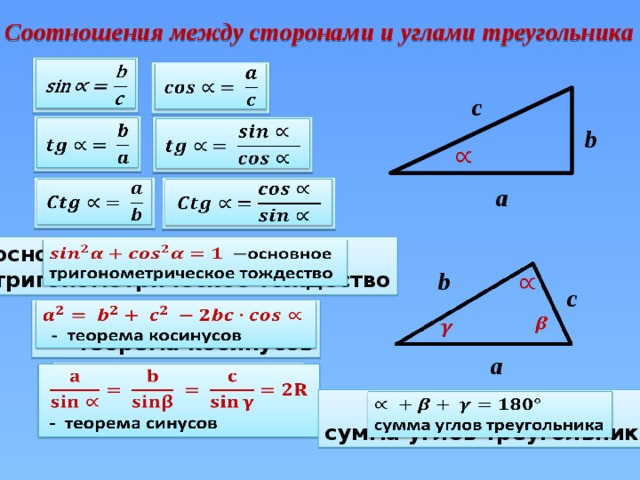
Вершины: А, В, С (точки)
Углы: ВАС, АВС, ВСА.
Стороны: АВ, ВС, СА (отрезки).
V. Физкультминутка:
8 раз ногою топнем,
9 раз руками хлопнем,
мы присядем 10 раз,
и наклонимся 6 раз,
мы подпрыгнем ровно
столько (показ треугольника)
Ай, да, счёт! Игра и только!
VI. Изучение нового материала.
Скоро углы подружились и стали неразлучны.
И теперь микрорайон мы будем так и называть: микрорайон Треугольники.
Третья остановка “Знайка”.
А как зовут эти треугольники?
Давайте дадим им имена. И попробуем сами сформулировать определение.
3 команда отвечает.
1 команда найдет и покажет тупоугольные треугольники.
2 команда найдёт и покажет прямоугольные треугольники.
3 команда найдёт и покажет остроугольные треугольники.
VIII. Следующая остановка “Соображай-ка”.
Задание всем командам.
Переложив 6 палочек, составьте из фонаря 4
равных треугольника.
Какие по виду углов получились треугольники? (Остроугольные).
IX. Итог урока.
В каком же микрорайоне мы с вами побывали?
С какими видами треугольников познакомились?
1 2 3 4 5 6 7 8 9 … 53 Bog’liq
1 2 3 4 5 6 7 8 9 … 53 Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©hozir.org 2022 | Bosh sahifa |
сторон треугольника — формула, свойства, правило, примеры
стороны треугольника — это прямые линии, которые соединяются тремя вершинами треугольника. Другими словами, мы можем сказать, что стороны треугольника — это отрезки, пересекающиеся в вершинах треугольника. Стороны прямоугольного треугольника можно найти с помощью различных методов, таких как теорема Пифагора или с помощью периметра треугольника. В случае, если некоторые углы и другие длины сторон заданы, мы можем использовать закон косинусов или закон синусов, чтобы найти длины сторон треугольника.
Другими словами, мы можем сказать, что стороны треугольника — это отрезки, пересекающиеся в вершинах треугольника. Стороны прямоугольного треугольника можно найти с помощью различных методов, таких как теорема Пифагора или с помощью периметра треугольника. В случае, если некоторые углы и другие длины сторон заданы, мы можем использовать закон косинусов или закон синусов, чтобы найти длины сторон треугольника.
В этой статье мы рассмотрим понятие сторон треугольника и его формулу. Мы также обсудим свойства и правила сторон треугольника и решим несколько примеров, основанных на концепции, для лучшего понимания.
| 1. | Каковы стороны треугольника? |
| 2. | Стороны треугольника Формула |
| 3. | Стороны треугольника Свойства |
| 4. | Стороны треугольника Правило |
| 5. | Часто задаваемые вопросы о сторонах треугольника |
Каковы стороны треугольника?
У каждого треугольника три стороны и три угла. Эти стороны треугольника представляют собой отрезки прямой линии, так что две стороны встречаются в каждой вершине треугольника, образуя трехстороннюю замкнутую фигуру. В прямоугольном треугольнике каждая сторона имеет имя. Самая длинная сторона прямоугольного треугольника называется гипотенузой, меньшая сторона треугольника называется основанием, а линия стояния, примыкающая к прямому углу, называется перпендикуляром. На концах каждой стороны треугольника, то есть в каждой вершине, образованы три угла. Теперь обсудим формулу, используемую для нахождения длин этих сторон.
Эти стороны треугольника представляют собой отрезки прямой линии, так что две стороны встречаются в каждой вершине треугольника, образуя трехстороннюю замкнутую фигуру. В прямоугольном треугольнике каждая сторона имеет имя. Самая длинная сторона прямоугольного треугольника называется гипотенузой, меньшая сторона треугольника называется основанием, а линия стояния, примыкающая к прямому углу, называется перпендикуляром. На концах каждой стороны треугольника, то есть в каждой вершине, образованы три угла. Теперь обсудим формулу, используемую для нахождения длин этих сторон.
Стороны треугольника Формула
Стороны треугольника. Формула данного треугольника для нахождения его сторон связана с тригонометрическими отношениями. К необходимым условиям относятся — одна сторона треугольника и острый угол и таким образом, мы можем узнать остальные стороны треугольника.
- В случае прямоугольного треугольника мы можем напрямую применить теорему Пифагора.
- В случае равнобедренного треугольника мы можем использовать формулу площади или периметра.

- В случае общего, некоторые из углов и некоторые длины сторон известны, мы можем использовать закон косинусов или закон синусов.
Формула сторон треугольника
1. Если нам известны угол и длина стороны прямоугольного треугольника,
- Синус θ = длина противоположной стороны / длина стороны гипотенузы
- Cos θ = длина прилегающей стороны / длина стороны гипотенузы
- Tan θ = длина противоположной стороны / длина соседней стороны
2. Закон синусов: sin(A)/a = sin(B)/b = sin(C)/c
Где,
- a, b и c — стороны противоположных треугольников.
- A, B и C — соответствующие углы.
3. Закон косинусов: c 2 = a 2 + b 2 — 2ab cos(C)
Где
- a, b и c — стороны треугольников.
- °С — угол, образованный сторонами а и b.
Используем приведенные выше формулы для нахождения длины сторон треугольника в зависимости от известных величин треугольника.
Свойства сторон треугольника
Теперь, когда мы обсудили формулы для нахождения длин сторон треугольника, давайте рассмотрим некоторые важные свойства сторон треугольника:
- Сторона, противоположная наибольшему углу треугольника, равна самая длинная сторона треугольника.
- Два треугольника называются конгруэнтными, если длины соответствующих сторон треугольника равны.
- Два треугольника называются подобными, если длины соответствующих сторон треугольника пропорциональны.
- Сумма трех сторон треугольника дает периметр треугольника.
- Площадь треугольника можно рассчитать, используя три стороны треугольника (формула Герона), формула которой:
- Площадь = √[s(s – a)(s – b)(s – c)], где a, b, c – три стороны треугольника, а s – полупериметр.
Стороны треугольника Правило
До сих пор мы обсуждали важные свойства сторон треугольника, теперь давайте разберемся с его основным правилом. Правило сторон треугольника состоит в том, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это правило также известно как теорема о неравенстве треугольника. Отсюда следует, что у нас не может быть треугольника с длинами 3, 4, 9.как 3 + 4 = 7 < 9. Давайте посмотрим на применение сторон формулы и правила треугольника в следующем разделе.
Правило сторон треугольника состоит в том, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это правило также известно как теорема о неравенстве треугольника. Отсюда следует, что у нас не может быть треугольника с длинами 3, 4, 9.как 3 + 4 = 7 < 9. Давайте посмотрим на применение сторон формулы и правила треугольника в следующем разделе.
Важные примечания о сторонах треугольника
- Стороны треугольника представляют собой прямые линии, которые соединяются тремя вершинами треугольника.
- В случае прямоугольного треугольника мы можем применить теорему Пифагора или формулу тригонометрических соотношений, чтобы найти стороны.
- Мы можем использовать закон косинусов или закон синусов, чтобы найти длины сторон треугольника.
☛ Статьи по теме:
- Типы треугольников
- Построение треугольников
- Подобные треугольники
Пример 1: Каковы стороны прямоугольного треугольника, гипотенуза которого равна 10 дюймам, а угол при основании равен 30°?
Решение: Найти: Стороны прямоугольного парка.

Дано,
Гипотенуза = 10 дюймов
Угол при основании = 30 градусов
Используя формулу сторон треугольника,
sin θ = длина противоположной стороны / длина стороны гипотенузы
⇒ sin 30° = x/10 — (Предположим, что длина противоположной стороны = x)
⇒ 1/2 = x/10
⇒ x = 5 в
И, cos θ = длина смежной стороны / длина стороны гипотенузы
⇒ cos 30°= y/10 — ( Предположим, что длина смежной стороны = y)
⇒ √3/2 = y/10
⇒ y = 5√3 в
Ответ: Остальные стороны треугольного парка равны 5 дюймам и 5√3 дюймам.
Пример 2: Длины двух сторон треугольника ABC равны 10 единицам и 9 единицам, а угол между ними равен 47°. Найдите длину третьей стороны треугольника.
Решение: Чтобы найти длину третьей стороны треугольника, воспользуемся законом косинусов.
Имеем a = 10, b = 9 и угол C = 47°. Нам нужно найти значение c.
 Итак, у нас
Итак, у насC 2 = A 2 + B 2 — 2AB COS (C)
⇒ C 2 = 10 2 + 2 — 2 × 10 × .
= 100 + 81 — 180 × 0,682
= 58,24
⇒ с = √58,24
= 7,63 ед.
Ответ: Длина третьей стороны треугольника равна 7,63 единицы.
Пример 3: В треугольнике ABC ∠C = 42° и ∠A = 33°, а сторона, противоположная углу C, равна 12,5 единицы. Найдите длину стороны треугольника, противоположной углу А.
Решение: Имеем ∠C = 42° и ∠A = 33°, c = 12,5 единиц. Нам нужно найти сторону «а». Итак, по закону синусов имеем
sinA / a = sinC / c
⇒ sin (33°) / a = sin (42°) / 12,5
⇒ 0,545 / a = 0,67 / 12,5
⇒ a = 12,5 × 0,545 ÷ 0,67
= 10,17 ед.
Ответ: Длина стороны, противоположной углу А, равна 10,17 ед.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Стороны треугольника Вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о сторонах треугольника
Какие стороны треугольника в геометрии?
Стороны треугольника представляют собой отрезки прямой линии, две стороны которых сходятся в каждой вершине треугольника, образуя трехстороннюю замкнутую фигуру.
Формула определения сторон треугольника?
Чтобы найти стороны треугольника, мы используем различные формулы в зависимости от известных значений для данного треугольника. Мы используем закон косинусов или закон синусов, если даны некоторые стороны и некоторые углы. Мы можем использовать теорему Пифагора, чтобы найти стороны прямоугольного треугольника. Мы также можем использовать формулу тригонометрического отношения в случае прямоугольного треугольника.
Когда использовать формулы сторон треугольника?
Мы можем использовать формулу тригонометрических соотношений или формулу теоремы Пифагора только в случае прямоугольного треугольника, так как она включает в себя тригонометрические соотношения, применяемые для нахождения сторон данного треугольника. В случае, если некоторые углы и другие длины сторон заданы, мы можем использовать закон косинусов или закон синусов.
Как использовать формулы сторон треугольника?
Если нам дан угол и длина стороны треугольника,
- Шаг 1: Проверка типа треугольника.
- Шаг 2. Проверьте наличие известных сторон или углов.
- Шаг 3: Подставьте данные значения сторонам треугольника по формуле: Синус θ = длина противоположной стороны / длина стороны гипотенузы, Cos θ = длина прилежащей стороны / длина стороны гипотенузы, Tan θ = длина противоположной стороны / Длина смежной стороны или напрямую использовать закон синуса или закон косинуса соответственно.

Каково применение сторон формулы треугольника?
Формула для сторон треугольника имеет приложения в тригонометрии, которая также имеет множество применений в нашей повседневной жизни, от создания карт до строительства зданий.
Каковы важные свойства сторон треугольника?
Некоторые важные свойства сторон треугольника:
- Сторона, противоположная наибольшему углу треугольника, является самой длинной стороной треугольника.
- Два треугольника называются конгруэнтными, если длины соответствующих сторон треугольника равны.
- Два треугольника называются подобными, если длины соответствующих сторон треугольника пропорциональны.
- Сумма трех сторон треугольника дает периметр треугольника.
Правило сторон треугольника?
Правило сторон треугольника состоит в том, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это правило также известно как теорема о неравенстве треугольника.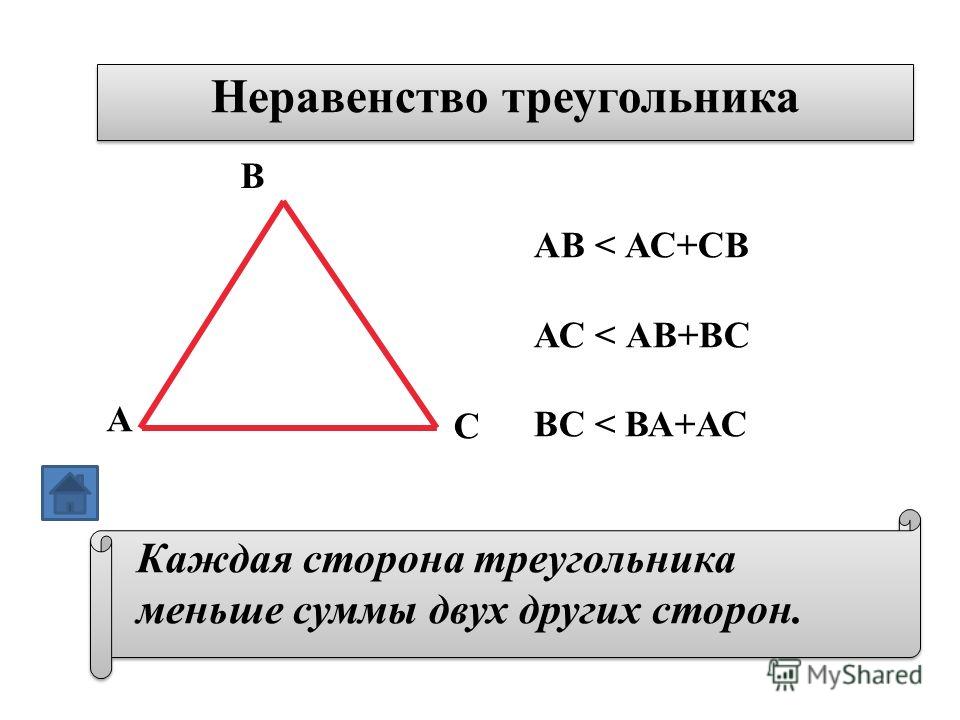
Каковы 3 стороны прямоугольного треугольника?
Три стороны прямоугольного треугольника — это Гипотенуза (самая длинная сторона), Перпендикуляр (также называемая противоположной стороной) и Основание (также называемая прилежащей стороной).
Как найти стороны треугольника с углами?
Чтобы найти длину стороны треугольника с углами, нам нужна хотя бы одна сторона. Затем мы можем использовать закон синусов, чтобы найти длину сторон треугольника.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист сторон треугольника
Калькулятор прямоугольного треугольника | Найти a, b, c и угол
Создано Ханной Памула, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 12 ноября 2021 г.
Содержание:- Как найти стороны прямоугольный треугольник
- Как найти угол прямоугольного треугольника
- Как решить прямоугольный треугольник только с одной стороной?
- Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
- Часто задаваемые вопросы
Найти недостающую сторону или угол не может быть проще, чем с помощью нашего замечательного инструмента — калькулятора сторон и углов прямоугольного треугольника. Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы нашего калькулятора.
Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы нашего калькулятора.
Как найти стороны прямоугольного треугольника
Существует несколько способов определения длины сторон прямоугольного треугольника. В зависимости от того, что дано, вы можете использовать разные отношения или законы, чтобы найти недостающую сторону:
- Учитывая две стороны
Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:
a² + b² = c²
, если катет
аявляется отсутствующей стороной, то преобразуем уравнение к виду, когда а находится на одной стороне, и извлекаем квадратный корень:а = √(c² - b²)если ножка
bнеизвестна, тоб = √(с² - а²)для гипотенузы c отсутствует, формула
с = √(а² + b²)
- Дан угол и гипотенуза
Примените закон синусов или тригонометрию, чтобы найти длины сторон прямоугольного треугольника:
- Дан угол и один катет
Найдите недостающую ногу с помощью тригонометрических функций:
а = b * тангенс (α)б = а * тангенс (β)
- Заданная площадь и одна ножка
Как мы помним из базовой формулы площади треугольника, мы можем вычислить площадь, умножив высоту треугольника и основание и разделив результат на два.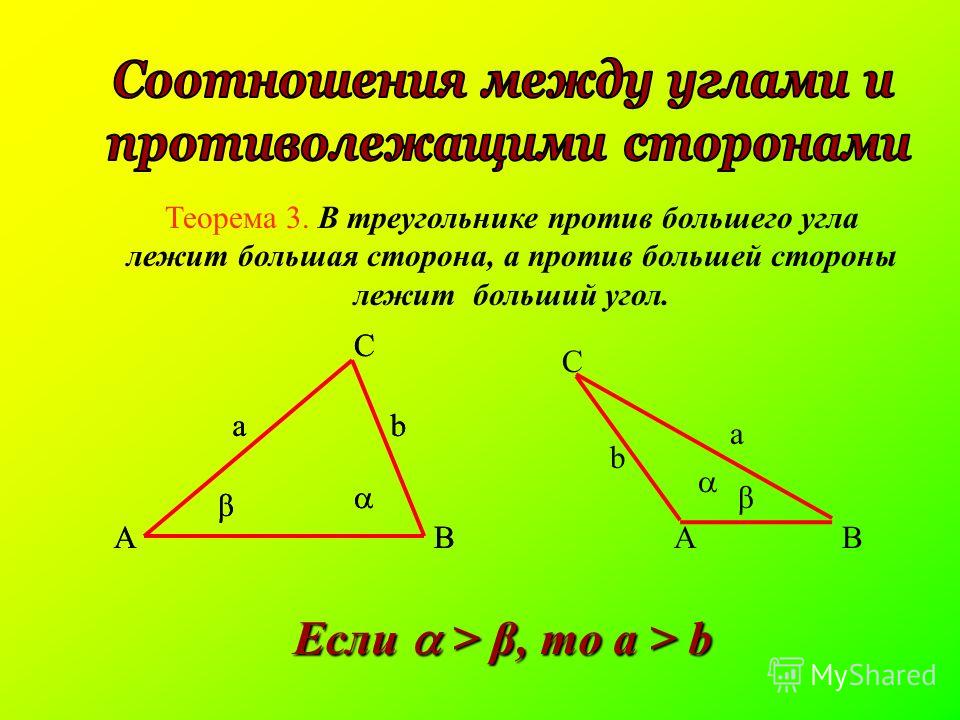 Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна сторона является высотой, а вторая — основанием, поэтому уравнение упрощается до:
Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна сторона является высотой, а вторая — основанием, поэтому уравнение упрощается до:
площадь = a * b / 2
Например, если мы знаем только площадь прямоугольного треугольника и длину катета a , мы можем вывести уравнение для других сторон:
-
b = 2 * площадь / a -
с = √(а² + (2 * площадь / а)²)
Как найти угол прямоугольного треугольника
Если кроме прямого угла известен еще один угол, вычисление третьего проще простого:
Дано β : α = 90 - β
Дано α : β = 90 - α
Однако, если даны только две стороны треугольника, нахождение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций:
для α 5 4
sin(α) = a/c поэтому α = arcsin(a/c) (обратный синус) cos(α) = b/c поэтому α = arccos(b/c) (арккосинус) tan(α) = a / b поэтому α = arctan(a / b) (арктангенс) cot(α) = b/a поэтому α = arccot(b/a) (арккотангенс) и для β
-
sin(β) = b/cпоэтомуβ = arcsin(b/c)(обратный синус) -
cos(β) = a/cпоэтомуβ = arccos(a/c)(арккосинус) -
tan(β) = b/aпоэтомуβ = arctan(b/a)(арктангенс) -
кроватка(β) = a / bпоэтомуβ = arccot(a / b)(арккотангенс)
Как решить прямоугольный треугольник только с одной стороной?
Чтобы решить треугольник с одной стороной, вам также понадобится один из непрямых углов .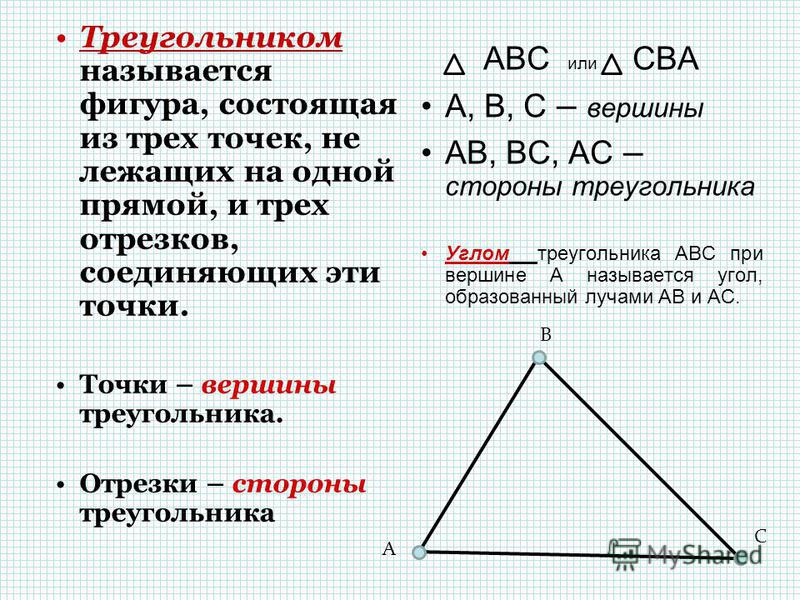 Если нет, то это невозможно:
Если нет, то это невозможно:
- Если у вас есть гипотенуза , умножьте ее на sin(θ) , чтобы получить длину стороны напротив угла.
- Можно также умножить гипотенузу на cos(θ), чтобы получить сторону, прилегающую к углу.
- Если у вас есть сторона , не являющаяся гипотенузой, примыкающая к углу , разделите ее на cos(θ) , чтобы получить длину гипотенузы .
- Можно также умножить эту длину на tan(θ), чтобы получить длину стороны, противоположной углу.
- Если у вас есть угол и сторона , противоположная , вы можете разделить длину стороны на sin(θ) , чтобы получить гипотенузу .
- Можно также разделить длину на tan(θ), чтобы получить длину стороны, примыкающей к углу.
Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
Давайте покажем, как найти стороны прямоугольного треугольника с помощью этого инструмента:
- Предположим, мы хотим найти недостающую сторону по заданной площади и одной стороне.
 Выберите нужный вариант из выпадающего списка . Это третий.
Выберите нужный вариант из выпадающего списка . Это третий. - Введите указанные значения . Например, площадь прямоугольного треугольника равна 28 кв. дюймов, а b = 9 дюймов.
- Наш калькулятор сторон и углов прямоугольного треугольника показывает недостающие стороны и углы! Теперь мы знаем, что:
- а = 6,222 дюйма
- с = 10,941 в
- α = 34,66°
- β = 55,34°
Теперь проверим, как работает нахождение углов прямоугольного треугольника:
- Обновите калькулятор. Выберите нужный вариант . Предположим, что у нас есть две стороны, и мы хотим найти все углы. Вариант по умолчанию правильный.
- Введите длины сторон . Наш прямоугольный треугольник имеет гипотенузу, равную 13 дюймам, и катет a = 5 дюймов.
- Отсутствуют стороны и углы . В нашем примере b = 12 дюймов, α = 67,38° и β = 22,62°.

Часто задаваемые вопросы
Сколько осей симметрии имеет прямоугольный треугольник?
Если прямоугольный треугольник равнобедренный (т. е. две его стороны, не лежащие в гипотенузе, имеют одинаковую длину), он имеет одну линию симметрии . В противном случае треугольник не будет иметь осей симметрии .
Может ли прямоугольный треугольник иметь равные стороны?
Нет, прямоугольный треугольник не может иметь все 3 стороны равные , так как все три угла не могут быть равными, так как один должен быть 90° по определению. Однако в прямоугольном треугольнике две стороны, не лежащие в гипотенузе, могут быть равны по длине. Это также означает, что два других угла равны 45°.
Все ли прямоугольные треугольники подобны?
Не все прямоугольные треугольники подобны , хотя некоторые могут быть. Они подобны, если все их углы имеют одинаковую длину или если отношение двух их сторон одинаково.
Ханна Памула, кандидат наук
Угол α
Угол β
Посмотреть 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… еще 15 найти длину стороны прямоугольного треугольника — Базовая геометрия
—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 Следующая →
Справка по базовой геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти длину стороны прямоугольного треугольника
Какова длина оставшейся стороны прямоугольного треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Переформулируйте теорему Пифагора, чтобы найти недостающую сторону.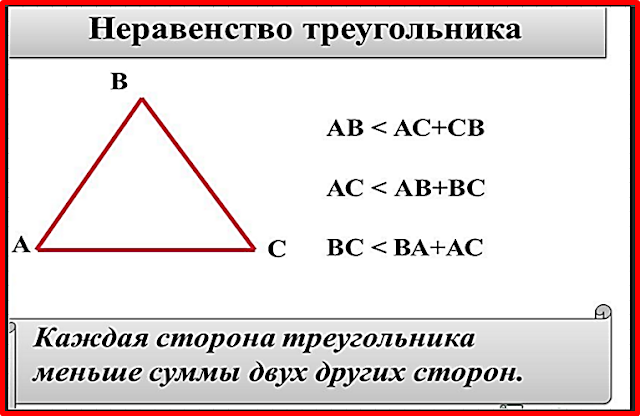 Теорема Пифагора:
Теорема Пифагора:
где – гипотенуза, а – стороны.
Сообщить об ошибке
Гипотенуза прямоугольного треугольника равна 26 дм, а катет равен 10 дм. Чему равна сумма двух кратчайших сторон?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы используем теорему Пифагора, поэтому проблема для решения становится где = неизвестная длина ноги
Итак и
Сумма двух сторон равна
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
2
22
Пояснение:
Сообщить об ошибке
Найдите длину неизвестной стороны прямоугольного треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно использовать теорему Пифагора, которая гласит, что .
Поскольку нам нужно найти длину «а», мы можем просто найти «а».
В нашем случае c = 12 и b = 9.
Таким образом, .
Сообщить об ошибке
Найдите недостающий катет прямоугольного треугольника, если один из катетов равен , а гипотенуза равна .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти недостающую сторону прямоугольного треугольника, вы должны использовать одну из двух вещей:
1. Теорему Пифагора
2. Тригонометрию.
Поскольку мы знаем только длины сторон, мы должны использовать теорему Пифагора.
a=4, b=x и c=5
Таким образом, недостающая длина стороны равна 3
Сообщить об ошибке
Учитывая, что гипотенуза прямоугольного треугольника равна и одна сторона равна , найдите длину другой стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти длину недостающей стороны, вы можете либо воспользоваться теоремой Пифагора, либо понять, что это случай особого прямоугольного треугольника со сторонами .
Таким образом, длина другой стороны равна .
Сообщить об ошибке
Найдите длину недостающей стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните теорему Пифагора для прямоугольного треугольника:
Поскольку недостающая сторона соответствует стороне , перепишите теорему Пифагора и решите для .
Теперь подставьте значения и в калькулятор, чтобы найти длину стороны . Округлите до десятичных разрядов.
Сообщить об ошибке
Найдите длину недостающей стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните теорему Пифагора для прямоугольного треугольника:
Поскольку недостающая сторона соответствует стороне , перепишите теорему Пифагора и решите для .
Теперь подставьте значения и в калькулятор, чтобы найти длину стороны . Округлите до десятичных разрядов.
Сообщить об ошибке
Найдите длину недостающей стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните теорему Пифагора для прямоугольного треугольника:
Поскольку недостающая сторона соответствует стороне , перепишите теорему Пифагора и решите для .
Теперь подставьте значения и в калькулятор, чтобы найти длину стороны . Округлите до десятичных разрядов.
Сообщить об ошибке
Найдите длину недостающей стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните теорему Пифагора для прямоугольного треугольника:
Поскольку недостающая сторона соответствует стороне , перепишите теорему Пифагора и решите для .
Теперь подставьте значения и в калькулятор, чтобы найти длину стороны . Округлите до десятичных разрядов.
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Авторские права Колледж SUNY в Кортленде, магистр образования, образование…
Посмотреть репетиторов
Сьюзен
Сертифицированный репетитор
Мичиганский университет в Дирборне, бакалавр искусств, английский язык. Мичиганский университет в Анн-Арборе, бакалавр искусств, английский язык.
Мичиганский университет в Анн-Арборе, бакалавр искусств, английский язык.
Посмотреть репетиторов
Натаниэль
Сертифицированный репетитор
Колумбийский университет Миссури, бакалавр искусств, история. Университет Миссури-Колумбия, магистр искусств, история.
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Как найти третью сторону треугольника по двум сторонам?
Треугольник — замкнутая фигура, образованная тремя отрезками. Он состоит из трех углов и трех вершин. Углы треугольников могут быть одинаковыми или разными в зависимости от типа треугольника. Существуют различные типы треугольников, основанные на свойствах линий и углов.
Свойства треугольника:
1. У каждого треугольника 3 стороны и 3 угла.
2. Сумма всех углов треугольника равна 180°
3. Периметр треугольника равен сумме всех трех сторон треугольника.
Периметр треугольника равен сумме всех трех сторон треугольника.
4. Треугольник имеет 3 вершины.
Типы треугольников на основе свойств линии
Разносторонний треугольник: Разносторонний треугольник — это тип треугольника, в котором все стороны имеют разную длину. Все углы разностороннего треугольника отличны друг от друга.
Равнобедренный треугольник: Равнобедренный треугольник — это другой тип треугольника, в котором две стороны равны, а третья сторона неравна. В этом треугольнике два угла также равны, а третий угол различен.
Прямоугольный треугольник: Прямоугольный треугольник следует теореме Пифагора, и один угол таких треугольников составляет 90 градусов, который образован основанием и перпендикуляром. Гипотенуза — самая длинная сторона в таких треугольниках.
Равносторонний треугольник: Равносторонний треугольник — это треугольник, в котором все три стороны имеют одинаковую величину и все углы таких треугольников также равны.
Нахождение третьей стороны треугольника по двум сторонам Предположим, что треугольник является прямоугольным, потому что найти третью сторону по двум сторонам можно только в прямоугольном треугольнике.
Мы знаем, что прямоугольный треугольник следует теореме Пифагора
Согласно теореме Пифагора сумма квадратов двух сторон равна квадрату третьей стороны.
(Перпендикуляр) 2 + (Основание) 2 = (Гипотенуза) 2
Используя приведенное выше уравнение, можно вычислить третью сторону, если известны две стороны.
Пример: Предположим, что даны две стороны, одна из которых равна 3 см, а другая — 4 см, тогда найдите третью сторону.
Возьмем перпендикуляр P = 3 см и основание B = 4 см.
Использование теоремы Pythagoras
P 2 + B 2 = H 2
(3) 2 + (4) 2 = H 2
9002 9087 2 = H 2 2 = H 2
9002 = H = H 2 9002 2 = H 2 2 = H 2 .
25 = H 2
H = 5
Примеры вопросов
Вопрос 1: Найдите меру основания, если даны перпендикуляр и гипотенуза, перпендикуляр = 12 см и гипотенуза = 13 см.
Решение:
Perpendicular = 12 cm
Hypotenuse = 13 cm
Using Pythagoras Theorem
P 2 + B 2 = H 2
B 2 = H 2 – P 2
B 2 = 13 2 — 12 2
B 2 = 169 — 144
B 2 = 25
B = 5
. Вопрос 2: Ferimeter 44448
. Вопрос 2: Perimeter 444448
. Вопрос 2: Perimeter 44448 . длина равностороннего треугольника 63см найдите сторону треугольника.
Решение:
Периметр равностороннего треугольника = 3 × сторона
3 × сторона = 64
Сторона = 63/3
Сторона = 21 см
ВОПРОС 3: Найдите меру из меры = 21 см
ВОПРОС 3: Найдите меру из меры из меры = 21 см
ВОПРОС 3: Найдите меру. третья сторона прямоугольного треугольника, если две стороны равны 6 см и 8 см.
третья сторона прямоугольного треугольника, если две стороны равны 6 см и 8 см.
Решение:
Перпендикуляр = 6 см
Основание = 8 см
Используя теорему Пифагора
H 2 = P 2 + B 2
H 2 = P 2 + B 2
H 2 = 6 2 + 8 2
H 2 = 36 + 64
H 2 = 100
H = 10 см
Вопрос 4. Определите, является ли данный треугольник прямоугольным или нет, стороны равны 48, 73, 55 ?
Решение:
Прямоугольный треугольник следует теореме Пифагора, поэтому нам нужно ее проверить.
Сумма квадратов двух меньших сторон должна быть равна квадрату большей стороны
поэтому 48 2 + 55 2 должно быть равно 73 2
2304 + 30295 что равно 53 73 2 = 5329
Следовательно, данный треугольник является прямоугольным, поскольку удовлетворяет теореме Пифагора.
Вопрос 5. Найдите гипотенузу прямоугольного треугольника с основанием 8 см и высотой 15 см?
Решение:
Использование теоремы Pythagorean, A 2 + B 2 = C 2
SO 8 2 + 15 2 = C 2 2 + 15 2 = C 2 2 + 15 2 = C 2 2 + 15 2 = C 2 . √(64 + 225)
c = √289
c = 17 см
Правила треугольника – стороны, углы, внешние углы, градусы и другие свойства
Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать
бесплатно загружаемое изображение вашего треугольника!)
90 $$
Правило 2:
Стороны треугольника — Теорема о неравенстве треугольника:
Эта теорема утверждает, что сумма длин любых двух сторон треугольника должна быть больше третьей стороны. )
)
Правило 3:
Соотношение между измерением сторон и углов в треугольнике:
Наибольший внутренний угол и сторона лежат друг против друга. Это же правило относится и к наименьшему размеру.
угол и сторона, а средний угол и сторона.
Правило 4
Удаленные внешние углы. Эта теорема утверждает, что мера внешнего угла $$ \angle A$$ равна сумме измерений удаленных внутренних углов. еще)
Чем отличаются внутренние и внешние углы треугольника?
На этот вопрос отвечает картинка ниже. Вы создаете внешний угол, продолжая любую сторону треугольника.
9{\circ} $$.
Чтобы проверить истинность этого правила, попробуйте
интерактивный треугольник Math Warehouse,
который позволяет вам перетаскивать разные стороны треугольника и исследовать взаимосвязь между углами
и стороны. Независимо от того, как вы расположите три стороны треугольника, сумма градусов всех
внутренние углы (три угла внутри треугольника) всегда равны 180°.
Это свойство внутренних углов треугольника является просто частным примером
общее правило для внутренних углов любого многоугольника.
Внутренние углы треугольника (рабочий лист)
Интерактивная демонстрация внутренних углов
∠ А ∠ Б ∠ С Всего 180
Перетащите точки треугольника, чтобы начать демонстрацию
Практические задачи (правило внутренних углов)
Проблема 1
Чему равен m$$\angle$$LNM в приведенном ниже треугольнике?
$$ \угол $$ LMN = 34°
$$ \угол $$ MLN = 29°
Используйте правило для внутренних углов треугольника:
м$$ \угол $$ LNM +m$$ \угол $$ LMN +m$$ \угол $$ MLN =180°
м$$ \угол $$ LNM +34° + 29° =180°
м$ $ \угол $$ LNM +63° =180°
м$$ \угол $$ LNM = 180° — 63° = 117°
Проблема 2
Внутренние углы треугольника равны $$ \angle $$ HOP, $$ \angle $$ HPO и $$ \angle $$ PHO. $$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.
$$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.
Что такое m$$ \angle $$ PHO?
Использовать внутренние углы правила треугольника:
м$$ \угол $$ PHO = 180° — 26° -64° = 90°
Взаимосвязь — Измерения сторон и углов
В любом треугольнике
- наибольший внутренний угол равен против наибольшей стороны
- наименьший внутренний угол против наименьшая сторона
- внутренний угол среднего размера равен напротив средняя сторона
Чтобы проверить истинность утверждений, вы можете использовать интерактивный треугольник Math Warehouse,
который позволяет вам перетаскивать разные стороны треугольника и исследовать отношения между мерами углов
и стороны. Независимо от того, как вы расположите три стороны треугольника, вы обнаружите, что утверждения в параграфе
выше верны.
(Хорошо, равнобедренный и равносторонний треугольник являются исключениями из-за того, что у них нет ни одного наименьшего
сторона или, в случае равностороннего треугольника, даже наибольшая сторона. Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)
Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)
Рабочий лист по взаимосвязи между длинами сторон и измерениями углов треугольника
Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать
бесплатно загружаемое изображение вашего треугольника!)
Рабочие листы треугольника
Интерактивировать: возведение треугольника в квадрат
Воспитатель: Сегодня мы будем работать с прямоугольными треугольниками. Прежде чем мы начнем, не могли бы вы рассказать мне, что
определение треугольника?
Ученик: Это трехсторонняя фигура.
Наставник: Хорошо, теперь, зная это, вы можете сказать мне, что такое прямоугольный треугольник?
Ученик: Прямой угол — это угол, равный 90 градусам, так что прямоугольный треугольник не будет
треугольник, сумма углов которого равна 90 градусов?
Наставник: Вы были правы в том, что это связано с прямым углом, но вместо сложения всех углов
до 90 градусов, значит один из углов треугольника равен 90 градусов. Это было бы
невозможно, чтобы все углы в сумме составляли 90 градусов, потому что во всех треугольниках углы должны
добавить до 180 градусов.
Это было бы
невозможно, чтобы все углы в сумме составляли 90 градусов, потому что во всех треугольниках углы должны
добавить до 180 градусов.
Ученик: Итак, прямоугольный треугольник — это треугольник, в котором есть прямой угол.
Наставник: Хорошо, теперь, зная, что такое прямоугольный треугольник, какова будет сумма двух других углов?
Ученик: Хорошо, если в треугольнике всего 180 градусов, а прямой угол равен 90 градусам, то другой
два угла, сложенные вместе, равны 90 градусов.
Наставник: Отлично. Теперь мы знаем основы прямоугольного треугольника. Сегодня мы будем учиться тому, как
Найдите длину третьей стороны прямоугольного треугольника, если длины двух других сторон равны
известен.
Ученик: Почему нельзя просто измерить длину?
Наставник: Ну, в некоторых ситуациях можно, но этот процесс может быть утомительным и оставляет место для человека. ошибка. Математический процесс намного точнее. Кроме того, бывают случаи, когда вы не можете
измерения, например, когда рядом нет линейки, треугольник нарисован не в масштабе или
даны только числа без сопроводительного рисунка.
ошибка. Математический процесс намного точнее. Кроме того, бывают случаи, когда вы не можете
измерения, например, когда рядом нет линейки, треугольник нарисован не в масштабе или
даны только числа без сопроводительного рисунка.
Ученик: Итак, если вы не можете полагаться на измерения, как бы вы это сделали?
Наставник: Чтобы найти неизвестные стороны в прямоугольных треугольниках, мы используем нечто, называемое
Теорема Пифагора. Он назван так потому, что был создан греческим философом и ученым по имени
Пифагор.
Ученик: Что такое теорема Пифагора и как мы ее используем?
Наставник: Теорема Пифагора утверждает, что A 2 +Б 2 =С 2 где A представляет собой одну сторону треугольника, B представляет другую сторону, а C представляет собой
гипотенуза, сторона, лежащая против прямого угла.
Ученик: Хорошо, но как мы можем использовать эту теорему, если задействованы три переменные?
Наставник: Ну, помните, в начале урока я сказал, что мы будем находить длину
третью сторону треугольника, используя длины двух других сторон.
Ученик: Теперь я вспомнил! Таким образом, мы можем заменить две из этих переменных сторонами, которые нам уже известны! Но
как узнать, какие длины представляют переменные?
Наставник: Хорошо, если я обозначу стороны моего треугольника A, B и C, где A и B — стороны треугольника.
треугольника, а C — гипотенуза, как эта информация может быть полезна при использовании
Теорема Пифагора?
Ученик: Ну, было бы логично, если бы А была бы длиной стороны А, а В была бы длиной стороны А.
сторона Б.
Наставник: Хорошо, а теперь давайте выясним, почему и как работает эта теорема, а затем попрактикуемся в ее использовании.
Несколько раз. Давай пойдем в
Квадрат треугольника.
Ученик: Есть треугольник с квадратом, прикрепленным к каждой стороне; это прямоугольный треугольник?
Наставник: Посмотрите на ту сторону, где написано угловых измерений и вы говорите мне, прямоугольный ли это треугольник.
Студент: Это! Угол С равен 90 градусов.
Наставник: Верно, в этом упражнении треугольник всегда прямоугольный. мы собираемся использовать это
деятельность по проверке теоремы Пифагора.
Ученик: Но подождите секунду, углы обозначены A, B и C, я думал, что теорема Пифагора
работает с длинами сторон.
Наставник: Вы правы в том, что теорема Пифагора работает с длинами сторон, но вам нужно
помните, что в разных ситуациях переменные означают разные вещи. Неважно, как
треугольник помечен, A, B и C всегда будут представлять стороны.
Ученик: Значит, в этом случае это будет (линия AC) 2 +(линия ВС) 2 = (линия АВ) 2 .
Ментор: Точно.
Ученик: Итак, для чего квадраты прикреплены к треугольнику? Я думал теорема пифагора
работает только для треугольников.
Наставник: Вы правы в том, что теорема Пифагора используется только для треугольников, но если вы посмотрите на
стороны в теореме Пифагора, вы увидите, что все они в квадрате. Итак, давайте посмотрим, что
действительно происходит, когда вы возводите число в квадрат. Возьми лист миллиметровки и возведи в квадрат 4.
Итак, давайте посмотрим, что
действительно происходит, когда вы возводите число в квадрат. Возьми лист миллиметровки и возведи в квадрат 4.
Ученик: Но это легко, это 16.
Ментор: Верно, но давайте сначала выясним, откуда взялось название «Квадрат».
Ученик: Итак, у меня есть лист миллиметровки, что мне делать?
Наставник: Сначала возьмите на миллиметровке четыре клетки подряд и заштрихуйте их.
Ученик: Четыре, потому что четыре — это число, которое мы пытаемся возвести в квадрат?
Наставник: Верно, если бы мы пытались возвести в квадрат девять, то вы бы заштриховали девять клеток подряд. Теперь ваша очередь
знаете, что четыре в квадрате — это всего лишь четырежды четыре, верно?
Ученик: Да, это всегда число, умноженное на само себя.
Наставник: Верно, а еще ты помнишь, что умножение — это просто сложение чисел в несколько раз?
раз, так что 5*3 на самом деле будет 5+5+5?
Ученик: Да, и поэтому 2*5 будет 2+2+2+2+2.
Ментор: Или, проще говоря, это может быть 5+5, но вы правильно поняли идею. Итак, 4*4 будет что?
Ученик: Ну, это будет 4+4+4+4, не так ли?
Наставник: Хорошо, первые четыре уже написаны на миллиметровке, так что давайте добавим еще 4 в
ряд прямо под первыми четырьмя. Итак, теперь мы добавили 4+4. Теперь давайте добавим еще 4 в ряд
прямо под вторыми четырьмя, и у нас есть 4+4+4. Можете ли вы догадаться, что мы будем делать дальше?
Ученик: Добавьте еще 4 в ряд ниже этого!
Ментор: Хорошо, а со всеми заштрихованными, что у вас есть?
Студент: Это квадрат!
Наставник: Верно, отсюда термин «квадрат», потому что результатом на самом деле является квадрат. К
закрепите эту идею, попробуйте три в квадрате.
Ученик: Это тоже квадрат!
Наставник: Хорошо, теперь вы можете догадаться, почему к сторонам треугольника в
Квадрат треугольника?
Ученик: Ну, это называется квадратурой треугольника, поэтому они возвели в квадрат каждую сторону треугольника.
Наставник: Но почему занятие называется «Квадратура треугольника», подумайте о пифагорейском
теорема.
Ученик: О точно! В теореме Пифагора все A, B и C возведены в квадрат, а A, B и C представляют
стороны треугольника, значит, они квадратуры сторон треугольника.
Наставник: Точно! Это задание было разработано, чтобы помочь людям понять теорему Пифагора, поэтому
нарисовал схему того, что на самом деле означает теорема. Теперь, используя эти квадраты, как вы можете
проверить, верна ли теорема Пифагора?
Ученик: Ну… если А 2 +Б 2 =С 2 не должен (квадратик, прикрепленный к стороне A)+ (квадратик, прикрепленный к стороне B)=(квадратик
прикреплен к стороне C)?
Наставник: Верно, но в какой части площади?
периметр?
Ученик: Ммм, я не знаю.
Воспитатель: Что ж, вернемся к квадрату, который вы нарисовали на миллиметровой бумаге. Вы сказали, прежде чем мы начали, что 4
в квадрате было 16, и вы были правы. Значит, периметр квадрата, который вы нарисовали, равен 16?
Вы сказали, прежде чем мы начали, что 4
в квадрате было 16, и вы были правы. Значит, периметр квадрата, который вы нарисовали, равен 16?
Ученик: Да, это так!
Наставник: Просто чтобы убедиться, что это правильно, попробуйте с квадратом, который вы нарисовали, на три квадрата. И что
периметр этого квадрата.
Ученик: 12…но три в квадрате 9.
Наставник: Правильно, это означает, что тот факт, что периметр первого квадрата такой же, как у
сторона в квадрате была случайностью. Причина, по которой это сработало, заключалась в том, что четыре в квадрате — это четыре раза.
четыре, то есть площадь, и длина стороны 4, и есть четыре стороны, так что (
длина стороны*4), которая является периметром. Теперь, когда мы знаем, что периметр неправильный, что
мы должны попробовать дальше?
Ученик: А как насчет
область?
Наставник: Хорошо, попробуй с квадратом четыре на четыре.
Студент: Это 16! Но давайте проверим это с помощью квадрата три на три, чтобы убедиться, что это правильно.
Наставник: Хорошая идея.
Ученик: Площадь квадрата три на три равна девяти! Оно работает!
Наставник: Хорошо, теперь мы обнаружили, что квадрат числа равен площади его квадрата. Так что же может
мы ожидаем для теоремы Пифагора теперь?
Ученик: Это будет (площадь квадрата, присоединенного к стороне A) + (площадь квадрата, присоединенного к
сторона B)=(площадь квадрата, присоединенного к стороне C).
Наставник: Отлично. Итак, если вы посмотрите на левую часть изображения в области, помеченной как «область», вы увидите
см площадь квадратов. Что вы в них замечаете?
Ученик: Квадрат AC+Квадрат BC=Квадрат AB.
Наставник: Поскольку область помечена как «область», вы можете сказать, что числа в этой области — это все области. Так
работает ли теорема Пифагора?
Так
работает ли теорема Пифагора?
Студент: Да!
Ментор: Будьте осторожны, мы уже обнаружили, что использование только одного фрагмента данных может привести вас к неверному пути.
Попробуйте изменить длины сторон AC и BC с помощью ползунков под диаграммой, все равно
Работа?
Студент: Да! Я не могу найти ни одной схемы, где бы она не работала.
Наставник: Хорошо, теперь, когда мы знаем, что теорема Пифагора работает и почему она работает, мы можем начать.
решение задач с его помощью. Помнишь, для чего я сказал, что мы его используем?
Ученик: Чтобы получить длину стороны, зная две другие стороны треугольника.
Наставник: Почти верно, это работает не для всех типов треугольников. К какому типу треугольника относится этот
работать на?
Ученик: Да, это работает только для прямоугольных треугольников.
Наставник: Хорошо, я дам вам длины двух сторон, а вы скажете мне, какова длина
третья сторона использует теорему Пифагора. Наличие калькулятора облегчило бы эту задачу.
Наличие калькулятора облегчило бы эту задачу.
Студент: Хорошо, у меня есть калькулятор; Я готов.
Наставник: Хорошо, я начну с двух катетов, а вы должны найти гипотенузу. хорошо, одна нога
равно 5, а другое равно 7. Что такое гипотенуза?
Ученик: Хорошо, значит 5 2 это 25 и 7 2 равно 49, поэтому 25+49=74. Гипотенуза равна 74!
Ментор: Не совсем, потому что помните, что это A 2 +Б 2 =С 2 . Вы сделали первую половину правильно, A 2 +Б 2 , но когда вы получили 74, вы забыли, что 74 равно только C 2 , а не C. Итак, что бы вы сделали, чтобы закончить решение этой задачи?
Ученик: Квадрат 74?
Ментор: Нет, подумайте об этом алгебраически, 74=C 2 , так как бы вы решили получить C сам по себе?
Ученик: Вы извлекаете квадратный корень из каждой стороны!
Наставник: Хорошо, так что закончите решать задачу.
Ученик: Хорошо, квадратный корень из 74 равен 8,6, поэтому C=8,6.
Наставник: Отлично, давайте попробуем еще один. Как насчет ног 3 и 4.
Ученик: Хорошо, 3 2 это 9 и 4 2 равно 16, поэтому 9+16=25. Тогда квадратный корень из 25 равен 5!
Наставник: Хорошая работа. Вы чувствуете, что понимаете, как получить длину гипотенузы, если задано
длины двух ног?
Студент: Да! Что дальше?
Воспитатель: Теперь попробуем найти длину второго участка, зная длины первого участка.
и гипотенуза. Итак, чтобы сделать это, нам придется немного заняться алгеброй. Можешь попробовать
сначала, а потом я помогу, если у вас возникнут какие-либо проблемы. Так что насчет 15 и 7.
Ученик: Какая из них гипотенуза, а какая катет?
Воспитатель: Ну, гипотенуза всегда самая длинная сторона в прямоугольном треугольнике. Это потому, что
самая длинная сторона будет напротив наибольшего угла, вторая самая длинная сторона будет напротив
второй по величине угол и самая короткая сторона напротив наименьшего угла. Мы знаем треугольник
имеет только 180 градусов и что гипотенуза должна быть самой длинной стороной, потому что самая большая
что в прямоугольном треугольнике может быть угол, отличный от прямого, равен 89.999. Итак, поскольку
прямой угол равен 90 градусов, а наибольший угол, который может быть равен 89,999, чем прямой
сторона напротив прямого угла должна быть самой длинной стороной, также известной как гипотенуза.
Зная это, можете ли вы сказать мне, является ли длина гипотенузы 15 или 7?
Это потому, что
самая длинная сторона будет напротив наибольшего угла, вторая самая длинная сторона будет напротив
второй по величине угол и самая короткая сторона напротив наименьшего угла. Мы знаем треугольник
имеет только 180 градусов и что гипотенуза должна быть самой длинной стороной, потому что самая большая
что в прямоугольном треугольнике может быть угол, отличный от прямого, равен 89.999. Итак, поскольку
прямой угол равен 90 градусов, а наибольший угол, который может быть равен 89,999, чем прямой
сторона напротив прямого угла должна быть самой длинной стороной, также известной как гипотенуза.
Зная это, можете ли вы сказать мне, является ли длина гипотенузы 15 или 7?
Ученик: Должно быть 15.
Наставник: Верно, поскольку 15 явно длиннее 7, теперь вы можете решить для другой ноги?
Ученик: Ну, это было бы 7 2 это 49 и 15 2 равно 225. Таким образом, это будет 49+B.




Сертифицированный репетитор
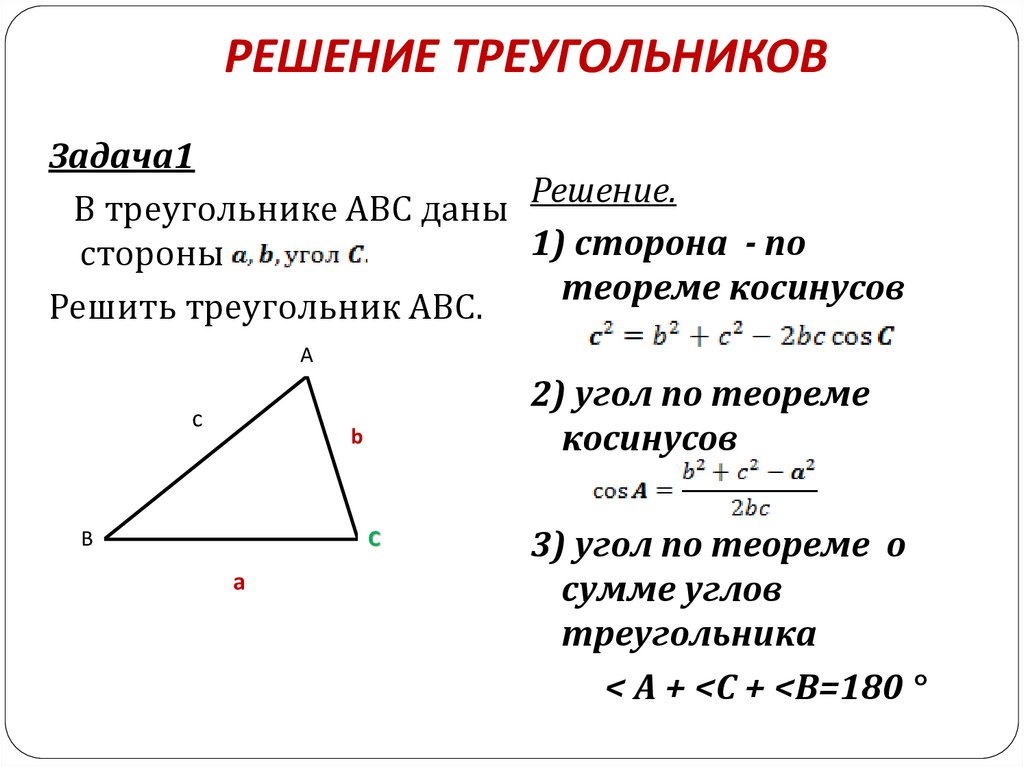 Мичиганский университет в Анн-Арборе, бакалавр искусств, английский язык.
Мичиганский университет в Анн-Арборе, бакалавр искусств, английский язык.Сертифицированный репетитор
 Периметр треугольника равен сумме всех трех сторон треугольника.
Периметр треугольника равен сумме всех трех сторон треугольника.
(Перпендикуляр) 2 + (Основание) 2 = (Гипотенуза) 2
Возьмем перпендикуляр P = 3 см и основание B = 4 см.
Использование теоремы Pythagoras
P 2 + B 2 = H 2
(3) 2 + (4) 2 = H 2
9002 9087 2 = H 22 = H 2
9002 = H = H 2 9002 2 = H 2 2 = H 2 .
25 = H 2
H = 5
Примеры вопросов
Вопрос 1: Найдите меру основания, если даны перпендикуляр и гипотенуза, перпендикуляр = 12 см и гипотенуза = 13 см.
Решение:
Perpendicular = 12 cm
Hypotenuse = 13 cm
Using Pythagoras Theorem
P 2 + B 2 = H 2
B 2 = H 2 – P 2
B 2 = 13 2 — 12 2
B 2 = 169 — 144
B 2 = 25
B = 5
. Вопрос 2: Ferimeter 44448
. Вопрос 2: Perimeter 444448
. Вопрос 2: Perimeter 44448 . длина равностороннего треугольника 63см найдите сторону треугольника. Решение: Периметр равностороннего треугольника = 3 × сторона 3 × сторона = 64 Сторона = 63/3 Сторона = 21 см ВОПРОС 3: Найдите меру из меры = 21 см ВОПРОС 3: Найдите меру из меры из меры = 21 см ВОПРОС 3: Найдите меру. Решение: Перпендикуляр = 6 см Основание = 8 см Используя теорему Пифагора H 2 = P 2 + B 2 H 2 = P 2 + B 2 H 2 = 6 2 + 8 2 H 2 = 36 + 64 H 2 = 100 H = 10 см Вопрос 4. Определите, является ли данный треугольник прямоугольным или нет, стороны равны 48, 73, 55 ? Решение: Прямоугольный треугольник следует теореме Пифагора, поэтому нам нужно ее проверить. Сумма квадратов двух меньших сторон должна быть равна квадрату большей стороны поэтому 48 2 + 55 2 должно быть равно 73 2 2304 + 30295 что равно 53 73 2 = 5329 Следовательно, данный треугольник является прямоугольным, поскольку удовлетворяет теореме Пифагора. Вопрос 5. Найдите гипотенузу прямоугольного треугольника с основанием 8 см и высотой 15 см? Решение: Использование теоремы Pythagorean, A 2 + B 2 = C 2 SO 8 2 + 15 2 = C 2 2 + 15 2 = C 2 2 + 15 2 = C 2 2 + 15 2 = C 2 . √(64 + 225) c = √289 c = 17 см Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать
бесплатно загружаемое изображение вашего треугольника!)
90 $$ Правило 2:
Стороны треугольника — Теорема о неравенстве треугольника:
Эта теорема утверждает, что сумма длин любых двух сторон треугольника должна быть больше третьей стороны. Правило 3:
Соотношение между измерением сторон и углов в треугольнике:
Наибольший внутренний угол и сторона лежат друг против друга. Это же правило относится и к наименьшему размеру.
угол и сторона, а средний угол и сторона. Правило 4
Удаленные внешние углы. Эта теорема утверждает, что мера внешнего угла $$ \angle A$$ равна сумме измерений удаленных внутренних углов. еще) На этот вопрос отвечает картинка ниже. Вы создаете внешний угол, продолжая любую сторону треугольника. третья сторона прямоугольного треугольника, если две стороны равны 6 см и 8 см.
третья сторона прямоугольного треугольника, если две стороны равны 6 см и 8 см. 
Правила треугольника – стороны, углы, внешние углы, градусы и другие свойства
 )
) Чем отличаются внутренние и внешние углы треугольника?
Чтобы проверить истинность этого правила, попробуйте
интерактивный треугольник Math Warehouse,
который позволяет вам перетаскивать разные стороны треугольника и исследовать взаимосвязь между углами
и стороны. Независимо от того, как вы расположите три стороны треугольника, сумма градусов всех
внутренние углы (три угла внутри треугольника) всегда равны 180°.
Это свойство внутренних углов треугольника является просто частным примером общее правило для внутренних углов любого многоугольника.
Внутренние углы треугольника (рабочий лист)
Интерактивная демонстрация внутренних углов
| ∠ А | |
| ∠ Б | |
| ∠ С | |
| Всего | 180 |
|---|
Перетащите точки треугольника, чтобы начать демонстрацию
Практические задачи (правило внутренних углов)
Проблема 1
Чему равен m$$\angle$$LNM в приведенном ниже треугольнике?
$$ \угол $$ LMN = 34°
$$ \угол $$ MLN = 29°
Используйте правило для внутренних углов треугольника:
м$$ \угол $$ LNM +m$$ \угол $$ LMN +m$$ \угол $$ MLN =180°
м$$ \угол $$ LNM +34° + 29° =180°
м$ $ \угол $$ LNM +63° =180°
м$$ \угол $$ LNM = 180° — 63° = 117°
Проблема 2
Внутренние углы треугольника равны $$ \angle $$ HOP, $$ \angle $$ HPO и $$ \angle $$ PHO.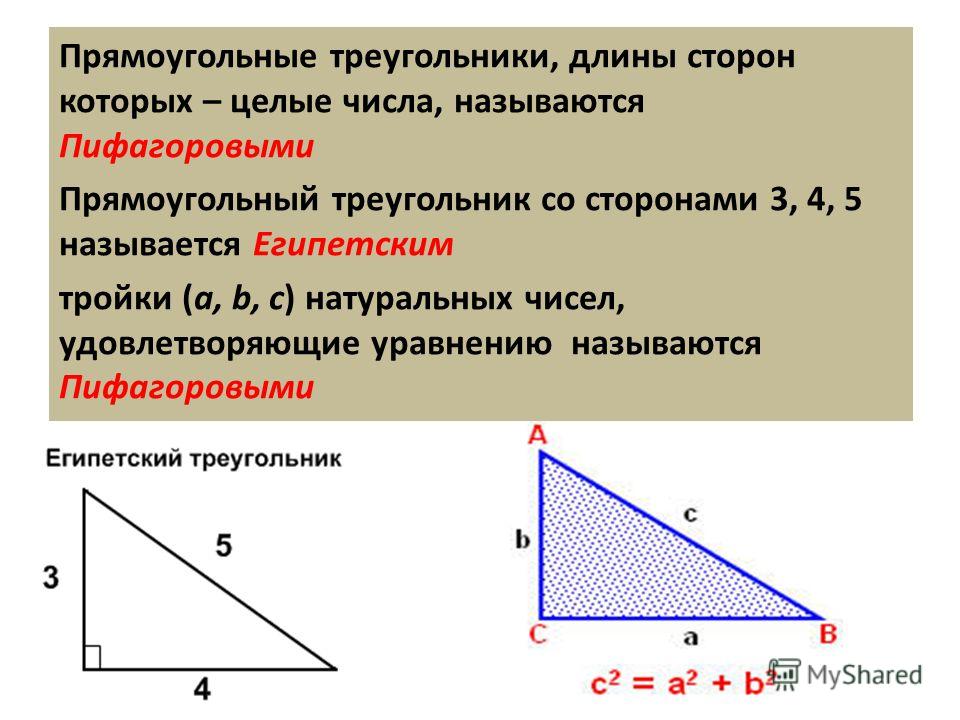 $$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.
$$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.
Что такое m$$ \angle $$ PHO?
Использовать внутренние углы правила треугольника:
м$$ \угол $$ PHO = 180° — 26° -64° = 90°
Взаимосвязь — Измерения сторон и углов
В любом треугольнике
- наибольший внутренний угол равен против наибольшей стороны
- наименьший внутренний угол против наименьшая сторона
- внутренний угол среднего размера равен напротив средняя сторона
Чтобы проверить истинность утверждений, вы можете использовать интерактивный треугольник Math Warehouse, который позволяет вам перетаскивать разные стороны треугольника и исследовать отношения между мерами углов и стороны. Независимо от того, как вы расположите три стороны треугольника, вы обнаружите, что утверждения в параграфе выше верны.
(Хорошо, равнобедренный и равносторонний треугольник являются исключениями из-за того, что у них нет ни одного наименьшего
сторона или, в случае равностороннего треугольника, даже наибольшая сторона.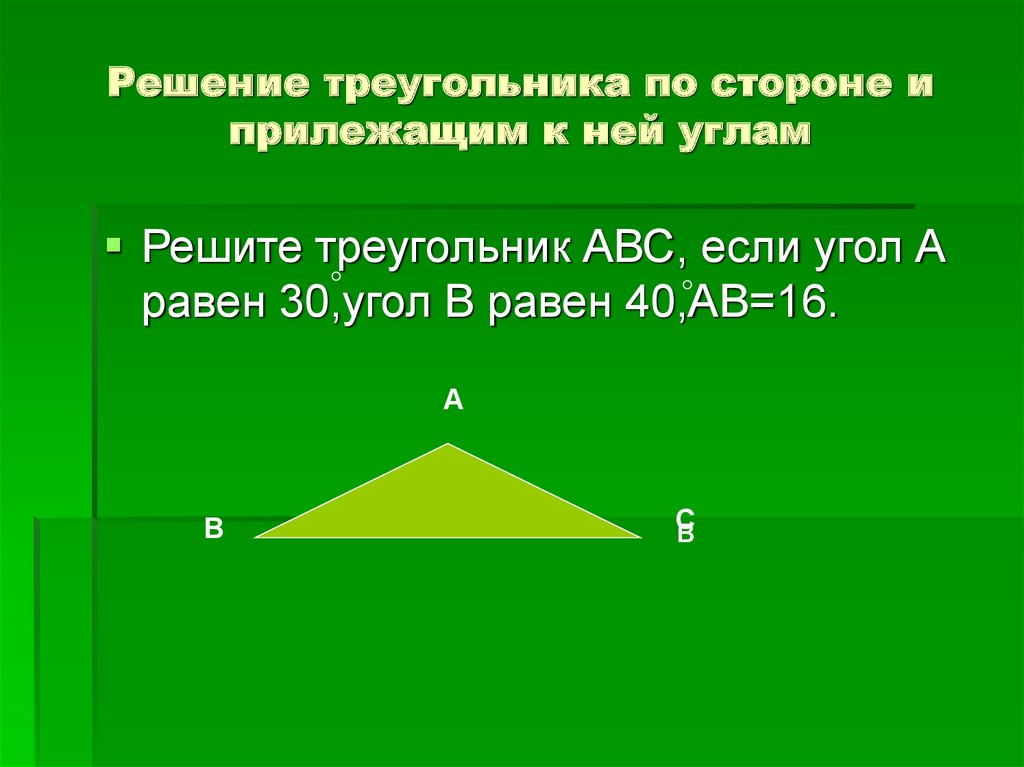 Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)
Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)
Рабочий лист по взаимосвязи между длинами сторон и измерениями углов треугольника
Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать бесплатно загружаемое изображение вашего треугольника!)
Рабочие листы треугольника
Интерактивировать: возведение треугольника в квадрат
Воспитатель: Сегодня мы будем работать с прямоугольными треугольниками. Прежде чем мы начнем, не могли бы вы рассказать мне, что определение треугольника?
Ученик: Это трехсторонняя фигура.
Наставник: Хорошо, теперь, зная это, вы можете сказать мне, что такое прямоугольный треугольник?
Ученик: Прямой угол — это угол, равный 90 градусам, так что прямоугольный треугольник не будет треугольник, сумма углов которого равна 90 градусов?
Наставник: Вы были правы в том, что это связано с прямым углом, но вместо сложения всех углов
до 90 градусов, значит один из углов треугольника равен 90 градусов. Это было бы
невозможно, чтобы все углы в сумме составляли 90 градусов, потому что во всех треугольниках углы должны
добавить до 180 градусов.
Это было бы
невозможно, чтобы все углы в сумме составляли 90 градусов, потому что во всех треугольниках углы должны
добавить до 180 градусов.
Ученик: Итак, прямоугольный треугольник — это треугольник, в котором есть прямой угол.
Наставник: Хорошо, теперь, зная, что такое прямоугольный треугольник, какова будет сумма двух других углов?
Ученик: Хорошо, если в треугольнике всего 180 градусов, а прямой угол равен 90 градусам, то другой два угла, сложенные вместе, равны 90 градусов.
Наставник: Отлично. Теперь мы знаем основы прямоугольного треугольника. Сегодня мы будем учиться тому, как Найдите длину третьей стороны прямоугольного треугольника, если длины двух других сторон равны известен.
Ученик: Почему нельзя просто измерить длину?
Наставник: Ну, в некоторых ситуациях можно, но этот процесс может быть утомительным и оставляет место для человека. ошибка. Математический процесс намного точнее. Кроме того, бывают случаи, когда вы не можете
измерения, например, когда рядом нет линейки, треугольник нарисован не в масштабе или
даны только числа без сопроводительного рисунка.
ошибка. Математический процесс намного точнее. Кроме того, бывают случаи, когда вы не можете
измерения, например, когда рядом нет линейки, треугольник нарисован не в масштабе или
даны только числа без сопроводительного рисунка.
Ученик: Итак, если вы не можете полагаться на измерения, как бы вы это сделали?
Наставник: Чтобы найти неизвестные стороны в прямоугольных треугольниках, мы используем нечто, называемое Теорема Пифагора. Он назван так потому, что был создан греческим философом и ученым по имени Пифагор.
Ученик: Что такое теорема Пифагора и как мы ее используем?
Наставник: Теорема Пифагора утверждает, что A 2 +Б 2 =С 2 где A представляет собой одну сторону треугольника, B представляет другую сторону, а C представляет собой гипотенуза, сторона, лежащая против прямого угла.
Ученик: Хорошо, но как мы можем использовать эту теорему, если задействованы три переменные?
Наставник: Ну, помните, в начале урока я сказал, что мы будем находить длину
третью сторону треугольника, используя длины двух других сторон.
Ученик: Теперь я вспомнил! Таким образом, мы можем заменить две из этих переменных сторонами, которые нам уже известны! Но как узнать, какие длины представляют переменные?
Наставник: Хорошо, если я обозначу стороны моего треугольника A, B и C, где A и B — стороны треугольника. треугольника, а C — гипотенуза, как эта информация может быть полезна при использовании Теорема Пифагора?
Ученик: Ну, было бы логично, если бы А была бы длиной стороны А, а В была бы длиной стороны А. сторона Б.
Наставник: Хорошо, а теперь давайте выясним, почему и как работает эта теорема, а затем попрактикуемся в ее использовании. Несколько раз. Давай пойдем в Квадрат треугольника.
Ученик: Есть треугольник с квадратом, прикрепленным к каждой стороне; это прямоугольный треугольник?
Наставник: Посмотрите на ту сторону, где написано угловых измерений и вы говорите мне, прямоугольный ли это треугольник.
Студент: Это! Угол С равен 90 градусов.
Наставник: Верно, в этом упражнении треугольник всегда прямоугольный. мы собираемся использовать это деятельность по проверке теоремы Пифагора.
Ученик: Но подождите секунду, углы обозначены A, B и C, я думал, что теорема Пифагора работает с длинами сторон.
Наставник: Вы правы в том, что теорема Пифагора работает с длинами сторон, но вам нужно помните, что в разных ситуациях переменные означают разные вещи. Неважно, как треугольник помечен, A, B и C всегда будут представлять стороны.
Ученик: Значит, в этом случае это будет (линия AC) 2 +(линия ВС) 2 = (линия АВ) 2 .
Ментор: Точно.
Ученик: Итак, для чего квадраты прикреплены к треугольнику? Я думал теорема пифагора работает только для треугольников.
Наставник: Вы правы в том, что теорема Пифагора используется только для треугольников, но если вы посмотрите на
стороны в теореме Пифагора, вы увидите, что все они в квадрате.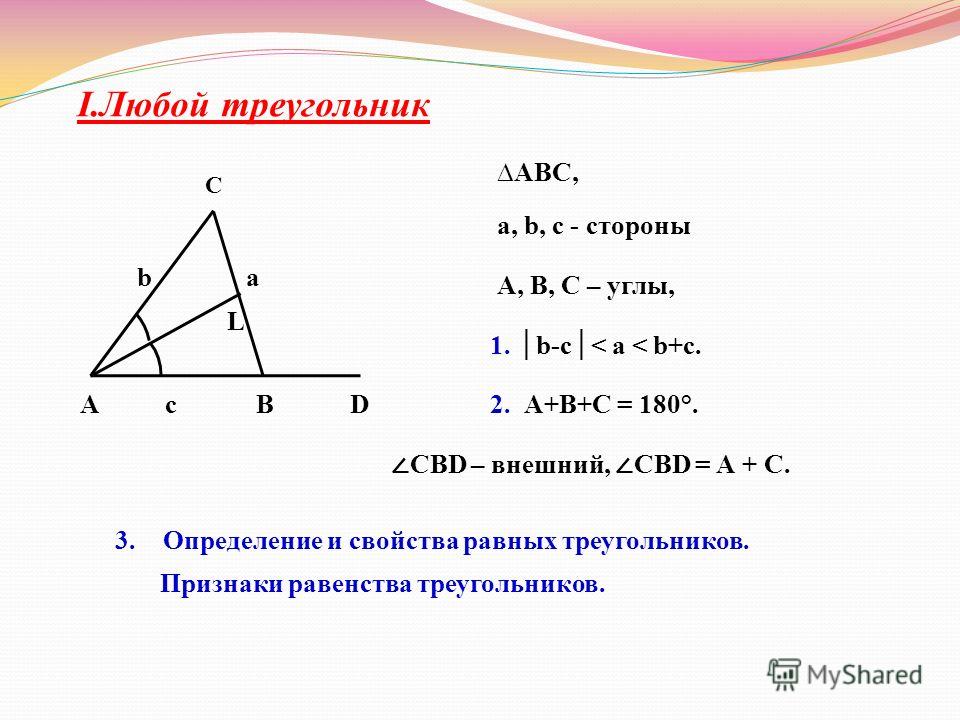 Итак, давайте посмотрим, что
действительно происходит, когда вы возводите число в квадрат. Возьми лист миллиметровки и возведи в квадрат 4.
Итак, давайте посмотрим, что
действительно происходит, когда вы возводите число в квадрат. Возьми лист миллиметровки и возведи в квадрат 4.
Ученик: Но это легко, это 16.
Ментор: Верно, но давайте сначала выясним, откуда взялось название «Квадрат».
Ученик: Итак, у меня есть лист миллиметровки, что мне делать?
Наставник: Сначала возьмите на миллиметровке четыре клетки подряд и заштрихуйте их.
Ученик: Четыре, потому что четыре — это число, которое мы пытаемся возвести в квадрат?
Наставник: Верно, если бы мы пытались возвести в квадрат девять, то вы бы заштриховали девять клеток подряд. Теперь ваша очередь знаете, что четыре в квадрате — это всего лишь четырежды четыре, верно?
Ученик: Да, это всегда число, умноженное на само себя.
Наставник: Верно, а еще ты помнишь, что умножение — это просто сложение чисел в несколько раз? раз, так что 5*3 на самом деле будет 5+5+5?
Ученик: Да, и поэтому 2*5 будет 2+2+2+2+2.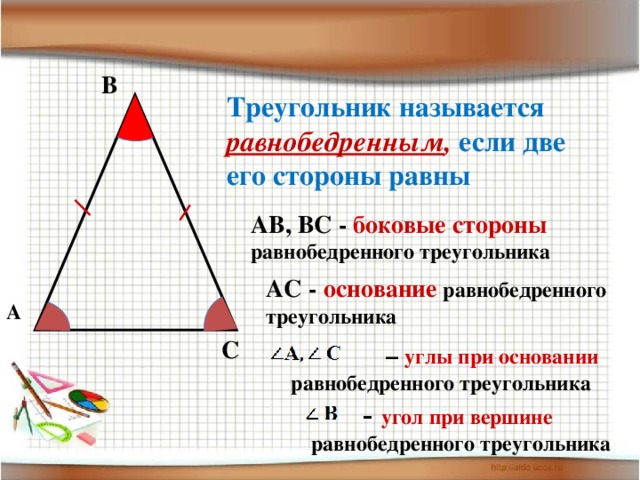
Ментор: Или, проще говоря, это может быть 5+5, но вы правильно поняли идею. Итак, 4*4 будет что?
Ученик: Ну, это будет 4+4+4+4, не так ли?
Наставник: Хорошо, первые четыре уже написаны на миллиметровке, так что давайте добавим еще 4 в ряд прямо под первыми четырьмя. Итак, теперь мы добавили 4+4. Теперь давайте добавим еще 4 в ряд прямо под вторыми четырьмя, и у нас есть 4+4+4. Можете ли вы догадаться, что мы будем делать дальше?
Ученик: Добавьте еще 4 в ряд ниже этого!
Ментор: Хорошо, а со всеми заштрихованными, что у вас есть?
Студент: Это квадрат!
Наставник: Верно, отсюда термин «квадрат», потому что результатом на самом деле является квадрат. К закрепите эту идею, попробуйте три в квадрате.
Ученик: Это тоже квадрат!
Наставник: Хорошо, теперь вы можете догадаться, почему к сторонам треугольника в Квадрат треугольника?
Ученик: Ну, это называется квадратурой треугольника, поэтому они возвели в квадрат каждую сторону треугольника.
Наставник: Но почему занятие называется «Квадратура треугольника», подумайте о пифагорейском теорема.
Ученик: О точно! В теореме Пифагора все A, B и C возведены в квадрат, а A, B и C представляют стороны треугольника, значит, они квадратуры сторон треугольника.
Наставник: Точно! Это задание было разработано, чтобы помочь людям понять теорему Пифагора, поэтому нарисовал схему того, что на самом деле означает теорема. Теперь, используя эти квадраты, как вы можете проверить, верна ли теорема Пифагора?
Ученик: Ну… если А 2 +Б 2 =С 2 не должен (квадратик, прикрепленный к стороне A)+ (квадратик, прикрепленный к стороне B)=(квадратик прикреплен к стороне C)?
Наставник: Верно, но в какой части площади? периметр?
Ученик: Ммм, я не знаю.
Воспитатель: Что ж, вернемся к квадрату, который вы нарисовали на миллиметровой бумаге. Вы сказали, прежде чем мы начали, что 4
в квадрате было 16, и вы были правы. Значит, периметр квадрата, который вы нарисовали, равен 16?
Вы сказали, прежде чем мы начали, что 4
в квадрате было 16, и вы были правы. Значит, периметр квадрата, который вы нарисовали, равен 16?
Ученик: Да, это так!
Наставник: Просто чтобы убедиться, что это правильно, попробуйте с квадратом, который вы нарисовали, на три квадрата. И что периметр этого квадрата.
Ученик: 12…но три в квадрате 9.
Наставник: Правильно, это означает, что тот факт, что периметр первого квадрата такой же, как у сторона в квадрате была случайностью. Причина, по которой это сработало, заключалась в том, что четыре в квадрате — это четыре раза. четыре, то есть площадь, и длина стороны 4, и есть четыре стороны, так что ( длина стороны*4), которая является периметром. Теперь, когда мы знаем, что периметр неправильный, что мы должны попробовать дальше?
Ученик: А как насчет область?
Наставник: Хорошо, попробуй с квадратом четыре на четыре.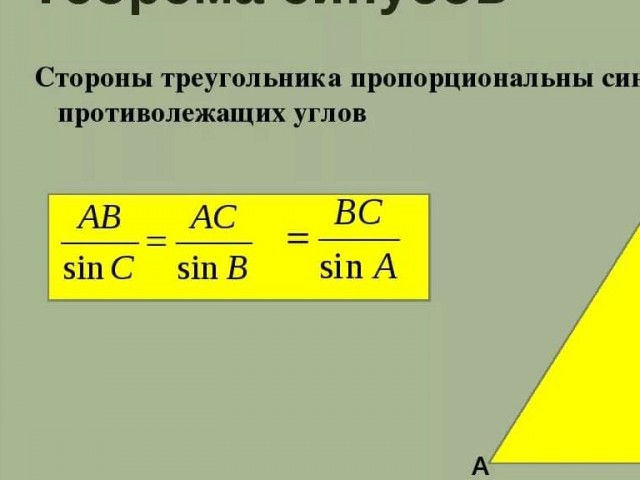
Студент: Это 16! Но давайте проверим это с помощью квадрата три на три, чтобы убедиться, что это правильно.
Наставник: Хорошая идея.
Ученик: Площадь квадрата три на три равна девяти! Оно работает!
Наставник: Хорошо, теперь мы обнаружили, что квадрат числа равен площади его квадрата. Так что же может мы ожидаем для теоремы Пифагора теперь?
Ученик: Это будет (площадь квадрата, присоединенного к стороне A) + (площадь квадрата, присоединенного к сторона B)=(площадь квадрата, присоединенного к стороне C).
Наставник: Отлично. Итак, если вы посмотрите на левую часть изображения в области, помеченной как «область», вы увидите см площадь квадратов. Что вы в них замечаете?
Ученик: Квадрат AC+Квадрат BC=Квадрат AB.
Наставник: Поскольку область помечена как «область», вы можете сказать, что числа в этой области — это все области. Так
работает ли теорема Пифагора?
Так
работает ли теорема Пифагора?
Студент: Да!
Ментор: Будьте осторожны, мы уже обнаружили, что использование только одного фрагмента данных может привести вас к неверному пути. Попробуйте изменить длины сторон AC и BC с помощью ползунков под диаграммой, все равно Работа?
Студент: Да! Я не могу найти ни одной схемы, где бы она не работала.
Наставник: Хорошо, теперь, когда мы знаем, что теорема Пифагора работает и почему она работает, мы можем начать. решение задач с его помощью. Помнишь, для чего я сказал, что мы его используем?
Ученик: Чтобы получить длину стороны, зная две другие стороны треугольника.
Наставник: Почти верно, это работает не для всех типов треугольников. К какому типу треугольника относится этот работать на?
Ученик: Да, это работает только для прямоугольных треугольников.
Наставник: Хорошо, я дам вам длины двух сторон, а вы скажете мне, какова длина
третья сторона использует теорему Пифагора. Наличие калькулятора облегчило бы эту задачу.
Наличие калькулятора облегчило бы эту задачу.
Студент: Хорошо, у меня есть калькулятор; Я готов.
Наставник: Хорошо, я начну с двух катетов, а вы должны найти гипотенузу. хорошо, одна нога равно 5, а другое равно 7. Что такое гипотенуза?
Ученик: Хорошо, значит 5 2 это 25 и 7 2 равно 49, поэтому 25+49=74. Гипотенуза равна 74!
Ментор: Не совсем, потому что помните, что это A 2 +Б 2 =С 2 . Вы сделали первую половину правильно, A 2 +Б 2 , но когда вы получили 74, вы забыли, что 74 равно только C 2 , а не C. Итак, что бы вы сделали, чтобы закончить решение этой задачи?
Ученик: Квадрат 74?
Ментор: Нет, подумайте об этом алгебраически, 74=C 2 , так как бы вы решили получить C сам по себе?
Ученик: Вы извлекаете квадратный корень из каждой стороны!
Наставник: Хорошо, так что закончите решать задачу.
Ученик: Хорошо, квадратный корень из 74 равен 8,6, поэтому C=8,6.
Наставник: Отлично, давайте попробуем еще один. Как насчет ног 3 и 4.
Ученик: Хорошо, 3 2 это 9 и 4 2 равно 16, поэтому 9+16=25. Тогда квадратный корень из 25 равен 5!
Наставник: Хорошая работа. Вы чувствуете, что понимаете, как получить длину гипотенузы, если задано длины двух ног?
Студент: Да! Что дальше?
Воспитатель: Теперь попробуем найти длину второго участка, зная длины первого участка. и гипотенуза. Итак, чтобы сделать это, нам придется немного заняться алгеброй. Можешь попробовать сначала, а потом я помогу, если у вас возникнут какие-либо проблемы. Так что насчет 15 и 7.
Ученик: Какая из них гипотенуза, а какая катет?
Воспитатель: Ну, гипотенуза всегда самая длинная сторона в прямоугольном треугольнике.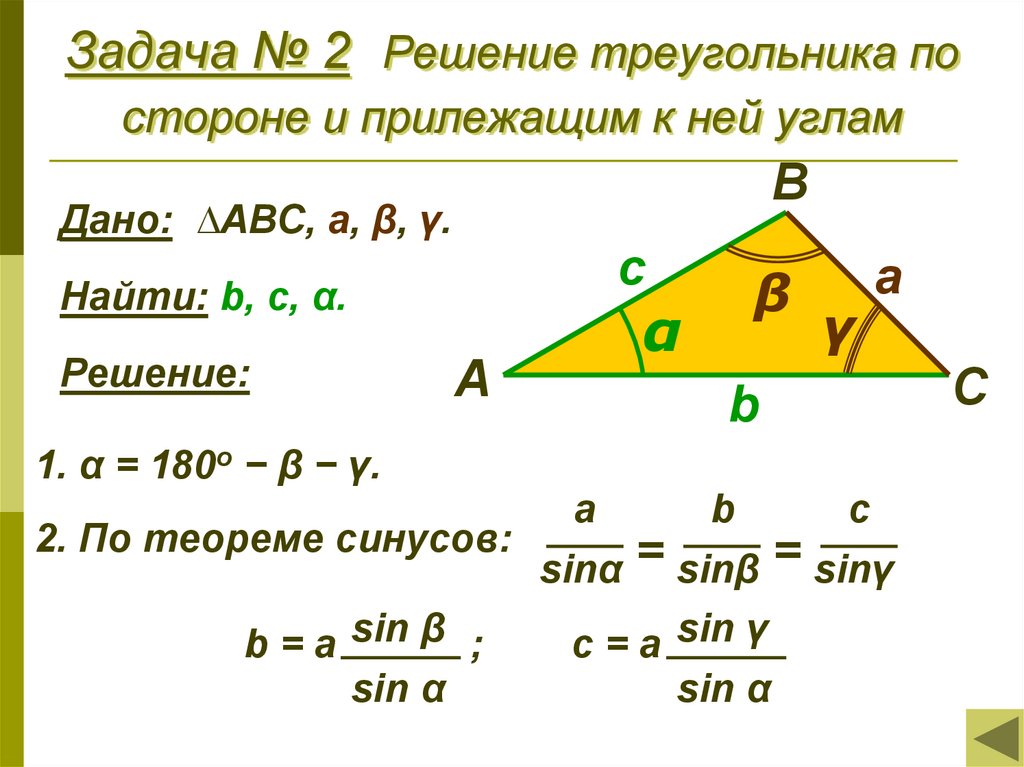 Это потому, что
самая длинная сторона будет напротив наибольшего угла, вторая самая длинная сторона будет напротив
второй по величине угол и самая короткая сторона напротив наименьшего угла. Мы знаем треугольник
имеет только 180 градусов и что гипотенуза должна быть самой длинной стороной, потому что самая большая
что в прямоугольном треугольнике может быть угол, отличный от прямого, равен 89.999. Итак, поскольку
прямой угол равен 90 градусов, а наибольший угол, который может быть равен 89,999, чем прямой
сторона напротив прямого угла должна быть самой длинной стороной, также известной как гипотенуза.
Зная это, можете ли вы сказать мне, является ли длина гипотенузы 15 или 7?
Это потому, что
самая длинная сторона будет напротив наибольшего угла, вторая самая длинная сторона будет напротив
второй по величине угол и самая короткая сторона напротив наименьшего угла. Мы знаем треугольник
имеет только 180 градусов и что гипотенуза должна быть самой длинной стороной, потому что самая большая
что в прямоугольном треугольнике может быть угол, отличный от прямого, равен 89.999. Итак, поскольку
прямой угол равен 90 градусов, а наибольший угол, который может быть равен 89,999, чем прямой
сторона напротив прямого угла должна быть самой длинной стороной, также известной как гипотенуза.
Зная это, можете ли вы сказать мне, является ли длина гипотенузы 15 или 7?
Ученик: Должно быть 15.
Наставник: Верно, поскольку 15 явно длиннее 7, теперь вы можете решить для другой ноги?
Ученик: Ну, это было бы 7 2 это 49 и 15 2 равно 225. Таким образом, это будет 49+B.


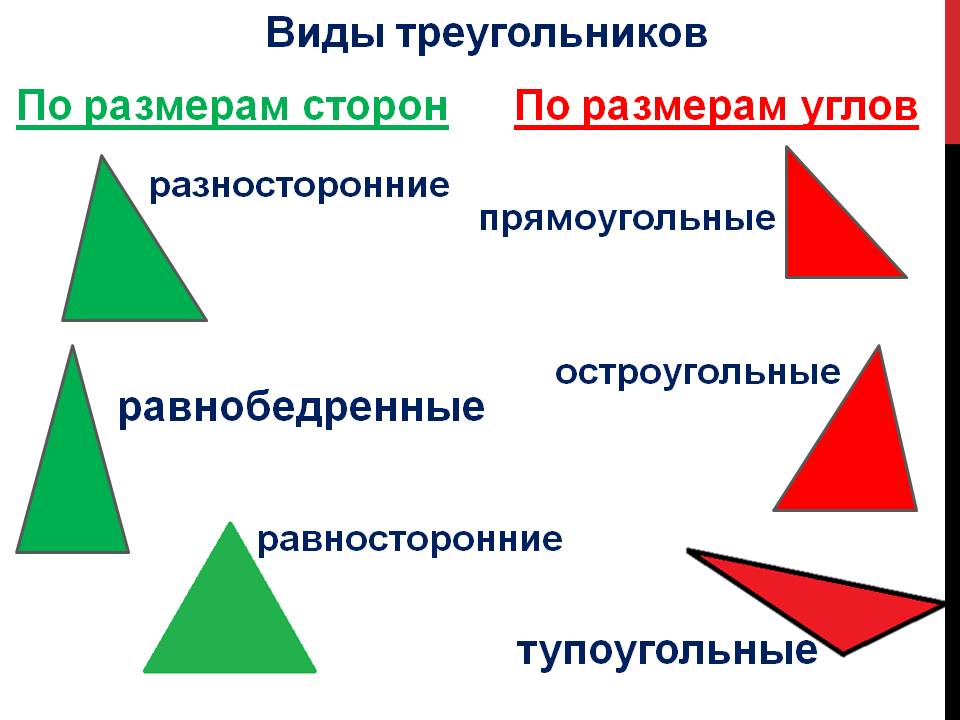




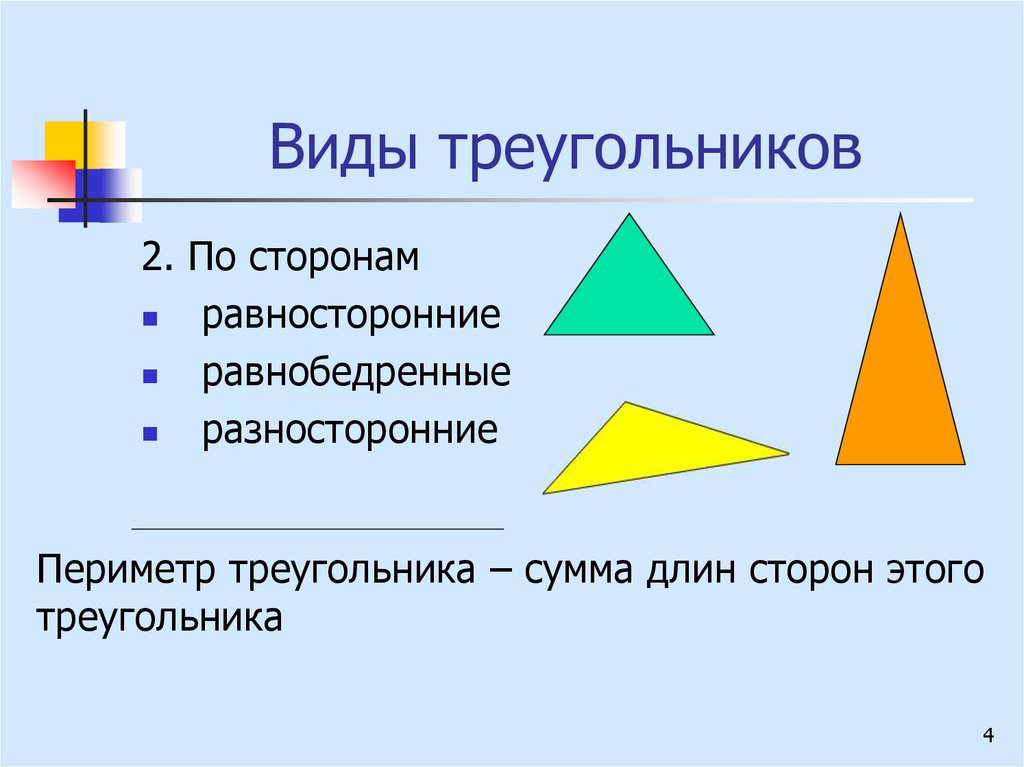 Самаров
Самаров В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.
В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
 Точка, из
которой проведена часть прямой, называется
началом луча.
Точка, из
которой проведена часть прямой, называется
началом луча.
 Запишите натуральные числа, которые лежат на координатном луче (числовом луче) между числами 995 и 1003. 4. Выразите в метрах: 3 км, 2 км 300 м, 1 км 50 м, 5 км 205 .
Запишите натуральные числа, которые лежат на координатном луче (числовом луче) между числами 995 и 1003. 4. Выразите в метрах: 3 км, 2 км 300 м, 1 км 50 м, 5 км 205 .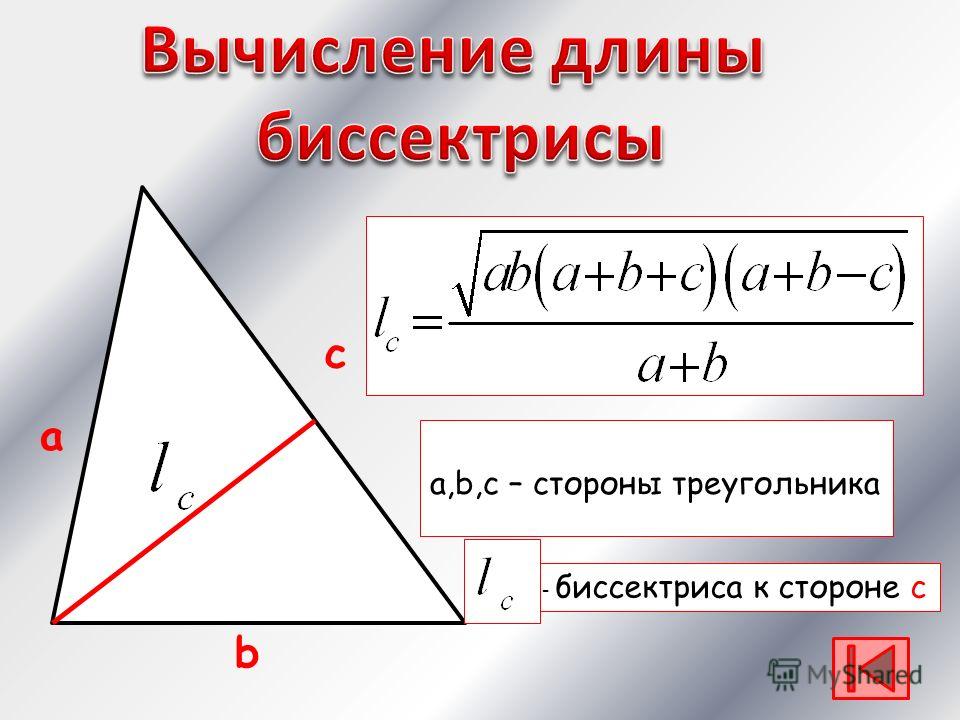 Запишите натуральные числа, которые лежат на координатном луче (числовом луче) между числами 995 и 1003.
Запишите натуральные числа, которые лежат на координатном луче (числовом луче) между числами 995 и 1003.


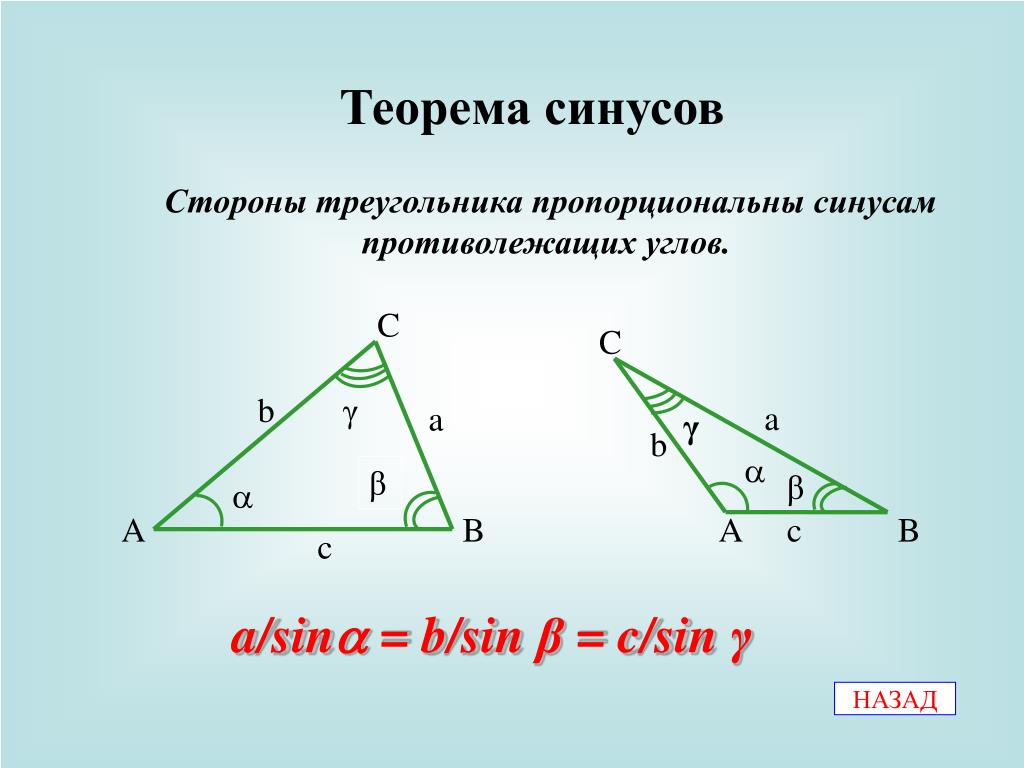
 Итак, у нас
Итак, у нас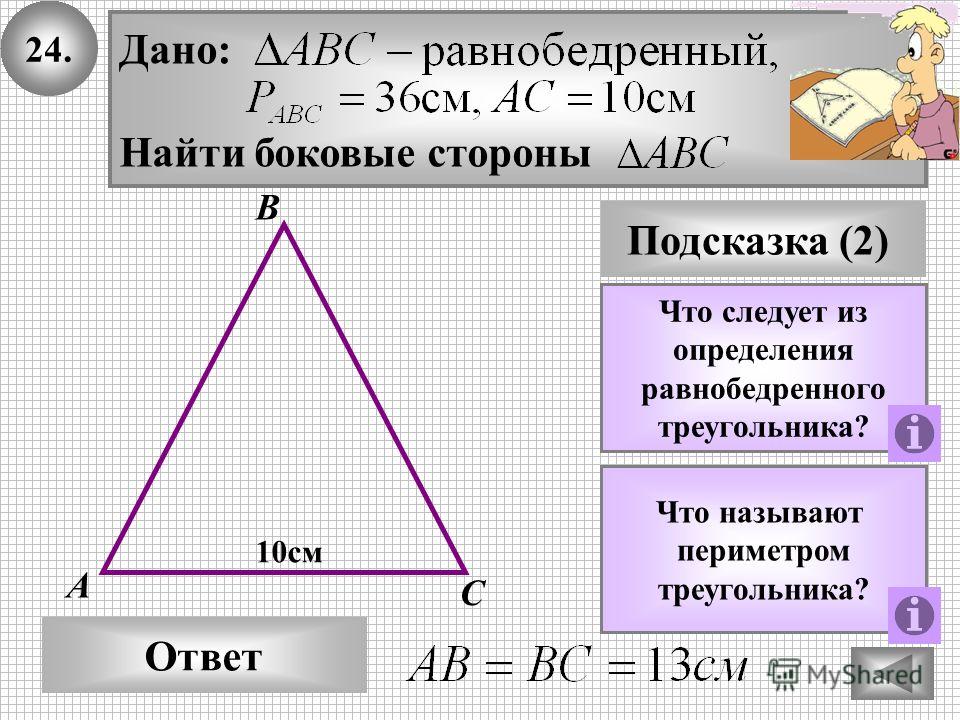
 Выберите нужный вариант из выпадающего списка . Это третий.
Выберите нужный вариант из выпадающего списка . Это третий.