Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выраженияНайдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выраженияВычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выраженияСколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выраженияНайдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выраженияВычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выраженияНайдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выраженияНайдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выраженияНужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения- Корни, степени, логарифмы и т.

- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выраженияВычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.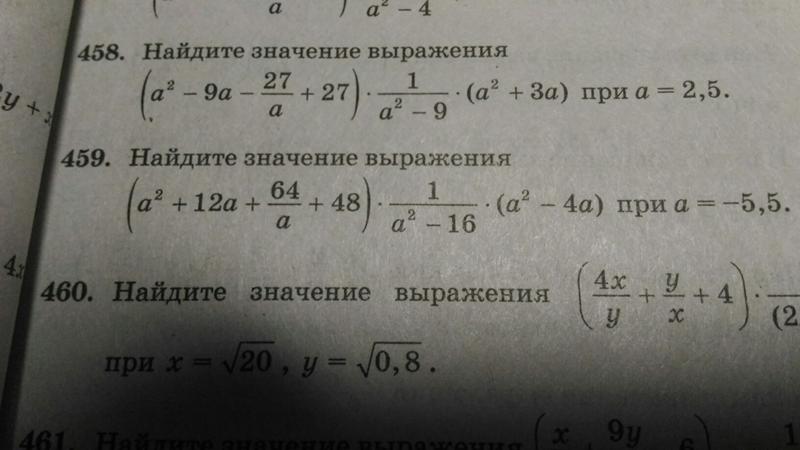
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными Пример 15. Значение выражения с переменными
Пример 15. Значение выражения с переменнымиВычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Найдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выраженияВычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выраженияСколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Найдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выраженияВычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.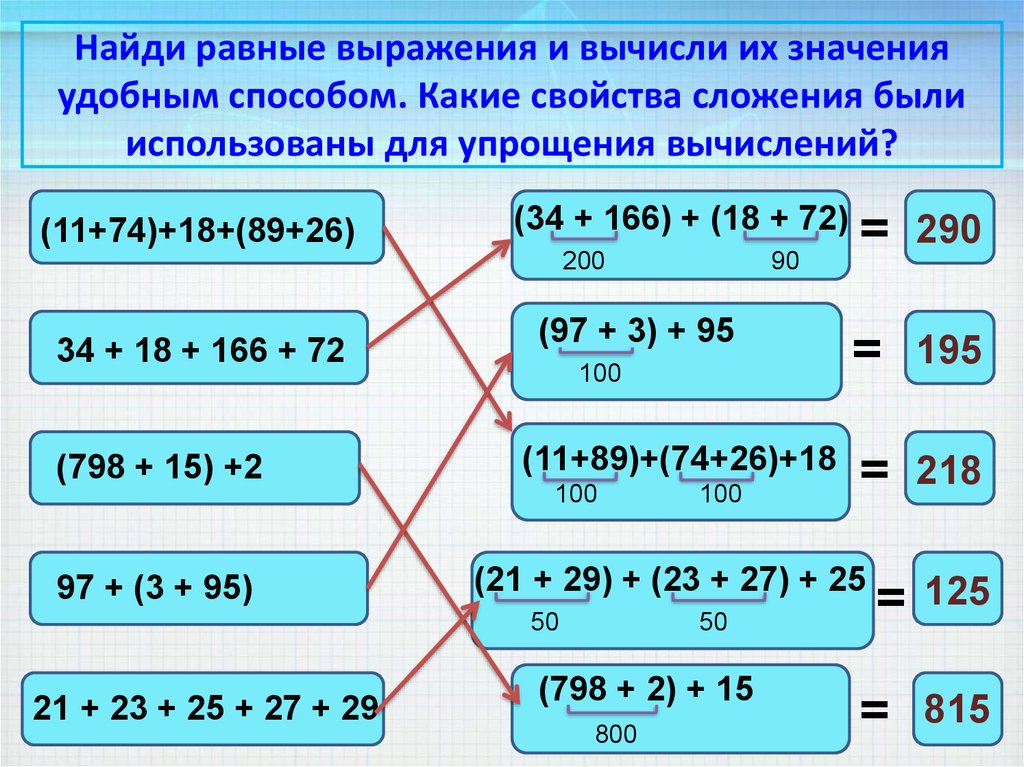
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выраженияНайдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выраженияВычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выраженияНайдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выраженияНайдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Поясним на примере.
Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выраженияВычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменнымиЧтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменнымиВычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выраженияНайдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Вычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выраженияВычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выраженияСколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выраженияНайдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выраженияВычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выраженияВычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выраженияНайдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Найдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выраженияНужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Сформулируем общее правило нахождения значений таких выражений.
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выраженияВычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Пример 15. Значение выражения с переменнымиВычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.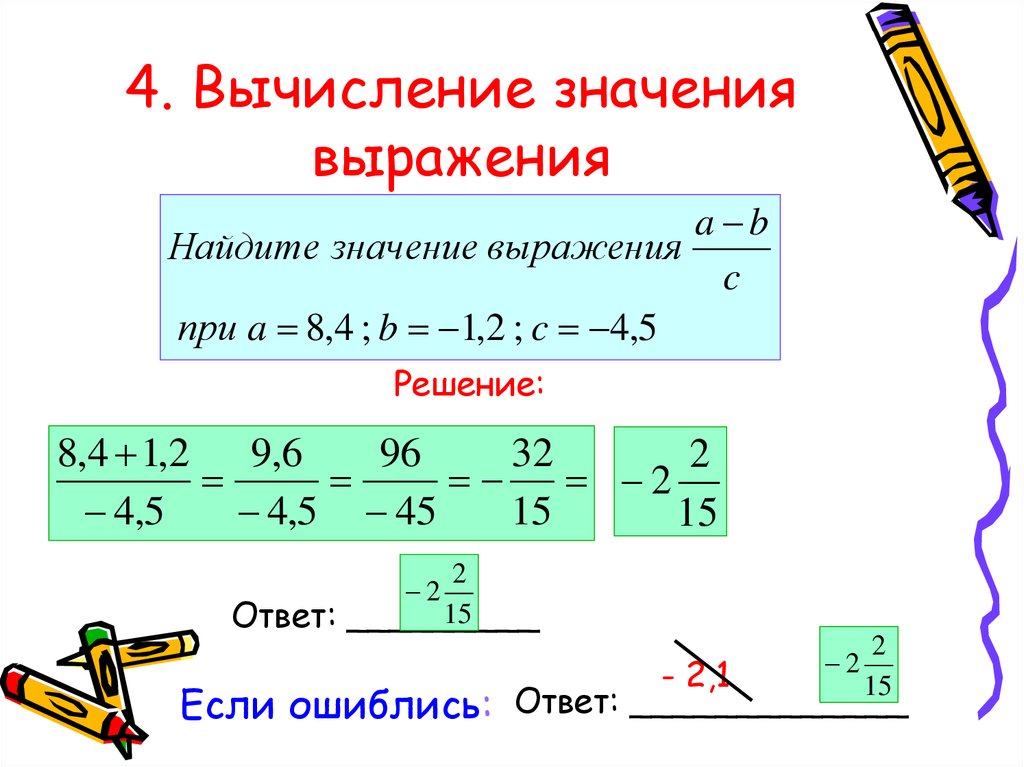
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+1318=141318.
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выраженияНайдем значение выражения 0,5·(0,76-0,06).
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0,5·(0,76-0,06)=0,5·0,7=0,35.
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выраженияВычислим значение 1+2·1+2·1+2·1-14.
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1+2·1+2·1+2·1-14=1+2·1+2·1+2·34
1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выраженияВычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.
Сначала вычисляем подкоренные выражения.
-2·3-1+60÷43=-6-1+153=83=2
2,2+0,1·0,5=2,2+0,05=2,25=1,5.
Теперь можно вычислить значение всего выражения.
-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выраженияСколько будет 3+13-1-1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
Однако, в данном случае можно применить формулу сокращенного умножения.
3+13-1=3-1.
Таким образом:
3+13-1-1=3-1-1=1.
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выраженияНайдем значение выражения 23·4-10+161-123,5-2·14.
Начинаем вычислять по порядку.
23·4-10=212-10=22=4
16·1-123,5-2·14=16*0,53=16·18=2.
Осталось только провести операцию сложение и узнать значение выражения:
23·4-10+161-123,5-2·14=4+2=6.
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выраженияВычислим значение следующего выражения: 2-25·45-1+3136.
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
Упростим исходное выражение, чтобы найти его значение.
2-25·45-1+3136=2-25·225-1+313·6
2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32
22·5-2-25+32=2-2+3=14+3=314
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выраженияНайдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3,22=3,2÷2=1,6
7-2·36=7-66=16
1+2+39-6÷2=1+2+39-3=66=1.
Перепишем наше выражение и вычислим его значение:
1,6-3·16÷1=1,6-0,5÷1=1,1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Вычислим выражение 25-1-25-74-3.
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
25-1=25+15-15+1=25+15-1=25+24
Исходное выражение принимает вид:
25-1-25-74-3=25+24-25-74-3.
Вычислим значение этого выражения:
25+24-25-74-3=25+2-25+74-3=94-3=-34.
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:
Имеем:
log5-6÷352+2+7=log327+7=3+7=10.
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выраженияНайдем значение выражения log2log2256+log62+log63+log5729log0,227.
log2log2256=log28=3.
По свойству логарифмов:
log62+log63=log6(2·3)=log66=1.
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.
Теперь можно переходить к вычислению значения исходного выражения.
log2log2256+log62+log63+log5729log0,227=3+1+-2=2.
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выраженияНайдите значение выражения: tg24π3-sin-5π2+cosπ.
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
tg4π3=3
sin-5π2=-1
cosπ=-1.
Подставляем значения в выражение и вычисляем его значение:
tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выраженияНужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения- Корни, степени, логарифмы и т.
 д. заменяются их значениями.
д. заменяются их значениями. - Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Разберем пример.
Пример 14. Значение числового выраженияВычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π
Теперь можно узнать значение синуса:
sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.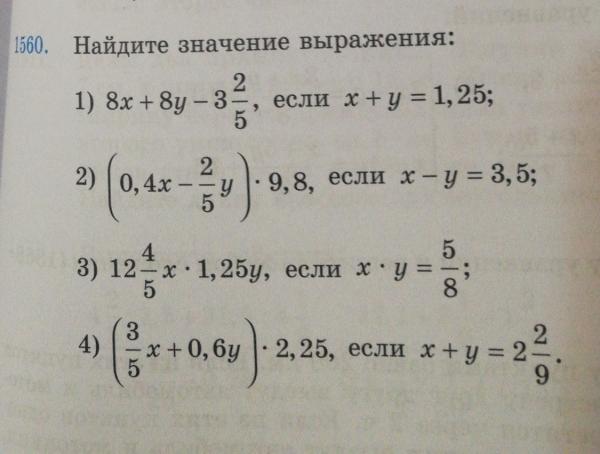
Вычисляем значение подкоренного выражения:
2·sinπ6+2·2π5+3π5+3=2·12+3=4
Отсюда:
2·sinπ6+2·2π5+3π5+3=4=2.
Со знаменателем дроби все проще:
lne2=2.
Теперь мы можем записать значение всей дроби:
2·sinπ6+2·2π5+3π5+3 lne2=22=1.
С учетом этого, запишем все выражение:
-1+1+39=-1+1+33=-1+1+27=27.
Окончательный результат:
-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменнымиЧтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.
Подставляем значения переменных в выражение и вычисляем:
0,5x-y=0,5·2,4-5=1,2-5=-3,8.
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения xx равно единице для всех положительных иксов.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как находить значение выражения 8 класс
Содержание
- Как найти значение числового выражения?
- Простейшие случаи
- Выражения со скобками
- Выражения с корнями
- Выражения со степенями
- Выражения с дробями
- Выражения с логарифмами
- Выражения с тригонометрическими функциями
- Общий случай числового выражения
- Вычисление значений выражений рациональными способами
- Нахождение значений выражений с переменными
- Информация
- Урок 1.
 Алгебра 8 класс
Алгебра 8 класс - Конспект урока «Рациональные выражения»
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки » + » , » · » , » — » , » ÷ » , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14 — 2 · 15 ÷ 6 — 3 .
Выполним сначала умножение и деление. Получаем:
14 — 2 · 15 ÷ 6 — 3 = 14 — 30 ÷ 6 — 3 = 14 — 5 — 3 .
Теперь проводим вычитание и получаем окончательный результат:
14 — 5 — 3 = 9 — 3 = 6 .
Вычислим: 0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 .
Сначала выполняем преобразование дробей, деление и умножение:
0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12
1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 · 4 11 · 11 12 = 1 2 — ( — 14 ) + 2 9 .
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
1 2 — ( — 14 ) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0 , 5 · ( 0 , 76 — 0 , 06 ) .
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0 , 5 · ( 0 , 76 — 0 , 06 ) = 0 , 5 · 0 , 7 = 0 , 35 .
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 .
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4
1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями — 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .
Сначала вычисляем подкоренные выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 = — 6 — 1 + 15 3 = 8 3 = 2
2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .
Теперь можно вычислить значение всего выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3 + 1 3 — 1 — 1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3 + 1 3 — 1 = 3 — 1 .
3 + 1 3 — 1 — 1 = 3 — 1 — 1 = 1 .
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 .
Начинаем вычислять по порядку.
2 3 · 4 — 10 = 2 12 — 10 = 2 2 = 4
16 · 1 — 1 2 3 , 5 — 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .
Осталось только провести операцию сложение и узнать значение выражения:
2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 = 4 + 2 = 6 .
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2 — 2 5 · 4 5 — 1 + 3 1 3 6 .
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2 — 2 5 · 4 5 — 1 + 3 1 3 6 = 2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6
2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6 = 2 — 2 5 · 2 2 · 5 — 2 + 3 2 = 2 2 · 5 — 2 — 2 5 + 3 2
2 2 · 5 — 2 — 2 5 + 3 2 = 2 — 2 + 3 = 1 4 + 3 = 3 1 4
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3 , 2 2 — 3 · 7 — 2 · 3 6 ÷ 1 + 2 + 3 9 — 6 ÷ 2 .
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6
7 — 2 · 3 6 = 7 — 6 6 = 1 6
1 + 2 + 3 9 — 6 ÷ 2 = 1 + 2 + 3 9 — 3 = 6 6 = 1 .
Перепишем наше выражение и вычислим его значение:
1 , 6 — 3 · 1 6 ÷ 1 = 1 , 6 — 0 , 5 ÷ 1 = 1 , 1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 2 5 — 1 — 2 5 — 7 4 — 3 .
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
2 5 — 1 = 2 5 + 1 5 — 1 5 + 1 = 2 5 + 1 5 — 1 = 2 5 + 2 4
Исходное выражение принимает вид:
2 5 — 1 — 2 5 — 7 4 — 3 = 2 5 + 2 4 — 2 5 — 7 4 — 3 .
Вычислим значение этого выражения:
2 5 + 2 4 — 2 5 — 7 4 — 3 = 2 5 + 2 — 2 5 + 7 4 — 3 = 9 4 — 3 = — 3 4 .
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 — 6 ÷ 3 5 2 + 2 + 7 . Имеем:
log 5 — 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .
log 2 log 2 256 = log 2 8 = 3 .
По свойству логарифмов:
log 6 2 + log 6 3 = log 6 ( 2 · 3 ) = log 6 6 = 1 .
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 — log 5 27 = — log 27 729 = — log 27 27 2 = — 2 .
Теперь можно переходить к вычислению значения исходного выражения.
log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + — 2 = 2 .
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: t g 2 4 π 3 — sin — 5 π 2 + cosπ .
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
t g 2 4 π 3 — sin — 5 π 2 + cosπ = 3 2 — ( — 1 ) + ( — 1 ) = 3 + 1 — 1 = 3 .
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 .
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 = cos 2 π 8 cos 5 π 36 + π 9 — 1 = cos π 4 cos π 4 — 1 = 1 — 1 = 0 .
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо.
 Сначала — умножение и деление, затем — сложение и вычитание.
Сначала — умножение и деление, затем — сложение и вычитание.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения — 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .
С учетом этого, запишем все выражение:
— 1 + 1 + 3 9 = — 1 + 1 + 3 3 = — 1 + 1 + 27 = 27 .
— 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 — 3 , 789 ln e 2 — 56 + 8 — 3 , 789 ln e 2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 2 3 — 1 5 + 3 · 289 · 3 4 3 · 2 3 — 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0 , 5 x — y при заданных x = 2 , 4 и y = 5 .
Подставляем значения переменных в выражение и вычисляем:
0 , 5 x — y = 0 , 5 · 2 , 4 — 5 = 1 , 2 — 5 = — 3 , 8 .
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х + 3 — х , очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.
Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© adminreshak.ru
Урок 1. Алгебра 8 класс
Конспект урока «Рациональные выражения»
На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.
Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.
Дробное выражение при некоторых значениях переменных может не иметь смысла.
Чтобы найти значение рационального выражения, надо:
1) подставить числовое значение переменной в данное выражение;
2) выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.
Как вы уже знаете, выражение вида называется дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Найдите значение дроби.
Найдите допустимые значения переменной в выражениях:
Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.
В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.
Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.
Чтобы найти значение рационального выражения, надо:
1) Подставить числовое значение переменной в данное выражение;
2) Выполнить все действия.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
Значение переменной a подставляется в исходное выражение.В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомните второй урок «Основные операции». Чтобы понять сложение мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия.
В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения 5 + x при x = 4
Найдите значение выражения 5 + x при x = 4
Показать решение
Задание 2. Найдите значение выражения a + 3 при a = 7
Показать решение
Задание 3. Найдите значение выражения a + a + a при a = 10
Показать решение
Задание 4. Найдите значение выражения a + b при a = 10 и b = 20
Показать решение
Задание 5. Найдите значение выражения b + b + b при b = 5
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
переменных выражений | Определение, примеры решений, вопросы
Содержание
1. | Введение в переменные выражения |
| 2. | Определение постоянной переменной, члена и коэффициента |
| 3. | Переменное выражение (алгебраическое выражение) |
| 4. | Типы переменных выражений |
| 5. | Нестандартное мышление! |
| 6. | Упражнение по вычислению переменных выражений |
| 7. | Решенные примеры для переменных выражений |
| 8. | Спорные вопросы по выражениям переменных |
| 9. | Практические вопросы по выражениям переменных |
| 10. | Важные темы |
| 11. | Образцы заданий олимпиады по математике |
| 12. | Часто задаваемые вопросы (FAQ) |
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на «почему», стоящем за «что». Учащиеся могут изучить огромное количество интерактивных рабочих листов, визуальных материалов, симуляций, практических тестов и многого другого, чтобы глубже понять концепцию.
Учащиеся могут изучить огромное количество интерактивных рабочих листов, визуальных материалов, симуляций, практических тестов и многого другого, чтобы глубже понять концепцию.
Запишитесь на БЕСПЛАТНОЕ пробное занятие уже сегодня! и участвуйте в LIVE онлайн-классе Cuemath вместе со своим ребенком.
Введение в переменные выраженияДжеймс и Натали играли со спичками и придумали составлять из них узоры из чисел.
Джеймс взял 4 спички и составил число \(4\)
Натали добавила еще 3 спички, чтобы сформировать узор из двух \(4\)s.
Затем Джеймс снова добавил еще 3 спички, чтобы сформировать узор из трех \(4\)s.
Внезапно Натали засомневалась, сколько нужно спичек, чтобы составить узор из десяти \(4\) s?
Из существующего шаблона они поняли, что им нужно \(4+ 9 (3)\) палочек, чтобы сделать это, так как им нужен шаблон с десятью \(4\)с.
Из этого они сделали вывод, что им нужно \(4+(n-1)3\) палочек, чтобы составить узор из \(n\) числа \(4\) палочек.
Здесь \(4+(n-1)3\) называется алгебраическим выражением.
Определение переменной, константы, члена и коэффициента
- Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
В приведенном выше примере \(n\) является переменной, и здесь она может принимать значения \(1,2,3,…\)
Некоторые примеры переменных в математике: \(a,b, х, у, г, м, \) и т. д.
- Символ, имеющий фиксированное числовое значение, называется константой.
Все числа являются константами.
Некоторые примеры констант: \(3, 6, \dfrac{-1}{2}, \sqrt{5}\) и т. д.
- Терм представляет собой переменную отдельно (или) отдельно константу (или) он может быть комбинацией переменных и констант посредством операции умножения или деления.
Некоторые примеры терминов: \(3x^2, \dfrac{-2}{3}y, \sqrt{5m},\) и т. д.
д.
Здесь числа, умножающие переменные, равны \(3, \dfrac{-2}{3} \) и \(5\), которые называются коэффициентами .
CLUEless по математике? Узнайте, как CUEMATH Учителя объяснят вашему ребенку Variable Expressions с помощью интерактивных симуляций и рабочих листов, чтобы им больше никогда не приходилось запоминать что-либо по математике!
Исследуйте живые, интерактивные и персонализированные онлайн-классы Cuemath, чтобы ваш ребенок стал экспертом по математике. Запишитесь на БЕСПЛАТНОЕ пробное занятие сегодня!
Переменное выражение (алгебраическое выражение)
Переменное выражение (или) алгебраическое выражение представляет собой комбинацию терминов с помощью таких операций, как сложение, вычитание, умножение, деление и т. д.
Пример переменного выраженияПример переменного выражения (или) алгебраическое выражение равно \(5x + 7\)
92+2(-2)+7 &= 5(4)-4+7 \\&= 20-4+7\\&= 23\end{align}\]Итак, ответ \(23\ )
Типы переменных выражений
Существует \(5\) типов переменных выражений (или) алгебраических выражений.
| Типы | Значение | Примеры |
|---|---|---|
Одночлен | 9{-1} +2г+3г\)
Think Tank
- Всякий ли многочлен является многочленом?
- Является ли каждый многочлен многочленом?
Вот упражнение с переменными выражениями.
Здесь вы можете выбрать одно из заданных выражений переменных и указать значение(я) для его переменной(й).
Затем вы можете оценить и ввести значение решения переменного выражения в соответствии с введенными вами значениями.
Не беспокойтесь, если вы введете неверный ответ на выражение.
Он покажет вам пошаговое объяснение правильного ответа.
Помогите своему ребенку получить более высокие баллы с помощью собственного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Проведите тест сейчас.
Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Проведите тест сейчас.
Решенные примеры
| Пример 1 |
В мешке \(25\) апельсинов. Напишите переменное выражение (алгебраическое выражение) для количества апельсинов в \(x\) количестве мешков.
Решение:
Количество апельсинов в одном мешке = \(25\)
Количество мешков = \(x\)
Таким образом, количество апельсинов в \(x\) мешках = \( 25x\)
| Требуемое выражение переменной \(= 25x \) |
| Пример 2 |
Вычислите данное выражение переменной для \(a = 7; b = -3\) и \(c = 2\)
\[6ab + 7bc + 9ca\]
Решение
Данное алгебраическое выражение равно \(6ab + 7bc + 9ca\)
Подставьте следующие значения в приведенное выше выражение:
\(a = 7; \;b = -3; \; c = 2\)
\[\begin{align}6ab \!+\! 7bc \!+\! 9ca&\!=\! 6(7)(-3) \!+\! 7(-3)(2) \!+\! 9(2)(7)\\[0,3см]&\!=\!\!-\!126\!-\!42\!+\!126\\[0,3см]&\!=\!\ !-\!42\end{align}\]
| \[6ab + 7bc + 9ca = — 42 \] |
| Пример 3 |
Укажите правильный вариант(ы).
\(4x+5\) является …
(a) Одночлен
(b) Двучлен
(c) Трехчлен 92-3x+2\) в \(x=2\)
Практические вопросыВажные темы
Ниже приведены список тем, которые тесно связаны с переменными выражениями. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Сложение и вычитание
- Факторизация
Образцы заданий олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, ежегодно проводимый для школьников. Это побуждает детей развивать свои навыки решения математических задач с точки зрения конкуренции.
Вы можете БЕСПЛАТНО скачать образцы бумаг по классам ниже:
- Образец бумаги IMO Class 1
- Образец бумаги IMO Class 2
- Образец бумаги IMO, класс 3
- Образец бумаги IMO класса 4
- Образец бумаги IMO Class 5
- Образец бумаги IMO класса 6
- Образец бумаги IMO класса 7
- Образец бумаги IMO Class 8
- Образец бумаги IMO класса 9
- Образец бумаги IMO Class 10
Чтобы узнать больше об олимпиаде по математике, нажмите здесь
Часто задаваемые вопросы (FAQ)
1.
 Как написать переменное выражение?
Как написать переменное выражение?Переменное выражение зависит от условия.
Например, «\(3\) больше, чем \(x\)» можно записать как выражение переменной \(x+3\)
«\(7\) меньше, чем сумма \(a\) ) и \(b\)» можно записать как выражение переменной \(a+b-7\)
2. Что такое пример переменной?
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: \(a,b,x,y,z,m,\) и т.д.
Дополнительную информацию можно найти в разделе «Определение переменной, константы, термина и коэффициента» на этой странице.
3. Какие существуют 3 типа переменных?
3 типа переменных:
- Независимые переменные
- Зависимые переменные
- Контролируемые переменные
4. Всегда ли выражения должны иметь переменную?
Нет, выражение не обязательно должно иметь переменную.
Например, такие константы, как \(2, -3, \dfrac{-3}{4}\), также называются выражениями.
5. Как определить переменную?
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: \(a,b,x,y,z,m,\) и т. д.
6. Что такое переменная? Приведите пример.
Символ, который не имеет фиксированного значения, в математике называется переменной. Может принимать любое значение.
Некоторые примеры переменных в математике: \(a,b,x,y,z,m,\) и т.д.
Оценка: вычисление выражений и многочленов
Функции
Purplemath
Что такое «оценка» в математике?
«Оценка» в основном означает «упрощение выражения до одного числового значения». Иногда вам будет дано числовое выражение, которое вам нужно будет только упростить; это скорее вопрос порядка операций. В этом уроке я сконцентрируюсь на аспекте оценки «подключи и пыхти»: подставляя значения для переменных и «пыхтя» мой путь к упрощенному ответу.
Содержимое продолжается ниже
MathHelp.
 com
comВычисление выражений
(Кстати, да, «подключи и пыхни» — довольно стандартная терминология. Это не «технический» термин, так что вы, вероятно, не увидите это есть в вашем учебнике, но вы наверняка услышите это от других учеников и, возможно, от своего преподавателя.)
Обычно единственной сложной частью оценивания является отслеживание знаков «минус». Я настоятельно рекомендую вам широко использовать круглые скобки, особенно когда вы только начинаете.
Что является примером оценки?
Чтобы найти ответ, я просто подставляю заданные значения, стараясь использовать круглые скобки, особенно вокруг знаков «минус». Особенно, когда я только начинаю, может быть полезно сначала нарисовать круглые скобки:
a 2 b
( ) 2 ( )
3 (−2) 906(4)(3)
12
Обратите внимание, как использование круглых скобок помогло мне отслеживать знак «минус» в значении и . Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2 и получить -4, что было бы неправильно.
Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2 и получить -4, что было бы неправильно.
Кстати, оказалось, что значения переменных c и d нам не нужны. Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будет та или иная переменная, которая не будет включена ни в одно конкретное упражнение в наборе.
В этом упражнении мне дали дополнительную информацию. нет b в выражении, которое они хотят, чтобы я оценил, поэтому я могу игнорировать это значение в своей работе:
(−2) − (−4)(4)
−2 − (−16)
−2 + 16
16 − 2
14
Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Показатели НЕ распределяются по сложению! Я никогда не должен пытаться сказать, что ( b + d ) 2 то же самое, что b 2 + d 2 906:30 . Это НЕ одно и то же! Я должен вычислить выражение в его нынешнем виде:
( (3) + (4) ) 2
( 7 ) 2
49
В этом выражении возведение в квадрат производится для каждой переменной отдельно.
(3) 2 + (4) 2
9 + 16
25
Обратите внимание, что этот последний ответ выше не соответствует ответу на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели степени не распределяются при сложении так, как это происходит при умножении.
На следующем тесте, а также на выпускном экзамене следует ожидать как минимум упражнения, аналогичные двум предыдущим. Эта склонность пытаться распределять показатель степени (а не умножение) над сложением является распространенной ошибкой учащихся, и ваш преподаватель почти наверняка захочет напоминать вам — и часто! — о разнице между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!
В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным в своем размещении, потому что это выражение не использует переменные в алфавитном порядке.
(3)(−4) 3 − (−2)(4)
(3)(−64) − (−8)
−192 + 8
−184
Самые общий тип «выражения», который вам, вероятно, потребуется оценить, будет полиномом. Чтобы вычислить полином, вы берете этот полином и подставляете переменную (обычно x ) в любое число, которое они вам дали.
Чтобы вычислить полином, вы берете этот полином и подставляете переменную (обычно x ) в любое число, которое они вам дали.
Какой пример вычисления многочлена?
Это мой первый многочлен для оценки, поэтому я снова начну с пустых скобок, показывающих, где нужно разместить значение переменной.
x 4 + 3 x 3 − x 2 + 6
( ) 4 + 3( ) 3 − ( ) 2 + 6
( −3) 4 + 3(−3) 3 − (−3) 2 + 6
81 + 3(−27) − (9) + 6
81 − 81 − 9 + 6
−3
Я рад, что научился использовать круглые скобки, чтобы сделать свои замены понятными. В этом случае эти скобки помогут мне отслеживать знаки «минус».
3(−2) 2 − 12(−2) + 4
3(4) + 24 + 4
12 + 24 + 4
40
Это другое. Мне дали уравнение с двумя переменными, но дали значение только одной из переменных. Я предполагаю, что они хотят, чтобы я подключил x и вычислил результирующее значение для y .
Я предполагаю, что они хотят, чтобы я подключил x и вычислил результирующее значение для y .
y = 4(−1) − 3
= −4 − 3 = −7
Тогда мой ответ будет уравнением:
y = −7
Примечание. В этом последнем упражнении выше мы подставляли значение одной из переменных и упрощали поиск значения другой переменной. Кроме того, часть, к которой мы подключались, была установлена равной имени, y . Из-за этого мы не просто вычисляли выражение; на самом деле мы оценивали полиномиальную функцию. Результат нашей операции plug-n-chug означает, что точка ( x , y ) = (−1, −7) находится на прямой y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных (или пропустите виджет и перейдите на следующую страницу). Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/evaluate.htm
Страница 2
Вычисление алгебраических выражений,… Пошаговое решение математических задач
3.1 Вычисление алгебраических выражений6 Тот же набор правил для порядка операций с целыми числами, который обсуждался в
Разделе 1.2, также используется с целыми числами. Правила изложены здесь для удобства справки по
.
Правила порядка выполнения операций
1. Работайте с символами включения (круглые, квадратные или фигурные скобки), начиная с самой внутренней пары. 92 = 8 ÷ 4-9 показателей
= 2-9 деление
= -7 Вычитание
2. (7+8) ÷ 5*4-20
(7+8) ÷ 5*4-20
(7+8) ÷ 5*4-20 = 15 ÷ 5*4-20 Сложений
= 3*4-20 Разделение
= 12-20 Умножение
= -8 Вычитание
3. 4*5- (6*2-3)+4 ÷ 2
4*5-(6*2-3)+4÷2=4*5-(9)+4÷2 круглые скобки
=20-9+2 0083
= 13 вычитание и добавление
4. (-5-6)/11+3 (-5)
(-5-6)/11+3 (-5) =-11/11+3 (— 5) Дробная полоса является символом включения
= -1+(-15) Разделение и умножение
= -16 Дополнение
Практическая викторина
| Вопросы | Ответы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найти значение каждого выражения 92 не являются той же степенью х. Числовая часть термина называется коэффициентом переменной или переменных в термине. Таким образом, в термине 8x,8 является коэффициентом x. Выражения с одинаковыми членами можно упростить, применив свойство дистрибутивности, обсуждавшееся в разделе 1. a(b+c)=ab+ac или ab+ac=a(b+c) или ba+ca=(b+c)a полезно, когда b и c являются числовыми коэффициентами. Например, 3x+5x=(3+5)x Коэффициенты складываются =8x Мы говорим, что 3x и 5x были объединены как слагаемые или что мы объединили 3x и 5x. Одинаковые члены можно комбинировать, добавляя (или вычитая) коэффициенты. Примеры Комбинируйте одинаковые термины, когда это возможно -7)+5(x+1)=4x-28+5x+5 Использовать распределительное свойство дважды. =4x+5x-28+5 92+2a 5. (x+3x)/2+x=(4x)/2+x Дробная черта — это символ включения, подобный скобкам. =2x+x=3x Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решите похожую задачуВведите свою задачу
3. Алгебра — это язык математики, и чтобы понимать математику, вы должны понимать язык. Мы хотим иметь возможность превращать английские фразы в их «алгебраические» эквиваленты и наоборот. Итак, если задача сформулирована на английском языке, мы можем перевести фразы в алгебраические символы и приступить к решению задачи по правилам, разработанным для алгебры. Следующие примеры иллюстрируют, как некоторые ключевые слова могут быть переведены в алгебраические символы. Примеры
Некоторые слова, например, выделенные жирным шрифтом в предыдущих примерах, являются ключами к операциям. Научитесь искать эти слова и слова из следующего списка.
Следует особо отметить слова «частное» и «разность». Как показано в задачах 3 и 6 практического теста, деление и вычитание выполняются со значениями в том порядке, в котором они даны в задаче. Например, разница между 3 и 5 равна 3-5=-2, а разница между 5 и 3 равна 5-3=2. 3.4 Решение уравнения Если уравнение содержит переменную, мы хотим найти значение (или значения) для переменной, которое даст истинное уравнение при замене переменной. Это значение (или значения) называется решением уравнения, и мы решили уравнение. Предположим, нам дано уравнение 2x-1 = x+3 , если мы заменим x = 4, то 2*4-1 = 7 и 4+3 = 7 SO 2*4-1 =4+3 и x=4 является решением Если мы подставим x=5, то 2*5-1=9 и 5+3=8 но 9!=8, * так что *! =5+3 и x=5 не является решением. Два уравнения эквивалентны, если они имеют абсолютно одинаковые решения. Например, 2x-1 = x+3 и x+1=5 эквивалентны, поскольку x=4 является решением каждого уравнения. Нам нужны некоторые процедуры, которые позволят нам шаг за шагом находить решения уравнений, содержащих переменные. Следующие две идеи являются основными. 1. Все, что делается с одной частью уравнения, должно быть сделано и с другой. 2. Цель состоит в том, чтобы найти простое уравнение, такое как x=4, которое эквивалентно исходному уравнению. В следующих примерах каждое уравнение решается поэтапно с объяснением каждого шага. Внимательно изучите каждый пример. Обратите внимание, что эквивалентные уравнения записываются одно под другим. Не пишите несколько уравнений в одной строке и не приравнивайте одно уравнение к другому уравнению. Примеры 1. x+7=12 Запишите уравнение. x+7-7=12-7 Добавить -7 к обеим сторонам x=5 Упрощение. 2. 2x-3=13 Запишите уравнение. 2x-3+3=13+3 Добавьте 3 к обеим сторонам. 2x=16 Упрощение. (2x)/2=16/2 Поделите обе части на 2, коэффициент при x. x=8 Упрощение. 3. 5x-1=-11 Запишите уравнение. 5x-1+1=-11+1 Добавьте +1 к обеим сторонам. 5x=-10 Упростить; теперь на одной стороне есть все термы с переменными и только термы с переменными. (5x)/5=-10/5 Поделите обе части на 5, коэффициент при x. x=-2 Упростите 4. 4x+1-x=13+x Запишите уравнение. 3x+1=13+x Упростить 3x+1-1=13+x-1 Добавить -1 к обеим сторонам. 3x=12+x Упростить 3x-x=12+x-x Добавить -x к обеим сторонам. 2x=12 Упрощение; теперь на одной стороне есть все термы с переменными и только термы с переменными. (2x)/2=12/2 Поделите обе части на 2, коэффициент при x. x=6 Упростить 5. (2x)/5+2=6 Запишите уравнение. (2x)/5+2-2=6-2 Добавьте -2 к обеим сторонам. (2x)/5 = 4 упростите 5*(2x)/5 = 4*5 Умножить обе стороны на 5. 2x = 20 Упрощение (2x)/2 = 20/2 Разделите обе стороны 2 x=10 Упрощение Давайте посмотрим, как наш решатель уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решите похожую задачуВведите свою задачу Каждое решение можно проверить, подставив его в исходное уравнение. Если выражение, представляющее ненулевое число, (а) прибавить, (б) разделить или (в) умножить на обе части уравнения, новое уравнение будет эквивалентно исходному уравнению. 3.5 Формулы Формулы — это общие правила или принципы, сформулированные математически. Например, в бизнесе простые проценты — это произведение основного долга, процентной ставки и времени в годах. Таким же правилом математически является формула {Iota}=PRT. Другие формулы приведены ниже. 92 Площадь (A) круга равна произведению PI на квадрат радиуса (r). p=4s Периметр (p) квадрата в 4 раза больше длины одной стороны (s). A=1/2bh Площадь (A) треугольника равна половине произведения основания (b) и высоты (h). d=rt Пройденное расстояние равно произведению скорости (r) и времени (t). C=5/9(F-32) Температура в градусах Цельсия (C) равна 5/9 разницы между температурой по Фаренгейту (F) и 32, В последней формуле предположим, что F = 212°, температура кипения воды на уровне моря. C=5/9(212-32)=5/9(180)=100 Предположим, что вопрос поставлен наоборот. Если C = 20°, каково будет соответствующее значение F? Подстановка 20 вместо C и решение для F дает 20=5/9(F-32) 20*9/5=9/5*5/9(F-32) Умножьте обе части на 9/5, взаимный 5/9. 36 = F-32 68 = F Решение для F с точки зрения C может быть сделано следующим образом: C = 5/9 (F-32) 9/5*C = 9 /5*5/9(F-32) 9/5C=F-32 9/5C+32=F Формула для C: и решено для F равно F=9/5C+32 Цель здесь состоит в том, чтобы решить формулы для одной из переменных в терминах других переменных. То есть, используя методы решения уравнений, которые имеют только одну переменную, рассматривайте другие переменные как константы и находите нужную переменную. Примеры 1. Найти b. Решение: P = A+B+C P-A-C = A+B+C-A-C P-A-C = B 2. Приведенный P = 2L+2w Formul прямоугольник Найти l Решение: P=2l+2w P-2w=2wl0083 P-2W = 2L (P-W)/2 = (2L)/2 (P-2W)/2 = L или P = 2L+W P/2 = (2L+ 2w)/2 P/2=(2l)/2+(2w)/2 P/2=l+w P/2-w=l Оба ответа верны, поскольку P/2- w=P/2-(2w)/2=(P-2w)/2 3. Учитывая 3y-4x+9=0, найдите y. Решение: 3y-4x+9 = 0 3y-4x+9+4x-9 = 0+4x-9 3y = 4x-9 y = (4x-9)/3 или y=(4x)/3-9/3=4/3x-3 Любая из этих форм верна. Если у вас есть один ответ, а другой находится в ключе ответов, вы должны признать свой ответ правильным, но в другой форме. Давайте посмотрим, как наш решатель уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Решить похожую задачуВведите свою задачу Решение: V=T/(P-5) V(P-5)=T/(P-5)(P-5) Умножьте обе части на P-5. V(P-5)=T (V(P-5))/V=T/V P-5=T/V P=T/V+5 3 900 задачи (Числа и последовательные целые числа) В разделе 3.3 мы обсуждали перевод английских фраз в алгебраические выражения. Фраза «8, добавленная к удвоенному числу» алгебраически переводится как 2x + 8. Как вы переводите «на 4 больше, чем число?» Если вы сказали x + 4, вы правы. Теперь цель состоит в том, чтобы перевести целое предложение в уравнение, а затем решить уравнение. Две приведенные выше фразы могут быть включены в предложение, подобное следующему: Алгебраически, 2x+8 = x+4 «Результат« переводится как = Решение, 2x+8 = x+4 2x+8-x = x+4-x x +8=4 x+8-8=4-8 x=-4 В этом разделе словесные задачи будут просто упражнениями на перевод предложений в уравнения и решение этих уравнений. Более сложные «прикладные» проблемы будут обсуждаться в последующих главах. Такие задачи будут включать геометрические формулы, расстояние, проценты, работу, неравенства и смешение. Примеры 1. Трижды сумма числа и 5 равна удвоенному числу плюс 5. Найдите число. Решение Пусть x : неизвестное число.
Число -10. 2. Если число уменьшить на 36, и результат будет на 76 меньше, чем удвоенное число, какое это будет число? Решение Пусть n = неизвестное число.
Число 40. Последовательные целые числа — это два целых числа, которые отличаются на 1, или второе целое число на 1 больше первого. Например, 21 и 22 — последовательные целые числа. -14 и -13 — последовательные целые числа. В общем случае, если n — одно целое число, то n + 1 — это следующее последовательное целое число. Примеры: последовательные целые числа 1. Найдите три последовательных целых числа таких, что сумма первого и третьего в 76 раз меньше второго. N+(n+2) = 3 (n+1) -76 2n+2 = 3n+3- 76 2n+2 = 3n-73 2n+2+73-2n = 3n-73+73-2n 75 = N 76 = N+1 77 = N+2 Три. последовательные целые числа равны 75, 76 и 77. 2. Три последовательных нечетных целых числа таковы, что их сумма равна -3. Что такое целые числа? let n = первое нечетное целое число n+(n+2)+(n+4) =-3 3n+6 =— 3 3n = -9 n = -3 N+2 = -1 N+4 =+1 Три последовательных нечетных целых числа составляют -3, -1 и +1. Разница между выражением и уравнением (со сравнительной таблицей) В математике вы, возможно, очень часто встречали термины выражение и уравнение. Однако, если оно не содержит знака равенства (=), то это просто выражение . Он содержит числа, переменные и операторы, которые используются для отображения значения чего-либо. Прочтите эту статью, чтобы понять основные различия между выражением и уравнением. Содержание: выражение и уравнение
Сравнительная таблица
Определение выражения В математике выражение определяется как фраза, которая объединяет числа (постоянные), буквы (переменные) или их комбинации, соединенные операторами (+, -, *, /), для представления ценность чего-либо. Выражение может быть арифметическим, алгебраическим, полиномиальным и аналитическим. Поскольку он не содержит знака равенства (=), он не показывает никакой связи. Следовательно, у него нет ничего похожего на левую или правую сторону. Выражение можно упростить, объединив одинаковые термины, или его можно вычислить, вставив значения вместо переменных, чтобы получить числовое значение. Примеры : 9x + 2, x – 9, 3p + 5, 4m + 10 Определение уравненияВ математике термин уравнение означает выражение равенства. Это предложение, в котором два выражения стоят равными друг другу. Чтобы удовлетворить уравнение, важно определить значение рассматриваемой переменной; это известно как решение или корень уравнения. Уравнение может быть условным или тождественным. Если уравнение условное , то равенство двух выражений верно для определенного значения вовлеченной переменной. Однако, если уравнение представляет собой identity , то равенство верно для всех значений, хранящихся в переменной. Существует четыре типа уравнений, которые обсуждаются ниже:
Основные различия между выражением и уравнениемПункты, приведенные ниже, обобщают важные различия между выражением и уравнением:
Заключение Таким образом, из приведенного выше объяснения становится ясно, что существует большая разница между этими двумя математическими понятиями. Выражение не раскрывает никакой связи, в отличие от уравнения. Уравнение содержит знак «равно», поэтому оно показывает решение или в конечном итоге представляет значение переменной. Примеры выраженийВ этой статье представлено множество примеров выражений в Access. Выражение — это комбинация математических или логических операторов, констант, функций, полей таблицы, элементов управления и свойств, результатом которой является одно значение. Вы можете использовать выражения в Access для вычисления значений, проверки данных и установки значения по умолчанию. В этой статье г.Все выражения форм и отчетов
Все выражения запросов и фильтров
Все табличные выражения
Все выражения макроса Формы и отчеты Таблицы в этом разделе содержат примеры выражений, которые вычисляют значение в элементе управления, расположенном в форме или отчете. Примечание Вы также можете использовать выражения в форме или отчете при выделении данных с условным форматированием. Текстовые операцииВ выражениях в следующей таблице используются операторы & (амперсанд) и + (плюс) для объединения текстовых строк, встроенных функций для управления текстовой строкой или других операций с текстом для создания вычисляемого элемента управления.
Верх страницы Верхние и нижние колонтитулыВы используете свойства Page и Pages для отображения или печати номеров страниц в формах или отчетах. Свойства Страница и Страница доступны только во время печати или предварительного просмотра, поэтому они не отображаются на странице свойств формы или отчета. Как правило, вы используете эти свойства, помещая текстовое поле в раздел верхнего или нижнего колонтитула формы или отчета, а затем используя выражение, подобное показанному в следующей таблице. Дополнительные сведения об использовании верхних и нижних колонтитулов в формах и отчетах см.
Верх страницы Арифметические операцииВы можете использовать выражения для сложения, вычитания, умножения и деления значений в двух или более полях или элементах управления. Вы также можете использовать выражения для выполнения арифметических операций с датами. Например, предположим, что у вас есть поле таблицы Date/Time с именем RequiredDate. В поле или в элементе управления, привязанном к полю, выражение =[RequiredDate] — 2 возвращает значение даты/времени, равное двум дням до текущих значений в поле RequiredDate.
Примечание Если в выражении используется арифметический оператор (+, -, * и /), а значение одного из элементов управления в выражении равно NULL, результатом всего выражения будет NULL — это известно как нулевое распространение. Если какие-либо записи в одном из элементов управления, которые вы используете в выражении, могут иметь нулевое значение, вы можете избежать распространения нулевого значения, преобразовав нулевое значение в ноль с помощью функции Nz — например, =Nz([Subtotal])+Nz ([Груз]). Верх страницы Значения в других элементах управления Иногда вам нужно значение, которое существует где-то еще, например, в поле или элементе управления в другой форме или отчете. В следующей таблице перечислены примеры выражений, которые можно использовать в вычисляемых элементах управления в формах.
Выражения в следующей таблице показывают некоторые способы использования вычисляемых элементов управления в отчетах. Выражения ссылаются на свойство отчета.
Верх страницы Подсчет, сумма и средние значения Вы можете использовать тип функции, называемый агрегатной функцией, для вычисления значений для одного или нескольких полей или элементов управления. Например, вы можете рассчитать итоговую сумму группы для нижнего колонтитула группы в отчете или промежуточную сумму заказа для позиций в форме. Вы также можете подсчитать количество элементов в одном или нескольких полях или рассчитать среднее значение. Выражения в следующей таблице показывают некоторые способы использования таких функций, как Avg, Count и Sum.
Дополнительные сведения об использовании агрегатных функций и суммировании значений в полях и столбцах см. в статьях Суммирование данных с помощью запроса, Подсчет данных с помощью запроса, Отображение итогов столбца в таблице с помощью строки итогов и Отображение итоговые значения столбца в таблице данных. Верх страницы агрегатные функции SQL Вы используете тип функции, называемый функцией SQL или агрегатной функцией домена, когда вам нужно выборочно суммировать или подсчитывать значения. «Домен» состоит из одного или нескольких полей в одной или нескольких таблицах или одного или нескольких элементов управления в одной или нескольких формах или отчетах.
Верх страницы Операции с датами Отслеживание даты и времени является фундаментальной деятельностью базы данных.
Верх страницы Условия только двух значений Примеры выражений в следующей таблице используют функцию IIf для возврата одного из двух возможных значений. Вы передаете функции IIf три аргумента: Первый аргумент — это выражение, которое должно возвращать значение True или False. Второй аргумент — это значение, которое будет возвращено, если выражение истинно, а третий аргумент — это значение, которое будет возвращено, если выражение ложно.
Верх страницы Запросы и фильтрыВ этом разделе содержатся примеры выражений, которые можно использовать для создания вычисляемого поля в запросе или для предоставления критериев запроса. Вычисляемое поле — это столбец в запросе, являющийся результатом выражения. Например, вы можете вычислить значение, объединить текстовые значения, такие как имя и фамилия, или отформатировать часть даты. Вы используете критерии в запросе, чтобы ограничить количество записей, с которыми вы работаете. Например, вы можете использовать оператор «Между», чтобы указать начальную и конечную даты и ограничить результаты вашего запроса заказами, которые были отправлены между этими датами. Ниже приведены примеры выражений для использования в запросах. Текстовые операции Выражения в следующей таблице используют операторы & и + для объединения текстовых строк, используют встроенные функции для работы с текстовой строкой или иным образом работают с текстом для создания вычисляемого поля.
Верх страницы Арифметические операции Вы можете использовать выражения для сложения, вычитания, умножения и деления значений в двух или более полях или элементах управления. Вы также можете выполнять арифметические операции над датами. Например, предположим, что у вас есть поле даты/времени с именем RequiredDate. Выражение =[RequiredDate] — 2 возвращает значение даты/времени, равное двум дням до значения в поле RequiredDate.
Дополнительные сведения об использовании агрегатных функций и суммировании значений в полях и столбцах см. в статьях Суммирование данных с помощью запроса, Подсчет данных с помощью запроса, Отображение итогов столбца в таблице с помощью строки итогов и Отображение итоговые значения столбца в таблице данных. Верх страницы Операции с датамиПочти все базы данных хранят и отслеживают дату и время. Вы работаете с датами и временем в Access, устанавливая поля даты и времени в своих таблицах на тип данных Дата/Время. Access может выполнять арифметические вычисления с датами; например, вы можете рассчитать, сколько дней прошло с даты выставления счета, чтобы определить возраст вашей дебиторской задолженности.
Верх страницы агрегатные функции SQL Выражения в следующей таблице используют функции SQL (язык структурированных запросов), которые объединяют или суммируют данные. В дополнение к агрегатным функциям Access также предоставляет «доменные» агрегатные функции, которые можно использовать для выборочного суммирования или подсчета значений. Например, вы можете подсчитать только значения в определенном диапазоне или найти значение в другой таблице. Набор агрегатных функций домена включает функцию DSum, функцию DCount и функцию DAvg. Для подсчета итогов часто требуется создать итоговый запрос. Например, для суммирования по группам необходимо использовать запрос «Итоги». Чтобы включить итоговый запрос из сетки дизайна запроса, нажмите Итого в меню Просмотр .
Верх страницы Поля с отсутствующими даннымиПоказанные здесь выражения работают с полями с потенциально отсутствующей информацией, например с полями, содержащими нулевые (неизвестные или неопределенные) значения. Вы часто сталкиваетесь с нулевыми значениями, такими как неизвестная цена нового продукта или значение, которое коллега забыл добавить в заказ. Возможность находить и обрабатывать нулевые значения может быть важной частью операций с базой данных, и выражения в следующей таблице демонстрируют некоторые распространенные способы работы с нулевыми значениями.
Верх страницы Вычисляемые поля с подзапросамиВы можете использовать вложенный запрос, также называемый подзапросом, для создания вычисляемого поля. Выражение в следующей таблице является одним из примеров вычисляемого поля, полученного в результате подзапроса.
Верх страницы Совпадение текстовых значенийПримеры выражений в этой таблице демонстрируют критерии, соответствующие целым или частичным текстовым значениям.
Верх страницы Критерии даты совпаденияВыражения в следующей таблице демонстрируют использование дат и связанных функций в выражениях критериев. Дополнительные сведения о вводе и использовании значений даты см. в статье Формат поля даты и времени.
Верх страницы Найти недостающие данные Выражения в следующей таблице работают с полями, в которых потенциально может отсутствовать информация – те, которые могут содержать нулевое значение или строку нулевой длины. Нулевое значение представляет отсутствие информации; он вообще не представляет ноль или какое-либо значение.
Верх страницы Совпадение с образцом записи с лайком Оператор Like обеспечивает большую гибкость, когда вы пытаетесь сопоставить строки, соответствующие шаблону, поскольку вы можете использовать Like с подстановочными знаками и определять шаблоны для сопоставления Access.
Верх страницы Сопоставление строк с агрегатами SQL Вы используете функцию агрегирования SQL или домена, когда вам нужно выборочно суммировать, подсчитывать или усреднять значения.
Верх страницы Сопоставление полей с подзапросамиВы используете подзапрос, также называемый вложенным запросом, для вычисления значения для использования в качестве критерия. Примеры выражений в следующей таблице сопоставляют строки на основе результатов, возвращенных подзапросом.
Верх страницы Запросы на обновление Вы используете запрос на обновление для изменения данных в одном или нескольких существующих полях в базе данных. Например, вы можете заменить значения или удалить их полностью. В этой таблице показаны некоторые способы использования выражений в запросах на обновление. Вы используете эти выражения в Обновление до строки в сетке дизайна запроса для поля, которое вы хотите обновить. Дополнительные сведения о создании запросов на обновление см. в статье Создание и выполнение запроса на обновление.
Верх страницы Операторы SQL Язык структурированных запросов, или SQL, — это язык запросов, который использует Access.
Верх страницы Табличные выражения Два наиболее распространенных способа использования выражений в таблицах — присвоение значения по умолчанию и создание правила проверки. Значения поля по умолчаниюПри разработке базы данных может потребоваться назначить значение по умолчанию для поля или элемента управления. Затем Access предоставляет значение по умолчанию при создании новой записи, содержащей поле, или при создании объекта, содержащего элемент управления. Выражения в следующей таблице представляют примеры значений по умолчанию для поля или элемента управления. Если элемент управления привязан к полю в таблице и поле имеет значение по умолчанию, значение по умолчанию элемента управления имеет приоритет.
Верх страницы Правила проверки полей Вы можете создать правило проверки для поля или элемента управления с помощью выражения. Примеры в следующей таблице демонстрируют выражения правил проверки для свойства ValidationRule и соответствующий текст для ValidationText свойство.
Дополнительные сведения о проверке данных см. в статье Создание правила проверки для проверки данных в поле. Верх страницы МакровыраженияВ некоторых случаях вам может понадобиться выполнить действие или серию действий в макросе, только если выполняется определенное условие. Например, предположим, что вы хотите, чтобы действие выполнялось только тогда, когда значение текстового поля Счетчик равно 10. Вы используете выражение для определения условия в поле 9.1973 Условие столбец макроса: Как и в случае свойства ValidationRule , выражение столбца Condition является условным выражением. Совет Чтобы заставить Access временно игнорировать действие, введите False в качестве условия. Это может быть полезно, когда вы пытаетесь найти проблемы в макросе.
Верх страницы Части выраженияАлгебраические выражения представляют собой комбинации переменные , числа и хотя бы одно арифметическое действие. Например, 2 Икс + 4 у − 9 является алгебраическим выражением. Срок: Каждое выражение состоит из терминов. Фактор: Что-то, что умножается на что-то другое. Фактор может быть числом, переменной, термином или более длинным выражением. Например, выражение 7 Икс ( у + 3 ) имеет три фактора: 7 , Икс , а также ( у + 3 ) . Коэффициент: Числовой коэффициент выражения умножения, содержащего переменную. Рассмотрим выражение на рисунке выше, 2 Икс + 4 у − 9. В первый срок, 2 Икс , коэффициент 2 : во второй срок, 4 у , коэффициент 4 . Постоянный: Число, которое не может изменить свое значение. Нравятся условия: Термины, содержащие одни и те же переменные, такие как 2 м , 6 м или же 3 Икс у а также 7 Икс у . Если выражение имеет более одного постоянного члена, они также похожи на термы.
Пример: Определите термины, такие как термины, коэффициенты и константы в выражении. 9 м − 5 н + 2 + м − 7 Во-первых, мы можем переписать вычитания как сложения. 9 м − 5 н + 2 + м − 7 знак равно 9 м + ( − 5 н ) + 2 + м + ( − 7 ) Итак условия находятся
9
м
,
(
−
5
н
)
,
м
,
2
, а также
(
−
7
)
. Нравятся условия являются терминами, которые содержат одни и те же переменные. 9 м а также 9м являются парой как термины . Постоянные условия 2 а также − 7 также как термины. Коэффициенты числовые части термина, содержащего переменную. Итак, вот коэффициенты находятся 9 , ( − 5 ) , а также 1 . ( 1 коэффициент члена м .) постоянный термины — это термины без переменных, в этом случае 2 а также − 7 . Алгебраические выражения должны быть тщательно написаны и интерпретированы. См. разницу между двумя выражениями в таблице ниже.
При записи выражений для неизвестных величин часто пользуются стандартными формулами. |


 д. заменяются их значениями.
д. заменяются их значениями. Алгебра 8 класс
Алгебра 8 класс Сначала — умножение и деление, затем — сложение и вычитание.
Сначала — умножение и деление, затем — сложение и вычитание.