График функции вида Z = F(X, Y)
График функции вида Z = F(X, Y) | QBASICBOOK.ru: сайт про QB64Опубликовано: 2020-04-27 08:00:00
Программа строит график функции Z = F(X, Y) в виде прозрачной сетки.
Рассмотрим исходный текст программы:
- REM PHUCKER_COPYRIGHT
- ‘FROM SCIENCE.CLANBB.RU WITH LOVE
- DECLARE FUNCTION F! (X!, Y!)
- SCREEN 12
- PI = 3.141592
- X0 = 320: Y0 = 240 ‘EKRANNOYE POLOZHENIYE PROYEKTSII NACHALA KOORDINAT
- M = 20 ‘MASSHTABNYY KOEFFITSIYENT DLYA OSEY X, Y, Z. POKAZYVAYET
- ‘ SKOLKIM PIKSELAM RAVEN YEDINICHNYY OTREZOK.
- ALPHA = -.3 * PI: BETA = .1 * PI ‘UGLY POVOROTA PROSTRANSTVA XYZ VOKRUG
- ‘ OSEY X I Y. UKAZYVAYUTSYA V RADIANAKH.

- MINX = -10: MAXX = 10 ‘OGRANICHENIYA PRYAMOUGOLNOY OBLASTI
- MINY = -10: MAXY = 10 ‘ PO OSYAM X I Y.
- KOLX = 32: KOLY = 32 ‘KOLICHESTVO RAZBIYENIY SETKI PO OSYAM X I Y.
- KOLX2 = 1024: KOLY2 = 1024 ‘KOLICHESTVO TOCHEK DLYA POSTROYENIYA
- ‘ «PRUTYEV» SETKI PO OSYAM X I Y.
- ‘SINUSY I KOSINUSY UGLOV ALPHA I BETA.
- COSA = COS(ALPHA): SINA = SIN(ALPHA)
- COSB = COS(BETA): SINB = SIN(BETA)
- ‘SHAGI MEZHDU «PRUTYAMI» SETKI PO OSYAM X I Y.
- DX = (MAXX — MINX) / KOLX: DY = (MAXY — MINY) / KOLY
- ‘SHAGI MEZHDU TOCHKAMI POSTROYENIYA «PRUTYEV».
- DX2 = (MAXX — MINX) / KOLX2: DY2 = (MAXY — MINY) / KOLY2
- ‘DVUKHUROVNEVYY TSIKL POSTROYENIYA «PRUTYEV» SETKI,
- ‘ PARALLELNYKH XZ.

- FOR Y = MINY TO MAXY * 1.001 STEP DY
- FOR X = MINX TO MAXX * 1.001 STEP DX2
- Z = F(X, Y)
- ‘BLOK PREOBRAZOVANIYA KOORDINAT PROSTRANSTVA.
- ‘SCHITAYEM, CHTO PROIZOSHLI POVOROTY TOCHEK PROSTRANSTVA
- ‘VOKRUG OSEY X I Y NA UGLY ALPHA I BETA SOOTVETSTVENNO.
- Y2 = Y * COSA — Z * SINA
- Z2 = Y * SINA + Z * COSA
- X2 = X
- ‘Z3 = Z2 * COSB — X2 * SINB
- X3 = Z2 * SINB + X2 * COSB
- Y3 = Y2
- PSET (X0 + X3 * M, Y0 — Y3 * M)
- NEXT X
- NEXT Y
- ‘DVUKHUROVNEVYY TSIKL POSTROYENIYA «PRUTYEV» SETKI,
- ‘ PARALLELNYKH YZ.

- FOR X = MINX TO MAXX * 1.001 STEP DX
- FOR Y = MINY TO MAXY * 1.001 STEP DY2
- Z = F(X, Y)
- ‘BLOK PREOBRAZOVANIYA KOORDINAT PROSTRANSTVA.
- ‘SCHITAYEM, CHTO PROIZOSHLI POVOROTY TOCHEK PROSTRANSTVA
- ‘VOKRUG OSEY X I Y NA UGLY ALPHA I BETA SOOTVETSTVENNO.
- Y2 = Y * COSA — Z * SINA
- Z2 = Y * SINA + Z * COSA
- X2 = X
- ‘Z3 = Z2 * COSB — X2 * SINB
- X3 = Z2 * SINB + X2 * COSB
- Y3 = Y2
- PSET (X0 + X3 * M, Y0 — Y3 * M)
- NEXT Y
- NEXT X
- ‘URAVNENIYE POVERKHNOSTI Z=F(X,Y).
 2))
2)) - END FUNCTION
Рисунок 1 – Исходный текст для графика функции вида Z = F(X, Y)
Рисунок 2 – Результат построения графика функции вида Z = F(X, Y)
Спасибо за прочтение этой статьи.
Прикрепленные файлы:
- graph-func-f-x-y.bas
< Предыдущая статья
Аналоговые часы
Выделите опечатку и нажмите Ctrl + Enter, чтобы отправить сообщение об ошибке.
НОУ ИНТУИТ | Лекция | Графика
< Дополнительный материал || Лекция 3: 123456
Аннотация:
В лекции представлены методы построения типичных графиков функций на плоскости и в пространстве, а также инструменты их редактирования, форматирования и настройки. Описаны разные технологические приемы построения графиков функций: автоматически, с помощью сетки и с применением специальных функций.
Ключевые слова: программа, координаты, панель инструментов, графика, меню, список, шаблон, прямоугольник, имя функции, курсор, область определения, функция, график, множества, значение, опция, радиус, массив
Цель лекции. Научить строить графики функций в разных системах координат с помощью различных технологических приемов. Показать способы форматирования и настройки разных типов графиков и диаграмм.
3.1. Инструменты графики
MathCAD предоставляет широкие возможности для построения графиков. Графические построения являются универсальными и легкими в использовании. Программа позволяет строить графики на плоскости и в трехмерном пространстве. Можно использовать декартовы и полярные координаты на плоскости, сферическую и цилиндрическую систему координат в пространстве.Панель Математика содержит панель инструментов графики.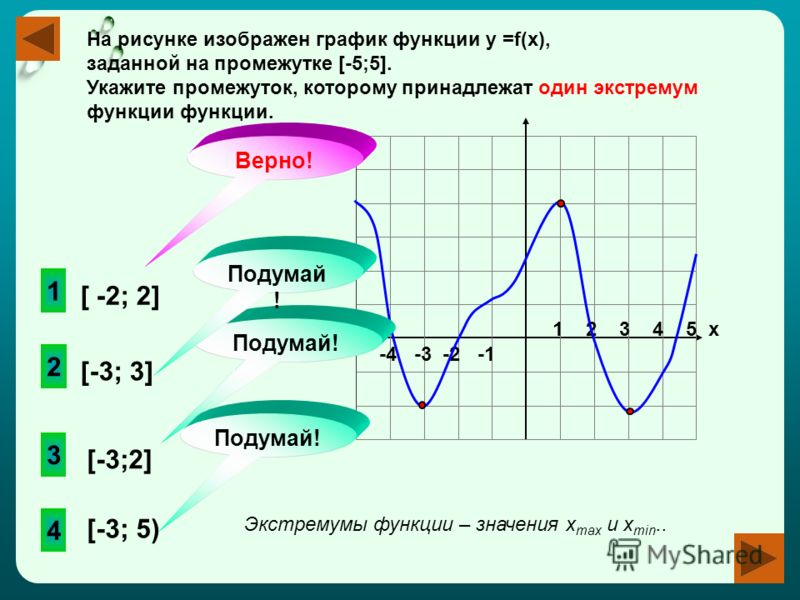 Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.
Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.
- Декартов график [@] —шаблон двухмерного графика;
- Полярный график [Ctrl+ 7] —шаблон графика в полярной системе координат;
- График поверхности [Ctrl+ 2] — шаблон для построения трехмерного графика;
- Карта линий уровня [Ctrl+ 5] —шаблон для контурного графика трехмерной поверхности; intuit.ru/2010/edi»>3D точечный график –шаблон для графика в виде точек в трехмерном пространстве;
- 3D столбиковая гистограмма –шаблон для изображения в виде совокупности столбиков в трехмерном пространстве;
- Векторное поле— создать шаблон для графика векторного поля на плоскости.
Для вывода шаблона двухмерной графики в декартовой системе координат служит кнопка декартов график на панели Graph [3, 8]. Она выводит в текущее положение курсора шаблон графиков в декартовых координатах (Рис.3.2). Незаполненный шаблон графика — пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика.
Рис. 3.2. Шаблон графика в декартовых координатах
intuit.ru/2010/edi»>В средние шаблоны данных надо поместить имя функции F(x) оси абсцисс x. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Масштабы, могут оказаться неудобными для представления целиком всего графика в максимальном размере. Рекомендуется всегда вначале использовать автоматическое масштабирование, а затем изменять масштабы на более подходящие. Для построения графика достаточно вывести курсор за пределы графического объекта.3.2. Построение графиков функций на плоскости
Для построения графика функции надо написать функцию, выбрать интервалы построения графика по оси X и Y и обозначить параметры графика. При этом следует учитывать область допустимых значений существования функции или область определения. Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.
3.2.1.Декартов график
Пример 3.1. Построить графики функций : , , . Функция не существует в точке . Но график строится и никаких дополнительных действий предпринимать не нужно. В отличие от построения графиков поверхности. Но эту проблему рассмотрим ниже.
Построение графика
Форматирование графика
Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) можно изменить, вызвав команду меню Format/Graph/X-Y Plot (Формат/График/декартов график) или щелкнув дважды по полю графика. Появится окно Formatting Currently Selected X-Y Plot
Появится окно Formatting Currently Selected X-Y Plot
Рис. 3.7. Окно форматирования декартова графика
- Вкладка X-Y оси устанавливает для осей X и Y : тип шкалы: логарифмическая Log scale, цифровая Numbered), линии сетки (Grid Lines), Сетку автоматическую (Auto Grid) или режим задания количества меток (Number of Grid). Внизу устанавливается стиль вида осей (Axes Style)/
- Вкладка Traces устанавливает условные обозначения различных кривых графика.
- Вкладка Надпись (Labels) расположение надписей.
Установка границ на осях координат
MathCAD обеспечивает следующие возможности устанавливать границы на осях координат:
- intuit.ru/2010/edi»>Автоматически, с включенным режимом Авто масштаб (Autoscale)(см. закладка » X-Y Оси » ).
- Автоматически, с выключенным режимом Авто масштаб.
- Вручную, вводя границы непосредственно на графике.
При включенном режиме Авто масштаб MathCAD устанавливает границу на каждой оси соответствующей первому главному делению, выходящему за пределы значений данных
При выключенном режиме Авто масштаб MathCAD устанавливает границы на осях точно равными пределам данных.
Добавление горизонтальных и вертикальных линий
Чтобы добавить горизонтальную или вертикальную линию к графику:
- вызвать окно форматирования графика в декартовых координатах, intuit.ru/2010/edi»>в диалоговом окне Форматирование— закладка » X-Y Оси » ,
- щёлкнуть » Нанести риски » (для X-оси, или Y-оси). MathCAD показывает два дополнительных пустых поля на каждой оси, для которой включена опция » Нанести риски «,
- впечатать значение, для которого нужно провести линию,
- чтобы удалить линию, удалить это число или щёлкните на поле » Нанести риски «
Дальше >>
< Дополнительный материал || Лекция 3: 123456
12. Функции двух переменных, их график, непрерывность
Рассмотрим два множества. Пусть множество D есть подмножество множества R2={(Х, y)} на плоскости, т. е. DÌR2, а множество Z есть подмножество множества R на прямой, т. е.ZÌR.
Соотношение между множеством D и множеством Z, при котором каждому элементу (Х,Y) множества D соответствует один и только один элемент Z множества Z, называется функцией двух переменных.
Множество D называется Областью определения функции и обозначается D(Z).
Для функции двух переменных вводится обозначение
Z=F(Х;Y), (Х;Y) Î D(Z).
Приведем примеры функций двух переменных, заданных аналитически.
Пример 1. Z = -2X+3Y+6, D(Z)=R2.
Здесь каждой паре действительных чисел (X0, Y0) соответствует одно и только одно действительное число
Z0 = -2X0,+ 3Y0+6.
Например, Z(0;0) =
и т. д.
Пример 2. Z = X2 + Y2, D(Z) = R2.
Очевидно, Z(0; 0) = 0; Z(-2; 3) = 13, Z(1; 4) = 17 и т. д.
Множество значений z, каждый элемент которого соответствует определенной точке (Х; Y)ÎD(Z), называется Областью значений этой функции. Область значений функции Z=F(Х;Y) принято обозначать Е(Z). Так, в примере 1 Е(Z)=R, а в примере 2 E(Z)=[0;+¥].
Так, в примере 1 Е(Z)=R, а в примере 2 E(Z)=[0;+¥].
Функция считается заданной, если указаны множества D(Z)ÌR2, E(Z)ÌR и соответствие F. Причем соответствие F может быть задано, как и в случае функций одной переменной, различными способами (аналитически, таблично, графически, описанием и т. д.).
Геометрическим изображением функции двух переменных Z=F(X; Y) будет служить некоторая поверхность, которая может быть названа графиком этой функции (рис.).
Пусть в пространстве выбрана прямоугольная система координат OXYZ. Рассмотрим функцию Z=F(X; Y), определенную в области D(Z). Как и ранее, область определения изображается некоторым множеством точек лоскости XOY. Каждой точке М0(Х0; Y0)ÎD(Z) ставится в соответствие точка пространства Р(Х0; Y0; Z0), аппликата которой равна значению функции в точке М0:
Z0 = F(X0; Y0).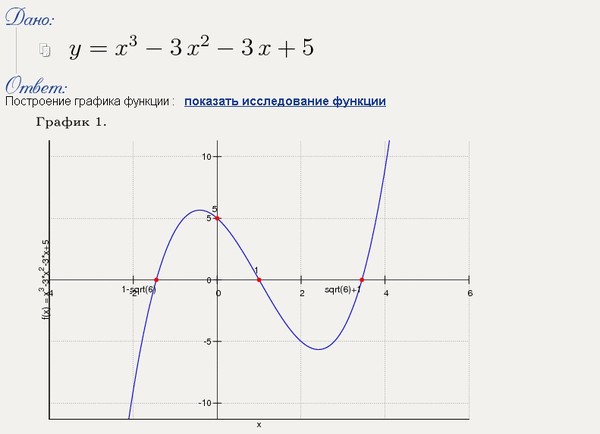
Множество всех таких точек пространства представляет собой некоторую поверхность, которую примем за график функции Z = F(X; Y). Так, например, графическим изображением функции Z = -2Х + 3Y + 6 примера 1 служит плоскость, проходящая через точки А(0;0; 6), В(+3; 0; 0), С (0; -2; 0).
Чтобы выяснить, что представляет собой график функции , можно обе части этого выражения предварительно возвести в квадрат и затем привести к виду X2 + Y2 + Z2 = 9. Если X2 + Y2=9 уравнение окружности, то очевидно наше уравнение – это уравнение поверхности шара. Рассматриваемая функция представляет, очевидно, только верхнюю половину поверхности шара.
Понятие предела функции двух переменных аналогично понятию предела функции одной переменной, за исключением того, что d-окрестностью на плоскости будет не интервал, а круг радиуса d.
Число А называется пределом функции F(X;Y) при Х®х0, Y®Y0, если для любого e >0 найдется такое de >0, что для всех точек Х(х;Y), таких, что
, выполняется неравенство
Заметим, что сформулированное выше определение предела функции двух аргументов в логическом отношении совпадает с определением предела функции одного аргумента.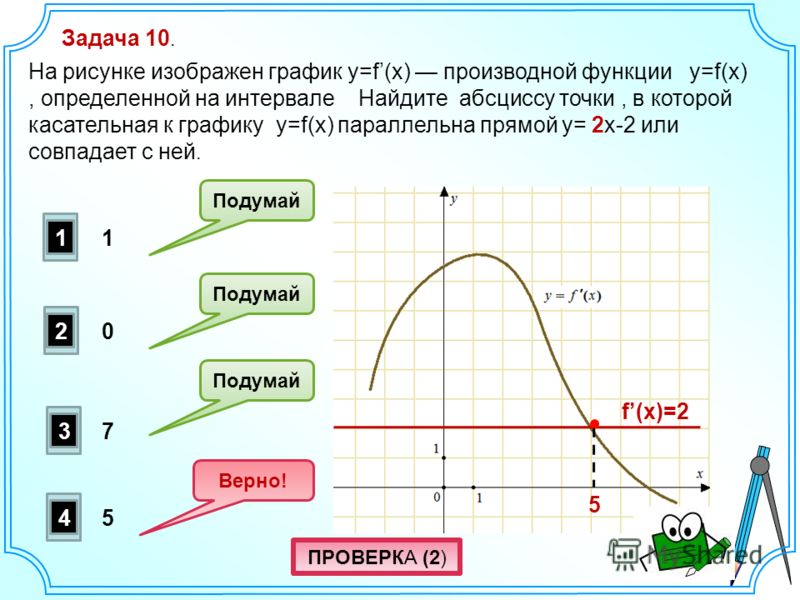 Следует ожидать, что все теоремы о пределах, изученные нами для случая функции одной переменной, переносятся на функции двух переменных. Здесь будут справедливыми теоремы о пределе суммы, произведения, частного и целый ряд других теорем теории пределов. Поэтому при вычислении пределов функций двух аргументов можно широко пользоваться этими теоремами.
Следует ожидать, что все теоремы о пределах, изученные нами для случая функции одной переменной, переносятся на функции двух переменных. Здесь будут справедливыми теоремы о пределе суммы, произведения, частного и целый ряд других теорем теории пределов. Поэтому при вычислении пределов функций двух аргументов можно широко пользоваться этими теоремами.
Например:
Пример 1. Вычислить
Решение. Применив теоремы о пределах, получим
Пример 2. Вычислить .
Решение. Воспользовавшись теоремами о пределах, получим
.
Так же, как и для функции одного переменного.
Функция F(X; Y) называется непрерывной в точке (Х0; Y0), если предел F(X; Y) при Х®х0, Y®Y0 существует и совпадает с F(х0; Y0), т. е.
Или
Функция F(X;Y) называется непрерывной в точке (X0;Y0), если ее приращение в этой точке стремится к нулю, когда приращения независимых переменных стремятся также к нулю .
Как и в случае функции одной переменной здесь можно говорить о Трех условиях непрерывности. Действительно, если предположить, что F(X; Y) непрерывна в точке (X0; Y0), то должны одновременно выполняться следующие условия:
I) F(X; Y) определена в точке (X0; Y0), т. е. F(X0; Y0) существует;
2) существует;
3) .
Если не выполнено хотя бы одно из этих условий, функция не будет непрерывной в точке. Говорят, что функция будет разрывной в точке, или функция терпит разрыв в точке.
Функция, непрерывная в каждой точке области D называется непрерывной в области D.
Для функции двух переменных точки разрыва могут обладать разнообразными особенностями. Множество точек разрыва может, в частности, состоять из точек некоторой линии. Такие линии называются Линиями разрыва. Так, функция будет иметь линией разрыва прямую Х=Y.
Заметим, что график непрерывной функции представляет собой поверхность без разрывов и дырок, даже точечных.
В заключение отметим, что все теоремы, устанавливающие свойства непрерывных функций одной переменной остаются справедливыми и при переходе к функциям двух аргументов.
| < Предыдущая | Следующая > |
|---|
Растяжение и сжатие графиков. Параллельный перенос графиков функций
ЦЕЛИ: 1) рассмотреть графики функций y=f(x), y=kf(x), y=f(x)+n, y=f(x-m) и y=f(x-m)+n и их свойства, используя ПК и программу Advanced Grapher;
2)расширить представления о преобразованиях графиков более сложных функций;
3)способствовать развитию у учащихся навыков чтения графиков и построения графиков функций.
I. Новый материал – объяснительная лекция.
Графики функций широко используются в
различных областях инженерных знаний, поэтому
умение строить, “читать”, прогнозировать их
“поведение” имеют огромную роль в практической
деятельности инженерных работников, гидро,
метеорологов и людей других “математических”
специальностей.
Выясним, какая связь существует между графиками функций y = f(x) и y = kf(x), где k-число, не равное нулю.
Пусть графиком функции y = f(x), область определения которой- промежуток[-2;4],является кривая, изображённая на рис.1а f(x) = x(x-3)(x+1).
Рассмотрим сначала случай, когда k>1.Построим
график функции y = kf(x), где k=2. Для этого расстояние
каждой точки графика функций y = f(x) от оси X
увеличим в 2раза, т.е.умножим её ординату на 2.
Построение выполним с помощью программы Advanced
Grapher, набрав формулу функции F1 с клавиатуры.
Заметим, что точки с абсциссами 0; 3; -1,
принадлежащие оси Х, останутся на месте, т.к.их
ординаты равны нулю (0*2х = 0).Все остальные точки
графиков у1, и у, имеющие одинаковые
абсциссы, будут лежать соответственно на
перпендикулярах к оси Х, причём каждая точка
графика функции у= 2f(x)
будет находиться от оси Х на расстоянии в 2 раза
большем, чем соответственная точка графика
функции y = f(x).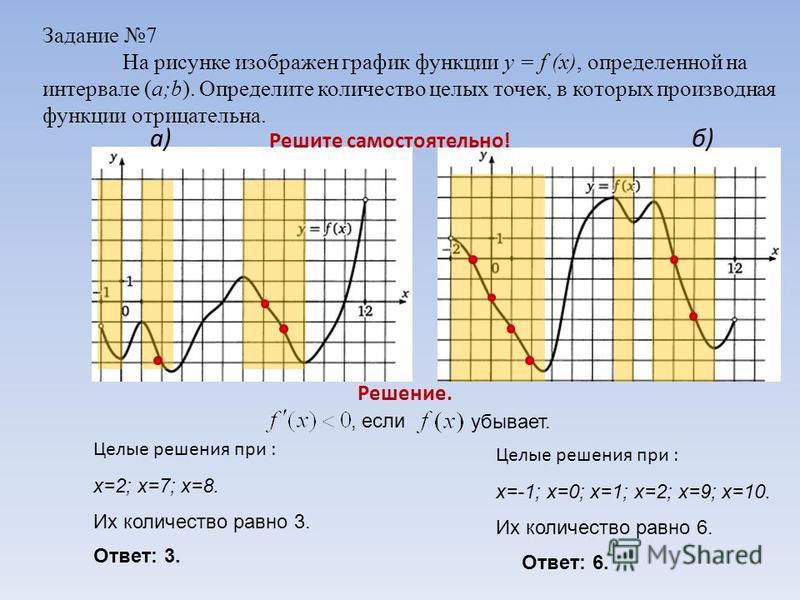 (рис. 1б).
(рис. 1б).
Рассмотрим теперь случай, когда О < k < 1, например k =, и построим график функции y= kf (x), при k = , используя программу Advanced Grapher.
Опять же заметим, что точки с абсциссами -1; 0 и 3, принадлежащие оси Х, останутся на месте ( 0* = 0 ), а каждая точка графика функции y= f (x), будет находиться от оси Х на расстоянии в 2 раза меньшем, чем соответственная точка графика функции y = f(x) (рис.1в).
Делаем вывод о том, что график функции y = f(x) при k < 1 можно получить из графика функции y = f(x) растяжением от оси Х исходного графика в k раз, а при О < k < 1- сжатием к оси Х графика функции y = f(x) в раз.
И рассмотрим случай, когда k< 0. Ограничимся значением k = -1, т.е. выясним, как можно построить график функции y= -f(x), зная график функции y = f(x).
Задав с клавиатуры формулу графика y = -f(x) и
получив соответствующее изображение на экране (рис. 1г), заметим, что каждой точке
графика y, кроме точек с
абсциссами -1; 0 и 3, соответствует точка графика y =
f(x) с противоположной ординатой.
1г), заметим, что каждой точке
графика y, кроме точек с
абсциссами -1; 0 и 3, соответствует точка графика y =
f(x) с противоположной ординатой.
Соответственно делаем вывод, что график функции y = -f(x) можно получить с помощью симметрии относительно оси Х.
Аналогично, графики функций y = kf(x) и y = -kf(x) при любом k0 симметричны относительно оси Х.
Иначе говоря, чтобы построить график функции y = kf(x), где k < 0, можно сначала построить график функции y = -kf(x), где -k > 0, а затем отобразить его симметрично относительно оси Х.
Выясним, как связаны между собой графики функций y = f(x) и y = f(x)+n, где n –произвольное число.
Рассмотрим графики функций y = x, y = x — 4 , y= x-4, y = x+ , y= x- (рис. 2).
Рассматривать будем попарно графики функций у и у(рис.2а), у и y(рис.2б), у и y(рис.2в), у и y(рис.2г).
Моментальное построение графика каждой из выше
указанных функций даст возможность сделать
вывод, что график функции y = f(x) + n можно получить
из графика функции y = f(x) с помощью сдвига вдоль
оси Y на n единиц вверх, если n>0, или на единиц вниз, если
n<0.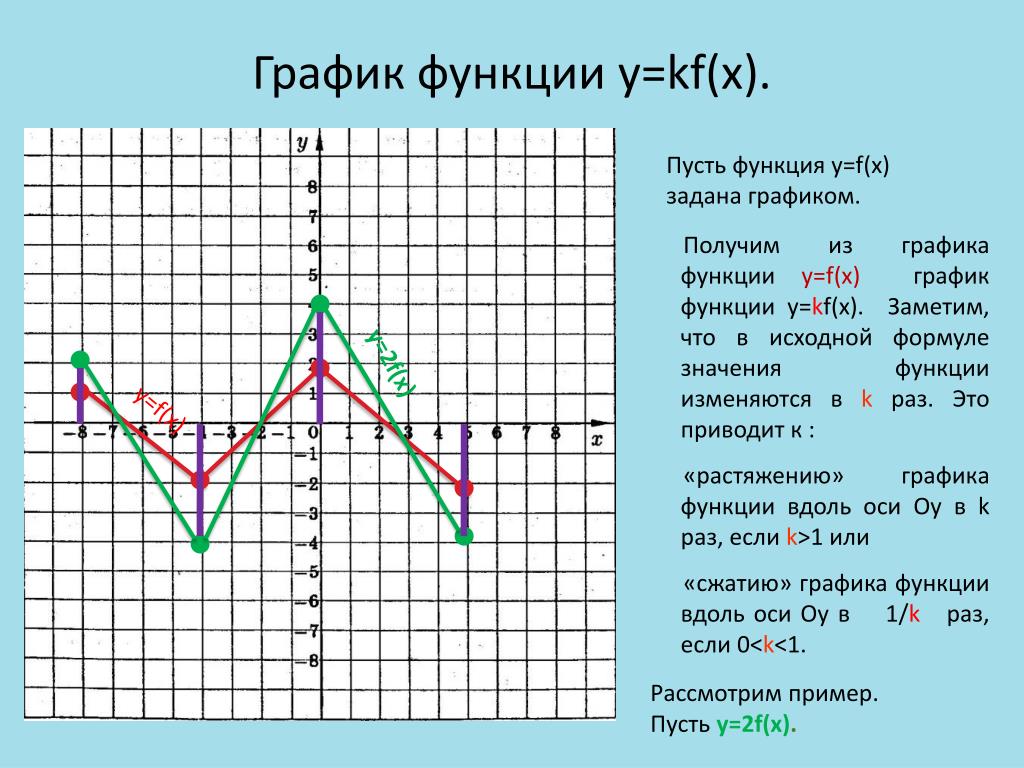
Выясним теперь, как связаны между собой графики функций y = f(x) и y = f(x-m), где m – произвольное число.
Рассмотрим графики функций y = (x-3), y = (x+2), y = (x), y = (x+).
Получаем рис.3 и делаем вывод, что график функции y = f(x) можно получить с помощью сдвига вдоль оси Х на m единиц вправо, если m>0, или на единиц влево, если m<0.
Из курса алгебры VII класса известно, что график функции y = x (парабола) симметричен относительно ось У. Точку пересечения параболы с осью симметрии называют вершиной параболы.
Построим, используя программу Advanced Grapher, в одной системе координат графики функций y = x, у== x+2, y= (х-3) и y= (х-3) +2 ( рис.4).
Учащимся наглядно видно, что у параболы у== x+2 осью симметрии является ось У, а у
параболы y= (х-3) — прямая х = 3. Графиком же
функции y= (х-3) +2 является парабола с
вершиной в точке (3;2) и осью симметрии её является
прямая х = 3.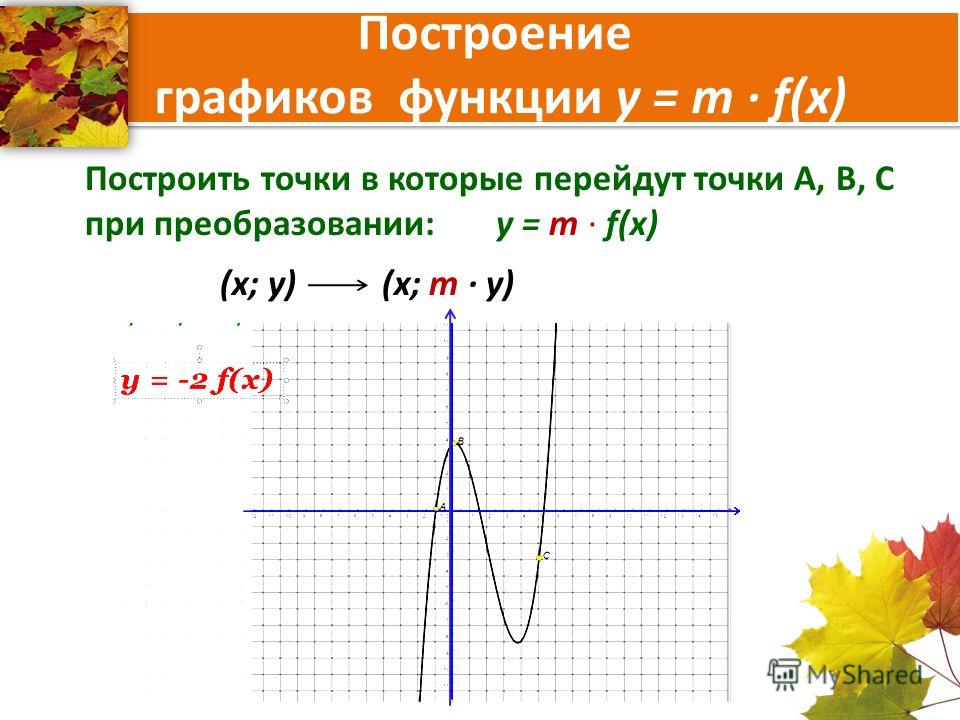
Из наглядного наблюдения учащиеся видят, что при построении графика функции у = (х-3) +2 нужно последовательно выполнить два параллельных переноса: один в направлении оси У на 2 единицы вверх, а другой в направлении оси Х на 3 единицы вправо.
Делаем вывод, что графиком функции вида у = (х-m) +n является парабола с вершиной в точке А(m;n) .А также обобщаем выше рассмотренные преобразования графиков и делаем вывод, что график функции y = f(x-m)+n может быть получен из графика функции y=f(x) в результате последовательно выполненных двух параллельных переносов: сдвига вдоль оси Х на m единиц и сдвига графика функции у = (х-m) вдоль оси У на n единиц.
II. Закрепление
.
У: Изобразите на координатной плоскости заданные точки и определите, используя обороты “выше на…” и “ниже…”, взаимное расположение соответствующих точек:
а) А(-1;7) и А1(-1;10) б) В(2;7) и В1(2;5) в) С (0;-6)
и С1(0;-5) г) Д (3;-4) и Д1(3;-7) .
У: Как найти расстояние между точками, имеющими одинаковые ординаты? Закончите предложение: “Если точки имеют одинаковые ординаты, то расстояние между ними равно…”
Обучающая исследовательская работа.
(карточки-распечатки см. Приложение 1)
I вариант.
1. Заданы функции y = f(x) и y = f(x) + 2. заполните таблицу значений этих функций и сделайте вывод о взаимном расположении точек данных функций и их графиков:
|
1 |
2 |
4 |
6 |
7 |
y=f(x) |
5 |
7 |
-5 |
||
y=f(x)+2 |
3 |
-11 |
Д: Любая точка графика y = f(x)+2 с абсциссой X находится на 2 единицы
“выше”, чем точка графика y = f(x) с той же самой
абсциссой; а график функции y = f(x)+2 можно получить из графика y = f(x)
параллельным переносом вдоль оси ординат на 2
единицы “вверх”.
II вариант.
1. Заданы функции y = f(x) и y = f(x) – 3. заполните таблицу значений этих функций и сделайте вывод о взаимном расположении точек данных функций и их графиков:
|
0 |
1 |
3 |
5 |
9 |
y=f(x) |
4 |
-6 |
5 |
||
y=f(x)-3 |
-3 |
0 |
Д: Любая точка графика y = f(x)-3 с абсциссой X находится на 3 единицы
“ниже”, чем точка графика y = f(x) с той же самой
абсциссой; а график функции y=f(x)-3 можно получить из графика y = f(x)
параллельным переносом вдоль оси ординат на 3
единицы “вниз”.
У: С помощью какого преобразования можно получить график функции y = f(x)+a, а0 из графика функции y = f(x).
Д: Обобщённый вывод (записать в тетрадь): График функции y1= f(x)+a, а0 можно получить из графика функции y = f(x) параллельным переносом вдоль оси ординат на единиц “вниз”, если а<0, и на единиц “вверх”, если а>0.
У: Пусть даны графики функций y = f(x) и y = f(x)+7. Известно, что один из них проходит через начало координат. Определите точку пересечения другого графика с осью ординат.
Д: A (0;7) или А (0;-7).
У: Пусть даны графики функций y = f(x) и y = f(x)+c. Известно, что один из них проходит через точку А(-11;231) и другой через точку А (-11;132). Найдите все возможные значения С.
Д: 99 или -99.
I вариант.
2. Постройте графики функций, используя известный график y = kx:
a) y = x-4 ; б) у = x+1; в) у = 2 x-1.
3.
II вариант.
2. Постройте графики функций, используя известный график y = kx:
а) у = -x+3; б) у = -0,5x+2; в) у = -2x-3.
3.
У: Изобразите на координатной плоскости заданные точки и определите, используя обороты “левее на …” и “правее на …” взаимное расположение следующих точек:
а) А (-1;7) и А (6;7) б) С (8;-6) и С (14;-6) в) В (2;3) и В (-2;3) г) Д (-13;_4) и Д (-3;-4).
У: Как найти расстояние между точками, имеющими одинаковые абсциссы? Закончите предложение: “Если точки имеют одинаковые абсциссы, то расстояние между ними равно…”
I, II вариант.
4. Заданы функции y=f(x), y= f(x+2) и y= f(x-3). Заполните таблицу значений этих функций:
У: Как взаимно расположены точки графиков функций y = f(x) и y = f(x+2)?
Каким образом можно получить график функции y= f(x+2) из графика функции y = f(x)?
Д: Любая точка графика y=
f(x+2) с абсциссой х-2
находится на 2 единицы “левее”, чем точка
графика y=f(x) с абсциссой х, а график функции y= f(x+2) можно получить из графика y = f(x),
“сдвинув” его на 2 единицы влево вдоль оси
абсцисс.
У: Как взаимно расположены точки графиков функций y = f(x) и y= f(x-3)?
Каким образом можно получить график функции y= f(x-3) из графика функции y = f(x)?
Д: Любая точка графика y= f(x-3) с абсциссой х+3 находится на 3 единицы “правее”, чем точка графика y = f(x) с абсциссой х, а график функции y= f(x-3) можно получить из графика функции y = f(x) “сдвинув” его на 3 единицы вправо вдоль оси абсцисс.
У: Попытайтесь сделать вывод о том как можно получить график функции y= f(x+а) из графика функции y = f(x)?
Д: График функции y= f(x+а) можно получить из графика функции y = f(x), “сдвинув” его на единиц вправо вдоль оси абсцисс, если а<0, и на единиц влево вдоль оси абсцисс, если а>0.
У: Пусть даны графики функций y = f(x) и y= f(x+7). Известно, что один из них проходит через начало координат. Какую точку пересечения графика с осью абсцисс можно указать наверняка?
Д: А(-7;0) и А (7;0).
У: Опишите как расположены относительно друг друга графики функций (задания 5-9 выполнены на карточках-распечатках, ответы в устной форме):
5. y = f(x-2) и y = f(x+7).
6. y = f(2x) и y = f(2x-4).
7. y = f(2x) и y = f(2x+1).
8. y = f(0,5x) и y = f(0,5x-4).
9. y = f() и . y = f(-1).
III . Лабораторно-исследовательская работа.(все задания выполнены на карточках-распечатках, ответы см. в приложении 2)
I вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = (x-4). б) у = (x+2).
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x+3)-4?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у = -4; б) у = (x+3)-4.
II вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = 2(x-1), б) у = -(x+3).
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x-5)+2?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =+2; б) у =(x-5)+2.
III вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = -0,5(x-4); б) у = (2x-3).
11. Пусть дан график функции y = f(x). Как получить график функции y = f(x+1)+3?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =+3; б) у = (x+1)+3.
IV вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = 4x+4х+1; б) у = —х-1.
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x-2)-1?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =-1; б) у = (x-2)-1.
Функция f(x,y)=min[x,y] : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| AchilleS |
| ||
13/08/06 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 13 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Функция двух и более переменных.
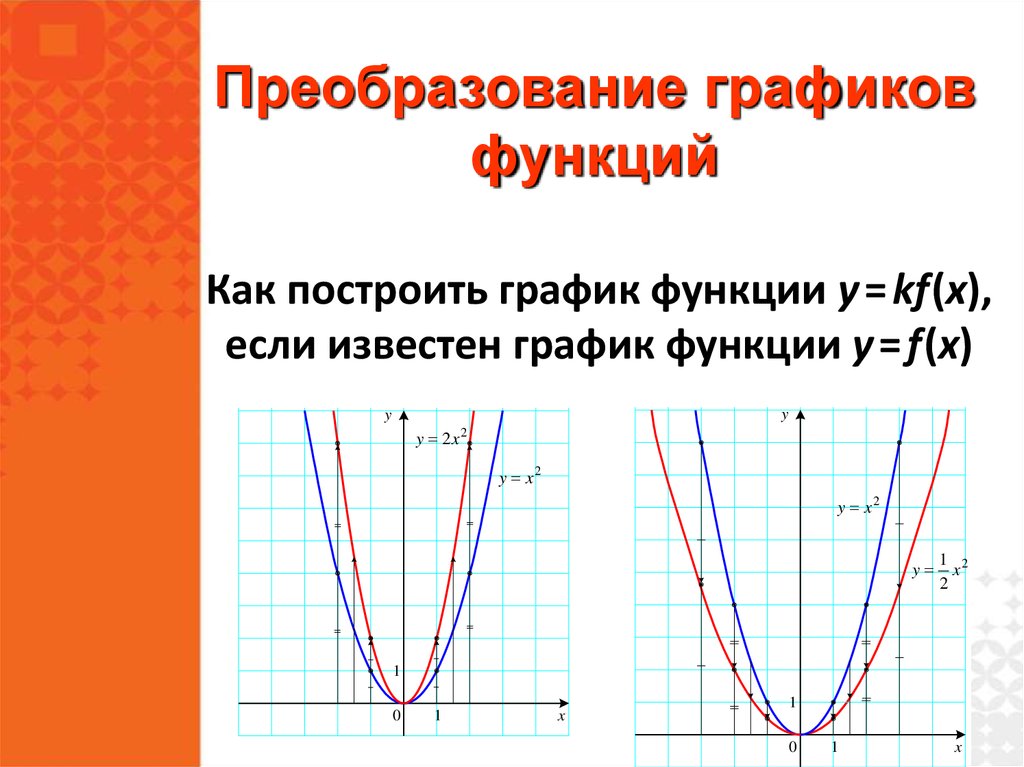 Её область определения
Её область определения- Функции нескольких переменных: основные определения
- Область определения функции нескольких переменных
- Функции нескольких переменных — пример из экономики
При изучении многих закономерностей в естествознании и экономике приходится встречаться с функциями от двух (и более) независимых переменных.
Определение (для функции двух переменных). Пусть X, Y и Z — множества. Если каждой паре (x, y) элементов из множеств соответственно X и Y в силу некоторого закона f ставится в соответствие один и только один элемент z из множества Z, то говорят, что задана функция двух переменных z = f(x, y).
В общем случае область определения функции двух переменных геометрически может
быть представлена некоторым множеством точек (x; y) плоскости xOy.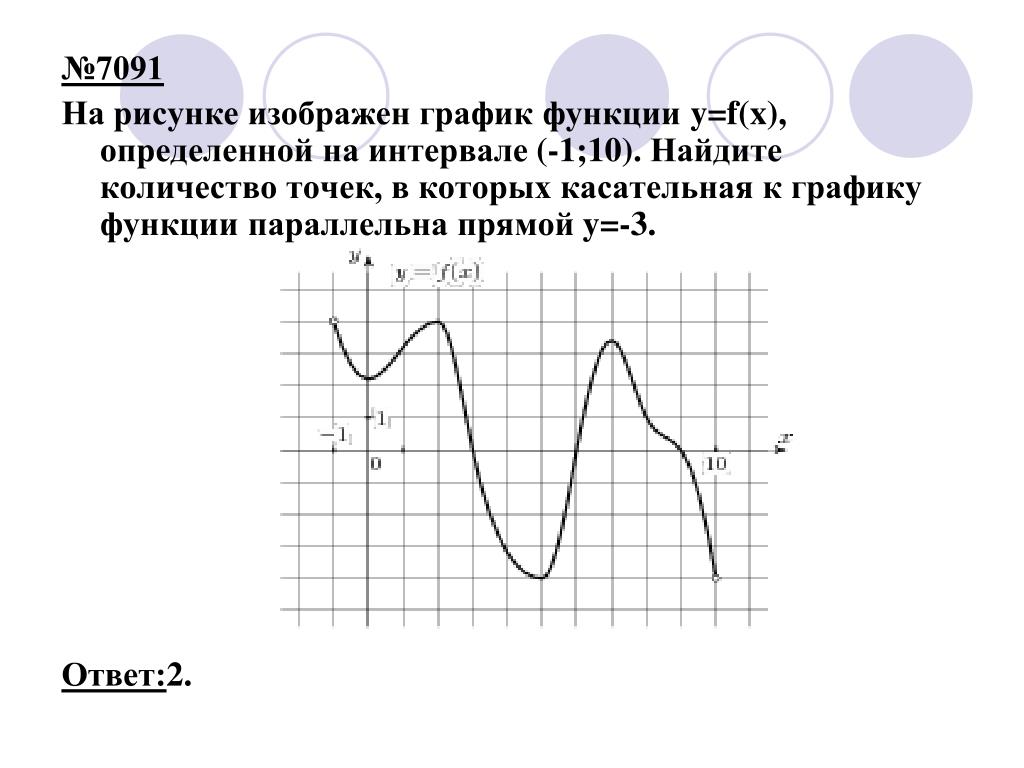
Подобно тому, как функция y = f(x) геометрически изображается графиком, можно геометрически истолковать и уравнение z = f(x, y).
Ставя в соответствие каждой точке аппликату z = f(x, y), мы получим некоторое множество точек (x; y; z) трёхмерного пространства – чаще всего некоторую поверхность. Поэтому равенство z = f(x, y) называют уравнением поверхности.
Из аналитической геометрии известно, что множество всех упорядоченных троек чисел (x; y; z) образует координатное пространство. При этом каждой тройке (x; y; z) в пространстве соответствует точка М(x; y; z) и наоборот.
Аналогично можно дать определение функции четырёх переменных u = f(x; y; z; t).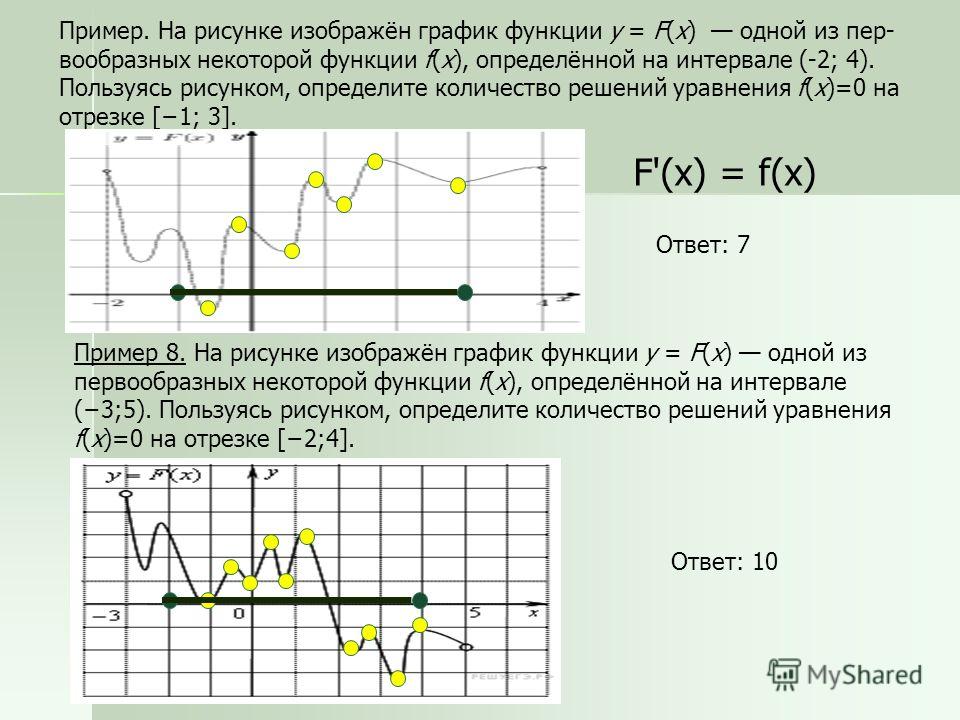 В этом случае
множество упорядоченных четвёрок чисел (x; y; z; t)
образуют так называемое четырёхмерное пространство, а каждая четвёрка (x; y; z; t)
называется точкой этого пространства. Однако область определения функции четырёх
переменных уже не имеет наглядного геометрического истолкования.
В этом случае
множество упорядоченных четвёрок чисел (x; y; z; t)
образуют так называемое четырёхмерное пространство, а каждая четвёрка (x; y; z; t)
называется точкой этого пространства. Однако область определения функции четырёх
переменных уже не имеет наглядного геометрического истолкования.
Забавный, хотя и нематематический случай функции нескольких переменных можно найти
в романе Джерома К. Джерома «Трое в лодке, не считая собаки». Герой романа сообщает: «Как-то раз я зашёл
в библиотеку Британского музея, чтобы навести справку о средстве против пустячной болезни, которую я
где-то подцепил, — кажется, сенной лихорадки. Я взял справочник и нашёл там всё, что мне было нужно…»
Итак, описана функция одной переменной — найти симптомы одного заболевания. Дальше: «… а потом, от
нечего делать, начал перелистывать книгу, просматривая то, что там сказано о разных других болезнях.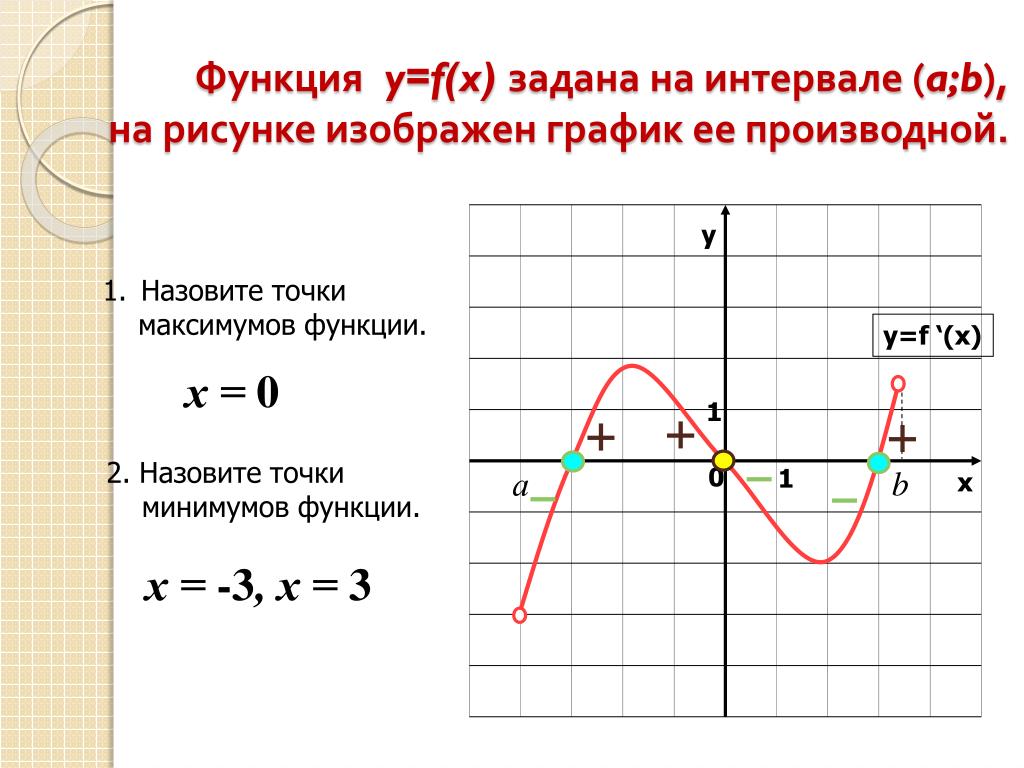 » И
герой находил у себя симптомы всех болезней, о которых читал: «Так я добросовестно перебрал все буквы
алфавита, и единственная болезнь, которой я у себя не обнаружил, была родильная горячка». То есть, самая
настоящая функция нескольких (многих) переменных — обнаружить у себя симптомы болезней (нескольких или даже
многих), о которых человек
прочёл. Впрочем, случай не такой уж и нематематический. Если условиться считать, что закон, которым задаётся
функция, заключается в суммировании чисел, означающих число симптомов, а на выходе — число, которое следует
толковать как степень нервного истощения героя. У этой функции есть и область определения — множество
симптомов всех болезней, которые можно найти в справочниках.
» И
герой находил у себя симптомы всех болезней, о которых читал: «Так я добросовестно перебрал все буквы
алфавита, и единственная болезнь, которой я у себя не обнаружил, была родильная горячка». То есть, самая
настоящая функция нескольких (многих) переменных — обнаружить у себя симптомы болезней (нескольких или даже
многих), о которых человек
прочёл. Впрочем, случай не такой уж и нематематический. Если условиться считать, что закон, которым задаётся
функция, заключается в суммировании чисел, означающих число симптомов, а на выходе — число, которое следует
толковать как степень нервного истощения героя. У этой функции есть и область определения — множество
симптомов всех болезней, которые можно найти в справочниках.
Пример 0 (наиболее общий). Рассмотрим температуру t в пункте p земной поверхности P. Таким образом, возникает
температурная функция ,
аргументом которой является точка p поверхности P, а значением t = T(p) —
температура в этой точке.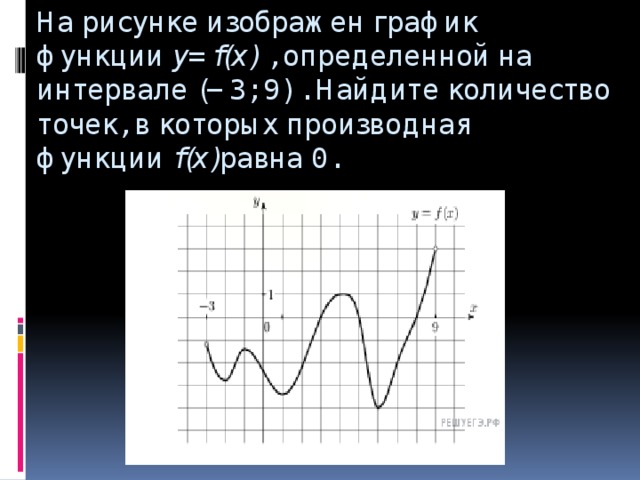 Чтобы привести эту функцию к числовой записи, точку p характеризуют некоторыми числовыми параметрами,
например, широтой и
долготой .
После этого вместо t = T(p)
пишут ,
где теперь t, ,
— числа.
И t оказывается, таким образом, зависящей не от одной,
а от двух переменных — и
, поэтому
такую числовую функцию называют функцией двух переменных. В этом же смысле температура
атмосферы в целом есть функция
трёх переменных: две первые (,
) указывают,
над какой точкой земной поверхности проводится измерение температуры, а последняя — H — задаёт высоту, на которой оно выполняется.
Чтобы привести эту функцию к числовой записи, точку p характеризуют некоторыми числовыми параметрами,
например, широтой и
долготой .
После этого вместо t = T(p)
пишут ,
где теперь t, ,
— числа.
И t оказывается, таким образом, зависящей не от одной,
а от двух переменных — и
, поэтому
такую числовую функцию называют функцией двух переменных. В этом же смысле температура
атмосферы в целом есть функция
трёх переменных: две первые (,
) указывают,
над какой точкой земной поверхности проводится измерение температуры, а последняя — H — задаёт высоту, на которой оно выполняется.
Таким образом, то, что раньше выглядело как функция одного аргумента, при переходе к числовой записи может оказаться функцией нескольких числовых аргументов.
Аналогично можно ввести понятия функции пяти и вообще n переменных .
Для функции нескольких переменных вводится понятие частных производных, а с помощью частных производных можно найти экстремумы функции нескольких переменных — у нас показано нахождение экстремумов функции двух переменных.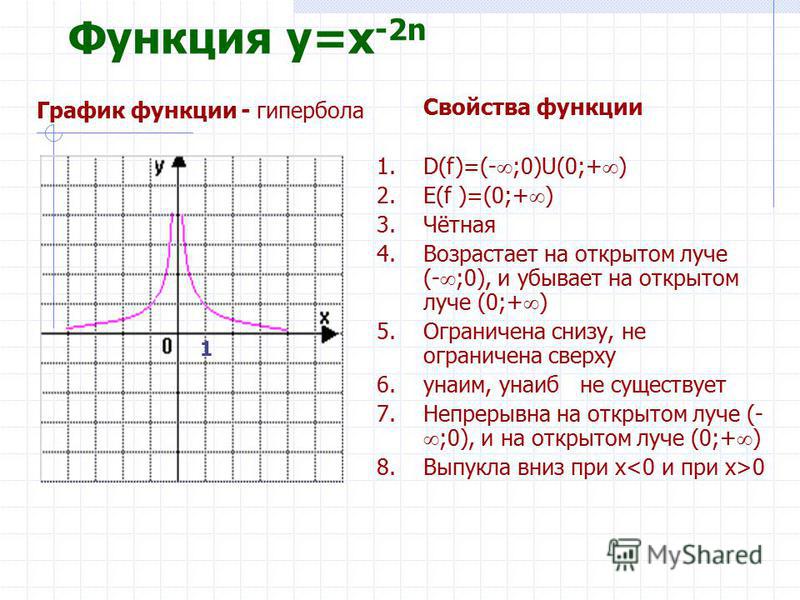
Основные определения, относящиеся к функциям нескольких переменных, являются обобщением соответствующих определений для функции одной переменной.
Множество D называется областью определения функции z, а множество E – множеством её значений. Переменные x и y по отношению к функции z называются её аргументами. Переменная z называется зависимой переменной.
Частным значениям аргументов
соответствует частное значение функции
Если функция нескольких переменных (например, двух переменных) задана формулой z = f(x, y),
то областью её определения является множество всех таких точек плоскости x0y,
для которых выражение f(x, y) имеет смысл и принимает действительные значения.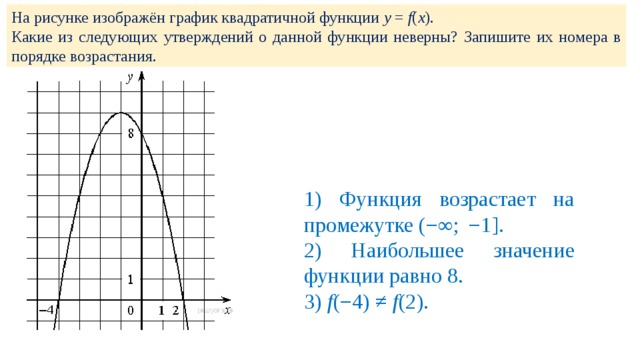 Общие правила для области определения функции
нескольких переменных выводятся из общих правил для области определения функции одной переменной. Отличие в том,
что для функции двух переменных областью определения является некоторое множество точек плоскости, а не
прямой, как для функции одной переменной. Для функции трёх переменных областью определения является
соответствующее множество точек трёхмерного пространства, а для функции n переменных —
соответствующее множество точек абстрактного n-мерного пространства.
Общие правила для области определения функции
нескольких переменных выводятся из общих правил для области определения функции одной переменной. Отличие в том,
что для функции двух переменных областью определения является некоторое множество точек плоскости, а не
прямой, как для функции одной переменной. Для функции трёх переменных областью определения является
соответствующее множество точек трёхмерного пространства, а для функции n переменных —
соответствующее множество точек абстрактного n-мерного пространства.
Область определения функции двух переменных с корнем
n-й степениВ случае, когда функция двух переменных задана формулой и n — натуральное число:
если n — чётное число, то областью определения функции является множество точек плоскости, соответствующих всем значениями подкоренного выражения, которые больше или равны нулю, то есть
если n — нечётное число, то областью определения функции является множество
любых значений , то есть
вся плоскость x0y.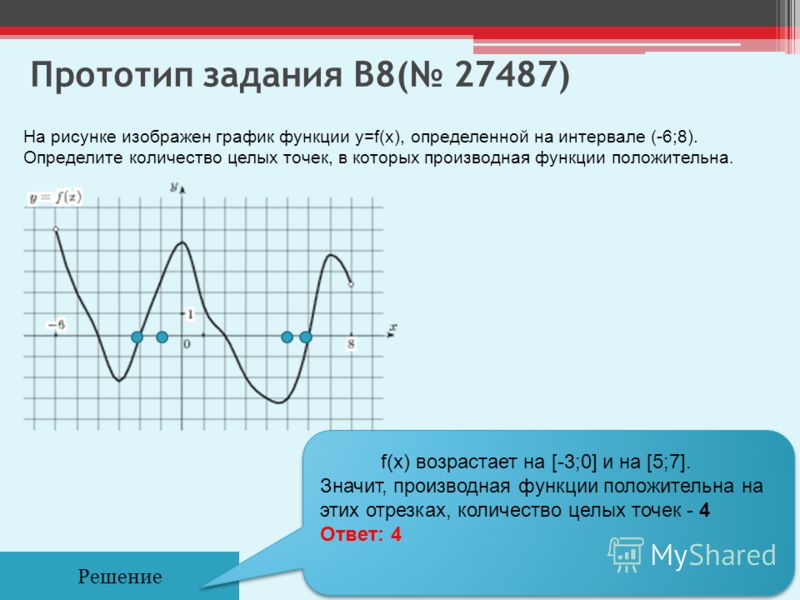
Область определения степенной функции двух переменных с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является вся плоскость x0y;
если a — отрицательное, то областью определения функции является множество значений , отличных от нуля: .
Область определения степенной функции двух переменных с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество тех точек плоскости, в которых принимает значения большие или равное нулю: ;
если — отрицательное, то областью определения функции является множество тех точек плоскости, в которых принимает значения, большие нуля: .
Область определения логарифмической функции двух переменных
Логарифмическая функция двух переменных
определена при условии, если её аргумент положителен, то есть, областью её определения является множество
тех точек плоскости, в которых принимает значения, большие нуля: .
Область определения тригонометрических функций двух переменных
Область определения функции — вся плоскость x0y.
Область определения функции — вся плоскость x0y.
Область определения функции — вся плоскость x0y, кроме пар чисел, для которых принимает значения .
Область определения функции — вся плоскость x0y, кроме пар чисел, для которых принимает значения .
Область определения обратных тригонометрических функций двух переменных
Область определения функции — множество таких точек плоскости, для которых .
Область определения функции — множество таких точек плоскости, для которых .
Область определения функции — вся плоскость x0y.
Область определения функции — вся плоскость x0y.
Область определения дроби как функции двух переменных
Если функция задана формулой ,
то областью определения функции являются все точки плоскости, в которых .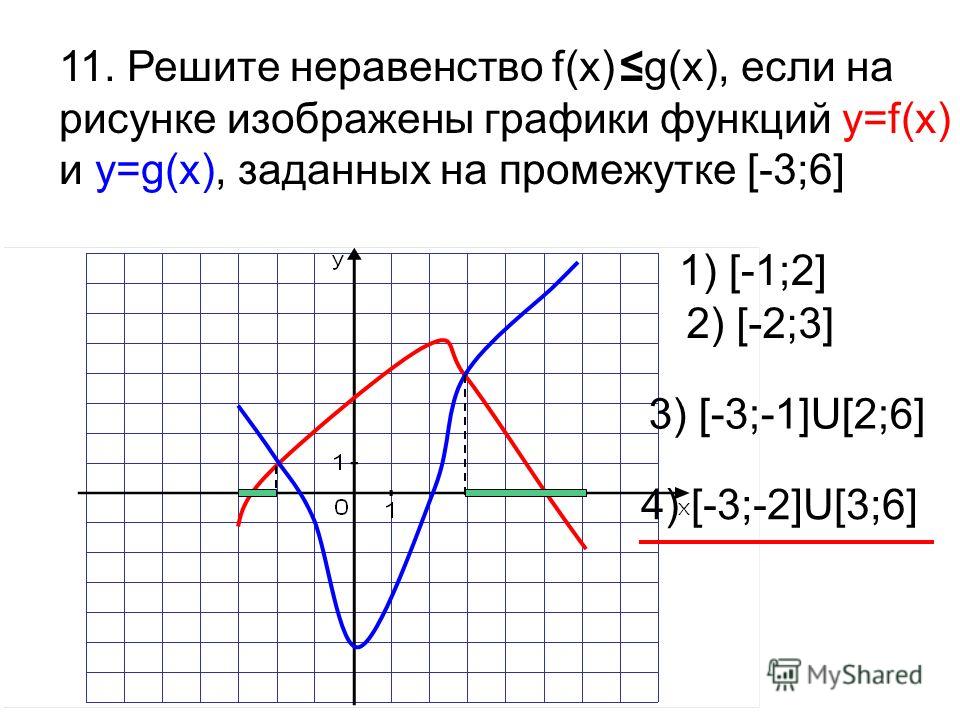
Область определения линейной функции двух переменных
Если функция задана формулой вида z = ax + by + c, то область определения функции — вся плоскость x0y.
Пример 1. Найти область определения функции двух переменных .
Решение. По правилам для области определения составляем двойное неравенство
.
Умножаем всё неравенство на и получаем
.
Полученное выражение и задаёт область определения данной функции двух переменных.
Пример 2. Найти область определения функции двух переменных .
Решение. По правилам для области определения составляем двойное неравенство
.
Переносим икс в правую часть и получаем
.
Полученное выражение и задаёт область определения данной функции двух переменных.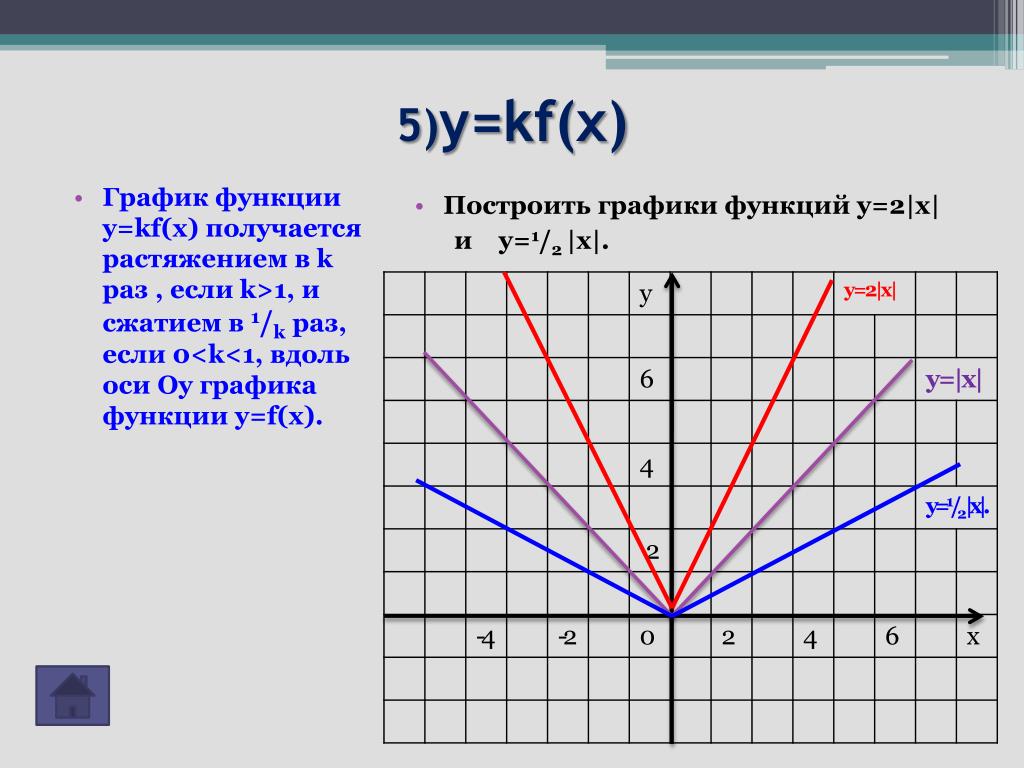
Пример 3. Найти область определения функции двух переменных S = xy и частное значение этой функции при при x = 3, y = 5.
Решение. Область определения функции S = xy, выражающей зависимость площади многоугольника от длин его сторон, может быть записана двумя неравенствами и , которые определяют I квадрант на плоскости xOy. Частное значение этой функции при x = 3, y = 5 составляет
Пример 4. Найти область и построить область определения функции двух переменных .
Решение. Область определения заданной функции двух переменных найдём из равенства т.е.
Это круг с центром в начале координат и радиусом r. Графиком функции является верхняя половина сферы .
Разрешив уравнение сферы относительно z, получим две однозначные функции z:
и
(рис.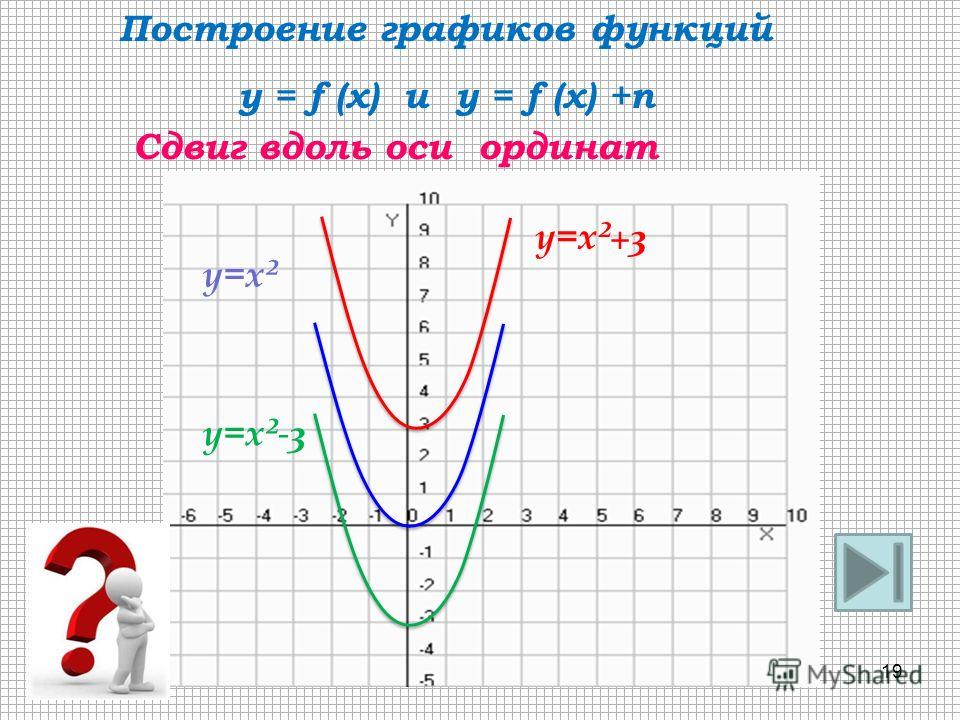 выше).
выше).
Пример 5. Рассмотрим производственную функцию (двухфакторную модель экономического роста)
где — национальный доход за год t; a – показатель приведения к единому масштабу продукции, затрат фондов и труда, оценивающий влияние на рост национального дохода неучтённых в модели факторов; — объём проиводственных фондов; — затраты живого труда в сфере материального производства; — показатели эластичности роста национального дохода в зависимости от роста производственных фондов и живого труда. Функция является функцией двух переменных:
Пройти тест по теме Функции нескольких переменных
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Функции нескольких переменных
- Функция двух и более переменных. Её область определения
- Поверхности второго порядка
- Частные производные
- Касательная плоскость и нормаль к поверхности
- Производная по направлению, градиент функции
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
4.
 1 Функции нескольких переменных. Расчет, том 3
1 Функции нескольких переменных. Расчет, том 3Цели обучения
- 4.1.1 Распознать функцию двух переменных и определить ее область определения и область значений.
- 4.1.2 Нарисуйте график функции двух переменных.
- 4.1.3 Нарисуйте несколько трасс или кривых уровня функции двух переменных.
- 4.1.4 Распознать функцию трех или более переменных и определить ее поверхности уровня.
Наш первый шаг — объяснить, что такое функция более чем одной переменной, начиная с функций двух независимых переменных. Этот шаг включает в себя определение домена и диапазона таких функций, а также обучение их графическому отображению. Мы также исследуем способы соотнесения графиков функций в трех измерениях с графиками более знакомых плоских функций.
Функции двух переменных
Определение функции двух переменных очень похоже на определение функции одной переменной. Основное отличие состоит в том, что вместо отображения значений одной переменной в значения другой переменной мы отображаем упорядоченные пары переменных в другую переменную.
Определение
Функция двух переменных z=f(x,y)z=f(x,y) отображает каждую упорядоченную пару (x,y)(x,y) в подмножестве DD вещественной плоскости ℝ2ℝ2 в уникальную вещественную номер з.з. Набор DD называется доменом функции. Диапазон числа ff — это множество всех действительных чисел zz, у которых есть хотя бы одна упорядоченная пара (x,y)∈D(x,y)∈D такая, что f(x,y)=zf(x,y) =z, как показано на следующем рисунке.
Рисунок 4.2 Область определения функции двух переменных состоит из упорядоченных пар (x,y).(x,y).
Определение домена функции двух переменных требует учета любых ограничений домена, которые могут существовать. Давайте взглянем.
Пример 4.1
Области определения и области значений для функций двух переменных
Найдите область определения и область значений каждой из следующих функций:
- f(x,y)=3x+5y+2f(x,y)=3x+5y+2
- г(х,у)=9-х2-у2г(х,у)=9-х2-у2
Решение
- Это пример линейной функции двух переменных.
 Нет значений или комбинаций xx и yy, из-за которых f(x,y)f(x,y) не определено, поэтому область определения ff составляет ℝ2,ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f(x,y)=z,f(x,y)=z или 3x+5y+2=z.3x+5y+2=z. Одно такое решение можно получить, установив сначала y=0,y=0, что дает уравнение 3x+2=z.3x+2=z. Решением этого уравнения является x=z−23,x=z−23, что дает упорядоченную пару (z−23,0)(z−23,0) как решение уравнения f(x,y)= zf(x,y)=z для любого значения z.z. Таким образом, областью действия функции являются все действительные числа или ℝ.ℝ.
Нет значений или комбинаций xx и yy, из-за которых f(x,y)f(x,y) не определено, поэтому область определения ff составляет ℝ2,ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f(x,y)=z,f(x,y)=z или 3x+5y+2=z.3x+5y+2=z. Одно такое решение можно получить, установив сначала y=0,y=0, что дает уравнение 3x+2=z.3x+2=z. Решением этого уравнения является x=z−23,x=z−23, что дает упорядоченную пару (z−23,0)(z−23,0) как решение уравнения f(x,y)= zf(x,y)=z для любого значения z.z. Таким образом, областью действия функции являются все действительные числа или ℝ.ℝ. - Чтобы функция g(x,y)g(x,y) имела действительное значение, величина под квадратным корнем должна быть неотрицательной:
9−x2−y2≥0,9−x2−y2≥0.
Это неравенство можно записать в видеx2+y2≤9.x2+y2≤9.
Следовательно, область определения g(x,y)g(x,y) равна {(x,y)∈ℝ2|x2+y2≤9}.{(x,y)∈ℝ2|x2+y2≤9 }. График этого набора точек можно описать как диск радиуса 33 с центром в начале координат. Домен включает граничный круг, как показано на следующем графике.
Домен включает граничный круг, как показано на следующем графике. Рисунок 4.3 Область определения функции g(x,y)=9−x2−y2g(x,y)=9−x2−y2 — замкнутый круг радиуса 3.
Чтобы определить диапазон g(x,y)=9−x2−y2g(x,y)=9− x2−y2 начнем с точки (x0,y0)(x0,y0) на границе области, которая определяется соотношением x2+y2=9.×2+y2=9. Отсюда следует, что x02+y02=9×02+y02=9 иg(x0,y0)=9−x02−y02=9−(x02+y02)=9−9=0.g(x0,y0)=9− х02-у02=9-(х02+у02)=9-9=0.
Если x02+y02=0x02+y02=0 (другими словами, x0=y0=0),x0=y0=0), тоg(x0,y0)=9−x02−y02=9−(x02 +y02)=9−0=3.g(x0,y0)=9−x02−y02=9−(x02+y02)=9−0=3.
Это максимальное значение функции. Для любого значения c между 0 и 3, 0 и 3 мы можем найти весь набор точек внутри области определения gg такой, что g(x,y)=c:g(x,y)=c:9−x2−y2 =c9-x2-y2=c2x2+y2=9-c2.9-x2-y2=c9-x2-y2=c2x2+y2=9-c2.
Поскольку 9−c2>0,9−c2>0, это описывает окружность радиуса 9−c29−c2 с центром в начале координат. Любая точка на этой окружности удовлетворяет уравнению g(x,y)=c.g(x,y)=c. Следовательно, диапазон этой функции можно записать в интервальной записи как [0,3].[0,3].
Любая точка на этой окружности удовлетворяет уравнению g(x,y)=c.g(x,y)=c. Следовательно, диапазон этой функции можно записать в интервальной записи как [0,3].[0,3].
Контрольно-пропускной пункт 4.1
Найдите область определения и область значений функции f(x,y)=36−9×2−9y2.f(x,y)=36−9×2−9y2.
Графические функции двух переменных
Предположим, мы хотим построить график функции z=(x,y).z=(x,y). Эта функция имеет две независимые переменные (xandy)(xandy) и одну зависимую переменную (z).(z). При построении графика функции y=f(x)y=f(x) одной переменной мы используем декартову плоскость. Мы можем изобразить любую упорядоченную пару (x,y)(x,y) на плоскости, и с каждой точкой на плоскости связана упорядоченная пара (x,y)(x,y). В функции двух переменных каждая упорядоченная пара (x, y) (x, y) в области определения функции отображается в действительное число z.z. Следовательно, график функции ff состоит из упорядоченных троек (x,y,z). (x,y,z). График функции z=(x,y)z=(x,y) двух переменных называется поверхностью.
(x,y,z). График функции z=(x,y)z=(x,y) двух переменных называется поверхностью.
Чтобы лучше понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте, что система координат (x,y)(x,y) лежит плоско. Тогда каждая точка в области определения функции ff имеет связанное с ней уникальное значение z-valuez. Если zz положительное, то точка на графике расположена выше плоскости xy, xy-plane, если zz отрицательно, то точка на графике расположена ниже плоскости xy.xy. Множество всех точек графика становится двумерной поверхностью, являющейся графиком функции f.f.
Пример 4.2
График функций двух переменных
Создайте график каждой из следующих функций:
- g(x,y)=9−x2−y2g(x,y)=9−x2−y2
- f(x,y)=x2+y2f(x,y)=x2+y2
Решение
- В примере 4.1 мы определили, что область определения g(x,y)=9−x2−y2g(x,y)=9−x2−y2 равна {(x,y)∈ℝ2|x2+y2≤9 }{(x,y)∈ℝ2|x2+y2≤9}, а диапазон равен {z∈ℝ2|0≤z≤3}.
 {z∈ℝ2|0≤z≤3}. Когда x2+y2=9×2+y2=9, мы имеем g(x,y)=0.g(x,y)=0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в плоскости x, y, плоскости x, y соответствует z=0z=0 в ℝ3.ℝ3. Если x2+y2=8,×2+y2=8, то g(x,y)=1,g(x,y)=1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x,y -planex,y-плоскость отображается в z=1z=1 в ℝ3.ℝ3. Когда x2+y2x2+y2 приближается к нулю, значение z приближается к 3. Когда x2+y2=0,×2+y2=0, тогда g(x,y)=3.g(x,y)=3. Это начало координат в плоскости x,y.x,y-plane. Если x2+y2x2+y2 равно любому другому значению между 0 и 9, 0 и 9, то g(x,y)g(x,y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат и радиусом 33, как показано на следующем графике.
{z∈ℝ2|0≤z≤3}. Когда x2+y2=9×2+y2=9, мы имеем g(x,y)=0.g(x,y)=0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в плоскости x, y, плоскости x, y соответствует z=0z=0 в ℝ3.ℝ3. Если x2+y2=8,×2+y2=8, то g(x,y)=1,g(x,y)=1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x,y -planex,y-плоскость отображается в z=1z=1 в ℝ3.ℝ3. Когда x2+y2x2+y2 приближается к нулю, значение z приближается к 3. Когда x2+y2=0,×2+y2=0, тогда g(x,y)=3.g(x,y)=3. Это начало координат в плоскости x,y.x,y-plane. Если x2+y2x2+y2 равно любому другому значению между 0 и 9, 0 и 9, то g(x,y)g(x,y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат и радиусом 33, как показано на следующем графике. Рисунок 4.4 График полушария представлен заданной функцией двух переменных.
- Эта функция также содержит выражение x2+y2.
 x2+y2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f(x,y)=x2+y2f(x,y)=x2+y2 равно нулю (достигается, когда x=y=0.).x=y=0.). Когда x=0,x=0, функция принимает вид z=y2,z=y2, а когда y=0,y=0, функция принимает вид z=x2.z=x2. Это сечения графика и параболы. Напомним из введения в векторы в пространстве, что имя графика f(x,y)=x2+y2f(x,y)=x2+y2 есть параболоид . График ff показан на следующем графике.
x2+y2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f(x,y)=x2+y2f(x,y)=x2+y2 равно нулю (достигается, когда x=y=0.).x=y=0.). Когда x=0,x=0, функция принимает вид z=y2,z=y2, а когда y=0,y=0, функция принимает вид z=x2.z=x2. Это сечения графика и параболы. Напомним из введения в векторы в пространстве, что имя графика f(x,y)=x2+y2f(x,y)=x2+y2 есть параболоид . График ff показан на следующем графике. Рисунок 4,5 Параболоид – это график заданной функции двух переменных.
Пример 4.3
Гайки и болты
Функция прибыли для производителя оборудования определяется выражением
f(x,y)=16−(x−3)2−(y−2)2,f(x,y)=16 −(x−3)2−(y−2)2,
, где xx — количество гаек, проданных в месяц (измеряется в тысячах), а yy — количество болтов, проданных в месяц (измеряется в тысячах). Прибыль измеряется тысячами долларов.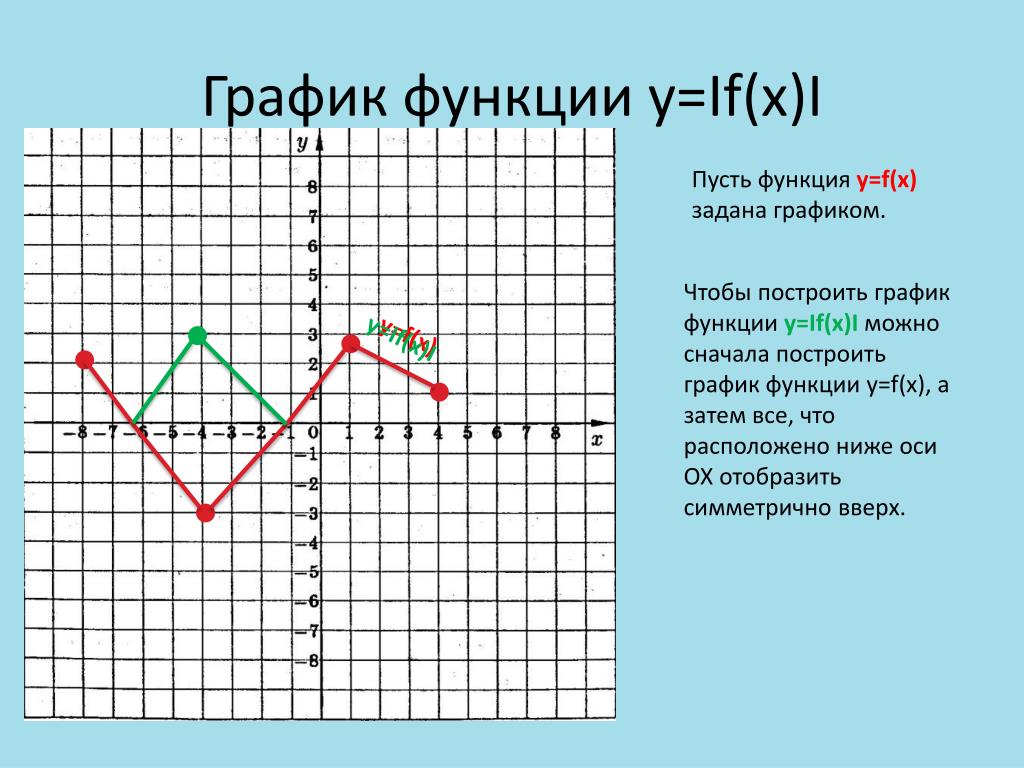 Нарисуйте график этой функции.
Нарисуйте график этой функции.
Решение
Эта функция является полиномиальной функцией от двух переменных. Область определения ff состоит из (x,y)(x,y) пар координат, которые дают неотрицательную прибыль:
16−(x−3)2−(y−2)2≥0(x−3)2+ (y−2)2≤16,16−(x−3)2−(y−2)2≥0(x−3)2+(y−2)2≤16.
Это диск радиуса 44 с центром в точке (3,2).(3,2). Еще одно ограничение состоит в том, что оба xandyxandy должны быть неотрицательными. Когда x=3x=3 и y=2,y=2,f(x,y)=16.f(x,y)=16. Обратите внимание, что любое значение может быть нецелым числом; например, в месяц можно продать 2,52,5 тыс. орехов. Таким образом, домен содержит тысячи точек, поэтому мы можем рассматривать все точки в пределах диска. Для любых z<16,z<16 можно решить уравнение f(x,y)=z:f(x,y)=z:
16-(x-3)2-(y-2)2=z(x-3)2+(y-2)2=16-z.16-(x-3)2-(y-2 )2=z(x−3)2+(y−2)2=16−z.
Поскольку z<16,z<16, мы знаем, что 16−z>0,16−z>0, поэтому предыдущее уравнение описывает окружность радиусом 16−z16−z с центром в точке (3,2).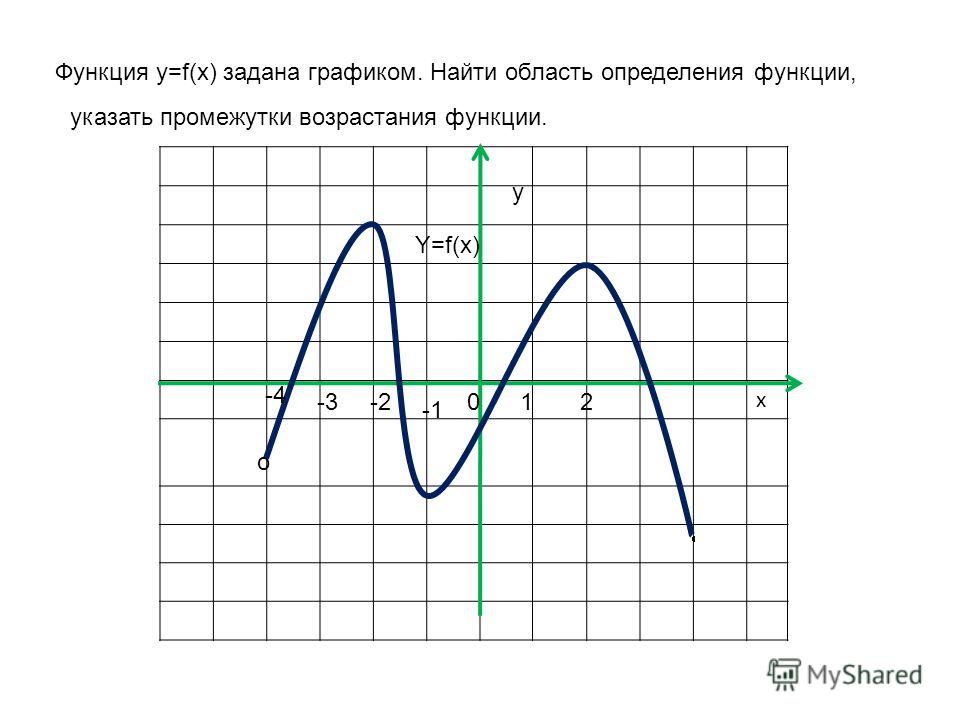 (3,2). Следовательно. диапазон f(x,y)f(x,y) равен {z∈ℝ|z≤16}.{z∈ℝ|z≤16}. График f(x,y)f(x,y) также является параболоидом, и этот параболоид направлен вниз, как показано.
(3,2). Следовательно. диапазон f(x,y)f(x,y) равен {z∈ℝ|z≤16}.{z∈ℝ|z≤16}. График f(x,y)f(x,y) также является параболоидом, и этот параболоид направлен вниз, как показано.
Рисунок 4.6 График данной функции двух переменных также является параболоидом.
Кривые уровня
Если туристы идут по извилистым тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются тропы. Топографическая карта содержит изогнутые линии, называемые контурными линиями . Каждая контурная линия соответствует точкам на карте, имеющим одинаковую высоту (рис. 4.7). Линия уровня функции двух переменных f(x,y)f(x,y) полностью аналогична изолинии на топографической карте.
Рисунок
4.7
(а) Топографическая карта Башни Дьявола, Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутую местность. (b) Перспективное фото Башни Дьявола показывает, насколько круты ее стороны.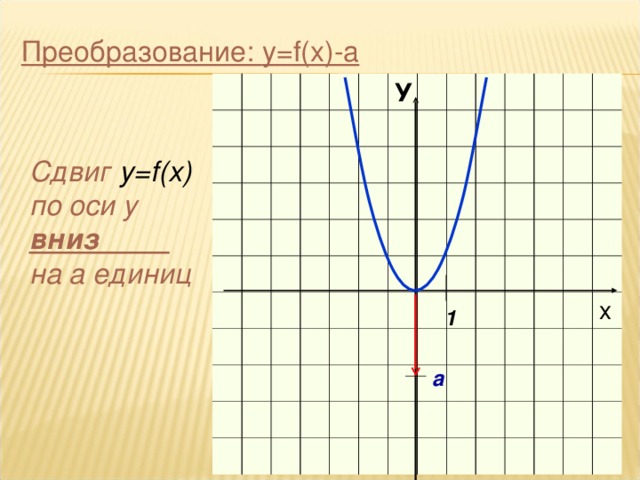 Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Определение
Для заданной функции f(x,y)f(x,y) и числа cc в диапазоне f,af,кривая уровня функции двух переменных для значения cc определяется как множество точек удовлетворяющее уравнению f(x,y)=c.f(x,y)=c.
Возвращаясь к функции g(x,y)=9−x2−y2,g(x,y)=9−x2−y2, мы можем определить кривые уровня этой функции. Диапазон gg — это закрытый интервал [0,3].[0,3]. Во-первых, мы выбираем любое число из этого замкнутого интервала, скажем, c=2.c=2. Кривая уровня, соответствующая c=2c=2, описывается уравнением
9-x2-y2=2,9-x2-y2=2.
Для упрощения возведите в квадрат обе части этого уравнения:
9-x2-y2=4,9-x2-y2=4.
Теперь умножьте обе части уравнения на −1−1 и прибавьте 99 к каждой стороне:
х2+у2=5.х2+у2=5.
Это уравнение описывает окружность с центром в начале координат и радиусом 5,5. Использование значений cc между 0 и 30 и 3 дает другие круги, также центрированные в начале координат. Если c=3,c=3, то окружность имеет радиус 0,0, поэтому она состоит только из начала координат. На рис. 4.8 представлен график кривых уровня этой функции, соответствующих c=0, 1, 2 и 3. c = 0, 1, 2 и 3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя в квадрат обе стороны. Здесь это не так, потому что диапазон функции квадратного корня неотрицательный.
Если c=3,c=3, то окружность имеет радиус 0,0, поэтому она состоит только из начала координат. На рис. 4.8 представлен график кривых уровня этой функции, соответствующих c=0, 1, 2 и 3. c = 0, 1, 2 и 3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя в квадрат обе стороны. Здесь это не так, потому что диапазон функции квадратного корня неотрицательный.
Рисунок 4,8 Кривые уровня функции g(x,y)=9−x2−y2,g(x,y)=9−x2−y2 при использовании c=0,1,2,c=0,1,2 и 33 (c=3(c=3 соответствует началу координат).
График различных кривых уровня функции называется контурной картой.
Пример 4.4
Составление контурной карты
Учитывая функцию f(x,y)=8+8x−4y−4×2−y2,f(x,y)=8+8x−4y−4×2−y2, найдите кривую уровня, соответствующую к с=0.с=0. Затем создайте контурную карту для этой функции. Каковы домен и диапазон f?f?
Решение
Чтобы найти кривую уровня для c=0,c=0, мы устанавливаем f(x,y)=0f(x,y)=0 и решаем.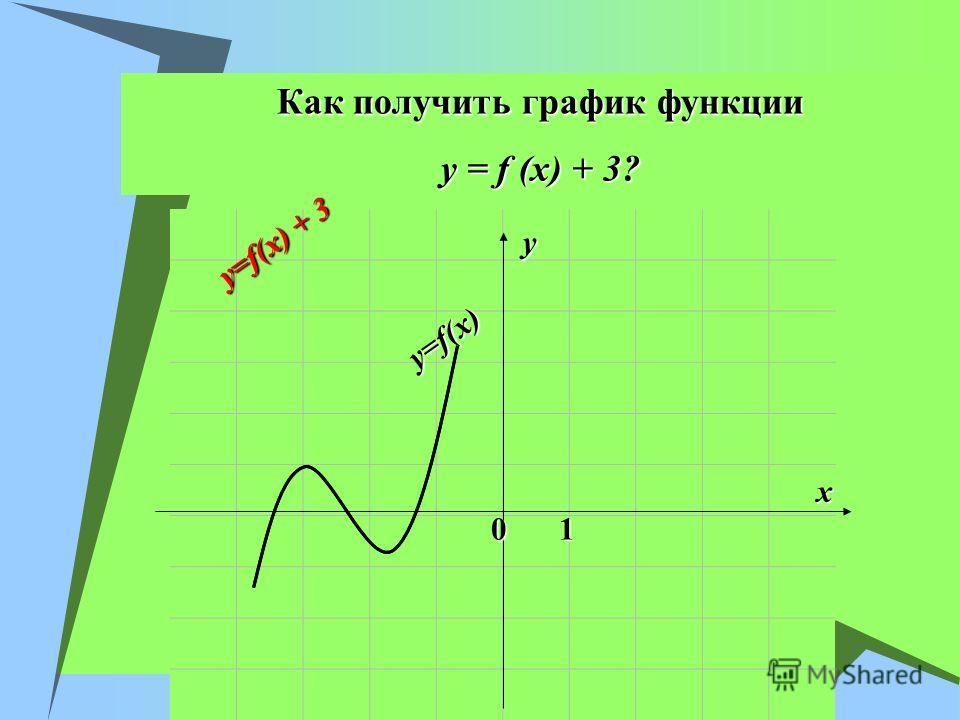 Это дает
Это дает
0=8+8x−4y−4×2−y2.0=8+8x−4y−4×2−y2.
Затем мы возводим обе части в квадрат и умножаем обе части уравнения на −1:−1:
4×2+y2−8x+4y−8=0,4×2+y2−8x+4y−8=0.
Теперь мы переставляем слагаемые, соединяя слагаемые xx и слагаемые yy, и прибавляем 88 к каждой стороне:
4×2−8x+y2+4y=8,4×2−8x+y2+4y=8.
Далее сгруппируем пары термов, содержащих одну и ту же переменную в скобках, и умножим на 44 из первой пары:
4(x2-2x)+(y2+4y)=8,4(x2-2x)+(y2+4y)=8.
Затем мы дополняем квадрат в каждой паре скобок и добавляем правильное значение в правую часть:
4(x2−2x+1)+(y2+4y+4)=8+4(1)+ 4.4(х2-2х+1)+(у2+4у+4)=8+4(1)+4.
Затем факторизуем левую часть и упрощаем правую:
4(x−1)2+(y+2)2=16,4(x−1)2+(y+2)2 =16.
Наконец, мы делим обе части на 16:16:
(x−1)24+(y+2)216=1.(x−1)24+(y+2)216=1.
(4.1)
Это уравнение описывает эллипс с центром в точке (1,−2).(1,−2). График этого эллипса показан на следующем графике.
Рисунок 4.9 Кривая уровня функции f(x,y)=8+8x−4y−4×2−y2f(x,y)=8+8x−4y−4×2−y2, соответствующая c=0.c=0.
Мы можем повторить тот же вывод для значений cc меньше 4,4. Тогда уравнение 4.1 принимает вид
4(x−1)216−c2+(y+2)216−c2=14(x−1)216−c2+(y+2)216−c2=1
для произвольного значения c.c. На рис. 4.10 показана контурная карта для f(x,y)f(x,y) с использованием значений c=0,1,2 и 3.c=0,1,2 и 3. Когда c=4,c=4, кривая уровня представляет собой точку (−1,2).(−1,2).
Рисунок 4.10 Контурная карта для функции f(x,y)=8+8x−4y−4×2−y2f(x,y)=8+8x−4y−4×2−y2 с использованием значений c=0,1,2,3 и 4 .с=0,1,2,3 и4.
Домен:x,y внутри эллипса (x-1)24+(y+2)216=1Диапазон: [0,∞)Домен:x,y внутри эллипса (x-1)24+(y+2)216 =1Диапазон: [0,∞) 90 919
Контрольно-пропускной пункт 4.2
Найдите и начертите кривую уровня функции g(x,y)=x2+y2−6x+2yg(x,y)=x2+y2−6x+2y, соответствующей c=15.c=15.
Еще один полезный инструмент для понимания графика функции двух переменных называется вертикальной трассировкой. Кривые уровня всегда изображаются в плоскости xy, плоскости xy, но, как следует из их названия, вертикальные трассы изображаются в плоскостях xzxz или yz-planes.yz.
Кривые уровня всегда изображаются в плоскости xy, плоскости xy, но, как следует из их названия, вертикальные трассы изображаются в плоскостях xzxz или yz-planes.yz.
Определение
Рассмотрим функцию z=f(x,y)z=f(x,y) с областью определения D⊆ℝ2.D⊆ℝ2. Вертикальный след функции может быть либо набором точек, решающим уравнение f(a,y)=zf(a,y)=z для данной константы x=ax=a, либо f(x,b)=zf (x,b)=z для заданной константы y=b.y=b.
Пример 4,5
Поиск вертикальных следов
Поиск вертикальных следов для функции f(x,y)=sinxcosyf(x,y)=sinxcosy, соответствующей x=−π4,0 и π4,x=−π4,0,иπ4, и y =-π4,0, и π4.y=-π4,0, и π4.
Решение
Первое множество x=−π4x=−π4 в уравнении z=sinxcosy:z=sinxcosy:
z=sin(−π4)cosy=−2cosy2≈−0,7071cosy.z=sin(−π4)cosy=−2cosy2 ≈−0,7071 уютный.
Это описывает косинусный график в плоскости x=−π4.x=−π4. Другие значения zz приведены в следующей таблице.
| куб.см | Вертикальная трассировка для x=cx=c |
|---|---|
| −π4−π4 | z=-2cosy2z=-2cosy2 |
| 00 | г=0г=0 |
| π4π4 | z=2cosy2z=2cosy2 |
Стол 4.1 Вертикальные трассы, параллельные xz-Planexz-Plane для функции f(x,y)=sinxcosyf(x,y)=sinxcosy
Аналогичным образом мы можем заменить y-значенияsy-значения в уравнении f(x ,y)f(x,y) для получения трасс в плоскости yz, плоскости yz, как указано в следующей таблице.
| дд | Вертикальная трасса на г=дд=д |
|---|---|
| −π4−π4 | z=2sinx2z=2sinx2 |
| 00 | z=sinxz=sinx |
| π4π4 | z=2sinx2z=2sinx2 |
Стол 4.2 Вертикальные трассы, параллельные плоскости yz-Planeyz, для функции f(x,y)=sinxcosyf(x,y)=sinxcosy
Три трассы в плоскости xz-xz являются функциями косинуса; три следа в плоскости yz-planeyz являются синусоидальными функциями. Эти кривые появляются на пересечениях поверхности с плоскостями x=−π4,x=0,x=π4x=−π4,x=0,x=π4 и y=−π4,y=0,y=π4y=− π4,y=0,y=π4, как показано на следующем рисунке.
Рисунок 4.11 Вертикальными следами функции f(x,y)f(x,y) являются косинусоидальные кривые в плоскостях xzxz-плоскостей (а) и синусоидальные кривые в плоскостях yz-syz (б).
Контрольно-пропускной пункт 4.3
Определите уравнение вертикального следа функции g(x,y)=−x2−y2+2x+4y−1g(x,y)=−x2−y2+2x+4y−1, соответствующей y=3 ,y=3, и описать его график.
Функции двух переменных могут создавать эффектные поверхности. На следующем рисунке показаны два примера.
Рисунок 4.12 Примеры поверхностей, представляющих функции двух переменных: (а) комбинация степенной функции и синусоидальной функции и (б) комбинация тригонометрической, экспоненциальной и логарифмической функций.
Функции более чем двух переменных
До сих пор мы рассматривали только функции двух переменных. Однако полезно кратко рассмотреть функции более чем двух переменных. Два таких примера
f(x,y,z)=x2−2xy+y2+3yz−z2+4x−2y+3x−6(многочлен от трех переменных)f(x,y,z)=x2−2xy+y2+3yz −z2+4x−2y+3x−6(многочлен от трех переменных)
и
g(x,y,t)=(x2−4xy+y2)sint−(3x+5y)cost. g(x,y,t)=(x2−4xy+y2)sint−(3x+5y)cost .
g(x,y,t)=(x2−4xy+y2)sint−(3x+5y)cost .
В первой функции (x,y,z)(x,y,z) представляет точку в пространстве, а функция ff сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра. Во второй функции (x,y)(x,y) может представлять точку на плоскости, а tt может представлять время. Функция может сопоставить точку на плоскости третьей величине (например, давлению) в данный момент времени t.t. Метод нахождения области определения функции более чем двух переменных аналогичен методу для функций одной или двух переменных.
Пример 4.6
Области определения функций трех переменных
Найдите область определения каждой из следующих функций:
- f(x,y,z)=3x−4y+2z9−x2−y2−z2f(x,y,z) =3x−4y+2z9−x2−y2−z2
- g(x,y,t)=2t−4×2−y2g(x,y,t)=2t−4×2−y2
Решение
- Чтобы функция f(x,y,z)=3x−4y+2z9−x2−y2−z2f(x,y,z)=3x−4y+2z9−x2−y2−z2 была определена (и была действительное значение), должны выполняться два условия:
- Знаменатель не может быть равен нулю.

- Подкоренное число не может быть отрицательным.
9−x2−y2−z2>0,9−x2−y2−z2>0.
Перемещение переменных на другую сторону и обращение неравенства дает домен какdomain(f)={(x,y,z)∈ℝ3|x2+y2+z2<9},domain(f)={( x,y,z)∈ℝ3|x2+y2+z2<9},
, который описывает шар радиуса 33 с центром в начале координат. ( Примечание : Поверхность шара не включена в этот домен.) - Знаменатель не может быть равен нулю.
- Чтобы функция g(x,y,t)=2t−4×2−y2g(x,y,t)=2t−4×2−y2 была определена (и была действительным значением), должны выполняться два условия:
- Подкоренное число не может быть отрицательным.
- Знаменатель не может быть равен нулю.
 Следовательно, домен gg равен
Следовательно, домен gg равенdomain(g)={(x,y,t)|y≠±x,t≥2}.domain(g)={(x,y,t)|y≠±x ,t≥2}.
Контрольно-пропускной пункт 4.4
Найдите область определения функции h(x,y,t)=(3t−6)y−4×2+4.h(x,y,t)=(3t−6)y−4×2+4.
Функции двух переменных имеют кривые уровня, которые отображаются в виде кривых в плоскости xy.xy-plane. Однако, когда функция имеет три переменные, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Определение
Для заданной функции f(x,y,z)f(x,y,z) и числа cc в диапазоне f,f поверхность уровня функции трех переменных определяется как множество точек удовлетворяющее уравнению f(x,y,z)=c.f(x,y,z)=c.
Пример 4.7
Поиск поверхности уровня
Найдите поверхность уровня для функции f(x,y,z)=4×2+9y2−z2f(x,y,z)=4×2+9y2−z2, соответствующей c=1.c= 1.
Решение
Поверхность уровня определяется уравнением 4×2+9y2-z2=1,4×2+9y2-z2=1. Это уравнение описывает гиперболоид из одного листа, как показано на следующем рисунке.
Это уравнение описывает гиперболоид из одного листа, как показано на следующем рисунке.
Рисунок 4.13 Гиперболоид одного листа с некоторыми его поверхностями уровня.
Контрольно-пропускной пункт 4,5
Найти уравнение поверхности уровня функции
g(x,y,z)=x2+y2+z2−2x+4y−6zg(x,y,z)=x2+y2+z2−2x+ 4y−6z
, соответствующие c=2,c=2, и опишите поверхность, если это возможно.
Раздел 4.1 Упражнения
В следующих упражнениях оцените каждую функцию при указанных значениях.
1.
W(x,y)=4×2+y2.W(x,y)=4×2+y2. Найдите W(2,−1),W(2,−1),W(−3,6).W(−3,6).
2.
W(x,y)=4×2+y2.W(x,y)=4×2+y2. Найдите W(2+h,3+h).W(2+h,3+h).
3.
Объем прямого кругового цилиндра рассчитывается как функция двух переменных: V(x,y)=πx2y,V(x,y)=πx2y, где xx — радиус правильного кругового цилиндра, а yy — высота цилиндра. Оцените V(2,5)V(2,5) и объясните, что это значит.
Оцените V(2,5)V(2,5) и объясните, что это значит.
4.
Баллон с кислородом состоит из правого цилиндра высотой yy и радиусом xx с двумя полусферами радиуса xx, установленными сверху и снизу цилиндра. Выразите объем бака как функцию двух переменных xandy,xandy, найдите V(10,2),V(10,2) и объясните, что это значит.
Для следующих упражнений найдите область определения функции.
5.
V(x,y)=4×2+y2V(x,y)=4×2+y2
6.
f(x,y)=x2+y2−4f(x,y)=x2+y2−4
7.
f(x,y)=4ln(y2−x)f(x,y)=4ln(y2−x)
8.
g(x,y)=16−4×2−y2g(x,y)=16−4×2−y2
9.
z(x,y)=y2−x2z(x,y)=y2−x2
10.
f(x,y)=y+2x2f(x,y)=y+2×2
Найдите диапазон функций.
11.
g(x,y)=16−4×2−y2g(x,y)=16−4×2−y2
12.
V(x,y)=4×2+y2V(x,y)=4×2+y2
13.
г = у2-х2г = у2-х2
Для следующих упражнений найдите кривые уровня каждой функции при указанном значении cc, чтобы визуализировать данную функцию.
14.
z(x,y)=y2−x2,z(x,y)=y2−x2,c=1c=1
15.
z(x,y)=y2−x2,z(x,y)=y2−x2,c=4c=4
16.
г(х,у)=х2+у2;с=4,с=9г(х,у)=х2+у2;с=4,с=9
17.
g(x,y)=4−x−y;c=0,4g(x,y)=4−x−y;c=0,4
18.
f(x,y)=xy;c=1;c=−1f(x,y)=xy;c=1;c=−1
19.
h(x,y)=2x−y;c=0,−2,2h(x,y)=2x−y;c=0,−2,2
20.
f(x,y)=x2−y;c=1,2f(x,y)=x2−y;c=1,2
21.
g(x,y)=xx+y;c=−1,0,2g(x,y)=xx+y;c=−1,0,2
22.
g(x,y)=x3−y;c=−1,0,2g(x,y)=x3−y;c=−1,0,2
23.
g(x,y)=exy;c=12,3g(x,y)=exy;c=12,3
24.
f(x,y)=x2;c=4,9f(x,y)=x2;c=4,9
25.
f(x,y)=xy−x;c=−2,0,2f(x,y)=xy−x;c=−2,0,2
26.
h(x,y)=ln(x2+y2);c=−1,0,1h(x,y)=ln(x2+y2);c=−1,0,1
27.
g(x,y)=ln(yx2);c=−2,0,2g(x,y)=ln(yx2);c=−2,0,2
28.
z=f(x,y)=x2+y2,z=f(x,y)=x2+y2,c=3c=3
29.
f(x,y)=y+2×2,f(x,y)=y+2×2,c=c= любая константа
Для следующих упражнений найдите вертикальные трассы функций при указанных значениях xx и y и начертите трассы.
30.
z=4-x-y;x=2z=4-x-y;x=2
31.
f(x,y)=3x+y3,x=1f(x,y)=3x+y3,x=1
32.
z=cosx2+y2z=cosx2+y2x=1x=1
Найдите область определения следующих функций.
33.
z=100−4×2−25y2z=100−4×2−25y2
34.
z=ln(x−y2)z=ln(x−y2)
35.
f(x,y,z)=136−4×2−9y2−z2f(x,y,z)=136−4×2−9y2−z2
36.
f(x,y,z)=49−x2−y2−z2f(x,y,z)=49−x2−y2−z2
37.
f(x,y,z)=16−x2−y2−z23f(x,y,z)=16−x2−y2−z23
38.
f(x,y)=cosx2+y2f(x,y)=cosx2+y2
Для следующих упражнений постройте график функции.
39.
z=f(x,y)=x2+y2z=f(x,y)=x2+y2
40.
г=х2+у2г=х2+у2
41.
Используйте технологию для построения графика z=x2y.z=x2y.
Нарисуйте следующее, найдя кривые уровня. Проверьте график с помощью технологии.
42.
f(x,y)=4−x2−y2f(x,y)=4−x2−y2
43.
f(x,y)=2−x2+y2f(x,y)=2−x2+y2
44.
z=1+e-x2-y2z=1+e-x2-y2
45.
г=cosx2+y2z=cosx2+y2
46.
z=y2−x2z=y2−x2
47.
Опишите контурные линии для нескольких значений cc для z=x2+y2-2x-2y.z=x2+y2-2x-2y.
Найдите поверхность уровня для функций трех переменных и опишите ее.
48.
w(x,y,z)=x−2y+z,c=4w(x,y,z)=x−2y+z,c=4
49.
w(x,y,z)=x2+y2+z2,c=9w(x,y,z)=x2+y2+z2,c=9
50.
w(x,y,z)=x2+y2−z2,c=−4w(x,y,z)=x2+y2−z2,c=−4
51.
w(x,y,z)=x2+y2−z2,c=4w(x,y,z)=x2+y2−z2,c=4
52.
w(x,y,z)=9×2−4y2+36z2,c=0w(x,y,z)=9×2−4y2+36z2,c=0
Для следующих упражнений найдите уравнение кривой уровня ff, содержащее точку P.P.
53.
f(x,y)=1−4×2−y2,P(0,1)f(x,y)=1−4×2−y2,P(0,1)
54.
g(x,y)=y2arctanx,P(1,2)g(x,y)=y2arctanx,P(1,2)
55.
g(x,y)=exy(x2+y2),P(1,0)g(x,y)=exy(x2+y2),P(1,0)
56.
Напряженность EE электрического поля в точке (x,y,z)(x,y,z), возникающего в результате бесконечно длинного заряженного провода, лежащего вдоль оси y, определяется выражением E(x,y,z )=k/x2+y2,E(x,y,z)=k/x2+y2, где kk — положительная константа. Для простоты положим k=1k=1 и найдем уравнения поверхностей уровня для E=10 и E=100.E=10 и E=100.
Для простоты положим k=1k=1 и найдем уравнения поверхностей уровня для E=10 и E=100.E=10 и E=100.
57.
Тонкая железная пластина расположена в xy-plane.xy-plane. Температура TT в градусах Цельсия в точке P(x,y)P(x,y) обратно пропорциональна квадрату ее расстояния от начала координат. Выразите TT как функцию xandy.xandy.
58.
См. предыдущую проблему. Используя найденную там температурную функцию, определите константу пропорциональности, если температура в точке P(1,2) равна 50°C. P(1,2) равна 50°C. Используйте эту константу для определения температуры в точке Q(3,4).Q(3,4).
59.
См. предыдущую проблему. Найдите кривые уровня для Т=40°С и Т=100°С, Т=40°С и Т=100°С и опишите, что представляют собой кривые уровня.
График функции двух переменных
Содержание
- 1 Определение
- 2 аспекта
- 2.
 1 Домен и диапазон
1 Домен и диапазон - 2.2 Проверка вертикальной линии
- 2.
- 3 Ограничение на одну переменную
- 3.1 График ограничения
- 3.2 Непрерывность каждой переменной и отдельная непрерывность в графическом выражении
- 3.3 Частные производные в графическом выражении
- 3.4 Производные по направлениям в графическом виде
- 3.5 Вектор градиента в графическом виде
Определение
Предположим, функция двух переменных , с областью определения подмножество . Граф представляет собой подмножество трехмерного евклидова пространства с координатами , заданное уравнением:
Эквивалентно, это набор точек:
Наглядно этот график выглядит как поверхность достаточно красивой функции.
Другой способ определения графика заключается в том, что для каждой точки на линии существует ровно одна точка графика, а именно точка с .
Оси — и — являются осями независимой переменной , а ось -, также называемая -осью, является осью зависимой переменной .
Аспекты
Домен и диапазон
| Аспект функции | Как это можно вывести из графика |
|---|---|
| домен | проецировать весь граф на -плоскость. |
| диапазон | спроецировать весь график на -ось. |
Проверка вертикальной линии
Проверка вертикальной линии для функции одной переменной говорит, что каждая вертикальная линия пересекает график ровно в одной точке, если -координата находится в домене и в нет точка, если -координата не находится в домене. Имеется аналогичный тест для функции двух переменных. Это говорит о том, что любая линия, параллельная -оси (оси значения функции), пересекает график ровно в одной точке, если -пара для линии находится в домене, и не пересекает график ни в одной точке, если -пара для линии не в домене. В частности, любая прямая, параллельная -оси, должна пересекать график функции не более чем в одной точке.
В частности, любая прямая, параллельная -оси, должна пересекать график функции не более чем в одной точке.
Если конкретное подмножество нарушает это условие, оно не может быть реализовано как график функции.
Ограничение на одну переменную
График ограничения
Предположим, мы фиксируем, но позволяем варьировать. Со стороны домена это эквивалентно рассмотрению горизонтальной линии в -плоскости. Предположим, нас интересует сужение функции на эту прямую (точнее, пересечение этой прямой с ). Другими словами, нас интересует изучение функции:
Это функция одна переменная , а именно . Далее график этой функции можно получить пересечением графика исходной функции плоскостью с плоскостью в . Обратите внимание, что эта плоскость параллельна -плоскости. В этой плоскости мы рассматриваем как независимую переменную, так и зависимую переменную.
Аналогично предположим, что мы фиксируем, но допускаем варьирование. Со стороны домена это эквивалентно рассмотрению вертикальной линии в -плоскости. Предположим, нас интересует сужение функции на эту прямую (точнее, пересечение этой прямой с ). Другими словами, нас интересует изучение функции:
Это функция одной переменной , а именно . Далее график этой функции можно получить пересечением графика исходной функции плоскостью с плоскостью в . Обратите внимание, что эта плоскость параллельна -плоскости. В этой плоскости мы рассматриваем как независимую переменную, так и зависимую переменную.
Непрерывность по каждой переменной и отдельная непрерывность в графическом выражении
Имеем следующее:
| Подтверждение непрерывности | Как мы можем проверить это по графику |
|---|---|
| непрерывен в точке | Рассмотрим граф, ограниченный плоскостью. Это непрерывно при . Это непрерывно при . |
| непрерывен в точке | Рассмотрим граф, ограниченный плоскостью. Это непрерывно при . |
| является раздельно непрерывным непрерывным по обеим переменным в точке . | Оба вышеуказанных состояния. |
| непрерывен везде. | Ограничения графика на все плоскости, параллельные -плоскости, дают графики непрерывных функций. |
| непрерывен везде. | Ограничения графика на все плоскости, параллельные -плоскости, дают графики непрерывных функций. |
| везде по отдельности непрерывна по обеим переменным. | Оба приведенных выше условия, т. е. ограничения графика на все плоскости, параллельные либо -плоскости, либо -плоскости, являются графиками непрерывных функций. |
Частные производные в графическом выражении
Для получения дополнительной информации см. Частные производные
У нас есть следующее:
| Частная производная | Графическая интерпретация |
|---|---|
| Частная производная в точке области определения функции | Наклон касательной at к сужению графика на плоскость . |
| Частная производная в точке области определения функции | Наклон касательной at к сужению графика на плоскость . |
Производные по направлению в графическом виде
Дополнительную информацию см.: Производная по направлению
Производную по направлению в направлении единичного вектора в точке можно определить следующим образом: сначала пересечь график функции с плоскостью . Эта плоскость перпендикулярна -плоскости, и ее пересечение с -плоскостью является линией, проходящей в направлении единичного вектора .
Это пересечение можно рассматривать как график функции одной переменной, где точка рассматривается как начало координат, направление — ось независимой переменной, а направление оси — ось зависимой переменной. Теперь производная по направлению — это наклон этого графика для значения зависимой переменной, равного 0.
Вектор градиента в графическом виде
Для получения дополнительной информации см.: Вектор градиента
Мы говорим, что это дифференцируемо в точке, если вектор градиента существует в точке. Это эквивалентно графику функции, имеющей четко определенную касательную плоскость в точке . Далее, уравнение этой касательной плоскости имеет вид:
Другой способ выразить это так:
Обратите внимание, что возможно, что обе частные производные существуют, но функция не дифференцируема. В этом случае поверхность не имеет четко определенной касательной плоскости в точке. Несмотря на то, что мы можем определить плоскость приведенным выше уравнением, это не касательная плоскость, потому что касательная плоскость не существует.
Рисование — Учебное пособие
Sage может создавать двухмерные и трехмерные графики.
Двумерные графики
В двух измерениях Sage может рисовать круги, линии и многоугольники; графики функций в прямоугольных координатах; а еще полярный графики, контурные графики и графики векторных полей. Мы приводим примеры некоторые из них здесь. Дополнительные примеры построения графиков с помощью Sage см. Решение дифференциальных уравнений и Максимумов, а также Мудрые конструкции документация.
Эта команда создает желтый круг радиусом 1 с центром в происхождение:
мудрец: круг((0,0), 1, rgbcolor=(1,1,0)) Графический объект, состоящий из 1 графического примитиваг.
Вы также можете создать закрашенный круг:
мудрец: круг((0,0), 1, rgbcolor=(1,1,0), fill=True) Графический объект, состоящий из 1 графического примитива
Вы также можете создать круг, назначив его переменной; это не рисует это:
мудрец: c = круг((0,0), 1, rgbcolor=(1,1,0))
Чтобы построить его, используйте c.show() или show(c) следующим образом:
мудрец: c.show()
В качестве альтернативы, оценка c.save('filename.png') спасет
заговорить с данным файлом.
Теперь эти «круги» больше похожи на эллипсы, потому что оси масштабируется по-разному. Вы можете исправить это:
мудрец: c.show(aspect_ratio=1)
Команда show(c, aspect_ratio=1) выполняет то же самое
вещь, или вы можете сохранить изображение, используя c.save('имя_файла.png', aspect_ratio=1) .
Легко построить график основных функций:
мудрец: сюжет(поскольку, (-5,5)) Графический объект, состоящий из 1 графического примитива 93), (х, 0,2 * пи), rgbcolor = оттенок (0,6)) мудрец: показать (p1+p2+p3, оси = ложь)
Хороший способ создания заполненных фигур — составить список
точки ( L в приведенном ниже примере), а затем используйте полигон команда построить фигуру с границей, образованной этими точками. За
например, вот зеленый дельтовидный:
мудрец: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)), .г....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] для i в диапазоне (200)] шалфей: p = многоугольник (L, rgbcolor = (1/8,3/4,1/2)) мудрец: п Графический объект, состоящий из 1 графического примитива
Введите show(p, axes=false) , чтобы увидеть это без каких-либо осей.
Вы можете добавить текст на график:
мудрец: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] для i в диапазоне (200)]
шалфей: p = многоугольник (L, rgbcolor = (1/8, 1/4, 1/2))
шалфей: t = текст ("гипотрохоид", (5,4), rgbcolor=(1,0,0))
мудрец: показать(p+t)
Учителя математики часто рисуют на доске следующий сюжет: не одна ветвь arcsin, а несколько из них: т. е. график \(y=\sin(x)\) для \(x\) между \(-2\pi\) и \(2\pi\), перевернутые относительно линии 45 градусов. Следующее Команды Sage строят это:
мудрец: v = [(sin(x),x) для x в srange(-2*float(pi),2*float(pi),0.1)] мудрец: линия (v) Графический объект, состоящий из 1 графического примитива
Поскольку функция тангенса имеет больший диапазон, чем синус, при использовании тот же трюк, чтобы построить арктангенс, вы должны изменить минимальные и максимальные координаты для оси x :
мудрец: v = [(tan(x),x) для x в srange(-2*float(pi),2*float(pi),0,01)] мудрец: показать (строка (v), xmin = -20, xmax = 20)
Sage также вычисляет полярные графики, контурные графики и графики векторного поля. (для специальных типов функций). Вот пример контура
сюжет:
(для специальных типов функций). Вот пример контура
сюжет:
мудрец: f = лямбда x,y: cos(x*y) шалфей: контур_сюжет (f, (-4, 4), (-4, 4)) Графический объект, состоящий из 1 графического примитива
Трехмерные графики
Sage также можно использовать для создания трехмерных графиков. В обоих блокнот и REPL, эти графики будут отображаться по умолчанию с помощью пакета с открытым исходным кодом [ThreeJS], который интерактивно поддерживает вращение и масштабирование фигуры с помощью мыши.
Используйте plot3d для построения графика функции вида \(f(x, y) = z\): 92
мудрец: parametric_plot3d([fx, fy, fz], (u, -1, 1), (v, -1, 1),
….: кадр = ложь, цвет = «желтый»)
Графика3d Объект
Крестовина:
мудрец: u, v = var('u,v')
мудрец: fx = (1+cos(v))*cos(u)
мудрец: fy = (1+cos(v))*sin(u)
мудрец: fz = -tanh((2/3)*(u-pi))*sin(v)
мудрец: parametric_plot3d([fx, fy, fz], (u, 0, 2*pi), (v, 0, 2*pi),
....: кадр = ложь, цвет = "красный")
Графика3d Объект
Скрученный тор:
мудрец: u, v = var('u,v')
мудрец: fx = (3+sin(v)+cos(u))*cos(2*v)
мудрец: fy = (3+sin(v)+cos(u))*sin(2*v)
мудрец: fz = sin(u)+2*cos(v)
мудрец: parametric_plot3d([fx, fy, fz], (u, 0, 2*pi), (v, 0, 2*pi),
. ...: кадр = ложь, цвет = "красный")
Графика3d Объект
92-4)
...: кадр = ложь, цвет = "красный")
Графика3d Объект
92-4) Прочие графики
√(4sin(2x))
√(4cos(2x))
Функции – Polar
Линии
2csc(θ)
2сек(θ)
1/(sin(θ) - cos(θ))
Круги
1
2
6sin(θ)
8cos(θ)
Спирали
θ
θ/5 дом=(0, 10π)
√(θ) дом=(0, 10π)
1/θ дом=(0, 10π)
Розы
4sin(3θ)
4sin(2θ)
4sin(5θ)
4sin(4θ)
Эллипсы
1/(1-.8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
Параболы
1/(1-sin(θ))
1/(1+cos(θ))
1/(1+sin(θ))
1/(1-cos(θ))
Гипербола
1/(1+2cos(θ))
4/(1+2sin(θ))
1/(1-2cos(θ))
4/(1-2sin(θ))
Кардиоиды
3+3cos(θ)
2+2sin(θ)
3-3cos(θ)
2-2sin(θ)
Лимакон
2+3cos(θ)
1+2sin(θ)
2-3cos(θ)
1-2sin(θ)
Лемнискат 92
грех (ху) = потому что (ху)
Уравнения — полярные
В настоящее время недоступно. 2, т] дом = (-4, 4)
95)] дом=(0, 12π)
2, т] дом = (-4, 4)
95)] дом=(0, 12π)
Параметрический – полярный
Линии
[2csc(t), t]
[2сек(т), т]
[1/(sin(t) - cos(t)), t]
Круги
[1, т]
[2, т]
[6sin(t), t]
[8cos(t), t]
Спирали
[т, т]
[t/5, t] dom=(0, 10π)
[√(t), t] дом=(0, 10π)
[1/t, t] dom=(0, 10π)
Розы
[4sin(3t), т]
[4sin(2t), т]
[4sin(5t), т]
[4sin(4t), т]
Эллипсы
[1/(1-.8cos(t)), т]
[1/(1-.8sin(t)), т]
[1/(1+.8cos(t)), т]
[1/(1+.8sin(t)), т]
Параболы
[1/(1-sin(t)), t]
[1/(1+cos(t)), t]
[1/(1+sin(t)), t]
[1/(1-cos(t)), t]
Гипербола
[1/(1+2cos(t)), t]
[4/(1+2sin(t)), t]
[1/(1-2cos(t)), t]
[4/(1-2sin(t)), t]
Кардиоиды
[3+3cos(t), t]
[2+2sin(t), t]
[3-3cos(t), t]
[2-2sin(t), t]
Лимаконс
[2+3cos(t), t]
[1+2sin(t), t]
[2-3cos(t), t]
[1-2sin(t), t]
Лемнискаты
[√(4sin(2t)), т]
[√(4cos(2t)), т]
Прочие параметрические графики
[5sin(t), 4cos(t)]
[5sin(t), 4cos(2t)]
[5sin(t), 4cos(3t)]
[5sin(2t), 4cos(t)]
[5sin(2t), 4cos(3t)]
[5sin(2t), 4cos(5t)]
[5sin(3t), 4cos(5t)]
[5sin(3t), 4cos(7t)]
[5sin(5t), 4cos(7t)]
[5sin(7t), 4cos(9t)]
РАД
Полярный
🔍+
1 🔍−
время построения графика (с)
Калькулятор загружается.
Пожалуйста, подождите....
Сделайте это прозрачным
Толщина графика Угловой режим
РАД
градус
ГРД График по мере ввода (взаимодействие)
Скрыть оси
Скрыть сетки
Показать интерфейс анимации осей ...
Медленно
Быстро
Показать угловые оси
Сделанный
подпись
Отключить программную клавиатуру
Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.
График функции — Словарь героев Википедии
Графическое представление см. в разделе График (графика). Чтобы узнать о комбинаторной структуре, см. График (дискретная математика) . Для теоретико-графового представления функции от множества к самой себе см. Функциональный график.
Эта статья нуждается в дополнительных ссылках для проверки . В математике график функции представляет собой набор упорядоченных пар (x, y) {\ displaystyle (x, y)}, где f (x) = y. {\ displaystyle f (x) = y.} В общем случае, когда x {\ displaystyle x} и f (x) {\ displaystyle f (x)} - действительные числа, эти пары представляют собой декартовы координаты точек в двумерном пространстве и, таким образом, образуют подмножество этой плоскости. В случае функций двух переменных, то есть функций, область определения которых состоит из пар (x, y), {\ displaystyle (x, y),} граф обычно относится к множеству упорядоченных троек (x, y, z) {\ displaystyle (x, y, z)}, где f (x, y) = z, {\ displaystyle f (x, y) = z,} вместо пар ((x, y), z) { \displaystyle ((x,y),z)} как в определении выше. Это множество является подмножеством трехмерного пространства; для непрерывной действительнозначной функции двух действительных переменных это поверхность. В науке, технике, технологиях, финансах и других областях графики используются для многих целей. График функции является частным случаем отношения. В современных основах математики и, как правило, в теории множеств функция фактически равна своему графику. [1] Однако часто полезно рассматривать функции как отображения, [2] , которые состоят не только из связи между входом и выходом, но и из того, какой набор является доменом, а какой набор является кодовым доменом. Например, чтобы сказать, находится ли функция на (сюръективной) или нет, следует учитывать кодовый домен. График функции сам по себе не определяет кодовый домен. Обычно [3] используют оба термина функция и график функции , поскольку даже если рассматривать один и тот же объект, они указывают на просмотр его с другой точки зрения. 9{x}} в интервале [−2,+3]. Также показаны два действительных корня и локальный минимум, находящиеся в интервале. Contents
Definition[edit ]Учитывая отображение f: X → Y, {\ displaystyle f: X \ to Y,}, другими словами, функцию f {\ displaystyle f} вместе с ее доменом X {\ displaystyle X} и кодоменом Y, {\ displaystyle Y,} график отображения равен 9{2}\right).} График функции f:{1,2,3}→{a,b,c,d}{\displaystyle f:\{1,2,3\}\to \{a,b,c,d\}}, определенное как , является подмножеством множества {1,2,3}×{a,b,c,d}{\displaystyle \{1,2,3\ }\times \{a,b,c,d\}} Из графика домен {1,2,3}{\displaystyle \{1,2,3\}} восстанавливается как набор первых компонент каждой пары в графе {1,2,3}={x: существует y, такой, что (x,y)∈G(f)}{\displaystyle \{1,2,3\}=\{ x:\ {\text{существует}}y,{\text{такое, что}}(x,y)\in G(f)\}}. График тригонометрической функции равен Если этот набор построить в трехмерной декартовой системе координат, результатом будет поверхность (см. рисунок). Часто бывает полезно показать на графике градиент функции и несколько кривых уровня. Кривые уровня можно нанести на функциональную поверхность или спроецировать на нижнюю плоскость. На втором рисунке показан такой рисунок графика функции: 9 Д. С. Бриджес (1991). Основы реального и абстрактного анализа . Спрингер. п. 285. ISBN 0-387-98239-6 .
|



 2))
2))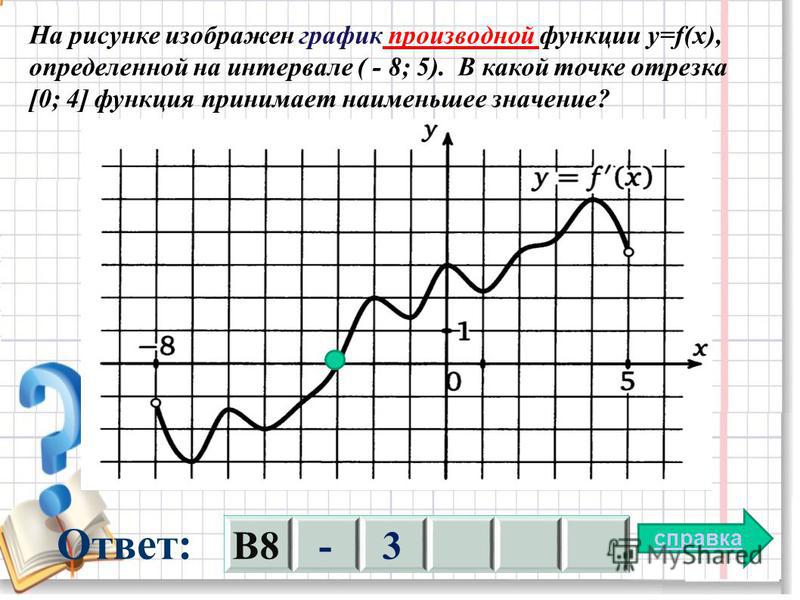 .. Спасибо.
.. Спасибо.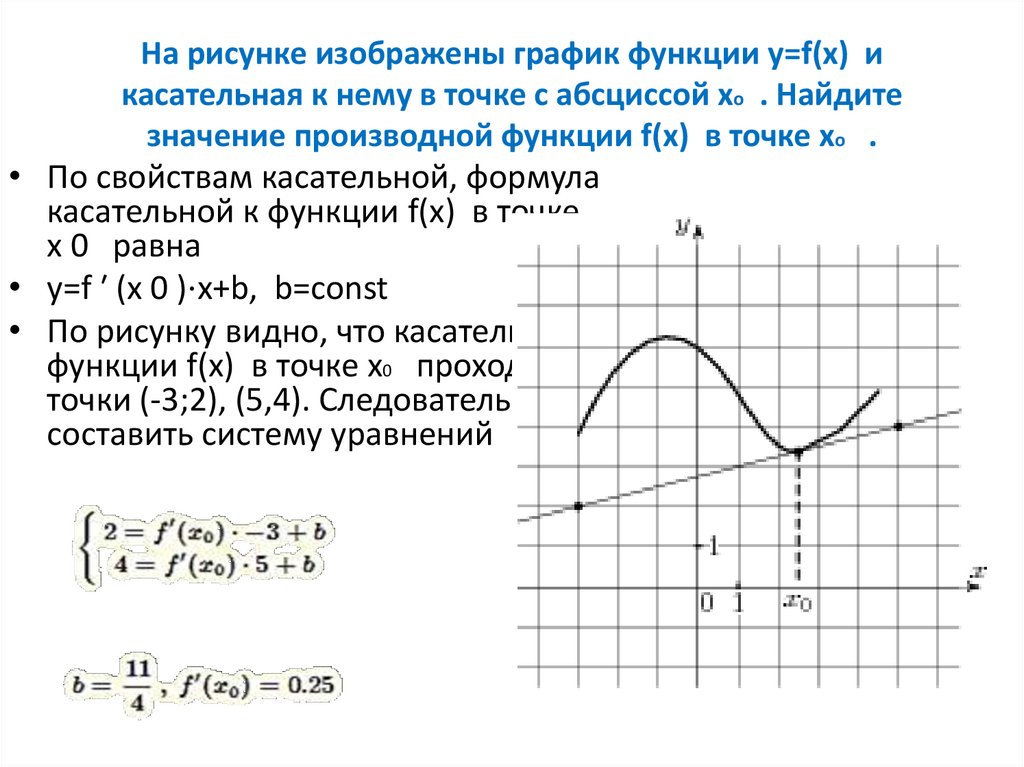 Подскажите, как выглядит график функции f(x,y)=min[x,y] и в чем заключается ее смысл?
Подскажите, как выглядит график функции f(x,y)=min[x,y] и в чем заключается ее смысл?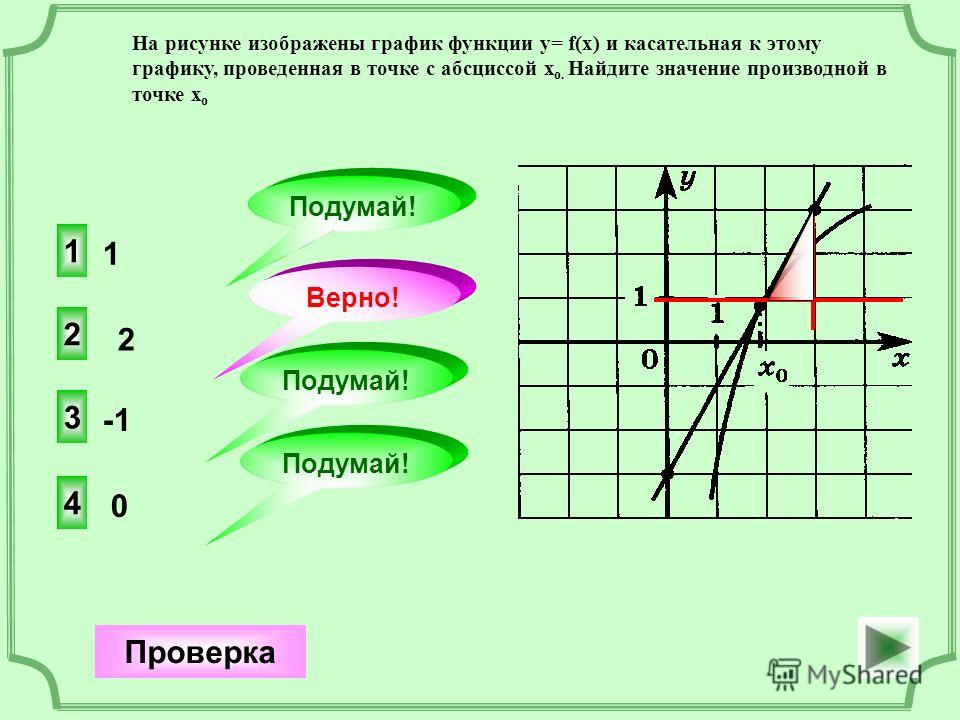 10.2007, 23:00
10.2007, 23:00 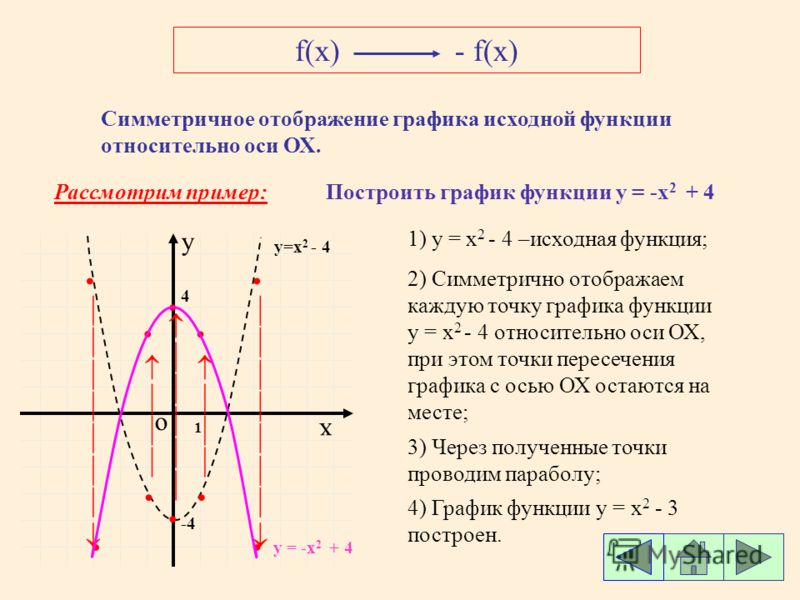 10.2007, 23:06
10.2007, 23:06 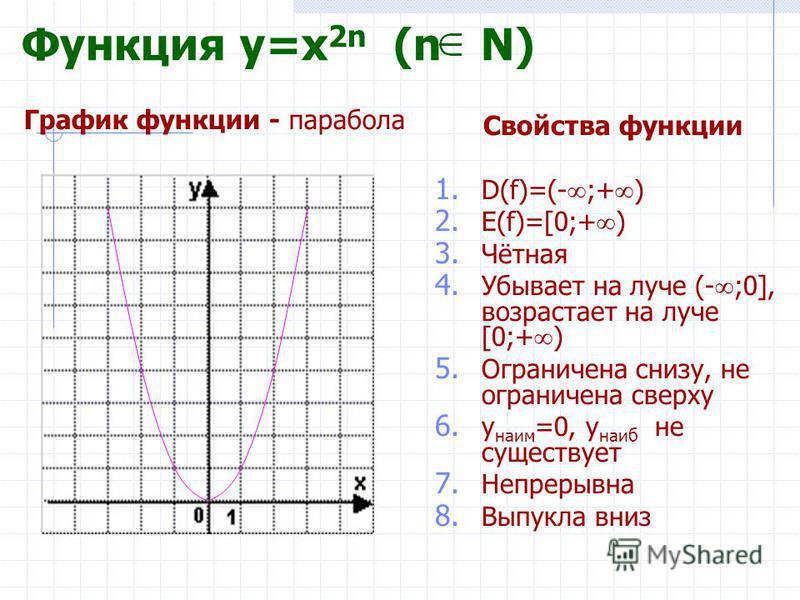 10.2007, 23:07
10.2007, 23:07 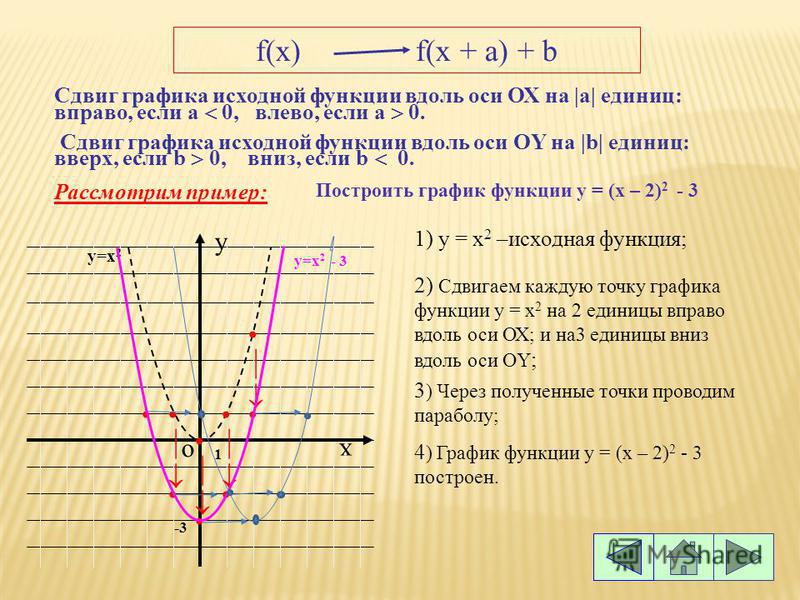 10.2007, 23:24
10.2007, 23:24 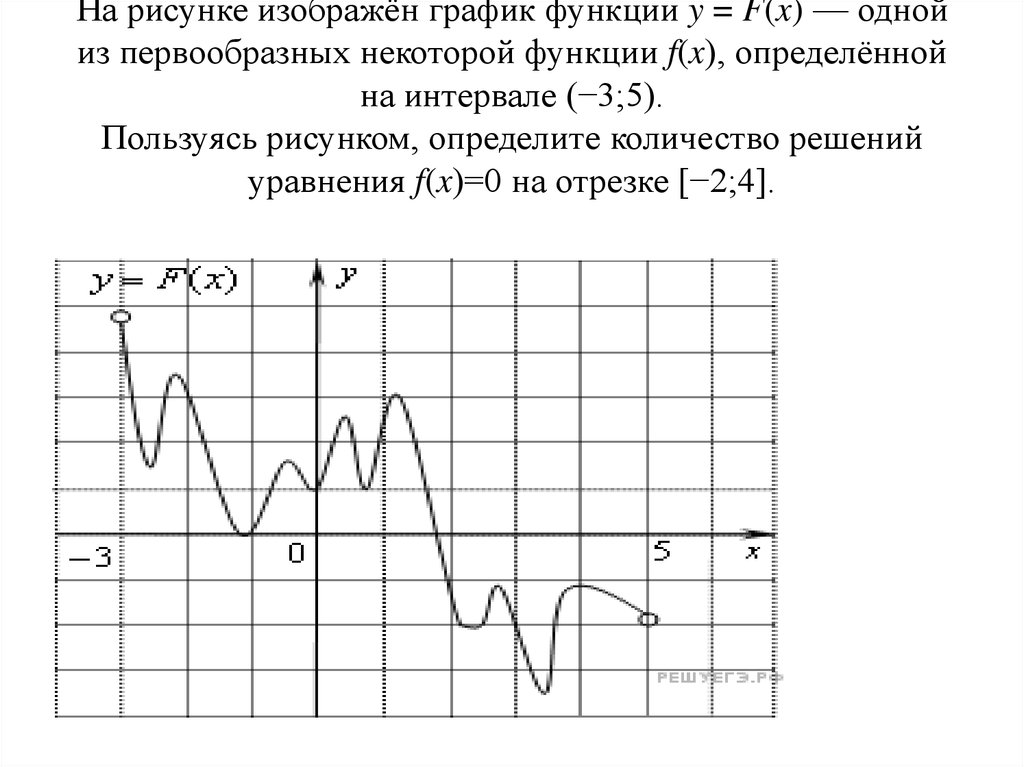 10.2007, 23:27
10.2007, 23:27 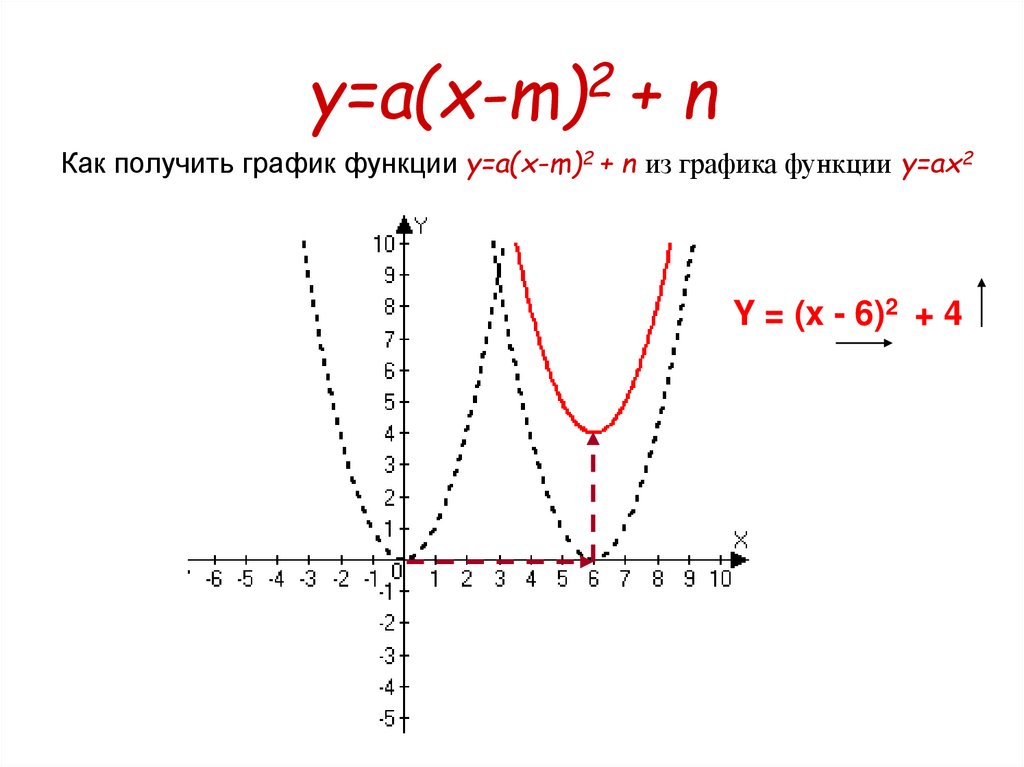 10.2007, 23:28
10.2007, 23:28 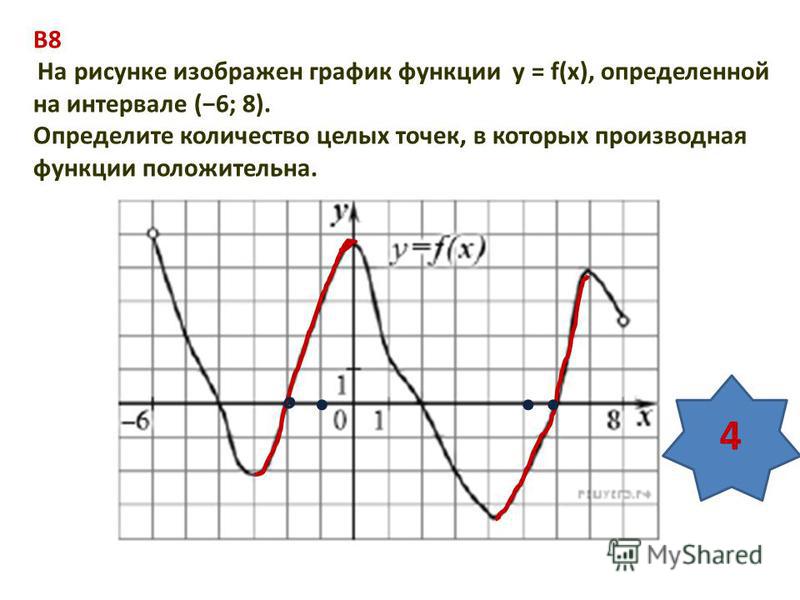 ..
.. 10.2007, 23:31
10.2007, 23:31 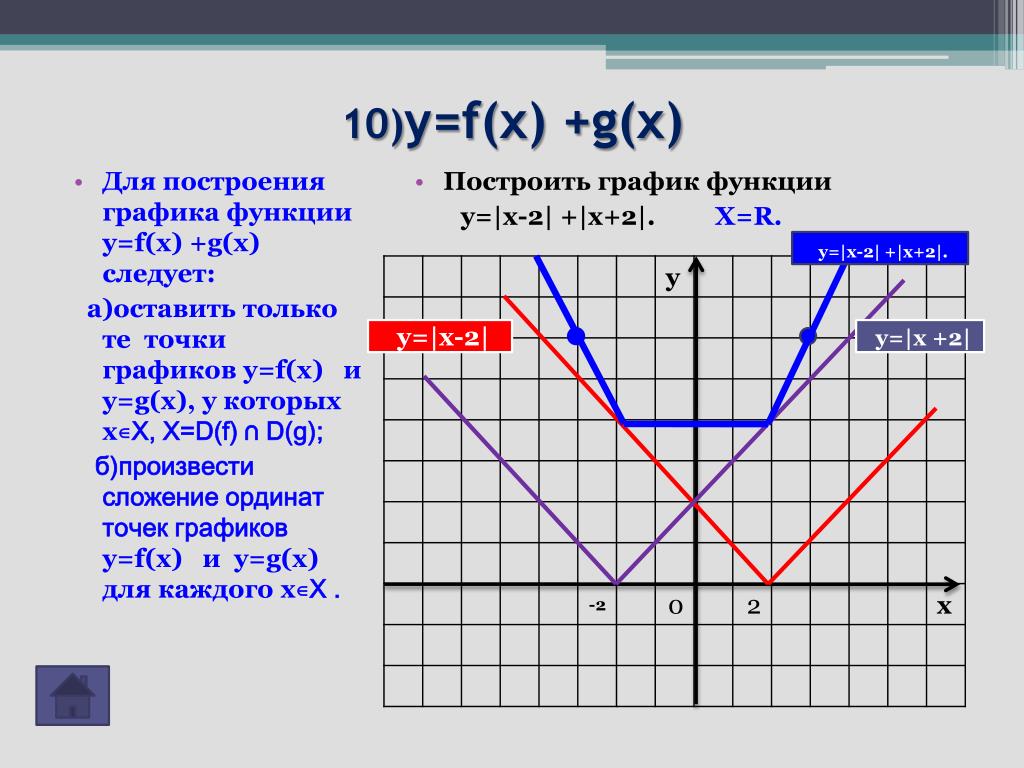 Нет значений или комбинаций xx и yy, из-за которых f(x,y)f(x,y) не определено, поэтому область определения ff составляет ℝ2,ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f(x,y)=z,f(x,y)=z или 3x+5y+2=z.3x+5y+2=z. Одно такое решение можно получить, установив сначала y=0,y=0, что дает уравнение 3x+2=z.3x+2=z. Решением этого уравнения является x=z−23,x=z−23, что дает упорядоченную пару (z−23,0)(z−23,0) как решение уравнения f(x,y)= zf(x,y)=z для любого значения z.z. Таким образом, областью действия функции являются все действительные числа или ℝ.ℝ.
Нет значений или комбинаций xx и yy, из-за которых f(x,y)f(x,y) не определено, поэтому область определения ff составляет ℝ2,ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f(x,y)=z,f(x,y)=z или 3x+5y+2=z.3x+5y+2=z. Одно такое решение можно получить, установив сначала y=0,y=0, что дает уравнение 3x+2=z.3x+2=z. Решением этого уравнения является x=z−23,x=z−23, что дает упорядоченную пару (z−23,0)(z−23,0) как решение уравнения f(x,y)= zf(x,y)=z для любого значения z.z. Таким образом, областью действия функции являются все действительные числа или ℝ.ℝ.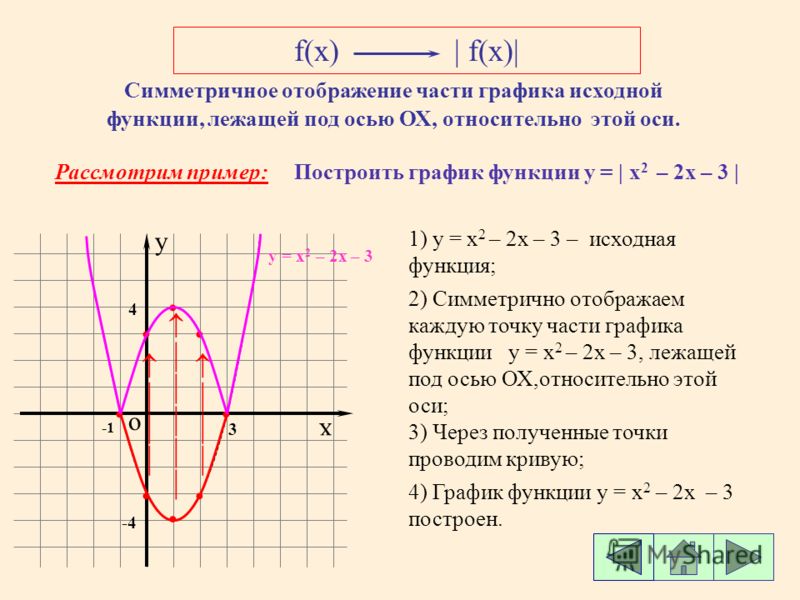 Домен включает граничный круг, как показано на следующем графике.
Домен включает граничный круг, как показано на следующем графике. 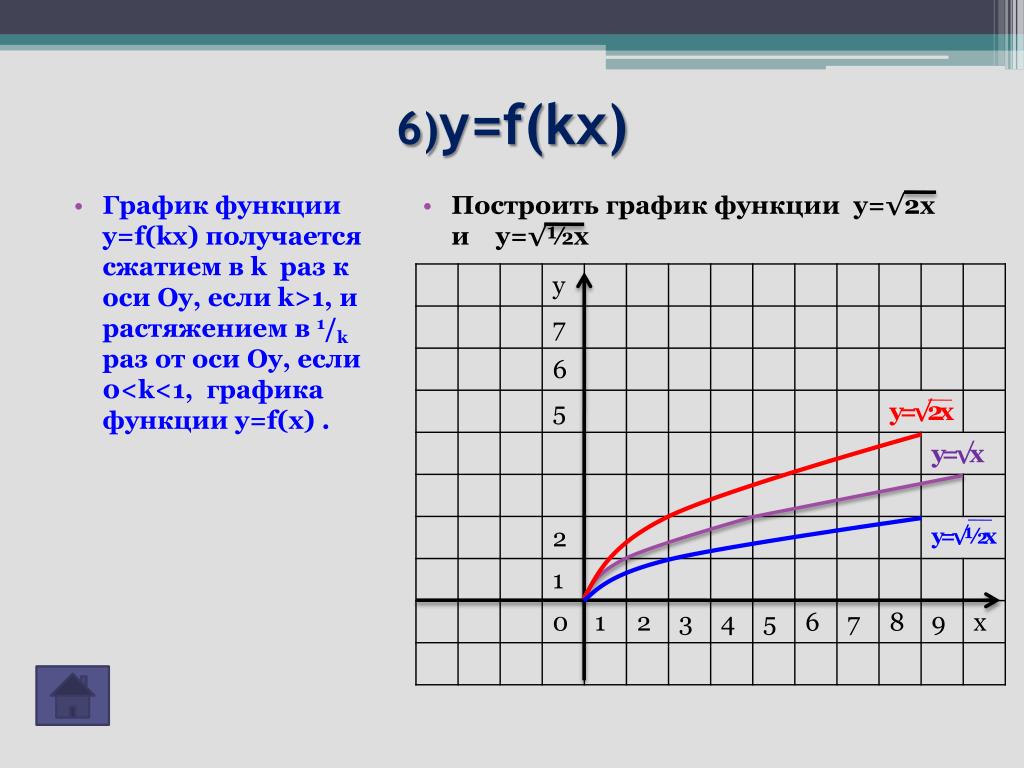 Любая точка на этой окружности удовлетворяет уравнению g(x,y)=c.g(x,y)=c. Следовательно, диапазон этой функции можно записать в интервальной записи как [0,3].[0,3].
Любая точка на этой окружности удовлетворяет уравнению g(x,y)=c.g(x,y)=c. Следовательно, диапазон этой функции можно записать в интервальной записи как [0,3].[0,3].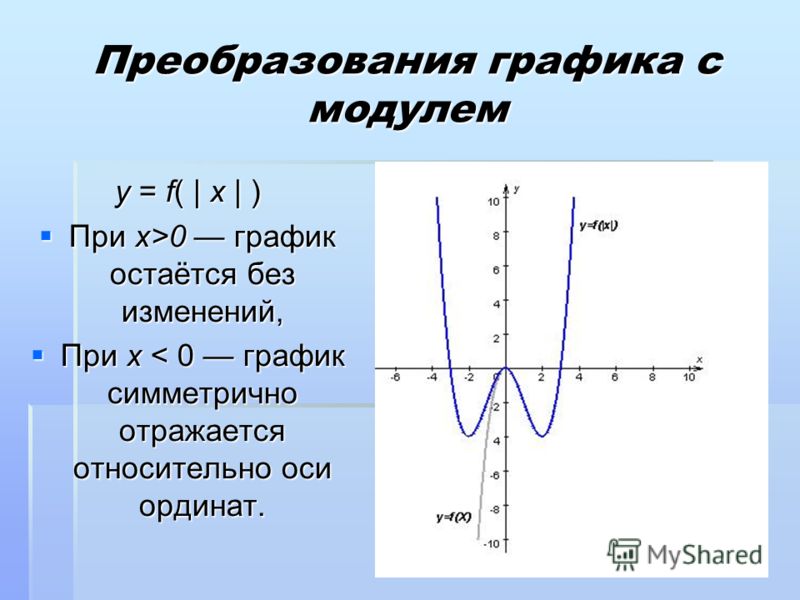 {z∈ℝ2|0≤z≤3}. Когда x2+y2=9×2+y2=9, мы имеем g(x,y)=0.g(x,y)=0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в плоскости x, y, плоскости x, y соответствует z=0z=0 в ℝ3.ℝ3. Если x2+y2=8,×2+y2=8, то g(x,y)=1,g(x,y)=1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x,y -planex,y-плоскость отображается в z=1z=1 в ℝ3.ℝ3. Когда x2+y2x2+y2 приближается к нулю, значение z приближается к 3. Когда x2+y2=0,×2+y2=0, тогда g(x,y)=3.g(x,y)=3. Это начало координат в плоскости x,y.x,y-plane. Если x2+y2x2+y2 равно любому другому значению между 0 и 9, 0 и 9, то g(x,y)g(x,y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат и радиусом 33, как показано на следующем графике.
{z∈ℝ2|0≤z≤3}. Когда x2+y2=9×2+y2=9, мы имеем g(x,y)=0.g(x,y)=0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в плоскости x, y, плоскости x, y соответствует z=0z=0 в ℝ3.ℝ3. Если x2+y2=8,×2+y2=8, то g(x,y)=1,g(x,y)=1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x,y -planex,y-плоскость отображается в z=1z=1 в ℝ3.ℝ3. Когда x2+y2x2+y2 приближается к нулю, значение z приближается к 3. Когда x2+y2=0,×2+y2=0, тогда g(x,y)=3.g(x,y)=3. Это начало координат в плоскости x,y.x,y-plane. Если x2+y2x2+y2 равно любому другому значению между 0 и 9, 0 и 9, то g(x,y)g(x,y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат и радиусом 33, как показано на следующем графике. 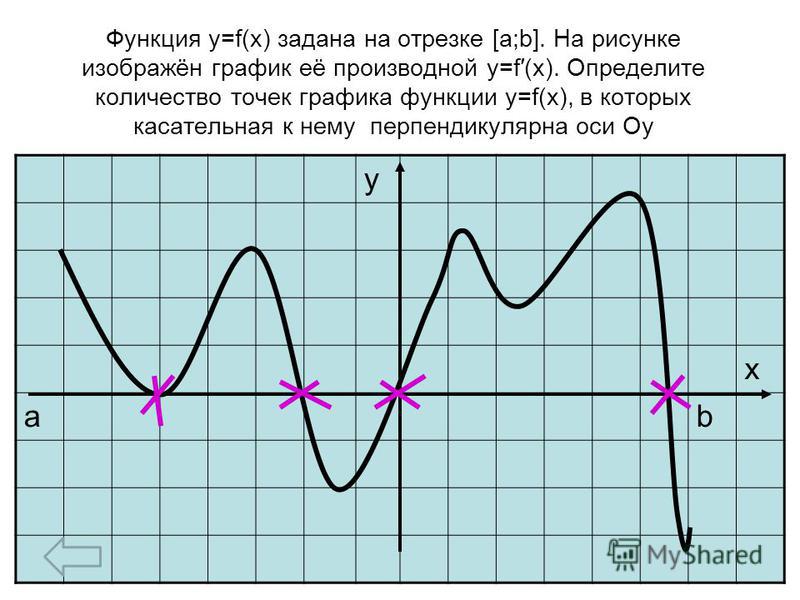 x2+y2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f(x,y)=x2+y2f(x,y)=x2+y2 равно нулю (достигается, когда x=y=0.).x=y=0.). Когда x=0,x=0, функция принимает вид z=y2,z=y2, а когда y=0,y=0, функция принимает вид z=x2.z=x2. Это сечения графика и параболы. Напомним из введения в векторы в пространстве, что имя графика f(x,y)=x2+y2f(x,y)=x2+y2 есть параболоид . График ff показан на следующем графике.
x2+y2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f(x,y)=x2+y2f(x,y)=x2+y2 равно нулю (достигается, когда x=y=0.).x=y=0.). Когда x=0,x=0, функция принимает вид z=y2,z=y2, а когда y=0,y=0, функция принимает вид z=x2.z=x2. Это сечения графика и параболы. Напомним из введения в векторы в пространстве, что имя графика f(x,y)=x2+y2f(x,y)=x2+y2 есть параболоид . График ff показан на следующем графике.