Транспонированная матрица
Если в матрице строки и столбцы поменять местами, то получим транспонированную матрицу.
Свойства:
дважды транспонированная матрица равна исходной
А = (А )= А;
(А+В) =А+ В;
(АВ) =ВА, т.е. (АВ) ≠ АВ;
Если А=А, то матрица А— симметричная
(аij=aji)
Обратная матрица
Обратной
матрицей по отношению к данной квадратной,
называется матрица, которая, будучи
умноженной как справа, так и слева на
данную матрицу, дает единичную матрицу.
Обозначим для матрица А обратную ей
матрицу через А-1.
АА-1=А-1А=Е.
Нахождение обратной матрицы для данной называется обращением данной матрицы.
Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы.
Пусть имеем матричное равенство
АС=В.
Умножим правую и левую часть равенства на обратную матрицу А-1
А-1АС= А-1В.
Поскольку известно, что А-1А=Е, то
ЕС= А-1В.
И поскольку известно, что ЕС=С, то
С= А-1В.
То
есть, мы равенство АС=В преобразовали
в равенство С= А -1В, выразив матрицу
С.
Если бы у нас были простые алгебраические числа а, bи с, то аналогичные преобразования были бы следующие:.
Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.
Алгоритм получения обратной матрицы
Вычисление det A;
Транспонирование матрицы ;
Определение алгебраических дополнений Аji,j=1,N;i=1,N;
Составление союзной матрицы ;
Вычисление обратной матрицы
;
Проверка А-1
Существуют
другие, более удобные способы вычисления
обратной матрицы, например, методом
Жордана – Гаусса, с которым познакомимся
позднее.
Классический метод получения обратной матрицы
Пусть данная матрица:
.
Транспортируем ее .
Найдем для каждого элемента аjiтранспортированной матрицыАТалгебраические дополненияАji.
Теперь составим для матрицы А так называемую присоединенную (или союзную) матрицу
.
Обратная матрица будет равна
.
Например: найти обратную матрицу для матрицы третьего порядка.
.
Основные свойства обратной матрицы
Учитывая, что det(AB)=detA∙ detB,можем записатьdetA-1 detA=detE=1.

Отсюда
.
Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
2. (АВ)-1=В-1А-1
3. (А-1)=(A1)-1.
Тема 2.1. Теория графов в электроэнергетике
Некоторые сведения об электрических системах
Следует иметь в виду, что предлагаемая дисциплина читается до изучения основных курсов по специальности 140204 (100100). Поэтому для того, чтобы приблизить излагаемый материал не только по содержанию, но и по форме к будущим специальным курсам, вспомним некоторые понятия, уже знакомые по курсу “Введение в специальность”.
Рис.1. Принципиальная схема энергосистемы
Энергетическая системаначинается с топлива и воды и кончается потребителем (рис.1).
Электрическая
системаначинается с генератора и
кончается потребителем, т. е. электрическая
система – это электрическая часть
энергетической системы, состоящая из
совокупности элементов, вырабатывающих,
преобразующих, передающих, распределяющих
и потребляющих электроэнергию.
е. электрическая
система – это электрическая часть
энергетической системы, состоящая из
совокупности элементов, вырабатывающих,
преобразующих, передающих, распределяющих
и потребляющих электроэнергию.
Работа электрической системы прежде всего характеризуется значениями мощностей в МВт (и энергии в МВт.час), вырабатываемых, преобразуемых, передаваемых и потребляемых всеми ее элементами.
Режим системы– это ее состояние в любой момент времени, которое характеризуется совокупностью параметров.
Параметры режима– это напряжение в различных точках системы, токи в ее элементах, углы расхождения векторов ЭДС и напряжений, активные и реактивные мощности генераторов, потоки активной и реактивной мощности в линиях и трансформаторах, потери мощности, энергии и напряжения в элементах системы и т.д.
При анализе различают два основных вида режимов электросистем:
установившийся режим (нормальный или послеаварийный) ;
переходный режим (нормальный или аварийный ).

Установившиеся режимы в электрической системе описываются законами Ома и Кирхгофа или вытекающими из них уравнениями узловых напряжений и контурных токов. Математический анализ установившихся режимов работы электрических систем сводится к составлению и решению систем линейных и нелинейных уравнений. Переходные процессы электрических систем описываются системами дифференциальных уравнений. Наиболее широко применяемые при анализе режимов электрических систем методы решения линейных, нелинейных и дифференциальных уравнений будут изложены во втором разделе данного курса.
Электрической
схемой системыназывается графическое
изображение последовательности
соединения ее элементов между собой.
Элементы электрической системы обладают
активными и реактивными (индуктивными
или емкостными) сопротивлениями, активной
и реактивной (индуктивной или емкостной)
проводимостями. Если заменить в
электрической схеме элементы системы
их сопротивлениями и проводимостями,
то получим схему замещения электрической
системы.
Рис.2. Электрическая схема сети
Рис.3. Схема замещения
Перед тем, как
начать рассчитывать режим работы
электрической системы (т.е. определять
параметры режима) составляют схему
замещения электрической системы (или
сети) и вычисляют все параметры схемы
замещения – сопротивления и проводимости.
Электрическая схема сети и ее схема
замещения, представленные на рис.1 и 2,
очень малы, и рассчитать режимы для
такой схемы можно “вручную”. Однако
реальные электрические системы достигают
больших размеров, их схемы замещения
очень сложны и без использования
современных ЭВМ выполнить анализ режимов
электрических систем невозможно.
Понятие обратной матрицы и способы ее нахождения.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Чурикова И.С. 1Муминов А.Ш. 1
1Академический лицей Международного Вестминстерского университета в Ташкенте
Хамраева Р.Р. 1
1WIUT
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
I ВВЕДЕНИЕ
Объект исследования: обратные матрицы.
Предмет исследования: подходы и методынахождения обратных матриц.
Цель работы: овладеть методами нахождения обратных матриц.
Задачи:
ознакомиться с понятием обратной матрицы и ее свойствами;
выделить основные методы нахождения обратных матриц;
Методы исследования: изучение литературы; обработка материалов и результатов; анализ; классификация; обобщение.
Актуальность работы: Обратные матрицы являются объектом изучения линейной алгебры и находят свое применение как в самой математике, так и в ее приложениях. Они часто используются в самых разнообразных исследованиях, упрощают решение системы уравнений с тремя и более неизвестными, находят широкое применение при программировании задач 3D-графики и компьютерных игр и др.
II ОСНОВНЫЕ ПОНЯТИЯ
Матрица — прямоугольная таблица, содержащая m строк и n столбцов и заполненная числами. Обозначается заглавными буквами A, B, С и т. д.
Элементы матрицы (числа) характеризуются их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса (aij).
Квадратная матрица – это матрица, содержащая одинаковое количество сток и столбцов.
Единичная матрица E – это диагональная матрица, диагональные элементы которой равны 1
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A-1 = A-1·A = E
Транспонированная матрица А’ – это матрица, полученная заменой строк матрицы A на ее столбцы и наоборот, ее столбцов на ее строки.
Присоединённая (союзная) матрица А* — матрица, элементами которой служат алгебраические дополнения элементов транспонированной матрицы A’.
Алгебраическим дополнением Aijк элементу aij определителя n-го порядка называется число Aij = (-1)i + j · Mij
Минор Mijк элементу aij определителя n-го порядка – это определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.
Определитель (детерминант) квадратной матрицы А называется число, которое обозначается detA (также |A| или Δ), и вычисляется определённым образом.
III КРИТЕРИЙ ОБРАТИМОСТИ МАТРИЦЫ
Лемма 1. Матрица, обратная к матрице А, будет существовать только, если матрица А является квадратной и их порядок будет одинаковым.
Доказательство:
Предположим, что существует матрица А=[m×n] А-1=[a×b]
Из определения обратной матрицы:
АА-1=Е
Из алгоритма перемножения матриц получаем:
[m×n][a×b]=[m×b]
n=a,
-где n и a «транзитны» и должны быть равны.
То же будет выполняться и для обратного:
А-1 А =Е
[a×b][m×n] =[a×n]
m=b
Отсюда можно заключить, что А=[m×n] А-1=[n×m].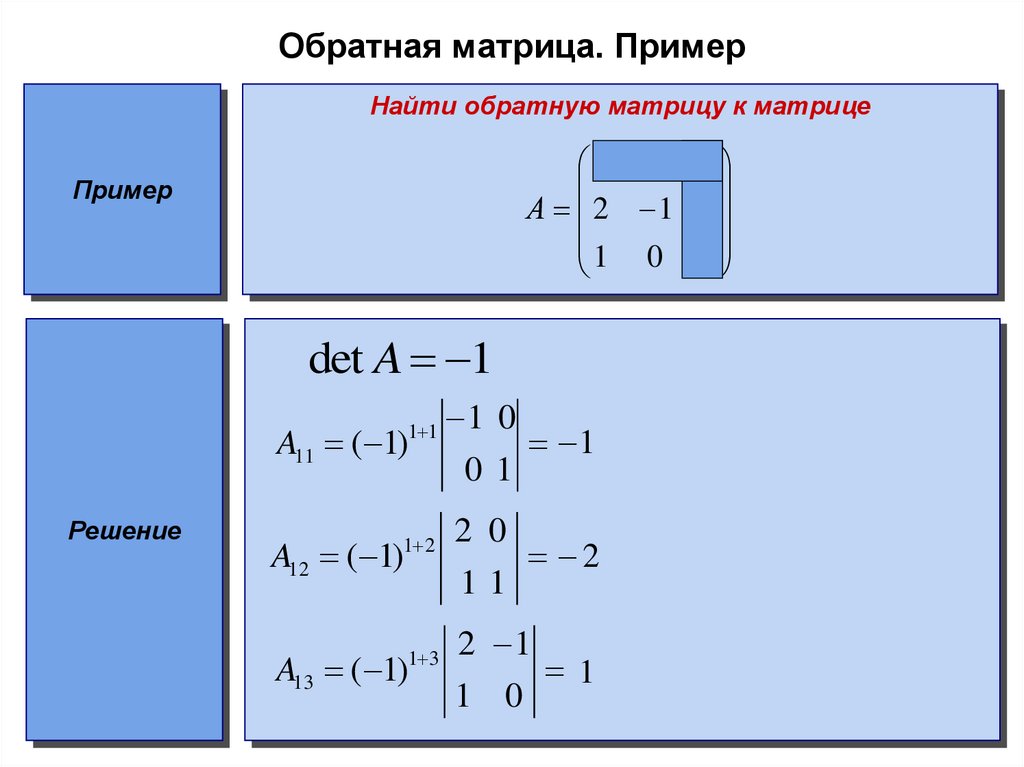 Согласно определению A·A1 = A-1·A = E, поэтому размеры матриц будет строго совпадать.
Согласно определению A·A1 = A-1·A = E, поэтому размеры матриц будет строго совпадать.
[m×n] =[n×m]
m=n
Что, в свою очередь, доказывает лемму 1.
Лемма 2. Если матрица А обратима, то для нее существует только одна обратная матрица.
Доказательство:
Предположим, что существуют две матрицы В и С, обратные к матрице А. При этом:
В≠С
Тогда по определению обратных матриц будет верным:
AB=BA=Е
AC=CA=Е
Из леммы 1 все четыре матрицы A, B, С и Е являются квадратными матрицами одинакового порядка. Отсюда следует:
ВАС
Так как умножение матриц является ассоциативным будет верным следующее:
BAC=(BA) C=EC=С
BAC=B (AC)=BE=B
BAC=C=B
C=B
Получаем две равные обратные матрицы, что доказывает утверждение об единственности обратной матрицы.
Лемма 3. Матрица, обратная к матрице А, существует только в том случае, когда она невырождена, то есть ее определитель |А| не равен нулю.
Доказательство:
Предположим, что |А|= 0 и существует матрица А-1, обратная к A. Тогда |A| = |A| · |B| = 0 по теореме определителя произведения матриц. В тоже время, по определению обратной матрицы: |AB| = |E| = 1. Полученное противоречие показывает, что матрица, обратная к A, существует только при |A| ≠0.
IV СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
|
1. |
Если квадратная матрица А имеет обратную, то: |
|
|
, где det – определитель. |
||
|
2. |
Если квадратные матрицы А и В порядок n имеют обратные матрицы, то их произведение AВ также имеет обратную матрицу: |
|
|
, для двух квадратных обратимых матриц A и B. |
||
|
3. |
Если матрица А порядка n имеет обратную, то транспонированная матрица AT также имеет обратную: |
|
|
, где обозначает транспонированную матрицу. |
||
|
4. |
Если квадратная матрица А имеет обратную, то: |
|
V НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ АЛГЕБРАИЧЕСКИХ ДОПОЛНЕНИЙ
Порядок нахождения обратной матрицы:
1. Нахождение определителя данной матрицы A (Если |А|=0, то обратная матрица не существует).
Нахождение определителя данной матрицы A (Если |А|=0, то обратная матрица не существует).
2. Вычисление дополнительных миноров и алгебраических дополнений и составление союзной матрицы А*.
3. Нахождение матрицы, транспонированной относительно A*.
4. Применение формулы:
где |A| — определитель матрицы А, а — транспонированная союзная матрица с матрицей А.
Пример:
Найти обратную матрицу для А= методом алгебраических дополнений.
Решение:
Найдем определитель матрицы А:
|A|=3·(-3)·1+ (-4)·1·3 + 5·2·(-5) — 5·(-3)·3 — 3·1·(-5) — (-4)·2·1 = -9 — 12 — 50 + 45 + 15 + 8= -3
|A|≠0 — следовательно, А-1 существует.
Найдем миноры и алгебраические дополнения для матрицы А
Составим союзную матрицу:
Транспонируем полученную союзную матрицу:
По формуле находим обратную матрицу:
5. Проверим полученный результат умножением данной матрицы A на обратную матрицу (При обратная матрица была найдена верно).
Проверим полученный результат умножением данной матрицы A на обратную матрицу (При обратная матрица была найдена верно).
Ответ:
VI НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ МАТРИЦЫ 2×2
Для квадратной матрицы второго порядка обратная матрица А-1 будет равна при .
Пример:
Найти обратную матрицу для
Решение:
Ответ:
VII НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
Порядок нахождения обратной матрицы:
Нахождение определителя данной матрицы A (Если |А|=0, то обратная матрица не существует).
Составление системы линейных уравнений вида
где aij — элементы матрицы A, для данной невырожденной матрицы A.
Решение полученной систему относительно y – нахождение обратного линейного преобразования
в котором Aij — алгебраические дополнения элементов матрицы A, |А| — определитель матрицы A.
Алгебраические дополнения располагаются как в транспонированной матрице*
Нахождение коэффициентов при y: , которые и будут элементами матрицы, обратной для матрицы A, и запись найденной обратной матрицы.
Метод линейных преобразований можно считать тем же методом алгебраических преобразований (союзной матрицы), но с другой формой записи.
Пример:
Найти обратную матрицу для А= методом линейных преобразований.
Решение:
Определитель для данной матрицы отличен от нуля, значит матрица обратима.
Для данной матрицы записываем линейное преобразование:
Находим линейное преобразование, обратное предыдущему, для этого потребуется алгебраические дополнения, найденные выше. Запишем обратное линейное преобразование:
Коэффициенты при иксах в обратном линейном преобразовании являются элементами A-1, следовательно
Ответ:
VIII НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ (МЕТОД ЖОРДАНА-ГАУССА)
1. Написание матрицы А и Е рядом через черту .
Написание матрицы А и Е рядом через черту .
2. Приведение полученной матрицы к виду с помощью элементарных преобразований* над ее строками.
3. Получение обратной матрицы .
*К элементарным преобразованиям матрицы относятся:
1) Отбрасывание нулевой строки (столбца).
2) Умножение всех элементов строки (столбца) на число.
3) Изменение порядка строк (столбцов) матрицы.
4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5) Транспонирование матрицы.
Пример:
Найти обратную матрицу для А= с помощью элементарных преобразований ее строк.
Решение:
Выпишем матрицу:
С помощью элементарных преобразований приводим левую часть к единичной матрице
=
=
Выписывает обратную матрицу A-1.
Ответ:
IX ЗАКЛЮЧЕНИЕ
Обратные матрицы являясь неотъемлемой частью изучения линейной алгебры, необходимы к применению в различных сферах. Помимо их практического применения при решении различных математических уравнений и задач, использовании их в программировании, они играют роль в формирование умения выделять главное, развивают логическое мышление, внимание и память.
X СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
А.Г. Курош, «Курс высшей алгебры», 1968 год;
А.С. Бортаковский «Линейная алгебра в примерах и задачах», 2005 год;
Д.К. Фаддеев, «Лекции по алгебре: Учебное пособие для вузов», 1984 год;
Б.М. Верников, «Лекция 11: Обратная матрица»;
Peeyush Chandra, «Notes on Mathematics – 102».
Просмотров работы: 39
Нахождение обратной матрицы | akak-ich.ru
Назад (Математика).В этой статье подробно разбирается нахождение обратной матрицы, рассмотрено построение союзной и транспонированной матрицы алгебраических
дополнений. Особое внимание уделяется решению примеров, в которых требуется построить обратную матрицу для заданной. Нахождение обратных матриц
является важной частью курса математического анализа. Умение работать с матрицами поможет в решении многих задач. Без этого навыка будет достаточно
сложно в дальнейшем. Например, в некоторых разделах экономики при помощи матриц производятся различные вычисления.
Особое внимание уделяется решению примеров, в которых требуется построить обратную матрицу для заданной. Нахождение обратных матриц
является важной частью курса математического анализа. Умение работать с матрицами поможет в решении многих задач. Без этого навыка будет достаточно
сложно в дальнейшем. Например, в некоторых разделах экономики при помощи матриц производятся различные вычисления.
Прежде чем приступить к рассмотрению примеров на нахождение обратной матрицы, рассмотрим один важный вопрос. Что необходимо знать и уметь для успешного изучения данного материала? А именно:
1. Что такое детерминант (определитель) матрицы?
Определитель матрицы — многочлен от элементов матрицы. Определитель можно найти только у квадратной матрицы, то есть у матрицы, у которой число строк равняется числу столбцов. читать далее…
2. Что такое минор матрицы?
Если в матрице выделить несколько произвольных строк и столько же столбцов, то определитель, составленный из
элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено k строк и столбцов, то полученный
минор называется минором порядка k. Примечательно то, что это свойство применимо не только к квадратным матрицам,
но и к прямоугольным. подробнее…
Если выделено k строк и столбцов, то полученный
минор называется минором порядка k. Примечательно то, что это свойство применимо не только к квадратным матрицам,
но и к прямоугольным. подробнее…
3. Уметь вычислять транспонированную матрицу.
О том, как транспонировать матрицу, будет рассказано ниже в этой статье.
4. Уметь вычислять союзную матрицу.
Сама процедура нахождения обратной матрицы называется обращением матрицы. Обращение матрицы возможно только для квадратных матриц (например: 2*2, 3*3, 4*4).
Обратная матрица — A-1. Условие: A*A-1 = A-1*A = I (единичная матрица).
Если определитель матрицы окажется равным нулю, то обратной матрицы не существует. Матрица, определитель которой отличен от нуля, называется неособенной или невырожденной или обратимой.
Иногда студент получает простое задание — найти обратную для матрицы 2*2. Тут особого мастерства от него не требуется, и вот почему…
Тут особого мастерства от него не требуется, и вот почему…
Чтобы найти обратную матрицу для матрицы 2*2, нужно число, обратное определителю матрицы (1/det), умножить на немного измененную исходную матрицу. А именно, в исходной матрице элементы главной диагонали переставляют местами, а у элементов побочной диагонали меняют знак:
Пример: найти обратную матрицу для матрицы 2*2:
Нахождение обратной матрицы для матриц 3*3, 4*4 и т.д. требует более углубленных знаний.
A-1 = 1/detA * CT, где CT — транспонированная союзная матрица.
Транспонирование — замена строк столбцами (AT = [aij=aji]).
Пример: транспонировать матрицу:
Решение:
Согласно определению, просто заменяем строки столбцами:
Союзная матрица — матрица, состоящая из алгебраических дополнений, соответствующих элементам исходной матрицы.
Алгебраическим дополнениемэлемента aij определителя называется его минор Mij, умноженный на (–1)i+j.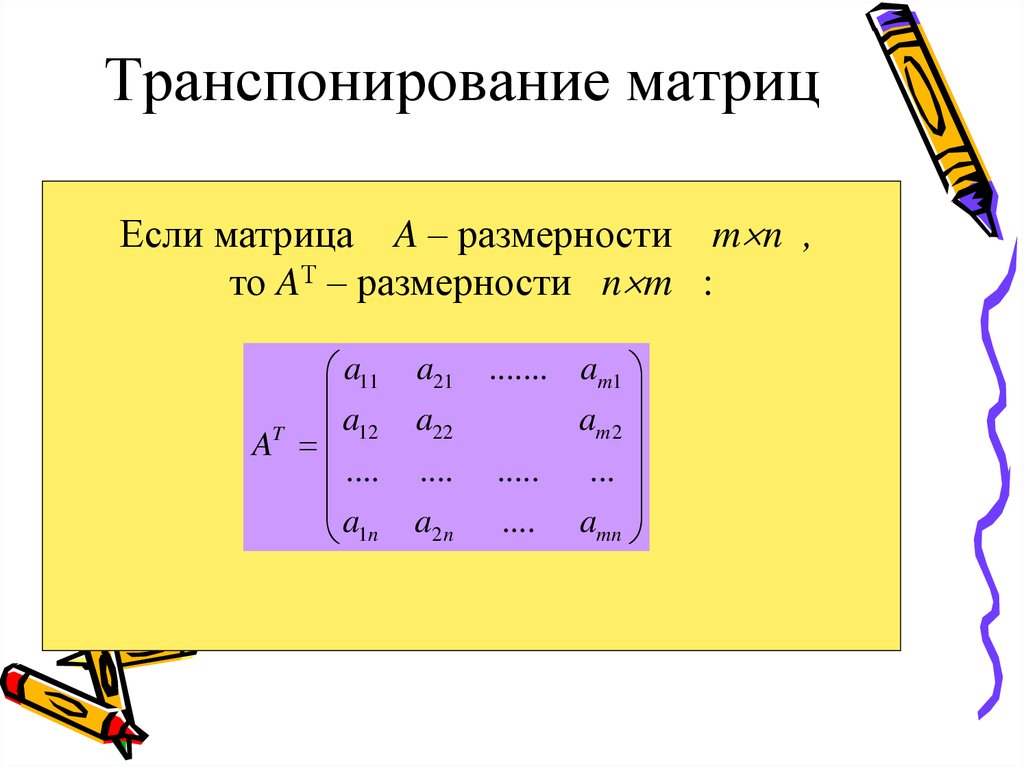 Формула нахождения алгебраического дополнения элемента:
Формула нахождения алгебраического дополнения элемента:
Aij = (-1)i+j*Mij.
Пример: найти обратную матрицу:
Решение:
1. Найдем детерминант матрицы:
2. Найдем союзную матрицу:
Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца , а второй — номер строки , в которые нужно записать вычисленное алгебраическое дополнение:
- A11 = (-1)1+1*0 = 0;
- A12 = (-1)1+2*(-2) = 2;
- A13 = (-1)1+3*(-3) = -3;
- A21 = (-1)2+1*(-6) = 6;
- A22 = (-1)2+2*4 = 4;
- A23 = (-1)2+3*6 = -6;
- A31 = (-1)3+1*0 = 0;
- A32 = (-1)3+2*4 = -4;
- A33 = (-1)3+3*3 = 3.

Транспонируем союзную матрицу:
Ну и, собственно, сам ответ — обратная матрица:
Нахождение обратной матрицы требует довольно громоздких вычислений и необычной расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Что такое обратная матрица и как её найти — Журнал «Код»
10.03.2021
Сложная тема из линейной алгебры.
Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:
Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.
С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Читать ли эту статью?
❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.
✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.
Обратное — это как?
В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:
Обратные числа при умножении друг на друга всегда дают единицу:
Обратная матрица
В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.
Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:
Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.
Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.
Как рассчитать обратную матрицу
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:
- Разделить единицу на матричный определитель.
- Найти транспонированную матрицу алгебраических дополнений.
- Перемножить полученные значения.
Далее мы по порядку во всём разберёмся.
Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополненийОпределитель — это особое число, которое «определяет» свойства матрицы.
Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.
Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.
Формула для расчёта определителя второго порядка
Пример расчёта определителя второго порядка
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.
Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.
Считаем определитель третьего порядка: 1-й этап — главная диагональ
Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.
Считаем определитель третьего порядка: 2-й этап — первый треугольник
Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.
Считаем определитель третьего порядка: 3-й этап — второй треугольник
Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.
Считаем определитель третьего порядка: 4-й этап — вторая диагональ
Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.
Считаем определитель третьего порядка: 5-й этап — третий треугольник
Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.
Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник
Общий вид формулы для расчёта определителя третьего порядка
Пример расчёта определителя третьего порядка
Транспонированная матрица алгебраических дополнений вычисляется в три шага:
- Мы из исходной матрицы находим матрицу миноров.
- Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.

- Находим транспонированную матрицу из матрицы алгебраических дополнений.
Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:
- Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
- Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
- Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
- Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.
Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.
Пример вычисления матрицы миноров из матрицы второго порядка
Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка
Матрица миноров третьего порядка рассчитывается по следующему принципу:
- Последовательно вычёркиваем строки и столбцы.
- Получаем четыре элемента и считаем определитель.
- Записываем результат в матрицу миноров третьего порядка.
Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:
- Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
- Найдите этот же элемент в исходной матрице и отметьте его точкой.
- Проведите от этой точки две линии: вдоль строки и вдоль столбца.
После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.
Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы
Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.
1-я строка 1-й элемент:
Δ = 5×1 — 8×6 = -43
1-я строка 2-й элемент:
Δ = 4×1 — 7×6 = -38
1-я строка 3-й элемент:
Δ = 4×8 — 7×5 = -3
2-я строка 1-й элемент:
Δ = 2×1 — 8×3 = -22
2-я строка 2-й элемент:
Δ = 1×1 — 7×3 = -20
2-я строка 3-й элемент:
Δ = 1×8 — 7×2 = -6
3-я строка 1-й элемент:
Δ = 2×6 — 5×3 = -3
3-я строка 2-й элемент:
Δ = 1×6 — 4×3 = -6
3-я строка 3-й элемент:
Δ = 1×5 — 4×2 = -3
Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.
Транспонируем полученную матрицу и можем переходить к последнему действию.
Получаем из матрицы третьего порядка матрицу миноров
Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:
Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось
Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными
Господи, зачем всё это?
Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?
Смотрите:
- Вам не нужно уметь решать все эти уравнения самостоятельно.
 Для этого давно есть мощные алгоритмы.
Для этого давно есть мощные алгоритмы. - Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
- В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
- И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.
«Программисты, которые умеют писать алгоритмы, — нишевая профессия»
Спокойствие, всё будет хорошо.
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Получите ИТ-профессию
В «Яндекс Практикуме» можно стать разработчиком, тестировщиком, аналитиком и менеджером цифровых продуктов. Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.
Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.
Начать карьеру в ИТ
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| SemDvs |
| ||
20/07/19 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Линейная алгебра: транспонирование матрицы и обратная матрица
вперед от:https://blog. csdn.net/yinhun2012/article/details/84236202
csdn.net/yinhun2012/article/details/84236202Эта статья предназначена для накопления математической основы эффекта раскраски. В большинстве случаев, когда мы использовали матрицу ранее, это прямое преобразование аффинного пространства, то есть преобразование аффинного пространства A в аффинное Пробел B, матрица использования также выглядит следующим образом:
Матрица T * однородных координат V = однородных координат V ‘
Детали вычисления являются точечным произведением строк матрицы и векторных столбцов, и его значение вычисления заключается в получении координатных компонентов в новом аффинном пространстве. Я много говорил.
На этот раз мы изучим работу двух матриц, одна — операция транспонирования матрицы (получить транспонированную матрицу), а другая — обратная операция матрицы (получить обратную матрицу).
First. Сначала рассмотрим, как математически определить транспонированную матрицу:
Новая матрица, полученная путем замены строк и столбцов матрицы, называется транспонированной матрицей, и определитель транспонированной матрицы не изменяется.
Здесь я использую матрицу 4х4 для демонстрации, потому что матрица 4х4 используется при разработке 3D-графики.
В то же время матрица транспонирования обладает следующими эксплуатационными свойствами:
Первые три не должны быть трудными для понимания, это может быть очевидно с первого взгляда, и четвертый рабочий характер должен быть продемонстрирован немного:
Вывод четвертой формулы может быть рассчитан с использованием матрицы 4×4, потому что мы в основном используем только матрицу 4×4 в трехмерной графике, и вывод может углубить впечатление.
Затем процесс вывода выводится в моей памяти, и соответствующие вычисления можно увидеть сразу.
Давайте посмотрим, как математически определить обратную матрицу:
Существуют матрица M и матрица N. Если M * N = матрица I (единичная матрица идентификации матрицы), то матрица M и матрица N являются обратными друг другу.
Таким образом, обратная матрица играет большую роль как «преобразование редукции». Что это означает, если предположить, что M и N являются взаимно обратными матрицами, то M · N · однородная координата A все еще получает исходную однородную координату A, тогда Это означает, что это преобразование восстанавливается. С точки зрения аффинного пространства, аффинное пространство A преобразуется в аффинное пространство B через матрицу M, а затем аффинное пространство B преобразуется в аффинное пространство посредством обратного преобразования N матрицы M A.
Что это означает, если предположить, что M и N являются взаимно обратными матрицами, то M · N · однородная координата A все еще получает исходную однородную координату A, тогда Это означает, что это преобразование восстанавливается. С точки зрения аффинного пространства, аффинное пространство A преобразуется в аффинное пространство B через матрицу M, а затем аффинное пространство B преобразуется в аффинное пространство посредством обратного преобразования N матрицы M A.
Каковы эксплуатационные свойства обратных матриц? следующим образом:
Первое ясно.
Второй нуждается в небольшом описании:
Третий также может быть необходимо рассчитать:
Итак, здесь демонстрируются свойства обычно используемых формул транспонированной матрицы и обратной матрицы. Кстати, почему мы должны наблюдать и изучать эти две матричные операции? Или каково специфическое использование этих двух матричных операций? Просто выпустить какие-то странные формулы для забавы? Nonono, который тесно связан со специальным пространственным выводом, который необходимо выполнить в 3D-графике позже, и здесь мы должны заранее поработать с хранилищем знаний, а затем перейти к реальному приложению CG-шейдеров.
Итак, продолжим дальше.
Интеллектуальная рекомендация
Принцип и Zookeeper Dubbo
Проблемы о проблемах, зоокедра не сложно, больше не публикуется. Отказ Отказ ВВЕДЕНИЕ ДУББО История развития программного обеспечения: (архитектура проекта) 1. Все в одном 🙁 все в одном) Это HodgePod…
Переменное улучшение
Переменные подъема: переменная подъем JavaScript часто одинакова, вызвана внутренними переменными и глобальными переменными. Пример 1: Предупреждение неопределено, потому что Декларация переменной буд…
Установка и конструкция SFTP Server под Windows
В течение десяти лет развития существует только эта система архитектуры! >>> Поскольку клиент недавнего проекта должен использовать SFTP, чтобы поставить меня в передачу файлов, с…
Опыт установки самой маленькой операционной системы Linux на диске U: MenuetOS
Существует не так много информации о системе MenuetOS. Пожалуйста, перейдите на Baidu или на официальный сайт, чтобы узнать:http://www.menuetos.net/Загрузите последнюю версию:http://www.menuetos.net/d…
Пожалуйста, перейдите на Baidu или на официальный сайт, чтобы узнать:http://www.menuetos.net/Загрузите последнюю версию:http://www.menuetos.net/d…
Двигатель Irrlicht: аппаратная анимация костей кожи кожи
Двигатель Irrlicht: аппаратная анимация костей кожи кожи Эта штука очень гладкая. Через полчаса я нашел путь. Самое поблагодарившее — Super Tuxkart (называется STK, эти три буквы ниже). Вы можете посе…
Вам также может понравиться
Start a ReactJS project
Build react app using create-react-app Build react app from scratch Start new project Update babel setting: .babelrc Build and serve Финансируется в: https://www.jianshu.com/p/feef65248696…
[Усыновление] [Технологические финансы] Взаимное золото контроль большие данные
Преступность Вспышка интернет-финансов в частности, является быстрым ростом интернет-кредита и разработки многокакретного бизнеса и кредитного бизнеса, особенно в денежных средствах кредитных отраслей…
Режим проектирования (2) -Факторный режим
Заводский режим Определите интерфейс для создания объектов, чтобы позволить подклассу определить, какой класс создан. Метод завода представляет собой экземплярный класс с задержкой дочернего ребенка. …
Метод завода представляет собой экземплярный класс с задержкой дочернего ребенка. …
Обновление содержимого в одной таблице clob для другой таблицы clob
…
Реагически возникают проблемы
1. Блокировка инцидента 2. Как пройти функцию OnClick 3. Динамически добавить класс Финансируется в: https: //juejin.im/post/5cd91a936fb9a0321a151afc…
транспонирование и инверсия
транспонирование и инверсия<<домой <<предыдущий следующий>>
Часто упоминается «транспонирование» матрицы, но что это значит?
Конечно, у него есть алгебраическая интерпретация, но я не знаю, возможно ли это.
быть выражено всего в нескольких словах. В любом случае, я лучше сделаю пару
примеры, чтобы узнать, что такое шаблон.
Ниже приведена матрица 2×2, как она используется в сложном умножении.
транспонирование квадратной матрицы можно считать зеркальной версией
это: зеркально по главной диагонали. Это диагональ с буквой а
в теме.
| |
Для квадратной матрицы любого размера действует тот же принцип. Просто
представьте, что главная диагональ — это линия, над которой расположены записи
перевернулся.
Просто
представьте, что главная диагональ — это линия, над которой расположены записи
перевернулся.
| |
Хотя представление с переворотом по диагонали помогает
вводите тему, она меня не удовлетворяет. Матрицу можно рассматривать
набор векторов, организованных в виде строк или столбцов. Тогда транспозиция может
выражаться:
| строки матрицы становятся столбцами при транспонировании |
То же самое относится и к большим матрицам. Обратите внимание, что средняя фигура
уже транспонировано, но все еще отображается в виде столбцов. Самый правый
рисунок подчеркивает ряды транспонирования. И вот как это будет
использоваться в практических приложениях.
Представление векторной вырезки и вставки показывает, что неквадратные
матрицы также имеют транспонирование. Ниже приведен пример блочной матрицы, который
может появиться еще несколько раз на моих страницах.
| |
Еще вопрос: в чем смысл транспонирования, в
алгебраический смысл? Я могу только проиллюстрировать значение транспонирования
на простейших примерах. Здесь снова матрица 2×2, поскольку она
может быть частью сложного умножения. Заметим, что такие матрицы
уже обладают симметрией, которой произвольные матрицы не обязательно обладают.
| |
Умножение на «единицу импульса» выполняется для нахождения ответов матрица и ее транспонирование.
| | |
Эти операции можно визуализировать на комплексной плоскости:
| | |
Первая матрица вращается против часовой стрелки, и ее
транспонирование вращается по часовой стрелке. Такие пары, которые
зеркально отраженные по оси x, называются комплексно-сопряженными. Для большего
матрицы, чем 2×2, такие визуализации не могут быть выполнены. Но эффект
транспозиции матриц в целом можно считать обращением
обороты в нем.
Для большего
матрицы, чем 2×2, такие визуализации не могут быть выполнены. Но эффект
транспозиции матриц в целом можно считать обращением
обороты в нем.
Давайте теперь проверим, что произойдет, если эта матрица и ее транспонирование
умножаются друг на друга.
| | |
0,8 2 +0,6 2 = 0,64+0,36 = 1, и
(0,6*0,8)-(0,8*0,6) равно нулю. Поэтому мы имеем совершенно особый результат
для этого случая: тождество.
| |
Я намеренно выбрал матрицу, транспонирование которой равно
обратный.
Обратите внимание, что это не всегда происходит с транспонированием только
произвольная матрица. Это касается только так называемых «ортонормированных».
матрицы. Как и в случае с действительными числами, когда вы умножаете матрицу на ее
обратный результат является тождеством. Сравните с мультипликативными обратными
как:
1*(1/1)=1 или 4*(1/4)=1.
Ниже представлена матрица, транспонирование которой не является обратным. Когда эти
перемножаются, результат не является единичной матрицей.
| | |
Тем не менее, вывод показывает хорошую закономерность. есть еще один
постоянным на единичной диагонали.
| |
Все матрицы 2×2 типа, которые появляются при комплексном умножении
показать этот результат постоянной диагонали при умножении на их
транспонировать. Для этого типа матрицы всегда будет существовать обратная.
Поэтому комплексные числа и их агрегаты являются фаворитами в ЦСП.
техника. Они предлагают систематический контроль над преобразованием данных, а
возможность достаточно точно обратить процесс вспять, если это необходимо.
| | |
На этой странице я показал, как умножение матрицы с
это инверсия приводит к единичной матрице. Но я не указал, как
можно найти обратную матрицу. Для вышеуказанного вида
матрица это просто. На самом деле это означает найти обратную
представленное в нем комплексное число. Вот как это сделать:
Но я не указал, как
можно найти обратную матрицу. Для вышеуказанного вида
матрица это просто. На самом деле это означает найти обратную
представленное в нем комплексное число. Вот как это сделать:
| |
Сначала найдите транспонирование. Транспонирование комплексного числа (a+ib) является сопряженным (a-ib). Затем вы делите на a 2 +b 2 . Что такое радиус (или «норма») в квадрате. Все это может быть написано:
(а+ib) -1 = (а 2 +b 2 ) -1 (а-ib)
А теперь, пожалуйста, инверсию других и более крупных матриц? Эхххм….
оставайтесь в тонусе.
Обратная матрица — поиск, формула, примеры
Обратная матрица для матрицы A обозначается A -1 . Обратную матрицу 2 × 2 можно вычислить по простой формуле. Далее, чтобы найти обратную матрицу порядка 3 и выше, нам нужно знать определитель и сопряженную матрицу. Обратной матрицей является другая матрица, которая при умножении на данную матрицу дает мультипликативную идентичность.
Далее, чтобы найти обратную матрицу порядка 3 и выше, нам нужно знать определитель и сопряженную матрицу. Обратной матрицей является другая матрица, которая при умножении на данную матрицу дает мультипликативную идентичность.
Обратная матрица используется для нахождения решения линейных уравнений методом обращения матриц. Здесь давайте узнаем о формуле, методах и терминах, связанных с обратной матрицей.
| 1. | Что такое обратная матрица? |
| 2. | Обратная матричная формула |
| 3. | Как найти обратную матрицу? |
| 4. | Термины, относящиеся к обратной матрице |
| 5. | Методы поиска обратной матрицы |
| 6. | Инверсия матрицы 2 x 2 |
| 7. | Обратная матрица 3 x 3 |
| 8. | Определитель обратной матрицы |
9. | Часто задаваемые вопросы об обратной матрице |
Что такое обратная матрица?
, обратная матрице , является другой матрицей, которая при умножении на данную матрицу дает мультипликативную идентичность. Для матрицы A ее обратной является A -1 , и A · A -1 = A -1 · A = I, где I — единичная матрица. Матрица, определитель которой отличен от нуля и для которой можно вычислить обратную матрицу, называется обратимой матрицей. Например, инверсия A = \(\left[\begin{array}{rr}
1&-1\\\
0 и 2
\end{массив}\right]\) равно \(\left[\begin{array}{cc}
1&1/2\\
0 и 1/2
\end{массив}\right]\) как
- A · A -1 = \(\left[\begin{array}{rr}
1&-1\\\
0 и 2
\end{массив}\right]\) \(\left[\begin{массив}{cc}
1&1/2\\
0 и 1/2
\end{массив}\right]\) = \(\left[\begin{массив}{cc}
1&0\\
0 и 1
\конец{массив}\справа]\) = I - A -1 · A = \(\left[\begin{array}{cc}
1&1/2\\
0 и 1/2
\end{массив}\right]\) \(\left[\begin{массив}{rr}
1&-1\\\
0 и 2
\end{массив}\right]\) = \(\left[\begin{массив}{cc}
1&0\\
0 и 1
\конец{массив}\справа]\) = I
Но как найти обратную матрицу? Давайте посмотрим в следующих разделах.
Формула обратной матрицы
В случае действительных чисел обратным любому вещественному числу a было число a -1 , такое, что a умножить на a -1 равно 1. Мы знали, что для a действительное число, число, обратное числу, было обратным числом, если число не равно нулю. Обратная квадратная матрица A, обозначаемая A -1 , является матрицей, так что произведение A и A -1 является единичной матрицей. Полученная единичная матрица будет того же размера, что и матрица A.
Поскольку |A| находится в знаменателе приведенной выше формулы, обратная матрица существует только в том случае, если определитель матрицы имеет ненулевое значение. т. е. |А| ≠ 0,
Как найти обратную матрицу?
Чтобы найти обратную квадратную матрицу A, мы используем следующую формулу: А -1 = прил(А) / |А| ; |А| ≠ 0
, где
- A — квадратная матрица.

- adj(A) — присоединенная матрица матрицы A.
- |А| является определителем A.
Примечание: Для матрицы, обратной которой существует:
- Данная матрица должна быть квадратной матрицей.
- Определитель матрицы не должен быть равен нулю.
Приведенные ниже термины помогают лучше понять и упростить расчет обратной матрицы.
Минор: Минор определяется для каждого элемента матрицы. Минором конкретного элемента называется определитель, полученный после исключения строки и столбца, содержащих этот элемент. Для матрицы A = \(\begin{pmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{ 33}\end{pmatrix}\), минор элемента \(a_{11}\) равен:
Минор элемента \(a_{11}\) = \(\left|\begin{matrix}a_{ 22}&a_{23}\\a_{32}&a_{33}\end{matrix}\right|\)
Кофактор: Кофактор элемента вычисляется путем умножения минора с -1 на показатель степени суммы элементов строки и столбца в порядке представления этого элемента.
Кофактор \(a_{ij}\) = (-1) i + j × минор \(a_{ij}\).
Определитель: Определитель матрицы — это представление единственного уникального значения матрицы. Определитель матрицы можно вычислить относительно любой строки или столбца данной матрицы. Определитель матрицы равен сумме произведения элементов и его сомножителей определенной строки или столбца матрицы.
Сингулярная матрица: Матрица, имеющая значение определителя, равное нулю, называется сингулярной матрицей. Для сингулярной матрицы A |A| = 0. Обратная сингулярная матрица не существует.
Несингулярная матрица: Матрица, значение определителя которой не равно нулю, называется невырожденной матрицей. Для невырожденной матрицы |A| ≠ 0 и, следовательно, существует обратное ему.
Сопряжение к матрице: Сопряжение к матрице представляет собой транспонирование матрицы элементов кофактора данной матрицы.
Правила для операций со строками и столбцами определителя:
Следующие правила полезны для выполнения операций со строками и столбцами над определителями.
- Значение определителя не изменится, если строки и столбцы поменять местами.
- Знак определителя меняется, если любые две строки или (два столбца) поменять местами.
- Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
- Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.
- Если элементы строки или столбца выражены в виде суммы элементов, то определитель может быть выражен в виде суммы определителей.
- Если элементы строки или столбца сложить или вычесть с соответствующими кратными элементам другой строки или столбца, то значение определителя остается неизменным.
Методы поиска обратной матрицы
Обратную матрицу можно найти двумя способами. Обратную матрицу можно вычислить с помощью элементарных операций и с помощью сопряженной матрицы. Элементарные операции над матрицей можно выполнять с помощью преобразований строк или столбцов.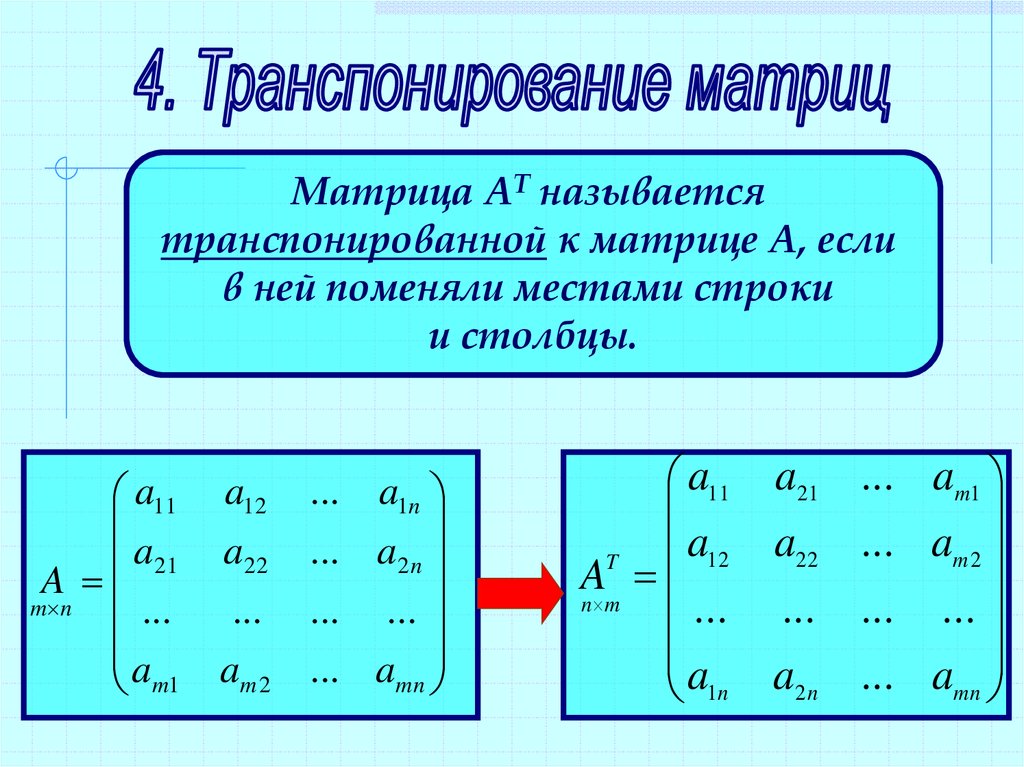 Кроме того, обратную матрицу можно вычислить, применяя формулу обратной матрицы с использованием определителя и сопряженной матрицы. Для выполнения обратной матрицы с помощью элементарных операций со столбцами мы используем матрицу X и вторую матрицу B в правой части уравнения.
Кроме того, обратную матрицу можно вычислить, применяя формулу обратной матрицы с использованием определителя и сопряженной матрицы. Для выполнения обратной матрицы с помощью элементарных операций со столбцами мы используем матрицу X и вторую матрицу B в правой части уравнения.
- Элементарные операции со строками или столбцами
- Обратная матричная формула (с использованием сопряженного и определителя матрицы)
Проверим каждый из способов, описанных ниже.
Элементарные операции со строками
Чтобы вычислить обратную матрицу A с помощью элементарных преобразований строк, мы сначала берем расширенную матрицу [A | I], где I — единичная матрица, порядок которой такой же, как у A. Затем мы применяем операции со строками, чтобы преобразовать левую часть A в I. Затем матрица преобразуется в [I | А -1 ]. Для получения более подробной информации о процессе нажмите здесь.
Элементарные операции со столбцами
Мы можем применить операции со столбцами так же, как это было объяснено для операций со строками, чтобы найти обратную матрицу.
Формула, обратная матрице
Обратная матрица A может быть вычислена с помощью формулы, обратной матрице, путем деления сопряженной матрицы на определитель матрицы. Обратную матрицу можно вычислить, выполнив следующие шаги:
- Шаг 1: Вычислите миноры всех элементов A.
- Шаг 2: Затем вычислите кофакторы всех элементов и напишите матрицу кофакторов, заменив элементы A соответствующими кофакторами.
- Шаг 3: Найдите сопряженный элемент A (записывается как adj A), взяв транспозицию кофакторной матрицы A.
- Шаг 4: Умножьте adj A на обратную величину определителя.
Adj A = транспонирование матрицы кофакторов
= Транспонирование \(\begin{pmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{ 33}\end{pmatrix}\)
=\(\begin{pmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13 }&A_{23}&A_{33}\end{pmatrix}\)
A -1 = \(\dfrac{1}{|A|}. \begin{pmatrix} A_{11}&A_{21} &A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\end{pmatrix}\)
\begin{pmatrix} A_{11}&A_{21} &A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\end{pmatrix}\)
В этом разделе мы узнали о различных методах вычисления обратной матрицы. Давайте лучше поймем это, используя несколько примеров для разных порядков матриц в разделе «Примеры» ниже.
Обратная матрица 2 x 2
Обратную матрицу 2 × 2 легче вычислить по сравнению с матрицами более высокого порядка. Мы можем вычислить обратную матрицу 2 × 2, используя общие шаги для вычисления обратной матрицы. Найдем обратную матрицу 2 × 2, приведенную ниже:
A = \(\begin{bmatrix} a & b \\ \\ c & d \end{bmatrix}\)
A -1 = (1/|A|) × Adj A
= [1/(ad — bc)] × \(\begin{bmatrix} d & -b \\ \\ -c & a \end{bmatrix}\)
Следовательно, чтобы вычислить обратную 2 × 2, нам нужно сначала поменять местами члены a и d и поставить отрицательные знаки для членов b и c, и, наконец, разделить его на определитель матрицы.
Инверсия матрицы 3 x 3
Мы знаем, что для каждой невырожденной квадратной матрицы A существует обратная матрица A -1 , такая что A × A -1 = I. Возьмем любую квадратную матрицу 3 × 3, заданную как
Возьмем любую квадратную матрицу 3 × 3, заданную как
A = \(\begin{bmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{bmatrix}\)
Обратную матрицу 3×3 можно вычислить по формуле обратной матрицы: A -1 = (1/|A|) × Adj A
Сначала мы проверим, является ли данная обратим, т. е. |A| ≠ 0. Если существует обратная матрица, мы можем найти сопряженную данную матрицу и разделить ее на определитель матрицы.
Аналогичным методом можно найти обратную любую матрицу размера n × n. Давайте посмотрим, можно ли использовать аналогичные шаги для вычисления обратной матрицы m × n, где m ≠ n.
Обратная матрица 2 × 3
Мы знаем, что первое условие существования обратной матрицы состоит в том, что данная матрица должна быть квадратной матрицей. Кроме того, определитель этой квадратной матрицы не должен быть равен нулю. Это означает, что обратной матрицы порядка m × n не будет, где m ≠ n. Следовательно, мы не можем вычислить обратную матрицу 2 × 3.
Обратная матрица 2 × 1
Как и обратная матрица 2 × 3, обратная матрица 2 × 1 также не существует, поскольку данная матрица не является квадратной матрицей.
Определитель обратной матрицы
Определитель обратной обратимой матрицы является обратным определителя исходной матрицы. т. е. det(A -1 ) = 1/det(A). Проверим доказательство предыдущего утверждения.
Мы знаем, что det(A • B) = det (A) × det(B)
Кроме того, A × A -1 = I
det(A × A -1 ) = det(I)
или det(A) × det(A -1 ) = det( I)
Поскольку det(I) = 1
det(A) × det(A -1 ) = 1
или det(A -1 ) = 1 / det(A)
Значит, доказано.
☛ Статьи по теме:
Следующие ссылки по теме помогут лучше понять обратную матрицу.
- Калькулятор обратной матрицы
- Калькулятор умножения матриц
- Калькулятор определителя
Важные моменты, касающиеся обратной матрицы:
Следующие пункты помогут лучше понять идею обратной матрицы.
- Обратная квадратная матрица (если существует) уникальна.
- Если A и B две обратимые матрицы одного порядка, то (AB) -1 = B -1 A -1 .
- Обратная квадратная матрица A существует, только если ее определитель не равен нулю, |A| ≠ 0,
- Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
- Определитель произведения двух матриц равен произведению определителей двух отдельных матриц. |АВ| = |А|.|В|
Давайте посмотрим, как использовать формулу обратной матрицы в следующем разделе решенных примеров.
Обратные примеры матриц
Пример 1: Найдите обратную матрицу A = \(\left(\begin{matrix}-3 & 4\\2 & 5 \end{matrix}\right)\).
Решение:
Дана матрица A = \(\left(\begin{matrix}-3 & 4\\ \\2 & 5 \end{matrix}\right)\).
Формула для вычисления матрицы, обратной A = \(\left(\begin{matrix}a&b\\\\c&d\end{matrix}\right)\) A -1 = \(\dfrac{ 1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\).

Используя эту формулу, мы можем вычислить A -1 следующим образом.
A -1 = \(\dfrac{1}{(-3)× 5 — 4 × 2}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix }\right)\)
= \(\dfrac{1}{-15 — 8}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\ )
= \(\dfrac{-1}{23}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\)
Ответ: Следовательно, A -1 = \(\dfrac{-1}{23}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\)
Пример 2: Найдите матрицу, обратную матрице A = \(\left(\begin{matrix}4 & -2 & 1\\5&0&3\\-1&2 & 6\end{matrix}\right)\) .
Решение:
Дана матрица A = \(\left(\begin{matrix}4 & -2 & 1\\5&0&3\\-1&2 & 6\end{matrix}\right)\)
Шаг — 1: Найдем определитель данной матрицы, используя Строку — 1 вышеприведенной матрицы.
|А| = \(4\left|\begin{matrix}0&3\\2 & 6\end{matrix}\right| -(-2)\left|\begin{matrix}5&3\\-1 & 6\end{matrix }\right|+1\left|\begin{matrix}5&0\\-1& 2\end{matrix}\right|\)
= 4(0 х 6 — 3 х 2) + 2(5 х 6 — (-1) х 3) +1(5 х 2 — 0 х (-1))
= 4(0 — 6) + 2(30 + 3) + 1(10 — 0)
= -24 + 66 + 10
= 52
Теперь определим сопряженную матрицу A, вычислив кофакторы каждого элемента, а затем взяв транспонирование кофакторной матрицы.

Adj A = \(\left(\begin{matrix}-6 & 14 & -6\\-33&25&-7\\10&-6 & 10\end{matrix}\right)\)
Инверсия матрица A задается формулой A -1 = \(\dfrac{1}{|A|}\).Adj A
A -1 = \(\dfrac{1}{52}\).\(\left(\begin {матрица}-6 и 14 и -6\\-33&25&-7\\10&-6 и 10\конец{матрица}\справа)\)
= \(\слева(\начало{матрица}-3/26 & 7/26 & -3/26\\-33/52&25/52&-7/52\\5/26&-3/26 & 5/26\end{matrix}\right)\)
Ответ: A -1 = \(\left(\begin{matrix}-3/26 & 7/26 & -3/26\\-33/52&25/52&-7/52\\5/26&-3/26 & 5/26\конец{матрица}\справа)\) 9{-1} = \dfrac{1}{22} \begin{pmatrix}5 & -2 \\\\ 1 & 4 \end{pmatrix} = \begin{pmatrix} 5/22 & -2/22 \\ \\ 1/22 & 4/22 \end{pmatrix} \)
Ответ: Обратная заданной матрицы \( = \begin{bmatrix} 5/22 & -1/11 \\\\ 1/22 & 2/11 \end{bmatrix}\)
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по обратной матрице
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об обратной матрице
Что означает обратная матрица?
, обратная матрице , является другой матрицей, которая умножается на данную матрицу и дает мультипликативную идентичность. Для матрицы A обратная матрица равна A -1 , а A · A -1 = I. Общая формула обратной матрицы равна присоединенной матрице, деленной на определитель матрицы. т. е. А -1 = \(\dfrac{1}{|A|}\) · Adj A. Обратная матрица существует только в том случае, если определитель матрицы имеет ненулевое значение.
Как найти обратную матрицу?
Обратная квадратная матрица находится в два простых шага. Сначала вычисляются определитель и сопряженный к данной квадратной матрице. Далее сопряженная матрица делится на определитель, чтобы найти обратную матрицу. Обратная матрица A равна \(\dfrac{1}{|A|}\).Adj A.
Далее сопряженная матрица делится на определитель, чтобы найти обратную матрицу. Обратная матрица A равна \(\dfrac{1}{|A|}\).Adj A.
Как найти обратную матрицу 2 × 2?
Обратная матрица 2 × 2 равна сопряженной матрице, деленной на определитель матрицы. Для матрицы A = \(\left(\begin{matrix}a&b\\ \\c&d\end{matrix}\right)\) ее сопряженный равен перестановке элементов первой диагонали и смене знака элементов второй диагонали. Формула обратной матрицы выглядит следующим образом.
A -1 = \(\dfrac{1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\)
Как использовать обратную матрицу?
Обратная матрица полезна при решении уравнений методом обращения матриц. Метод обращения матриц с использованием формулы X = A -1 B, где X — переменная матрица, A — матрица коэффициентов, а B — постоянная матрица.
Можно ли вычислить обратную матрицу для обратимой матрицы?
Да, для обратимой матрицы можно вычислить обратную матрицу. Матрица, определитель которой не равен нулю, является невырожденной матрицей. А для невырожденной матрицы мы можем найти определитель и обратную матрицу.
Матрица, определитель которой не равен нулю, является невырожденной матрицей. А для невырожденной матрицы мы можем найти определитель и обратную матрицу.
Когда обратная матрица не существует в некоторых случаях?
Матрица, обратная матрице, существует только в том случае, если значение ее определителя не равно нулю и данная матрица является квадратной матрицей. Поскольку сопряженная матрица делится на определитель матрицы, чтобы получить обратную матрицу. Матрица, определитель которой не равен нулю, называется невырожденной матрицей. Обратная матрица не определена для прямоугольных матриц.
Какова формула обратной матрицы?
Формула обратной матрицы используется для определения обратной матрицы для любой заданной матрицы. Обратная квадратная матрица A равна A -1 только тогда, когда: A × A -1 = A -1 × A = I . Формула обратной матрицы может быть представлена как A -1 = adj(A)/|A|; |А| ≠ 0, где A — квадратная матрица.
Для данной матрицы 2 × 2. Какова формула для нахождения обратной матрицы?
Для заданной матрицы 2×2 A = \(\left(\begin{matrix}a&b\\ \\c&d\end{matrix}\right)\) , обратная дается A -1 = \(\dfrac{1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\). Здесь A -1 является инверсией A.
Что такое инверсия матрицы идентичности?
Инверсия единичной матрицы сама по себе. Это связано с тем, что для любой единичной матрицы порядка I мы имеем I × I = I × I = I. Для получения дополнительной информации нажмите здесь.
Как использовать формулу обратной матрицы?
Формулу обратной матрицы можно использовать, выполнив указанные шаги:
- Шаг 1: Найдите матрицу миноров для данной матрицы.
- Шаг 2: Затем найдите матрицу кофакторов.
- Шаг 3: Найдите сопряженное, транспонировав матрицу кофакторов.
- Шаг 4: Разделите на определитель.

Что такое формула обратной матрицы 3 × 3?
Формула обратной матрицы для матрицы 3 × 3: A -1 = adj(A)/|A|; |А| ≠ 0, где A = квадратная матрица, adj(A) = сопряженная квадратная матрица, A -1 = обратная матрица.
Что такое обратная диагональная матрица?
Обратная диагональная матрица снова является диагональной матрицей, в которой элементы главной диагонали обратной матрицы являются величинами, обратными соответствующим элементам исходной матрицы. Чтобы узнать, как это доказать, нажмите здесь.
Матричная алгебра
Матричная алгебраМатричная алгебра
Что такое единичная матрица?
Что такое скаляр?
Что такое обратная матрица?
Когда (для какой матрицы) транспонированная матрица равна исходной матрице?
Выполнить умножение матриц.
Имея матрицу и матричную операцию, определите содержимое результирующей матрицы (например, SSCP, ковариация, корреляция).
Определения
«Матрица представляет собой прямоугольник n на k чисел или символов, обозначающих числа» (Pedhazur, 1997, стр. 983). Размер матрицы называется ее порядком и обозначается строками и столбцами. По соглашению строки всегда упоминаются первыми. Таким образом, матрица порядка 3 на 2 называется может выглядеть так:
A
=Матрица B порядка 4 на 4 может выглядеть так:
B
=По соглашению матрицы в тексте печатаются жирным шрифтом .
Элементы (элементы) матрицы обозначаются по имени матрицы в нижнем регистре с заданными строкой и столбцом (опять же, сначала идет строка). Например, а 31 = 2, б 22 =1. В общем, a ij означает элемент A в i-й строке и j-м столбце. По соглашению элементы печатаются курсивом .
Транспонирование матрицы получается путем перестановки строк и столбцов, так что первая строка становится первым столбцом, и так далее. Транспонирование матрицы обозначается одинарными кавычками и называется простым числом. Например, A ‘(простое число):
Транспонирование матрицы обозначается одинарными кавычками и называется простым числом. Например, A ‘(простое число):
А
=А’ =
Обратите внимание, что A ‘ — это не просто A , «опрокинутое» на бок (если это так, мы увидим первый столбец как 1 3 вместо 3 1). Это как если бы карты или доски с номерами для каждой строки были вытянуты 1 на 1 и размещены в порядке для транспонирования. Транспонирование B:
В
=В’ =
(Для некоторых матриц транспонирование равно исходной матрице.)
Если n = k, количество строк равно количеству столбцов, а матрица равна квадрат . Квадратная матрица может быть симметричной или асимметричной . Симметричная матрица обладает тем свойством, что элементы выше и ниже главной диагонали одинаковы, так что element(i,j) = element(j,i), как в нашей матрице B . (Главная или главная диагональ в матрице B состоит из элементов, равных 1. ) В случае квадратной симметричной матрицы транспонированная матрица является исходной матрицей. Матрица корреляции всегда будет квадратной симметричной матрицей, поэтому транспонирование будет равно оригиналу.
) В случае квадратной симметричной матрицы транспонированная матрица является исходной матрицей. Матрица корреляции всегда будет квадратной симметричной матрицей, поэтому транспонирование будет равно оригиналу.
Вектор-столбец представляет собой матрицу чисел размером n на 1. Например:
б =
| .4 |
.5 | |
.2 | |
.1 |
(Я собираюсь использовать прямоугольники для матриц, а не стандартные скобки из-за проблем с форматированием.) Итак, b — вектор-столбец. Вектор-строка представляет собой матрицу чисел размером 1 на k. Например,
б ‘= | . | .5. | 2. | .1 |
Итак, b ‘ — это вектор-строка. Обратите внимание, что b’ является транспонированием b . По соглашению, векторы печатаются жирным шрифтом в нижнем регистре, а векторы-строки представляются транспонированными векторами-столбцами.
Диагональная матрица — это квадратная симметричная матрица, которая имеет нули везде, кроме главной диагонали. Например:
С =
| 12 | 0 | 0 |
0 | 10 | 0 | |
0 | 0 | 5 |
C — диагональная матрица.
Особенно важная диагональная матрица называется единичной матрицей I . Эта диагональная матрица имеет 1 на главной диагонали.
я =
| 1 | 0 | 0 |
0 | 1 | 0 | |
0 | 0 | 1 |
I — единичная матрица. Бывает, что корреляционная матрица, в которой все переменные ортогональны, является единичной матрицей.
Скаляр — это матрица с одним элементом. Например
д = | 12 |
d
— скаляр.
Операции с матрицами
Сложение и вычитание
Матрицы можно складывать и вычитать тогда и только тогда, когда они одного порядка (одинаковые по количеству строк и столбцов). Матрицы, над которыми допустима операция, говорят, что соответствуют операции.
Нам повезло, что сложение и вычитание матриц просто означает сложение или вычитание соответствующих элементов двух матриц.
Дополнение
4 |
+
| 6 |
=
| 10 |
1 | 2 | 3 | ||
5 | 3 | 8 | ||
|
|
| ||
| х | г | з |
Дополнение
1 | 2 |
+
| 3 | 4 |
=
| 4 | 6 |
1 | 2 | 5 | 6 | 6 | 8 | ||
1 | 2 | 7 | 8 | 8 | 10 | ||
|
|
|
|
|
| ||
| Х |
| Д |
| З |
|
Вычитание
1 | 2 |
—
| 3 | 4 |
=
| -2 | -2 |
1 | 2 | 5 | 6 | -4 | -4 | ||
1 | 2 | 7 | 8 | -6 | -6 | ||
|
|
|
|
|
| ||
| Х |
| Д |
| З |
|
Умножение
В отличие от сложения и вычитания матриц, умножение матриц не является прямым расширением обычного умножения. Умножение матриц включает в себя как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Умножение матриц включает в себя как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Чтобы его получить, мы сначала умножаем соответствующие элементы, а затем складываем их.
|
|
|
| б1 |
=
|
|
|
|
а1 | а2 | а3 | б2 | а1b1 | +a2b2 | +a3b3 | ||
|
|
| б3 |
|
|
| ||
|
|
|
|
|
|
| ||
| а’ |
| б |
| с |
|
Для числового примера
|
|
|
| 0 |
=
|
|
=
|
|
1 | 2 | 3 | 2 | 0+4+12 | 16 | |||
|
|
| 4 |
|
|
Результат умножения двух таких векторов называется скалярным произведением. Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Например,
|
|
|
| 7 |
|
|
|
|
1 | 1 | 1 |
| 8 | = | 7+8+9 | = | 24 |
|
|
|
| 9 |
|
|
|
|
1’x
= S X
Мы можем найти сумму перекрестных произведений с помощью таких операций:
|
|
|
| 1 |
|
|
|
|
2 | 4 | 6 |
| 3 | = | 2+12+30 | = | 44 |
|
|
|
| 5 |
|
|
|
|
х’у
= С ХУИ если мы вычтем среднее значение из вектора-столбца, мы можем найти сумму квадратов:
|
|
|
| -1 |
|
|
|
|
-1 | 0 | 1 |
| 0 | = | 1+0+1 | = | 2 |
|
|
|
| 1 |
|
|
|
|
х’х
= С х 2 В отличие от обычного умножения, умножение матриц не является симметричным, так что в общем случае x’y не равно y’x , то есть предварительное и постумножение обычно не дают одного и того же результата. В общем случае первая матрица будет иметь порядок r1xc1, а вторая — порядка r2xc2.
В общем случае первая матрица будет иметь порядок r1xc1, а вторая — порядка r2xc2.
Чтобы соответствовать умножению, c1 должно быть равно r2. Порядок полученной матрицы будет r1xc2. Внутренние числа должны быть равны для умножения числа. Если да, то результат будет порядка внешних чисел. Некоторые примеры
А(1 ст ) |
|
| Б(2 и ) |
|
| АБ |
|
строки | Кол-во |
| строки | Кол-во |
| строки | Кол-во |
1 | 5 |
| 5 | 1 |
| 1 | 1 |
1 | 10 |
| 10 | 1 |
| 1 | 1 |
1 | 6 |
| 5 | 1 |
| ДНЦ |
|
5 | 1 |
| 1 | 5 |
| 5 | 5 |
3 | 2 |
| 2 | 3 |
| 3 | 3 |
3 | 3 |
| 2 | 3 |
| ДНЦ |
|
2 | 4 |
| 4 | 3 |
| 2 | 3 |
То, что именно происходит с умножением матриц, зависит от порядка матриц (хотя схема шагов всегда одна и та же).
Если мы умножим вектор-столбец на вектор-строку, мы получим матричное произведение векторов, а не скаляр.
Пример
1 |
|
|
|
|
| 1 | -2 | 0 |
2 |
| 1 | -2 | 0 | = | 2 | -4 | 0 |
3 |
|
|
|
|
| 3 | -6 | 0 |
| и |
|
| б’ |
| = | С |
|
|
3×1 |
|
| 1×3 |
|
| 3×3 |
|
|
Возьмите первую строку a (1), умножьте на первый столбец b (1) и установите результат в c 1,1 . Возьмите вторую строку a (2), умножьте на 1 st col of b (1), установите результат c 2,1 и т. д.
Возьмите вторую строку a (2), умножьте на 1 st col of b (1), установите результат c 2,1 и т. д.
Тот же шаблон используется для матриц большего порядка, за исключением того, что для каждой комбинации мы и умножаем, и складываем. Например
2 | 1 |
|
|
|
|
| 7 | 8 | 9 |
3 | 1 |
| 2 | 3 | 4 |
| 9 | 11 | 13 |
4 | 2 |
| 3 | 2 | 1 |
| 14 | 16 | 18 |
| А |
|
| Б |
|
|
| С |
|
|
3×2 |
|
| 2×3 |
|
|
| 3×3 |
|
|
Чтобы получить значения C
(2)2+(1)3=7 (1,1) | (2)3+(1)2=8 (1,2) | (2)4+(1)1=9 (1,3) |
(3)2+(1)3=9 (2,1) | (3)3+(1)2=11 (2,2) | (3)4+(1)1=13 (2,3) |
(4)2+(2)3=14 (3,1) | (4)3+(2)2=16 (3,2) | (4)4+(2)1=18 (3,3) |
Перейти по строкам первой матрицы и столбцам второй. Чтобы получить c(1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Чтобы получить c(1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Умножение матриц полезно для нахождения матрицы сумм квадратов и перекрестных произведений (матрица SSCP).
Мы можем найти либо необработанные оценки, либо суммы оценок отклонений квадратов и перекрестных произведений. Первые необработанные баллы:
| 1 | 2 | 0 | |||||||||||
| 1 | 2 | 2 | 3 | 2 | 2 | 2 | 3 | 2 | 26 | 37 | 14 | ||
| 2 | 3 | 4 | 3 | 4 | 2 | 2 | 4 | 2 | 37 | 58 | 20 | ||
| 0 | 2 | 2 | 2 | 0 | 0 | 3 | 3 | 2 | 14 | 20 | 12 | ||
| 2 | 4 | 0 | |||||||||||
| 2 | 2 | 0 | |||||||||||
| Х’ | Х | SSCP | |||||||||||
| 3×6 | 6×3 | 3×3 |
Содержимое матрицы SSCP
Сим | Сим | |
Сим | ||
Теперь баллы отклонения от тех же данных:
| -1 | -1 | -1 | |||||||||||
| -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 2 | ||
| -1 | 0 | 1 | 0 | 1 | -1 | 0 | 1 | 1 | 1 | 4 | 2 | ||
| -1 | 1 | 1 | 1 | -1 | -1 | 1 | 0 | 1 | 2 | 2 | 6 | ||
| 0 | 1 | -1 | |||||||||||
| 0 | -1 | -1 | |||||||||||
| Х’ | Х | SSCP | |||||||||||
| 3×6 | 6×3 | 3×3 |
Содержимое матрицы SSCP
Если мы умножаем или делим матрицу на скаляр, каждый элемент матрицы умножается (делится) на этот скаляр. Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
2/6 | 1/6 | 2/6 | .33 | .17 | .33 | |
| 1/6 | 4/6 | 2/6 | = | .17 | .66 | .33 |
| 2/6 | 2/6 | 6/6 | . | .33 | 1 |
Матрица SSCP, деленная на N (или N-1), называется матрицей дисперсии-ковариации. В нем у нас есть отклонения по диагонали и ковариации вне главной диагонали.
Если мы далее разделим на стандартное отклонение для каждой строки и каждого столбца, мы получим матрицу корреляции:
Корреляционная матрица для наших данных:
1 | ||
| .35 | 1 | |
| .58 | .41 | 1 |
Детерминанты
Определитель — это забавное свойство или значение матрицы. Мы (на самом деле, компьютер) будем находить детерминанты корреляции, дисперсии-ковариации или матрицы сумм квадратов и перекрестных произведений (SSCP). Вы можете думать о детерминанте как о мере свободы варьирования или отсутствия предсказуемости в матрице (я говорю это, чтобы дать вам некоторое представление о том, что это такое, даже если это не совсем правильно или точно). Помимо общего представления о том, что это такое, и связанной с ним номенклатуры, вам необходимо знать (а) что определитель используется для нахождения обратной матрицы (обсуждается в следующей теме) и (б) что это означает, когда определитель нуль.
Мы (на самом деле, компьютер) будем находить детерминанты корреляции, дисперсии-ковариации или матрицы сумм квадратов и перекрестных произведений (SSCP). Вы можете думать о детерминанте как о мере свободы варьирования или отсутствия предсказуемости в матрице (я говорю это, чтобы дать вам некоторое представление о том, что это такое, даже если это не совсем правильно или точно). Помимо общего представления о том, что это такое, и связанной с ним номенклатуры, вам необходимо знать (а) что определитель используется для нахождения обратной матрицы (обсуждается в следующей теме) и (б) что это означает, когда определитель нуль.
Определитель матрицы A записывается
дет( А ) = | А | или
1 | .5 |
.5 | 1 |
| А | |
Определитель обозначен вертикальными черточками вместо скобок. Определитель сложно вычислить, если матрица не имеет порядка 2×2. В этом случае определитель равен 9.0922 11 ( 22 )- 21 ( 12 ). Для нашего примера выше определитель будет равен 1(1)-(0,5)(0,5) = 0,75.
Определитель сложно вычислить, если матрица не имеет порядка 2×2. В этом случае определитель равен 9.0922 11 ( 22 )- 21 ( 12 ). Для нашего примера выше определитель будет равен 1(1)-(0,5)(0,5) = 0,75.
Большой определитель означает свободу варьирования; определитель, равный нулю, означает, что свободы варьирования нет, в матрице полная предсказуемость. Например, если бы корреляции между нашими двумя показателями были равны 1,0, то определитель матрицы корреляции был бы равен (1)(1)-(1)(1) = 0. Нулевой определитель получается, когда существует линейная зависимость в матрица. То есть, если одна переменная является линейной комбинацией других переменных в матрице, определитель будет равен нулю. Например, предположим, что я хочу использовать удовлетворенность работой для прогнозирования текучести кадров. У меня есть пять шкал удовлетворенности работой из JDI (Job Descriptive Index, известная мера): работа, зарплата, продвижение по службе, надзор и коллеги. Теперь предположим, что я хочу предсказать оборот по этим пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общую удовлетворенность, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + совместная работа).
Теперь предположим, что я хочу предсказать оборот по этим пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общую удовлетворенность, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + совместная работа).
Если я положу все шесть шкал в корреляционную матрицу, определитель будет равен нулю. Матрица с определителем, равным нулю, называется сингулярной . Это своего рода плохая вещь, как будет объяснено в ближайшее время. Сингулярные матрицы доставляют нам неприятные проблемы. Матрица будет сингулярной, если любые две переменные в матрице идеально коррелированы (либо r = 1, либо r = -1). Матрица также будет сингулярной всякий раз, когда любая переменная в матрице точно предсказывается любой комбинацией других переменных в матрице. То есть, если мы выберем какую-либо одну переменную в качестве зависимой и используем любую комбинацию других переменных в матрице для вычисления линейной регрессии, и мы найдем R 2 из 1. 0, матрица вырожденная. Сингулярная матрица не имеет обратной .
0, матрица вырожденная. Сингулярная матрица не имеет обратной .
1 | 0 | 0 |
|
|
|
|
|
|
0 | 1 | 0 |
| | А | | = 1 |
|
|
|
0 | 0 | 1 |
|
|
|
|
|
|
| А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 | . | .25 |
|
|
|
|
|
|
.5 | 1 | .25 |
| | Б | | = 0,69 |
|
|
|
.25 | .25 | 1 |
|
|
|
|
|
|
| Б |
|
|
|
|
|
|
|
1 | 1 | 0 |
|
|
|
|
|
|
1 | 1 | 0 |
| | С | | = 0 |
|
|
|
0 | 0 | 1 |
|
|
|
|
|
|
| С |
|
|
|
|
|
|
|
Обратите внимание, что определитель для A больше, чем для B , потому что у A больше свободы для изменения, и, конечно же, определитель для C равен нулю, потому что две переменные идеально коррелированы.
Матрица, обратная
, обратное , является матричным аналогом деления действительных чисел. В действительных числах x -1 равно 1/x. А в действительных числах, если умножить х на х -1 , имеем (x)(1/x)=1. Только квадратная матрица может иметь обратную. Обратная матрица обладает тем свойством, что когда мы умножаем матрицу на обратную, получается единичная матрица I . Другими словами, АА -1 = А -1 А = I . Это особенное во многих отношениях. Во-первых, обычно не бывает так, что предварительное и постумножение двух матриц дает один и тот же результат ( AX обычно не равно XA ). Во-вторых, единичная матрица обладает тем свойством, что ее умножение на любую подходящую матрицу приводит к той же самой матрице. то есть АИ = ИА = А . Умножение матрицы на единичную матрицу аналогично операции действительного числа умножения числа или переменной на 1: результирующий результат идентичен введенным числам. Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В действительных числах, когда вы делите число на его обратную («обратную»), результат равен 1. Когда вы умножаете матрицу на обратную, результат равен I . В обоих случаях (1 и I ), умножение на что-то оставляет исходное значение неизменным.
Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В действительных числах, когда вы делите число на его обратную («обратную»), результат равен 1. Когда вы умножаете матрицу на обратную, результат равен I . В обоих случаях (1 и I ), умножение на что-то оставляет исходное значение неизменным.
1 | .5 | .25 |
| 1 | 0 | 0 |
| 1 | .5 | .25 |
.5 | 1 | .25 |
| 0 | 1 | 0 |
| . | 1 | .25 |
.25 | .25 | 1 |
| 0 | 0 | 1 |
| .25 | .25 | 1 |
| Б |
|
|
| я |
|
|
| БИ |
|
|
|
|
|
|
|
|
|
|
|
|
1 | . | .25 |
| 1,36 | -.64 | -.18 |
| 1 | 0 | 0 |
.5 | 1 | .25 |
| -.64 | 1,36 | -.18 |
| 0 | 1 | 0 |
.25 | .25 | 1 |
| -.18 | -. | 1,36 |
| 0 | 0 | 1 |
| Б |
|
|
| Б -1 |
|
| ББ -1 | ||
Проверить умножение.
БИ(1,1) = 1+0+0; БИ(2,1) = 0,5+0+0; BI(3,1) = .25+0+0 и т. д. BB -1 (1,1) = (1)1,36–0,5(0,46)–0,25(0,18) = 1; BB -1 (2,1) = 0,5(1,36)-(1).64-0,25(0,18)=0 и т. д.
Третья основная причина, по которой нас это волнует, заключается в том, что для нахождения весов b и b из матриц данных используется инверсия. Если мы умножим корреляционную матрицу на обратную, мы получим единичную матрицу I . Это позволяет нам умножать обе части уравнения на обратную для решения матричного уравнения (так же, как деление обеих частей уравнения в обычной алгебре).
Если мы умножим корреляционную матрицу на обратную, мы получим единичную матрицу I . Это позволяет нам умножать обе части уравнения на обратную для решения матричного уравнения (так же, как деление обеих частей уравнения в обычной алгебре).
Обратное позволяет нам найти веса b .
Во всяком случае, нет обратной, когда матрица вырожденная (когда определитель равен нулю). Когда нет обратного, мы не можем найти веса b . Итак, если у нас есть сингулярная матрица, мы не можем использовать множественную регрессию.
Матричные функции
| template | ||
| Detail::tmat2x2< valType > ::value_type | определитель (detail::tmat2x2< valType > const &m) | |
| template | ||
| определитель (detail::tmat3x3< valType > const &m) | ||
| template | ||
| x detail::tvalmat > tval5289 :: value_type | Detriminant (Detail :: tmat4x4 | |
| Tempalt valType > const & m) | ||
| template | ||
| detail::tmat3x3< valType > | inverse (detail::tmat30017 | |
| template | ||
| detail::tmat4x4< valType > | inverse (detail::tmat4x4< valType > const &m) | |
| template | ||
| matType | matrixCompMult (matType const &x, matType const &y) | |
| template | ||
| matType | outerProduct (vecType const &c, vecType const &r) | |
| template | ||
| matType::transpose_type | transpose (matType const &x) | |
Для каждой из следующих встроенных матричных функций существует как версия с плавающей запятой одинарной точности, где все аргументы и возвращаемые значения имеют одинарную точность, так и версия с плавающей запятой двойной точности, где все аргументы и возвращаемые значения имеют двойную точность.
Показана только версия с плавающей запятой одинарной точности.
| detail::tmat2x2 | ( | detail::tmat2x2< valType > const & | м | ) |
Возвращает определитель матрицы mat2.
- Параметры шаблона
valType Скалярные типы с плавающей запятой.
- См. также
- Справочная страница определителя GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| detail::tmat3x3 | ( | detail::tmat3x3< valType > const & | м | ) |
Возвращает определитель матрицы mat3.
- Параметры шаблона
valType Скалярные типы с плавающей запятой. 
- См. также
- Справочная страница определителя GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| detail::tmat4x4 | ( | detail::tmat4x4< valType > const & | м | ) |
Возвращает определитель матрицы mat4.
- Параметры шаблона
valType Скалярные типы с плавающей запятой.
- См. также
- Справочная страница определителя GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| detail::tmat2x2 | ( | detail::tmat2x2< valType > const & | м | ) |
Возвращает обратную матрицу mat2.
- Параметры шаблона
valType Скалярные типы с плавающей запятой.
- См. также
- Инверсная справочная страница GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| detail::tmat3x3 | ( | detail::tmat3x3< valType > const & | м | ) |
Возвращает обратную матрицу mat3.
- Параметры шаблона
valType Скалярные типы с плавающей запятой.
- См. также
- Инверсная справочная страница GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| detail::tmat4x4 | ( | detail::tmat4x4< valType > const & | м | ) |
Возвращает обратную матрицу mat4.
- Параметры шаблона
valType Скалярные типы с плавающей запятой.
- См. также
- Инверсная справочная страница GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
| matType glm::matrixCompMult | ( | matType const & | х , |
| matType const & | г | ||
| ) |
Умножить матрицу x на матрицу y покомпонентно, т. е. result[i][j] является скалярным произведением x[i][j] и y[i][j].
- Параметры шаблона
matType Типы матриц с плавающей запятой.
- См. также
- Справочная страница GLSL matrixCompMult
- Спецификация GLSL 4.
 20.8, раздел 8.6 Матричные функции
20.8, раздел 8.6 Матричные функции
| matType glm::outerProduct | ( | vecType const & | с , |
| vecType константа & | р | ||
| ) |
Первый параметр c рассматривается как вектор-столбец, а второй параметр r — как вектор-строка, и линейная алгебраическая матрица умножается c * r.
- Параметры шаблона
matType Типы матриц с плавающей запятой.
- См. также
- Справочная страница GLSL externalProduct
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
- Задачи:
- Уточните объявление, чтобы указать, что при использовании matType не требуется указывать.

| matType::transpose_type glm::transpose | ( | matType const & | х | ) |
Возвращает транспонированную матрицу x.
- Параметры шаблона
matType Типы матриц с плавающей запятой.
- См. также
- Справочная страница транспонирования GLSL
- Спецификация GLSL 4.20.8, раздел 8.6 Матричные функции
Обратная матрица
Марко Табога, доктор философии
Понятие обратного матрица представляет собой многомерное обобщение понятия обратного числа:
Table of contents
Definition
Existence of the inverse
Singular matrix
Uniqueness of the inverse
Right and left inverse
Inverse of a product
Обратное к транспонированию
Решенные упражнения
Упражнение 1
Упражнение 2
Упражнение 3
Определение
Начнем с определения обратного.
Определение Позволять быть матрица. Его обратным, если он существует, является матрица что удовлетворяетгде это единичная матрица. Если существует, то мы говорим, что обратим.
Когда , тогда а также который ясно показывает, что приведенное выше определение обобщает понятие взаимного число.
Пример Рассмотрим матрицу Затем, мы можем проверить тем самым проведение умножение между два матрицы:
Существование обратной
При каких условиях квадратная матрица обратима? Следующее предложение отвечает на этот вопрос.
Предложение А матрица обратим тогда и только тогда, когда полный ранг.
Доказательство
Сначала докажем часть «если» (полный ранг
подразумевает обратимость). Обозначим через
в
колонны
единичная матрица
. Если
полноранговый, то его
столбцы линейно
независимый. Это подразумевает, что любой
-размерный
вектор можно записать как
линейная комбинация
столбцы
(см. лекцию о стандартных
основания для доказательства). Следовательно, для
,
мы можем написать
как линейная комбинация столбцов
:куда
– коэффициенты линейной комбинации. Используя представленные результаты
в лекции о
матрица
умножение и линейные комбинации, эти коэффициенты можно складывать
сформировать
вектор
такой
чтоКроме того,
векторы-столбцы
можно расположить рядом, образуя
матрица
такой
чтоТаким образом,
обратим и
Мы
теперь собираемся доказать часть «только если» (обратимость подразумевает полный ранг).
Если инверсия
существуют,
thenПост-умножение
обе части уравнения любым
вектор
,
мы
getor Таким образом,
любой вектор
может быть записана как линейная комбинация столбцов
,
с коэффициентами, взятыми из
.
Если
полноранговый, то его
столбцы линейно
независимый. Это подразумевает, что любой
-размерный
вектор можно записать как
линейная комбинация
столбцы
(см. лекцию о стандартных
основания для доказательства). Следовательно, для
,
мы можем написать
как линейная комбинация столбцов
:куда
– коэффициенты линейной комбинации. Используя представленные результаты
в лекции о
матрица
умножение и линейные комбинации, эти коэффициенты можно складывать
сформировать
вектор
такой
чтоКроме того,
векторы-столбцы
можно расположить рядом, образуя
матрица
такой
чтоТаким образом,
обратим и
Мы
теперь собираемся доказать часть «только если» (обратимость подразумевает полный ранг).
Если инверсия
существуют,
thenПост-умножение
обе части уравнения любым
вектор
,
мы
getor Таким образом,
любой вектор
может быть записана как линейная комбинация столбцов
,
с коэффициентами, взятыми из
. Другими словами, столбцы
охватывать пространство всех
векторы. Если бы они не были линейно независимыми, то мы могли бы
исключить некоторые из них и получить набор линейно независимых векторов,
1) является основой пространства
из всех
векторы; 2) имеет мощность меньше
.
Но это невозможно, потому что любое основание
имеет мощность, равную
(см. лекцию о стандартных
базы). Таким образом, столбцы
должны быть линейно независимыми, а это означает, что
имеет полный ранг.
Другими словами, столбцы
охватывать пространство всех
векторы. Если бы они не были линейно независимыми, то мы могли бы
исключить некоторые из них и получить набор линейно независимых векторов,
1) является основой пространства
из всех
векторы; 2) имеет мощность меньше
.
Но это невозможно, потому что любое основание
имеет мощность, равную
(см. лекцию о стандартных
базы). Таким образом, столбцы
должны быть линейно независимыми, а это означает, что
имеет полный ранг.
Сингулярная матрица
Матрица, которая не является обратимой, называется сингулярной матрицей . По предложению выше, сингулярная матрица — это матрица, не имеющая полный ранг. По этой причине сингулярную матрицу также иногда называют без ранга .
Единственность обратного
Предложение Если инверсия матрица существует, то она единственна.
Доказательство
В доказательстве того, что матрица
обратима тогда и только тогда, когда она полноранговая, мы показали, что обратная
можно построить столбец за столбцом, найдя векторы
что
решить это
есть, записав векторы канонического базиса в виде линейных комбинаций
колонны
. Поскольку представление вектора в терминах базиса единственно,
векторы
уникальны. Но последние являются колоннами
.
Следовательно, также
уникален.
Поскольку представление вектора в терминах базиса единственно,
векторы
уникальны. Но последние являются колоннами
.
Следовательно, также
уникален.
Правая и левая инверсия
Важным фактом является то, что дает единичную матрицу не только при предварительном умножении, но и при умножается на .
Предложение Позволять быть матрица. Если его инверсия существует, она удовлетворяет не только условиено так же состояниегде это единичная матрица.
Доказательство
Пост-умножение обеих сторон
уравнение
,
а также
получатель
Но
у нас также есть
чтоСейчас,
может показаться интуитивно понятным, что уравнения (1) и (2) подразумевают, что
Тем не менее,
это нужно доказать. Доказательство следующее. Уравнение (1) говорит о том, что
столбцы
,
в правой части уравнения можно рассматривать как линейные комбинации
колонны
себя, в левой части, с коэффициентами, взятыми из
. Уравнение (2) говорит о том, что столбцы
,
в правой части уравнения можно рассматривать как линейные комбинации
колонны
себя, в левой части, с коэффициентами, взятыми из
.
С
является полноранговым, его столбцы являются основой пространства всех
векторов и единственностью представления в терминах базиса (см.
лекция под названием «Основы
линейного пространства), коэффициенты линейных комбинаций должны быть
то же, что
есть,
Уравнение (2) говорит о том, что столбцы
,
в правой части уравнения можно рассматривать как линейные комбинации
колонны
себя, в левой части, с коэффициентами, взятыми из
.
С
является полноранговым, его столбцы являются основой пространства всех
векторов и единственностью представления в терминах базиса (см.
лекция под названием «Основы
линейного пространства), коэффициенты линейных комбинаций должны быть
то же, что
есть,
Обратное произведение
Справедливо следующее предложение.
Предложение Позволять а также быть двумя матрицы. Затем продукт обратим тогда и только тогда, когда а также обратимы. Кроме того,
Доказательство
Две матрицы
а также
обратимы тогда и только тогда, когда они полноранговые (см. выше). Если
а также
полноранговые, то
полноранговый (см. лекцию о
матричные продукты и
классифицировать). Наоборот, если хотя бы одна из двух матриц не
полноранговые, то ранг их продукта меньше
потому что в
Другими словами, продукт является полноценным, только если
а также
являются полноценными. Кроме того, легко проверить, что
удовлетворяет определению обратного
:
Наоборот, если хотя бы одна из двух матриц не
полноранговые, то ранг их продукта меньше
потому что в
Другими словами, продукт является полноценным, только если
а также
являются полноценными. Кроме того, легко проверить, что
удовлетворяет определению обратного
:
Инверсия транспонирования
Следующее предложение показывает, как вычислить обратную операцию транспонирования матрица.
Предложение Позволять быть матрица и его транспонировать. Если обратим, то обратим и
Доказательство
У нас есть чтоПо переставляя обе части уравнения, мы получитьпотому что единичная матрица равна своей транспонированной. Используя формулу для транспонирование продукта, мы получитьТак, удовлетворяет определению обратного .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Определить
Проверять что
Решение
Нам нужно провести умножение между двумя матрицы:Их произведение равно единичной матрице, поэтому действительно является обратным .
Упражнение 2
Позволять , а также быть матрицы полного ранга. Экспресс инверсия условия, обратные , а также .
Решение
Приходится многократно применять формулу для обратной продукт:
Упражнение 3
Показывать что
Решение
По определению, обратное нуждается в удовлетворятьButAs следствие,
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Обратная матрица», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/обратная матрица.
Транспонирование матрицы — свойства и формулы —
| Definition | |
|---|---|
| — | Definition |
| — | Examples |
| Properties | |
|---|---|
| — | Product |
| — | Inverse |
| — | Определитель |
| — | Трассировка |
| — | Линейность |

Примеры
Транспонированная матрица матрицы
является
. Транспонированная матрица матрицы
является
.
Продукт
Транспонированная матрица произведения двух матриц равно произведению транспонированных матриц, в которых порядок произведений обратный:
.
Доказательство
Пусть $A$ — матрица размером $l \times m$, и
$B$ — матрица $m \times n$, записанная в виде
9{T}|$ равен определителю $A$, т. е.
Доказательство
По определению,
определитель транспонирования произвольной $n \times n$ матрицы $A$
записывается как
,
где $\sigma$ обозначает функцию,
называется перестановкой,
который переупорядочивает набор целых чисел,
$
\{
1,2,\cdots,n
\}
$
$S_{n}$ обозначает
множество всех таких перестановок,
$\mathrm{sgn}(\sigma) $ это
знак, зависящий от перестановки,
а также
сумма $\sum_{\sigma \in S_{n}}$ включает все перестановки. (Подробнее см. «Определение определителя».)
9{-1} $
такой, что
(Подробнее см. «Определение определителя».)
9{-1} $
такой, что
, где $i=1,2,\cdots,n$. Используя это, мы имеем
$$ \тег{5.1} $$ . Так как $\sigma$ это карта, которая отображает $\{1,2,\cdots,n\}$ к тому же набору $\{1,2,\cdots,n\}$, существует $j$ $(j=1,\cdots,n)$ такой, что $\sigma(j) = 1$. Поэтому $(5.1)$ можно записать в виде
, куда , в последней строке, просто изменился порядок умножения. Аналогично, существует $k$ $(k=1,\cdots,n, k\neq j)$ такой, что $\sigma(k) = 2$. Мы видим, что
9{T}$ равен следу $A$: Доказательство
Пусть $A$ — матрица $n \times n$,
и $A_{ij}$
$i$-я строка,
$j$-й элемент столбца $A$.
По определению транспонирования,
у нас есть
, где ($i,j=1,2 \cdots , n$). Это и определение следа дают
Линейность
Пусть $A$ и $B$ — матрицы $m \times n$, а alpha — скаляр.






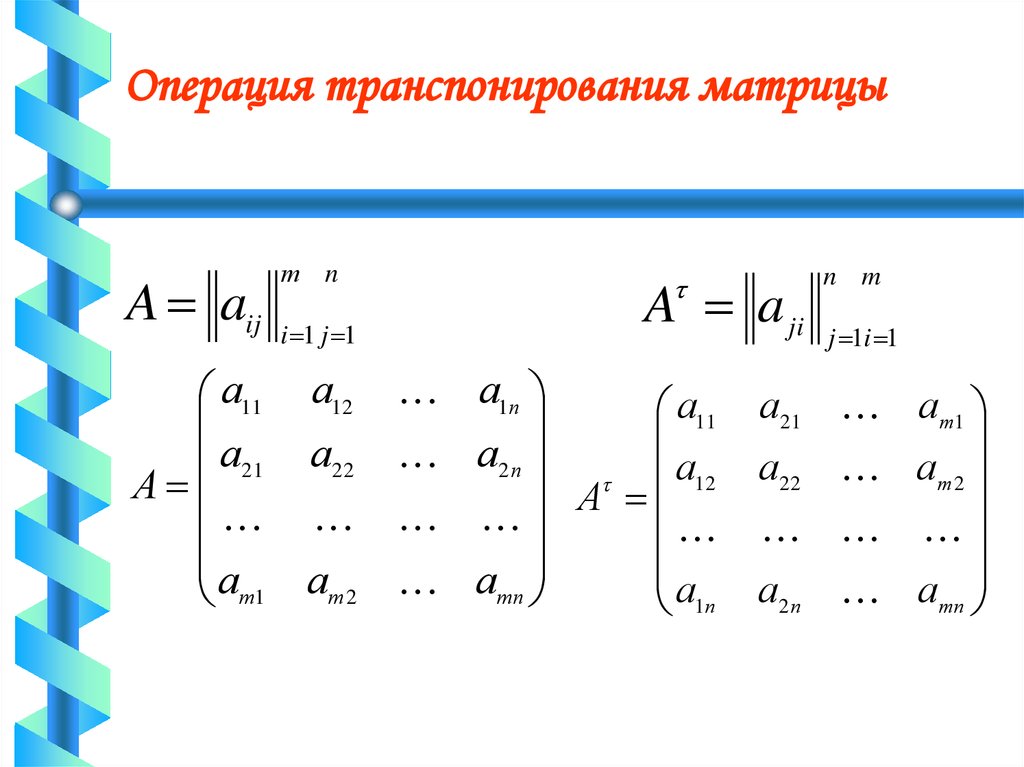 Для этого давно есть мощные алгоритмы.
Для этого давно есть мощные алгоритмы.  е. в столбцах которой представлены новые базисные вектора через старый базис). В таком случае, матрица является переходом от нового к старому.
е. в столбцах которой представлены новые базисные вектора через старый базис). В таком случае, матрица является переходом от нового к старому.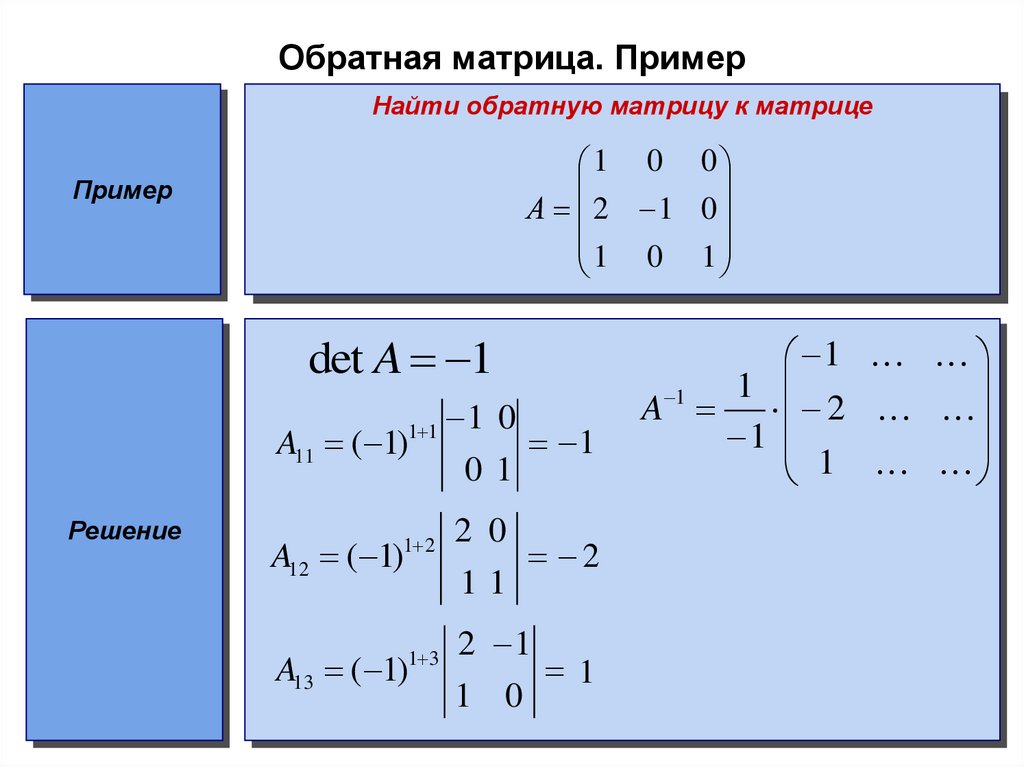 09.2019, 13:14
09.2019, 13:14  Возможно у меня где-то неправильное логическое рассуждение?
Возможно у меня где-то неправильное логическое рассуждение?

 09.2019, 15:47
09.2019, 15:47  09.2019, 15:58
09.2019, 15:58  И не понимаю, где логика сворачивает не туда (рассуждения описал выше)..
И не понимаю, где логика сворачивает не туда (рассуждения описал выше)..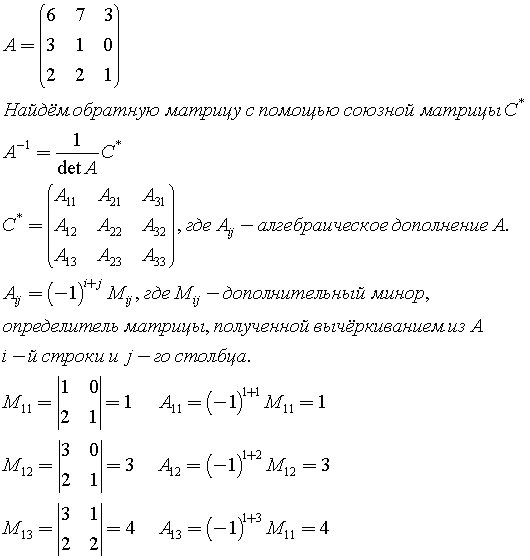
 С учётом того, что матрица линейного отображения определена для любого отображения , будь только выбраны базисы в , нам не обязательно интересоваться транспонированными матрицами, пока мы не начнём говорить о каких-нибудь евклидовых или гильбертовых . Когда начнём, тогда сможем например умножать матрицу на транспонированную к ней с осмысленным результатом.
С учётом того, что матрица линейного отображения определена для любого отображения , будь только выбраны базисы в , нам не обязательно интересоваться транспонированными матрицами, пока мы не начнём говорить о каких-нибудь евклидовых или гильбертовых . Когда начнём, тогда сможем например умножать матрицу на транспонированную к ней с осмысленным результатом.

 Надо с обеих сторон, чтобы оба перевести в другой.
Надо с обеих сторон, чтобы оба перевести в другой.


