Карточки по геометрии для подготовки к ОГЭ
Модуль «Геометрия» (базовый уровень) Вариант 2
1. На рисунке треугольник АВС – равнобедренный с основанием АС, АD – его высота, ВD = 16 см, СD =4 см. Найдите высоту АD.
Ответ: ____________
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Ответ: ____________
3.Основания прямоугольной трапеции равны 12 и 4. Её площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Ответ: ____________
4.Периметр параллелограмма АВСD равен 32 см, а его диагональ ВD равна 9 см. Найдите периметр треугольника АВD.
Ответ: ____________
5.Найдите радиус окружности, вписанной в
правильный треугольник, высота которого равна 6.
Ответ: ____________
6.Какое из следующих утверждений верно?
1) Вертикальные углы равны.
2) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
3) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
7. Катеты прямоугольного треугольника равны 6 и 8. Найдите синус наименьшего угла этого треугольника.
Ответ: ____________
Модуль «Геометрия» (базовый уровень) Вариант 3
1.Найдите длину отрезка МВ, если в изображённой на рисунке трапеции МNPK известно: МK = 24, NP = 18, BP = 12.
Ответ: ____________
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Ответ: ____________
3.Точка D на стороне АВ
треугольника АВС выбрана так, что AD = AC. Известно, что Найдите
угол DCB. Ответ дайте
в градусах.
Известно, что Найдите
угол DCB. Ответ дайте
в градусах.
Ответ: ____________
5.Найдите периметр треугольника АВС, изображённого на рисунке, если точка О – центр вписанной окружности, ВМ = 6 см, МС = 8 см, АС = 12 см.
Ответ: ____________
6.Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 16. Найдите диаметр окружности.
Ответ: ____________
7.Какое из следующих утверждений верно?
1) Все хорды одной окружности равны между собой.
2) Диагональ равнобедренной трапеции делит её на два равных треугольника.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
8. В треугольнике АВС Найдите АВ.
Ответ: ____________
Модуль «Геометрия» (базовый уровень) Вариант 4
1. На
стороне ВС прямоугольника АВСD, у которого АВ = 3 и АD =
7, отмечена точка Е так, что Найдите ED.
На
стороне ВС прямоугольника АВСD, у которого АВ = 3 и АD =
7, отмечена точка Е так, что Найдите ED.
Ответ: ____________
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Ответ: ____________
3.В параллелограмме АВСD диагональ АС перпендикулярна стороне СD. Найдите тупой угол между диагоналями, если диагонали АС и BD равны 6 см и соответственно.
Ответ: ____________
5.В трапецию вписана окружность. Найдите периметр этой трапеции, если её основания равны 8 см и 12 см.
Ответ: ____________
6.Найдите угол ВАD четырёхугольника АВСD,
вписанного в окружность, если внешний угол четырёхугольника при вершине С
равен 1080.
Ответ: ____________
7.Какое из следующих утверждений верно?
1) Все квадраты имеют равные площади.
2) Основания равнобедренной трапеции равны.
3) Центр окружности, описанной около прямоугольного треугольника, находится на стороне этого треугольника.
8. В треугольнике АВС Найдите ВС.
Ответ: ____________
Модуль «Геометрия» (базовый уровень) Вариант 5
1.Высота равнобедренной трапеции, проведённая из вершины С, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания ВС.
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3.Четырёхугольник АВСD вписан в окружность.
Угол АВС равен 1280, угол CAD
равен 730. Найдите угол ABD.
Ответ дайте градусах.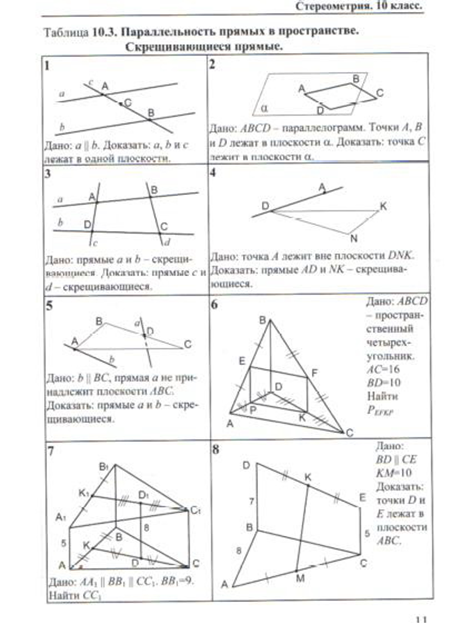
4.Найдите длину разности векторов (размеры клеток ).
5.Периметр равнобедренного треугольника равен 80, а боковая сторона – 25. Найдите площадь треугольника.
6.На отрезке АВ выбрана точка С так, что АС = 80 и ВС = 2. Построена окружность с центром А, проходящая через С. Найдите длину отрезка касательной, проведённой из точки В к этой окружности.
7.Какое из следующих утверждений верно? 1) В прямоугольном треугольнике гипотенуза равна сумме катетов. 2) Если в ромбе один из углов равен 90градусам, то такой ромб – квадрат. 3) Для точки, лежащей на окружности, расстояние до центра окружности равно диаметру.
8. В треугольнике АВС Найдите
Модуль «Геометрия» (базовый уровень) Вариант 6
1. В
треугольнике
В
треугольнике
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3.В параллелограмме АВСD высота BH в два раза меньше стороны СD. Найдите градусную меру угла АВС.
4. Найдите длину суммы векторов (размеры клеток ).
5.Отрезок NО – высота трапеции MNLK. Найдите площадь трапеции, если MN = 10 см, МО = 6 см, ОК = 12 см, NL = 8 см.
6. На окружности по разные стороны от диаметра АВ отмечены M и N. Известно, что Найдите угол NM
В.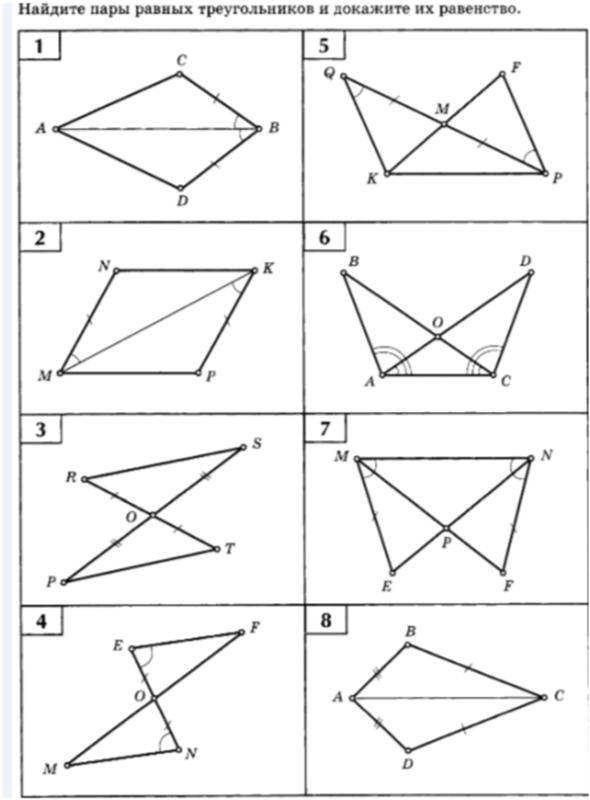 Ответ дайте в градусах.
Ответ дайте в градусах. 7.Какое из следующих утверждений верно? 1) Сумма углов вписанного в окружность четырёхугольника равна 3600. 2) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны. 3) Если при пересечении двух прямых третьей внутренние односторонние углы равны 900, то прямые параллельны. 8. Катеты прямоугольного треугольника равны 4 и 3. Найдите синус наименьшего угла этого треугольника.
Модуль «Геометрия» (базовый уровень) Вариант 7
1. Диагональ АС
параллелограмма АВСD образует со стороной АВ угол 200.
Найдите сторону CD параллелограмма,
если его периметр равен 20 см, а угол АDС равен
1400.
Диагональ АС
параллелограмма АВСD образует со стороной АВ угол 200.
Найдите сторону CD параллелограмма,
если его периметр равен 20 см, а угол АDС равен
1400.
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3.В трапеции АВСD стороны АВ, ВС и CD равны. Основание АD в два раза больше основания ВС. Найдите угол СDА.
4.Найдите длину суммы векторов (размеры клеток ).
5. На рисунке Р и Н – середины сторон, СК – высота треугольника. Найдите площадь треугольника, если РН = 7 см, СК = 12 см.
6.В окружности с диаметром 20 см проведены
две параллельные хорды, длина каждой из которых равна 16 см. Найдите
расстояние между хордами.
Найдите
расстояние между хордами.
7.Какое из следующих утверждений верно?
1)Любые два равносторонних треугольника подобны.
2) Каждая сторона треугольника равна сумме двух других сторон.
3) Сумма углов выпуклого четырёхугольника равна 1800.
8. В треугольнике АВС угол С прямой, АС = 6, ВС = 8. Найдите синус внешнего угла при вершине А.
Модуль «Геометрия» (базовый уровень) Вариант 8
1. В прямоугольном треугольнике АВС из вершины прямого угла проведена высота CD. Найдите гипотенузу АВ, если угол АCD равен 300, а отрезок АD равен 5 см.
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3.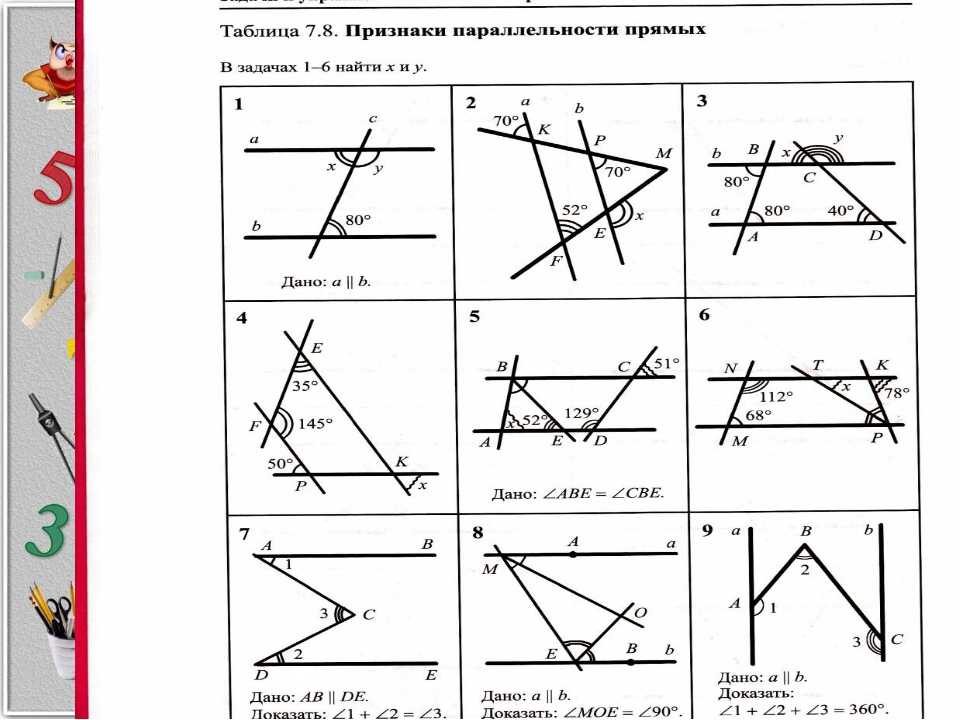 В параллелограмме АВСD диагонали
пересекаются в точке О, причём диагональ ВD вдвое
больше стороны АВ. Угол между диагоналями равен 1120, а угол САD равен 400.
Найдите угол СDА.
В параллелограмме АВСD диагонали
пересекаются в точке О, причём диагональ ВD вдвое
больше стороны АВ. Угол между диагоналями равен 1120, а угол САD равен 400.
Найдите угол СDА.
4.Две стороны прямоугольника АВСD равны 7 и 24. Найдите длину разности векторов
5.Найдите периметр параллелограмма, изображённого на рисунке. АН = 9 см, ВН = 12 см, ВК = 20 см.
6. Угол между диаметром АВ и хордой АС окружности равен 300. Через точку С проведена касательная к окружности, которая пересекает прямую АВ в точке D. Найдите угол СDА. Ответ дайте в градусах.
7.Какое из следующих утверждений верно?
1) Смежные углы равны.
2) Через любую точку, лежащую вне окружности, можно провести две
касательные к этой окружности. 3)
Площадь параллелограмма равна половине произведения его диагоналей.
3)
Площадь параллелограмма равна половине произведения его диагоналей.
8. В треугольнике АВС Найдите
Модуль «Геометрия» (базовый уровень) Вариант 9
1.В треугольнике АВС ВМ – медиана и ВН – высота. Известно, что АС = 53 и ВС = ВМ. Найдите АН.
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3. В равнобедренной трапеции АВСD тупой угол при основании равен 1300. Найдите угол AQD, образованный биссектрисами острых углов А и D.
4.Найдите длину вектора (размеры клеток ).
5.В
трапеции АВСD АD = 4, ВС = 1, а
её площадь равна 35. Найдите площадь треугольника АВС.
Найдите площадь треугольника АВС.
6.Найдите радиус окружности, описанной около прямоугольника со сторонами 7 см и 24 см.
7.Какое из следующих утверждений верно?
1) У любой трапеции основания параллельны.
2) Все углы ромба равны.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
8. В треугольнике АВС Найдите sin A.
Модуль «Геометрия» (базовый уровень) Вариант 10
1.В треугольнике АВС со сторонами 10 см, 15 см и 17 см проведена биссектриса ВD к большей стороне АС. Найдите меньший из отрезков, на которые точка D делит сторону АС.
2.Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
3.В равнобедренной трапеции с большим
основанием AD
диагональ АС перпендикулярна боковой стороне СD и
является биссектрисой угла BAD. Найдите угол DAB.
Найдите угол DAB.
4.Найдите длину суммы векторов (размеры клеток ).
5.Найдите площадь треугольника BCD, если CD = 12 см, DN = 6 см, BD = 10 см.
6.В окружности проведены хорда СР и диаметр АВ. Найдите радиус окружности, если РМ = 6, СМ = 8, ВМ = 4.
7.Какие из следующих утверждений верны?
1) Диагональ параллелограмма делит его на два равных треугольника.
2) Все углы ромба равны.
3) Площадь квадрата равна произведению двух его смежных сторон.
8. В треугольнике АВС Найдите
Зачетная система по геометрии в 8-м классе
Цель: реализовать триединые
дидактические задачи: обучение, развитие,
воспитание.
Подбор заданий на тематических зачетах основывается на уровнях:
- минимальный (государственный стандарт);
- базовый;
- вариативный (творческий).
Основными принципами разноуровневой технологии являются:
- всеобщая талантливость — нет бесталанных людей, а есть занятые не своим делом;
- взаимное превосходство – если у кого-то что-то получается хуже, чем у других, значит что – то должно получиться лучше; это что – то нужно искать;
- неизбежность перемен – ни одно суждение о человеке не может считаться окончательным.
Что ведет к формированию и воспитанию разносторонней личности.
Включение ученика в познавательную
деятельность, её организация влечёт за собой
неизбежное возникновение затруднений, пути
выхода известны не только учителю, но и учащимся.
Здесь мы видим рефлексивные действия учеников по выявлению собственных изменений: вспомнить, выявить, осознать основные компоненты деятельности, её смысл, способы, проблемы, пути их решения, полученные результаты.
Рефлексия помогает осознать способы решения задачи, зафиксировать достигнутый образовательный результат, корректировать путь, самостоятельно проектировать индивидуальную учебную деятельность.
Поскольку рефлексия становится не только звеном механизма саморазвития личности, но и мерой культуры мышления, она приводит к изменению характера и содержания подготовки к учебным занятиям, воспитывает характер учащегося.
Зачет проводится как заключительный этап
проверки знаний учащихся в конце изучаемой темы.
Заранее сообщается о предстоящем зачете, его
содержании, особенности организации и сроках
сдачи. Учащимся предварительно сообщается
примерный перечень заданий, выносимых на зачет. Каждому ученику предоставляется индивидуальная
карточка с заданиями , включающая основные и
дополнительные упражнения.
Каждому ученику предоставляется индивидуальная
карточка с заданиями , включающая основные и
дополнительные упражнения.
В начале урока учитель работает с более подготовленными учащимися — консультантами. Он проверяет и оценивает их знания, и разъясняет методику проверки заданий. Консультанты принимают у учащихся выполнение каждого задания и оценивают их, ведя учетные карточки. Собрав учетные карточки, учитель выводит итоговые отметки и подводит итог зачета. Помощь в работе учителя оказывает листы учета.
| Ф.И. ученика |
Обязательная часть | Дополнительная часть оценка | ||||||||||
С целью отслеживания результатов обучения и последующей рефлексии можно составить и проанализировать таблицу:
Ф. И. И.ученика |
Отметка за курс …класса | “Прогноз” ученика | “Прогноз” учителя | Отметки за зачеты | Итоговая отметка за год | ||||
| № 1 | № 2 | № 3 | № 4 | № 5 | |||||
Материал по теме усвоен, настроение приподнятое. Дети настроены на дальнейшее приобретение новых знаний. Ребята ждут подобные зачеты, где можно проявить себя, показав не только уровень знаний, эрудицию, но и смекалку.
Данная методика помогает провести диагностику развития личности в обучении, учитывая элементы:
- воспитанность; познавательный интерес;
- общеучебные умения и навыки;
- фонд действенных знаний (по уровням);
мышление; память; тревожность; темперамент.

ЛИСТ УЧЁТА
“зачет” или “3”;
“ 4 и 5 ”.
| Ф.И. ученика |
Обязательная часть | Дополнительная часть | Оценка | |||||||||||||
| Аристова Настя | ||||||||||||||||
| Приходько Алёна | ||||||||||||||||
| Шестакова Ира | ||||||||||||||||
| Германов Иван | ||||||||||||||||
| Травкова Света | ||||||||||||||||
| Жукова Алиса | ||||||||||||||||
| Харитонов Иван | ||||||||||||||||
Черкасов Артем. |
||||||||||||||||
| Мурашкин Рома | ||||||||||||||||
| Барсукова Наташа | ||||||||||||||||
| Нагорнов Иван | ||||||||||||||||
“Зачет” – при выполнении задания
обязательного уровня с незначительными
недочетами.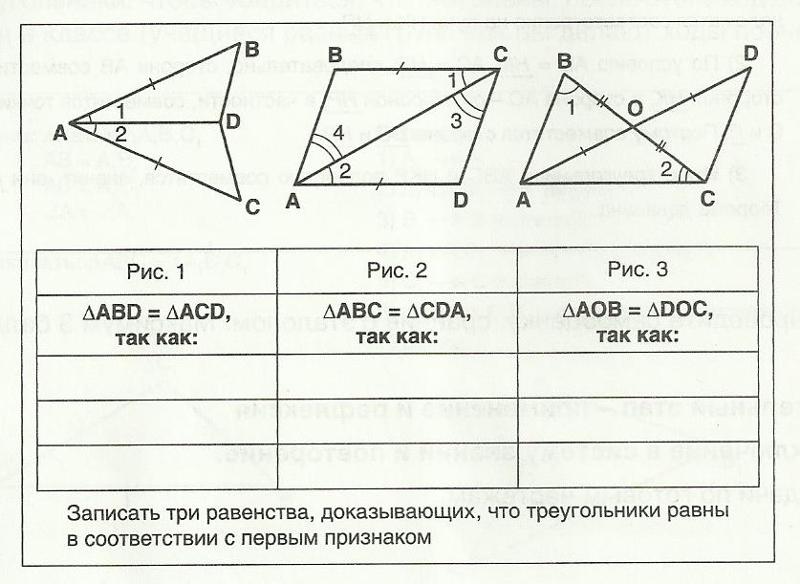
“3” – при выполнении задания обязательного
уровня без ошибок.
“4”– выполнены задания обязательного уровня и
на 4.
“5” – выполнены задания всех уровней.
“незачет”– при не выполнении заданий (учитывается
любой уровень).
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Тема: “Четырехугольники”. Всего 14 час.
ЦЕЛИ:
- Дать систематические сведения о четырехугольниках и их свойствах.
- Сформировать представления о фигурах, симметричных относительно точки или прямой.
- Повторить признаки равенства треугольников.
- Научить доказывать теоремы с опорой на признаки равенства треугольников с применением новых теоретических факторов.
- Ознакомить с понятием симметричных фигур
относительно точки или прямой.

Планирование: 14 /час/.
- Многоугольники. (2)
- Параллелограмм и трапеция. (2)
- Прямоугольник. Квадрат. Ромб. (3)
- Симметричные фигуры. (2)
- Закрепление. (1)
- Зачёт 1. (1)
- Задачи на построение. (2)
- КОНТРОЛЬНАЯ РАБОТА (1)
Основные понятия и определения:
- понятия многоугольника,
- понятие выпуклого многоугольника,
- определение параллелограмма,
- определение трапеции,
- определение прямоугольника,
- определение ромба,
- определение квадрата,
- осевая и центральная симметрия.
Зачёт по теме: «Многоугольник».
1.
ЗАДАЧИ: НА “3” Дано: Доказать: АВСD – параллелограмм. НА “4 И 5” Дано: АВСD – параллелограмм. Дано: АВСD – трапеция. |
2.
ЗАДАЧИ: НА “3” Дано: Доказать : АВСD – параллелограмм. НА “4 И 5” Дано: АВСD – параллелограмм. Дано: АВСD – трапеция. |
3.
ЗАДАЧИ: НА “3” Дано: Доказать: АВСD – параллелограмм. НА “4 И 5” Дано: АВСD – прямоугольник. Дано: АВСD – трапеция. |
Тема: “Площади фигур”. Всего 14 час.
ЦЕЛИ:
- Сформировать понятие площади многоугольника;
- Развивать умение вычислять площади фигур, применяя изученные свойства фигур и формулы;
- Формировать навыки применения теоремы Пифагора при нахождении площадей многоугольников.
Планирование: 14 /час/.
- Площадь многоугольника. (2)
- Площади параллелограмма и трапеции. (5)
- Теорема Пифагора. (3)
- Повторение. (1)
- Зачёт 2. (2)
- КОНТРОЛЬНАЯ РАБОТА. (1)
Основные понятия и определения:
- дать понятие площади многоугольника,
- понятие площади прямоугольника,
- понятие площади параллелограмма,
- понятие площади треугольника,
- понятие площади трапеции.

- теорема Пифагора.
Зачет по теме: “ПЛОЩАДИ МНОГОУГОЛЬНИКОВ ”. №2
Игра «Умники и Умницы».
ЦЕЛИ зачета:
- Закрепить полученные знания по изученной теме “площади многоугольников”.
- Применять теоретические знания на практике при решении задач.
- Развивать математическую речь, память, логическое мышление.
- Развивать сознательное воспроизведение математических понятий.
- Развивать познавательный интерес.
- В игровой форме показать свой уровень воспитанности. Учить достойно выходить из трудной ситуации.
ПОВТОРИТЬ К ЗАЧЁТУ:
- Параллелограмм.
- Прямоугольник. Квадрат.
- Ромб.
- Треугольник.
- Трапеция.
- Теорема Пифагора.

ПОВТОРИТЬ: признаки равенства треугольников, способы построения биссектрисы, высоты, медианы треугольника, виды углов.
ЗАЧЁТ ПО ГЕОМЕТРИИ 8 КЛАСС. Тема: “Площади многоугольников”.
1. Отборочный тур.
- Задания обязательного уровня. (по разным типам) “3”.
- Повышенного уровня . “4”
- Углубленного уровня. “5”
На подготовку идёт 5-10 минут. Сдают решения (в любом порядке) ареопагу.
На игру желательно брать задания , которые на подготовку не займут много времени.
ЗАДАНИЯ НА “ТРОЙКУ”: Найти площадь .
ЗАДАНИЯ НА “ЧЕТЫРЕ”: Найти площадь .
ЗАДАНИЯ НА “ПЯТЬ”: Найти площадь .
В зависимости от набранного количества баллов получают ордена.
На “3” – один орден.
На “4” – два.
На “5” – три ордена.
2. Вопросы по теории (5 различных билетов) /лежат на столе обратной стороной, дети выбирают сами/.
1.
- Основные свойства площадей многоугольников.
- Сформулировать и доказать теорему о вычислении площади трапеции.
2.
- Площадь прямоугольника. Сформулировать и доказать теорему о площади параллелограмма.
- Расскажите, как измеряются площади многоугольников.
3.
- Сформулируйте и докажите теорему о вычислении площади треугольника.
- Как вычислить площадь прямоугольного треугольника по его катетам ?
4.
- Сформулируйте теорему о вычислении площади двух треугольников , имеющих по равному углу.
- Сформулируйте и докажите теорему ПИФАГОРА.
5.
- Сформулируйте и докажите теорему, обратную
теореме Пифагора.

- Приведите примеры пифагоровых треугольников. Какие треугольники называются пифагоровыми?
На подготовку 5 минут. Нет ошибок – ещё один орден.
3. Вопросы на эрудицию. (20 занимательных вопросов).
- Назовите фамилию автора школьного учебника по геометрии.
- Какие бывают дроби?
- Единица измерения скорости на море. (узел)
- Третья буква греческого алфавита. (гамма)
- Объём 1 кг воды.
- Какое число в Древнем Риме записывалось буквой Д? (500)
- Чьи это слова: “ПОЛЁТ — ЭТО МАТЕМАТИКА! ” (В.Чкалов)
- Рост Дюймовочки? (дюйм – 2,5 см)
- Какую часть тела составляет вода в организме человека? (2/3)
- Количество путешествий Мюнхгаузена на Луну? (два)
- О каких числах идёт речь?Один – долг, другие –
имущество (положит.
 и отриц.числа).
и отриц.числа). - Какая геометрическая теорема в старину называлась “ТЕОРЕМОЙ НЕВЕСТЫ”? (теорема Пифагора)
- В честь какой женщины математика назван один из цветков? (В честь французской вычислительницы Гортензии Лекарт назван цветок гортензия, привезенный из Индии.)
- Кем было предложено обозначать отношение длины окружности к её диаметру буквой “п”? (Леонардом Эйлером).
- Сколько лет Балда служил у попа? (1 год).
- Количество нот. (7 нот ).
- В каком веке жил и творил Архимед? (3 век до н. эр.).
- Автор книги “НАЧАЛО”? (Евклид)
- Чему равны стороны египетского треугольника? (3 см ; 4 см ;5 см )
- Кто автор слов: “Вдохновенье нужно в геометрии не меньше, чем в поэзии. ”? (А.С.Пушкин)
Продолжение статьи.
Приложения к статье.
Геометрия 7. Карточки-задания | Учебно-методический материал по геометрии (7 класс):
Тема «Длина отрезка» (1 уровень) Геометрия – 7 , п. 7.
№ 1. На отрезке АВ взяты точки С и D. Найдите длину отрезка CD, если АВ = 12 см, АС = 3 см, BD = 4 см.
№ 2. На отрезке АВ длиной 36 см взята точка К. Найдите длину отрезков АК и ВК, если АК больше ВК на 4 см.
№ 3. На прямой отмечены точки А, В, С так, что АВ = 27 м, АС = 11 м, ВС = 16 м. Какая из этих точек лежит между двумя другими?
Тема «Длина отрезка» (2 уровень) Геометрия – 7 , п. 7.
№ 1. На отрезке АВ взяты точки М и N. Известно, что АВ = 12 см, АМ = 8 см, BN = 10 см. Найдите длину отрезка МN.
№ 2. На отрезке АВ длиной 36 см взята точка К. Найдите длину отрезков АК и ВК, если АК : ВК = 4 : 5.
№ 3. Дан отрезок АВ = 16 см. Точка М – середина отрезка АВ, точка К – середина отрезка МВ. Найдите длину отрезка АК.
Найдите длину отрезка АК.
Тема «Длина отрезка» (3 уровень) Геометрия – 7 , п. 7.
№ 1. На отрезке АВ взята точка С. Известно, что АВ = 9 см, ВС = 4 см. Какую длину может иметь отрезок АС?
№ 2. На отрезке АВ длиной 36 см взята точка К. Найдите длину отрезков АК и ВК, если .
№ 3. На отрезке АВ = 40 см взята точка Р. Найдите расстояние между серединами отрезков АР и РВ.
…………………………………………………………………………………………………
Тема «Смежные и вертикальные углы» (1 уровень) Геометрия – 7 , п. 11.
Найдите угол, образованный:
а) биссектрисами двух смежных углов;
б) биссектрисами двух вертикальных углов.
Тема «Смежные и вертикальные углы» (2 уровень) Геометрия – 7 , п. 11.
1) Смежные углы относятся как 1 : 2. Найдите эти смежные углы.
2) Один из углов, образовавшихся при пересечении двух прямых, равен 21˚. Найдите остальные углы.
Тема «Смежные и вертикальные углы» (3 уровень) Геометрия – 7 , п. 11.
11.
1) Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.
2) Сумма трех углов, образовавшихся при пересечении двух прямых, равна 325˚. Найдите остальные углы.
3) Даны углы α, β и γ . Известно, что α > β, а γ
Тема «Смежные и вертикальные углы» (3 уровень) Геометрия – 7 , п. 11.
1) одного из смежных углов и другого составляют в сумме прямой угол. Найдите эти смежные углы.
2) Сумма вертикальных углов в 2 раза меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.
3) один из четырех углов, образовавшихся при пересечении двух прямых, в 11 раз меньше суммы трех остальных углов. Найдите эти четыре угла.
………………………………………………………………………………………………….
Тема «Треугольник» (2 уровень) Геометрия – 7 , п. 14.
Дано: ΔАВС, ΔАDC,
АВ = АС = ВС, AD = DC,
PABC = 36 см, PADC = 40 см.
Найти: стороны ΔАВС, ΔАDC.
…………………………………………………………………………………………………
Тема «Первый признак равенства треугольников»(2 уровень)Геометрия – 7 , п. 15.
1) Равные отрезки АВ и CD точкой пересечения О делятся пополам. Докажите, что ΔАОС = ΔВОD и найдите АС, если ВD = 12 см.
2) Известно, что ΔАВС = ΔА1В1С1, причем ∠А = ∠А1, ∠В = ∠В1. На сторонах АС и А1С1 отмечены точки D и D1 так, что CD = C1D1.
Докажите, что ΔСВD = ΔC1B1D1.
………………………………………………………………………………………………….
Тема «Равнобедренный треугольник» (2 уровень) Геометрия – 7 , п. 18.
1) Дано: ΔАВС, D Є АС,
AD = DC, AC ⊥ BD.
Доказать: ΔАВС – равнобедренный.
2) Периметр равнобедренного треугольника равен 36 см, а основание – 10 см. Найдите боковую сторону этого треугольника.
Тема «Равнобедренный треугольник» (2 уровень) Геометрия – 7 , п. 18.
1) Дано: ΔАВС – равнобедренный,
АС – основание,
АМ и СК – высоты, пересекаются в точке О.
Доказать: ΔАОС – равнобедренный.
2) Периметр равнобедренного треугольника равен 37 см. Основание меньше боковой стороны на 5 см. Найдите стороны этого треугольника.
Тема «Равнобедренный треугольник» (3 уровень) Геометрия – 7 , п. 18.
1) Дано: ΔАВС, М Є АС, N Є АС,
ΔMBN – равнобедренный, MN – основание,
AN = CM.
Доказать: ΔАВС – равнобедренный.
2) Сумма двух сторон равнобедренного треугольника равна 26 см, а периметр равен 36 см. Какими могут быть стороны этого треугольника?
…………………………………………………………………………………………………
Тема «Второй признак равенства треугольников» Геометрия – 7 , п. 19.
- В ΔАВС на продолжении стороны ВС за точку С отложен отрезок CD, равный СА, а точки А и D соединены отрезком. СЕ – биссектриса треугольника АСВ, а CF – медиана треугольника ACD. Докажите, что CF ⊥ CE.
- На одной стороне угла с вершиной А отмечены точки D и В, на другой стороне – С и Е так, что АD = АС = 3 см, АВ = АЕ = 4 см.
 Докажите, что : а) ВС = ED; б) КВ = КЕ, где К – точка пересечения отрезков ВC и ЕD.
Докажите, что : а) ВС = ED; б) КВ = КЕ, где К – точка пересечения отрезков ВC и ЕD.
…………………………………………………………………………………………………
Тема «Третий признак равенства треугольников» Геометрия – 7 , п. 20.
На стороне АС как на основании построены по одну сторону от неё два равнобедренных треугольника АВС и АМС. Докажите, что прямая МВ пересекает сторону АС в её середине.
Тема «Третий признак равенства треугольников» Геометрия – 7 , п. 20.
- На отрезке АС как на основании построены по разные стороны от него два равнобедренных треугольника АВС и ADC. Докажите, что BD ⊥ AC.
- Отрезок прямой АВ точками P и Q делится на три равные части. Вне отрезка АВ по одну сторону от него взяты точки C и D так, что АВ = BD, CQ = DP, ∠DPB + ∠CQA = 140˚. Найти: ∠DPB и ∠CQA.
……………………………………………………………………………………………………
Тема «Признаки равенства треугольников» Геометрия – 7 , п. 20.
20.
На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки ВМ и ВN . BD – медиана треугольника. Докажите, что MD = ND.
Тема «Признаки равенства треугольников» (2 уровень) Геометрия – 7 , п. 20.
- Дан равнобедренный треугольник АВС с основанием АС. Точки D и Е лежат соответственно на сторонах АВ и ВС, AD = CE. DC пересекает АЕ в точке О. Докажите, что ΔАОС – равнобедренный.
- На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки АМ и CN. BD, медиана треугольника АВС , пересекает отрезок MN в точке О. Докажите, что ВО – медиана треугольника MBN.
Тема «Признаки равенства треугольников» (3 уровень) Геометрия – 7 , п. 20.
- ΔМNP – равнобедренный с основанием МР, точка К – середина отрезка МР, МЕ = РF, где Е Є MN, F Є NP. Докажите, что луч KN – биссектриса угла ЕКF.
- В равнобедренном треугольнике АВС точка D – середина основания АС.
 На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно так, что ВМ = ВN. Докажите, что ΔBDM = ΔBDN.
На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно так, что ВМ = ВN. Докажите, что ΔBDM = ΔBDN.
Поиск материала «Геометрия. Карточки. 11 класс. Комбинации тел. Часть 3 №1. Дудницын Ю.П., Кронгауз В.Л. 1996» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Карточки по геометрии_11 класс — София Октябриновна…
Карточки по геометрии_11 класс. Карточки_геометрия11_многогранники_Дудницын_Кронгауз.rar Скачать 2 Мб. ОБСУЖДЕНИЕ. Комментариев пока нет.
proshkolu.ru
- Геометрия. Карточки. 11 класс. Комбинации тел. Часть…
Часть 3 №1.
 Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школах
Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школахПри подготовке комплекта к использованию следует сгруппировать карточки по темам, затем упорядочить их в каждой группе. Для этого используйте шифр, помешенный в правом верхнем углу карточки. Первое число указывает номер темы, второе—порядковый номер карточки в…
x-uni.com
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Геометрия. Карточки. 11 класс. Комбинации тел. Часть.
 ..
..Часть 3 №3. Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школах
При подготовке комплекта к использованию следует сгруппировать карточки по темам, затем упорядочить их в каждой группе. Для этого используйте шифр, помешенный в правом верхнем углу карточки. Первое число указывает номер темы, второе—порядковый номер карточки в…
x-uni.com
- Геометрия 11 класс — Дидактические материалы — Каталог файлов…
Геометрия 11 класс. Карточки для уровневого обучения.Ю.П.Дудницын,В.Л.Кронгауз. Часть2.Тела вращения.
sosninasent.ucoz.ru
- Учебно — методические материалы по ГЕОМЕТРИИ. | ВКонтакте
В этой теме Вы сможете ознакомиться с учебно-методическими материалами по ГЕОМЕТРИИ.
 Напоминаем, что выложенные здесь материалы, предназначены только..
Напоминаем, что выложенные здесь материалы, предназначены только..1.3 МБ.
vk.com
- Дудницын Ю.П., Кронгауз В.Л. Геометрия. Карточки для…
Дидактические материалы. — М.: Образование, 1995. — 120 с. Содержание: Двугранный угол. Призма и ее элементы. Сечение призмы. Площадь поверхности призмы. Объем призмы. Пирамида и ее элементы. Сечение пирамиды. Усеченная пирамида. Площадь поверхности пирам…
www.studmed.ru
- Дудницын Ю.П., Кронгауз В.Л. Геометрия. 7 класс.
Автор: Дудницын Ю.П., Кронгауз В.Л. Название: Геометрия. 7 класс. Тренировочные задания Формат: PDF Размер: 14,58 Мб Язык: Русский. Скачать по прямой ссылке. Пособие «Тренировочные задания» является дополнением к учебнику «Геометрия. 7-9 классы» А.В. Погорелова и предназначено для организации самостоятельной работы учащихся, направленной на усвоение и отработку ими основных теоретических фактов и на овладение практическими умениями в процессе решения задач.
 Пособие содержит 19 тренировочных работ в шести…
Пособие содержит 19 тренировочных работ в шести…www.psyoffice.ru
- Геометрия. Карточки. 11 класс. Комбинации тел. Часть…
Часть 3 №2. Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школах
При подготовке комплекта к использованию следует сгруппировать карточки по темам, затем упорядочить их в каждой группе. Для этого используйте шифр, помешенный в правом верхнем углу карточки. Первое число указывает номер темы, второе—порядковый номер карточки в…
x-uni.com
- Дудницын Ю.П., Кронгауз В.Л. Контрольные работы по геометрии.
Автор: Дудницын Ю.П., Кронгауз В.
 Л. Название: Контрольные работы по геометрии. 10 класс Формат: PDF Размер: 1,34 Мб Язык: Русский.
Л. Название: Контрольные работы по геометрии. 10 класс Формат: PDF Размер: 1,34 Мб Язык: Русский.Данное пособие от издательства «Просвещение» предназначается для учителей и преподавателей старших классов, которые выстраивают свою работу по учебнику Л.С.Атанасяна «Геометрия, 10-11». В книге имеется выстроенный тематический план, полный комплект контрольных работ на весь период обучения по предмету.
www.psyoffice.ru
- textbooks1—11.ru Контрольные работы по геометрии. 10 класс…
10 класс — Дудницын Ю.П., Кронгауз В.Л. cкачать в PDF. Данное пособие от издательства «Просвещение» предназначается для учителей и преподавателей старших классов, которые выстраивают свою работу по учебнику Л.С.Атанасяна «Геометрия, 10-11». В книге имеется выстроенный тематический план, полный комплект контрольных работ на весь период обучения по предмету.
textbooks1-11.
 ru
ru - Дудницын Ю.П., Кронгауз В.Л. Геометрия. Карточки для…
Карточки для уровневого обучения. 10 класс. Файлы.
Комплект карточек по стереометрии трех уровней сложности по следующим разделам: Аксиомы стереометрии и простейшие следствия из них/ Параллельные прямые в пространстве. Параллельность прямой и плоскости.
www.studmed.ru
- Геометрия. Карточки для уровневого обучения. Часть…
Часть 1. Многогранники. 11 класс. Дудницын Ю.П., Кронгауз В.Л.
b-ok.asia
- Ю.П. Дудницын В.Л. Кронгауз Контрольные по геометри
«Геометрия. 10-11 классы». класс. Учебно-методический комплект. Ю.П. Дудницын. B.J. Кронгауз. Контрольные работы по геометрии. К учебнику Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. . «Геометрия, 10-. (М.: Просвещение).
 класс. Рекомендовано. Российской Академией Образования. Издание второе, стереотипное. Издательство «ЭКЗАМЕН» МОСКВА • 2009. УДК 372.8:514(075.3) ББК 74.262.22 я72. учеб. для об- щеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадом- M.: Просвещение» приведено на обложке данного изда…
класс. Рекомендовано. Российской Академией Образования. Издание второе, стереотипное. Издательство «ЭКЗАМЕН» МОСКВА • 2009. УДК 372.8:514(075.3) ББК 74.262.22 я72. учеб. для об- щеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадом- M.: Просвещение» приведено на обложке данного изда…teacher-andreeva.ru
- Карточки. Геометрия. 10 класс. Для уровневого обучения.
ГЕОМЕТРИЯ 10 Ю.П. Дудницын, В.Л. Кронгауз КАРТОЧКИ с заданиями по геометрии для 10 класса (16 тем, 315 карточек, из них 76 рисунков) Москва НПО «ОБРАЗОВАНИЕ» 1997 Аксиомы стереометрии и некоторые следствия из них Всего карточек 16 1 уровень 7 2 уровень 5 3 уровень 4 2 Параллельные прямые в пространстве Всего карточек 14 1 уровень 4 2 уровень 6 3 уровень.
djvu.online
- Геометрия. Карточки для уровневого обучения. Часть…

Часть 1. Многогранники. 11 класс. Геометрия. Карточки для уровневого обучения. Часть 1. Многогранники. 11 класс. Дудницын Ю.П., Кронгауз В.Л.
Какого качества скаченный файл? Скачайте книгу, чтобы оценить ее качество.
ru.1lib.education
- Дидактические материалы, сборники задач — @дневники…
Дудницын Ю.П., Кронгауз В.Л. Карточки. Геометрия для уровневого обучения.
Задачи каждой таблицы соответствуют определенной теме школьного курса геометрии 10-11 классов и расположены внутри таблицы в порядке возрастания их сложности. Книга предоставлена гость100 Скачать (djvu, 600dpi, 1,3 Мб) ifolder или mediafire.com.
diary.ru
- 1—11klasses Алгебра. Тематические тесты. 9 класс — Дудницын…
9 класс — Дудницын Ю.П., Кронгауз В.Л. cкачать в PDF. Пособие содержит тесты по важнейшим разделам курса алгебры 9 класса основной школы.
 С их помощью можно осуществлять тематический контроль знаний девятиклассников.
С их помощью можно осуществлять тематический контроль знаний девятиклассников.1-11klasses.ru
- Авторы: Дудницын | Все Контрольные
Математика 6 Дудницын Контрольные работы по математике 6 класс с ответами для любого УМК.
Дидактические материалы дополняют учебник по алгебре и началам анализа для 10–11 классов под редакцией Колмогорова А.Н. и др. При постоянном использовании контрольных работ по алгебре в 10 классе рекомендуем купить книгу: Дудницын, Семенов: Алгебра и начала математического анализа.10 класс.Контрольные работы в новом формате.Учебное пособие.
xn--b1agatflbfbtgq5jm.xn--p1ai
- Контрольные работы по геометрии. 10 класс. Дудницын…
10 класс. Дудницын Ю.П., Кронгауз В.Л. 2-е изд., стер. — М.: 2009.
Размер: 1,3 Мб. Смотреть, скачать: drive.google. Содержание К учителю 5 I. Материалы к учебнику «Геометрия 10 -11» Л.
 С. Атанасяна и др 11 Примерное поурочное планирование 11 Тематика контрольных работ 15 Контрольная работа№ 1 16 Контрольная работа№ 2 18 Контрольная работа № 3 20 Контрольная работа № 4 22 Контрольная работа № 5 24 Контрольная работа№6 26 Ответы к контрольным работам 28 II.
С. Атанасяна и др 11 Примерное поурочное планирование 11 Тематика контрольных работ 15 Контрольная работа№ 1 16 Контрольная работа№ 2 18 Контрольная работа № 3 20 Контрольная работа № 4 22 Контрольная работа № 5 24 Контрольная работа№6 26 Ответы к контрольным работам 28 II.www.at.alleng.org
- Контрольные работы по геометрии. 10 класс — Дудницын…
Пособие предназначено учителям математики старших классов, которые ведут преподавание курса геометрии по учебнику Л.С.Атанасяна Геометрия, 10-11 издательства Просвещение.
10 класс — Дудницын Ю.П., Кронгауз В.Л. Данное пособие от издательства «Просвещение» предназначается для учителей и преподавателей старших классов, которые выстраивают свою работу по учебнику Л.С.Атанасяна «Геометрия, 10-11». В книге имеется выстроенный тематический план, полный комплект контрольных работ на весь период обучения по предмету.
11klasov.
 net
net - Контрольные работы по алгебре и началам анализа. 11 класс…
11 класс — Дудницын Ю.П., Кронгауз В.Л. Пособие адресовано учителям и одиннадцатиклассникам, использующим при изучении курса алгебры и начал анализа учебник «алгебра и начала анализа, 10-11 кл.»
11klasov.net
- Алгебра. Карточки с заданиями для 7 класса. Ю. Дудницын…
В брошюре приведены карточки с заданиями различных уровней сложности, что поможет учителю дифференцированно подходить к школьникам на уроках. Карточки составлены по основным темам курса 7-го класса.. Алгебра, Уроки, 7 класс, Сборники.
Ю. Дудницын, В. Кронгауз.
multiurok.ru
- 1—11klasses Контрольные работы по геометрии. 10 класс…
10 класс — Дудницын Ю.П., Кронгауз В.Л. cкачать в PDF. Данное пособие от издательства «Просвещение» предназначается для учителей и преподавателей старших классов, которые выстраивают свою работу по учебнику Л.
 С.Атанасяна «Геометрия, 10-11». В книге имеется выстроенный тематический план, полный комплект контрольных работ на весь период обучения по предмету.
С.Атанасяна «Геометрия, 10-11». В книге имеется выстроенный тематический план, полный комплект контрольных работ на весь период обучения по предмету.1-11klasses.ru
- Ю.П. Дудницын В.Л. Кронгауз Контрольные по геометри
«Геометрия. 10-11 классы». класс. Учебно-методический комплект. Ю.П. Дудницын. B.J. Кронгауз. Контрольные работы по геометрии. К учебнику Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. . «Геометрия, 10-. (М.: Просвещение). класс. Рекомендовано. Российской Академией Образования. Издание второе, стереотипное. Издательство «ЭКЗАМЕН» МОСКВА • 2009. УДК 372.8:514(075.3) ББК 74.262.22 я72. учеб. для об- щеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадом- M.: Просвещение» приведено на обложке данного изда…
5splusom-school.ru
- Геометрия, 7 класс / Ю. П. Дудницын, В. Л. Кронгауз — Search RSL
Геометрия, 7 класс / Ю.
 П. Дудницын, В. Л. Кронгауз. Карточка. Дудницын, Юрий Павлович.
П. Дудницын, В. Л. Кронгауз. Карточка. Дудницын, Юрий Павлович.(Карточки для уровневого обучения) Шифр хранения: FB 13 99-1/159-4 Электронный заказ.
search.rsl.ru
- Дудницын, Юрий Павлович — Контрольные работы по геометрии.
«Геометрия, 10-11» (М.: Просвещение). Карточка. Дудницын, Юрий Павлович. Контрольные работы по геометрии.
Контрольные работы по геометрии. 11 класс : к учебнику Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. «Геометрия, 10-11» (М.: Просвещение). Дата поступления в ЭК.
search.rsl.ru
- Дудницын Ю.П., Кронгауз В.А. Геометрия. 8 класс.
Автор: Дудницын Ю.П., Кронгауз В.А. Название: Геометрия. 8 класс. Тренировочные задания Формат: PDF Размер: 20,98 Мб Язык: Русский. Скачать по прямой ссылке. Пособие «Тренировочные задания» является дополнением к учебнику «Геометрия.
 7—9 классы» А. В. Погорелова и предназначено для организации самостоятельной работы учащихся, направленной на усвоение и отработку ими основных теоретических фактов и на овладение практическими умениями в процессе решения задач.
7—9 классы» А. В. Погорелова и предназначено для организации самостоятельной работы учащихся, направленной на усвоение и отработку ими основных теоретических фактов и на овладение практическими умениями в процессе решения задач.www.psyoffice.ru
- Геометрия для разноуровневого обучения. 11 класс. Часть…
11 класс. Часть 2. Тела вращения. Карточки». Дудницын Ю.П., Кронгауз В.Л.. 1995. Геометрия для уровневого обучения. 11 класс. Часть 2. Тела вращения КАРТОЧКИ.
knigirossii.ru
- ЛитРес, LitRes – большая библиотека электронных книг, где можно купить, скачать и читать онлайн бесплатно
ЛитРес — это самая большая библиотека электронных книг. Покупай, скачивай, читай и слушай лицензионные электронные книги и аудиокниги для компьютеров, телефонов и планшетов. На LitRes публикуются отзывы, рейтинги книг, рекомендации, рецензии, информация об авторах.

www.litres.ru
- My-shop.ru – купить книги, учебники, пособия. Здесь можно заказать и купить книги, новинки, бестселлеры с доставкой по всей России
Интернет-магазин My-shop.ru — интернет магазин, где можно купить более 700 тысяч книг любого жанра, автора и тематики. Учебники по выгодным ценам с доставкой в Москве, Санкт-Петербурге и других городах России! Книги почтой с доставкой на дом и самовывозом.
my-shop.ru
- Интернет-магазин канцтоваров
Канцтовары. Низкие цены на любые канцтовары для детей и взрослых, для работы и учёбы. Письменные принадлежности. Карандаши, ручки, стержни, фломастеры, чернила, тушь, маркеры – любые письменные принадлежности. Бумажные канцтовары. Широкий выбор тетрадей, дневников, альбомов быстро и дёшево купить бумажные канцтовары. Ранцы, рюкзаки, сумки.
 Всевозможные сумки и косметички, ранцы с наполнением и без, рюкзаки со скидками и сумки для ноутбуков.
Канцелярские мелочи.
Ластики, ножницы, точилки, подставки и линейки, степлеры, дыроколы, корректоры, скотч и клей.
Всевозможные сумки и косметички, ранцы с наполнением и без, рюкзаки со скидками и сумки для ноутбуков.
Канцелярские мелочи.
Ластики, ножницы, точилки, подставки и линейки, степлеры, дыроколы, корректоры, скотч и клей.
my-shop.ru
- Лабиринт – большой книжный интернет магазин, где можно заказать и купить книги, бестселлеры и новинки с доставкой по всей России и в другие страны
Лабиринт — это самый большой интернет магазин бумажных книг. Покупай и заказывай книги! Доставка почтой, курьером, через сеть пунктов самовывоза в Москве, Санкт-Петербурге и других 30 городах России. Доставляем также в другие страны СНГ и мира! На официальном сайте «Лабиринта» публикуются рейтинги книг, отзывы, рекомендации, рецензии и информация об авторах, издательствах, правообладателях, сериях книг.
www.labirint.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Геометрия. Карточки. 11 класс. Комбинации тел. Часть 3 №1. Дудницын Ю.П., Кронгауз В.Л. 1996»
Карточки. 11 класс. Комбинации тел. Часть 3 №1. Дудницын Ю.П., Кронгауз В.Л. 1996»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 48 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Урок № 1 по геометрии в 7 классе «Прямая и отрезок»
Ф.И.О. Белянина Светлана Николаевна
Должность: учитель математики
Место работы: МОУ СОШ д.Сарафановоим.Героя России Ю.П.ЯковлеваЧебаркульского района Челябинской области
Предмет: геометрия
Урок 1
Класс | 7 | ||
Тема урока | Прямая и отрезок | ||
Тип урока | Вводный урок, первый в тематическом планировании по геометрии | ||
Цель урока | Систематизировать знания учащихся об основных свойствах простейших геометрических фигур, таких как прямая и отрезок. | ||
Задачи урока | Образовательные: 1.Начать введение геометрической терминологии. 2.Познакомить учащихся со свойством прямой. 3.Рассмотреть приём практического проведения прямых на плоскости. Развивающие: 1.Развивать навыки изображения планиметрических фигур и простейших геометрических конфигураций, связанных с условием решаемых задач. 2.Формировать у учащихся навыки применения свойств геометрических фигур как опоры при решении задач. 3.Формировать логическое мышление и навыки самостоятельной работы с информацией. 4.Учить анализировать информацию, обобщать, делать выводы. 5.Развивать умение работать в парах и группах. Воспитательные: 1.Воспитывать уважительное отношение к мнению других, умение слушать и слышать окружающих. 2.Создание условий для развития трудолюбия и аккуратности у учащихся. 3.Способствовать формированию и развитию культуры учащихся, повышению уровня познавательного интереса к предмету. | ||
Планируемые результаты | Научатсяиспользовать полученные знания о прямой и отрезке при решении практических задач. Овладеютнавыком построения прямой и отрезка с помощью линейки. Узнаюткраткую историю развития геометрии. Научатся взаимодействовать со своими сверстниками, получат навыки работы в группе, в паре. | ||
Образовательные ресурсы | Компьютер, проектор, презентация, дидактическая карточка на парту (приложение 1), пустой кластер для заполнения каждому учащемуся (приложение 2). | ||
План урока | Организационный момент (1 мин) Актуализация знаний, целеполагание и мотивация (4 мин) Изучение нового материала: — просмотр видеоролика (5 мин) -выполнение практической работы (5 мин) Первичное осмысление и закрепление изученного (в том числе и в ходе изучения нового материала) (15мин) Выполнение теста (5мин) Домашнее задание (5мин) Итоги урока. | ||
Методы обучения | Проблемный диалог, фронтальная работа, индивидуальная работа, работа в паре, работа в группе, репродуктивный метод обучения. | ||
Формы обучения | Интерактивная, словесная, наглядная, практическая работа, выполнение интерактивного теста. | ||
Основные понятия | Геометрия, прямая, отрезок, точка, свойство прямой. | ||
Планируемые результаты | |||
Предметные | Метапредметные УУД | Личностные УУД | |
Сформировать знания учащихся по изучаемой теме «Прямая и отрезок»,использовать полученные знания при решении конкретных практических задач. | Регулятивные: проверять результаты построений; адекватно воспринимать указания на ошибки и исправлять найденные ошибки; оценивать собственные успехи в результате выполнения геометрических задач на построение; планировать шаги по устранению пробелов. Познавательные: сопоставлять информацию, представленную в разных видах; осознанное построение устного рассказа, использовать известные приемы построения геометрического чертежа; понимать информацию, представленную в виде ребуса, текста, схемы, таблицы. Коммуникативные: сотрудничать с товарищами при выполнении заданий в паре: устанавливать и соблюдать очерёдность действий, сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках; задавать вопросы с целью получения нужной информации; организовывать взаимопроверку и самопроверку выполненной работы; высказывать свое мнение при обсуждении задания, умение строить монологическую речь | Учиться развивать адекватную самооценку, развивать познавательный интерес и учебную мотивацию, уметь оказывать взаимопомощь. | |
ХОД УРОКА
Организационный момент (1 мин)
Слайд №2.
— Добрый день, ребята! Рада видеть вас на своем уроке здоровыми и счастливыми, с хорошим настроением. Начинаем урок и я предлагаю вам продолжить предложения.
На уроке наши глаза внимательно
Смотрят и все … (видят).
Уши внимательно слушают
И всё …(слышат).
Голова хорошо … (думает).
Молодцы!
Актуализация знаний, целеполагание и мотивация (стадия вызова) (4 мин)
(разгадывание ребусов)
Слайд №3
А теперь посмотрите на слайди вставьте пропущенные слова в нужном падеже в предложение, предварительно решив ребусы.
Сегодня на уроке геометрии нам пригодятся линейка и карандаш.
Слайд№4Ребята разгадайте ребусы и назовите тему урока.
Тема урока «Прямая и отрезок».
Ребята, какую цель вы поставите перед собой сегодня на уроке?
(формируется цель совместно с учителем в процессе беседы)
Слайд №5: Систематизировать знания о взаимном расположении точек и прямых.
Какие задачи нужно решить для достижения этой цели?
Слайд№6:
1. Вспомнить понятие о прямой, отрезке и точке.
2. Выполнить практические задания.
Итак, мы начинаем изучать новый предмет, который называется «Геометрия». Предлагаю вам посмотреть небольшой видеоролик. С помощью него вы узнаете, что означает наука геометрия, когда появилась, имена великих геометров, в каких государствах зародилась, какая бывает геометрия и на какие разделы делится геометрия, которую мы будем изучать. По ходу видеоролика выполнить следующее задание. Вам нужно заполнить кластер.
(приложение 1, лежит на парте у каждого учащегося)
Изучение нового материала (стадия осмысления):
1. Просмотр видеоролика о истории геометрии.(Слайд №7). (5 мин)
Просмотр видеоролика о истории геометрии.(Слайд №7). (5 мин)
По окончании фильма ребята сравнивают свой заполненный кластер с образцом
(слайд№7)
Ребята давайте посмотрим, что у вас в результате получилось. Пожалуйста кто может продемонстрировать свой заполненный кластер. Остальным предлагаю, по необходимости, отредактировать заполненный кластер.(Слайд 8)
(Один ученик выходит и рассказывает по своей схеме)
2.Усвоение новых знаний проходит в виде беседы и выполнения практической работы.
Предлагаю поработать в парах и выполнить следующее задание.
Дидактическая карточка(на каждой парте, приложение 2)(5 мин)
Содержание карточки ( приложение №2):
Внимательно рассмотрите рисунок. Распределите известные вам геометрические фигуры на две группы. Заполните таблицу.
1 группа | 2 группа |
|
|
Слайд №7
1 группа | 2 группа |
Прямая Ломаная Отрезок Луч Прямоугольник Квадрат Многоугольник
| Куб Цилиндр Шар Конус Пирамида Параллелепипед |
Ответьте на вопросы:
По какому принципу данные геометрические фигуры записаны в двух различных группах?
Какие слова не распределены в группы? Почему?
Попытайтесь объяснить известные вам термины.
Запишите в тетради число и тему урока.
Выполним практическую работу. Проверяем выполнение заданий с помощью слайдов самостоятельно.
Практическая работа (5 мин)
- Начертить прямую. Обозначить. Как ее можно обозначить? (Слайд №10).
- Отметить точку С, не лежащую на данной прямой, и точки D, Е, К лежащие на этой прямой.
- Используя символы принадлежности, запишите предложение
«Точка D принадлежит прямой АВ,а точка С не принадлежит прямой a»(Слайд №11)
- Используя рисунок (Слайд №11) и символы , запишите какие точки принадлежат прямой b? а какие-нет.
- Сколько прямых можно провести через заданную точку А?
- Сколько прямых можно провести через две точки?
- Через любые две точки можно провести прямую? Сформулируйте данное свойство прямых.(Слайд№12)
- Начертите прямые КМ и DP, пересекающиеся в точке О.
 Запишите с помощью символов. (Слайд№13)
Запишите с помощью символов. (Слайд№13) - Ответьте на вопрос: Сколько общих точек могут иметь две прямые? (Слайд№13)
- На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки. (Слайд №14)
- Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М. (Слайд№15) Ответьте на вопросы с обоснованием.
- Являются ли прямые МN и а различными прямыми?
- Может ли прямая b проходить через точку N?
- Дана прямаяEF, A EF, В EF.Может ли прямая АВ не пересекать отрезок EF?(Слайд№15)
Итак, ребята, какие выводы можно сделать из выполнения практической работы?
4 этап. Закрепление нового материала. (10мин)
Решение задач №2,5,6 из учебника.
Творческая работа в группах.Каждой группе (в группе 4 человека) выдается карточка (приложение № 3)с заданием для выполнения. Время на решение 4 минуты. По истечении времени группы рассказывают решение. Если у одной группы, ответ не полный, то добавляет другая группа. Рисунки выполняют на листе формата А4, фломастером и с помощью линейки.
Время на решение 4 минуты. По истечении времени группы рассказывают решение. Если у одной группы, ответ не полный, то добавляет другая группа. Рисунки выполняют на листе формата А4, фломастером и с помощью линейки.
Карточка.
1.Сколько точек пересечения могут иметь три прямые? Рассмотреть всевозможные случаи, сделать соответствующие рисунки.
2.На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите всевозможные случаи и сделайте рисунки.
https://learningapps.org/display?v=pzdv0so2519 |
5 этап. Выполнение интерактивного теста:(5мин)
Учащиеся, не имеющие возможности выхода в интернет, получают тест в бумажном варианте.
6 этап. Задание на дом:(5мин)
Задание на дом:(5мин)
Обязательное задание:
Прочитать параграф 1,2.Ответить на вопросы 1-3, решить задачи №1,3,4,7.
Задание по желанию:По кластеру составленному в начале урока составить устный рассказ.
7 этап. Этап рефлексии.5(мин)
Ребята, подведем итоги урока. Предлагаю Вам назвать три момента, которые получились хорошо в процессе урока, и предложить одно действие, которое улучшит вашу работу на следующем уроке.
Литература:
1. Учебник Геометрия 7-9 Л.С.Атанасян.
2. Методическое пособие. Поурочные разработки по геометрии 7 класс. Авт.Н.Ф.Гаврилова
Конспект урока
DOCX / 158.48 Кб
Тема»Прямая и отрезок»
PPTX / 47.46 Мб
Приложение №1
DOCX / 137.47 Кб
Приложение №2
DOCX / 138.05 Кб
/data/files/e1563951900.docx (Приложение №3)
приложение №4
DOCX / 3. 16 Мб
16 Мб
Видеоролик
Сервис «облако слов»
Генератор ребусов
Интерактивный тест по геометрии 7 класс. тема «Прямая и отрезок»
Карточки для подготовки к ОГЭ. Геометрия. Четырехугольникиматериал для подготовки к егэ (гиа) по геометрии (8, 9 класс) на тему
Карточки по геометрии 9 класс подготовка к огэ 24 варианта ответы
Карточки на нахождение углов и сторон в трапеции, параллелограмме, прямоугольнике, а также периметра параллелограмма, площади квадрата. Можно использовать на уроках в 8 классе при изучении темы: Четырехугольники
Скачать:
| chetyrehugolniki. docx | 59.11 КБ |
Предварительный просмотр:
1.Диагональ прямоугольника образует угол 56° с одной
Из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
1.Диагональ прямоугольника образует угол 44° с одной
Из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ дайте в градусах.
2. В равнобедренной трапеции известны высота, меньшее основание и угол
При основании (см. рисунок). Найдите большее основание.
2. В равнобедренной трапеции известны высота, меньшее основание и угол
При основании (см. рисунок). Найдите большее основание.
3.Периметр квадрата равен 32. Найдите площадь этого квадрата.
3.Периметр квадрата равен 68. Найдите площадь этого квадрата.
4.Найдите больший угол равнобедренной трапеции ABCD, если диагональ
АС образует с основанием AD и боковой стороной
АВ углы, равные 25° и 40° соответственно. Ответ дайте в градусах.
4.Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
1.Диагональ прямоугольника образует угол 70° с одной
Из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
1.Диагональ прямоугольника образует угол 54° с одной
Из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
2.В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.
2. В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.
3.Периметр квадрата равен 160. Найдите площадь этого квадрата.
3.Периметр квадрата равен 60. Найдите площадь этого квадрата.
4.Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
4.Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 25° и 100° соответственно.
1. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
1. Разность углов, прилежащих к одной стороне параллелограмма, равна 20°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Найдите меньший угол параллелограмма. Ответ дайте в градусах.
2. Разность углов, прилежащих к одной стороне параллелограмма, равна 10°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
2. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
3.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 9, CK = 6.
3. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 5, CK = 19.
4. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ ACD = 124°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
4. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ ACD = 80°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Карточки на нахождение углов и сторон в трапеции, параллелограмме, прямоугольнике, а также периметра параллелограмма, площади квадрата. Можно использовать на уроках в 8 классе при изучении темы: Четырехугольники
Можно использовать на уроках в 8 классе при изучении темы: Четырехугольники
| chetyrehugolniki. docx | 59.11 КБ |
Можно использовать на уроках в 8 классе при изучении темы Четырехугольники.
Nsportal. ru
18.11.2017 17:20:42
2017-11-18 17:20:42
Источники:
Https://nsportal. ru/shkola/geometriya/library/2016/11/12/kartochki-dlya-podgotovki-k-oge-geometriya-chetyrehugolniki
Карточка для подготовки к ГИА-9 география, 9 класс | Тест по географии (9 класс) по теме: | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Карточки по геометрии 9 класс подготовка к огэ 24 варианта ответы
По теме: методические разработки, презентации и конспекты
Карточка для подготовки к ГИА, география. 9 класс
Карточка для подготовки к ГИА погеографии 9 класс включает названия географических объектов, которые необходимо классифицировать в таблицу: горы, озера. реки, равнины, острова по материкам.
реки, равнины, острова по материкам.
Карточки для проверки знаний и умений 11 класса по географии
Карточки с заданиями для проверки усвоения знаний и умей у учащихся 11 классе по учебнику Максаковского. В карточках предлагаются разные задания: заполнить схему, таблицы или ответьть развернутыми отв.
Комплексная карточка №2 для подготовки к ОГЭ по географии
В карточке содержатся вопросы разного уровня сложности и по разным темам курса школьной географии.
Карточки для подготовки к ОГЭ по геометрии. 9 класс
Карточки для подготовки к ОГЭ по геометрии для 9 класса по всему курсу. 24 варианта с ответами.
Карточка для подготовки учащихся 11 классов к сдаче устной части ЕГЭ по английскому языку
Данная карточка сделана для вебинара «Эффективные приёмы подготовки учащихся 11 классов к сдаче устной части ЕГЭ по английскому языку с новым пособием издательства «Просвещение» «Английский язык.
Карточки для подготовки к ОГЭ в 9 классе.

Тренировочные карточки предназначены для систематического повторения материала по темам: «Словосочетание», «Виды придаточных», «Пунктуация в сложном предложении».
Карточки для подготовки к впр математика 6 класс
В карточках предложены примеры на отработку действий с пложительными и отрицательными числами. При создании карточек использовался задания с сайта РЕШУ ВПР.
Карточка для подготовки к ГИА, география. 9 класс
Карточка для подготовки к ГИА погеографии 9 класс включает названия географических объектов, которые необходимо классифицировать в таблицу: горы, озера. реки, равнины, острова по материкам.
Карточки для проверки знаний и умений 11 класса по географии
Карточки с заданиями для проверки усвоения знаний и умей у учащихся 11 классе по учебнику Максаковского. В карточках предлагаются разные задания: заполнить схему, таблицы или ответьть развернутыми отв.
Комплексная карточка №2 для подготовки к ОГЭ по географии
В карточке содержатся вопросы разного уровня сложности и по разным темам курса школьной географии.
Карточки для подготовки к ОГЭ по геометрии. 9 класс
Карточки для подготовки к ОГЭ по геометрии для 9 класса по всему курсу. 24 варианта с ответами.
Карточка для подготовки учащихся 11 классов к сдаче устной части ЕГЭ по английскому языку
Данная карточка сделана для вебинара «Эффективные приёмы подготовки учащихся 11 классов к сдаче устной части ЕГЭ по английскому языку с новым пособием издательства «Просвещение» «Английский язык.
Карточки для подготовки к ОГЭ в 9 классе.
Тренировочные карточки предназначены для систематического повторения материала по темам: «Словосочетание», «Виды придаточных», «Пунктуация в сложном предложении».
Карточки для подготовки к впр математика 6 класс
В карточках предложены примеры на отработку действий с пложительными и отрицательными числами. При создании карточек использовался задания с сайта РЕШУ ВПР.
Карточки для проверки знаний и умений 11 класса по географии
В карточках предлагаются разные задания заполнить схему, таблицы или ответьть развернутыми отв.
Nsportal. ru
04.06.2019 15:15:07
2019-06-04 15:15:07
Источники:
Https://nsportal. ru/shkola/geografiya/library/2011/12/17/kartochka-dlya-podgotovki-k-gia-9-geografiya-9-klass
Карточки для подготовки к ОГЭ по геометрии №15-20 | Методическая разработка по геометрии (9 класс): | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Карточки по геометрии 9 класс подготовка к огэ 24 варианта ответы
По теме: методические разработки, презентации и конспекты
Карточка для подготовки к ГИА, география. 9 класс
Карточка для подготовки к ГИА погеографии 9 класс включает названия географических объектов, которые необходимо классифицировать в таблицу: горы, озера. реки, равнины, острова по материкам.
Карточка для подготовки к ГИА-9 география, 9 класс
Карточка для подготовки к ГИА-9 география, 9 класс включает 2 задания. 1 задание — найти соответствие: субъект-столица. 2 задание — рассчитать годовую амплитуду.
2 задание — рассчитать годовую амплитуду.
Карточка ученика «Подготовка к сочинению-описанию»
Карточка для ученика. Тема урока: «Подготовка к сочинению-описанию по картине К. Ф.Юона «Конец зимы. Полдень».
Геометрия (карточка для подготовки к ОГЭ)
Геометрия (карточка для подготовки к ОГЭ).
Карточки для подготовки к ОГЭ модуль «Геометрия»
Карточки очень эффективны для подготовки и тренировки к огэ.
Карточки для подготовки к ОГЭ. Геометрия. Четырехугольники
Карточки на нахождение углов и сторон в трапеции, параллелограмме, прямоугольнике, а также периметра параллелограмма, площади квадрата. Можно использовать на уроках в 8 классе при изучении темы: Четыр.
Карточки для подготовки к ОГЭ по геометрии. 9 класс
Карточки для подготовки к ОГЭ по геометрии для 9 класса по всему курсу. 24 варианта с ответами.
Карточка для подготовки к ГИА, география. 9 класс
Карточка для подготовки к ГИА погеографии 9 класс включает названия географических объектов, которые необходимо классифицировать в таблицу: горы, озера. реки, равнины, острова по материкам.
реки, равнины, острова по материкам.
Карточка для подготовки к ГИА-9 география, 9 класс
Карточка для подготовки к ГИА-9 география, 9 класс включает 2 задания. 1 задание — найти соответствие: субъект-столица. 2 задание — рассчитать годовую амплитуду.
Карточка ученика «Подготовка к сочинению-описанию»
Карточка для ученика. Тема урока: «Подготовка к сочинению-описанию по картине К. Ф.Юона «Конец зимы. Полдень».
Геометрия (карточка для подготовки к ОГЭ)
Геометрия (карточка для подготовки к ОГЭ).
Карточки для подготовки к ОГЭ модуль «Геометрия»
Карточки очень эффективны для подготовки и тренировки к огэ.
Карточки для подготовки к ОГЭ. Геометрия. Четырехугольники
Карточки на нахождение углов и сторон в трапеции, параллелограмме, прямоугольнике, а также периметра параллелограмма, площади квадрата. Можно использовать на уроках в 8 классе при изучении темы: Четыр.
Карточки для подготовки к ОГЭ по геометрии.
 9 класс
9 классКарточки для подготовки к ОГЭ по геометрии для 9 класса по всему курсу. 24 варианта с ответами.
Карточка ученика «Подготовка к сочинению-описанию»
1 задание — найти соответствие субъект-столица.
Nsportal. ru
23.04.2018 10:18:02
2018-04-23 10:18:02
Источники:
Https://nsportal. ru/shkola/geometriya/library/2019/01/25/kartochki-dlya-podgotovki-k-oge-po-geometrii-no15-20
Соединение SET с геометрией — чудо математики
SET — это карточная игра, которая вызывает множество математических вопросов у игроков всех уровней — от учеников начальной школы до математиков-исследователей. Математические идеи в SET включают подсчет и комбинаторику, вероятность, геометрию, модульную арифметику, векторы и линейную алгебру. Книга «Радость SET» представляет собой очень доступное глубокое погружение во многие из этих тем. Я описал некоторые из моих любимых вопросов по счету в этой ранней записи в моем блоге и во второй половине этой записи в блоге, рассказывающей о математическом лагере с учащимися начальной школы.
В этом посте я сосредоточусь на связях между геометрией и игрой SET. В частности, я рассмотрю ключевые вопросы и моменты семинаров, которые я провожу, и примерно проследю за слайдами из моего семинара в Twitter Math(s) Camp в 2018 году. Они находятся в этой папке, которая также битком набита другими ресурсами. .
Внимание: этот пост будет содержать много спойлеров.
Знакомство с SET (краткий обзор)
Представляя SET, я люблю начинать с разложения карточек и вопроса: «Что вы заметили? Что вас интересует?» Это отличный способ выделить атрибуты, а также некоторые другие наблюдения и вопросы, которые могут возникнуть у людей изначально.
Карточка SET имеет четыре атрибута. На трех карточках ниже показаны все возможные значения атрибутов.
Вопрос: Если колода SET содержит ровно одну карту каждой возможной комбинации атрибутов, сколько карт в колоде?
Я хотел бы перейти к этому вопросу, попросив людей найти способ упорядочить карточки так, чтобы они были уверены, что у них есть ровно одна карточка с каждой комбинацией атрибутов. Мы можем подсчитать количество карт, а также разработать комбинаторный/счетный аргумент.
Мы можем подсчитать количество карт, а также разработать комбинаторный/счетный аргумент.
Я заметил, что когда люди упорядочивают карты таким образом, у них естественным образом возникает идея НАБОРА. Это намного сильнее, чем то, что я им говорю!
Вопрос: Можете дать определение SET?
Я показываю четыре тщательно отобранных примера SET и прошу людей дать определение того, что представляет собой SET. Это отличный способ изучить точность определений, а также примеры и не-примеры.
А НАБОР – это группа из трех карточек, в которой для каждого из четырех атрибутов характеристики одинаковы для всех трех карточек или различаются для всех трех карточек. Три карточки ниже представляют собой НАБОР, потому что форма у них одинаковая, заполнение одинаковое, номера разные, цвета разные.
Интерлюдия: Сыграйте в игру
Чтобы сыграть в SET с другими, выложите на стол двенадцать карт. Тот, кто первым найдет SET, называет «SET» и показывает его остальным игрокам. Затем пустые места пополняются из колоды. Если игроки согласны с тем, что на столе нет сета, раздаются еще три карты. В конце игры побеждает тот, у кого больше всего наборов. У Дэвида Батлера есть хороший вариант игры, который включает в себя игру в командах и уравновешивает конкуренцию, когда одни участники быстрее находят наборы, чем другие.
Затем пустые места пополняются из колоды. Если игроки согласны с тем, что на столе нет сета, раздаются еще три карты. В конце игры побеждает тот, у кого больше всего наборов. У Дэвида Батлера есть хороший вариант игры, который включает в себя игру в командах и уравновешивает конкуренцию, когда одни участники быстрее находят наборы, чем другие.
Игра позволит участникам попрактиковаться в поиске наборов, которые пригодятся позже.
Вопрос: Выберите две карты наугад. Сколько карт, если они есть, можно использовать для завершения НАБОР?
Спойлер: ответ 1. (Вы можете объяснить, почему?) Это называется Фундаментальной Теоремой SET, и она необходима для многих геометрических аргументов, которые возникнут позже.
Вопрос: Сколько СЕТов возможно (включая те, где карта используется более чем в одном СЕТЕ) среди всех карт в колоде?
Спойлер: краткое объяснение. Существует 81 вариант выбора для первой карты в НАБОРЕ, 80 вариантов для второй карты и 1 вариант для третьей карты (согласно основной теореме НАБОР). Это дает 81*80*1. Но! Порядок, в котором вытягиваются наши карты, не имеет значения, поэтому мы пересчитали. Нам нужно разделить на количество способов расставить три карты, то есть 3*2*1 = 3! = 6 способов. Таким образом, общее количество возможных сетов равно (81*80*1)/(3*2*1) = 1080.
Это дает 81*80*1. Но! Порядок, в котором вытягиваются наши карты, не имеет значения, поэтому мы пересчитали. Нам нужно разделить на количество способов расставить три карты, то есть 3*2*1 = 3! = 6 способов. Таким образом, общее количество возможных сетов равно (81*80*1)/(3*2*1) = 1080.
Вопрос: Какое наибольшее количество сетов среди девяти карт?
Возможно, лучше задать этот вопрос в виде задачи: найти девять карт с наибольшим количеством наборов среди них. Этот вопрос плавно переходит в наше геометрическое представление.
Представление SET в двумерной аффинной геометрии
Предположим, мы представляем каждую карту SET точкой в пространстве. Линия — это набор из трех точек, образующих МНОЖЕСТВО. Мы можем визуализировать 12 наборов среди наших девяти карт, как показано на диаграмме ниже. Обратите внимание, что наши линии изгибаются; это нормально!
Здесь мы построили самолет в космосе. Есть несколько способов помочь людям изучить этот факт. Один из них — начать со знакомых представлений о геометрической плоскости, то есть «три не лежащие на одной прямой точки определяют плоскость» и «если две точки лежат в плоскости, то любая линия, содержащая эти две точки, также лежит в этой плоскости».
Один из них — начать со знакомых представлений о геометрической плоскости, то есть «три не лежащие на одной прямой точки определяют плоскость» и «если две точки лежат в плоскости, то любая линия, содержащая эти две точки, также лежит в этой плоскости».
На языке SET это означает, что мы должны начать с трех карт (точек), которые не образуют SET (не лежат на одной прямой). Тогда для любых двух карт в нашей плоскости SET, определяемый этими картами, должен быть в плоскости. Это означает, что третья карта, необходимая для завершения SET, также должна быть частью самолета. Начиная с наших трех неколлинеарных точек, мы продолжаем добавлять карты на плоскость, пока не исчерпаем все варианты.
В нашем самолете осталось девять карт. Эта коллекция из девяти карт называется закрытых. То есть, если мы выберем любую пару точек, точка, завершающая прямую, будет лежать на плоскости.
Вопрос: Какое максимальное количество карт мы можем удалить из нашей коллекции из девяти и при этом восстановить все двенадцать наборов?
Вместо того, чтобы начинать с определения самолета, я хотел бы начать с постановки вопроса выше. В конце концов люди приходят к трем картам, которые не принадлежат одному и тому же НАБОРУ. Когда мы начинаем устанавливать связи отсюда с геометрией, это кажется немного более конкретным.
В конце концов люди приходят к трем картам, которые не принадлежат одному и тому же НАБОРУ. Когда мы начинаем устанавливать связи отсюда с геометрией, это кажется немного более конкретным.
Интерлюдия: конечная аффинная геометрия
Знаете ли вы, что существует множество различных видов геометрии? Чтобы дать крайне нетехническое объяснение, евклидова геометрия (та, с которой мы лучше всего знакомы) построена на наборе аксиом (утверждений, которые мы считаем заданными истинами). Аксиомы являются строительными блоками математики и геометрии. Каждая ветвь геометрии имеет свой собственный набор аксиом или, другими словами, каждый набор аксиом порождает уникальную ветвь геометрии (цитата по стр. 9).9 «Радости SET»).
Наша геометрия SET принадлежит к неевклидовой ветви геометрии, называемой конечной аффинной геометрией: «конечная», потому что у нас есть конечное число точек и линий, и «аффинная», потому что допускаются параллельные линии. (Возможно, вы захотите подумать о том, что значит иметь две параллельные линии SET!)
До сих пор мы исследовали аффинную плоскость, называемую AG(2,3). (2 для двух измерений, 3 для трех точек на линии). Мы можем считать объекты в этой геометрии: 9 точек, 12 линий, 1 плоскость. И помните, нам нужно всего 3 (неколлинеарных) карты, чтобы построить наш самолет.
(2 для двух измерений, 3 для трех точек на линии). Мы можем считать объекты в этой геометрии: 9 точек, 12 линий, 1 плоскость. И помните, нам нужно всего 3 (неколлинеарных) карты, чтобы построить наш самолет.
Теперь перейдем к трем измерениям!
SET в трех измерениях
Чтобы перейти к трем измерениям, мы используем плоскость SET и одну точку вне плоскости. Затем мы завершаем нашу гиперплоскость, как и раньше. То есть мы выбираем любые две точки на гиперплоскости и добавляем третью точку, завершающую линию. Я начал строить гиперплоскость ниже. Вы видите карту, которая может быть помещена рядом?
Я использовал карту «два пустых зеленых овала», чтобы поместить еще три карты на «самую верхнюю» плоскость.
Какие карты вы могли бы добавить дальше? Что ж, мы могли бы закончить «самую переднюю» плоскость (тот, что образован тремя картами на верхнем уровне, одной картой на среднем уровне и тремя передними картами на нижнем уровне).
Мы также можем использовать верхнюю переднюю левую карту (два полосатых фиолетовых ромба) и нижнюю заднюю правую карту (три полосатых зеленых овала), чтобы заполнить центр среднего уровня (один полосатый красный арахис/волнистая штука).
Если мы будем продолжать в том же духе, мы построим AG(3,3). (Первые 3 для трех измерений, 3 для трех точек на линии). Мы можем считать объекты в этой геометрии: 27 точек, 117 линий, 39плоскости, 1 гиперплоскость. (Эти числа не очевидны; вам потребуются хитрые счетные и комбинаторные конструкции.)
Какое минимальное количество точек необходимо для построения гиперплоскости? Ну, нам нужны три неколлинеарные точки, чтобы построить плоскость, а затем одна точка вне плоскости. Таким образом, мы использовали четыре карты, чтобы построить наш гиперплан.
SET в четырех измерениях
Точно так же мы можем перемещаться в четыре измерения. Нам просто нужна наша гиперплоскость (сделанная ранее) и точка вне гиперплоскости. Фотография ниже была сделана Крисси Ньюэлл на вечере игр в Twitter Math(s) Camp 2018.
Мы построили АГ(4,3), который имеет 81 очко (количество карт в колоде SET), 1080 линий (все возможные SET в колоде), 1170 плоскостей и 120 гиперплоскостей.
Но зачем останавливаться сейчас?
Что, если мы добавим в нашу колоду SET еще один атрибут, например размер? Вы представляете, как сейчас выглядела бы наша пятимерная гиперплоскость? Я оставлю это вам, чтобы попробовать!
Практические вопросы
Я провожу семинары SET с большими группами, иногда в разных городах. Мне нужен был быстрый, дешевый и портативный набор материалов для пар/троек. Мой метод пластиковых стаканчиков и плотного картона (или даже прозрачного плексигласа) работает довольно хорошо, и его относительно легко таскать с собой. (Однако тяжелая карта и сами карты SET немного тяжеловаты в моем чемодане.)
Я также сделал эти великолепные кубики SET.
Кубики созданы с любовью. Они включают в себя разрезание, складывание и склейку каждой стороны 81 маленького кубика. Их изготовление занимает лет (много часов), но они прекрасны. Сети находятся в папке, которой я поделился ранее. Инструкции нет, но думаю разберетесь. Вы также можете попробовать наклеить наклейки на готовые кубики или даже на напечатанные на 3D-принтере кубики. Если вы найдете что-то, что работает, дайте мне знать!
Вы также можете попробовать наклеить наклейки на готовые кубики или даже на напечатанные на 3D-принтере кубики. Если вы найдете что-то, что работает, дайте мне знать!
С кубиками очень весело играть …
Нравится:
Нравится Загрузка…
Математические программы для средней школы
ЗАПИСАТЬ ОЦЕНКУ
Учебник по классической алгебре и геометрии
Наши учащиеся средних классов свободно овладевают алгеброй и геометрией, становятся уверенными в себе и готовы преуспеть.
Как это работает
Мы проводим наших студентов через глубокое изучение алгебраических понятий, помогая им решать сложные математические задачи. Геометрия преподается с упором на формальные доказательства, что является ключом к дальнейшему развитию логики и навыков рассуждения.
Абстрактное мышление
Мы вводим элементы алгебры более высокого уровня и геометрии, основанной на доказательствах, оттачивая ум наших студентов и их способность рассуждать на основе сложных идей.
Умственная гибкость
Учащиеся совершенствуют свои знания, регулярно решая нестандартные интересные задачи, заставляя их применять существующую математическую основу для получения новых концепций.
Задание
Учащиеся выходят из своей зоны комфорта, чтобы решить сложные задачи, которые углубят их понимание и подготовят к экзаменам и математическим соревнованиям, которые могут их ожидать.
Классная среда
Учащиеся вовлечены в научный дискурс и дебаты, должны представить логические аргументы в поддержку своих идей и регулярно участвуют в здоровом соревновании друг с другом.
I — Ускоренный уровень
Эта учебная программа, часто лучше всего подходящая для новых учащихся, разработана для того, чтобы помочь учащимся достичь того уровня, на котором они находятся, и вывести их на уровень международных стандартов.
II — Продвинутый уровень
Большинство учащихся переходят на этот уровень, где мы предлагаем сложную учебную программу по математике, которая обеспечивает глубокое понимание, навыки рассуждения и уверенность, необходимые для успеха от начальной до средней школы с отличием и далее.
III — уровень с отличием
В этой строгой учебной программе очень подробно рассматриваются темы, изучаемые на продвинутом уровне, и регулярно используются задачи соревновательного уровня, которые побуждают учащихся расширять границы своих способностей. Многие учащиеся с отличием также предпочитают участвовать в математических олимпиадах.
Конкурсные программы
Успех в математических олимпиадах прежде всего зависит от глубокой и широкой основы, которая лучше всего реализуется на наших основных занятиях. Для тех, кто заинтересован в более целенаправленном изучении конкурсных материалов, мы предлагаем программу выборочных соревнований, которая готовит как новичков, так и опытных участников к полному спектру национальных и международных математических соревнований.
Узнать больше
Узнать больше
2–3,5 часа в неделю
Учащиеся могут выбрать алгебру, геометрию или оба предмета, продолжительность занятий от 2 до 3,5 часов.
Классная комната
Атмосфера в классе является ключом к нашей методологии. Классы состоят в среднем из 12 учеников, а опытный учитель ведет интерактивный урок.
Домашнее задание
Домашнее задание задается каждую неделю, чтобы закрепить то, чему учили в классе.
Уникальная учебная программа
Наша учебная программа, совершенствовавшаяся в течение двух десятилетий нашей командой талантливых ученых, вдохновлена элитными математическими школами бывшего Советского Союза и адаптирована для образовательной среды США.
1 место
Лучшая школа мира по версии Центра талантливой молодежи Джонса Хопкинса!
4-й
Каждый 4-й студент RSM, участвовавший в программе, попал в 5% лучших на AMC8!
21к
21 000 победителей Math Kangaroo по всей стране!
50k+
Выпускники RSM поступают в лучшие университеты мира
Читать далее
Просмотреть все результаты
icon. openЦитата
openЦитатаДорогая мисс Р.! С вами я обрел уверенность в математике, которой раньше не было. Вы помогли мне получить отличные оценки в школе и развить сильную трудовую этику. Вы были таким замечательным учителем.
RSM Студент
7 класс
Почему вас называют «русской» математической школой?
«Русский» происходит от нашего подхода, который основан на элитных математических школах бывшего Советского Союза, адаптированных к условиям США. По русской традиции изучение математики является важнейшим средством умственного развития. Мы преподаем математику таким образом, чтобы не только развивать математические способности, но и развивать интеллект и характер.
Откуда взялась ваша учебная программа?
Мы предлагаем одну непрерывную учебную программу, начиная с K-12. Наша учебная программа и методология, совершенствовавшиеся в течение 20 лет нашей командой талантливых ученых, вдохновлены элитными математическими школами бывшего Советского Союза и адаптированы к американской образовательной среде.
Насколько велики ваши классы? Каково соотношение учителей и учеников?
В нашем классе в среднем 12 человек, и с тремя уровнями в классе мы можем гарантировать, что каждый ребенок будет помещен в класс, который будет достаточно сложным. Классы являются неотъемлемой частью нашей методологии и учебной программы, поскольку окружающая среда позволяет учащимся озвучивать и обсуждать свои идеи и знакомит их с различными способами мышления.
Сколько времени длятся ваши занятия?
В средней школе продолжительность занятий зависит от того, изучает ли учащийся алгебру, геометрию или и то, и другое. Курсы алгебры проходят раз в неделю по 2,5 часа, геометрии по 1,5 часа.
Зачем моему ребенку геометрия?
Математическое образование не обходится без геометрии. Это новый язык, на освоение которого уходят годы, как с точки зрения продвинутого логического, так и пространственного мышления. Большинство государственных школ предлагают геометрию не более одного года, а некоторые даже меньше, но невозможно полностью выучить геометрию менее чем за три года.
Если ваш ребенок увлекается олимпиадами, подготовка по геометрии также необходима, так как регулярно встречаются задачи по геометрии.
Большинство государственных школ предлагают геометрию не более одного года, а некоторые даже меньше, но невозможно полностью выучить геометрию менее чем за три года.
Если ваш ребенок увлекается олимпиадами, подготовка по геометрии также необходима, так как регулярно встречаются задачи по геометрии.
Сколько домашних заданий я должен ожидать?
Целью домашнего задания является закрепление того, что было изучено в классе. Наши учителя задают ровно столько, чтобы закрепить навыки, полученные в классе. Домашнее задание — отличный инструмент для оценки знаний вашего ребенка. Это должно занять примерно половину продолжительности урока вашего ребенка. Если домашнее задание занимает неоправданно много времени или слишком мало, это может быть красным флажком, указывающим на то, что ваш ребенок не находится на соответствующем уровне.
Кто ваши учителя?
Все наши учителя имеют опыт работы в области математики или смежных областях и страстно увлечены этим предметом. Они также проходят обширную подготовку, чтобы преподавать в соответствии с нашей специальной методологией и учебным планом.
Они также проходят обширную подготовку, чтобы преподавать в соответствии с нашей специальной методологией и учебным планом.
В каком возрасте лучше всего присоединиться?
Требуется много лет, чтобы разработать глубокую математическую основу, а также тип мышления, на формировании которого мы сосредоточены. С математикой, как с языком или спортом, чем раньше ребенок начнет, тем лучше. Наши ученики начинают рассуждать абстрактными понятиями в начальной школе, а к средней школе они не только знакомы с основными элементами алгебры, но и могут легко применять их при решении задач.
Сколько у вас стоит обучение?
Для получения подробной информации об обучении посетите раздел «обучение» в выбранном вами отделении RSM.
Подходит ли ваша программа для моего ребенка?
Мы разработали несколько уровней для каждого класса специально для того, чтобы способствовать развитию каждого ребенка на основе его знаний и способностей. Мы рекомендуем запланировать бесплатную оценку, так как эти занятия позволяют нам понять потребности каждого ребенка и порекомендовать класс, который лучше всего подходит для него или нее.
Мы рекомендуем запланировать бесплатную оценку, так как эти занятия позволяют нам понять потребности каждого ребенка и порекомендовать класс, который лучше всего подходит для него или нее.
Не будет ли ваша программа путать моего ребенка в школе?
Понятия, которые мы рассматриваем, являются фундаментальными, и мы изучаем их глубоко. Дети видят понятия с разных сторон. Это не приводит к путанице, а скорее расширяет возможности учащихся, углубляя их понимание. Поскольку наша учебная программа, как правило, опережает общеобразовательную школу, дети часто сначала изучают понятия в RSM. Как только они освоят их, мы обнаружим, что они могут адаптироваться к любому школьному формату.
15 заданий по геометрии для вовлечения учащихся всех классов
Если вы оглянетесь в своем классе, то, скорее всего, везде увидите геометрию — в квадратиках календаря, длинных шестиугольных карандашах или прямоугольных ковриках.
Геометрия полна важных основополагающих понятий, но не все студенты лучше всего усваивают ее на лекциях и бесконечных практических задачах. К счастью, ваши планы уроков геометрии легко связать с реальными приложениями! Занятия по геометрии могут дать вашим ученикам практический опыт и вовлечь их в учебный процесс.
К счастью, ваши планы уроков геометрии легко связать с реальными приложениями! Занятия по геометрии могут дать вашим ученикам практический опыт и вовлечь их в учебный процесс.
Попробуйте эти 15 увлекательных занятий , которые помогут вам преподавать геометрию и сделать из ваших учеников любознательных и увлеченных учеников.
Юные ученики: попробуйте эти интерактивные задания по геометрии
Практические задания — отличный способ познакомить учащихся с такими математическими понятиями, как фигуры и узоры .
Эти увлекательные занятия помогут им изучить свойства 2D- и 3D-фигур в реальном мире и дадут им возможности для обучения, которые заложат основу для дальнейшего обучения.
1. Создавайте трехмерные фигуры с помощью зубочисток и пластилина
Раздайте учащимся зубочистки, пластилин или зефир и предложите им построить трехмерные фигуры, такие как призмы и кубы. Это отличный способ для учащихся понять свойства трехмерных фигур в реальной жизни!
Кроме того, учащиеся могут использовать это задание, чтобы оживить двухмерные фигуры и понять соответствующие понятия, такие как вершины, углы и стороны.
2. Создавайте 2D-фигуры с помощью танграмм
Головоломки Tangram — родом из Китая и привезенные в Европу в начале 19 века.через торговые пути — используйте семь плоских геометрических фигур, чтобы составить силуэты. Хотя танграмы обычно делаются из дерева, вы можете сделать наборы для своего класса из цветной плотной бумаги или войлока.
Танграммы — отличный инструмент для учащихся, которым нравится управлять своей работой, и могут помочь юным учащимся понять свойства различных форм. Кроме того, есть много разных шаблонов для учащихся! Дайте им разные узоры и наблюдайте, как шестиугольник, трапеция и четырехугольник превращаются в зайчика, домик или солнце.
3. Создавайте геометрические узоры из блоков узоров
Для учащихся начальной школы частью понимания форм является также понимание геометрических узоров. Блоки шаблонов помогают учащимся создавать шаблоны, практиковать вращение фигур и сортировать различные фигуры.
Создание моделей важно не только для геометрии — это основополагающая концепция критического мышления и анализа, которая может помочь учащимся устанавливать связи между различными концепциями.
4. Решайте геометрические загадки с наборами LEGO
Будь то головоломки или загадки, математические головоломки могут помочь учащимся решить сложные задачи, сделать выводы и углубить свое понимание.
LEGO — отличный многоцелевой инструмент для вашего класса, который может помочь учащимся лучше понять свойства форм. Дайте учащимся описания различных 2D- и 3D-форм (количество сторон, вершин и длина сторон) и попросите их построить правильный объект!
5. Потренируйтесь формировать фигуры с помощью геобордов
Геоборды — это классический геометрический инструмент, который помогает учащимся создавать фигуры с помощью резинок, натянутых на колышки.
Особенно удобно для кинестетических учащихся. Используйте геоборды, чтобы учащиеся могли создавать различные формы, описывать их свойства и измерять их. Они могут воспроизводить уже знакомые формы или использовать их для изучения новых.
В вашем классе нет геобордов? Без проблем! Предложите учащимся получить доступ к этой цифровой версии на компьютере или планшете.
Старшие классы: развивайте понимание геометрии с помощью различных средств
Когда учащиеся перейдут в старшие классы начальной или средней школы, они начнут больше узнавать о свойствах фигур , а не только об их внешнем виде.
Они начнут использовать геометрические инструменты и смогут более глубоко изучить применение геометрии в реальной жизни. Используйте эти задания с 3 по 5 класс, чтобы приступить к ним весело и совместно!
1. Создание линейных сегментов с геобордами
Возможно, ваши ученики удивятся, узнав, что на уроке математики строка — это не , а строка. Независимо от того, изучаете ли вы перпендикулярные линии или сегменты линий, используйте геоборды для практического отображения различных концепций.
Когда дело доходит до геометрии, нужно знать много слов, поэтому используйте геодоски, чтобы пополнить новый словарный запас и поощрить математические разговоры в классе.
2. Нарисуйте геометрические идеи с помощью карандаша и бумаги
Иногда написание новых понятий является лучшим способом их запоминания учащимися! Все прямые углы, вершины и линии геометрии особенно хорошо подходят для визуальной среды.
Каждый учащийся может практиковаться в рисовании геометрических фигур от руки и делать наглядные заметки о новых концепциях. Они также смогут попрактиковаться в использовании таких инструментов, как линейки, компасы и транспортиры для измерения углов и длины.
Чтобы получить дополнительные ресурсы, разместите в классе опорные схемы или предложите учащимся сделать свои собственные с помощью маркеров и цветной бумаги.
3. Дополните уроки в школе с помощью онлайн-игр
Цифровое игровое обучение сочетает в себе все удовольствие от видеоигры с эффективными результатами обучения, согласованными с учебным планом.
Prodigy Math Game позволяет вам легко направлять процесс обучения учащихся, пока они играют онлайн! Зарегистрируйте бесплатную учетную запись учителя, чтобы отправлять оценки ученикам, пока они исследуют увлекательный фэнтезийный мир. Кроме того, Prodigy позаботится об оценке за вас!
Создайте мою бесплатную учетную запись учителя сейчас Другие онлайн-инструменты, такие как Geogebra, также могут помочь учащимся одновременно развивать свои навыки работы с компьютером по геометрии и .
4. Практикуйте геометрические понятия с помощью карточек с заданиями
Карточки с заданиями помогают разбивать более сложные идеи и задания на более мелкие и выполнимые части. Это отличный способ помочь учащимся сосредоточиться на одном вопросе за раз, не перегружая себя, независимо от того, работают ли они:
- С партнером
- В небольших группах
- В одиночку во время смены станции
Попробуйте бесплатно Печатные карточки с заданиями по геометрии от учителей Платите учителям или создавайте свои собственные, чтобы получить еще больше возможностей для настройки! Какую бы концепцию геометрии ни изучают учащиеся, для этого есть карточка с заданием.
5. Совершенствуйте навыки с помощью рабочих листов по геометрии
Интернет — прекрасный инструмент, особенно когда дело доходит до поиска рабочих листов по геометрии. Просто зайдите на свой любимый сайт и распечатайте что-нибудь в качестве домашнего задания или для тех, кто раньше всех закончит.
Используйте рабочие листы по геометрии, чтобы учащиеся практиковали понятия на подходящем для них уровне, или используйте Prodigy для отправки онлайн-задания, над которым они могут работать в школе или дома.
Создайте мою бесплатную учетную запись учителя сейчас6. Какой формы ваша земля?
В этом умном геометрическом задании учащиеся должны создать фигуру с наибольшей площадью поверхности из предварительно нарезанной нити.
Учащиеся могут использовать геоборд или веревку и гвозди, чтобы сделать свою фигуру. Им придется использовать формулы, которые они уже выучили, для нахождения площади поверхности, или они могут считать квадраты на бумаге с сеткой или на геобордах.
7. Лента Мёбиуса
Это магия? Это геометрия? Ваши ученики будут настолько поражены, что им может быть трудно понять это. Пусть они смоделируют задачу с помощью полосок бумаги и сами увидят, как эта задача о площади поверхности работает в реальной жизни.
Предложите учащимся поиграть со своими лентами Мёбиуса и провести вокруг них линии, разрезать их посередине или поэкспериментировать с различными поворотами, чтобы посмотреть, что получится.
Другие способы разнообразить изучение геометрии в разных классах
1. Организуйте поиск предметов по геометрии
Предложите учащимся искать различные геометрические фигуры в вашем классе. Попросите их найти:
- Восемь прямых углов
- Призму с квадратным основанием
- Наибольшее количество кружков
Или что-то еще, что, по вашему мнению, они могли бы искать в вашем классе!
Для получения дополнительной информации попросите учащихся вычислить площадь поверхности фигур, записать свои выводы в математический журнал и описать их свойства самостоятельно или в небольших группах.
2. Сыграйте в геометрическую игру для всего класса. Игра «Опасность»
«Опасность» — это проверенное временем занятие, в котором участвует весь класс. Используйте бесплатный шаблон, чтобы настроить его в соответствии с тем, что вы изучаете в классе, с разными категориями для разных подтем геометрии.
Предложите учащимся идентифицировать фигуры по картинкам или описать свойства фигур и назвать их.
3. Для младших школьников попробуйте форму БИНГО
Для дополнительного сопоставления и идентификации формы попробуйте классическую игру в классное бинго! Распечатайте наш шаблон карты BINGO и добавьте к каждой из них разные формы.
Либо назовите фигуры, чтобы помочь учащимся попрактиковаться в их идентификации, либо опишите форму и попросите дать ответ. Выигрывает тот, кто первым заполнит полный ряд!
Помогите своим учащимся получить максимальную отдачу от вашего раздела геометрии
Каждый учащийся вашего раздела геометрии найдет что-то для себя — практические занятия, практические приложения и возможности для увлекательных игр в классе.
Используйте эти 15 заданий, чтобы закрепить ключевые понятия и поддерживать интерес учащихся к процессу обучения. Скоро они станут мастерами геометрии!
Присоединяйтесь к Prodigy Math Game, чтобы узнать больше о способах проведения увлекательных занятий по геометрии в соответствии с учебным планом. Ваша бесплатная учетная запись учителя включает инструменты, которые помогут вам согласовывать вопросы, на которые учащиеся отвечают во время игры, с тем, что вы преподаете в классе! Кроме того, всего за несколько кликов вы сможете получать информацию об учащихся и легко различать их.
Ваша бесплатная учетная запись учителя включает инструменты, которые помогут вам согласовывать вопросы, на которые учащиеся отвечают во время игры, с тем, что вы преподаете в классе! Кроме того, всего за несколько кликов вы сможете получать информацию об учащихся и легко различать их.
Преподавание геометрии для более глубокого понимания
18.05.2017 5 комментариев
Что должно происходить на каждом уровне и как включать мероприятия, ведущие учащихся с одного уровня на следующий
Что делает понятия геометрии такими сложными для некоторых учащихся? Было много учителей, которые пытались облегчить формальное понимание с помощью новых программ и методов. Иногда они успешны, иногда не очень. Огромной проблемой может быть решение двухстолбцовых доказательств, которые, казалось бы, оторваны от практических жизненных приложений, впервые. Если вы знаете, что делает этот предмет сложным и на каком уровне в настоящее время находятся ваши ученики, вы можете использовать эти предложения, чтобы выяснить, что вы можете сделать, чтобы помочь своим ученикам учиться. |
ЧАСТЬ 1. Итак, почему преподавать (и изучать!) геометрию так сложно?
Недостаточно доказательств в дошкольном образовании
Основа для изучения геометрии не закладывается в старшей школе. Она начинается в начальной и средней школе. Учащиеся должны научиться доказывать и объяснять, почему что-то происходит, еще до того, как они поступят в класс средней школы. Это помогает заложить основу для геометрии, а также других предметов в средней школе. Если бы студентов познакомили с простыми неформальными доказательствами и потребовали разумно обосновать утверждения, они были бы гораздо лучше подготовлены к формальным доказательствам.
Конечно, конкретные понятия геометрии не будут на том же уровне, но лучше ввести шаблон мыслей раньше. Учащиеся должны уметь объяснять, доказывать и показывать почему задолго до того, как они начнут изучать геометрию в средней школе.
Низкий уровень концептуального понимания
Мы все знаем, что семестр пролетает незаметно. Учителя не могут тратить столько времени, сколько нужно, чтобы по-настоящему охватить все уровни понимания, необходимые для достижения успеха. Более того, из-за того, что понятия геометрии не вводятся заранее, всегда есть очень запутанные ученики. В то время как некоторые студенты могут легко понять это, другим остается хвататься за соломинку понимания.
Уровни Ван Хиле помогают нам лучше понять непонимание, с которым сталкиваются слишком многие ученики. Модель Ван Хиле — это теория, которая описывает, как учащиеся изучают геометрию. Он основан на докторской работе мужа и жены Дины ван Хиле-Гелдоф и Пьера ван Хиле.
Согласно их модели и другим исследованиям, учащиеся начинают изучать геометрию с низким уровнем понимания Ван Хиле. Изучение сложных понятий, таких как доказательства, требует гораздо более высокого уровня (уровень 4 из 5), и большинство учащихся поступают в класс на уровне 2 или 3. Учащиеся, не имеющие базовых знаний или способности обосновывать утверждения, легко настраиваются на провал в классе. .
Общее когнитивное развитие
Даже когда понятия геометрии вводятся рано, некоторые учащиеся просто не готовы на уровне развития. Жан Пиаже и его теории когнитивного развития помогают пролить свет на это. Индивидуум должен достичь формальной операционной стадии, чтобы понять, формально рассуждать и строить доказательства.
Проблема в том, что некоторые учащиеся еще не достигли этого этапа, поскольку он может охватывать период от подросткового возраста до начала взрослой жизни (11–20 лет). Это означает, что если ученик не достиг такого уровня когнитивного развития, ему будет довольно сложно понять геометрию. Хотя мы мало что можем с этим поделать, важно знать, что это фактор.
Хотя мы мало что можем с этим поделать, важно знать, что это фактор.
Часть 2: Об уровнях Ван Хиле для изучающих геометрию
Уровни основаны на идее, что учащиеся могут понимать геометрию визуально в раннем возрасте, а затем развивать понятия, лежащие в основе свойств, до такой степени, что они могут сначала просто определите, а затем подумайте более абстрактно о принципах. Они доходят до анализа фигуры или формы. В конце концов, они переходят к вычетам. Студенты на более высоком уровне знают, как работают аксиомы, теоремы и конверсии, достаточно, чтобы расширить свойства. На самом высоком уровне учащиеся способны мыслить как математик. Они осознают, что аксиомы более произвольны, чем конкретны, и поэтому могут, наконец, расширить свое мышление, чтобы принять неевклидову геометрию.
Уровень учащегося определяется его/ее опытом, а не возрастом. Добавление серии заданий, позволяющих учащимся взаимодействовать с геометрическими фигурами, помогает им перейти на следующий уровень.
Еще один момент, о котором следует помнить, это то, что весь язык и словарный запас, которые вы используете, должны соответствовать конкретному уровню учащегося. Всегда используйте правильную терминологию, но имейте в виду, что если вы не поддержите своих учеников подробными инструкциями по словарному запасу, чтобы убедиться, что вы все понимаете термины, когда вы их используете, вы потеряете некоторых учеников. Те, кто отстают, смогут только запоминать и царапать. Они не будут полностью понимать, и это может помешать им когда-либо достичь следующей фазы/уровня.
Даже учащиеся двух разных уровней, работающие вместе, могут столкнуться с трудностями при обсуждении геометрических свойств в игре. Партнеры должны будут использовать один и тот же уровень словарного запаса для эффективной совместной работы.
Часть 3. Способы преподавания геометрии для более глубокого понимания с использованием уровней Ван Хиле
Как и в большинстве случаев обучения, чем раньше, тем лучше. Преимущество в начальных классах — единственный способ убедиться, что ученики имеют более высокий уровень ван Хиле, когда они переходят к геометрии в старших классах. Крайне важно, чтобы мы улучшили основы обучения в начальной и средней школе для абстрактного и реляционного уровней. Как мы можем включить это?
Преимущество в начальных классах — единственный способ убедиться, что ученики имеют более высокий уровень ван Хиле, когда они переходят к геометрии в старших классах. Крайне важно, чтобы мы улучшили основы обучения в начальной и средней школе для абстрактного и реляционного уровней. Как мы можем включить это?
- Зрительное распознавание в начальной школе (2-5 классы)
- Практика рисования (для точности)
- Практика отношений разных форм (6-8 классы)
- Практическая деятельность (с манипулятивными действиями), в идеале с некоторым уровнем исследования/исследования
- Обучение студентов объяснять, доказывать и показывать, почему
Геометрия — это предмет, который строится сам на себе. Учащийся, который потерялся в начале, скорее всего, будет потерян на протяжении всей школьной карьеры. Вот почему крайне важно, чтобы базовые концепции преподавались на всех уровнях образования.
Вот несколько примеров того, что вы увидите на каждом уровне, и виды деятельности, которые помогут учащимся закрепить свое обучение, чтобы перейти на следующий уровень.
Уровень 0: ВИЗУАЛИЗАЦИЯ
Понимание: Ребенок может узнавать и классифицировать отдельные формы на основе классических примеров.
Мыслительный процесс: Это прямоугольник, потому что он похож на коробку.
Вызовы: Когда фигуры повернуты по-другому или не соответствуют «типичному» визуальному представлению, ребенок может подумать, что это не соответствует требованиям (примеры: ребенок может подумать, что очень тонкий разносторонний треугольник не является треугольником, поскольку это не классическая равносторонняя форма). они узнали. Он/она может подумать, что перевернутый квадрат на самом деле не квадрат, а «ромб». видеть, что формы конгруэнтны при повороте и т. д.)
 Когда учащиеся могут перетаскивать вершины и отображать меры, они действительно начинают понимать, как работают свойства каждой фигуры.
Когда учащиеся могут перетаскивать вершины и отображать меры, они действительно начинают понимать, как работают свойства каждой фигуры. Уровень 1: АНАЛИЗ
Понимание: Учащийся может идентифицировать фигуры или их составные части. Он принимает основные, отдельные свойства геометрии.
Мыслительный процесс: Этот набор мер угла взят из равнобедренного треугольника, так как две меры совпадают, а сумма составляет 180 градусов.
Проблемы: Учащийся может испытывать трудности при переходе от одного свойства к другому. Последовательность шагов может быть туманной, а способность «увидеть», с чего начать в более сложной фигуре или задаче, требующей двух свойств, может отсутствовать.
Занятия для учащихся средних и старших классов на уровне 1:
|
- Позвольте учащимся попрактиковаться в определении ситуаций, в которых может иметь место определенное свойство. Им нужно много практиковаться в распознавании фигур и закреплении свойств, прежде чем они смогут начать применять более абстрактные понятия. Эта игра «скрученные пальцы» похожа на настольный твистер для отработки специальных пар углов вдоль поперечной.
- Уделяйте время четким и кратким заметкам. Во время лекции обязательно сосредоточьтесь на новых словарных терминах. Создавайте основы. Попробуйте «заметки-каракули», которые сочетают в себе графику и текст, чтобы помочь учащимся запомнить важные идеи и новые термины.
Уровень 2: АБСТРАКЦИЯ
Понимание: Учащийся может делать выводы и может упорядочивать и связывать свойства. Он/она понимает условия и может начать ИСПОЛЬЗОВАТЬ дедуктивную логику, но еще не понимает смысла дедукции или того, как формально представить доказательство.
Он/она понимает условия и может начать ИСПОЛЬЗОВАТЬ дедуктивную логику, но еще не понимает смысла дедукции или того, как формально представить доказательство.
Мыслительный процесс: У этой фигуры две пары конгруэнтных сторон, так что это может быть прямоугольник или параллелограмм…. Ах, но прямых углов нет, а противоположные пары углов конгруэнтны, так что это должен быть параллелограмм.
Проблемы: У учащегося могут возникнуть проблемы с расширением определения за пределы его самой базовой интерпретации. Трудно объяснить или следовать последовательности дедуктивных рассуждений, которая представляет собой формальное доказательство со многими шагами.
Задания для учащихся 2-го уровня:
- Включите задачи, в которых учащиеся должны использовать несколько свойств, наложенных друг на друга, чтобы найти недостающие меры или решить проблемы. Угловые головоломки предлагают веселую и сложную задачу, которая хорошо подходит для этого уровня учащихся.
 Этот набор рассматривает свойства углов в треугольниках, а вот еще один — теоремы об окружности.
Этот набор рассматривает свойства углов в треугольниках, а вот еще один — теоремы об окружности.
|
Опять же, не забудьте включить разнообразную входную информацию. Используйте некоторые карточки с диаграммами, некоторые с пояснениями и определениями слов, а некоторые с измерениями, чтобы учащиеся сочетали практику со всеми формами и могли строить ментальные связи. |
Уровень 3: ВЫЧИСЛЕНИЕ
Понимание: Учащийся понимает рассуждения и логику и может передать это другим. Он/она может построить формальные доказательства.
Мыслительный процесс: Поскольку a подразумевает b, а b подразумевает c, то a подразумевает c. В этом случае а истинно, поэтому я могу заключить, что с также должно быть истинным.
Проблемы: Учащиеся на этапе 3 понимают теоремы, неопределенные термины, определения и аксиомы, но имеют фиксированное представление о них. Они воспринимают аксиомы как нечто конкретное и с трудом понимают неевклидову геометрию.
Они воспринимают аксиомы как нечто конкретное и с трудом понимают неевклидову геометрию.
Мероприятия для учащихся старших классов на уровне 3:
|
|
Уровень 4: ТОЧНОСТЬ
Понимание: Понимание геометрии расширилось до уровня математика. Учащийся понимает неевклидову геометрию и может сравнивать изучение геометрии с другими областями.
(Большинство наших старшеклассников еще не достигли этого уровня.)
Вы не можете просто бросить ребенка в воду и ожидать, что он умеет плавать. Им нужно видеть воду, прикасаться к ней, практиковаться, экспериментировать и испытывать ее. Затем они постепенно изучают более сложные аспекты плавания, такие как плавание, манипулирование конечностями для движения, задержку дыхания под водой и так далее.
Это очень похоже на геометрию. Студенты, у которых никогда не было фактического понимания основ геометрии, будут потеряны. Они могут легко утонуть в информационном натиске геометрии. Независимо от того, какой уровень математики преподается, в какой-то момент урок, включающий базовую геометрию, не просто необходим, он имеет решающее значение. Не забудьте дать своим ученикам время, пространство и основательную практику, которая позволит им перейти с одного уровня на другой!
Для получения дополнительных советов по обучению математике, обновлений и ресурсов введите свой адрес электронной почты здесь:
Далее читать:
Геометрия, часть 2: Континуум обучения (ван Хиле)
К. Элкинс, OK Math and Reading Lady
Сегодняшняя статья будет посвящена аспекту геометрии, включающему уровни мышления. Мы знаем, что учащиеся PreK или KG не готовы к формальным определениям форм. Начиная примерно со 2-го класса учащиеся могут быть готовы описывать формы, используя определенные атрибуты. Пьер и Дина ван Хиле — голландские преподаватели математики, у которых есть отличный способ описать, как дети проходят через эти уровни геометрического мышления. Они называются «Уровни Ван Хиле геометрического мышления». Нажмите на эту ссылку для получения полного описания: Модель ван Хиле Также – несколько полезных ресурсов в конце этого поста.
Пьер и Дина ван Хиле — голландские преподаватели математики, у которых есть отличный способ описать, как дети проходят через эти уровни геометрического мышления. Они называются «Уровни Ван Хиле геометрического мышления». Нажмите на эту ссылку для получения полного описания: Модель ван Хиле Также – несколько полезных ресурсов в конце этого поста.
Меня заинтересовали эти уровни, когда я проводил исследования о лучших способах помочь учащимся освоить стандарты по геометрии. (Дополнительную информацию об этих уровнях см. ниже.) Должен ли я учить их «правильному определению» квадрата в KG? В какой момент учащиеся должны начать понимать специфические свойства квадрата — что это на самом деле определенный тип прямоугольника. А также . . . когда уместно помочь учащимся понять, что квадрат также классифицируется как ромб, прямоугольник, параллелограмм и четырехугольник? Нажмите на ссылку, чтобы получить копию таблицы в формате PDF: Ван Хиле Уровни 0, 1, 2
Что мы, учителя, можем сделать, чтобы помочь им пройти уровни? По словам ван Хиле, уровни нельзя пропускать — дети должны продвигаться по каждой иерархии мысли. Поэтому, несмотря на то, что к этим уровням не привязан уровень обучения, мне нравится думать о уровне визуализации как о начальной точке, наиболее подходящей для учащихся 1-го или 2-го класса PreK. Уровень 1 мышление может проявиться во 2 или 3 классе (и выше). Учащиеся, способные к Уровень 2 мышление может начаться с 3-8 класса. Учащиеся, изучающие геометрию в старших классах, могут мыслить на уровне 3 .
Поэтому, несмотря на то, что к этим уровням не привязан уровень обучения, мне нравится думать о уровне визуализации как о начальной точке, наиболее подходящей для учащихся 1-го или 2-го класса PreK. Уровень 1 мышление может проявиться во 2 или 3 классе (и выше). Учащиеся, способные к Уровень 2 мышление может начаться с 3-8 класса. Учащиеся, изучающие геометрию в старших классах, могут мыслить на уровне 3 .
Одно из свойств описанных им уровней носит название «Разделение». В статье, указанной выше, говорится: «Учитель, который рассуждает на одном уровне, говорит на другом «языке», отличном от ученика на более низком уровне, что препятствует пониманию». Когда учитель говорит о «квадрате», он или она имеет в виду особый тип прямоугольника. Студент на уровне 0 или 1 не будет иметь такого же понимания этого термина. Ученик не понимает учителя, а учитель не понимает, как рассуждает ученик. Ван Хилес считал это свойство одной из главных причин неудач в геометрии. Учителя считают, что они выражают свои мысли ясно и логично, но их рассуждения 3-го или 4-го уровня непонятны учащимся более низких уровней. В идеале учителю и ученикам нужен общий опыт, лежащий в основе их языка.
Учителя считают, что они выражают свои мысли ясно и логично, но их рассуждения 3-го или 4-го уровня непонятны учащимся более низких уровней. В идеале учителю и ученикам нужен общий опыт, лежащий в основе их языка.
Вот уровни поближе.
Уровень 0 Визуализация: Опишите формы на основе их внешнего вида.
- На этом уровне учитель может сказать: «Вот как выглядит квадрат». (без описания свойств).
- Сортировка и классификация фигур по внешнему виду «Они подходят друг другу, потому что все заостренные». или «У них у всех прямые углы». или «У них кривые». или «Они имеют ту же форму, что и печенье». или «Все эти фигуры катятся». или «Это выглядит как треугольник со срезанной вершиной (трапеция)».
- Учащиеся работают над тем, чтобы сгруппировать фигуры, которые похожи на .
- Действия учащихся: наблюдение, ощупывание, сборка, сортировка, разборка, сборка (с использованием 2D- и 3D-моделей, шаблонов, бумажных форм и изображений)
Анализ уровня 1: Описывать формы на основе их свойств.
- Учащиеся узнают, какими свойствами обладает каждая фигура. Пример: «Все прямоугольники имеют 4 стороны с равными и параллельными противоположными сторонами и 4 прямыми углами». или «Перпендикулярные линии образуют прямой угол».
- Может быть много способов ориентировать фигуру, и фигуры могут быть разных размеров (без изменения имени фигуры).
- Действия учащихся: описывать и сортировать модели и изображения по свойствам
Уровень 2 Абстракция: Распознавание отношений между свойствами геометрических фигур.
- Учащиеся понимают, что некоторые фигуры можно классифицировать по-разному. Пример: «Квадрат — это особый вид прямоугольника». или «Все прямоугольники — параллелограммы». или «Перпендикулярные линии — это особый тип пересекающихся линий». или «Прямоугольники — это параллелограммы с прямыми углами». или «Если фигура представляет собой четырехугольник с 4 равными сторонами и без прямых углов, то это ромб».

- Действия учащихся: Сортировка, классификация, рисование и построение 2D- и 3D-фигур
Следующие 2 уровня обычно охватывают мышление, связанное со старшей школой, поэтому я не буду подробно рассказывать о них в этом посте.
Уровень 3 Дедукция: Переход от размышлений о свойствах к рассуждениям или доказательству теорий.
Уровень 4 Строгость: Установление и анализ теорем в различных системах постулирования.
Геометрические ресурсы
- БЕСПЛАТНЫЕ 2D- и 3D-клипарты — отлично подходят для создания собственных рабочих листов или для сортировки детьми (Jen Hart Design @ TPT)
- БЕСПЛАТНЫХ 3D-фигур для сортировки или построения графиков от srenaud @ TPT
- БЕСПЛАТНЫХ карточек с заданиями по геометрии (упражнение 1 или 2 уровня) от Кэтрин Уиллис @ TPT
- Карточки с заданиями для составления фигур из блоков шаблонов — простые (составление более крупных фигур с использованием блоков шаблонов) 2 доллара США от Келли Смит @ TPT
- плакатов и карточек с линиями и углами (уровень 1 или 2 — атрибуты различных линий и углов) 2,50 долл.
 США от Кимберли Майнер @ TPT
США от Кимберли Майнер @ TPT - 2D-маты для сортировки фигур за 2 доллара от Little Academics @ TPT
- Набор Movin’ it Match 2D и 3D Shapes (8 долларов США от The Math Maniac): на мой взгляд, оно того стоит, особенно если вы ищете множество рисунков 2D и 3D фигур черными линиями, которые можно использовать для сортировки и игр.
Для тех из вас, кто интересуется более подробной теорией ван Хиле и конкретными способами применения к различным темам геометрии, вот еще одна статья: Модель геометрического мышления Ван Хиле (Департамент образования Огайо)
Я знаю, что в этом посте не слишком много внимания уделяется идеям урока, НО это очень важно в отношении уровней развития понимания геометрии. Впереди еще идеи для уроков.
160 Табель успеваемости по математике Комментарии для начальной и средней школы
Табель успеваемости — отличный способ для учителей кратко изложить свои мысли родителям и учащимся. Однако написание комментариев в табеле успеваемости по математике иногда может быть утомительным, повторяющимся и занимать очень много времени.
Если вы обнаружили, что откладываете написание табелей успеваемости до последней минуты, мы вам поможем! В этом посте мы рассмотрим более 100 комментариев к табелям успеваемости по математике, которые вы можете использовать в качестве шаблонов, чтобы упростить написание табелей успеваемости.
Для студентов, изучающих математику, получение обратной связи имеет решающее значение для обучения и повышения успеваемости. Учащимся важно видеть, что они делают правильно, а что неправильно, чтобы они знали, что нужно улучшить и что продолжать делать.
Кроме того, комментарии в табеле успеваемости создают связь между учителем и учеником или родителем. Это дает возможность получить качественную обратную связь как для родителей, так и для учащихся.
Чем может помочь Text Blaze?
Хотя эти комментарии важны, их написание может быть утомительным или утомительным. Если в вашем классе 25 учеников, и каждый ученик получает 3 комментария в своем табеле успеваемости по математике, то вам нужно написать целых 75 комментариев. Это может занять много времени. Text Blaze может помочь сделать написание этих комментариев более эффективным. Фрагменты текста можно использовать для вставки в комментарии, а поля формы можно использовать для настройки таких аспектов, как имя учащегося, дата и т. д.
Это может занять много времени. Text Blaze может помочь сделать написание этих комментариев более эффективным. Фрагменты текста можно использовать для вставки в комментарии, а поля формы можно использовать для настройки таких аспектов, как имя учащегося, дата и т. д.
Вот видео, которое даст вам представление о том, как создать фрагмент.
Попробуйте
- Чтобы настроить эти шаблоны, нажмите кнопку «Копировать в Text Blaze». Затем вы можете вставлять комментарии в любом месте онлайн с помощью сочетаний клавиш!
Кроме того, попробуйте приведенный ниже фрагмент кода, выбрав или отменив выбор черты учащегося, чтобы создать комментарии в табеле успеваемости по математике.
Демонстрация генератора комментариев к табелю успеваемости по математике
Генератор комментариев к табелю успеваемости по математике для {formtext: name=first name; столбцы=9} :
- Способности решать проблемы: {formtoggle: name=постепенно улучшается; по умолчанию=да}{formtext: имя=имя; cols=8} постепенно улучшает свои {formtext: name=insert математические навыки; cols=13}, но прогресс идет медленно из-за {formtext: name=insert Problem; столбцы=12}.
 {endformtoggle}{formtoggle: name=переполняется; default=no}При решении сложных математических задач {formtext: name=first name; cols=8} иногда становится перегруженным информацией, особенно для более длинных математических задач. {endformtoggle}{formtoggle: name=хороший словарный запас; default=no}{formtext: name=имя; cols=8} имеет отличный словарь, который помогает {formmenu: name=gender; его; default=her} решать математические задачи.{endformtoggle}
{endformtoggle}{formtoggle: name=переполняется; default=no}При решении сложных математических задач {formtext: name=first name; cols=8} иногда становится перегруженным информацией, особенно для более длинных математических задач. {endformtoggle}{formtoggle: name=хороший словарный запас; default=no}{formtext: name=имя; cols=8} имеет отличный словарь, который помогает {formmenu: name=gender; его; default=her} решать математические задачи.{endformtoggle} - Математические понятия: {formtoggle: name=дополнение понимание; по умолчанию=да}{formtext: имя=имя; cols=8} имеет {formmenu: name=rating; сильный; по умолчанию=средний; слабое} понимание основного сложения.{endformtoggle}{formtoggle: name=борется с; default=no}{formtext: name=имя; cols=8} явно проявляет большие усилия на уроке математики, но по-прежнему борется с {formtext: name=insert математическое умение; cols=13}.{endformtoggle}{formtoggle: name=не удалось запомнить; default=no}{formtext: name=имя; cols=8} испытывает трудности с запоминанием расписания.
 {endformtoggle}{formtoggle: name=сильное понимание; default=no}{formtext: name=имя; cols=8} демонстрирует {formmenu: name=rating; сильный; по умолчанию=средний; слабое} понимание {formtext: name=вставить математический навык; cols=13}.{endformtoggle}
Арифметика: {formtoggle: name=хорошо в арифметике; по умолчанию=да}{formtext: имя=имя; cols=8} умеет складывать и вычитать и может применять оба понятия к задачам со словами.{endformtoggle}{formtoggle: name=нужно больше практики; default=no}{formtext: name=имя; cols=8} требует дополнительной практики, чтобы преуспеть в арифметике.{endformtoggle} {formtoggle: name=должен тренироваться в запоминании; default=no}{formtext: name=имя; cols=8} имеет четкое представление о том, как работает умножение, но ему было бы полезно больше практиковаться в запоминании расписания. {endformtoggle}{formtoggle: name=хорошо разбирается в алгебре; default=no}{formtext: name=имя; cols=8} хорошо разбирается в алгебре и может решать задачи с несколькими переменными.
{endformtoggle}{formtoggle: name=сильное понимание; default=no}{formtext: name=имя; cols=8} демонстрирует {formmenu: name=rating; сильный; по умолчанию=средний; слабое} понимание {formtext: name=вставить математический навык; cols=13}.{endformtoggle}
Арифметика: {formtoggle: name=хорошо в арифметике; по умолчанию=да}{formtext: имя=имя; cols=8} умеет складывать и вычитать и может применять оба понятия к задачам со словами.{endformtoggle}{formtoggle: name=нужно больше практики; default=no}{formtext: name=имя; cols=8} требует дополнительной практики, чтобы преуспеть в арифметике.{endformtoggle} {formtoggle: name=должен тренироваться в запоминании; default=no}{formtext: name=имя; cols=8} имеет четкое представление о том, как работает умножение, но ему было бы полезно больше практиковаться в запоминании расписания. {endformtoggle}{formtoggle: name=хорошо разбирается в алгебре; default=no}{formtext: name=имя; cols=8} хорошо разбирается в алгебре и может решать задачи с несколькими переменными. {endformtoggle}
{endformtoggle}
_
Посетите нашу страницу для учителей, где вы найдете больше шаблонов, которые вы можете использовать уже сегодня!
Способности решать проблемы Шаблон 1
{formtext: name=first name; cols=8} постепенно улучшает свои {formtext: name=insert математические навыки; cols=13}, но процесс идет медленно из-за {formtext: name=insert Problem;cols=12}.
_
Способность к решению задач Шаблон 2
При решении сложных математических задач {formtext: name=first name; cols=8} иногда становится перегруженным информацией, особенно для более длинных математических задач.
_
Способности решать проблемы Шаблон 3
{formtext: name=first name; cols=8} имеет отличный словарь, который помогает {formmenu: name=gender; его; default=her} решать математические задачи.
_
Способности решать проблемы Шаблон 4
{formtext: name=first name; cols=8} имеет ограниченный словарный запас, который не позволяет {formmenu: name=gender; его; default=her} от понимания математических словесных задач.
_
Шаблон навыков решения проблем 5
{текст формы: имя=имя; cols=8} точно решает текстовые задачи, когда {formmenu: name=gender; он; default=she} получает помощь от учителя.
_
Способности решать проблемы Шаблон 6
{formtext: name=first name; cols=8} испытывает трудности с {formtext: name=вставить математический навык; cols=13}, даже при наличии приспособлений.
_
Способности решать проблемы Шаблон 7
{formtext: name=first name; cols=8} не всегда оправдывает ответы на математические задачи доказательствами.
_
Способности решать проблемы Шаблон 8
{formtext: name=first name; cols=8} общается и последовательно объясняет {formmenu: name=gender; его; default=her} мыслительные процессы со словами, числами и картинками.
_
Способность решать проблемы Шаблон 9
{formtext: name=first name; cols=8} обычно не просит помощи при решении математической задачи.
_
Шаблон навыков решения проблем 10
{текст формы: имя=имя; cols=8} последовательно применяет надежные стратегии решения проблем при работе над текстовыми задачами.
_
Способности решать проблемы Шаблон 11
{formtext: name=first name; cols=8} с трудом выполняет инструкции по решению задач на мышление.
_
Способности решать проблемы Шаблон 12
{formtext: name=first name; cols=8} последовательно следует инструкциям для решения задач на мышление.
_
Способность решать проблемы Шаблон 13
{formtext: name=first name; cols=8} имеет выдающуюся математическую основу.
_
Способности решать проблемы Шаблон 14
{formtext: name=first name; cols=8} успевает ниже среднего по {formtext: name=insert математический навык; столбцы=13}.
_
Способности решать проблемы Шаблон 15
{formtext: name=first name; cols=8} неизменно обеспечивает отличную работу при решении текстовых задач.
_
Способности решать проблемы Шаблон 16
{formtext: name=first name; cols=8} обладает отличными коммуникативными навыками и всегда обосновывает ответы на текстовые задачи четкими доказательствами.
_
Способности решать проблемы Шаблон 17
{formtext: name=first name; cols=8} точно решает текстовые задачи со здравым стратегическим мышлением и практически не требует помощи учителя.
_
Шаблон навыков решения проблем 18
{текст формы: имя=имя; cols=8} может понимать концепции словесных задач, но часто торопится с {formmenu: name=gender; его; default=her} работает, что вызывает ошибки.
_
Способность решать проблемы Шаблон 19
{formtext: name=first name; cols=8} понимает, но иногда игнорирует важную информацию в текстовых задачах.
_
Способности решать проблемы Шаблон 20
{formtext: name=first name; cols=8} всегда может переварить информацию в словесной задаче, выразить ее и кратко передать коллегам.
_
Понимание математических понятий Шаблон 1
{formtext: name=first name; cols=8} имеет {formmenu: name=rating; сильный; по умолчанию=средний; слабое} понимание основного сложения.
_
Понимание математических понятий Шаблон 2
{formtext: name=first name; cols=8} явно проявляет большие усилия на уроке математики, но по-прежнему борется с {formtext: name=insert математическое умение; столбцы=13}.
_
Понимание математических понятий Шаблон 3
{текст формы: имя=имя; cols=8} испытывает трудности с запоминанием расписания.
_
Понимание математических понятий Шаблон 4
{formtext: name=first name; cols=8} демонстрирует {formmenu: name=rating; сильный; по умолчанию=средний; слабое} понимание {formtext: name=вставить математический навык; столбцы=13}.
_
Понимание математических понятий Шаблон 5
Даже если учитель объясняет {formtext: name=insert math concept; cols=16} несколько раз, {formtext: name=first name; cols=8} все еще пытается сохранить его.
_
Понимание математических понятий Шаблон 6
{formtext: name=first name; cols=8} быстро и точно отвечает на математические факты.
_
Понимание математических понятий Шаблон 7
{formtext: name=first name; cols=8} выполняет выдающуюся работу в {formtext: name=insert math concept; столбцы=16}.
_
Понимание математических понятий Шаблон 8
{formtext: name=first name; cols=8} в изучении {formtext: name=insert математической концепции; cols=16} несовместимо.
_
Понимание математических понятий Шаблон 9
{formtext: name=first name; cols=8} работает ниже среднего, не из-за неспособности, а из-за отвлечения внимания или {formtext: name=insert поведенческой проблемы; столбцы=21}.
_
Понимание математических понятий Шаблон 10
{formtext: name=first name; cols=8} основан на {formtext: name=insert математической концепции; столбцы=16}.
_
Понимание математических понятий Шаблон 11
{текст формы: имя=имя; cols=8} постоянно может применять математические навыки и {formmenu: name=gender; его; default=ее} понимание {formtext: name=вставить несколько математических понятий; cols=24} ко всем учебным занятиям.
_
Понимание математических понятий Шаблон 12
{formtext: name=first name; cols=8} имеет проблемы с {formtext: name=вставить математическое понятие; cols=16} из-за низкой мотивации и усилий.
_
Понимание математических понятий Шаблон 13
{текст формы: имя=имя; cols=8} делает сознательное усилие, чтобы понять {formtext: name=insert математическое понятие; cols=16}, но с трудом применяется при написании тестов.
_
Понимание математических понятий Шаблон 14
{formtext: name=first name; cols=8} чрезвычайно способны сочетать свое понимание {formtext: name=insert математической концепции; cols=16} и эффективно применять их к сложным задачам.
_
Понимание математических понятий Шаблон 15
{текст формы: имя=имя; cols=8} продемонстрировали прогресс и рост в понимании и применении {formtext: name=insert математической концепции; столбцы=16}.
_
Понимание математических понятий Шаблон 16
{formtext: name=first name; cols=8} испытывает трудности с запоминанием некоторых математических понятий, но проявляет большую инициативу в их решении, делая заметки и практикуясь после уроков.
_
Понимание математических понятий Шаблон 17
{текст формы: имя=имя; cols=8} проявляет инициативу в изучении математических понятий, посещая занятия после школы и обращаясь за помощью в классе, когда это необходимо.
_
Понимание математических понятий Шаблон 18
{formtext: name=first name; cols=8} демонстрирует непоследовательную работу в {formtext: name=insert математическое понятие или навык; столбцы=22}.
_
Понимание математических понятий Шаблон 19
{formtext: name=first name; cols=8} показывает безупречное мастерство в сохранении математических процессов и концепций.
_
Понимание математических понятий Шаблон 20
{formtext: name=first name; cols=8} имеет проблемы с сортировкой и классификацией {formmenu: name=concept; по умолчанию=фигуры; цвета; графики; простые числа}.
_
Арифметический шаблон 1
{formtext: name=first name; cols=8} умеет складывать и вычитать и может применять обе концепции к задачам со словами.
_
Арифметический шаблон 2
{formtext: name=first name; cols=8} требует дополнительной практики, чтобы преуспеть в арифметике.
_
Арифметический шаблон 3
{formtext: имя=имя; cols=8} имеет четкое представление о том, как работает умножение, но ему было бы полезно больше практиковаться в запоминании расписания.
_
Арифметический шаблон 4
{formtext: name=first name; cols=8} хорошо разбирается в алгебре и может решать задачи с несколькими переменными.
_
Арифметический шаблон 5
{formtext: name=first name; cols=8} имеет проблемы с пониманием дробей и преобразованием их в десятичные.
_
Арифметический шаблон 6
{formtext: name=first name; cols=8} демонстрирует последовательное и правильное понимание арифметики, но требует много времени для решения задач.
_
Арифметический шаблон 7
{formtext: name=first name; cols=8} демонстрирует уверенность при решении задач на сложение, вычитание, умножение и деление.
_
Арифметический шаблон 8
{formtext: name=first name; cols=8} может точно и уверенно решать вопросы по алгебре.
_
Арифметический шаблон 9
{formtext: name=first name; cols=8} внимательно относится к деталям и эффективно использует их для интерпретации и ответов на вопросы по алгебре.
_
Арифметический шаблон 10
{formtext: name=first name; cols=8} понимает основные арифметические функции, но не может их эффективно применять.
_
Арифметический шаблон 11
{formtext: name=first name; cols=8} продемонстрировали значительное улучшение запоминания расписаний.
_
Арифметический шаблон 12
{formtext: name=first name; cols=8} использует числовые знаки, такие как плюс, минус и равенство, для создания правильных математических предложений.
_
Арифметический шаблон 13
{formtext: name=first name; cols=8} уверен, когда {formmenu: name=operators; добавление; по умолчанию = вычитание; умножение; деление} чисел.
_
Арифметический шаблон 14
{formtext: name=first name; cols=8} иногда проявляет нетерпение при решении длинных вопросов по алгебре, что приводит к ошибкам.
_
Арифметический шаблон 15
{formtext: name=first name; cols=8} хорошо разбирается в умножении и делении, но с трудом применяет эти знания при решении текстовых задач.
_
Арифметический шаблон 16
{formtext: name=first name; cols=8} не прикладывает достаточно усилий для понимания основных арифметических операций.
_
Арифметический шаблон 17
{formtext: name=first name; cols=8} плохо учится на уроках математики и не пытается понять арифметику.
_
Арифметический шаблон 18
{formtext: name=first name; cols=8} прилагает сознательные усилия для совершенствования {formmenu: name=gender; его; default=her} применение математических процессов для тестовых задач.
_
Арифметический шаблон 19
{formtext: name=first name; cols=8} не соответствует {formmenu: name=gender; его; default=her} полный потенциал в арифметике.
_
Арифметический шаблон 20
{formtext: name=first name; cols=8} с трудом решает арифметические задачи, но было бы полезно чаще обращаться за помощью.
_
Геометрический шаблон 1
{formtext: name=first name; cols=8} имеет четкое представление об основных углах и треугольниках.
_
Геометрический шаблон 2
{formtext: name=first name; cols=8} изо всех сил пытается понять основные понятия площади и периметра.
_
Геометрический шаблон 3
{formtext: name=first name; cols=8} демонстрирует четкое понимание объема и массы.
_
Геометрический шаблон 4
{текст формы: имя=имя; cols=8} понимает понятие объема и массы, но не может применить это понимание к математическим задачам.
_
Геометрический шаблон 5
{formtext: name=first name; cols=8} демонстрирует четкое понимание {formtext: name=вставить навык геометрии; cols=16}, но с трудом применяет это понимание к текстовым задачам.
_
Геометрический шаблон 6
{formtext: name=first name; cols=8} знает основные формы и может четко идентифицировать и описать их.
_
Геометрический шаблон 7
{formtext: name=first name; cols=8} знает разницу между {formtext: name=insert двумя похожими понятиями геометрической математики; столбцы=34}.
_
Геометрический шаблон 8
{formtext: name=first name; cols=8} имеет четкое представление об основах {formtext: name=геометрической концепции; cols=15}, но не может развить эти знания, чтобы понять более сложные темы.
_
Геометрический шаблон 9
{текст формы: имя=имя; cols=8} быстро и эффективно определяет и различает прямые, тупые и острые углы.
_
Геометрический шаблон 10
{formtext: name=first name; cols=8} имеет проблемы с пониманием многих геометрических понятий, и ему будет полезна дополнительная поддержка, если {formmenu: name=gender; он; default=она} обратилась за помощью.
_
Геометрический шаблон 11
{formtext: name=first name; cols=8} преуспел и показал значительный прогресс в {formmenu: name=gender; его; default=her} понимание точек и линий.
_
Геометрический шаблон 12
{formtext: name=first name; cols=8} демонстрирует устойчивый прогресс в применении геометрических понятий.
_
Геометрический шаблон 13
{formtext: name=first name; cols=8} всегда делает все возможное, чтобы обратиться за помощью, когда борется с математическим вопросом по геометрии.
_
Геометрический шаблон 14
{formtext: name=first name; cols=8} хорошо разбирается во всех геометрических понятиях и отлично справляется со своими задачами.
_
Геометрический шаблон 15
{formtext: name=first name; cols=8} прекрасно понимает радиус, диаметр и длину окружности.
_
Геометрический шаблон 16
Пока {formtext: name=first name; cols=8} имеет среднее представление об окружности и площади, {formmenu: name=gender; он; default=she} иногда возникают проблемы с их связью.
_
Геометрический шаблон 17
{formtext: name=first name; cols=8} борется с дополнительными, вертикальными и дополнительными углами.
_
Геометрический шаблон 18
{formtext: name=first name; cols=8} понимает характеристики различных видов треугольников, но с трудом создает их с помощью транспортира.
_
Геометрический шаблон 19
{formtext: name=first name; cols=8} отлично разбирается во всех геометрических понятиях и оказывает большую поддержку некоторым из его одноклассников, у которых возникают проблемы с некоторыми понятиями.
_
Геометрический шаблон 20
{текст формы: имя=имя; cols=8} плохо разбирается во всех геометрических концепциях и нуждается в большей поддержке в решении простых геометрических задач.
_
Шаблон графиков 1
{formtext: name=first name; cols=8} отлично читает и интерпретирует диаграммы и графики, но испытывает трудности с их созданием.
_
Шаблон графиков 2
{formtext: name=first name; cols=8} превосходно разбирается в нескольких графических методах.
_
Шаблон графиков 3
{formtext: name=first name; cols=8} хорошо разбирается в интерпретации и создании линейных, круговых и гистограмм.
_
Шаблон графиков 4
{formtext: name=first name; cols=8} может четко отображать сложные данные в различных графиках, включая линейные графики и круговые диаграммы.
_
Шаблон графиков 5
С помощью {formtext: name=first name; cols=8} может отображать сложные данные во многих типах графиков.
_
Шаблон графиков 6
{formtext: name=first name; cols=8} понимает, как работают графики, но не может интерпретировать представленные в них данные.
_
Шаблон графиков 7
{formtext: name=first name; cols=8} имеет проблемы с использованием линейки и созданием аккуратных графиков из-за небрежности.
_
Шаблон графиков 8
{formtext: name=first name; cols=8} имеет четкое представление о линейных графиках, круговых диаграммах и столбчатых диаграммах, но затрудняется решить, какой график лучше всего подходит для каждого конкретного сценария.
_
Шаблон графиков 9
{formtext: name=first name; cols=8} имеет четкое представление о том, какой граф лучше всего подходит для различных задач.
_
Шаблон графиков 10
{formtext: name=first name; cols=8} может создавать графики, используя как простые, так и сложные данные.
_
Шаблон графиков 11
С помощью {formtext: name=first name; cols=8} может создавать графики, используя простые и сложные данные.
_
Шаблон графиков 12
{formtext: name=first name; cols=8} отлично подходит для создания графиков, но с трудом объясняет корреляции.
_
Шаблон графиков 13
{formtext: name=first name; cols=8} показал значительное улучшение в {formmenu: name=gender; его; default=her} способность интерпретировать данные в виде графиков.
_
Шаблон графиков 14
{formtext: name=first name; cols=8} может создавать точные и аккуратные графики практически без помощи.
_
Шаблон графиков 15
{formtext: name=first name; cols=8} отлично разбирается в круговых диаграммах и гистограммах, но {formmenu: name=gender; он; default=she} изо всех сил пытается интерпретировать линейные графики.
_
Шаблон графиков 16
{formtext: name=first name; cols=8} может создавать таблицы, но иногда неправильно маркирует данные, спеша {formmenu: name=gender; его; default=ее} работа.
_
Шаблон графиков 17
{formtext: name=first name; cols=8} требует больше усилий для эффективного создания линейных графиков.
_
Шаблон графиков 18
{formtext: name=first name; cols=8} создает удовлетворительные линейные графики, гистограммы и круговые диаграммы, но потенциально может создавать превосходные.
_
Шаблон графиков 19
{formtext: name=first name; cols=8} уверенно и точно интерпретирует и создает все графики.
_
Шаблон графиков 20
{formtext: name=first name; cols=8} неуверенно работает с графиками.
_
Шаблон измерения 1
{текст формы: имя=имя; cols=8} понимает основные единицы измерения длины, ширины и высоты, такие как дюймы, футы, сантиметры и метры.
_
Шаблон измерения 2
{formtext: имя=имя; cols=8} понимает и эффективно использует единицы измерения температуры, включая градусы Фаренгейта и Цельсия.
_
Шаблон измерения 3
{formtext: name=first name; cols=8} хорошо разбирается в инструментах измерения времени, таких как часы, минуты и секунды, и может эффективно интерпретировать часы.
_
Шаблон измерения 4
{текст формы: имя=имя; cols=8} точно использует линейку и может измерять различные расстояния в метрах, сантиметрах и миллиметрах.
_
Шаблон измерения 5
{formtext: имя=имя; cols=8} знает о различных единицах измерения и способах их преобразования, т. е. о переводе килограммов в граммы.
_
Шаблон измерения 6
{formtext: имя=имя; cols=8} имеет четкое представление об основных единицах измерения объема, массы и веса, но с трудом переводит их друг в друга для текстовых задач.
_
Шаблон измерения 7
{текст формы: имя=имя; cols=8} может использовать некоторые инструменты измерения, но не может использовать транспортир при решении задач.
_
Шаблон измерения 8
{formtext: name=first name; cols=8} может эффективно использовать все инструменты измерения, включая линейки, транспортиры и весы.
_
Шаблон измерения 9
{formtext: имя=имя; cols=8} понимает, как считать основные денежные единицы, включая пенни, десять центов, пятаки, четвертаки и доллары.
_
Шаблон измерения 10
{formtext: имя=имя; cols=8} понимает основные единицы валюты, но изо всех сил пытается их конвертировать, то есть конвертировать доллары в пенни.
_
Шаблон измерения 11
{formtext: name=first name; cols=8} хорошо разбирается в денежных единицах и может легко их конвертировать.
_
Шаблон измерения 12
{formtext: имя=имя; cols=8} понимает, как работают единицы валюты, и с помощью может точно произвести сдачу.
_
Шаблон измерения 13
{formtext: имя=имя; cols=8} изо всех сил пытается преобразовать измерения в метрические измерения, включая {formmenu: name=measurements; миллиметры; по умолчанию=сантиметры; стоградусная; несколько=да}.
_
Шаблон измерения 14
{formtext: имя=имя; cols=8} отлично разбирается в единицах измерения и может применять их для решения текстовых задач с ясностью и точностью.
_
Шаблон измерения 15
{текст формы: имя=имя; cols=8} понимает единицы измерения, но изо всех сил пытается применить эти знания к текстовым задачам.
_
Шаблон измерения 16
{formtext: name=first name; cols=8} с легкостью решает сложные словесные задачи об измерениях и подкрепляет свои ответы вескими доказательствами.
_
Шаблон измерения 17
{formtext: name=first name; cols=8} с трудом понимает различные единицы измерения расстояния, такие как футы, ярды, мили, километры и т. д.
_
Шаблон измерения 18
{formtext: имя=имя; cols=8} прекрасно разбирается в единицах измерения и способах их преобразования.
_
Шаблон измерения 19
{formtext: имя=имя; cols=8} показывает результаты ниже уровня оценки в тестах с проблемами измерения.
_
Шаблон измерения 20
{formtext: имя=имя; cols=8} показал значительное улучшение в {formmenu: name=gender; его; default=her} применение знаний об основных единицах измерения объема, массы и веса.
_
Шаблон начальной школы 1
{formtext: name=first name; cols=8} позитивно и с энтузиазмом относится к решению математических задач.
_
Шаблон начальной школы 2
{formtext: name=first name; cols=8} можно сосредоточиться на {formmenu: name=gender; его; default=her} работают в течение длительного периода времени, хотя {formmenu: name=gender2; он; default=she} требует для этого несколько напоминаний.
_
Шаблон начальной школы 3
{текст формы: имя=имя; cols=8} часто «забывает» заполнить {formmenu: name=gender; его; default=ее} домашнее задание.
_
Шаблон начальной школы 4
{formtext: name=first name; cols=8} всегда руки в {formmenu: name=gender; его; default=her} домашнее задание вовремя.
_
Шаблон начальной школы 5
{formtext: name=first name; cols=8} иногда прерывает {formmenu: name=gender; его; default=her} одноклассников, когда говорит, но в целом активно участвует в математических дискуссиях.
_
Шаблон начальной школы 6
{formtext: name=first name; cols=8} нуждается в постоянных напоминаниях, чтобы уделять внимание урокам математики.
_
Шаблон начальной школы 7
{formtext: name=first name; cols=8} имеет сильное чувство ответственности и дисциплины.
_
Шаблон начальной школы 8
{formtext: name=first name; cols=8} иногда требуется дополнительное время для выполнения заданий, но {formmenu: name=gender; он; default=she} всегда отлично работает в таких случаях.
_
Шаблон начальной школы 9
{formtext: name=first name; cols=8} иногда мешает и отвлекает других учеников в классе.
_
Шаблон начальной школы 10
{formtext: name=first name; cols=8} демонстрирует высокий уровень уверенности при решении математических задач.
_
Шаблон начальной школы 11
{formtext: name=first name; cols=8} завершает все {formmenu: name=gender; его; default=her} домашнее задание, но обычно сдает его с опозданием.
_
Шаблон начальной школы 12
{formtext: name=first name; cols=8} не всегда проверяет {formmenu: name=gender; его; default=her} работают, что приводит к глупым ошибкам.
_
Шаблон начальной школы 13
{formtext: name=first name; cols=8} понимает математические понятия лучше, чем большинство {formmenu: name=gender; его; по умолчанию=ее} ровесники, но {formmenu: name=gender; его; default=her} работа очень грязная и неопрятная.
_
Шаблон начальной школы 14
{formtext: name=first name; cols=8} побуждает других учеников говорить и иным образом прерывает урок математики.
_
Шаблон начальной школы 15
{formtext: name=first name; cols=8} во время математических дискуссий выглядит застенчивым.
_
Шаблон начальной школы 16
{formtext: name=first name; cols=8} иногда имеет проблемы с математикой, но ему было бы полезно научиться обращаться за помощью.
_
Шаблон начальной школы 17
{formtext: name=first name; cols=8} может точно, но медленно решать различные математические задачи.
_
Шаблон начальной школы 18
{formtext: name=first name; cols=8} отсутствует много дней подряд, и ему могут быть полезны дополнительные занятия с репетиторами.
_
Шаблон начальной школы 19
{formtext: name=first name; cols=8} не хватает самодисциплины и иногда следует за другими одноклассниками, которые замышляют что-то нехорошее.
_
Шаблон начальной школы 20
{formtext: name=first name; cols=8} нужно больше возможностей практиковать свои математические навыки дома.
_
Шаблон средней школы 1
{formtext: name=first name; cols=8} демонстрирует энтузиазм и интерес к математике.
_
Шаблон средней школы 2
{formtext: name=first name; cols=8} продемонстрировал значительное улучшение в освоении {formtext: name=insert математической концепции или навыка; столбцы=16}.
_
Шаблон средней школы 3
{formmenu: name=gender; он; default=she} теперь готова к изучению дифференциального исчисления.
_
Шаблон средней школы 4
{formtext: name=first name; cols=8} изо всех сил пытается найти мотивацию для интереса к математике.
_
Шаблон средней школы 5
{formtext: name=first name; cols=8} требует больше усилий в {formtext: name=вставьте математические навыки; столбцы=13}.
_
Шаблон средней школы 6
{formtext: name=first name; cols=8} могут быть полезны дополнительные занятия по математике.
_
Шаблон средней школы 7
{formtext: name=first name; cols=8} прилагает сознательные усилия для точного решения математических задач.
_
Шаблон средней школы 8
{formtext: name=first name; cols=8} проявляет интерес к математике, но не уверен в {formmenu: name=gender; его; default=ее} способность.
_
Шаблон средней школы 9
{formtext: name=first name; cols=8} разбирается в математике, но его часто отвлекают {formtext: name=insert отвлекающие факторы; столбцы=14}.
_
Шаблон средней школы 10
{formtext: name=first name; cols=8} понимает большинство математических понятий, но часто делает ошибки по невнимательности.
_
Шаблон средней школы 11
{formtext: name=first name; cols=8} продемонстрировал более медленный, чем ожидалось, прогресс в изучении {formtext: name=insert math concept; столбцы=16}.
_
Шаблон средней школы 12
{formtext: name=first name; cols=8} уверен в себе и имеет достаточно полномочий, чтобы обратиться за помощью в случае необходимости.
_
Шаблон средней школы 13
{formtext: name=first name; cols=8} быстро и с энтузиазмом усваивает математические понятия.
_
Шаблон средней школы 14
{formtext: name=first name; cols=8} — прекрасный математик.
_
Шаблон средней школы 15
{текст формы: имя=имя; cols=8} обладает очень логичным мышлением, которое помогает ему преуспеть в математике.
_
Шаблон средней школы 16
{formtext: name=first name; cols=8} не может слушать указания из {formmenu: name=gender; его; по умолчанию=ее} учитель.
_
Шаблон средней школы 17
{formtext: name=first name; cols=8} бросается решать математические задачи и не обращает внимания на детали.
_
Шаблон средней школы 18
{текст формы: имя=имя; cols=8} легко перегружается, когда {formmenu: name=gender; он; default=она} не может решить математическую задачу.
_
Шаблон средней школы 19
{formtext: name=first name; cols=8} отрицательно относится к математике и часто не решается решить математические задачи.
_
Шаблон средней школы 20
{formtext: name=first name; cols=8} задает много вопросов и прилагает сознательные усилия, чтобы попросить о помощи, когда это необходимо.

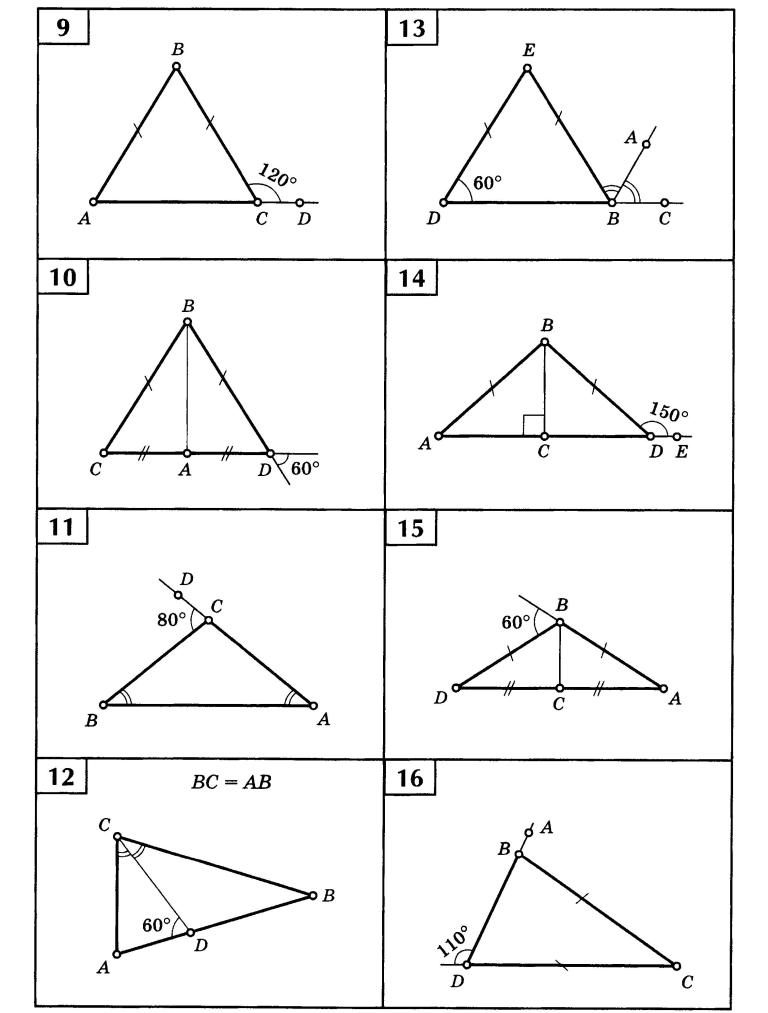
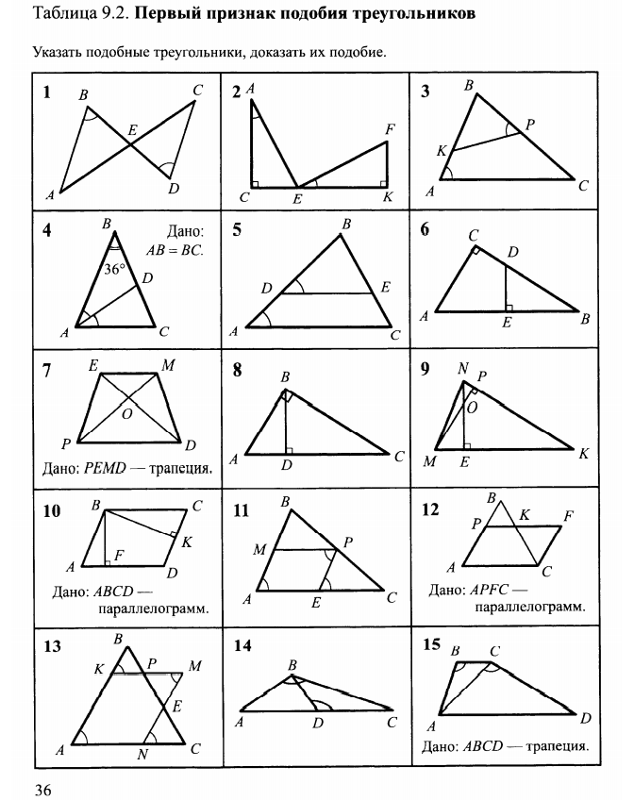




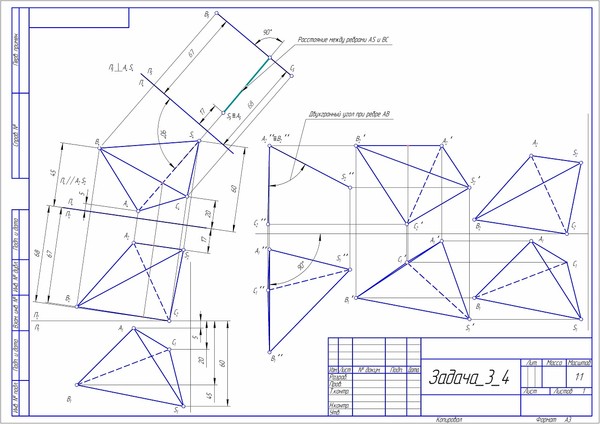

 и отриц.числа).
и отриц.числа). Докажите, что : а) ВС = ED; б) КВ = КЕ, где К – точка пересечения отрезков ВC и ЕD.
Докажите, что : а) ВС = ED; б) КВ = КЕ, где К – точка пересечения отрезков ВC и ЕD. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно так, что ВМ = ВN. Докажите, что ΔBDM = ΔBDN.
На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно так, что ВМ = ВN. Докажите, что ΔBDM = ΔBDN.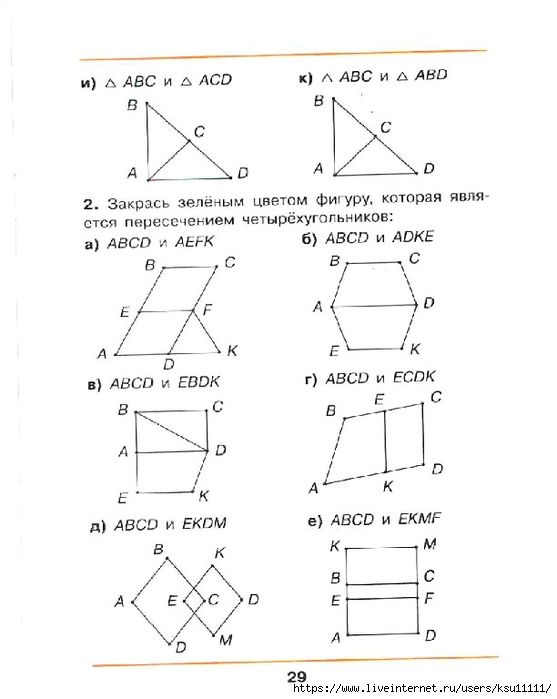 Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школах
Автор: Дудницын Ю.П., Кронгауз В.Л. 1996 Содержание заданий на карточках соответствует программе и учебникам по геометрии для 11 класса полной средней общеобразовательной школы. Поэтому новое пособие можно использовать в школах ..
..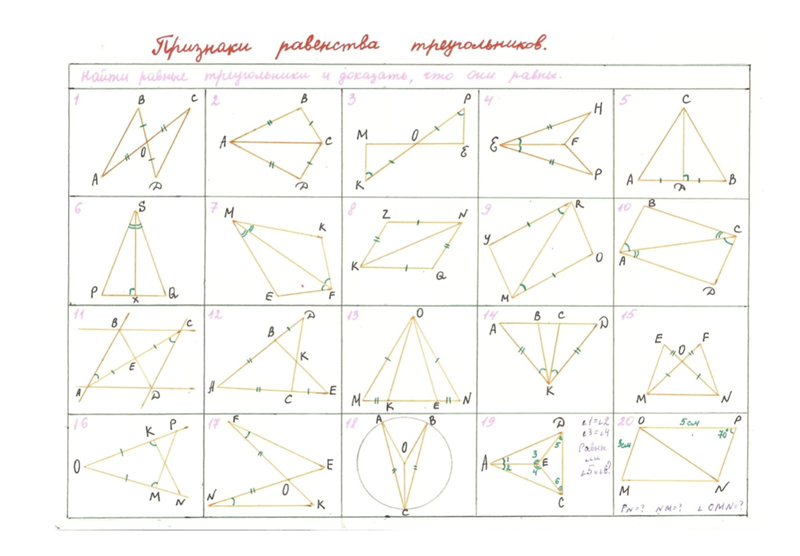 Напоминаем, что выложенные здесь материалы, предназначены только..
Напоминаем, что выложенные здесь материалы, предназначены только.. Пособие содержит 19 тренировочных работ в шести…
Пособие содержит 19 тренировочных работ в шести… Л. Название: Контрольные работы по геометрии. 10 класс Формат: PDF Размер: 1,34 Мб Язык: Русский.
Л. Название: Контрольные работы по геометрии. 10 класс Формат: PDF Размер: 1,34 Мб Язык: Русский.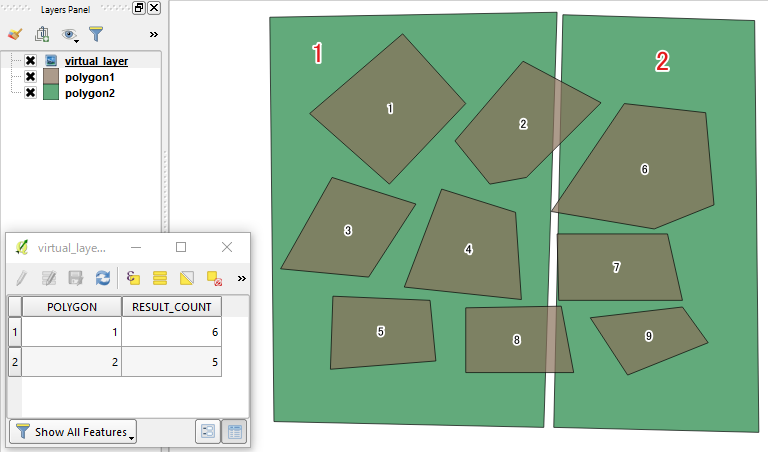 ru
ru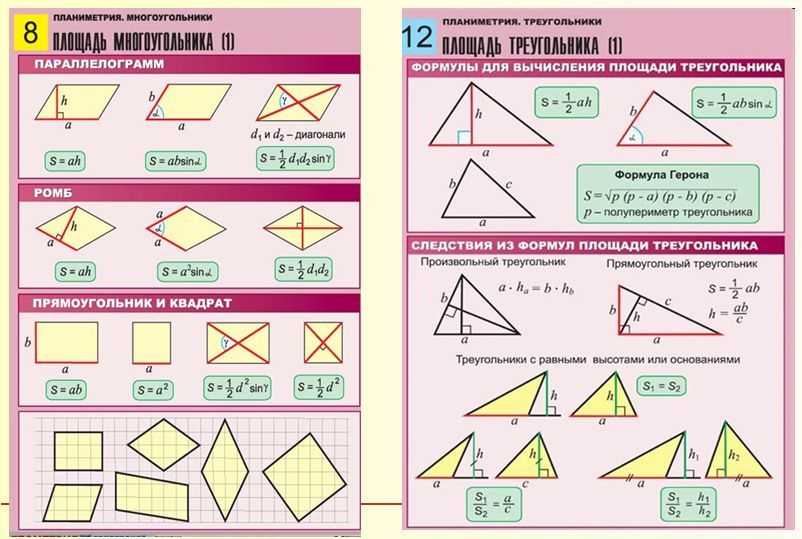 класс. Рекомендовано. Российской Академией Образования. Издание второе, стереотипное. Издательство «ЭКЗАМЕН» МОСКВА • 2009. УДК 372.8:514(075.3) ББК 74.262.22 я72. учеб. для об- щеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадом- M.: Просвещение» приведено на обложке данного изда…
класс. Рекомендовано. Российской Академией Образования. Издание второе, стереотипное. Издательство «ЭКЗАМЕН» МОСКВА • 2009. УДК 372.8:514(075.3) ББК 74.262.22 я72. учеб. для об- щеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадом- M.: Просвещение» приведено на обложке данного изда…