Нелинейное взвешивание вероятностей: Поведенческая и экспериментальная экономика

Нормальное распределение (распределение Гаусса) с примерами решения…

Привет, сегодня поговорим про нормальное распределение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое нормальное распределение, распределение гаусса, примеры решения задач на распределение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

нормальное распределение , также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей сфункцией Гаусса:

где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений.

Многомерный случай описан в статье «Многомерное нормальное распределение».

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.

Нормальное распределение

Плотность вероятности Зеленая линия соответствует стандартному нормальному распределению
Функция распределения Цвета на этом графике соответствуют графику наверху
Обозначение
Параметры	μ — коэффициент сдвига(вещественное число) σ > 0 — коэффициент масштаба(вещественный, строго положительный)
Носитель
Плотность вероятности
Функция распределения
Математическое ожидание
Медиана
Мода
Дисперсия
Коэффициент асимметрии
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов
Характеристическая функция

Значение стандартного распределения

Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Свойства стандартного распределения

Моменты

Моментами и абсолютными моментами случайной величины X называются математические ожидания X ^p и , соответственно. Если математическое ожидание случайной величины μ = 0, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целыхp.

Если X имеет нормальное распределение, то для нее существуют (конечные) моменты при всех p с действительной частью больше −1. Для неотрицательных целых p, центральные моменты таковы:

Здесь n — натуральное число, а запись (p − 1)!! означает двойной факториал числа p − 1, то есть (посколькуp − 1 в данном случае нечетно) произведение всех нечетных чисел от 1 до p − 1.

Центральные абсолютные моменты для неотрицательных целых p таковы:

Последняя формула справедлива также для произвольных p > −1.

Бесконечная делимость

Нормальное распределение является бесконечно делимым.

Если случайные величины и независимы и имеют нормальное распределение с математическими ожиданиями и и дисперсиями и соответственно, то также имеет нормальное распределение с математическим ожиданием и дисперсией Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Максимальная энтропия

Нормальное распределение является непрерывным распределением с максимальной энтропией при заданном математическом ожидании и дисперсии.

Моделирование нормальных псевдослучайных величин

Простейшие приближенные методы моделирования основываются на центральной предельной теореме . Об этом говорит сайт https://intellect.icu . Именно, если сложить несколько независимых одинаково распределенных величин с конечной дисперсией, то сумма будет распределена приблизительно нормально. Например, если сложить 100 независимых стандартноравномерно распределенных случайных величин, то распределение суммы будет приближенно стандартным нормальным.

Для программного генерирования нормально распределенных псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределенную величину на базе одной равномерно распределенной.

Нормальное распределение в природе и приложениях

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе.
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют не нормальные распределения).
• некоторые характеристики живых организмов в популяции.

Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например, биномиальное и пуассоновское. Этим распределением моделируются многие не детерминированные физические процессы.

Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование свойств личности человека в психологии и психиатрии.

Из пункта ведется стрельба из орудия вдоль прямой . Предполагается, что дальность полета распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадет с перелетом от 5 до 70м.

Классика жанра.

Решение: в задаче рассматривается нормально распределенная случайная величина – дальность полета снаряда, и по условию .

Так как речь идет о перелете за цель, то . Вычислим вероятность – того, что снаряд упадет в пределах этой дистанции.

Если в нашем распоряжении есть таблица значений функции , то используем формулу :

Для самопроверки можно задействовать экселевскую функцию =НОРМСТРАСП(z) или напрямую «забить» и затем в Пункт 9 расчетного макета

.

Если же в нашем распоряжении есть таблица значений функции Лапласа , то решаем через нее:

Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.

Напоминаю, что , и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.

Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:

– с перелетом от 5 до 70 м упадет примерно 15,87% снарядов

Тренируемся самостоятельно:

Пример 3

Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.

В образце решения и далее я буду использовать функцию Лапласа, как самый распространенный вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.

И уже в этом примере нам встретился особый случай – когда интервал симметричен относительно математического ожидания. В такой ситуации его можно записать в виде и, пользуясь нечетностью функции Лапласа, упростить рабочую формулу:

Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство можно «упаковывать» с помощью модуля:

– вероятность того, что значение случайной величины отклонится от математического ожидания менее чем на .

Хорошо то решение, которое умещается в одну строчку:)
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.

Результат этой задачи получился близким к единице, но хотелось бы еще бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счет? Существует! На поставленный вопрос отвечает так называемое

правило «трех сигм»

Его суть состоит в том, что практически достоверным является тот факт, что нормально распределенная случайная величина примет значение из промежутка .

И в самом деле, вероятность отклонения от матожидания менее чем на составляет:
или 99,73%

В «пересчете на подшипники» – это 9973 штуки с диаметром от 1,38 до 1,62 см и всего лишь 27 «некондиционных» экземпляров.

В практических исследованиях правило «трех сигм» обычно применяют в обратном направлении: если статистически установлено, что почти все значения исследуемой случайной величины

укладываются в интервал длиной 6 стандартных отклонений, то появляются веские основания полагать, что эта величина распределена по нормальному закону. Проверка осуществляется с помощью теории статистических гипотез.

Продолжаем решать суровые советские задачи:

Пример 4

Случайная величина ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.

Решение

очень простое. По условию, и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение и по формуле :

– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.

Ответ:

Прорешанная задача принципиально отличается от вроде бы похожего Примера 3 урока о равномерном распределении. Там была погрешность округления результатов измерений, здесь же речь идет о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине экспериментатора – когда мы, например, «на глазок» снимаем показания со стрелки тех же весов.

Помимо прочих, существуют еще так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно «прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически ведь можно обсчитать. Однако, в любом случае, случайной такая ошибка не будет, и ее матожидание отлично от нуля.

…срочно разрабатываю курс по подготовке продавцов =)

Самостоятельно решаем обратную задачу:

Пример 5

Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно мм.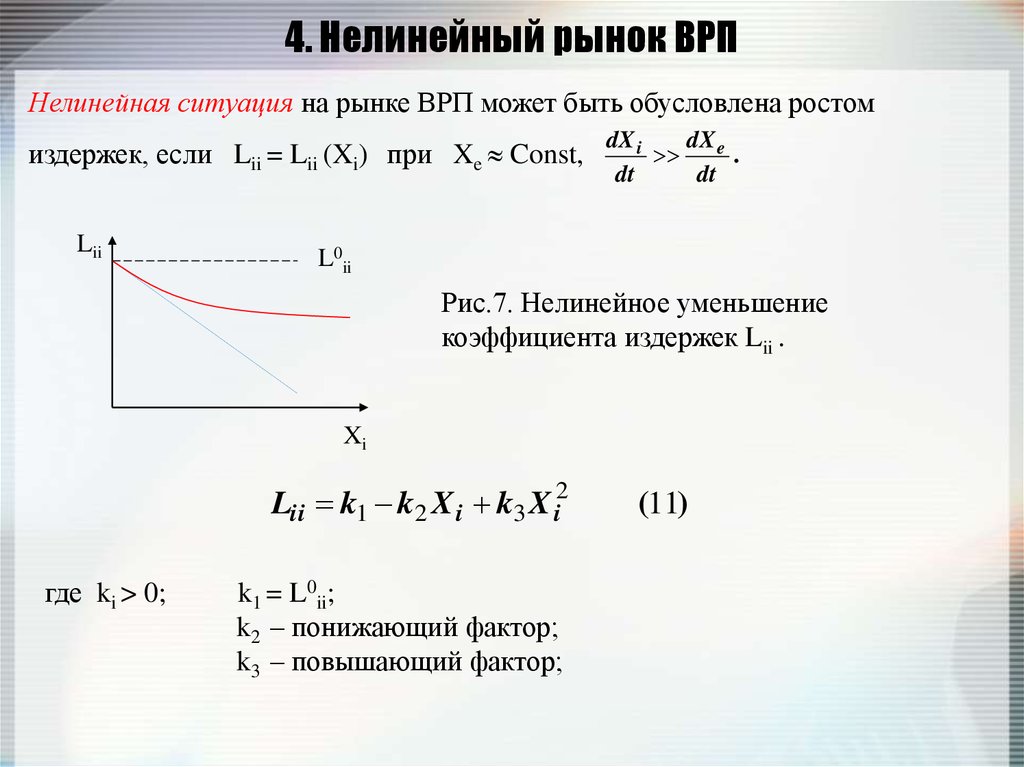 Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью попадет длина диаметра валика.

Пункт 5* расчетного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.

И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:

Пример 6

Нормально распределенная случайная величина задана своими параметрами (математическое ожидание) и (среднее квадратическое отклонение). Требуется:

а) записать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что примет значение из интервала ;
в) найти вероятность того, что отклонится по модулю от не более чем на ;
г) применяя правило «трех сигм», найти значения случайной величины .

Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц 😉

Ну а я разберу пример повышенной сложности:

Пример 7

Плотность распределения вероятностей случайной величины имеет вид . Найти , математическое ожидание , дисперсию , функцию распределения , построить графики плотности и функции распределения, найти .

Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по себе присутствие экспоненты еще ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения еще нужно обосновать:

Так как функция определена при любом действительном значении , и ее можно привести к виду , то случайная величина распределена по нормальному закону.

Приводим. Для этого выделяем полный квадрат и организуем трехэтажную дробь:

Обязательно выполняем проверку, возвращая показатель в исходный вид:

, что мы и хотели увидеть.

Таким образом:
– по правилу действий со степенями «отщипываем» . И здесь можно сразу записать очевидные числовые характеристики:

Теперь найдем значение параметра . Поскольку множитель нормального распределения имеет вид и , то:
, откуда выражаем и подставляем в нашу функцию:
, после чего еще раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид .

Построим график плотности:

и график функции распределения :

Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке функция распределения принимает значение и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти еще хотя бы пару точек. Берем традиционное значение и стандартизируем его по формуле . Далее с помощью таблицы значений функции Лапласа находим: – желтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: и:
.

После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.

Да, и еще нужно вычислить:
– вероятность того, что случайная величина примет значение из данного отрезка.

Ответ:

См. также

• моделирование нормально распределенных случайных величин ,
• Аддитивный белый гауссовский шум
• Логнормальное распределение
• Центральная предельная теорема
• Двумерное нормальное распределение
• Многомерное нормальное распределение
• Статистический критерий
• Частотное распределение

Напиши свое отношение про нормальное распределение. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое нормальное распределение, распределение гаусса, примеры решения задач на распределение и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Бутстреп, малые выборки, применение в анализе данных

Основная идея

Теоретический бэкграунд

Приложения бутстрепа

Аппроксимация стандартной ошибки выборочной оценки

Метод процентилей

Центрированный метод бутстреп-процентилей

Бутстреп-t критерий

Пример реальных данных

Основная идея

Метод бутстрепа предложен Б. Эфроном как развитие метода складного ножа в 1979 году.

Опишем основную идею бутстрепа.

Цель анализа данных – получить максимально точные выборочные оценки и распространить результаты на всю популяцию.

Технический термин, которым обозначаются численные данные, построенные по выборке, это выборочная статистика.

Основные описательные статистики это выборочные среднее, медиана, стандартное отклонение и т.д.

Итоговая статистика, например, выборочное среднее, медиана, корреляция будут меняться от выборки к выборке.

Исследователю требуется знать размер этих отклонений в зависимости от популяции. На основании этого рассчитывается предел погрешности.

Исходная картина всех возможных значений выборочной статистики в форме распределения вероятностей называется выборочным распределением.

Ключевым является размер выборки. Что делать, если размер выборки небольшой? Один из разумных подходов состоит в том, чтобы случайным образом извлекать данные из имеющейся выборки.

Идея бутстрепа в том, чтобы использовать результаты вычислений по выборкам как “фиктивную популяцию” с целью определить выборочное распределение статистики. Фактически, при этом анализируется большое число “фантомных” выборок, называемых бутстреп-выборками.

Обычно случайным образом генерируется несколько тысяч выборок, из этого набора можно найти бутстреп-распределение интересующей нас статистики.

Итак, пусть имеем выборку выберем на первом шаге случайным образом  один из элементов выборки, возвратим этот элемент в выборку, вновь случайным образом выберем элемент и тд.

Повторим описанную процедуру случайного выбора n раз.

В бутстрепе проводится случайный выбор с возвращением, выбранные элементы исходной выборки возвращается в выборку и далее могут быть снова выбраны.

Формально на каждом шаге мы выбираем элемент исходной выборки с вероятностью 1/n.

Всего имеем n элементов исходной выборки, вероятность получить выборку с номерами (N1 … Nn), где Ni меняется от 0 до n описывается полиномиальным распределением.

Таких выборок генерируется несколько тысяч, что вполне достижимо для современных компьютеров.

Для каждой выборки строится оценка интересующей величины, далее оценки усредняются.

Так как выборок много, можно построить эмпирическую функцию распределения оценок, далее рассчитать квантили, вычислить доверительный интервал.

Ясно, что бутстреп метод является модификацией метода Монте-Карло.

Если выборки генерируются без возвращения элементов, то получается известный метод складного ножа.

Вопрос: зачем это делать и когда метод разумно использовать в реальном анализе данных?

В бутстрепе мы не получаем новой информации, но разумно используем имеющиеся данные, исходя из поставленной задачи.

Например, бутстреп можно использовать для малых выборок, для оценок медианы, корреляций, построения доверительных интервалов и в других ситуациях.

В исходной работе Эфрона рассматривались оценки парной корреляции для размера выборки n = 15.

Генерируется B = 1000 бутстреп выборок (bootstrap replication).

На основе полученных коэффициентов ro1 … roВ строится общая оценка коэффициента корреляции и оценка стандартного отклонения.

Стандартная ошибка выборочного коэффициента корреляции, вычисленная с помощью нормального приближения, имеет вид:

где коэффициент корреляции равен 0.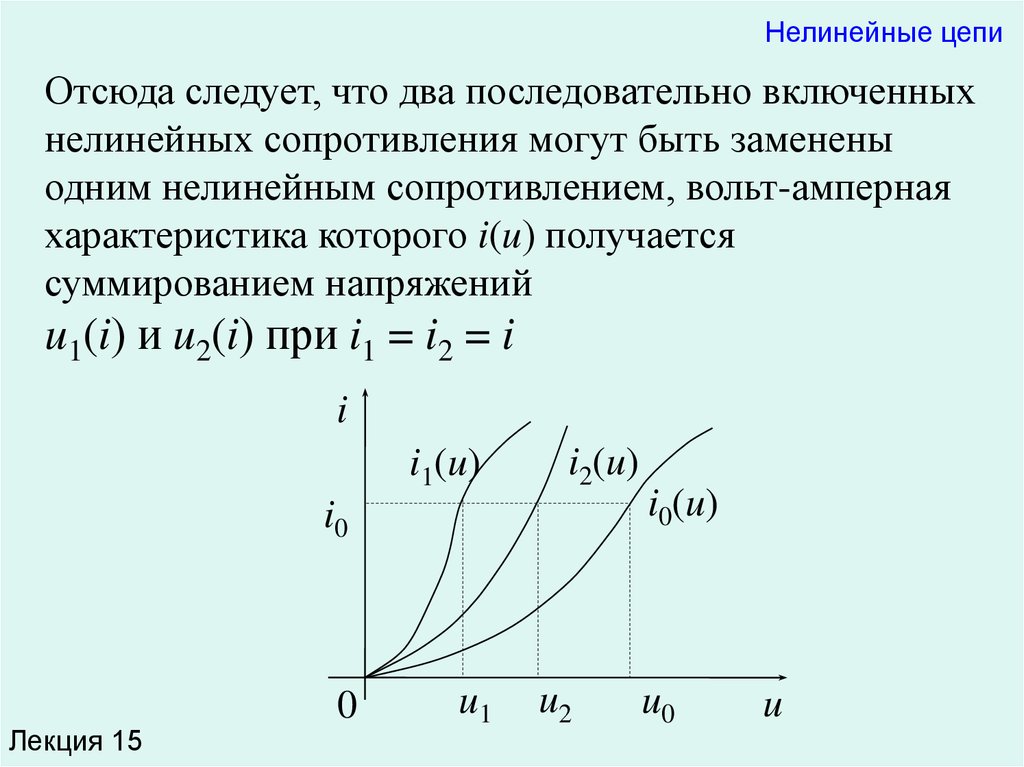 776, размер исходной выборки n = 15.

Бутстреп оценка стандартной ошибки равна 0.127, см. Efron, Gall Gong, 1982.

Теоретический бэкграунд

Пусть — целевой параметр исследования, например, средний доход в выбранном обществе.

По произвольной выборке размера  получаем набор данных  Пусть соответствующая выборочная статистика —  

Для большинства выборочных статистик при большом значении  (>30) выборочное распределение представляется из себя нормальную кривую с центром  и стандартным отклонением , где положительный параметр  зависит от популяции и вида статистики  

Этот классический результат известен как центральная предельная теорема.

Зачастую при оценке требуемого стандартного отклонения по данным возникают серьезные технические трудности.

Например, если  медиана или выборочная корреляция.

Метод бутстрепа позволяет обойти эти трудности.

Идея простая: обозначим через  произвольную величину, представляющую собой такую же статистику, вычисленную по бутстреп-выборке, которая получена из исходной выборки 

Что можно сказать про выборочное распределение , если “исходная” выборка  фиксирована?

В пределе  выборочное распределение  также является колоколообразным с параметрами  и 

Таким образом, бутстреп-распределение  хорошо аппроксимирует выборочное распределение 

Заметим, что когда мы переходим от одной выборки к другой, в выражении  меняется только , так как  вычислена по  

По сути это является бутстреп версией центральной предельной теоремы.

Также было установлено, если предельное выборочное распределение статистической функции  не включает в себя неизвестные по популяции, бутстреп-распределение позволяет получить более хорошее приближение к выборочному распределению, чем центральная предельная теорема.

В частности, когда статистическая функция имеет вид  где через  обозначена истинная, или выборочная оценка стандартной ошибки  при этом предельное выборочное распределение обычно стандартное нормальное.

Этот эффект получил название коррекции второго порядка с помощью бутстреппинга.

Пусть т.е. среднее по популяции, и  т.е. среднее по выборке; — стандартное отклонение в популяции,  — выборочное стандартное отклонение, вычисленное по исходным данным, а  — вычисленное по бутстреп-выборке.

Тогда выборочное распределение величины  где , будет аппроксимироваться бутстреп-распределением , где — среднее по бутстреп-выборке, .

Аналогично, выборочное распределение  будет аппроксимироваться бутстреп-распределением , где .

Первые результаты по коррекции второго порядка были опубликованы Бабу и Сингхом в 1981-83 годах.

Приложения бутстрепа

Аппроксимация стандартной ошибки выборочной оценки

Предположим, что для популяции известен параметр 

Пусть  — оценка  сделанная на основе случайной выборки размера  т.е.  это функция от Так как выборка меняется на множестве всех возможных выборок, то для того, чтобы оценить стандартную ошибку  используется следующий подход:

Вычислим  используя ту же формулу, что использовалась для  но на этот раз на основе  различных бутстреп-выборок размера  каждая. Грубо говоря, можно принять  если только  не сильно велико. В этом случае можно сократить до nlnn. Тогда можно определить исходя, собственно, из сути бутстреп-метода: популяция (выборка) заменяется эмпирической популяцией(выборкой).

Байесовская коррекция с помощью бутстреп метода

Среднее выборочного распределения  часто зависит от  обычно как  для больших То есть,  Байесовская аппроксимация:

 где — это бутстреп-копии . Тогда скорректированное значение будет —

Стоит отметить, что предыдущий метод ресэмплинга(замен выборки), называемый методом складного ножа, является более популярным.

Доверительные интервалы

Доверительные интервалы (ДИ) для заданного параметра это основанные на выборке диапазоны .

Этот диапазон обладает тем свойством, что значение  с очень высокой (заранее установленной) вероятностью принадлежит ему. Это называется уровнем значимости. Конечно, эта вероятность должна относиться к любой выборке из возможных, т.к. каждая выборка привносит свой вклад в определение доверительного интервала. Два наиболее часто используемых уровня значимости это 95% и 99%. Здесь мы ограничимся значением 95%.

Традиционно ДИ зависят от выборочного распределения величины точнее в пределе . Есть два основных вида доверительных интервалов, которые могут быть построены с помощью бутстрепа.

Метод процентилей

Этот метод уже упоминался во введении, он очень популярен благодаря своей простоте и естественности. Предположим, что у нас есть 1000 бутстреп копий обозначим их через  Тогда в доверительный интервал попадут значения из диапазона Возвращаясь к теоретическому обоснованию метода, стоит отметить, что в нем требуется симметрия выборочного распределения  вокруг Причина этого заключается в том, что в методе аппроксимируется выборочное распределение с помощью бутстреп-распределения , хотя по логике получается, что оно должно аппроксимироваться значением  то есть противоположным по знаку.

Центрированный метод бутстреп-процентилей

Предположим, что выборочное распределение  аппроксимируется с помощью бутстреп распределения то есть как изначально и предполагалось в бутстреппинге. Обозначим 100-й процентиль  (в бутстреп-повторениях) через  Тогда предположение, что значение  лежит в диапазоне от  до  будет верным с вероятностью 95%. Это же выражение легко преобразуется в аналогичное для диапазона от  до  Этот интервал и называется центрированным доверительным интервалом по бутстреп-процентилям (при уровне значимости 95%).

Бутстреп-t критерий

Как уже было отмечено, в бутстрепе используется функция вида  где  есть выборочная оценка стандартной ошибки 

Это дает дополнительную точность.

В качестве основного примера возьмем стандартную t-статистику (отсюда название метода): то есть частный случай, когда (популяционное среднее), (выборочное среднее) и — выборочное стандартное отклонение. Бутстреп аналогом такой функции является  где  вычисляется также, как и только по бутстреп-выборке.

Обозначим 100-й бутстреп-процентиль  через и будем полагать, что значение  лежит в интервале  

Используя равенство  можно переписать предыдущее утверждение, т.е. лежит в интервале  

Этот промежуток называется бутстреп t-доверительным интервалом для при уровне 95%.

В литературе он используется для достижения большей точности, чем предыдущий подход.

Пример реальных данных

Возьмем для первого примера данные из работы Холландера и Вольфе 1999 года, стр. 63, которые представляют собой эффект влияния света на скорость вылупления цыплят.

Стандартный бокс-график предполагает отсутствие нормальности по данным популяции. Мы провели бутстреп анализ медианы и среднего.

 

 

Отдельно стоит отметить отсутствие симметрии на бутстреп t-гистограмме, которая отличается от стандартной предельной кривой. 95%-е доверительные интервалы для медианы и среднего (вычисленные с использованием бутстреп метода процентилей), грубо говоря, покрывают диапазон  

Этот диапазон представляет общую разницу (нарастание) в результатах скорости вылупления цыплят в зависимости от подсветки.

В качестве второго примера рассмотрим данные из работы Девора (Devore) 2003 г., стр 553, в которой рассматривалась корреляция между показателем биохимической потребности в кислороде (БПК, BOD) и результатами гидростатического взвешивания (HW)  профессиональных спортсменов — футболистов.

Двумерные данные состоят их  пар и пары можно произвольно выбирать во время бутстреп ресэмплинга. Например, сначала взять  затем  и т.д.

На рисунке график ящики-усы показывает отсутствие нормальности для основных популяций. Гистограммы корреляций, вычисленные на основе бутстреп двумерных данных, являются асимметричными (сдвинутыми влево).

По этой причине, центрированный метод бутстреп процентилей является в данном случае более подходящим.

В результате анализа выяснилось, что измерения скоррелированы  для как минимум 78% популяции.

Данные для примера 1:

-8.5 -4.6 -1.8 -0.8 1.9 3.9 4.7 7.1 7.5 8.5 14.8 16.7 17.6 19.7 20.6 21.9 23.8 24.7 24.7 25.0 40.7 46.9 48.3 52.8 54.0

Данные для примера 2:

BOD

2.5 4.0 4.1 6.2 7.1 7.0 8.3 9.2 9.3 12.0 12.2 12.6 14.2 14.4 15.1 15.2 16.3 17.1 17.9 17.9

HW

 8.0 6.2 9.2 6.4 8.6 12.2 7.2 12.0 14.9 12.1 15.3 14.8 14.3 16.3 17.9 19.5 17.5 14.3 18.3 16.2

В литературе часто предлагаются различные схемы для бутстреппинга, которые могли бы давать достоверные результаты в различных статистических ситуациях.

То, что обсуждалось выше — лишь самые базовые элементы, и других вариантов схем на самом деле очень много. Например, какой метод лучше использовать в случае двухступенчатой выборки или стратифицированной выборки?

Естественную схему в этом случае нетрудно придумать. Бутстрэппинг в случае данных с моделями регрессии вообще привлекает много внимания. Есть два основных метода: в первом ковариации и переменные отклика ресэмплируются вместе (парный бутстреппинг), во втором — бутстреппинг производится по остаткам (остаточный бутстреппинг).

Парный метод остается корректным (в смысле результатов при ) даже если дисперсии ошибок в моделях не равны. Второй метод в этом случае некорректен. Этот недостаток компенсируется тем, что такая схема дает дополнительную точность в оценке стандартной ошибки.

Гораздо сложнее применять бутстреппинг для данных временных рядов.

Анализ временных рядов, однако, является одной из ключевых областей в эконометрике. Здесь можно выделить две основные трудности: во-первых, данные по временным рядам обладают свойством быть последовательно зависимыми. То есть,  зависит от ,  и т.д.

Во-вторых, статистическая популяция со временем меняется, то есть появляется нестационарность.

Для этого разработаны методы, которые переносят зависимость в исходных данных на бутстреп-выборки, в частности, блоковая схема.

Вместо бутстреп выборки сразу строится блок данных, сохраняющий в себе зависимости из исходной выборки.

В области приложения бутстреппинга к разделам эконометрики в настоящий момент проводится довольно много исследований, в целом метод активно развивается.

В начало

Содержание портала

Нелинейное взвешивание вероятностей может отражать искажения внимания при последовательной выборке

. 2021 9 авг.

doi: 10.1037/rev0000304. Онлайн перед печатью.

Вероника Зилкер ¹ , Торстен Пачур ¹

принадлежность

• ¹ Центр адаптивной рациональности.

• PMID: 34370495
• DOI: 10.1037/rev0000304

Вероника Зилкер и др. Психолог преп. 2021 .

. 2021 авг 9.

doi: 10.1037/rev0000304. Онлайн перед печатью.

Авторы

Вероника Зилкер ¹ , Торстен Пачур ¹

принадлежность

• ¹ Центр адаптивной рациональности.

• PMID: 34370495
• DOI: 10.1037/rev0000304

Абстрактный

Нелинейное взвешивание вероятностей позволяет кумулятивной теории перспектив (CPT) учитывать ключевые явления при принятии решений в условиях риска (например, эффект уверенности, четырехчастный образец отношения к риску). Он описывает влияние рискованных исходов на предпочтения с точки зрения зависящего от ранга нелинейного преобразования их объективных вероятностей. Модель рассеяния внимания (aDDM) формализует вывод о том, что предвзятость внимания в отношении варианта может формировать предпочтения в рамках последовательного процесса выборки. Здесь мы связываем эти два влиятельных фреймворка. Мы использовали aDDM для имитации выбора между двумя вариантами, систематически изменяя силу предвзятости внимания к любому варианту. Полученные варианты были смоделированы с помощью CPT. Изменения в предпочтениях из-за смещения внимания в aDDM отражались в высоко систематизированных подписях в параметрах весовой функции CPT (кривизна, возвышение). При повторном анализе большого набора ранее опубликованных данных мы показываем, что искажения внимания также эмпирически связаны с моделями взвешивания вероятностей, как это было предложено моделированием. Наш анализ также выявил ранее упускаемую из виду связь между паттернами взвешивания вероятностей и временем отклика. Эти результаты подчеркивают, что искажения при взвешивании вероятностей могут возникать из-за простых искажений внимания при поиске информации, связанных с конкретными вариантами, и предлагают альтернативу общепринятым интерпретациям параметров весовой функции с точки зрения чувствительности к вероятности и оптимизма. Они также указывают на новые, основанные на внимании объяснения эмпирических явлений, связанных с характерными формами функции взвешивания вероятности CPT (например, эффект уверенности, разрыв между описанием и опытом). Результаты продвигают интеграцию двух известных вычислительных структур для принятия решений. (Запись базы данных PsycInfo (c) 2021 APA, все права защищены).

Похожие статьи

• Теория перспективы отражает выборочное распределение внимания.

  Пачур Т., Шульте-Мекленбек М., Мерфи Р.О., Хертвиг ​​Р. Пачур Т. и др. J Exp Psychol Gen. 2018 Feb; 147 (2): 147–169. дои: 10.1037/xge0000406. J Exp Psychol Gen. 2018. PMID: 29369680 Клиническое испытание.

• Как эти двое могут встретиться: теория перспектив и модели эвристики в рискованном выборе.

  Пачур Т., Сутер Р.С., Хертвиг ​​Р. Пачур Т. и др. Когн Психол. 2017 март;93:44-73. doi: 10.1016/j.cogpsych.2017.01.001. Epub 2017 9 февраля. Когн Психол. 2017. PMID: 28189037

• Учет предвзятости последней выборки при перцептивном принятии решений.

  Чжу Т. Чжу Т. Познание. 2022 июнь;223:105049. doi: 10.1016/j.cognition.2022.105049. Epub 2022 4 фев. Познание. 2022. PMID: 35131576

• Случайное счастье, вызванное музыкой, модулирует взвешивание вероятности во время рискованных лотерейных выборов.

  Шульрайх С., Хойссен Ю.Г., Герхардт Х., Мор П.Н., Бинкофски Ф.С., Кельш С., Хекерен Х.Р. Шульрайх С. и соавт. Фронт Псих. 2014 7 января; 4:981. doi: 10.3389/fpsyg.2013.00981. Электронная коллекция 2014 7 января. Фронт Псих. 2014. PMID: 24432007 Бесплатная статья ЧВК.

• Метааналитический обзор двух способов обучения и разрыв между описанием и опытом.

  Wulff DU, Mergenthaler-Canseco M, Hertwig R. Вульф Д.Ю. и соавт. Психологический бык. 2018 февраль; 144(2):140-176. дои: 10.1037/bul0000115. Epub 2017 14 декабря. Психологический бык. 2018. PMID: 29239630 Обзор.

Посмотреть все похожие статьи

Цитируется

• Дорсолатеральная префронтальная кора играет причинную роль в оценке вероятности во время рискованного выбора.

  Паниди К., Воробьева А.Н., Феурра М., Ключарев В. Паниди К. и др. Научный представитель 2022 г., 27 сентября; 12 (1): 16115. doi: 10.1038/s41598-022-18529-6. Научный представитель 2022. PMID: 36167703 Бесплатная статья ЧВК.

• К повороту внимания в исследованиях рискованного выбора.

  Зилкер В., Пачур Т. Зилкер В. и др. Фронт Псих. 2022 6 сент.; 13:953008. doi: 10.3389/fpsyg.2022.953008. Электронная коллекция 2022. Фронт Псих. 2022. PMID: 36148098 Бесплатная статья ЧВК.

Значение теории перспектив как инвестиционный фактор

Значение теории перспектив как инвестиционный фактор

Значение теории перспектив является допустимым инвестиционным фактором, особенно в периоды очевидной неэффективности рынка. Теория перспектив — популярная модель иррационального принятия решений. Он подчеркивает реалистичное мысленное представление ожидаемых прибылей и убытков, а также индивидуальную оценку таких представлений. Теория перспектив объясняет асимметричное неприятие потерь (см. пост здесь) и игровые предпочтения (см. пост здесь). Поскольку мысленные представления об ожидаемой доходности и волатильности часто основаны на графиках цен, ценность теории перспектив можно оценить на основе распределения доходности активов за прошлые периоды. Активы с высокой теоретической ценностью должны иметь низкую последующую доходность, и наоборот. Это утверждение остается в силе, даже если часть рынка полностью рациональна, пока существуют балансовый отчет и пределы риска. Эмпирические научные работы подтвердили ценность теории перспектив на международных фондовых рынках, рынках корпоративных облигаций и валютных рынках.

Ниже приведены в основном цитаты из трех эмпирических статей, ссылки на которые приведены в конце поста. Курсив и текст в скобках добавлены для ясности.

Этот пост связан с обзором этого сайта о неявных субсидиях на финансовых рынках.

Что такое теория перспектив?

«Несмотря на популярность теории ожидаемой полезности, экспериментальные данные… показывают, что поведение инвесторов в реальном мире… отклоняется от того, что предсказывает теория ожидаемой полезности… Теория перспектив, представленная Канеманом, — это более реалистичная схема принятия решений для оценки риска ». [Сюй, Кожан и Тейлор]

«Теория перспектив широко считается наиболее успешной описательной теорией для принятия решений». [Чжун и Ван]

«Принятие решений в соответствии с теорией перспектив [включает] два этапа: «представление» и «оценка». Во-первых, для любого риска, который рассматривает агент, он формирует мысленное представление этого риска. Точнее… агент формирует мысленное представление о прибылях и убытках, которые он связывает с принятием риска. Во-вторых, агент оценивает это представление — это распределение прибылей и убытков — чтобы убедиться, что оно привлекательно… Тверски и Канеман (19).92) содержат подробные формулы, определяющие значение, которое агент теории перспектив присвоил бы любому заданному распределению прибылей и убытков». [Барберис, Мукерджи и Ван]

«Теория перспектив отличается от теории ожидаемой полезности двумя важными аспектами.

• Во-первых, в рамках модели ожидаемой полезности предполагается, что функция полезности непрерывно дифференцируема и является вогнутой функцией конечного богатства. Напротив, функция ценности теории перспектив является функцией прибылей и убытков по отношению к .0149 опорная точка . Функция изгибается в нуле и вогнута при выигрыше [уменьшение удовольствия], но выпукла при убытке [увеличении боли]. Таким образом, функция ценности теории перспектив лучше отражает неприятие реальных потерь инвестора и сосредоточенность на постепенном изменении богатства , а не на конечном уровне богатства.
• Во-вторых, в то время как отношение между вероятностями событий и весами является линейным в рамках ожидаемой полезности, теория перспектив вводит нелинейную функцию взвешивания вероятности. Такая весовая функция отражает предпочтения инвесторов в азартных играх в реальном мире экстремальным событиям . Теория также моделирует восприятие инвесторами вероятностей прибыли иначе, чем вероятностей убытков.

В совокупности эти свойства гарантируют, что теория перспектив предлагает более реалистичное описание того, как инвесторы оценивают риск, по сравнению с рациональной моделью ожидаемой полезности». [Сюй, Кожан и Тейлор]

«Для многих инвесторов их мысленное представление об акциях дается распределением прошлых доходов по акциям… Наиболее очевидный способ, которым Инвесторы могут узнать о распределении доходности акций в прошлом, взглянув на график движения цены акции в прошлом — в частности, на график, который обычно появляется спереди и в центре, когда они ищут информацию об акции… Они верят прошлому. распределения доходности, чтобы быть хорошим и легкодоступным показателем объекта, в котором они действительно заинтересованы, а именно распределения будущей доходности акций… Это мнение может быть ошибочным». [Барберис, Мукерджи и Ван]

«Индивидуальные инвесторы отдают предпочтение лотерейному спросу, в то время как институциональные инвесторы склоняются к страховому спросу». [Чжун и Ван]

Стоимость по теории перспектив и доходность активов

«Модель делает простой прогноз… акции с высокой стоимостью по теории перспектив будут иметь в среднем низкую последующую доходность, в то время как акции с низкой стоимостью по теории перспектив будут иметь высокую последующую доходность . Интуиция ясна: акции с высокой теоретической стоимостью привлекательны для некоторых инвесторов; эти инвесторы склоняются к этим акциям в своих портфелях, в результате чего они становятся переоцененными и получают низкую последующую доходность». [Барберис, Мукерджи и Ван]

«Предположим, что… рынок состоит из двух типов инвесторов: рациональные инвесторы, мыслящие в соответствии с рамками ожидаемой полезности, и иррациональные инвесторы, оценивающие риск так, как это описано в теории перспектив. Тогда эти иррациональные инвесторы с большей готовностью сохранят высокую теоретическую стоимость [активов] … Если эти инвесторы составляют нетривиальную долю … их торговая деятельность изменит спрос … и, следовательно, повлияет на ожидаемую прибыль в равновесии. В частности, они будут предлагать высокую стоимость [активов] по теории перспектив, чтобы они были временно оценены и переоценены. [Сюй, Кожан и Тейлор]

«Арбитражники, не склонные к риску, не используют агрессивно существующую неверную оценку из-за страха увеличения разрыва в оценке в ближайшем будущем. Следовательно, даже если прогностическая модель не полностью охвачена обычными факторами риска, она все равно может быть сгенерирована подверженностью шумовому торговому риску». [Сюй, Кожан и Тейлор]

Эмпирические данные по акциям

«Каждый месяц мы вычисляем для каждой акции в поперечном разрезе теоретическую стоимость акции… представлением распределения прошлой доходности акции является распределение ее ежемесячной доходности за предыдущие пять лет». [Барберис, Мукерджи и Ван]

«В соответствии с нашей гипотезой мы обнаруживаем, что коэффициент при теоретической стоимости акций, усредненный по всем ежемесячным регрессиям, значительно отрицателен: акции с более высокими теоретическими значениями имеют более низкую последующую доходность . Мы также обнаруживаем, опять же в соответствии с нашей концепцией, что этот результат особенно силен среди акций с малой капитализацией… предсказательная сила теории перспектив для последующей доходности акций сильнее среди акций, которые менее подвержены арбитражу, например, среди неликвидных акций. и акции с высокой идиосинкразической волатильностью». [Барберис, Мукерджи и Ван]

«Предыдущие исследования проверяли последствия теории перспектив для доходности акций при допущении, что инвесторы используют перспективное представление доходности акций… В этой статье мы проверяем теорию перспектив при предположении, что инвесторы используют ретроспективное представление. Оба… представляют доказательства, подтверждающие их соответствующие предположения. Этот предполагает не только то, что теория перспектив полезна для понимания поперечного сечения доходности, но также и то, что инвесторы могут широко использовать как прогнозные, так и ретроспективные представления акций 9.0134». [Барберис, Мукерджи и Ванг]

«Мы обнаружили, что значительная часть предсказательной силы теории перспектив в отношении доходности исходит из компонента «взвешивания вероятностей» теории перспектив. При взвешивании по вероятности агент перевешивает хвосты распределения доходности, прием, который, среди прочего, улавливает широко распространенное предпочтение лотерейных азартных игр. Тот факт, что взвешивание вероятностей играет важную роль в наших результатах, предполагает — и мы подтверждаем это в данных — что акции с высокой стоимостью теории перспектив — это акции, прошлые доходности которых имеют положительную асимметрию. Таким образом, часть того, что может повлиять на наши результаты, заключается в том, что когда инвесторы наблюдают за распределением доходности акций в прошлом, возможно, глядя на ценовой график, они видят асимметрию, которая, в свою очередь, заставляет их думать об акциях как об азартной игре, похожей на лотерею, и, следовательно, находить их привлекательными ». [Барберис, Мукерджи и Ванг]

Эмпирические данные об облигациях

«Наш основной эмпирический прогноз заключается в том, что теоретическая стоимость облигации, основанная на распределении ее исторической доходности, имеет предсказательную силу для ее будущей доходности с отрицательным знаком . Эта предсказательная сила должна быть сильнее для бросовых облигаций, в которых индивидуальные инвесторы играют более важную роль». [Чжун и Ван]

«Как портфельный, так и регрессионный анализ показывают, что облигации с более высокой (более низкой) теоретической стоимостью будут приносить более низкую (более высокую) доходность в будущем. Другими словами, значения теории перспектив могут предсказывать будущие доходы. Наши результаты устойчивы к различным спецификациям ценности теории перспектив и спецификациям модели». [Чжун и Ван]

«Из-за страха быть менее уважаемыми сверстниками, институциональные инвесторы, как правило, более склонны к потерям, чем индивидуальные инвесторы . Неприятие потерь институциональными инвесторами объясняет, почему именно неприятие потерь объясняет наибольшую прогностическую силу теории перспектив на рынке облигаций». [Чжун и Ван]

Эмпирические данные по иностранной валюте

«Наша статья… эмпирически исследует роль теории перспектив в объяснении сечения доходности валюты… Если часть валютных инвесторов действительно отклоняется от ожидаемой полезности в своем решении -процессы производства и оценивать валютный риск в соответствии с теорией перспектив, то их торговая деятельность в соответствии с теорией перспектив должна влиять на ожидаемую доходность валюты в равновесии». [Сюй, Кожан и Тейлор]

«Спотовые и месячные форвардные обменные курсы с ежедневной периодичностью с 1 января 1985 г. по 28 февраля 2018 г. собираются из Barclays и Reuters через Datastream… Наш основной эмпирический анализ сосредоточен на выборке, состоящей из пятнадцати обменных курсов развитых стран. валюты по отношению к доллару США». [Сюй, Кожан и Тейлор]

«Нам необходимо построить меру ценности теории перспектив на уровне валюты. Эмпирическое использование теории перспектив требует двух шагов.

• Во-первых, инвесторы должны сформировать мысленное представление о риске… инвесторы мысленно представляют риск валюты, используя прошлое распределение доходности обменного курса. Исторический график обменного курса — это, пожалуй, первая часть информации, которая появится у инвесторов при поиске информации о валюте. Следовательно, инвесторы, скорее всего, будут использовать графики цен (и, следовательно, прошлые распределения обменного курса) для формирования мысленного представления о том, насколько рискованной является валюта.
• Второй шаг заключается в том, что инвесторы должны оценить привлекательность такого представления или нет. Мы применяем формулу Тверски и Канемана к прошлому распределению изменений обменного курса и строим стоимость теории перспектив на уровне валюты, которая отражает, насколько привлекательна валюта для инвестора теории перспектив». [Сюй, Кожан и Тейлор]

«[Мы предоставляем] эмпирические доказательства того, что значение теории перспектив является важным… фактором, определяющим перекрестные колебания избыточной доходности валюты». [Сюй, Кожан и Тейлор]

«Мы обнаружили, что значение теории перспектив , полученное на основе исторического распределения изменений обменного курса, отрицательно и существенно прогнозирует поперечное сечение будущих доходов от избытка валюты . Прогностическое отношение является не только статистически значимым, но и экономически значимым. Увеличение значения теории перспектив на одно стандартное отклонение связано с годовым падением валютных доходов на 3,6% в следующем месяце. Предсказательная сила остается сильной при контроле других характеристик валюты». [Сюй, Кожан и Тейлор]

«Кроме того, отсортировав валюты по пяти портфелям на основе значений теории перспектив, мы обнаружили, что валюты с высокой стоимостью теории перспектив значительно уступают своим парам с более низкой стоимостью примерно на 5% в год. Стратегия покупки (короткой продажи) валют с низкой (высокой) теоретической стоимостью имеет лишь умеренную корреляцию с другими факторами валютного риска, факторами риска акций и факторами хедж-фондов. Аномальная доходность (альфа) после учета этих факторов остается статистически значимой на уровне 1%… Наши 9Выводы 0133 говорят в пользу существования неправильной оценки на уровне отдельных валют, а не объяснения систематического риска ». [Сюй, Кожан и Тейлор]

«Для дальнейшей проверки гипотезы неправильной оценки мы взаимодействуем между переменной ценности теории перспектив и косвенными показателями пределов арбитража, спекулятивного спроса и внимания инвесторов. Мы обнаружили, что предсказательная сила усиливается, когда волатильность валютного рынка, глобальное неприятие риска и стресс на финансовом рынке высоки, а именно, когда арбитражеры более сложны для исправления неправильной цены. Кроме того, прогностическая связь также сильнее, когда глобальные настроения инвесторов высоки, и связь слабее, когда инвесторы уделяют больше внимания макроэкономическим показателям и, следовательно, уделяют меньше внимания историческим показателям валюты из-за ограниченной способности внимания.

No related posts.