Сумма квадратов всех целых чисел: онлайн калькулятор
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b)2 = a2 ± 2ab + b2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c)3, однако формулы сокращенного умножения для простого выражения как:
a2 + b2
в учебниках по математике вы не найдете.
Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a2 + b2 = (a + ib) × (a — ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a2 + b2 = (a + b)2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш).
Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат.
Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f2 = a2 + b2 + c2 + d2,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725.
Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Формулы простого умножения. Калькулятор онлайн.Упрощение многочлена.Умножение многочленов
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять.
Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3.
Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х — у) 3
= х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Yandex.RTB R-A-339285-1
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения
- формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
- формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
- формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
- формула разности квадратов: a 2 — b 2 = a — b a + b
- формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
- формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть.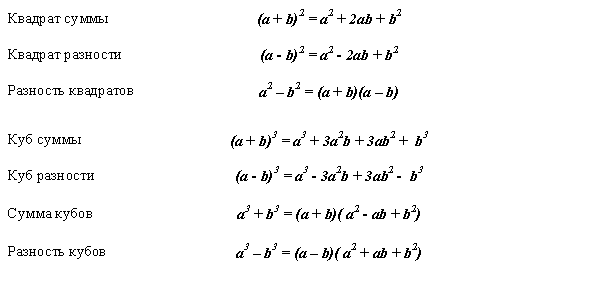
Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.
Дополнительные формулы сокращенного умножения
Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.
Во-первых, рассмотрим формулу бинома Ньютона.
a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n
Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:
C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !
Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.
Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.
a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n
Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.
a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1
Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.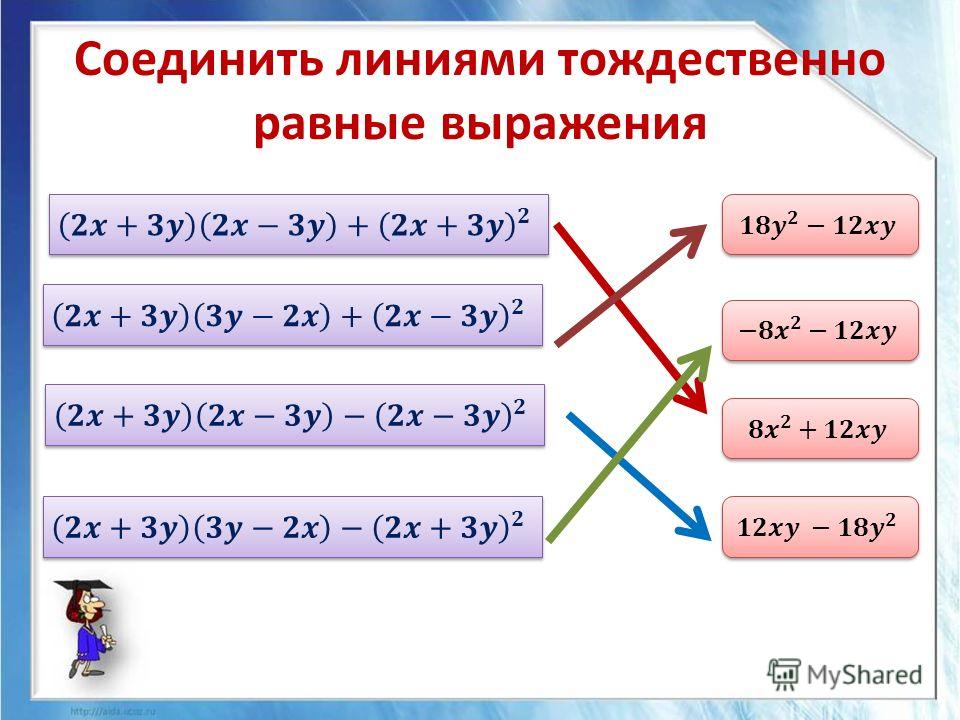
Для четных показателей 2m:
a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2
Для нечетных показателей 2m+1:
a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m
Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .
Как читать формулы сокращенного умножения?
Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.
a + b 2 = a 2 + 2 a b + b 2 .
Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.
Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:
квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.
Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.
Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.
Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.
С учетом этого, формулы суммы и разности кубов прочитаются так:
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Доказательство ФСУ
Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.
Для примера рассмотрим формулу квадрата разности.
a — b 2 = a 2 — 2 a b + b 2 .
Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.
a — b 2 = a — b a — b .
Раскроем скобки:
a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .
Формула доказана. Остальные ФСУ доказываются аналогично.
Примеры применения ФСУ
Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.
Пример 1. ФСУ
Упростим выражение 9 y — (1 + 3 y) 2 .
Применим формулу суммы квадратов и получим:
9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2
Пример 2.
ФСУ
Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .
Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.
8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .
Сокращаем и получаем:
8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z
Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.
Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:
79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .
Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.
Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения .
Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
a 2 — b 2 = (a — b)(a + b)
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(a + b) 2 = a 2 + 2ab + b 2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел , не используя калькулятор или умножение в столбик. Поясним на примере:
Найти 112 2 .
Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
112 2 = (100 + 12) 2
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
(8a + с) 2 = 64a 2 + 16ac + c 2
Предостережение!!!
(a + b) 2 не равно a 2 + b 2
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
(a — b) 2 = a 2 — 2ab + b 2
Также стоит запомнить весьма полезное преобразование:
(a — b)
2
= (b — a)
2
Формула выше доказывается простым раскрытием скобок:
(a — b)
2
= a
2
— 2ab + b
2
= b
2
— 2ab + a
2
= (b — a)
2
Куб суммы
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Запомнить эту «страшную» на вид формулу довольно просто.
Выучите, что в начале идёт a 3 .
Два многочлена посередине имеют коэффициенты 3.
В
спомним, что любое число в нулевой степени есть 1. (a 0 = 1, b 0 = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3
Предостережение!!!
(a + b) 3 не равно a 3 + b 3
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a 3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
(a — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сумма кубов ( Не путать с кубом суммы!)
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a 3 + b 3 = (a + b)(a 2 — ab + b 2)
Сумма кубов — это произведение двух скобок.
Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
A 2 — ab + b 2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубов (Не путать с кубом разности!!!)
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a 3 — b 3 = (a — b)(a 2 + ab + b 2)
Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.
Разложим, например, :
В этой записи легко запоминается, что вначале стоит куб первого, а в конце — куб второго числа. А вот что посередине — запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго — увеличивается — несложно заметить и запомнить, труднее дело обстоит с запоминанием коэффициентов и знаков (плюс там или минус?).
Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее — ага, уже треугольник получается:
Первая строка, с одной единичкой — нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:
Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:
Ну а знаки запомнить еще проще: первый — такой же, как в раскладываемом двучлене (раскладываем сумму — значит, плюс, разность — значит, минус), а дальше знаки чередуются!
Вот такая это полезная штука — треугольник Паскаля.
Пользуйтесь!
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие
Примеры применения формул сокращенного умножения
Пример 1.
7.
Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты
Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад
Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку.
В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные.
Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
{2}) \] Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Используйте
Это калькулятор факторинга, если специально для факторизации разности двух квадратов. Если входное уравнение можно представить в виде 92 = (a + b)(a — b) \)
Факторизованные члены, которые содержат дополнительные разности двух квадратов, также будут факторизованы.
Разность двух квадратов, когда а отрицательно
и не может быть преобразован в эту форму.Если а отрицательно и у нас есть сложение такое, что у нас есть -а 2 + b 92 \)
Завершить разложение а 2 — b 2 на (a + b)(a — b)
\( 4(3 + y)(3 — y) \)
Окончательный ответ :
\( 4(3 + у)(3 — у) \)
Подписаться на калькуляторSoup:
Калькулятор квадратов разности коэффициентов
| Дом | |
| Многочлены | |
| Нахождение наибольшего общего делителя | |
| Факторинг трехчленов | |
| Функция абсолютного значения | |
| Краткий обзор полиномов факторинга | |
| Решение уравнений с одним радикальным членом | |
| Добавление дробей | |
| Вычитание дробей | |
| Метод ФОЛЬГИ | |
| График сложных неравенств | |
| Решение абсолютных неравенств | |
| Сложение и вычитание многочленов | |
| Использование уклона | |
| Решение квадратных уравнений | |
| Факторинг | |
| Свойства умножения показателей степени | |
| Завершение квадрата | |
| Решение систем уравнений методом подстановки | |
| Объединение одинаковых радикальных терминов | |
| Исключение с помощью умножения | |
| Решение уравнений | |
| Теорема Пифагора 1 | |
| Нахождение наименьших общих кратных | |
| Умножение и деление в экспоненциальном представлении | |
| Сложение и вычитание дробей | |
| Решение квадратных уравнений | |
| Сложение и вычитание дробей | |
| Умножение на 111 | |
| Добавление дробей | |
| Умножение и деление рациональных чисел | |
| Умножение на 50 | |
| Решение линейных неравенств с одной переменной | |
| Упрощение кубических корней, содержащих целые числа | |
| График сложных неравенств | |
| Простые трехчлены как произведения двучленов | |
| Написание линейных уравнений в форме наклона-пересечения | |
| Решение линейных уравнений | |
| Линии и уравнения | |
| Пересечения параболы | |
| Функция абсолютного значения | |
| Решение уравнений | |
| Решение сложных линейных неравенств | |
| Комплексные номера | |
| Разложение на множители разности двух квадратов | |
| Умножение и деление рациональных выражений | |
| Сложение и вычитание радикалов | |
| Умножение и деление чисел со знаком | |
| Решение систем уравнений | |
| Факторизация противоположности GCF | |
| Умножение специальных многочленов | |
| Свойства показателей степени | |
| Научное обозначение | |
| Умножение рациональных выражений | |
| Сложение и вычитание рациональных выражений с отличающимися знаменателями | |
| Умножение на 25 | |
| Десятичные дроби | |
| Решение квадратных уравнений путем заполнения квадрата | |
| Частное правило для экспонент | |
| Упрощение квадратных корней | |
| Умножение и деление рациональных выражений | |
| Независимые, противоречивые и зависимые системы уравнений | |
| Склоны | |
| Графические линии на координатной плоскости | |
| Графические функции | |
| Силы десяти | |
| Свойство нулевой мощности экспонентов | |
| Вершина параболы | |
| Рационализация знаменателя | |
| Тест факторизуемости для квадратных трехчленов | |
| Трехчленные квадраты | |
| Решение двухшаговых уравнений | |
| Решение линейных уравнений, содержащих дроби | |
| Умножение на 125 | |
| Свойства экспоненты | |
| Умножение дробей | |
| Сложение и вычитание рациональных выражений с одинаковым знаменателем | |
| Квадратные выражения — Заполнение квадратов | |
| Сложение и вычитание смешанных чисел с разными знаменателями | |
| Решение формулы для заданной переменной | |
| Факторинг трехчленов | |
| Умножение и деление дробей | |
| Умножение и деление комплексных чисел в полярной форме | |
| Степенные уравнения и их графики | |
| Решение линейных систем уравнений подстановкой | |
| Решение полиномиальных уравнений с помощью факторинга | |
| Законы экспонентов | |
| индекс casa mÃo | |
| Системы линейных уравнений | |
| Свойства рациональных показателей | |
| Мощность произведения и мощность частного | |
| Факторизация разностей идеальных квадратов | |
| Деление дробей | |
| Разложение полинома на множители путем нахождения GCF | |
| Графики линейных уравнений | |
| Шаги факторинга | |
| Свойство умножения показателей степени | |
| Решение систем линейных уравнений с тремя переменными | |
| Решение экспоненциальных уравнений | |
| Нахождение НОК набора одночленов | |
- Выражение
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Solve
- Graph
- System
- Математический решатель на вашем сайте
Калькулятор квадратов разности факторов
Связанные темы:
упростить квадратный корень из 36 x в 16 степени |
прикладная математика поместите следующие уравнения в стандартную форму квадратного уравнения |
бесплатный решатель вопросов по алгебре 7-го класса |
программное обеспечение калькулятора промежуточной алгебры |
энный корень на ти-83 |
смешивать числа и дроби |
маршрутов из точки a в точку b вероятность комбинации конечных математических задач |
математика третьего класса трива |
базовый математический расчет м |
вероятность и перестановки и комбинации, решенные примеры |
решение производных функций онлайн |
пример математического стихотворения |
онлайн математические задачи |
методы решения дифференциальных уравнений в частных производных первого порядка
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| Бнойпренс Дата регистрации: 13. |
| ||||||
| Наверх | |||||||
| Вофий Тимидов Дата регистрации: 06.07.2001 |
| ||||||
| Наверх | |||||||
| СанГ Зарегистрирован: 31.08.2001 |
| ||||||
| Вернуться к началу | |||||||
| Матдейс Дата регистрации: 08.12.2001 |
| ||||||
| Наверх | |||||||
| elesdla Зарегистрирован: 30.10.2001 |
| ||||||
| Наверх | |||||||
| СанГ Зарегистрирован: 31.08.2001 |
| ||||||
02.2003 
Кто-нибудь, пожалуйста, направьте меня.
Я никогда не призываю своих учеников получать готовые ответы из Интернета, однако я призываю их использовать Алгебратор. Со временем я полюбил это программное обеспечение. Это помогает студентам изучать математику в удобной форме.
Я использовал его в алгебре среднего уровня, алгебре среднего уровня и алгебре 2. Это помогло мне понять самые сложные математические задачи. Я благодарен этому.
По-настоящему замечательная программа для алгебры — это программа Algebrator. Если просто ввести задачу из книги, пошаговое решение появится при нажатии кнопки «Решить». Я использовал его на многих математических занятиях — промежуточной алгебре, предварительной алгебре и исправительной алгебре. Очень рекомендую программу.
