Неравенства с одной переменной. Числовые промежутки. Решение систем неравенств с одной переменной 8 класс
Неравенство
Неравенство, содержащее одну переменную, называется неравенством с одной переменной (неизвестной).
Решением неравенства называется такое значение переменной, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или доказать, что их нет.
Два неравенства называются равносильными, если они имеют одни и те же решения, или они оба не имеют решений.
При решении неравенств используют основные их свойства:
- Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
- Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

Решение неравенств обозначают на координатной прямой.
Пусть a – некоторое число. Все числа, не превосходящие а – это часть координатной прямой левее точки a вместе с точкой a (черный закрашенный кружок):
Все числа, меньшие а – это часть координатной прямой левее точки a, но не включая точку.
Аналогично для чисел, не меньших а, и больших а:
Обозначения числовых множеств на координатной прямой носят название числовые промежутки.
Пример 1. Записать, используя обозначения числовых промежутков, множество точек заштрихованной части координатной прямой.
Ответ: (-∞;-6) U [-3;0) U [2;5) U (5; ∞)
Читается так: промежуток от минус бесконечности до минус 6 (шесть не входит) объединить с промежутком от минус 3 до нуля (минус три входит, ноль не входит) объединить с промежутком от двух до пяти (два входит, пять не входит) объединить с промежутком от 5 до бесконечности (5 не входит).
Пример 2. Решим неравенство x3-x2<2.
Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, т.е. на 6. Получим
2x-3x<12
-x<12
x>-12
Ответ (-12;∞).
В рассмотренном примере мы заменили заданное неравенство равносильным ему неравенством вида ax<b, где a и b – некоторые числа. Неравенства вида ax<b или ax>b, где a и b – некоторые числа, называют линейными неравенствами с одной переменной
Может случиться, что при решении неравенства мы придем к линейному неравенству вида 0x>b или 0x<b. Неравенство такого вида, а значит, и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число.
Неравенство такого вида, а значит, и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число.
Пример 3. Турист вышел по направлению к железнодорожной станции, расположенной на расстоянии 10 км от него. Если турист увеличит скорость на 2 км/ч, то за 2 часа он пройдет расстояние, большее 10 км. Если он уменьшит скорость на 2 км/ч, то даже за 3 ч не успеет дойти до станции. Какова скорость туриста?
Пусть скорость туриста равна х км/ч. Если турист будет идти со скоростью (х+2) км/ч, то за 2 часа он пройдет 2(х+2) км. По условию задачи 2(х+2)>10. Если турист будет идти со скоростью (х-2) км/ч, то за 3 часов он пройдет 3(х-2) км. По условию задачи 3(х-2)<10.
Требуется найти значения х, при которых верно как неравенство 2(х+2)>10, так и неравенство 3(х-2)<10, т.е. найти общие решения этих неравенств. В таких случаях говорят, что надо решить систему неравенств.
2х+2>103x-2<10
Заменив каждое неравенство системы равносильным ему неравенством, получим
x>3x<16/3
Значит, значение х должно удовлетворять условию 3<x<5(1/3).
Ответ: скорость туриста больше 3 км/ч, но меньше 5 (1/3) км/ч
Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Решить систему – значит найти все ее решения или доказать, что решений нет.
Неравенства с переменными, их частные и общее решение
Неравенства, содержащие переменную, занимают основную долю в общем объеме изучения темы «Неравенства» школьной программы математики и алгебры. Данная статья содержит базовый материал: определение понятия неравенства с переменными и их решений, способ записи решений неравенств. Также для наглядности приведем решение практических задач.
Определение неравенств с переменными
Числовые неравенства мы разобрали в соответствующей статье, выяснив что числовыми неравенствами являются два числовых выражения, между которыми располагается какой-либо из знаков неравенства. Заменив хотя бы одно из числовых выражений выражением с переменной, мы получим неравенство с переменными. Такое определение дано по виду записи подобных неравенств. Выделяют неравенства с одной, двумя, тремя и большим количеством переменных по числу переменных, использующихся в записи неравенства.
Такое определение дано по виду записи подобных неравенств. Выделяют неравенства с одной, двумя, тремя и большим количеством переменных по числу переменных, использующихся в записи неравенства.
Неравенства с одной переменной
Определение 1Неравенство с одной переменной – это неравенство, в записи которого используется одна переменная.
К примеру, k < 7 – неравенство с одной переменной k; 8 ≥ d2 – 3 – неравенство с одной переменной d. При этом возможно, что переменная будет участвовать в записи несколько раз, например:
((2·x — 5·t2) · (t-1) < 1t или t-1+ 4 ≥ 1t- t3t+3
Неравенства с двумя переменными Определение 2Неравенство с двумя переменными – это неравенство, в записи которого используются две неодинаковые переменные.
Например, m3+15· n2>13 – неравенство с двумя переменными m и n;
(f+2·g)37+3< 7 — ff2+1 – неравенство с двумя переменными f и g.
По записи неравенства с двумя переменными схожи с неравенствами с параметром и одной переменной. Но тогда, как правило, в условиях всегда указывается, какие буквы служат обозначением параметров, поэтому вопрос о том, сколько переменных в заданном неравенстве, обычно не возникает.
Но тогда, как правило, в условиях всегда указывается, какие буквы служат обозначением параметров, поэтому вопрос о том, сколько переменных в заданном неравенстве, обычно не возникает.
Неравенства с тремя или больше переменными
Определение 3Неравенства с тремя, четырьмя и т.д. переменными
– это неравенства, в записи которых используются три, четыре и т.д. переменных.В школьной программе подобные неравенства встречаются редко, но тем не менее существуют. Например, шар, радиус которого равен 2 и центр которого совпадает с началом координат, возможно определить неравенством с тремя переменными: x2 + y2 + z2 ≤ 4.
Решения неравенства: частное, общее и простое решение
Определение 4Решение неравенства с одной переменной – такое значение переменной, которое обращает исходное неравенство в верное числовое неравенство.
В качестве примера возьмем простое неравенство вида y > 9. Пусть y=13. Подставим это значение в исходное неравенство и получим числовое неравенство 13 > 9. Оно является верным, а значит 13 является решением исходного неравенства y > 9. А вот число y=5 не станет решением данного неравенства, поскольку, подставив такое значение переменной, мы получим неверное числовое неравенство: 5 > 9.
Оно является верным, а значит 13 является решением исходного неравенства y > 9. А вот число y=5 не станет решением данного неравенства, поскольку, подставив такое значение переменной, мы получим неверное числовое неравенство: 5 > 9.
Логичным следствием является вопрос о возможном количестве решений конкретного неравенства. Отметим, что неравенство с одной переменной может не иметь решений, иметь конечное количество решений или иметь бесконечно много решений. Мы рассмотрим это утверждение, имеющее большую значимость в практике, более детально в изучении самого процесса нахождения решений неравенств.
Резюмируем:
- неравенство может не иметь решений. К примеру: z2<-2. В самом деле, при любом действительном значении переменной z, мы будем иметь неверное числовое неравенство, опираясь на то, что, согласно свойствам степени, квадрат любого числа является неотрицательным числом. Оно, в свою очередь, никак не может быть меньше -2.
- неравенство может иметь лишь одно решение.
 Например, неравенство f=1≤0 имеет решение f=1, и оно единственно;
Например, неравенство f=1≤0 имеет решение f=1, и оно единственно; - неравенство может иметь конечное количество решений: три, шесть и т.п. Как пример, рассмотрим неравенство |x2 — 1| ≤ 0, решений которого существует ровно два: 1 и -1;
- неравенство может иметь бесконечно много решений. Например: t > 5. Решением данного неравенства станет любое действительное число, большее 5: 13, 87, 601, 825 и т.п.
Все вышесказанное верно и для неравенств с двумя, тремя и более переменными.
Определение 5Решение неравенства с двумя переменными – это пара значений заданных переменных, при которых исходное неравенство с переменными преобразуется в верное числовое неравенство.
В качестве примера рассмотрим неравенство с двумя переменными y и z: y + 1>2·z. Пара значений переменных y и z: 1 и 0 соответственно, являются решением заданного неравенства, поскольку подставив их, мы получим верное числовое неравенство: 1+1>2·0. В то же время пара значений y=2, z=4 не будет служить решением исходного неравенства: их подстановка создаст неверное числовое неравенство 2+1>2·4.
Пара значений переменных зачастую записывается в скобках наподобие координат точек в прямоугольной системе координат. Например, для вышеуказанного примера решение запишется так: (1, 0).
Все вышесказанное верно и для неравенств с большим количеством переменных.
Определение 6Решение неравенства с тремя, четырьмя и более переменными – это тройка, четверка и т.п. значений заданных переменных, при которых исходное неравенство преобразуется в верное числовое неравенство.
Например, рассмотрим неравенство с четырьмя переменными a2+b2+c2+d2≤ 36. Четверка значений этих переменных, такие как: a=1, b=2, c=3, d=4, являются решением исходного неравенства, поскольку, подставив их, мы получим верное числовое неравенство: 12+22+32+42≤ 36.
Также рассмотрим такие понятия как «частное решение неравенства» и «общее решение неравенства».
Определение 7Частное решение неравенства – это некоторое отдельно взятое решение исходного неравенства.
К примеру,17 – частное решение неравенства m<101. Еще одним частным решением указанного неравенства будет число 7.
Еще одним частным решением указанного неравенства будет число 7.
Общее решение неравенства – множество всех частных решений исходного неравенства.
Рассмотрим на том же примере: m<101. Общим решением этого неравенства будет множество чисел, меньших 101.
Несмотря на частоту использования указанной терминологии, все же намного чаще применяют понятие решения неравенства без неких уточнений, наделяя при этом смыслом общего решения. В случае, когда необходимо определить отдельное решение, в исходном задании так и указывают.
Способ записи общего решения неравенства
Навык записи общего решения неравенства нужен для формирования ответа при решении задач. Сначала разберем принятые правила записи на примере решений неравенств с одной переменной.
Напомним, что решение неравенства с одной переменной – это либо число, либо множество чисел, т.е. числовое множество.
Определение 9Когда равенство не имеет решений, пишут буквально – «нет решений», либо применяют знак пустого множества ∅ .
Когда общее решение – одно число, так его и записывают: 2, -1,15 ли 817. А также можно заключить его в фигурные скобки.
Когда общее решение – несколько чисел (при этом их немного), нужно либо записать их по очереди, отделив запятой или точкой с запятой, либо – через запятую, заключив в фигурные скобки. Например: 6, 12, 45 или {6, 12, 45} .
Наконец, когда общее решение включает в себя бесконечно много решений, то применяют общепринятые обозначения множеств натуральных чисел (N), целых чисел (N), рациональных чисел (Q), действительных чисел (R), а также числовых промежутков, множеств отдельных чисел и т.п. В практике чаще встречаются простейшие неравенства и числовые промежутки. Пусть, решением некоторого неравенства станут: число 3, полуинтервал (5;9] и луч [13; +∞), тогда ответ запишется так: 3, (5, 9], [13, +∞), или: 3 ꓴ (5, 9] ꓴ [13, +∞), или: x=3, 5<x≤9, x≥13.
Чтобы записать общее решение неравенства с двумя, тремя и более переменными при небольшом количестве решений, перечисляют их все; либо делают описание множеств переменных. К примеру, d – любое целое число, s равно 0 или 1, t=-3, m=17.
К примеру, d – любое целое число, s равно 0 или 1, t=-3, m=17.
Зачастую решение для неравенства с двумя переменными не записывают, а «зарисовывают», изображая решения неравенства на координатной плоскости. Пусть задано неравенство: 2·х-у≥5; его решение – все точки, расположенные на и ниже прямой, определяемой формулой: у=2·х-5.
Решением неравенства с тремя переменными станет некое множество точек трехмерного пространства.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Как найти решение неравенства с вычитанием
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Алгебра 1 Помощь » Уравнения / Неравенства » Системы неравенств » Как найти решение неравенства с вычитанием
Решить неравенство:
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала объедините одинаковые члены в правой части неравенства, чтобы получить . Далее попытайтесь изолировать переменную:.
Далее попытайтесь изолировать переменную:.
Следовательно, ответ .
Сообщить об ошибке
Решить неравенство:
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала распределите отрицательный знак: становится . Поскольку по одну сторону от знака неравенства нет похожих членов для объединения, мы попытаемся изолировать переменную: . Поэтому ответ таков.
Сообщить об ошибке
Какое из следующих значений является допустимым для ?
Возможные ответы:
Правильный ответ:
Объяснение:
Так как неравенство включает абсолютное значение, у вас есть две возможности рассмотреть: когда результат положительный и когда он отрицательный. Когда вы рассматриваете отрицательный результат, вы должны перевернуть знак неравенства, чтобы найти :
Когда вы рассматриваете отрицательный результат, вы должны перевернуть знак неравенства, чтобы найти :
Это означает, что меньше положительного 20 И больше отрицательного 20:
И
Для каждого случая сначала вычтите 4 слева направо. Затем вы разделите обе стороны на 4 на изоляцию:
и
и
Это дает вам интервал для действительных значений:
Отчет о ошибке
Каково возможное допустимое значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Это неравенство можно переписать как:
4 x + 14 > 30 ИЛИ 4 x + 14 < –30
Решить каждое относительно x:
> 4
7 x 90; 4
х > 16; x > 44 x + 14 < –30; 4 х < –44; x < –11
Следовательно, значения от –11 до 4 (включительно) не будут работать. Следовательно, ответ равен 7.
Следовательно, ответ равен 7.
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала вычтите по 2п с обеих сторон:
п + 5 < 12.
Затем вычтите по 5 с обеих сторон:
п < 7
Сообщить об ошибке
Решите следующее неравенство.
Возможные ответы:
Правильный ответ:
Объяснение:
Изолируйте термин с на одной стороне и константами на другой стороне.
Сначала вычтите 7x с обеих сторон и добавьте 5 к обеим сторонам.
Затем разделите на 3, чтобы найти x.
Сообщить об ошибке
Найдите:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти переменную, нам нужно изолировать переменную с одной стороны неравенства и все остальные константы с другой стороны. Для этого выполните обратные операции.
Для этого выполните обратные операции.
Сначала вычтем 7 с обеих сторон, получим:
Затем вычтем 2x с обеих сторон:
Наконец, разделите обе части на 2:
Сообщить об ошибке
Найдите все решения этого неравенства.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить неравенство, изолируйте переменную с одной стороны от всех остальных констант с другой. Для этого выполните противоположные операции для управления неравенством.
Сначала изолируйте x, добавив по шесть с каждой стороны.
Все, что вы делаете с одной стороны, вы должны делать и с другой стороной.
Это дает вам:
Таким образом, ответ таков: .
Сообщить об ошибке
Решите следующее неравенство:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы изолировать переменную, нам нужно вычесть 10 из обеих частей уравнения.
Упростите левую и правую часть уравнения.
Ответ:
Отчет о ошибке
Решить для x:
Возможные ответы:
Правильный ответ:
Объяснение:
Когда вы решаете неравенство, проще всего рассматривать знак неравенства как знак равенства, пока вы решаете x.
Чтобы найти x, вам нужно получить x отдельно с одной стороны. Первое, что вам нужно сделать, это вычесть 6 из обеих сторон. Это оставило бы вас с . Чтобы получить x сам по себе, нужно обе части разделить на 9.. Это приведет вас к ответу .
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept
Решатели неравенств — документация SymPy 1.
 11
11Переключить боковую панель оглавления
- sympy.solvers.inequalities.solve_rational_inequalities ( eqs ) [источник]
Решите систему рациональных неравенств с рациональными коэффициентами.
Примеры
>>> из sympy.abc импортировать x >>> из sympy importsolve_rational_inequities, Poly
>>> решить_рациональные_неравенства([[ ... ((Поли(-х + 1), Поли(1, х)), '>='), ... ((Poly(-x + 1), Poly(1, x)), '<=')]]) {1}>>> решить_рациональные_неравенства([[ ... ((Поли(х), Поли(1, х)), '!='), ... ((Poly(-x + 1), Poly(1, x)), '>=')]]) Союз(Интервал.открыть(-oo, 0), Интервал.Lоткрыть(0, 1))
См. также
solve_poly_inequality
- sympy.solvers.inequalities.solve_poly_inequality( poly , rel )[источник]
Решите полиномиальное неравенство с рациональными коэффициентами.

Примеры
>>> из sympy importsolve_poly_inequality, Poly >>> из sympy.abc импортировать x
>>>solve_poly_inequality(Poly(x, x, domain='ZZ'), '==') [{0}]>>>solve_poly_inequality(Poly(x**2 - 1, x, domain='ZZ'), '!=') [Interval.open(-oo, -1), Interval.open(-1, 1), Interval.open(1, oo)]
>>>solve_poly_inequality(Poly(x**2 - 1, x, domain='ZZ'), '==') [{-1}, {1}]См. также
solve_poly_inequalities
- sympy.solvers.inequalities.solve_poly_inequalities( polys )[источник]
Решение полиномиальных неравенств с рациональными коэффициентами.
Примеры
>>> из Симпи Импорт Поли >>> из sympy.solvers.inequalities импортироватьsolve_poly_inequalities >>> из sympy.abc импортировать x >>> решить_поли_неравенства((( ... Poly(x**2 - 3), ">"), ( ... Poly(-x**2 + 1), ">"))) Union(Interval.open(-oo, -sqrt(3)), Interval.
 open(-1, 1), Interval.open(sqrt(3), oo))
open(-1, 1), Interval.open(sqrt(3), oo))
- sympy.solvers.inequalities.reduce_rational_inequalities ( exprs , gen , реляционное = True ) [источник]
Сократить систему рациональных неравенств с рациональными коэффициентами.
Примеры
>>> из sympy import Symbol >>> из sympy.solvers.inequalities импортировать reduce_rational_inequalities
>>> x = Символ('x', реальное=Истина)>>> уменьшить_рациональные_неравенства ([[х**2 <= 0]], х) Уравнение (х, 0)
>>> уменьшить_рациональные_неравенства ([[х + 2 > 0]], х) -2 < х >>> уменьшить_рациональные_неравенства([[(х + 2, ">")]], х) -2 < х >>> уменьшить_рациональные_неравенства([[х + 2]], х) Уравнение (х, -2)
Эта функция находит небесконечное множество решений, поэтому, если неизвестный символ объявлен как расширенный реальный, а не реальный, тогда результат может включать условия конечности:
>>> y = Symbol('y', extended_real=True) >>> уменьшить_рациональные_неравенства([[у + 2 > 0]], у) (-2 < у) и (у < оо)
- sympy.
 solvers.inequalities.reduce_abs_inequality( expr , rel , gen )[источник]
solvers.inequalities.reduce_abs_inequality( expr , rel , gen )[источник] Сокращение неравенства с вложенными абсолютными значениями.
Примеры
>>> from sympy import reduce_abs_inequality, Abs, Symbol >>> x = Символ('x', реальный=Истина)>>> reduce_abs_inequality(Abs(x - 5) - 3, '<', x) (2 < х) и (х < 8)
>>> reduce_abs_inequality(Abs(x + 2)*3 - 13, '<', x) (-19/3 < х) & (х < 7/3)
См. также
reduce_abs_inequalities
- sympy.solvers.inequalities.reduce_abs_inequalities ( exprs , gen ) [источник]
Сократить систему неравенств с вложенными абсолютными значениями.
Примеры
>>> from sympy import reduce_abs_inequalities, Abs, Symbol >>> x = Symbol('x', extended_real=True)>>> reduce_abs_inequality([(Abs(3*x - 5) - 7, '<'), ... (Абс(х + 25) - 13, '>')], х) (-2/3 < x) & (x < 4) & (((-oo < x) & (x < -38)) | ((-12 < x) & (x < оо)))
>>> reduce_abs_inequality([(Abs(x - 4) + Abs(3*x - 5) - 7, '<')], x) (1/2 < х) & (х < 4)
См.
 также
такжеreduce_abs_inequality
- sympy.solvers.inequalities.reduce_inequalities ( неравенств , символов = [] ) [источник]
Сократите систему неравенств с рациональными коэффициентами.
Примеры
>>> из sympy.abc импортировать x, y >>> из симпи импорта reduce_inequalities
>>> уменьшить_неравенства (0 <= х + 3, []) (-3 <= х) & (х < оо)
>>> уменьшить_неравенства (0 <= х + у * 2 - 1, [х]) (х < оо) и (х >= 1 - 2 * у)
- sympy.solvers.inequalities.solve_univariate_inequality( expr , gen , относительный = True , домен = Reals , Continuous = False ) [источник]
Решает действительное одномерное неравенство.
- Параметры:
выражение : Реляционный
Целевое неравенство
поколение : Символ
Переменная, для которой решается неравенство
реляционный : логический
Ожидается вывод реляционного типа или нет
домен : Установить
Область, в которой решается уравнение
непрерывный: логическое значение
Истинно, если известно, что expr является непрерывным в данной области (и поэтому для него не нужно вызывать Continuous_domain())
- Поднимает:
Нереализованная ошибка
Решение неравенства не может быть определено из-за ограничения в
sympy.. solvers.solveset.solvify()
solvers.solveset.solvify()
Примечания
В настоящее время мы не можем решить все неравенства из-за ограничений в
sympy.solvers.solveset.solvify(). Также вернулось решение для тригонометрических неравенств ограничены в своем периодическом интервале.Примеры
>>> from sympy importsolve_univariate_inequality, Symbol, sin, Interval, S >>> х = Символ('х')>>>solve_univariate_inequality(x**2 >= 4, x) ((2 <= x) & (x < оо)) | ((-оо < х) & (х <= -2))
>>>solve_univariate_inequality(x**2 >= 4, x, относительное = False) Союз(Интервал(-оо,-2), Интервал(2, оо))
>>> домен = Интервал (0, S. Бесконечность) >>>solve_univariate_inequality(x**2 >= 4, x, False, домен) Интервал(2, оо)
>>>solve_univariate_inequality(sin(x) > 0, x, относительное = False) Интервал.открыть(0, пи)
См. также
-
sympy.solvers.solveset.


 Например, неравенство f=1≤0 имеет решение f=1, и оно единственно;
Например, неравенство f=1≤0 имеет решение f=1, и оно единственно;
 open(-1, 1), Interval.open(sqrt(3), oo))
open(-1, 1), Interval.open(sqrt(3), oo))
 solvers.inequalities.reduce_abs_inequality( expr , rel , gen )[источник]
solvers.inequalities.reduce_abs_inequality( expr , rel , gen )[источник] также
также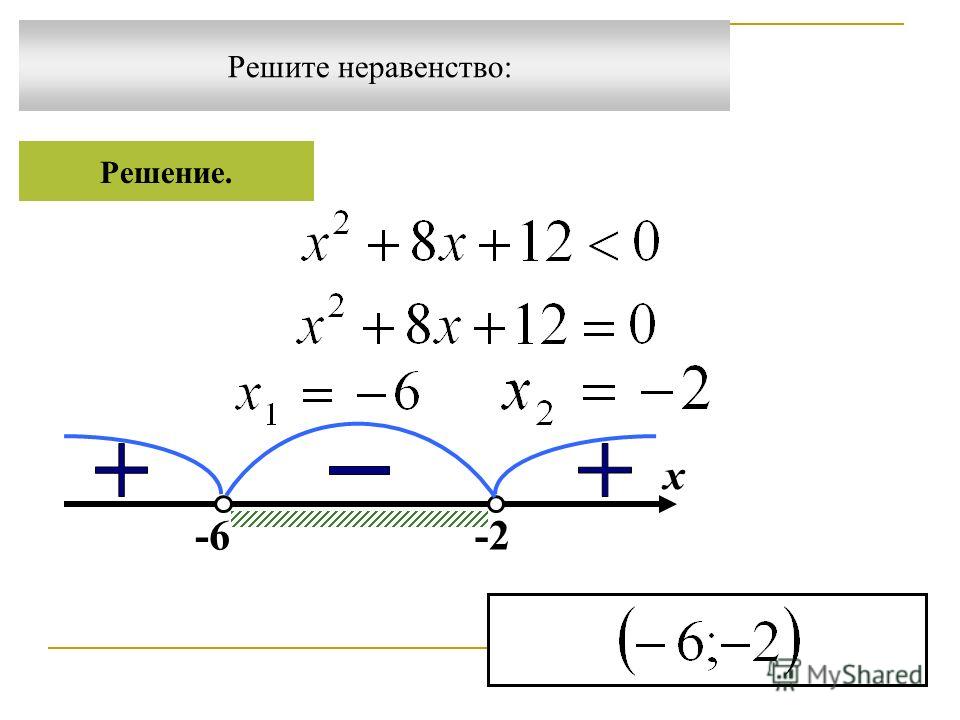 solvers.solveset.solvify()
solvers.solveset.solvify()