Правило периметр и площадь: Вычислите периметр и площадь прямоугольника со сторонами a и b если a=15 см b=100 см

Периметр и площадь. Почему дети в начальной школе путаются в том, что кажется взрослым очень простым

Нам, взрослым, некоторые вещи кажутся очевидными. Всем мы знаем, как вычислить периметр и площадь у фигуры, например. А вот для детей в началке это сложно. Как им помочь, рассказывает наш блогер, учитель начальных классов Ольга Катаева.

Родители по-разному относятся к вопросу выполнения домашнего задания. Некоторые помогают, корректируют, контролируют. Некоторые делают задания за ребёнка. А кто-то считает, что выполнение домашнего задания — ответственность ребёнка, и не вмешиваются.

Есть родители, которые предпочитают с детьми не заниматься совсем (это касается не только домашних заданий). Восхищают родители, которые занимаются со своими детьми, помогают им понять то, что решали в классе, разбирают ошибки в контрольных. А есть такие, которые не разбирают материал вместе с ребёнком, а требуют полного заучивания программы, не интересуясь, понял он что-то или нет.

Много раз объясняла родителям, что у детей начальных классов другое мышление

Они не могут думать абстрактными понятиями. Они не могут понять материал, заучив правило или формулу. Чтобы научиться говорить определениями и формулами, младшие школьники должны усвоить понятие на практике.

В начальной школе есть совсем простые темы, а есть темы потруднее. Есть очень трудные. Одна из них — «Площадь и периметр». Взрослым, у которых логическое мышление уже сформировано, эта тема не кажется трудной, поэтому они с лёгкостью объясняют её дома детям, не придерживаясь рекомендаций и объяснений учителя. Родители помнят, как учили эту тему в школе. Правда, не в начальных классах, а в среднем звене и старшем — то есть тогда, когда начинает формироваться логическое и абстрактное мышление. Поэтому подросткам дают формулы.

Дети начальной школы часто путают понятия «площадь» и «периметр»

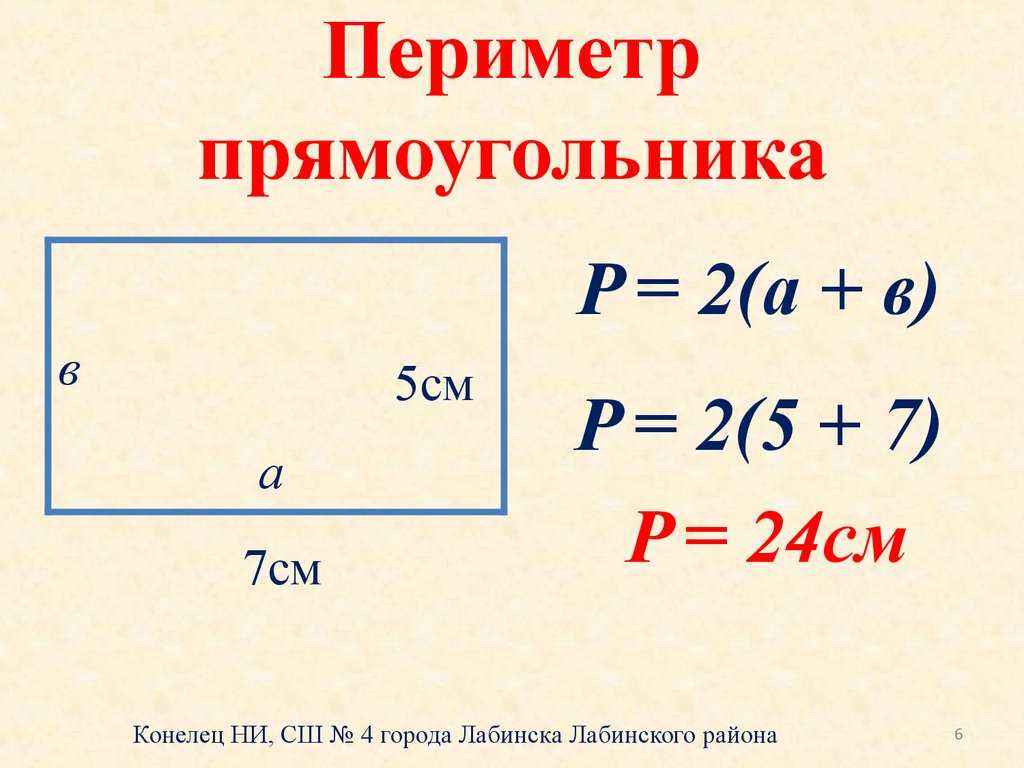
Объяснению и повторению этой темы уделяется не так уж много времени. Родители, видя двойки за контрольные с такими заданиями, пытаются по своему объяснить, как решать. Дают формулу на периметр: P=2а+2b, но не объясняют, что она обозначает.

Вспомним формулу площади S=ab. И в той, и в другой формулах присутствует умножение — это первая причина, почему дети путаются (другие причины надо выяснять, это могут быть пространственно-конструктивные нарушения и др.).

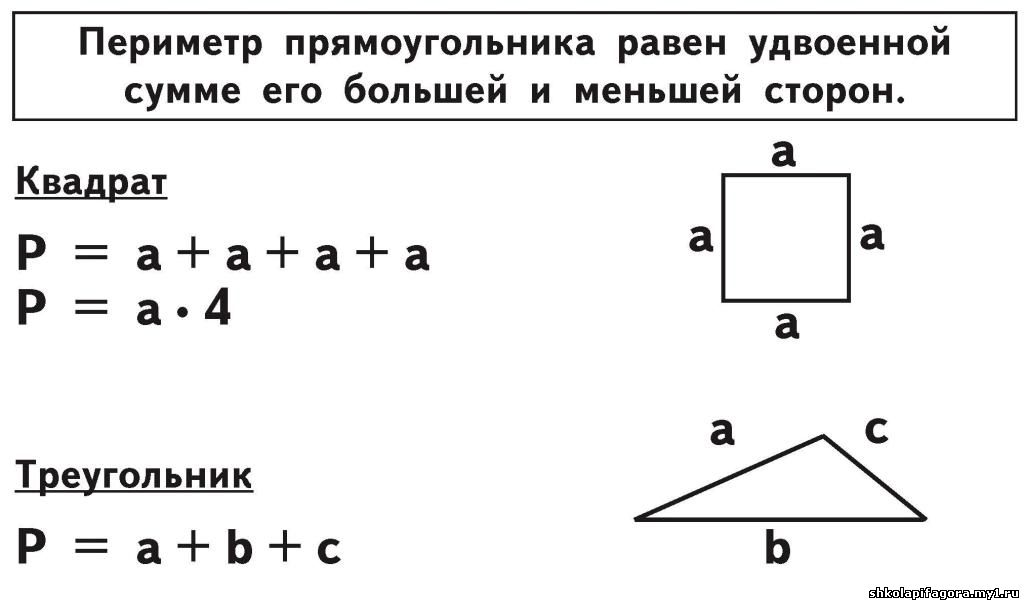
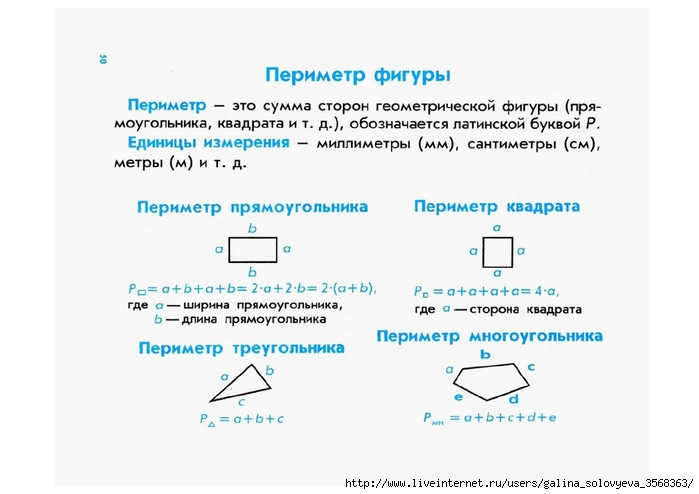
Как можно объяснить эту тему, чтобы ребёнок ее понял? Обратимся к определению периметра: «Пери́метр — общая длина границы фигуры», или «Периметр — длина контура замкнутой плоской фигуры», или так: «Периметр — сумма длины всех сторон плоской геометрической фигуры». В начальной школе даётся такое определение: «Периметр — это сумма длин всех сторон фигуры». Важно понять, что периметр — это весь контур фигуры, то есть мы складываем вместе длины всех сторон.

Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее). Если фигура — прямоугольник, её делят на равные квадратики и считают их.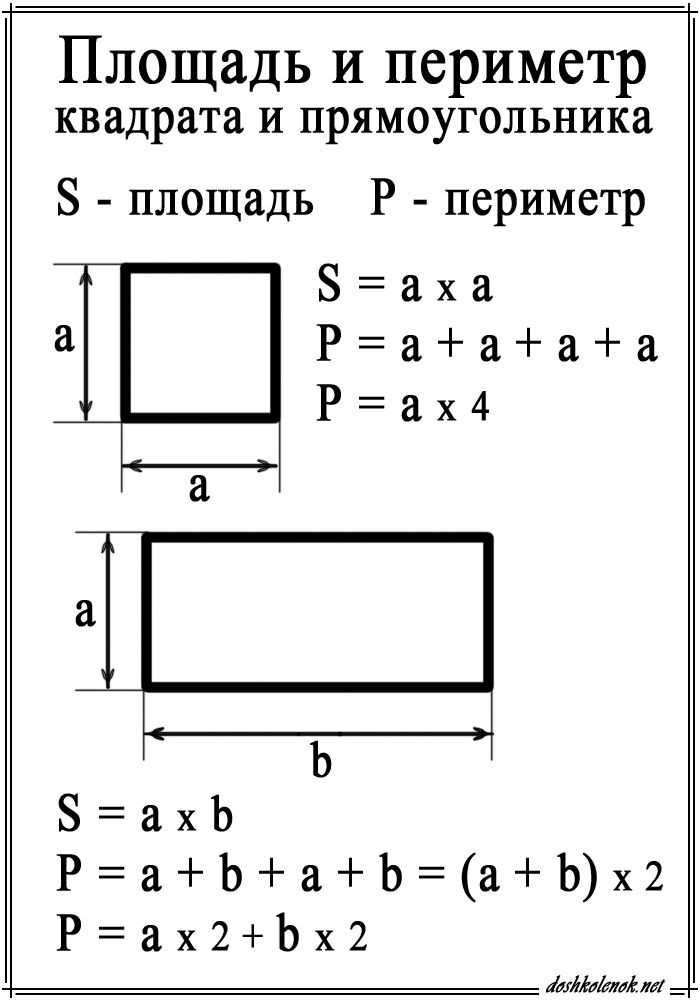 Так можно делать с небольшими фигурами, которые помещаются в тетрадках.

Находить площадь «Красной площади», которая в Москве, так нельзя

Есть формула. Для нахождения площади больших фигур, прямоугольной формы, достаточно знать длину и ширину и перемножить их (можно ввести ассоциацию с таблицей Пифагора, которая тоже поделена на квадратики и значение произведения находят путём умножения чисел).

Вот оно — существенное отличие: периметр — сложение, площадь — умножение. Поэтому в период, когда идёт отработка этих понятий, не следует вводить формулу периметра прямоугольника с умножением. Если ученик поймёт суть понятия «периметр», он сможет найти периметр любого многоугольника. Если зациклить его на формуле для нахождения периметра прямоугольника, школьник не сможет перенести знание для нахождения периметра другой фигуры.

Не надо заучивать с детьми формулы и определения. Надо понимать возрастные особенности младших школьников и объяснять на понятном для них «языке» — через образы, ассоциации, через практику, через действование.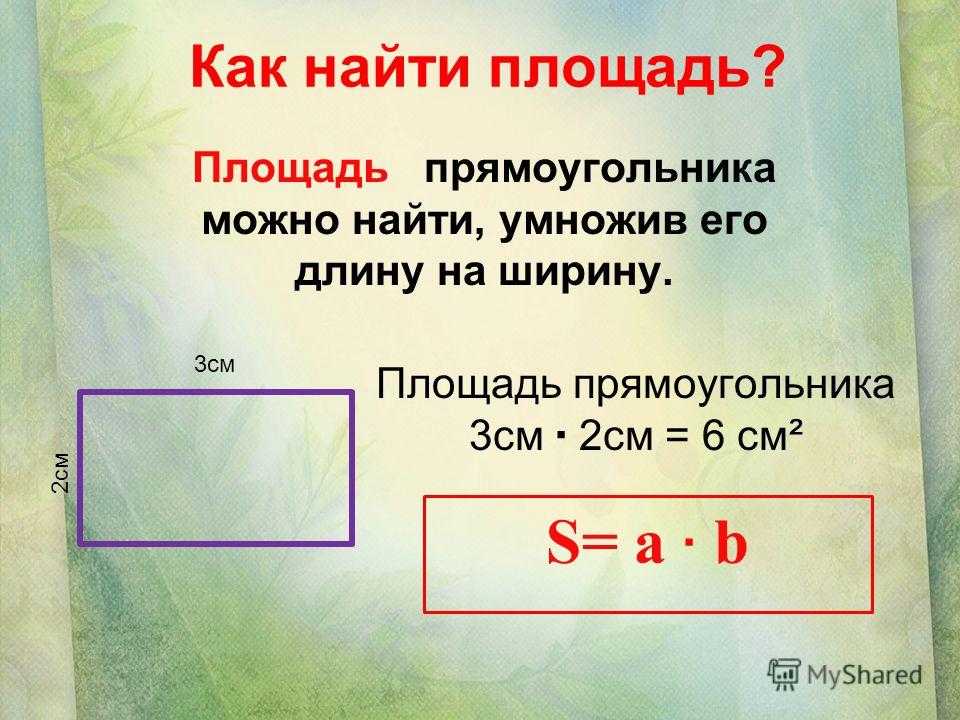

Удачи родителям, которые понимают своих детей и помогают им в нелёгкой учебной жизни.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Фото: Shutterstock / pupunkkop

7 способов найти площадь прямоугольника

10 марта 2020ЛикбезОбразование

Выбирайте формулу, ориентируясь на известные величины.

Поделиться

0

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

• S — искомая площадь прямоугольника;
• a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• d — любая диагональ прямоугольника;
• α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• R — радиус описанной окружности;
• α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

• ТЕСТ:​ ​​Умеете ли вы считать в уме?
• Как легко и быстро считать проценты в уме
• Как найти площадь любого треугольника
• ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
• Как освоить устный счёт школьникам и взрослым

Формула площади и периметра

Как мы знаем, геометрия изучает формы. Геометрия имеет дело с плоскими формами и объемными формами. Мы вычисляем различные термины, связанные с фигурами, такие как длина, ширина, высота, площадь, периметр, объем и т. д. Площадь и объем — два важных понятия, используемых в нашей повседневной жизни. Мы сталкиваемся со многими формами, для которых необходимо рассчитать необходимое пространство и расстояние вокруг них, и это называется площадью и периметром фигур. Мы видим много форм вокруг, таких как квадраты, прямоугольники, круги, многоугольники и т. д. Каждая форма имеет свои уникальные свойства и размеры. Следовательно, каждая форма имеет различную площадь и периметр в зависимости от ее размеров. Итак, здесь, на этой странице, мы будем изучать математические формулы площади и периметра, связанные с различными формами.

Определение площади и периметра

Площадь — это пространство, занимаемое любой двумерной геометрической фигурой, а периметр — это расстояние вокруг фигуры или, можно сказать, граница фигуры.

Способы измерения площади и периметра совершенно разные.

Площадь

Площадь – это измерение пространства, занимаемого любой двумерной геометрической фигурой. Или мы можем сказать, что количество пространства, занимаемого любой формой, предметом или плоской поверхностью, определяется как площадь формы, предмета или плоской поверхности. Фактическая площадь фигуры, объекта или плоской поверхности определяется общим количеством квадратных единиц, которые могут быть включены в нее. Следовательно, площадь фигуры рассчитывается в квадратных единицах (квадратных единицах).

Площадь любой формы зависит от ее размеров. Разные формы имеют разную площадь. Например, площадь квадрата отличается от площади прямоугольника.

Пример 1. Используя бумагу с квадратной сеткой, можно просто применить концепцию определения местоположения области. Общее количество единичных квадратов, включенных в фигуру, равно площади фигуры в квадратных метрах.

Предположим, что любой синий квадрат занимает 9 квадратных единиц, что означает, что квадрат имеет площадь поверхности 9квадратных единиц.

Напр. 2. Предположим, если вы хотите покрасить прямоугольную стену своего дома, вам нужно знать площадь стены, чтобы рассчитать количество краски, необходимой для покраски стены, и стоимость покраски.

Если две фигуры имеют одинаковую форму, нет необходимости, чтобы они имели одинаковую площадь, пока их размеры не станут равными. Предположим, что два квадрата имеют стороны s и s1, поэтому площади двух квадратов будут равны: s = s₁

Также есть много примеров из жизни, например:

• Использование концепции площади для определения площади стены, которую необходимо покрасить.

• Площадь пола комнаты, которую необходимо покрыть плиткой.

• Количество места на заднем дворе, которое необходимо засадить цветами и так далее.

Периметр

Слово «периметр» происходит от греческого слова «периметрон». «Пери» — это латинское слово, означающее «около», а «Метрон» — греческое слово, означающее «мера».

Сложение длин всех сторон формы или измерение внешней границы формы или объекта дает периметр этой формы или объекта. Периметр – это длина границы, ограниченной любой геометрической фигурой. Периметр формы зависит от длины формы.

Например, металлическая проволока длиной 10 см может образовывать как круг, так и квадрат.

Предположим, вам нужно обнести свой дом забором. Длина ограждения – это периметр дома.

Периметры двух фигур могут быть равны, только если их длина одинакова.

Некоторые реальные применения периметра включают:

Нахождение периметров мелких предметов можно выполнить, обмотав веревку или нить вокруг объекта, периметр которого необходимо определить.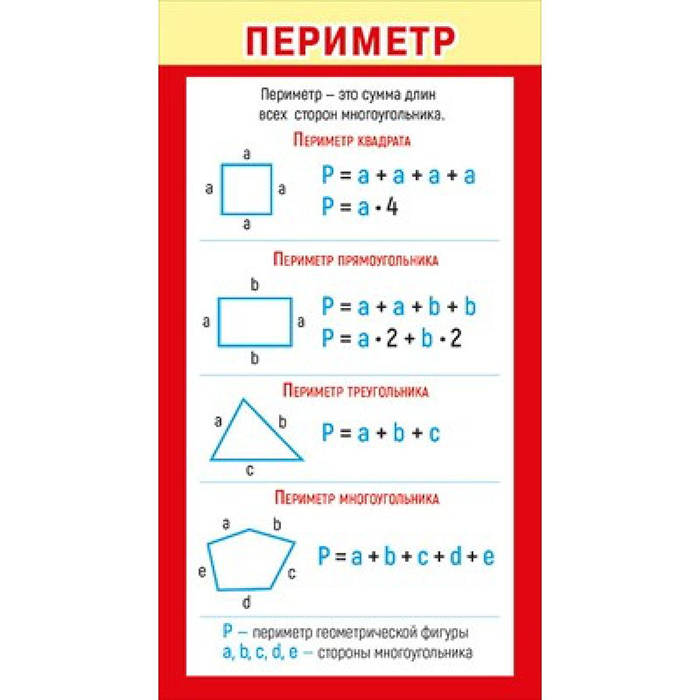

Для многоугольников периметр вычисляется путем суммирования сторон многоугольника и их выражения в предоставленных единицах измерения.

Формулы площади и периметра для всех фигур

Существуют разные типы форм с разными размерами. Поэтому формулы их площади и периметра также различаются. Вот различные формулы площади и периметра для всех фигур. Ниже приведена таблица формул площади и периметра, которая предоставит вам формулы площади и периметра для всех фигур.

Таблица формул площади и периметра0002 Figure

Area Formula

Perimeter Formula

Variables

Rectangle

(image will be uploaded soon)

Area = l x w

Perimeter = 2(д+ш)

Д = длина

Ш = ширина

Квадрат

(изображение скоро будет загружено)

0077

Область = A ²

Периметр = 4A

A = Стороны квадрата

. ½ x b x h

Периметр = сумма всех сторон

b = основание

H = высота

Трейпезоид

(изображение вскоре будет загружено)

(изображение будет загружено)0003

Область = ½ (a+b) H

Периметр = сумма всех сторон

A = BASE1

B = BASE2

H = вертикальная высота

4449 29.0077779 9000 2

9000007 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000007 9000 2

9000 29007 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2

9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2

9000 2.

(изображение будет загружено в ближайшее время)

Площадь = B x H

Периметр = 2 (A+B)

A = сторона

B = База

H = Vertical Height

9007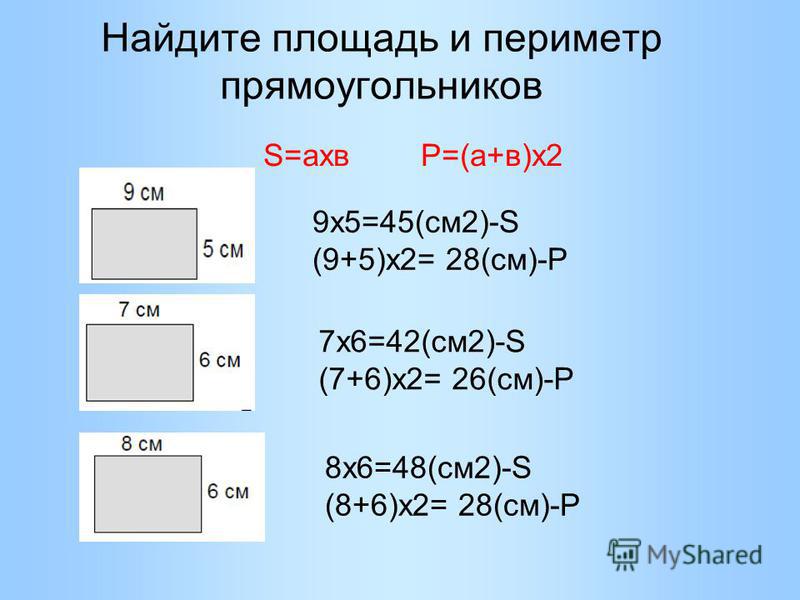4444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444 40002. 0073

Rhombus

(image will be uploaded soon)

Area = a x h

Perimeter = 4a

a = side of the rhombus

h = height

Circle

(изображение будет загружено в ближайшее время)

Область = πr ²

Периметр/окружность =

2πr

R = радиус из круга

R = радиус.0003

= 22/7 or 3.1416

Semicircle

(image will be uploaded soon)

Area =½ πr ²

Perimeter = πr + 2r

r = радиус окружности

Эта таблица формул площади и периметра поможет вам запомнить эти формулы с первого взгляда.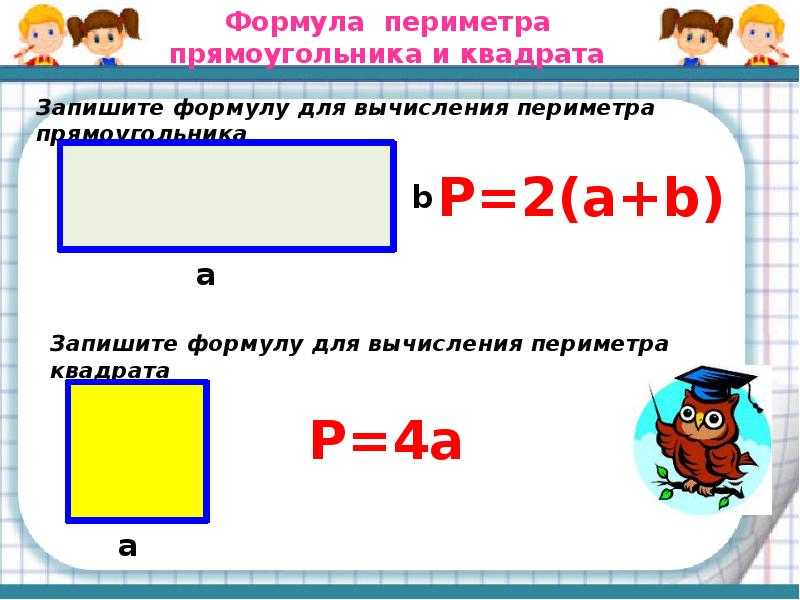 Всегда держите эту область и таблицу формул под рукой.

Решенные примеры

Вот несколько решенных примеров, основанных на формулах площади и периметра различных форм.

Пример 1: Если радиус окружности равен 7 см. Найдите его площадь и длину окружности.

Решение: Учитывая, что радиус = 7 см

Площадь A = π × r ²

A = 22/7 × 7 × 7

A = 154 см ² .

Длина окружности, C = 2πr 

C = 2 x 22/7 x 7

C  = 44 см

Пример 2. Если длина стороны квадрата равна 9см. Затем найдите его площадь и общую длину его границы.

Решение: Учитывая, что длина стороны квадрата, a = 9 см

Мы имеем формулу площади как A = a ²

 = (9) ²

= 81 см ²

9 Итого длина его границы равна периметру квадрата

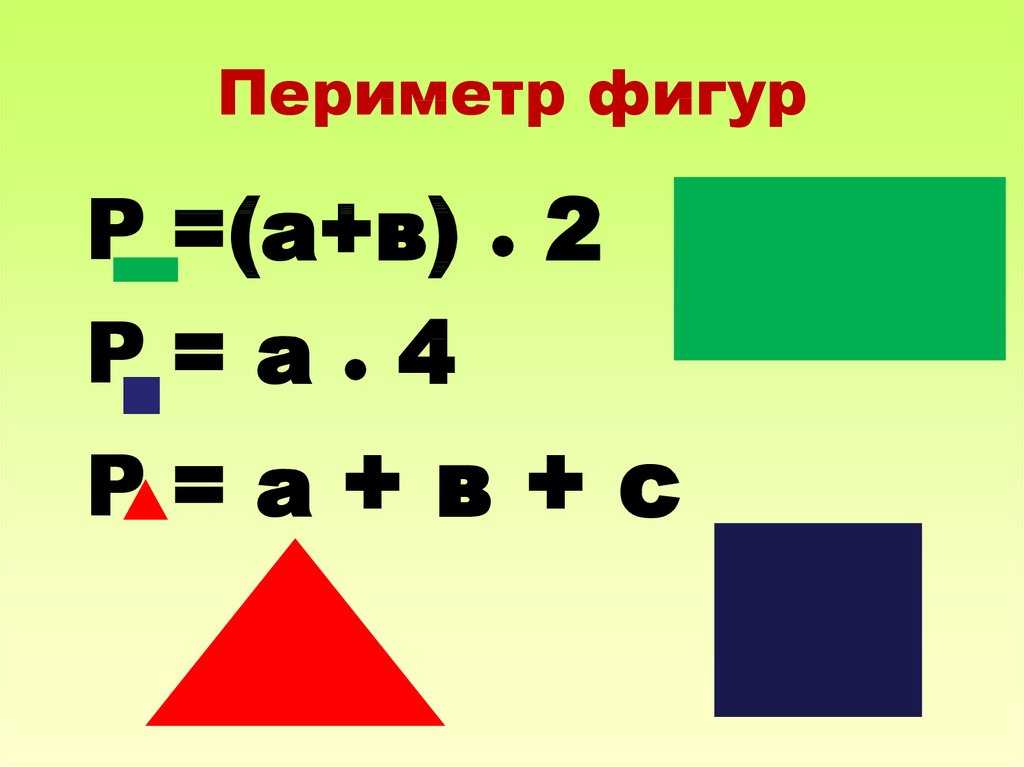. Имеем периметр = 4a

= 4 x 9

= 36см.

Следовательно, площадь квадрата равна 81 см ² , а общая длина его границы равна 36 см.

Пример 3: Длина прямоугольного поля составляет 15 м, а ширина — 6 м. Найдите площадь и периметр поля.

Решение: Учитывая, что, длина = 15m

Ширина = 6m

, мы имеем, площадь формулы A = длина x ширина

= 15 x 6

= 90 M ²

и периметр Формула P = 2 (2 (2 ( длина + ширина)

   = 2 x (15 + 6)

   = 2 x 21

   = 42 м.

Время викторины

Проверьте свои успехи, решив еще несколько задач на площадь и периметр различной формы.

1. Найти стоимость коврового покрытия комнаты длиной 13 м и шириной 9 м из расчета 12,40 рупий за метр.

2. Площадь квадрата 121кв.см. Найдите его сторону.

Заключение:

Математические выводы и приложения становятся трудными для понимания без правильного руководства. Вы можете обратиться к этой статье для полного понимания и лучших результатов.

Периметр круга — веб-формулы

Периметр — это расстояние вокруг замкнутой фигуры, обычно измеряемое в миллиметрах (мм), сантиметрах (см), метрах (м) и километрах (км). Эти единицы связаны следующим образом:

 

10 мм = 1 см

100 см = 1 м

1000 м = 1 км

 

Слово «периметр» также иногда используется вместо окружности.

 

Если мы знаем радиус

Зная радиус окружности, длину окружности или периметр можно рассчитать по формуле bwloe:

 

Периметр (P) = 2 · π · R

где:
R  радиус окружности
π  пи, примерно 3,142

 

Если мы знаем диаметр

Если нам известен диаметр круга, длину окружности можно найти по формуле

Периметр (P) = π · D

где:
D  диаметр круга
π  – число Пи, примерно 3,142.

 

Если мы знаем площадь

Если мы знаем площадь круга, длину окружности можно найти по формуле:

Периметр (P) = √ ( 4 · π · A )

 

где:
A  – площадь круга
π  – число Пи, приблизительно 3,142.

 

 

Пример 1:

Круглая клумба радиусом 9 м. Найдите периметр/длину клумбы.

Решение :

Р = 2 · π · R

Р = 2 · 3,1416 · 9

Р = 56,5487 см

 

Итак, периметр/окружность клумбы составляет 56,5487 м.

 

 

Пример 2: Найдите периметр данного круга, диаметр которого равен 4,4 см.

 

Решение :

Учитывая, что:

Диаметр круга (D) = 4,4 см.

Мы знаем формулу для нахождения периметра круга, если известен диаметр, а именно π· D.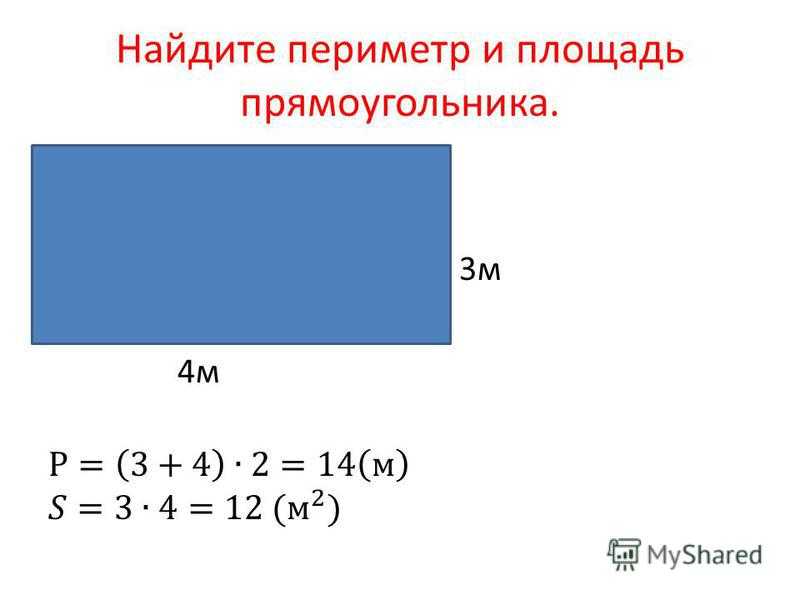

Подставьте диаметр 4,4 и значение Pi на 3,14 в приведенной выше формуле.

 

Периметр = (3,14)(4,4) = 13,82

 

Следовательно, периметр данной окружности равен 13,82 см.

 

 

Пример 3: Если радиус равен 11,7 см. Найдите периметр (длину окружности) круга.

Решение :

 

Учитывая, что:

Радиус (r) = 11,7 см

Периметр (длина окружности) круга P = 2 π r

Подставим значение r в формулу, получим:

Р = 2 х 3,14 х 11,7

Р = 79,56 см

 

Таким образом, периметр круга равен 79,56 см.

 

 

Пример 4: Найдите периметр и площадь круга, если радиус круга равен 8 см.

Решение : Мы задали радиус, который равен 8 см. Итак, воспользовавшись формулой периметра круга, имеем:

Р = 2πr

Р = 2×3,14×8

Р = 50,24 см

 

А для площади круга:-

А = π r ²

А = 3,14×(8) ²

А = 200,96 см ²

 

 

Пример 5: Колесо воловьей повозки имеет радиус 6 м.

No related posts.