7.ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка с постоянными коэффициентами называется уравнение вида
y(n) + a1y(n-1) +….. + an-1y′ + any = f(x), | (7.1) |
где a1, a2,a3 ….,an-1,an – действительные числа; y = f(x) – данная функция.
Рассмотрим ЛНДУ второго порядка |
|
y′′+ a1 y′+ a2 y = f (x) | (7.2) |
и соответствующее ему однородное уравнение (ЛОДУ) |
|
y′′+ a1 y′+ a2 y = 0. | (7.3) |
Пусть y1 и y2 – фундаментальная система решений уравнения (7.3), тогда
есть общее решение уравнения (7.3).
Теорема (о структуре общего решения ЛНДУ).
Общее решение неоднородного уравнения (7.2) равно сумме общего решения соответствующего однородного (7.3) и частного решения неоднородного уравнения (7.2):
yон = yоо + yчн .
Доказательство. Так как yоо- общее решение уравнения (7.3), то по определению решения эта функция обращает уравнение (7.3) в верное равенство. Так как учн- частное решение уравнения (7.2), то функция учн
также обращает это уравнение в тождество. | Имеем два тождества: | |||
| ′′ | ′ |
|
|
| уоо | + a1 yоо + a2 yоо ≡ 0 | ||
|
|
|
| — найдем их сумму: |
( yчн)′′+ a1( yчн)′+ a2 yчн ≡ f (x) | ||||
′′ | ′′ | ′ | ′ |
|
( yоо + yчн) + a1( yоо + yчн) + a2 ( yоо + yчн) ≡ f (x) или | ||||
( yоо + yчн)′′+ a1( yоо + yчн)′+ a2 ( yоо + yчн) ≡ f (x). | ||||
Следовательно, | yон = yоо + yчн является общим решением | |||
уравнения (7.2). | # |
|
|
|
7.1. Нахождение частного решения ЛНДУ со специальной правой частью
В том случае, когда правая часть дифференциальных уравнений (7.1) и (7.2) в общем случае имеет вид
f (x) = eαx [Pm (x) cos βx +Qn (x)sin βx],
где Pm(x) и | Qn(x) — многочлены переменной x степеней m и n;α, β — | |||
действительные | числа, | используется | метод | неопределенных |
коэффициентов (или метод подбора). |
|
| ||
Частное решение yчн | дифференциального уравнения (7.2) зависит в | |||
каждом конкретном случае от вида функции f(x) и от выражения α ±iβ
(где | i = −1 ), | которое | сравнивается | с | корнями характеристического | |
уравнения, составленного для соответствующего ЛОДУ (7.3). |
| |||||
Возможны случаи: |
|
|
| r | ||
1. | Если | α ±iβ | является | корнем кратности | ||
| характеристического уравнения |
|
|
| ||
|
|
| k 2 + a k + a | = 0 | (*) | |
|
|
| 1 | 2 |
|
|
(r – означает сколько раз α ±iβ совпадет с корнями характеристического уравнения). Тогда частное решение находится в виде
|
|
|
| y | = xreαx [M | l | (x)cos βx + N | (x)sin βx], | |||||||
|
|
|
| чн |
|
|
|
|
|
|
|
| l |
| |
Ml (x) и Nl (x) — | многочлены со | своими неопределенными | |||||||||||||
коэффициентами, при этом l = max{m, n}. |
|
| |||||||||||||
Например, если |
|
|
|
|
|
|
|
|
|
|
| ||||
l = 0, | то |
|
| M0 (x) = Ax0 = A |
| — многочлен нулевой степени, | |||||||||
l =1, | то |
|
| M1(x) = Ax + B |
|
| — |
|
| многочлен первой степени, | |||||
l = 2, | то |
|
| M 2 (x) = Ax2 + Bx +C — | многочлен второй степени, | ||||||||||
l = 3, | то |
|
| M3 (x) = Ax3 + Bx2 +Cx + D — | многочлен 3-й степени, | ||||||||||
l, то | M | l | (x) = A xl + A xl −1 +… + A | — многочлен степени l. | |||||||||||
|
|
| 0 |
| 1 |
|
|
|
|
| l |
|
|
| |
2. | Если | α ±iβ | не |
| является | корнем характеристического | |||||||||
уравнения |
| (*), то | r = 0 | и |
| x0 =1, | тогда частное решение yчн имеет | ||||||||
вид |
|
|
| y | = eαx [M | l | (x)cos βx + N | (x)sin βx]. | |||||||
|
|
|
| чн |
|
|
|
|
|
|
| l |
|
| |
Пример 1. Найти общее решение уравнения
y′′−6 y′+9 y = 5e3x
Решение. Находим общее решение соответствующего ЛОДУ:
y′′−6 y′+9 y = 0 .
Его характеристическое уравнение k 2 −6k +9 = 0 имеет корни k1 = k2 = 3. Общее решение однородного уравнения при равных корнях характеристического уравнения имеет вид
yоо = C1e3x +C2 xe3x = e3x (C1 +C2 x) .
Правая часть неоднородного уравнения имеет вид f (x) = 5e3x.
α = 3, β = 0 α ±iβ = 3 — является кратным корнем кратности r = 2
характеристического уравнения, l = max{0,0} = 0 , поэтому
yчн = x2e3x [M0 (x)cos0x + N0 (x)sin 0x] = Ax2e3x.
Дважды дифференцируем yчн:
( yчн)′ = 2Axe3x +3Ax2e3x
( yчн)′′ = 2Ae3x + 6Axe3x + 6Axe3x +9Ax2e3x =
=2Ae3x +12Axe3x +9Ax2e3x
иподставляем полученные выражения в данное уравнение:
2Ae3x +12Axe3x | +9Ax2e3x −12Axe3x −18Ax2e3x +9x2e3x = 5e3x. | ||||||||||||||||||||
В результате получим |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
| 2Ae3x | = 5e3x 2A = 5 A = 2,5. | ||||||||||||||||
Тогда y | = 2,5x2e3x. А общее решение неоднородного уравнения | ||||||||||||||||||||
чн |
|
|
|
|
|
|
|
|
|
|
| = e3x |
|
|
| x) + 2,5x2e3x. | |||||
y | он | = y |
| + y |
| (C +C | 2 | ||||||||||||||
|
|
|
|
| оо |
| чн |
|
| 1 |
|
|
|
|
|
| |||||
Ответ: y = e3x (C +C | 2 | x) + 2,5x2e3x. ■ |
|
|
|
|
|
|
| ||||||||||||
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Пример 2. Решить задачу Коши для уравнения |
| ′ | |||||||||||||||||||
y | ′′ | + y | ′ | − 2 y = cos x −3sin x , |
|
|
|
|
| ||||||||||||
|
|
| если y(0) =1, y (0) = 2. | ||||||||||||||||||
Решение. Находим общее решение соответствующего ЛОДУ | |||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| y′′+ y′− 2 y = 0. |
|
|
|
| |||||
Его характеристическое уравнение: | k 2 + k − 2 = 0, | ||||||||||||||||||||
|
|
|
|
|
| k = −1 ±3; |
| k =1;k | 2 | = −2. | |||||||||||
|
|
|
|
|
|
| 1,2 |
|
|
| 2 |
|
| 1 |
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Общее решение ЛОДУ | при различных корнях характеристического | ||||||||||||||||||||
уравнения имеет вид |
| = C ek1x + C |
| ek2 x = C e x |
|
|
| e−2x . | |||||||||||||
|
|
| y | оо | 2 |
| + C | 2 | |||||||||||||
|
|
|
|
|
|
| 1 |
|
|
|
|
| 1 |
|
|
| |||||
Правая часть данного уравнения: | f (x) = cos x −3sin x. | ||||||||||||||||||||
α = 0, β =1 α ±iβ = ±i | — не являются корнями характеристического | ||||||||||||||||||||
уравнения r = 0, |
| l = max{0,0} = 0 . |
|
|
|
|
|
|
| ||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yчн = x r eαx | [M l (x) cos βx + Nl (x) sin βx] = A cos x + B sin x. | ||||||||||||||||||||
Дифференцируя, получим |
|
|
|
|
|
|
|
|
|
|
| ||||||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
| , | ′′ | = −A cos x − B sin x . | |||||
yчн = −Asin x + B cos x | yчн | ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ′ | ′′ |
|
|
|
|
|
|
| |
Подставим значения yчн , yчн , y | чн в данное уравнение, будем иметь | ||||||||||||||||||||
− Acos x − Bsin x − Asin x + B cos x −
− 2A cos x − 2B sin x ≡ cos x − 3sin x .
Приравнивая коэффициенты при сosx | и sinx в левой и правой частях, | |
получим систему |
|
|
−3A + B =1 |
| A = 0, |
| B =1. | |
− A −3D = −3 |
| |
Тогда | y | чн | = sin x, а |
| y | он | = y | оо | + y | чн | = C e x +C | 2 | e−2x +sin x — | ||||||||
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
| |||||||
общее решение данного уравнения. |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
Найдем | ′ | = C1e | x | − 2C2e | −2x | + cos x. |
|
|
|
|
|
|
|
|
| ||||||
yон |
|
|
|
|
|
|
|
| y =1, y′ = 2 : | ||||||||||||
Используя начальные условия, найдем С1 и С2 | при | x=0, | |||||||||||||||||||
|
| 1 = C | +C |
|
|
|
| C | +C |
| =1 |
| C |
| =1, | ||||||
|
|
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
|
|
| |||||
| 2 | = C2 − 2C2 +1 |
| C1 − 2C2 =1 |
| C2 = 0. | |||||||||||||||
Подставляя значения С1 и С2 в общее решение, получим частное
решение yчаст. = ex + sin x . Ответ: yчаст. = ex + sin x . ■
7.2. Принцип наложения (суперпозиции)
Этот метод основан на следующей теореме:
Теорема. Если правая часть f (x) ЛНДУ (7.1) представляет сумму двух функций, т.е. f (x) = f1(x) + f2 (x) , то частное решение такого ДУ можно получить как сумму частных решений аналогичных уравнений с правыми частями соответственно f1(x) и f2 (x) , т.е.
yчн = y1чн(x) + y2чн(x) .
Доказательство. Рассмотрим два уравнения:
y′′+ a1 y′+ a2 y = f1(x) и y′′+ a1 y′+ a2 y = f2 (x) .
Пусть y1чн(x) и y2чн(x) являются частными решениями этих уравнений соответственно, тогда имеем два тождества:
( y1чн)′′+ a1( y1чн)′+ a2 y1чн ≡ f1(x) — найдем их сумму:
( y2чн)′′+ a1( y2чн)′+ a2 y2чн ≡ f2 (x)
[( y1чн)′′+( y2чн)′′] + a1[( y1чн)′+( y2чн)′] +
+ a2 ( y1чн + y2чн) ≡ f1(x) + f2 (x)
или ( y1чн + y2чн)′′+ a1( y1чн + y2чн)′+ a2 ( y1чн + y2чн) ≡ f1(x) + f2 (x).
Следовательно, yчн = y1чн + y2чн является решением уравнения
y′′+ a1 y′+ a2 y = f1(x) + f2 (x) . #
Пример. Найти общее решение уравнения
y′′+ y′ = x + e2x .
Решение. Так как правая часть уравнения
f (x) = x + e2x = f (x) + f | 2 | (x) , | то | по | теореме общее решение | ||||||||||||||||
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
данного уравнения будет иметь вид |
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
| yон = yоо + yчн1 + yчн2 . |
|
|
| |||||||||||||
Найдем | yоо. Для этого рассмотрим уравнение y′′+ y′ = 0, его | ||||||||||||||||||||
характеристическое уравнение |
| k 2 + k = 0 имеет корни k1=0; k2= -1. | |||||||||||||||||||
Тогда | y | оо | = C ek1x | +C | 2 | ek2 x | = C e0x +C | 2 | e−x | = C +C | 2 | e−x | |||||||||
|
|
| 1 |
|
|
|
|
|
|
|
| 1 |
|
| 1 |
| |||||
Найдем у1чн. |
|
|
|
|
|
|
|
|
|
| y′′+ y′ = x |
|
|
|
| ||||||
Для этого рассмотрим уравнение |
|
|
|
| |||||||||||||||||
Правая часть |
| f1(x) = x α1 = 0; β1 = 0;l =1. |
|
|
| ||||||||||||||||
Так как | α1 ±iβ1 = 0 ± 0i = 0 — является простым корнем |
|
| ||||||||||||||||||
характеристического уравнения r =1, тогда |
|
|
|
|
|
| |||||||||||||||
|
| y |
| = xr eα1x | [M | l | (x) cos β x + N | l | (x) sin β x] = |
| |||||||||||
|
| 1чн |
|
|
|
|
|
|
|
|
|
| 1 |
|
| 1 |
|
| |||
| = x[(Ax + B)cos0x + (Cx + D)sin 0x] = x( Ax + B). | ||||||||||||||||||||
Подставим y1чн = Ax2 + Bx , ( y1чн)′ = 2Ax + B , | ( y1чн)′′ = 2A в | ||||||||||||||||||||
рассматриваемое уравнение | y′′+ y′ = x : |
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
| 2A + 2Ax + B = x , |
|
|
|
|
| ||||||||||
используя условие равенства многочленов, получим |
|
|
| ||||||||||||||||||
|
|
|
|
| 2A =1 |
|
| 1 |
|
|
|
|
| ||||||||
|
|
|
|
|
| A = 2 , |
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| 2A + B = 0 |
| B =1. |
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 x2 |
|
|
| ||||
Таким образом, получим |
| y |
|
|
| = | − x. |
|
|
|
|
|
| ||||||||
Найдем у2чн . |
|
|
|
|
| 1чн |
| 2 |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
| y′′+ y′ = e2x |
|
|
| ||||||||
Для этого рассмотрим уравнение |
|
|
| ||||||||||||||||||
Правая часть | f2 (x) = e2x . Для | f2 (x) :α2 = 2; β2 = 0; l = 0 . | |||||||||||||||||||
α2 ± β2i = 2 ± 0i = 2 — |
| не |
|
|
| является | корнем | характеристического | |||||||||||||
уравнения r = 0, поэтому
y2чн = xr eα2 x [Ml (x) cos β2 x + Nl (x) sin β2 x]= = x0e2x [Acos 0x + B sin 0x]= Ae2x ;
studfiles.net
Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.
Рассмотрим уравнение вида
С учетом обозначения можно записать:
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале ( конечном или бесконечном).
Теорема. Общее решение линейного неоднородного дифференциального уравнения в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.
Доказательство. Пусть Y – некоторое решение неоднородного уравнения.
Тогда при подстановке этого решения в исходное уравнение получаем тождество:
Пусть — фундаментальная система решений линейного однородного уравнения. Тогда общее решение однородного уравнения можно записать в виде:
Далее покажем, что сумма является общим решением неоднородного уравнения.

Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением.
Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором.
На практике удобно применять метод вариации произвольных постоянных.
Для этого сначала находят общее решение соответствующего однородного уравнения в виде:
Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:
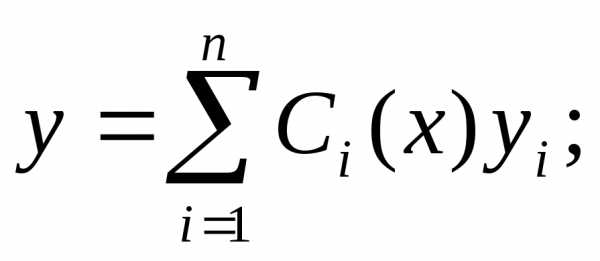
Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:

Пример. Решить уравнение
Решаем линейное однородное уравнение
Решение неоднородного уравнения будет иметь вид:
Составляем систему уравнений:
Решим эту систему:
Из соотношения найдем функциюА(х).
Теперь находим В(х).
Подставляем полученные значения в формулу общего решения неоднородного уравнения:
Окончательный ответ:
Таким образом, удалось избежать нахождения частного решения неоднородного уравнения методом подбора.
Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.
Линейные неоднородные дифференциальные уравнения с постоянными
коэффициентами.
Уравнения с правой частью специального вида.
Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.
Различают следующие случаи:
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
где — многочлен степениm.
Тогда частное решение ищется в виде:
Здесь Q(x)— многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Пример. Решить уравнение .
Решим соответствующее однородное уравнение:
Теперь найдем частное решение исходного неоднородного уравнения.
Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.
Частное решение ищем в виде: , где
Т.е.
Теперь определим неизвестные коэффициенты А и В.
Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.
Итого,
частное решение: 
Тогда общее решение линейного неоднородного дифференциального уравнения:
II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:
где
число r показывает сколько раз число 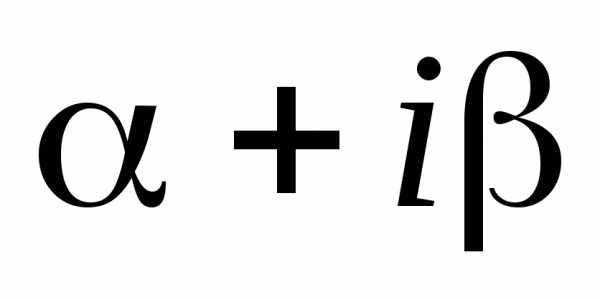 является корнем характеристического
уравнения для соответствующего
однородного уравнения, аQ1(x) и Q2(x) – многочлены степени не выше m,
где m—
большая из степеней m1 и m2.
является корнем характеристического
уравнения для соответствующего
однородного уравнения, аQ1(x) и Q2(x) – многочлены степени не выше m,
где m—
большая из степеней m1 и m2.
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т.е. если уравнение имеет вид: , то частное решение этого уравнения будет гдеу1 и у2 – частные решения вспомогательных уравнений
и
Для иллюстрации решим рассмотренный выше пример другим способом.
Пример. Решить уравнение
Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (—sinx).
Составим и решим характеристическое уравнение:
Для функции f1(x) решение ищем в виде .
Получаем: Т.е.
Итого: 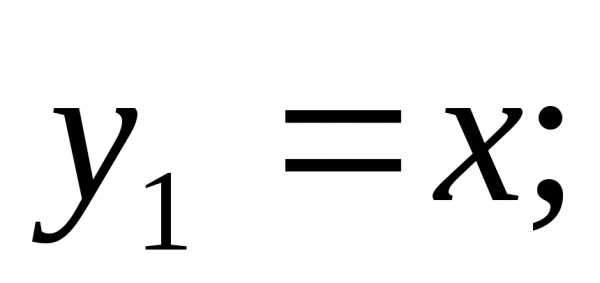
Для функции f2(x) решение ищем в виде: .
Анализируя функцию f2(x), получаем:
Таким образом,

Итого: 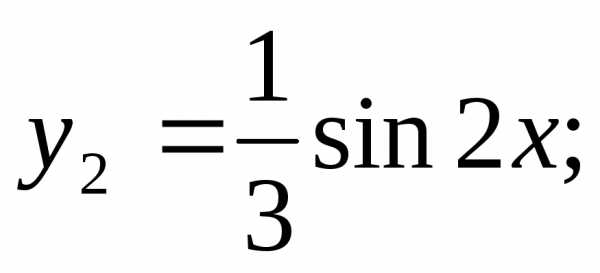
Т.е. искомое частное решение имеет вид:
Общее решение неоднородного дифференциального уравнения:
Рассмотрим примеры применения описанных методов.
Пример. Решить уравнение
Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
Общее решение однородного уравнения:
Теперь найдем частное решение неоднородного уравнения в виде:
Воспользуемся методом неопределенных коэффициентов.
Подставляя в исходное уравнение, получаем:
Частное
решение имеет вид: 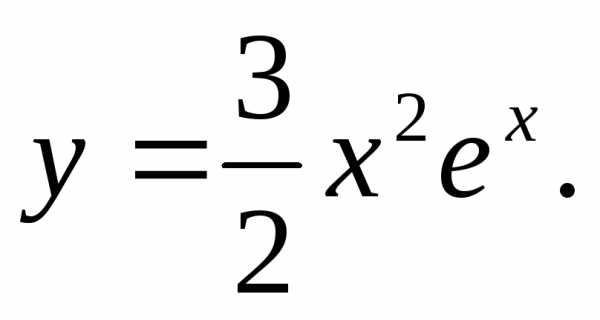
Общее решение линейного неоднородного уравнения:
Пример. Решить уравнение
Характеристическое уравнение:
Общее решение однородного уравнения:
Частное решение неоднородного уравнения: .
Находим производные и подставляем их в исходное неоднородное уравнение:
Получаем общее решение неоднородного дифференциального уравнения:
Нормальные системы обыкновенных дифференциальных уравнений.
Определение. Совокупность соотношений вида:
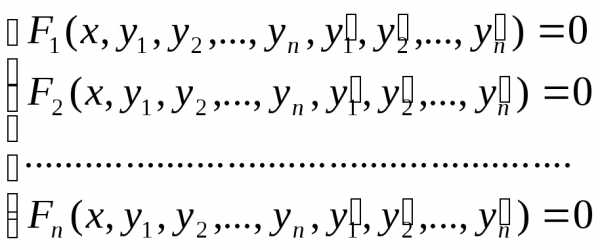
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.
Такая система имеет вид:
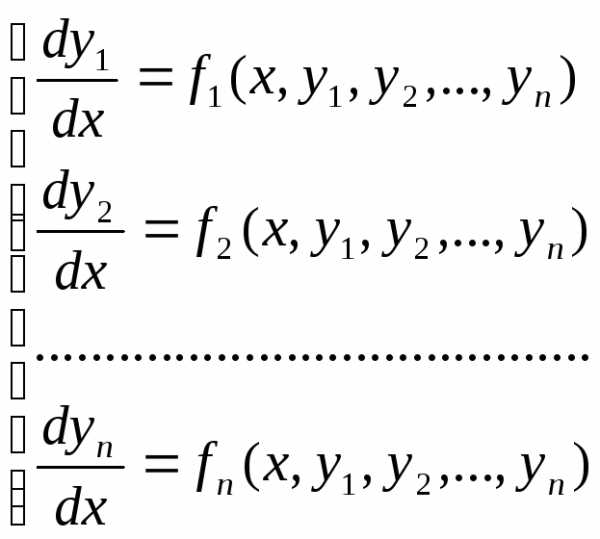 (1)
(1)
Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.
Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции …непрерывны и имеют непрерывные частные производные по, то для любой точкиэтой области существует единственное решение
системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям
Определение. Общим решением системы дифференциальных уравнений вида (1) будет совокупность функций ,, …, которые при подстановке в систему (1) обращают ее в тождество.
studfiles.net
Линейные неоднородные дифференциальные уравнения
Линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка с постоянными коэффициентами — это уравнения вида
\[y» + py’ + qy = f(x)\]
Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами можно записать как сумму
\[y = {y_o} + Y,\]
где \({y_o}\) — это общее решение линейного однородного уравнения с постоянными коэффициентами
\[y» + py’ + qy = 0,\]
Y- частное решение ЛНДУ.
В некоторых специальных случаях частное решение ЛНДУ может быть найдено методом неопределенных коэффициентов, в общем случае используют метод вариации произвольных постоянных. В данном пункте мы рассмотрим неоднородные дифференциальные уравнения с правой частью специального вида и применим метод неопределенных коэффициентов, а метод вариации произвольных постоянных будет изложен позже.
Общее решение неоднородного дифференциального уравнения второго порядка ищем в зависимости от вида правой части, то есть от функции f(x).
I
\[f(x) = {e^{ax}}{P_n}(x)\]
где \({P_n}(x)\) — многочлен степени n.
Ia. Если a не является корнем характеристического уравнения, то есть
\[a \ne {k_1},a \ne {k_2},\]
то частное решение ЛНДУ ищем в виде
\[Y = {e^{ax}}{Q_n}(x),\]
где \({Q_n}(x)\) — многочлен степени n с постоянными коэффициентами.
(Подробно. Это значит, что если степень Р равна 0 (то есть f(x) — произведение е в какой-либо степени и некоторого числа, либо f(x) — только число (в этом случае степень e равна нулю)), то и Q — многочлен нулевой степени, то есть число. В этом случае Q=A. А — неопределенный коэффициент, который будем искать.
Если степень P равна 1 (то есть, f(x) равна произведению е в какой-либо степени и mx, где m — некоторое число, либо f(x) — только mx (если e в нулевой степени)), то и Q — многочлен первой степени, значит, его будем искать в виде Q=Ax+B, где A и B — неопределенные коэффициенты.
Если степень P — вторая (то есть, f(x) есть произведение e в какой-либо степени и mx², или f(x) — только mx² (если e в нулевой степени)), то и Q — многочлен второй степени, его будем искать в виде Q=Ax²+Bx+C, где A,B,C — неопределенные коэффициенты. И т.п.)
Iб. Если a — один из корней характеристического уравнения, то если верно только одно из равенств
\[a = {k_1},a = {k_2},\]
, то частное решение ЛНДУ ищем в виде
\[Y = x{e^{ax}}{Q_n}(x).\]
Iв. Если a — кратный корень характеристического уравнения, то есть
\[a = {k_1} = {k_2},\]
(например, при дискриминанте, равном 0), то частное решение неоднородного дифференциального уравнения второго порядка в этом случае есть
\[Y = {x^2}{e^{ax}}{Q_n}(x).\]
II
\[f(x) = {e^{ax}}[{P_n}(x)\cos bx + {Q_m}(x)\sin bx].\]
IIa. Если a+bi не является корнем характеристического уравнения, то есть
\[a \pm bi \ne \alpha \pm \beta i,\]
то частное решение неоднородного дифференциального уравнения ищем как
\[Y = {e^{ax}}[{S_N}(x)\cos bx + {T_N}(x)\sin bx],\]
где \({S_N}(x),{T_N}(x) — \) многочлены степени N, N — больная из степеней n и m.
IIб. Если a+bi является корнем характеристического уравнения, то есть
\[a \pm bi = \alpha \pm \beta i,\]
то для этого случая частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами ищем в виде
\[Y = x{e^{ax}}[{S_N}(x)\cos bx + {T_N}(x)\sin bx].\]
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
calcsbox.com
Линейные неоднородные дифференциальные уравнения (лнду)
1.Структура общего решения лнду второго порядка.
Рассмотрим ЛНДУ второго порядка
(20)
Где  — заданные непрерывные на (a,b)
функции ,уравнениелевая часть которого совпадает с левой
частью нашего уравнения называетсясоответствующим емуоднородным
уравнением .
— заданные непрерывные на (a,b)
функции ,уравнениелевая часть которого совпадает с левой
частью нашего уравнения называетсясоответствующим емуоднородным
уравнением .
Теорема : Общим решением уравнения (20) (y) является сумма его произвольного частного решенияy* и общего решениясоответствующего однородного уравнения т.е.. Доказательство этой теоремы опустим.
2.Метод вариации произвольных постоянных.
Рассмотрим ЛНДУ (20) .Его общим решением,
согласно только, что приведенной теоремы
является соотношение .
Чаcтное решениеy*
уравнения (20) можно найти ,если известно
общее решение соответствующего
однородного уравнения
соответствующего
однородного уравнения методом
вариации произвольных постоянных
(метод Лагранжа) состоящий в следующем:
пусть- общее решение однородного уравнения.
методом
вариации произвольных постоянных
(метод Лагранжа) состоящий в следующем:
пусть- общее решение однородного уравнения. Заменим
в общем решении постоянные
Заменим
в общем решении постоянные и
и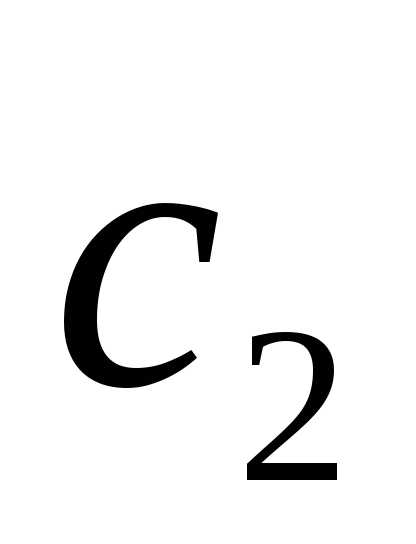 неизвестными
функциями
неизвестными
функциями и
и и
подберем их так, чтобы функциябыла
решением уравнения (20).Найдем производную
и
подберем их так, чтобы функциябыла
решением уравнения (20).Найдем производную
Подберем функции  и
и так, чтобы,
(21), тогда
так, чтобы,
(21), тогда
, а .
Подставляя выражения для y*
, и
и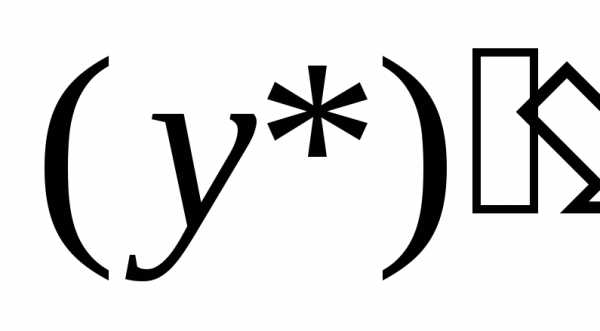 в уравнение (20) получим
в уравнение (20) получим
Или
Поскольку 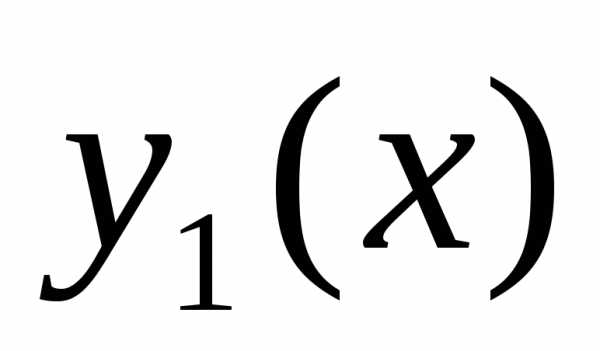 и
и — решение соответствующего однородного
уравнения, то выражения в квадратных
скобках равны нулю, и поэтому
— решение соответствующего однородного
уравнения, то выражения в квадратных
скобках равны нулю, и поэтому
 (22)
(22)
Таким образом, функция y*
будет частным решением уравнения (20)
если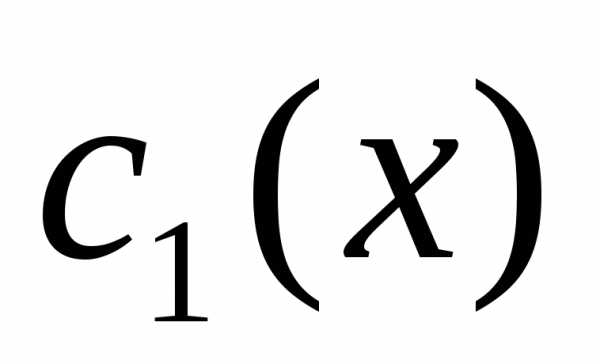 и
и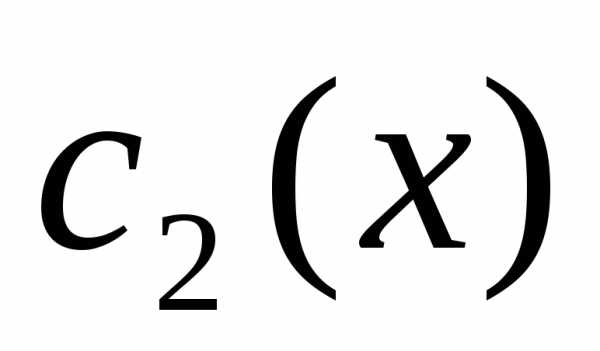
удовлетворяют системе уравнений (21) и (22).
(23)
Определитель системы 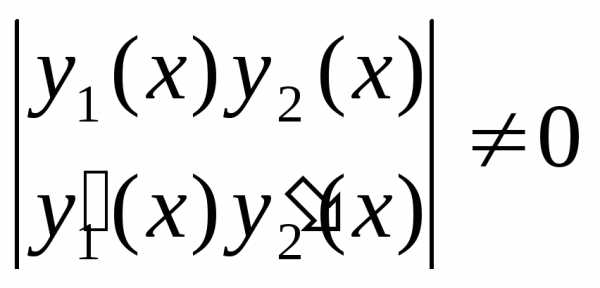 ,так как это определитель для фундаментальной
системы частных решений
,так как это определитель для фундаментальной
системы частных решений и
и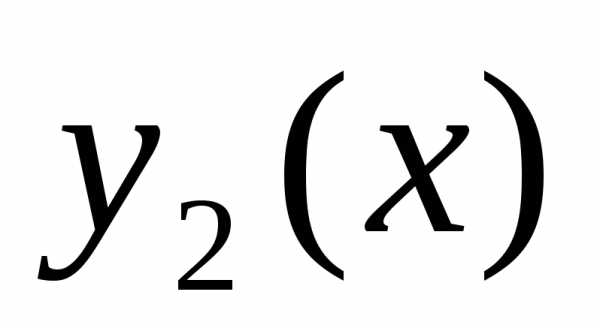 однородного уравнения .Поэтому система
(23) должна иметь единственное решениеи,
где
однородного уравнения .Поэтому система
(23) должна иметь единственное решениеи,
где и
и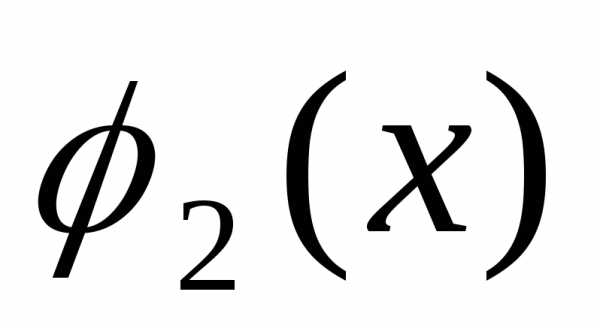 —
некоторые функции отx.
Интегрируя эти функции находим
—
некоторые функции отx.
Интегрируя эти функции находим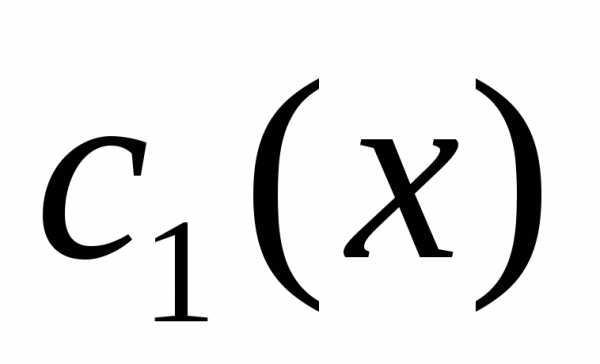 и
и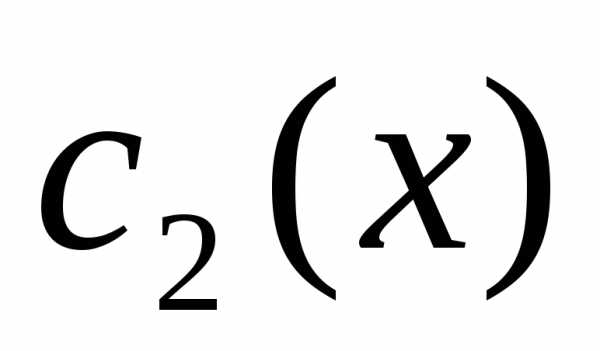 ,
а затем , в соответствии с формулой для
у* составляем частное решение уравнения
(20).
,
а затем , в соответствии с формулой для
у* составляем частное решение уравнения
(20).
Пример: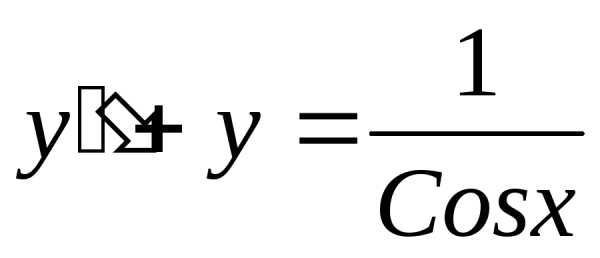 ;
;
Найдем общее решение  соответствующего однородного уравнения.
Имеем
соответствующего однородного уравнения.
Имеем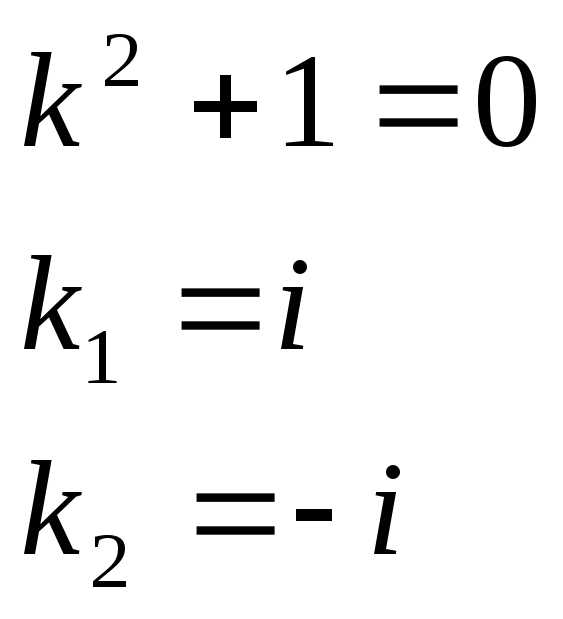

Следовательно,
.Теперь
найдем частное решение у* исходного
уравнения .Оно, как говорилось выше,
ищется в виде.Для
нахождения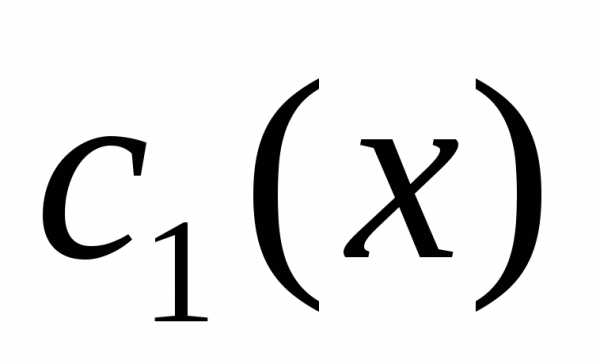 и
и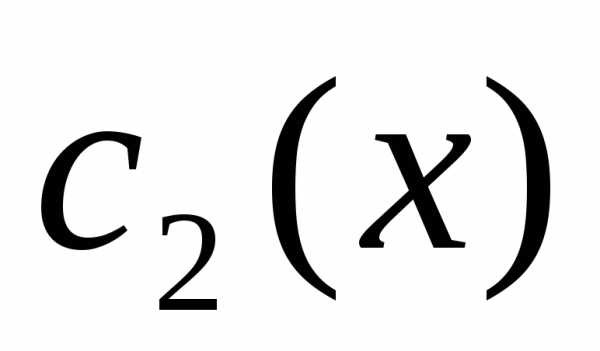 составим
систему уравнений
составим
систему уравнений
Решаем ее
;
Запишем частное решение данного уравнения .Следовательно, общее решение данного уравнения имеет вид
.
При нахождении частных решений ЛНДУ может оказаться полезной следующая теорема:
Теорема: Если правая часть
уравнения (20) представляет собой сумму
двух функций,
а и
и —
частные решения уравненийисоответственно, то функцияявляется частным решением данного
уравнения.
—
частные решения уравненийисоответственно, то функцияявляется частным решением данного
уравнения.
3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами т.е. уравнение
(24)
Где pиg–
некоторые числа согласно вышеприведенной
теореме. Общее
решение этого уравнения представляет
собой сумму общего решения
Общее
решение этого уравнения представляет
собой сумму общего решения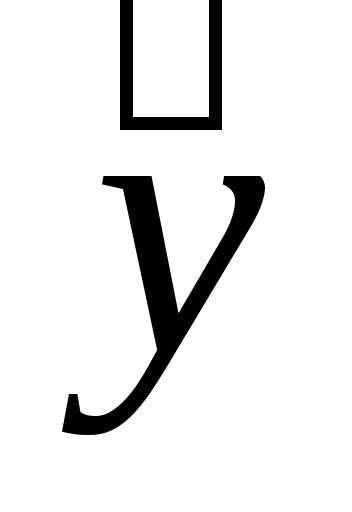 соответствующего
однородного уравнения и частного решения
у* неоднородного. Частное решение может
быть найдено методом вариации произвольных
постоянных.
соответствующего
однородного уравнения и частного решения
у* неоднородного. Частное решение может
быть найдено методом вариации произвольных
постоянных.
Однако, для уравнений с постоянными
коэффициентами существует более простой
способ нахождения у* ,если правая часть  уравнения имеет «специальный вид»:
уравнения имеет «специальный вид»:
I . илиII.
Cуть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой частиf(x) уравнения (24) записывают ожидаемую форму частного решения с неопределенными коэффициентами , затем подставляют его в уравнение (24) и из полученного тождества находят значение коэффициентов.
Вариант 1. Правая часть имеет вид,
где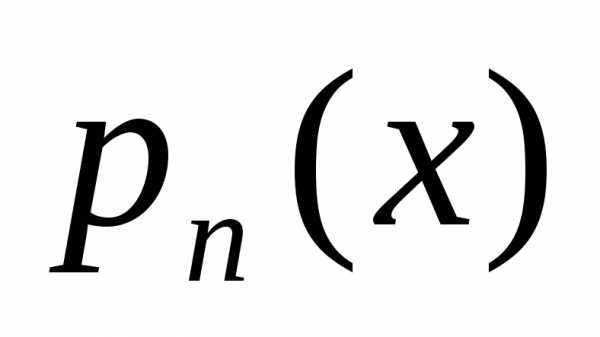 —
многочлен степениn.
—
многочлен степениn.
Уравнение (24) запишется в виде (25)
В этом случае частное решение y*
ищется в виде.
Здесьr– число кратности ,
как корня характеристического уравнения.
,
как корня характеристического уравнения.
(т.е.r– число, показывающее,
сколько раз является корнем уравнения),
а- многочлен степениn,
записанный неопределенными коэффициентами
является корнем уравнения),
а- многочлен степениn,
записанный неопределенными коэффициентами
а) Пусть  не является корнем характеристического
уравненият.е.
не является корнем характеристического
уравненият.е.
 .
Следовательно,
.
Следовательно,
После подстановки функции y*
и ее производных в уравнение (25) и
сокращения на ,
получим :(26)
,
получим :(26)
Слева многочлен степени nс неопределенными коэффициентами, справа – многочлен степениn, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях, получим систему (n+ 1) алгебраических уравнений для определения коэффициентов.
б) Пусть  является однократным (простым) корнем
характеристического уравнения
является однократным (простым) корнем
характеристического уравнения
,т.е.. В этом случае искать решение в форме
нельзя , т.к., и уравнение (26)принимает вид
.
В левой части многочлен степени (n-1) , а в правой многочлен степениn.Чтобы получить тождество многочленов в решении у* нужно иметь многочлен тоже степени
(n-1), поэтому частное решение у* следует искать в виде(в частном решении (25) положить (r= 1)).
в) Пусть  является двукратным корнем
характеристического уравнения,
т.е..
В этом случае,
а поэтому уравнение (26) принимает вид.
Слева стоит многочлен степениn-2.
Понятно, что чтобы иметь слева многочлен
степениn,частное решение
у* следует искать в виде
является двукратным корнем
характеристического уравнения,
т.е..
В этом случае,
а поэтому уравнение (26) принимает вид.
Слева стоит многочлен степениn-2.
Понятно, что чтобы иметь слева многочлен
степениn,частное решение
у* следует искать в виде
( т.е. в частном решении уравнения (25) надо положитьr=2).
Вариант 2. Правая часть уравнения (24) имеет вид
, где- многочлены степениnиmсоответственно,- действительные числа. Уравнение (24) запишется в виде(27)
Можно показать, что в этом случае частное решение у* последнего уравнения следует искать в виде
(28) , где
r– число , равное кратности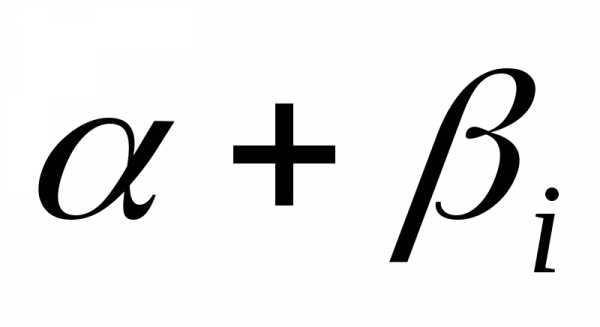 , как корня характеристического уравнения,-
многочлены степени
, как корня характеристического уравнения,-
многочлены степени с
неопределенными коэффициентами,
с
неопределенными коэффициентами,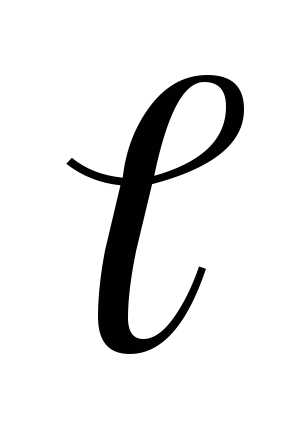 —
наивысшая степень многочленов,т.е.
—
наивысшая степень многочленов,т.е.
 =max(n,m).
=max(n,m).
Примечания:
При подстановке функции (28) в (27) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения .
Формула (28) сохраняется и в случаях, когда .
Если правая часть уравнения (24) есть сумма вида I илиII то для нахождения у* следует использовать теорему о наложении решений.
Пример:
Найдем общее решение  ЛОДУ,
его характеристическое уравнение
ЛОДУ,
его характеристическое уравнение
имеет корень кратности 2. Значит.
Находим частное решение исходного
уравнения .В нем правая частьесть формула вида
кратности 2. Значит.
Находим частное решение исходного
уравнения .В нем правая частьесть формула вида
 ,
причем
,
причем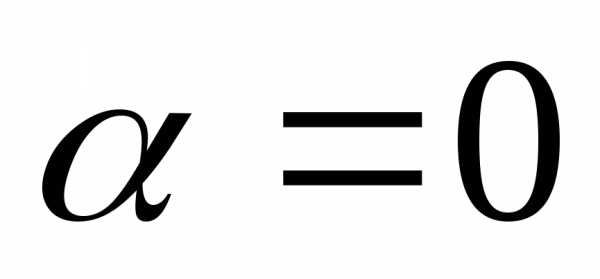 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения .
Поэтому , частное решение ищем как
частное решение уравнения (25) в виде,т.е.,
гдеAиB–
неопределенные коэффициенты .Тогда.
Подставивв исходное уравнение получим,
или.
Приравнивая коэффициенты при одинаковых
степенях
.
Поэтому , частное решение ищем как
частное решение уравнения (25) в виде,т.е.,
гдеAиB–
неопределенные коэффициенты .Тогда.
Подставивв исходное уравнение получим,
или.
Приравнивая коэффициенты при одинаковых
степенях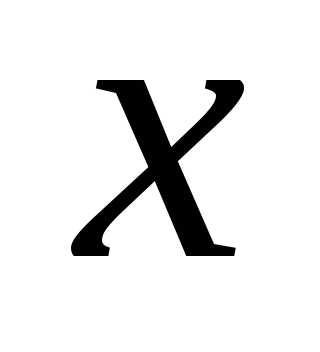 получаем систему уравнений
получаем систему уравнений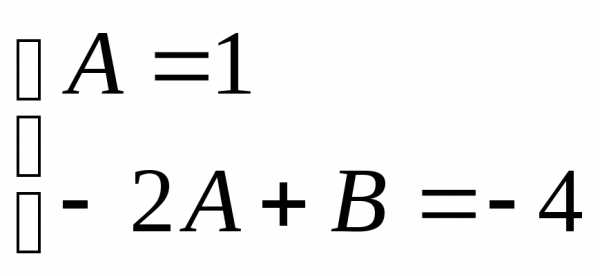 ,
отсюда А=1,В=-2.
,
отсюда А=1,В=-2.
Поэтому частное решение данного уравнения имеет вид . Следовательно,
— искомое общее решение уравнения.
studfiles.net
Линейные неоднородные дифференциальные уравнения
II-го порядка с постоянными коэффициентами
Общий вид линейного неоднородного дифференциального уравнения с постоянными коэффициентами записывается следующим образом:
(8.15)
здесь -постоянные,.
Структура общего решения уравнения (8.15) может определяться на основе теоремы 8.3.
Теорема 8.3. Общим решением дифференциального уравнения (8.15) при постоянных коэффициентах и непрерывной функцииесть сумма общего решения соответствующего однородного дифференциального уравнения и любого частного решения неоднородного уравнения, т.е.
(8.16)
Общее решение уравнения (8.15) можно определить при помощи теоремы 8.4.
Теорема 8.4.Общее решение линейного неоднородного уравнения (8.15) в некоторой области может быть найдено в квадратурах, если известно общее уравнение соответствующего однородного уравнения.
В общем случае, задача подбора частного решения вызывает определенные трудности, в связи с чем представляет интерес метод вариации произвольной постоянной (метод Лагранжа). Этот метод позволяет найти общее решение линейного неоднородного уравнения в квадратурах по известной фундаментальной системе решений соответствующего однородного уравнения с постоянными коэффициентами. Идея метода состоит в следующем. Пусть известна фундаментальная система решения соответствующего однородного уравнения. Тогда общее решение неоднородного уравнения отыскивают в виде
(8.16)
где — неизвестные функции.
Такие функции для дифференциального уравнения второго порядка определяются из решения следующей системы:
(8.17)
Таким образом, для решения неоднородного дифференциального уравнения II порядка необходимо:
1) решить однородное дифференциальное уравнение и записать его общее решение;
2) записать общее решение неоднородного уравнения в форме общего решения однородного уравнения, однако с переменными коэффициентами;
3) построить систему (8.17) и решить ее;
4) решение системы (8.17) подставить в выражение (8.16) и получить при этом общий интеграл линейного неоднородного уравнения.
Задача 8.9.Методом вариации произвольной постоянной проинтегрировать уравнение
.
На первом этапе составим характеристическое уравнение
.
Решение такого уравнения имеет вид:
.
Фундаментальная система решений общего однородного уравнения представляется функциями:
.
Тогда общее решение линейного однородного уравнения записывается в виде
.
Общее решение линейного неоднородного уравнения представляется соотношением
.
Функции находим из системы
Решая такую систему, имеем
Общее решение линейного неоднородного уравнения имеет вид
.
Определение частного решения линейного неоднородного уравнения методом неопределенных коэффициентов
Вновь рассмотрим линейное неоднородное дифференциальное уравнение II-го порядка с постоянными коэффициентами:
, (8.18)
Уравнение (8.18), как было показано ранее, всегда можно проинтегрировать в квадратурах методом вариации произвольной постоянной.
Однако, необходимо отметить, что в ряде случаев, уравнение (8.18) можно проинтегрировать без квадратур, чисто алгебраическими методами. Оказывается, что если функция — правая часть уравнения (8.18) — имеет специальный вид, то частное решение линейного неоднородного уравнения может быть определено методом неопределенных коэффициентов.
Теорема 8.5.Если правая часть уравнения (8.18) имеет вид
,
где — многочлен степени, то его частное решение можно отыскать в виде
,
где — некоторый многочлен степени,- число, которое показывает, сколько разесть корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Задача 8.10.Найти общее решение дифференциального уравнения
.
Составим характеристическое уравнение
.
Здесь .
Тогда .
Поскольку а=2 не есть корнем характеристического уравнения, тои имеем:
.
Определим и
,
.
Подставляя выражение для в исходное уравнение, имеем
.
Частное решение линейного неоднородного уравнения записывается следующим образом
.
Общее решение линейного неоднородного уравнения представляется соотношением
.
Задача 8.11.Найти общее решение дифференциального уравнения
.
Составим характеристическое уравнение:
.
Здесь .
Тогда
.
Подберем частное решение. Поскольку есть двукратным корнем характеристического уравнения, то имеем.
Частное решение исходного уравнения имеем в виде
.
Определим .
После подстановки , у’ и у» в исходное уравнение, имеем:
.
Таким образом:
.
В свою очередь, общее решение линейного неоднородного уравнения записывается в виде
.
Теорема 8.6.Если правая часть уравнения (8.18) имеет вид
,
где — многочлены степени соответственното его частное решение можно отыскать в виде
.
Здесь — многочлены степени не выше, где- большая из степеней- число, которое показывает, сколько разявляется корнем характеристического уравнения.
Задача 8.12.Определить общее решение уравнения
.
Составим характеристическое уравнение
.
Здесь .
Тогда
.
Частное решение исходного уравнения будем отыскивать в виде
.
Здесь , значит,.
Тогда
.
При этом
.
.
Подставляя в исходное уравнение, имеем
.
Общее решение исходного уравнения выражается зависимостью
.
128
studfiles.net
Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q(x)0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Бернулли.
(Якоб Бернулли (1654-1705) – швейцарский математик.)
Суть
метода заключается в том, что искомая
функция представляется в виде произведения
двух функций 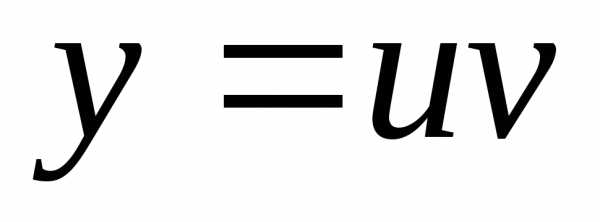 .
.
При
этом очевидно, что 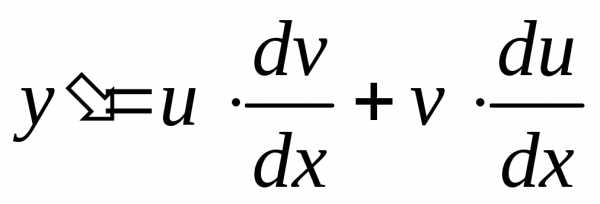 — дифференцирование по частям.
— дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Например,
функция  может быть представлена как
может быть представлена как
и т.п.
Таким
образом, можно одну из составляющих
произведение функций выбрать так, что
выражение 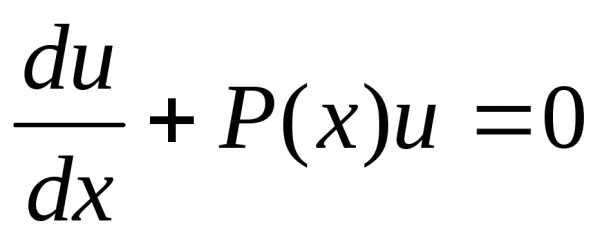 .
.
Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.
Интегрируя, можем найти функцию v:
; ;
Т.е.
была получена вторая составляющая
произведения 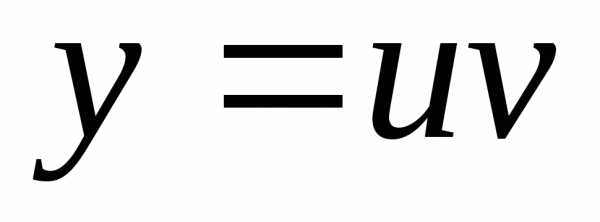 ,
которое и определяет искомую функцию.
,
которое и определяет искомую функцию.
Подставляя полученные значения, получаем:
Окончательно получаем формулу:
, С2 — произвольный коэффициент.
Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
Метод Лагранжа.
( Ларганж Жозеф Луи (1736-1813) — французский математик, през. Берлинской АН,
поч. чл. Пет. АН (1776)).
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.
Вернемся к поставленной задаче:
Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.
Далее находится решение получившегося однородного дифференциального уравнения:
.
Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.
Тогда по правилам дифференцирования произведения функций получаем:
Подставляем полученное соотношение в исходное уравнение
Из этого уравнения определим переменную функцию С1(х):
Интегрируя, получаем:
Подставляя это значение в исходное уравнение, получаем:
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.
Пример. Решить уравнение
Сначала
приведем данное уравнение к стандартному
виду: 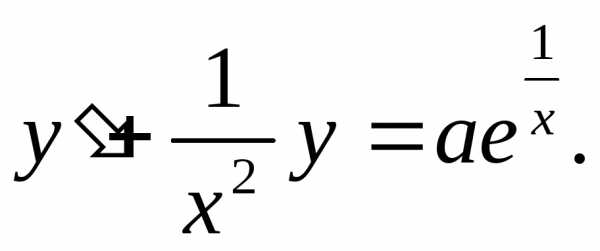
Применим
полученную выше формулу: 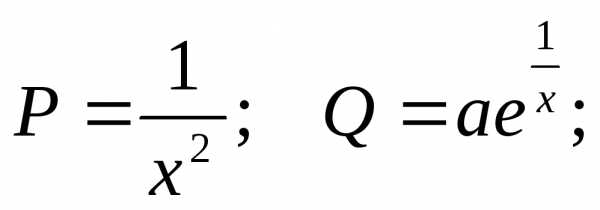
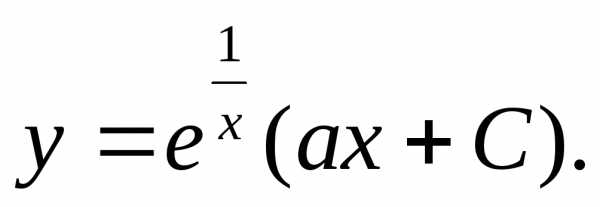
Уравнение Бернулли.
Определение. Уравнением Бернулли называется уравнение вида
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для
решения уравнения Бернулли применяют
подстановку 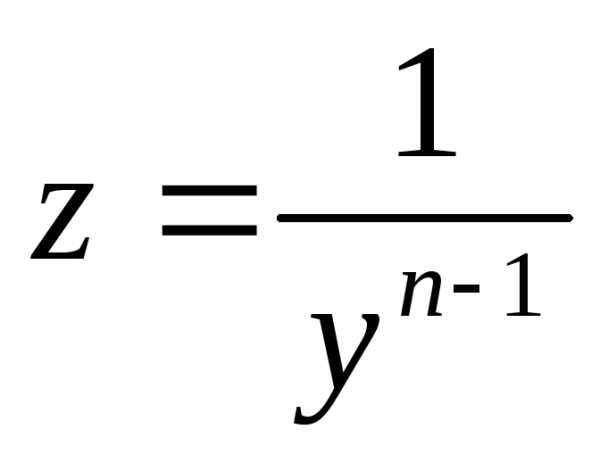 ,
с помощью которой, уравнение Бернулли
приводится к линейному.
,
с помощью которой, уравнение Бернулли
приводится к линейному.
Для этого разделим исходное уравнение на yn.
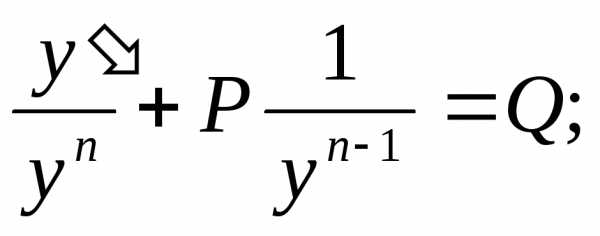
Применим подстановку, учтя, что .
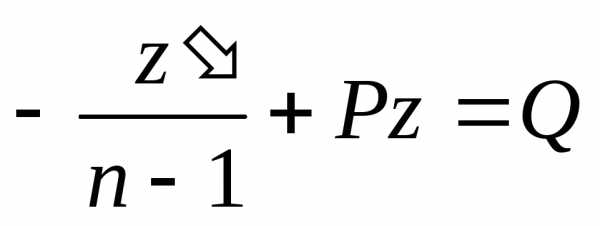
Т.е. получилось линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:
Пример. Решить уравнение
Разделим
уравнение на xy2: 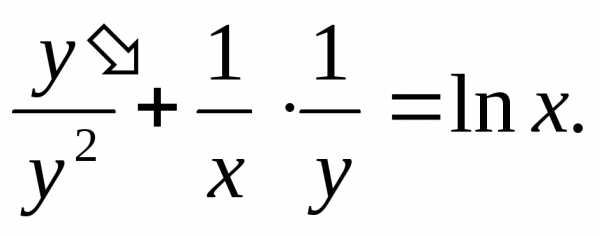
Полагаем 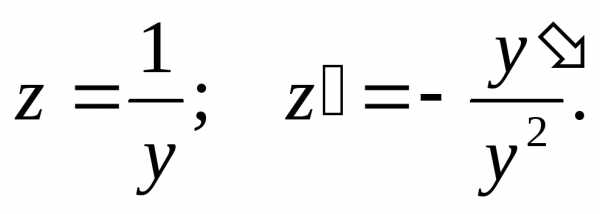
.
Полагаем
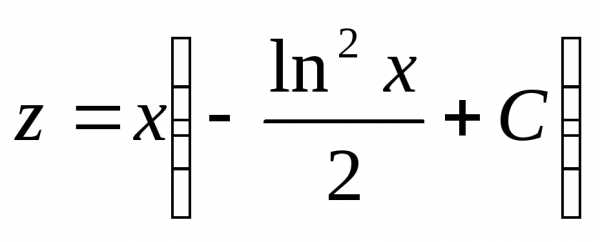
Произведя обратную подстановку, получаем:

Пример. Решить уравнение
Разделим
обе части уравнения на 
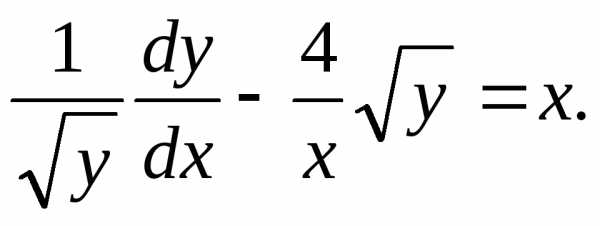
Полагаем
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
Получаем: 
Применяя обратную подстановку, получаем окончательный ответ:
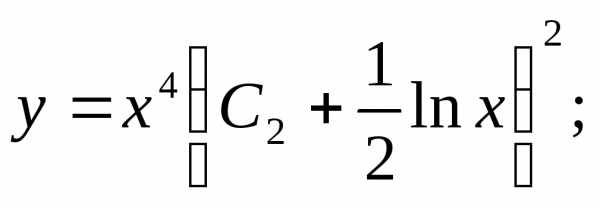
studfiles.net
3.5. Линейные неоднородные дифференциальные уравнения
Рассмотрим линейное неоднородное дифференциальное уравнение (ЛНДУ) порядка
Или коротко , где .
Уравнение , левая часть которого совпадает с левой частью ЛНДУ, называют Соответствующим данному ЛНДУ однородным уравнением.
Теорема (о структуре общего решения ЛНДУ).
Общее решение ЛНДУ Порядка с непрерывными на некотором интервале коэффициентами равно сумме общего решения соответствующего однородного уравнения и любого частного решения ЛНДУ, т. е. .
Доказательство. В первую очередь, подставим функцию В исходное уравнение и убедимся в том, что она действительно является решением ЛНДУ:
При выводе были использованы линейные свойства линейного дифференциального оператора и то, что функция Есть общее решение ОЛДУ, так что , а функция Есть частное решение НЛДУ, так что .
Далее, чтобы доказать, что данное решение является общим, необходимо для заданных начальных условий найти единственную комбинацию Произвольных постоянных, обеспечивающих решение задачи Коши.
Дифференцируя функцию Раз, и подставляя в нее и во все ее производные заданные начальные условия, получим систему линейных уравнений относительно произвольных постоянных следующего вида:
Определителем этой системы является Вронскиан , который не равен нулю, поскольку по условию теоремы решения образуют фундаментальную систему решений соответствующего ОЛДУ. При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое обозначим как .
Таким образом, сумма линейной комбинации фундаментальных решений вида и частного решения Является решением, получена из общего решения при некоторых значениях Произвольных постоянных и по построению удовлетворяет начальным условиям, что и требовалось доказать.
Если известна фундаментальная система решений соответствующего ОЛДУ и, следовательно, его общее решение , то для определения частного решения НЛДУ порядка можно воспользоваться Методом Лагранжа вариации произвольных постоянных.
Этот метод заключается в том, что частное решение НЛДУ ищут в виде
,
Т. е. в виде линейной комбинации неизвестных функций и заранее вычисленных фундаментальных решений соответствующего ОЛДУ.
Предварительно находят производные из системы алгебраических уравнений следующего вида:
Определителем этой системы является Вронскиан , который не равен нулю при любом , поскольку решения образуют фундаментальную систему решений соответствующего ОЛДУ.
При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое представим в виде равенств .
Интегрируя каждое из полученных равенств, получим набор первообразных для функций .
Окончательно, получаем функцию ,
Которая, как доказано в общей теории, является частным решением ЛНДУ при условии непрерывности на некотором интервале функций .
Отметим, что для произвольного НЛДУ порядка нет общего способа построения системы фундаментальных решений . Таким образом, методом Лагранжа можно воспользоваться только тогда, когда эту фундаментальную систему каким-либо способом удается найти. Если НЛДУ порядка имеет числовые коэффициенты , то фундаментальная система решений , соответствующего ОЛДУ, находится всегда и достаточно просто. В этом случае для нахождения частного решения всегда можно использовать метод Лагранжа.
Теорема (о наложении решений ЛНДУ).
Если правая часть ЛНДУ представлена в виде суммы нескольких функций, так что
, и есть частные решения неоднородных уравнений , то сумма этих частных решений есть некоторое частное решение исходного ЛНДУ.
Доказательство. Подставим функцию В исходное уравнение и убедимся в том, что эта функция действительно является решением ЛНДУ:
.
При выводе были использованы линейные свойства линейного дифференциального оператора и условия теоремы. Таким образом, теорема полностью доказана.
Частным случаем ЛНДУ являются линейные неоднородные дифференциальные уравнения порядка с постоянными числовыми коэффициентами вида .
Так как постоянные функции непрерывны на любом промежутке, то по теореме о структуре общего решения ЛНДУ для того, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений соответствующего однородного уравнения, найти некоторое частное решение ЛНДУ и представить общее решение в следующем виде:
.
Рассмотрим на примере ЛНДУ второго порядка с постоянными коэффициентами, как находится его общее решение с использованием метода Лагранжа для отыскания частного решения.
Пример. Найти общее решение уравнения .
На первом этапе ищется общее решение соответствующего однородного уравнения Его характеристическое уравнение имеет вид Корни характеристического уравнения находятся по общей формуле вычисления корней квадратного уравнения и в данном случае равны , .
В соответствии с общей теорией функции , являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.
Таким образом, общее решение соответствующего однородного уравнения имеет вид
.
Заменим в общем решении Постоянные Неизвестными функциями И в соответствии с методом неопределенных коэффициентов будем искать частное решение НЛДУ в виде .
Предварительно для НЛДУ второго порядка решается система уравнений
Линейная относительно производных неизвестных функций .
Для данного уравнения указанная система имеет вид
Определителем этой системы является Вронскиан который всегда отличен от нуля, что позволяет найти неизвестные по формулам Крамера
, .
Интегрируя полученные дифференциальные уравнения и выделяя первообразные их правых частей , , находим неизвестные функции в виде , . Отсюда, частное решение данного НЛДУ равно
.
Окончательно, общее решение данного уравнения записывается в виде
.
Пример. Найти общее решение уравнения .
На первом этапе ищется общее решение соответствующего однородного уравнения Его характеристическое уравнение имеет вид Корни характеристического уравнения находятся с использованием общей формулы вычисления корней квадратного уравнения и в данном случае равны , , .
В соответствии с общей теорией функции , , являются линейно независимыми, и для уравнения третьего порядка образует фундаментальную систему решений.
Таким образом, общее решение соответствующего однородного уравнения имеет вид
.
Заменим в общем решении Постоянные Неизвестными функциями И в соответствии с методом неопределенных коэффициентов Лагранжа будем искать частное решение НЛДУ в следующем виде:
.
Для данного НЛДУ третьего порядка система уравнений, линейная относительно производных неизвестных функций имеет вид:
Определителем этой системы является Вронскиан
Который отличен от нуля, что позволяет найти неизвестные По формулам Крамера в следующем виде: , , .
Интегрируя полученные дифференциальные уравнения, находим неизвестные функции , , . Отсюда, частное решение данного НЛДУ равно .
Окончательно, общее решение данного уравнения записывается в виде
.
Пусть правая часть линейного неоднородного дифференциального уравнения порядка с постоянными числовыми коэффициентами имеет Специальный вид:
1) ,
2) ,
Где – вещественные числа, И– полиномы степеней и .
Как и ранее, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений соответствующего однородного уравнения, найти некоторое частное решение ЛНДУ и представить общее решение в виде .
Однако если правая часть ЛНДУ имеет специальный вид, то частное решение уравнения также имеет структуру, аналогичную правой части, и может быть найдено по Методу неопределенных коэффициентов. Этот метод несколько проще метода вариации произвольных постоянных, так как не включает в себя операцию интегрирования функций.
1) Рассмотрим вначале ЛНДУ с постоянными коэффициентами второго порядка со специальной частью первого вида .
В этом случае частное решение дифференциального уравнения ищем в виде
,
Т. е. выбираем полином той же степени, что и в правой части, только с неизвестными заранее коэффициентами , а число назначаем равным числу в правой части.
Показатель степенной функции выбирают равным нулю, если число не совпадает ни с одним корнем характеристического уравнения, и равным кратности корня характеристического уравнения в случае совпадения числа с каким-либо корнем.
Рассмотрим на конкретных примерах ЛНДУ второго порядка, как находится его общее решение с использованием метода неопределенных коэффициентов для отыскания частного решения .
Пример. Найти общее решение уравнения .
На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет корни , . Следовательно, фундаментальная система решений имеет вид ,, а общее решение соответствующего однородного уравнения есть .
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как не совпадает ни с одним корнем характеристического уравнения, то и частное решение будем искать в виде
.
Вычислив производные ,И подставив , и в исходное уравнение получим (после сокращения на ) следующее тождество:
.
Сравнивая коэффициенты обеих частей этого тождества, получим систему трех линейных уравнений для определения неизвестных коэффициентов:
,
Откуда .
Итак, , и, следовательно, общее решение уравнения имеет вид .
Пример. Найти общее решение уравнения .
На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет двукратный корень . Следовательно, фундаментальная система решений имеет вид ,, а общее решение соответствующего однородного уравнения есть .
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как совпадает с двукратным корнем характеристического уравнения, то и частное решение будем искать в виде
.
Вычислив производные ,И подставив , и в исходное уравнение получим (сократив на и сравнив коэффициенты при одинаковых степенях ) следующие значения для неопределенных коэффициентов: .
Следовательно, , а общее решение данного уравнения имеет вид .
2) Рассмотрим далее ЛНДУ с постоянными коэффициентами второго порядка со специальной частью второго вида .
В этом случае частное решение уравнения ищем в виде
,
Т. е. выбираем полиномы при косинусе и синусе наибольшей степени, из имеющихся в правой части, с неизвестными заранее коэффициентами и , а числа , назначаем равными числам , , стоящим в правой части.
Показатель степенной функции выбирают равным нулю, если комплексное число , не совпадает ни с одним комплексным корнем характеристического уравнения, и равным кратности комплексного корня характеристического уравнения в случае совпадения числа с каким-либо комплексным корнем.
Рассмотрим на конкретных примерах ЛНДУ второго порядка, как находится его общее решение с использованием метода неопределенных коэффициентов для отыскания частного решения .
Пример. Найти частное решение уравнения .
На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет два различных комплексных корня ,. Следовательно, фундаментальная система вещественных решений имеет вид , , а общее решение соответствующего однородного уравнения есть .
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как комплексная пара сопряженных чисел правой части исходного уравнения совпадает с комплексной парой корней кратности один характеристического уравнения, то и частное решение будем искать в виде
.
Вычислив производные ,И подставив , и в исходное уравнение получим следующее тождество: . Сравнивая коэффициенты при синусе и косинусе, найдем следующие значения для неопределенных коэффициентов: . Следовательно, , а общее решение данного уравнения имеет вид .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
