Неполные квадратные уравнения | Алгебра
Как решать неполные квадратные уравнения? Решение и количество корней зависят от вида уравнения.
Неполные квадратные уравнения бывают трёх видов.
Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.
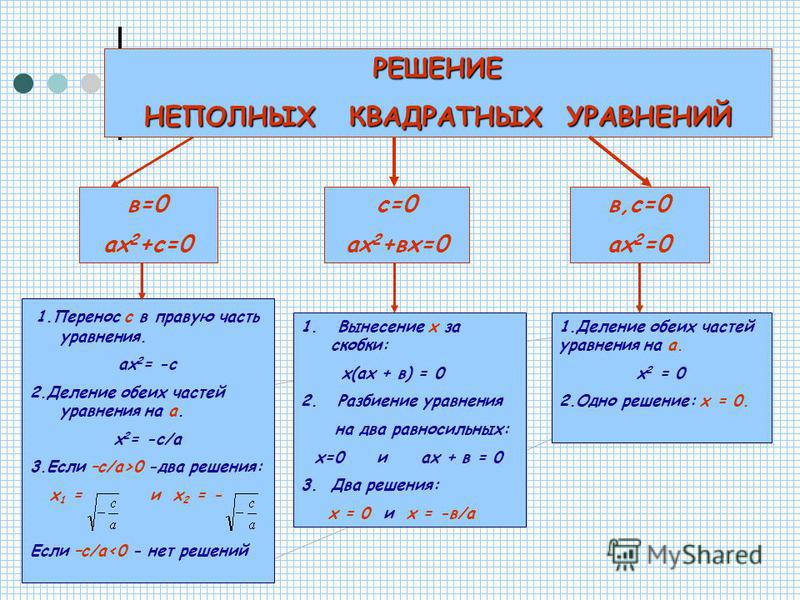
I. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
Общий множитель x выносим за скобки:
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Второе уравнение — линейное. Решаем его:
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
Общий множитель x выносим за скобки:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; -18.
Общий множитель 5x выносим за скобки:
Приравниваем к нулю каждый множитель:
Ответ: 0; 3.
II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).
Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.
1. Если знаки a и c — разные, уравнение имеет два корня.
В курсе алгебры 7 класса такие уравнения решают разложением левой части на множители по формуле разности квадратов (поскольку квадратные корни начинают учить только в курсе 8 класса, коэффициенты a и c в 7 классе обычно являются квадратами некоторых рациональных чисел):
Уравнение типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Приравниваем к нулю каждый из множителей:
Раскладываем левую часть уравнения по формуле разности квадратов:
Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:
Ответ: 7; -7.
Ответ: 2,25; -2,25.
2. Если знаки a и c — одинаковые, уравнение не имеет корней.
Корней нет, так как сумма положительных чисел не может равняться нулю.
Ответ: нет корней.
Корней нет, так как сумма отрицательных чисел не может равняться нулю.
Ответ: нет корней.
В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:
Примеры.
Ответ:±2.
Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:
Ответ:
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Нет корней, так как квадратный корень не может быть равным отрицательному числу.
Ответ: нет корней.
III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.
Уравнение такого рода имеет единственный корень x=0
В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:
Примеры.
Ответ: 0.
Ответ: 0.
Ответ: 0.
В следующий раз рассмотрим примеры решения полных квадратных уравнений.
Неполное квадратное уравнение: формулы, алгоритм решений, примеры
Математика
12.11.21
14 мин.
Неполные квадратные уравнения чаще всего встречаются в различных математических задачах школьной программы. Главное их отличие от обычных в том, что они содержат меньше членов, поэтому и решать их довольно легко. Минимум существует 3 способа. Зная их, можно будет решить пример любой сложности, в некоторых случаях даже устно, причём даже за считаные секунды.
Оглавление:
- Понятие и термины
- Стандартный алгоритм
- Вычисление неполных выражений
- Решение задач
Понятие и термины
Под уравнениями в математике понимают равенства, где неизвестны некоторые члены. Их принято обозначать маленькими латинскими буквами. Чаще всего используют x, y, a, b, c. Решение уравнений подразумевает нахождение неизвестных величин. При этом они могут принимать как конкретное значение, так и быть переменными.
Решение уравнений подразумевает нахождение неизвестных величин. При этом они могут принимать как конкретное значение, так и быть переменными.
Числа, которые заменяют буквами, называют корнями. Это такие значения переменных, при которых выражение имеет смысл и обращается в верное равенство. Другими словами, слова «корень» и «решение» — синонимы. Для уравнений характерно, что число действительных ответов может быть не только конечное число. Например, a — 2 = 4 имеет один корень, он равняется шести, a 2 = 9 — 2 решения: 3 и -3, а n = n — бесконечное число.
В алгебраическом виде уравнение записывают так: P (x1, x2…, xn) = 0, где: P — сумма одночленов от неизвестных. Все известные виды уравнений разделяют на 5 типов:
- Линейные. В записи многочлена самой высокой степенью является единица: ax + a2x2 +…anxn + y = 0.
- Квадратичные. Выражения, в которых стоит значение переменной x2, при этом в записи есть свободные переменные и коэффициенты.
 Например, ax2 + bx + c = 0. Главное условие — первый коэффициент (a) не должен быть равен нулю.
Например, ax2 + bx + c = 0. Главное условие — первый коэффициент (a) не должен быть равен нулю. - Кубические. График функции представляет собой параболу. Они имеют вид: ax3+ bx2 + c x + n = 0 или ax3 + bx + c = 0.
- Биквадратные. Наивысшая степень в уравнении не превышает 4.
Кроме этого, существуют иррациональные и рациональные равенства. К первым относят уравнения, где неизвестное стоит под знаком корня или возведения в степень и является дробным, а ко вторым — выражения, использующие операции сложения, вычитания, деления и умножения, а также возведения целого числа в степень.
Выражения, в которых второй или третий коэффициент равняется нулю, называют неполными. Решение уравнений такого типа имеет свои особенности. Корни можно находить по упрощённому алгоритму, а не по стандартному через дискриминант или теорему Виета. Формулы будут проще, соответственно, сложные преобразования делать не придётся.
Стандартный алгоритм
Перед тем как перейти непосредственно к решению, нужно приравнять выражение к нулю, то есть если равенство имеет вид ax2 + bx = c, его нужно привести к следующей форме записи: ax2 + bx — c = 0. Затем можно использовать алгоритм, разработанный, чтобы можно было быстро решать полные квадратные уравнения.
Пошаговое решение выглядит следующим образом:
- в случае необходимости привести равенство до вида квадратного уравнения;
- найти дискриминант;
- проанализировать его значение: если оно будет меньше нуля, дальнейшее решение не имеет смысла;
- при равенстве дискриминанта нулю воспользоваться формулой: x = -b / 2*a;
- если полученное число больше нуля, уравнение имеет 2 корня, найти их можно, воспользовавшись равенством: x1 = (-b + √D) / 2a; x1 = (-b — √D) / 2a.
Для многочленов кубического и квадратного вида формулы для расчёта будут сложнее: D = b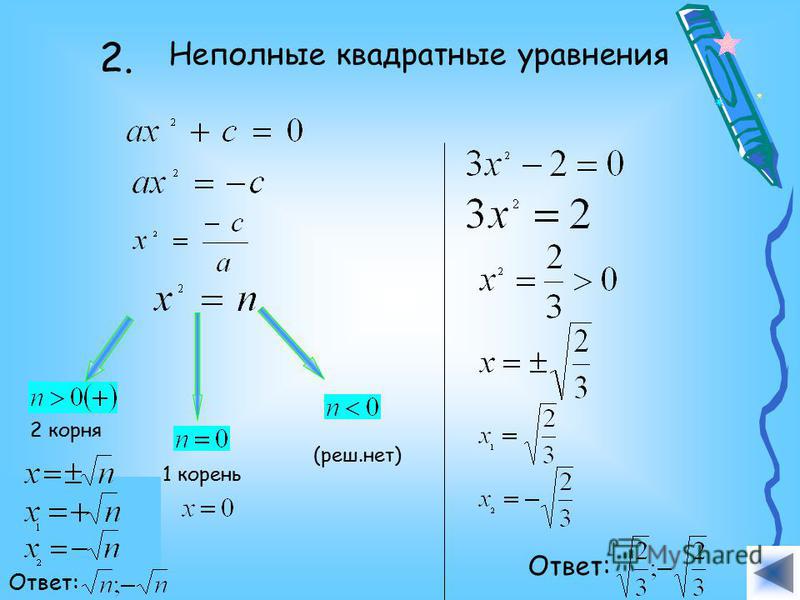 В частности, для кубического уравнения формула примет упрощённый вид: -27q2 — 4p3. Это выражение называется уравнением Кардано.
В частности, для кубического уравнения формула примет упрощённый вид: -27q2 — 4p3. Это выражение называется уравнением Кардано.
Этот алгоритм можно использовать и при решении неполных выражений. Важным этапом является нахождение дискриминанта. Под ним понимают выражение вида b2 — 4ac. Обозначают его большой латинской буквой D. Величина представляет собой симметрический многочлен, если его рассматривать относительно корней.
Найти корни квадратного уравнения можно, используя теорему Виета. Но применять её возможно не ко всем выражениям. Использовать правило разрешено только с приведёнными равенствами. Это уравнения, где первый коэффициент равен единице: n2 + pn + n = 0. Определение Виета позволяет найти корни по следующим формулам: n1 + n2 = -p; n1 * n2 = q, где неизвестные будут искомыми корнями.
Доказать справедливость формул Виета можно следующим образом. Корни квадратного равенства можно найти из выражения: n1 = (-b + √D) / 2; n1 = (-b — √D) / 2, где дискриминант D = p2 — 4q. Если найти сумму корней, в ответе получится: n1 + n2 = (-b + √D) / 2 + (-b — √D) / 2 = (-b — √D) — p — √D) / 2 = -2p/2 = -p. Произведение же равно: n1 * n2 = (-b + √D) / 2 * (-b — √D) / 2 = (-b)2 — √D)2 / 4 = (p2 — D) / 4 = p2 — (p2 — 4q) / 4 = 4q / 4 = q. Соответственно, полученные равенства n1 + n2 = -p; n1 * n2 = q.
Если найти сумму корней, в ответе получится: n1 + n2 = (-b + √D) / 2 + (-b — √D) / 2 = (-b — √D) — p — √D) / 2 = -2p/2 = -p. Произведение же равно: n1 * n2 = (-b + √D) / 2 * (-b — √D) / 2 = (-b)2 — √D)2 / 4 = (p2 — D) / 4 = p2 — (p2 — 4q) / 4 = 4q / 4 = q. Соответственно, полученные равенства n1 + n2 = -p; n1 * n2 = q.
Теорема Виета даёт важную информацию о корнях квадратного уравнения. При небольшой тренировке с её помощью можно научиться выполнять решение в уме, потратив на это совсем немного времени.
Вычисление неполных выражений
Чтобы решать неполные уравнения, необязательно использовать формулы корней. Найти результат можно, используя только правила сокращённого умножения и деления. Всего таких формул 7. Учат их в седьмом классе средней школы при изучении правил сокращения дробей.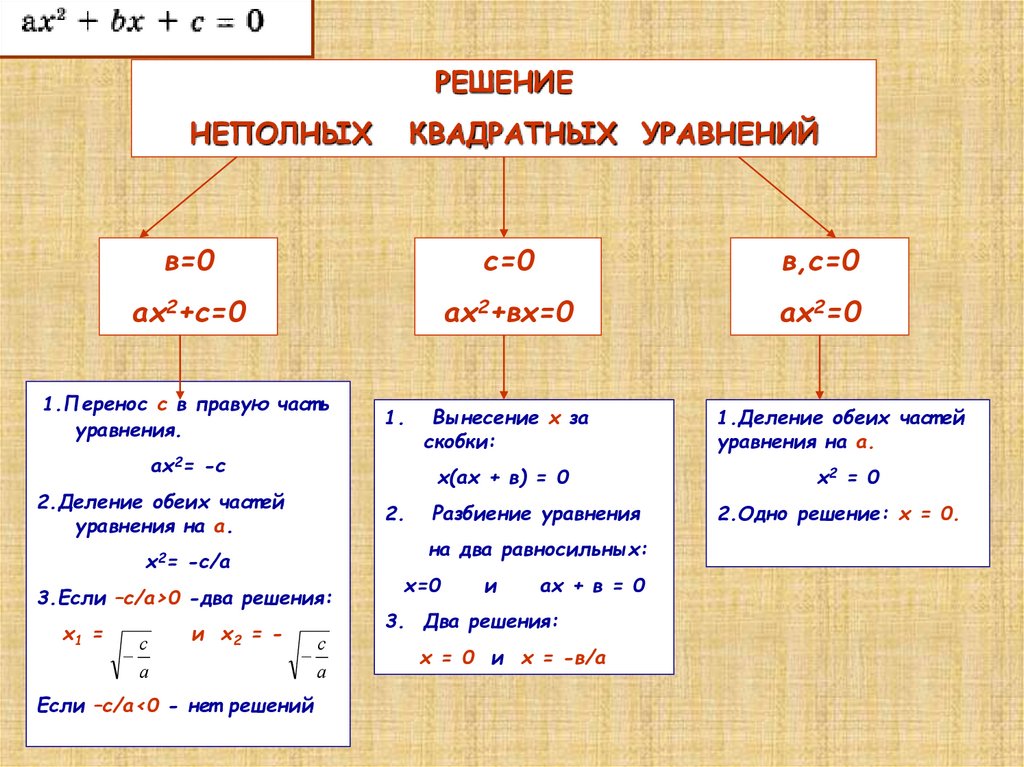 Вот их перечень:
Вот их перечень:
- Разность квадратов. Вычитание выражений, стоящих в квадрате, можно заменить произведением разности и суммы их членов: t2 — n2 = (t — n) * (t + n).
- Квадрат суммы. Сложение двух чисел в квадрате — однотипная операция прибавления квадрата первого числа к удвоенному произведению первого и второго и квадрату второго: (t + n)2 = t2 + 2tn + n2.
- Квадрат разности. Правило, сходное с квадратом суммы, лишь вместо сложения в первом действии ставится вычитание: (t — n)2 = t2 — 2tn + n2. Следует отметить, что часто используется и следующее равенство: (t — n)2 = (t — n)2.
- Сумма куба. Сумма двух чисел в третьей степени равна первому многочлену в третьей степени плюс утроенное произведение квадрата первого слагаемого на второе плюс сумма утроенного произведения первого на квадрат куба второго числа.
- Куб разности.
 Он равен кубу первого числа минус утроенное произведение квадрата уменьшаемого на вычитаемое плюс тройное произведение первого числа на квадрат второго минус куб вычитаемого.
Он равен кубу первого числа минус утроенное произведение квадрата уменьшаемого на вычитаемое плюс тройное произведение первого числа на квадрат второго минус куб вычитаемого. - Сумма кубов. Заменить такое выражение можно произведением суммы слагаемых на неполный квадрат разности: t3 + n3 = (t + n) * (t 2 — tn + n 2) .
- Разность кубов. Правило, аналогичное прибавлению кубов, но во втором множителе стоит неполный квадрат суммы: t3 — n3 = (t − n) * (t2 + t n + n2).
Кроме этих правил, нужно знать свойство деления и метод разложения на множители. Согласно закону, любое равенство можно разделить на одно число, но делить нужно одновременно и левую, и правую часть. Разложение же позволяет приводить сложные и громоздкие уравнения к простому виду.
Например, f2 — 33f + 200 = 0. Хотя это и полный трёхчлен, не стоит спешить искать дискриминант. На самом деле, исходное выражение можно представить как произведение множителей неполных одночленов. Так, f2 — 33* f + 200 = (f — 8) * (f — 25) = 0. Решением будут корни равные 25 и 8.
На самом деле, исходное выражение можно представить как произведение множителей неполных одночленов. Так, f2 — 33* f + 200 = (f — 8) * (f — 25) = 0. Решением будут корни равные 25 и 8.
Решение задач
Практические задания помогают лучше усвоить теоретический материал и запомнить нужные для решения формулы. Существуют различные задачи, с помощью которых можно довольно быстро проработать весь изученный курс. Вот некоторые примеры с решением неполных квадратных уравнений, которые наверняка помогут при выполнении самостоятельных вычислений:
- Найти неизвестное в уравнении: f2 = 12 * f. В соответствии с алгоритмом нужно правую часть перенести влево и приравнять выражение к нулю: f2 — 12 * f. = 0. Неизвестное можно вынести за скобки: f * (f — 12) = 0. Так как ноль в ответе может получиться, лишь при условии, что один из множителей будет нулевым, множимые можно рассмотреть отдельно.
 Корнями уравнения будут числа 0 и 12.
Корнями уравнения будут числа 0 и 12. - Вычислить корни выражения: 4x * (x + 3) = 12x + 1. В первую очередь нужно раскрыть скобки. Для этого каждое слагаемое следует умножить на то, что стоит перед скобками. После этого пример примет вид: 4x2 + 12 = 12 x + 1. Теперь все члены неравенства можно собрать слева и привести подобные: 4x2 + 12x — 12x — 1 = 4x2 — 1 = 0. Полученное выражение есть не что иное, как разность квадратов, поэтому его можно переписать так: 4x2 — 12 = 0. Отсюда (2x2) — 12 = (2x — 1) * (2x + 1) = 2x — 1 = 0. Далее решается простое линейное выражение. В ответе получится: x = ± 1 / 2.
- Определить возможные решения для уравнения: 6p2 — (2p — 1) = p * (p + 4). Очевидно, что в левой части стоит разность квадратов. Но использовать правило умножения здесь будет нерационально. Дело в том, что смысл преобразований заключается в приведении уравнения к виду без скобок, поэтому следует вычитаемое расписать по формуле квадрата разности: 2p — 1 = (2p)2 — 2 * 2p * 1 + 1.
 Таким образом, получится равенство: 6p2 — 4p2 + 4p — 1 = p2 + 4p. Теперь можно действовать по алгоритму: перенести все члены в одну сторону и привести подобные: 6p2 — 4p2 + 4p — 1 — p2 + 4p = m2 — 1 = 0. Это уже простое неполное квадратное уравнение, которое можно решить в уме. Корни, удовлетворяющие условию, буду равны ± 1.
Таким образом, получится равенство: 6p2 — 4p2 + 4p — 1 = p2 + 4p. Теперь можно действовать по алгоритму: перенести все члены в одну сторону и привести подобные: 6p2 — 4p2 + 4p — 1 — p2 + 4p = m2 — 1 = 0. Это уже простое неполное квадратное уравнение, которое можно решить в уме. Корни, удовлетворяющие условию, буду равны ± 1.
Таким образом, квадратные и уравнения высших порядков можно решать по классической схеме, используя дискриминант. Но при этом неполные выражения гораздо проще вычислять, преобразуя их до простого вида. В этом как раз и помогают правила сокращённого умножения.
{{2}}-{7}{x}={0}$$$.Перепишем уравнение в следующем виде: $$${3}{x}\cdot{x}-{7}{x}={0}$$$.
Теперь перепишите уравнение, используя распределительное свойство умножения: $$${x}{\left({3}{x}-{7}\right)}={0}$$$.
Когда произведение чисел равно 0?
Когда хотя бы один множитель равен 0.
Итак, либо $$${x}={0}$$$, либо $$${3}{x}-{7}={0}$$$.
Второе уравнение линейное, его корень $$${x}=\frac{{7}}{{3}}$$$.
Ответ 9{{2}}-{9}={0}$$$.
Ответ : $$${0}$$$ и $$$-\frac{{9}}{{4}}$$$.
Неполные квадратные уравнения с примерами
Неполное квадратное уравнение — это квадратное уравнение, которое не имеет ни одного члена вида ax²+bx+c=0 (при условии, что всегда присутствует член x²). Эти уравнения обычно легче решить, чем полное квадратное уравнение. В зависимости от пропущенного члена у нас есть два типа неполных квадратных уравнений.
В этой статье мы подробно узнаем о двух типах неполных квадратных уравнений. Мы научимся решать эти типы уравнений и рассмотрим несколько практических примеров.
АЛГЕБРА
Актуально для …
Обучение решению неполных квадратных уравнений.
См. примеры
Содержание
АЛГЕБРА
Актуально для …
Обучение решению неполных квадратных уравнений.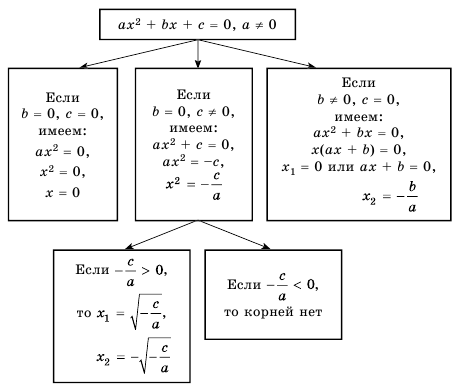

 Например, ax2 + bx + c = 0. Главное условие — первый коэффициент (a) не должен быть равен нулю.
Например, ax2 + bx + c = 0. Главное условие — первый коэффициент (a) не должен быть равен нулю.
 Он равен кубу первого числа минус утроенное произведение квадрата уменьшаемого на вычитаемое плюс тройное произведение первого числа на квадрат второго минус куб вычитаемого.
Он равен кубу первого числа минус утроенное произведение квадрата уменьшаемого на вычитаемое плюс тройное произведение первого числа на квадрат второго минус куб вычитаемого. Корнями уравнения будут числа 0 и 12.
Корнями уравнения будут числа 0 и 12.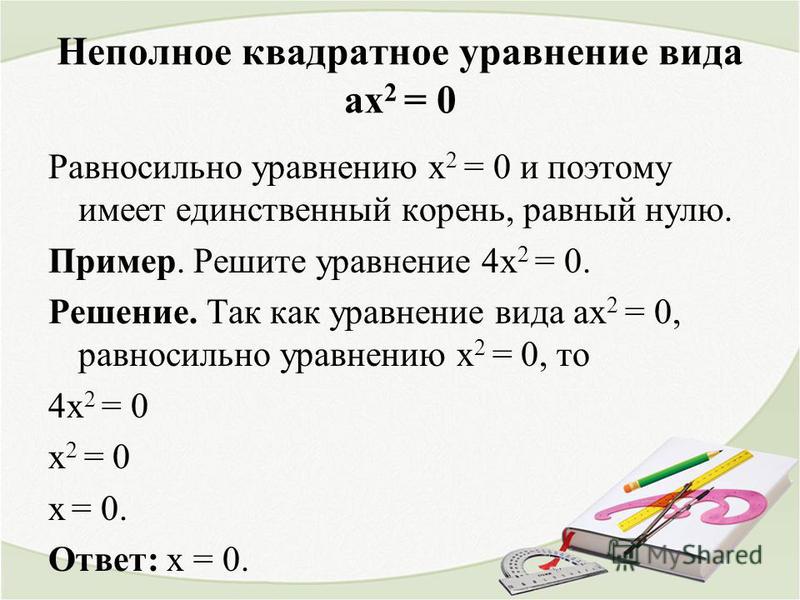 Таким образом, получится равенство: 6p2 — 4p2 + 4p — 1 = p2 + 4p. Теперь можно действовать по алгоритму: перенести все члены в одну сторону и привести подобные: 6p2 — 4p2 + 4p — 1 — p2 + 4p = m2 — 1 = 0. Это уже простое неполное квадратное уравнение, которое можно решить в уме. Корни, удовлетворяющие условию, буду равны ± 1.
Таким образом, получится равенство: 6p2 — 4p2 + 4p — 1 = p2 + 4p. Теперь можно действовать по алгоритму: перенести все члены в одну сторону и привести подобные: 6p2 — 4p2 + 4p — 1 — p2 + 4p = m2 — 1 = 0. Это уже простое неполное квадратное уравнение, которое можно решить в уме. Корни, удовлетворяющие условию, буду равны ± 1.