Непрерывной случайной величины пример – L№4(Случайные Величины)

10.Непрерывные случайные величины.Функция распределениянепрерывной случайной величины и ее свойства.

Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси. Например: температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента и т.д.

Одним из возможных способов задания непрерывной случайной величины является использование с этой целью соотв. функции распределения. Функция F(x), равная вероятности того, что случайная величина Х в результате испытания примет значение , меньше х, называется функцией распределения данной случайной величины :F(x)=P(X<x)

Свойства функции распределения: 1) Функция распределения удовлетворяет неравенству: 0≤F(x)≤1 ; 2) Функция распределения является неубывающей функцией, т.е. из х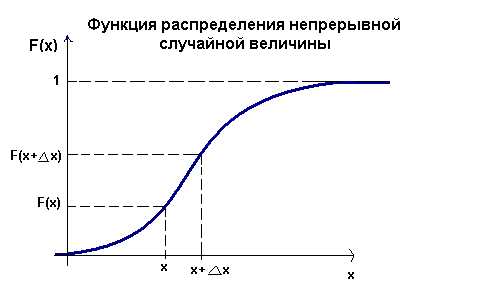

2>х₁ следует F(x2)≥F(x1). 3)Функция распределения стремится к 0 при неограниченном убывании еаргумента и стремится к 1 при его неограниченном возрастании.

График функции распределения

11.Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Основные числовые характеристики непрерывной случайной величины.

Плотностью распределения вероятностей (плотностью вероятности) f(x) непрерывной случайной величины Х называется производная функции распределения F(x) этой величины: f(x)=F’(x)

Свойства плотности распределения вероятностей: 1) Плотность вероятности является неотрицательной функцией: f(x)≥0; 2) Вероятность того, что в результате испытания непрерывная случайная величина примет какие либо значения из интервала (a,b) равна: 3) Определенный интеграл в пределах от –бесконечности до + бесконечности от плотности вероятности непрерывной случайной величины равен единице :

  4)Определенный интеграл в пределах от минус бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины:

Под основными числовыми характеристиками непрерывной случайной величины понимают, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Математическое ожидание непрерывной случайной величины:

Дисперсия непрерывной случайной величины D(X) = M[X – M(X)]². (добавить)

Среднее квадратическое отклонение: σ(х)= √D(X)

12. Нормальный закон распределения. Вероятность попадения нормально распределенной случайнойвеличиныв заданный интервал.Правило трех сигм.

Из всех видов распределения непрерывных случайных величин наиболее часто используют нормальное распределение, которое задается законом Гаусса. Так, если мы имеем сумму большого числа независимых величин, подчиненных каким угодно законам распределения, то при некоторых общих условиях она будет приближенно подчиняться нормальному закону. Непрерывная случайная величина

называется распределенной по нормальному закону, если ее плотность вероятности имеет вид : (увеличить,дописать), где М-математическое ожидание, σ в квадрате – дисперсия, σ-среднее квадратическое отклонение этой величины.это кривая Гаусса:

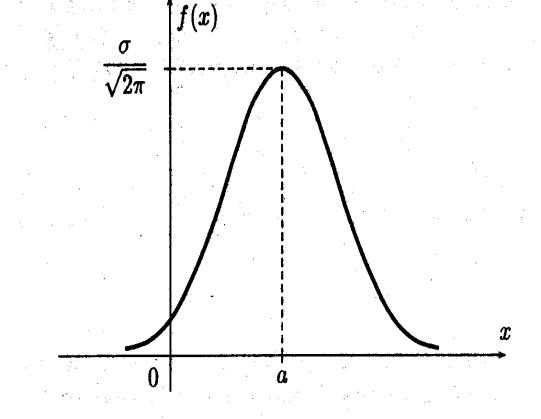
Подставив выражение для плотности вероятности нормально распределенной случайной величины в выражение , получим вероятность того, что в результате испытания нормально распределенная случайная величина

примет значение из заданного интервала : P(a<X<b)=____________________

Правило трех сигм: отклонения значений нормального распределения случайной величины от ее математического ожидания по абсолютной величине практически не превышает ее утроенного среднего квадратического отклонения.

studfiles.net

Лекция 13. Понятие непрерывной случайной величины (нсв). Формула вычисления вероятно­стей.

Непрерывной случайной величиной называют случайную величину, которая может принимать любые значения на числовом интервале.

Примеры непрерывных случайных величин: возраст студентов, длина ступни ноги человека, масса детали и т. д. Это положение относится ко всем случайным величинам, измеряемым на непрерывной шкале, таким как меры веса, длины, времени, температуры, расстояния. Измерение может быть проведено с точностью до какого-нибудь десятичного знака, но случайная величина – теоретически непрерывная величина. В экономическом анализе находят широкое применение относительные величины, различные индексы экономического состояния, которые также вычисляются с определенной точностью, скажем, до двух знаков после запятой, хотя теоретически их значения – непрерывные случайные величины.

У непрерывной случайной величины возможные значения заполняют некоторый интервал (или сегмент) с конечными или бесконечными границами.

Закон распределения непрерывной случайной величины можно задать в виде интегральной функции распределения, являющейся наиболее общей формой задания закона распределения случайной величины, а также в виде дифференциальной функции (плотности распределения вероятностей), которая используется для описания распределения вероятностей только непрерывной случайной величины.

Функция распределения (или интегральная функция) F(x) – универсальная форма задания закона распределения случайной величины. Для непрерывной случайной величины функция распределения также определяет вероятность того, что случайная величина X примет значение, меньшее фиксированного действительного числа х, т. е.

F(x) = F(X < x).

При изменении х меняются вероятности Р(Х < x) = F(x). Поэтому F(x) и рассматривают как функцию переменной величины. Принято считать, что случайная величина X известна, если известна ее функция распределения F(x).

Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференци-руемая функция с непрерывной производной.

1. Функция распределения есть неотрицательная функция, заключенная между 0 и 1, т.е. 0 ≤ F(x) ≤ 1.

2. Функция распределения есть неубывающая функция, т. е. F(x₂) ≥ F(x₁), если х₂> х₁. Тогда P(x₁ ≤ Х < х₂) = P(Х < х₂) – P(Х < х₁) = F(x₂) – F(x

1).

Так как любая вероятность есть число неотрицательное, то P(x₁ ≤ ≤ Х < х₂)  0, а следовательно, F(x₂) – F(x₁) ≥ 0 и F(x₂) ≥ F(x₁).

Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (α, β), равна приращению функции распределения на этом интервале, т. е.

P(α ≤ Х < β) = F(β) – F(α).

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Р(Х = х₁) = 0.

Согласно сказанному, равенство нулю вероятности Р(Х = х₁) не всегда означает, что событие Х = х₁ невозможно. Говоря о вероятности события Х = х₁, априорно пытаются угадать, какое значение примет случайная величина в опыте.

Если х

1лежит в области возможных значений непрерывной случайной величины X, то с некоторой уверенностью можно предсказать область, в которую случайная величина может попасть. В то же время невозможно хотя бы с малейшей степенью уверенности угадать, какое конкретное значение из бесконечного числа возможных примет непрерывная случайная величина.

Например, если метеослужба объявляет, что температура воздуха в полдень составила 5 °С, то это не означает, что температура будет точно равна этому значению. Вероятность такого события равна нулю.

3. Если все возможные значения случайной величины принадлежат интервалу (α, β), то

F(х) = 0 при х ≤ α; F(х) = 1 при х > β.

В самом деле, F(x) = 0 для всех значений х ≤ α и F(х) = 1 при х > β, поскольку события X < х для любого значения х ≤ α, являются в этом случае невозможными, а для любого значения х > β – достоверными.

Следствие. Если возможные значения непрерывной случайной личины расположены на всей оси ОХ, то справедливы следующие предельные соотношения:

,

или F(– ∞) = 0; F(+ ∞) = 1. Это следствие справедливо и для дискретных случайных величин.

studfiles.net

Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случай­ных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (18.5) и (18.10) берутся их интегральные аналоги.

Определение 4. Математическим ожиданием непрерывной случайной величины X, возможные значения которой находят­ся на отрезке [а, b], называется определенный интеграл:

В том случае, когда возможные значения случайной вели­чины Х заполняют всю ось Ох, пределы интегрирования а и b бесконечны: а = —,b = . Возможны также случаи, ког­да один из пределов интегрирования бесконечен (возможные значенияХ лежат на полупрямой).

Определение 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

Все сказанное выше о случаях бесконечных пределов интегрирования остается справедливым и для дисперсии.

Среднее квадратичекое отклоенние непрерывной случайной величины определяется, как и прежде, по формуле (18.15):

σ(Х) = .

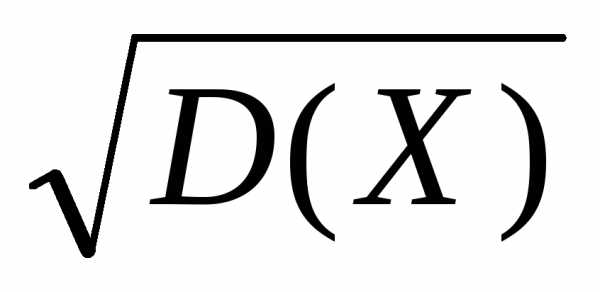Для вычисления дисперсии употребляется более удобная фор­мула, которая выводится из (18.37):

Пример 4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной плотностью распределения на отрезке [0, 1]:

Решение. Согласно формулам (18.36), (18.38) и (18.15) по­следовательно вычисляем искомые величины:

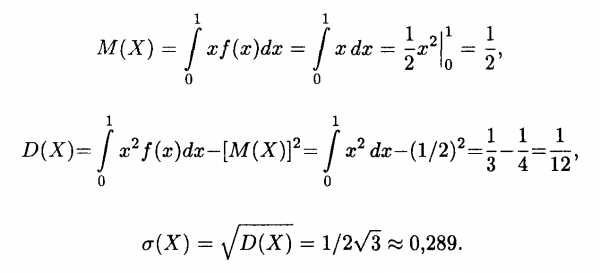
Пример 5. Найти основные числовые характеристики непре­рывной случайной величины X, заданной функцией распреде­ления на положительной полуоси Ох:

Решение. Найдем сначала плотность распределения:

Затем, как и в предыдущем примере, вычисляем соответствуцющие интегралы; при их вычислении применяем правило интегрирования по частям для определенного интеграла. В итоге получаем искомые величины:

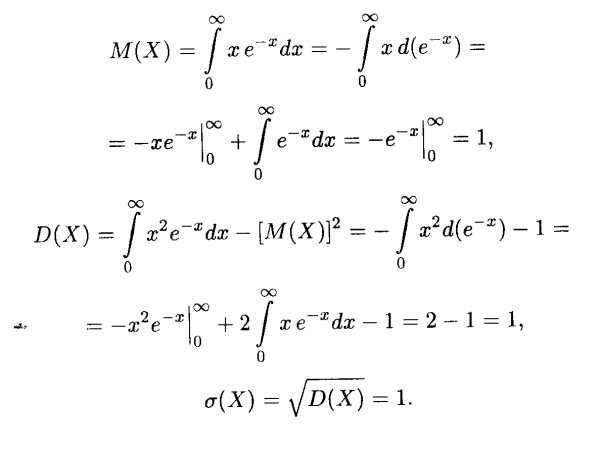
18.5. Основные распределения непрерывных случайных величин Равномерное распределение

Определение 1. Распределение вероятностей называется рав­номерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

Пусть на интервале (a, b) плотность распределения являет­ся постоянной величиной: f(x) = С. Определим значение С из условия (18.35):

откуда получаем, что f(x) = С = 1/(b — а). Значит, искомая плотность равномерного распределения дается формулой

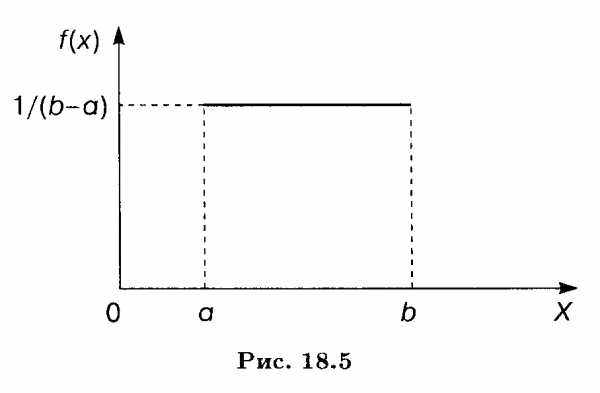
График плотности равномерного распределения указан на рис. 18.5.

Пример 1. Найти среднеквадратическое отклонение случай­ной величины X, распределенной равномерно на интерва­ле (1, 5).

Решение. Согласно формуле (18.39), плотность распреде­ления указанной случайной величины является ненулевой и равна 0,25 на интервале (1, 5). По формулам (18.36) и (18.38) последовательно вычисляем:

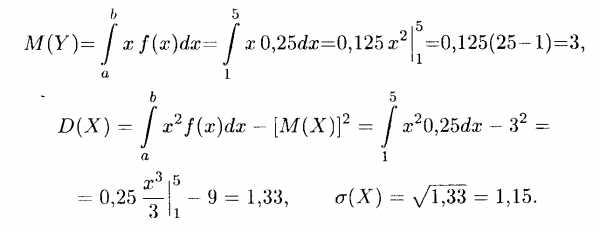
Пример 2. Радиус круга измерен приближенно на интервале (а, b). Полагая, что радиус является случайной величиной X, распределенной равномерно в этом интервале, найти матема­тическое ожидание и дисперсию площади круга.

Решение. Площадь круга также является случайной ве­личиной, вычисляемой по формуле Y = πX²; она имеет то же равномерное распределение, что и случайная величина X. По формулам (18.36) и (18.38) получаем

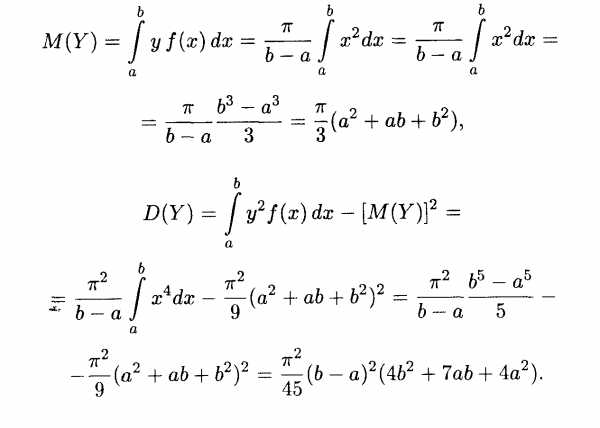
studfiles.net

Непрерывная случайная величина

Этот интеграл предполагается абсолютно сходящимся. В противном случае, т.е. когда интеграл расходится или сходится условно, считают, что случайная величина X не имеет математического ожидания.

Вероятностный смысл этой формулы такой же, что и для дискретной случайной величины. Это ее среднее значение, точнее — средневзвешенное значение с весовой функцией, равной плотности вероятности.

Математическое ожидание непрерывной случайной величины обладает теми же свойствами, что и математическое ожидание дискретной случайной величины.

Определение дисперсии случайной величины X, данное ранее с помощью формулы

2	˜ 2	),
DX = M[(X − mX )	] = M(X

является общим как для дискретной, так и для непрерывной случайной величины. По

этой формуле имеем

+∞

Z

DX = (x − mX )2f(x)dx.

−∞

Свойства дисперсии, сформулированные для дискретных случайных величин, сохраняются и для случая непрерывных случайных величин.

Определение. Модой непрерывной случайной величины называется точка максимума ее плотности вероятности.

Определение. Медианой (Me X, Me) непрерывной случайной величины называется ее значение, обладающее свойством — вероятности попадания случайной величины X левее и правее медианы равны:

P (X < Me) = P (X > Me).

С помощью функции распределения данное равенство записывается в виде F (Me) = 1 − F (Me) откуда

F (Me) = 1/2.

Если F (x) строго возрастает, то медиана единственна. В случае отсутствия математического ожидания его роль, как среднего, обычно выполняет медиана.

Определение. Коэффициентом асимметрии распределения (скошенности), или просто асимметрией называется число, равное отношению третьего центрального момента случайной величины к кубу ее среднего квадратического отклонения:

aX = µ3/σX3 .

Для непрерывной случайной величины aX > 0, если график одномодальной плотности имеет пологую часть справа, а крутую слева от моды; aX < 0, если наоборот; aX = 0 для симметричного распределения.

Определение. Квантилем порядка p непрерывной случайной величины X называется ее значение xp, удовлетворяющее уравнению

F (xp) = p.

Квантили порядков p = 1/4 и p = 3/4 называются соответственно нижней и верхней квартилями.

Если F (x) строго возрастает, то квантиль xp единственна. Квантиль порядка p = 1/2 есть медиана распределения.

studfiles.net

Примеры законов распределения непрерывной случайной величины

Основными законами распределения непрерывной случайной величины являются: равномерное, экспоненциальное , нормальное и другие. Рассмотрим равномерное распределение.

Равномерное распределение

Равномерным считается распределение, при котором все значения случайной величины (в области ее существования, например, в интервале [a,b]) равновероятны. Функция распределения для такой случайной величины имеет вид:

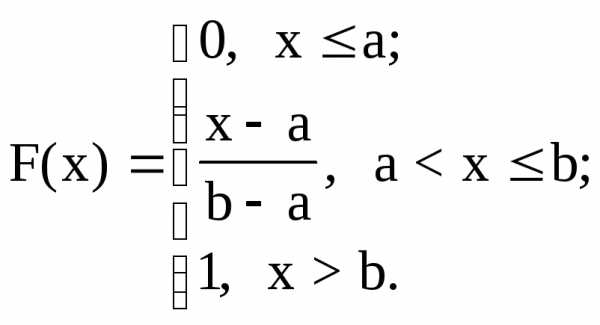
Плотность распределения:

F(x) f(x)

1

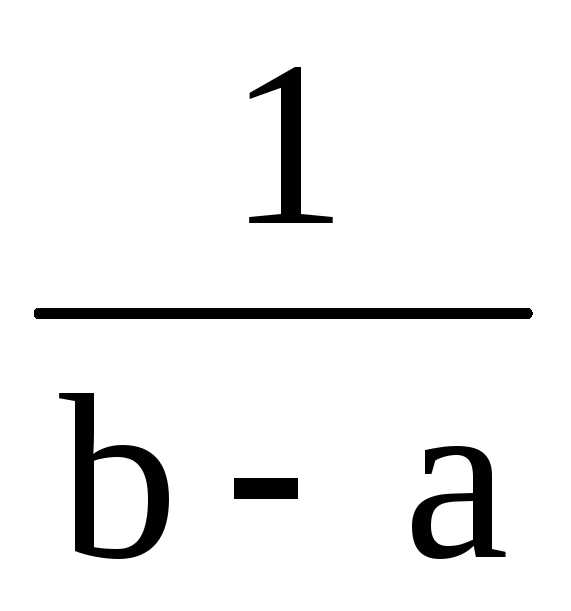
0 a b x 0 a b x

Рис. Графики функции распределения (слева) и плотности распределения (справа).

Числовые характеристики случайных величин

Исчерпывающей характеристикой случайных величин является закон распределения. Как известно, закон распределения представляет собой некоторую функцию, указание которой полностью описывает случайную величину с вероятностной точки зрения. На практике бывает трудно построить закон распределения случайной величины (да и нет потребности в таком полном описании). Достаточно указать отдельные числовые параметры, характеризующие существенные черты распределения, например, 1) среднее, вокруг которого разбросаны значения случайной величины; 2) число, характеризующее величину этого разброса и т.д.

Числа, в сжатой форме выражающие наиболее существенные черты распределения, называются числовыми характеристиками случайной величины.

Среди них рассмотрим прежде всего характеристики положения, фиксирующие положение случайной величины на числовой оси, т.е. некоторое среднее, ориентировочное значение случайной величины, около которого группируются её возможные значения. Из характеристик положения в теории вероятности наибольшую роль играет математическое ожидание, иногда его называют средним значением случайной величины.

Математическое ожидание

Определение 1: Математическим ожиданием или средним значением случайной величины X, заданной на вероятностном пространстве <W,F,P>, называется число

M[X]=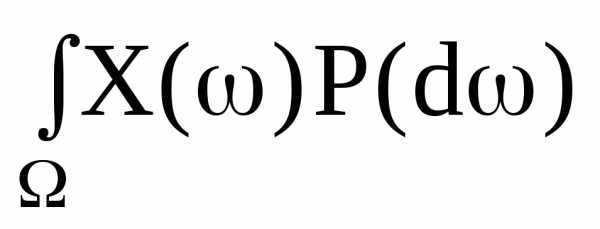

если. интеграл, стоящий в правой части, существует.

Мы знаем, что случайная величина Х(w) индуцирует меру Р_х на прямой, задаваемую равенством: P_x=P{X<x}=F(x), поэтому М[X] мы можем определить также как

, (1)

где F(x) — функция распределения случайной величины Х.

Из определения следует, что M[X] существует, если M½[X]½<¥. Практически редко встречаются случаи, когда математическое ожидание не существует. Если F(x) ─ ступенчатая функция (рассматривается дискретная случайная величина), то интеграл Стилтьеса в формуле (1) превращается в сумму

, Р(Х=х_i)=р_i ,

— математическое ожидание для дискретной случайной величины.

Если F(x) имеет плотность f(x), то

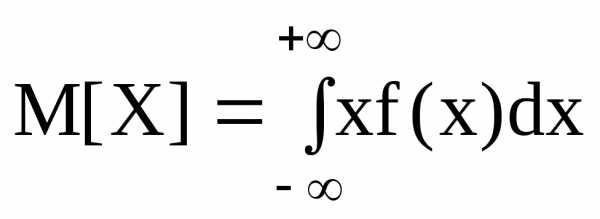
— математическое ожидание для непрерывной случайной величины.

Математическое ожидание M[X] можно рассматривать как координату «центра тяжести» распределения F единичной массы на прямой и это соответствует естественному пониманию среднего значения этого распределения.

studfiles.net

Раздел V. Непрерывные случайные величины

Y = cX получаются из значений случайной величины Х умножением на множитель c, а вероятности соответствующих значений новой случайной величины никак не изменяются.

Еще раз подчеркнем, что математическое ожидание есть усредненная характеристика случайной величины. Оно всегда определяется только одним числом, которое находится на интервале между наименьшим и наибольшим из возможных значений случайной величины. В отличие от функции и плотности распределения, которые дают полную информацию о случайной величине и позволяют находить вероятности ее значений или вероятности того, что они находятся в любом интервале, знание математического ожидания недостаточно для определения таких вероятностей.

Дисперсия случайных величин характеризует средний разброс квадрата отклонений значений случайной величины X от ее математического ожидания M ( X ) . Аналогично тому, как это было для дискретных случайных величин,

вводится следующее определение.

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

D( X ) = M (( X − M ( X ))2 )

(5.8)

Поэтому размерность D(X ) равна квадрату размерности X . Удобнее D( X ) является среднее квадратичное отклонение σ = D( X ) . Дисперсии случайных

величин удовлетворяют следующим свойствам:

1. Дисперсия постоянной величины C равна нулю:

D(C) = 0

2. Постоянный множитель выносится за знак дисперсии в квадрате, т.е.:

D(cX ) = c2 D( X )

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, т.е.:

D( X +Y ) = D( X ) + D(Y )

4. Для вычисления D( X ) удобнее использовать равенство
D( X ) = M (X 2 )−(M ( X ))2	(5.9)

Заметим, что отклонение случайной величины X от числа, равного ее математическому ожиданию M ( X ) , т.е. Z = X − M ( X ) – также случайная вели-

чина. При этом M (Z ) всегда равно нулю, т.е. M (X − M (X )) = 0 . Действительно, используя свойства (1) – (3), получаем:

M (Z) = M ( X ) − M (M ( X )) = M ( X ) − M (X ) = 0

Именно по этой причине разброс значений X относительно M ( X )	харак-
теризуется дисперсией D( X ) и средним квадратичным уклонением σ =	D(X ) .

Пример 7. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X , которая имеет плотность распределения:

studfiles.net

8.2. Числовые характеристики непрерывных случайных величин

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

Где Р(Х) — плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу , то

Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством

Если интеграл сходится, или равносильным равенством

В частности, если все возможные значения Х принадлежат интервалу , то

Или

Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин.

Среднее квадратическое отклонение непрерывной случайной величины определяется равенством

.

Модой непрерывной случайной величины Х называется ее наиболее вероятное значение (для которого плотность вероятности Р(Х) достигает максимума).

Медианой непрерывной случайной величины Х называется такое ее значение, для которого

.

Вертикальная прямая , проходящая через точку с абсциссой, равной , геометрически делит площадь фигуры под кривой распределения на две равные части (рис. 8.7).

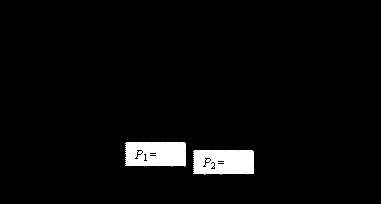Рис. 8.7

Очевидно, что .

Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством

.

Центральный теоретический момент порядка K непрерывной случайной величины Х определяется равенством

.

Если все возможные значения Х принадлежат интервалу , то

, .

Очевидно, что ; ; ; ; . Центральные моменты выражаются через начальные моменты по формулам:

,

,

.

Математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение распределения случайной величины Х; второй центральный момент, или дисперсия , — степень рассеяния распределения Х относительно М(Х).

Третий центральный момент служит для характеристики асимметрии распределения.

Величина называется Коэффициентом асимметрии случайной величины.

А = 0, если распределение симметрично относительно математического ожидания.

Четвертый центральный момент характеризует крутость распределения.

Эксцессом случайной величины называется число

.

Кривые более островершинные, чем кривая для нормального распределения, обладают положительным эксцессом, более плосковершинные — отрицательным эксцессом.

Пример 8.7. Дана функция

При каком значении параметра С эта функция является плотностью распределения некоторой непрерывной случайной величины Х? Найти математическое ожидание и дисперсию случайной величины Х.

Решение. Для того чтобы Р(Х) была плотностью вероятности некоторой случайной величины Х, она должна быть неотрицательна, т. е. , откуда и она должна удовлетворять свойству 4 плотности вероятности.

Следовательно,

Откуда

.

Найдем интеграл , применив метод интегрирования по частям

Таким образом,

И плотность распределения имеет вид

Следовательно,

Дисперсия

Вначале найдем

Теперь

Пример 8.8. Случайная величина Х распределена по «закону прямоугольного треугольника» в интервале (рис. 8.8).

1. Написать выражение плотности распределения.

2. Найти функцию распределения F(Х).

3. Найти вероятность попадания случайной величины Х на участок от до А.

4. Найти характеристики величины Х: М(Х), D(Х), , .

Решение. Так как площадь прямоугольного треугольника есть площадь фигуры, ограниченной кривой распределения и осью абсцисс, то она равна единице: И, следовательно, . Уравнение прямой АВ в отрезках имеет вид , откуда , то есть функция плотности распределения имеет вид

Найдем функцию распределения F(Х):

Если , то

Если , то

Если , то

Таким образом,

Вероятность попадания случайной величины Х на участок от До А определяется по формуле

.

Найдем математическое ожидание:

Следовательно,

,

.

Так как , а , ,

,

То .

Пример 8.9. По данным задачи 8.5 найти математическое ожидание М(Х), дисперсию D(Х), моду М0(Х) и медиану Ме(Х).

Решение. Так как

То .

Дисперсия

Вначале найдем

.

Следовательно,

График плотности вероятности Р(Х) имеет вид (рис. 8.9)

Рис. 8.9

Плотность вероятности р(Х) максимальна при х = 2, это означает, что М0(Х) = 2.

Из условия Найдем медиану Ме(Х): ; откуда

Пример 8.10. Дана функция

Найти коэффициент асимметрии и эксцесс случайной величины Х.

Решение. Плотность распределения случайной величины Х равна

Так как асимметрия , эксцесс , то найдем начальные моменты первого, второго, третьего и четвертого порядков:

Тогда

Так как то Следовательно,

Пример 8.11. Плотность случайной величины Х задана следующим образом:

Найти моду, медиану и математическое ожидание Х.

Решение. Найдем математическое ожидание Х:

.

Так как плотность распределения достигает максимума при Х = 1, то М0(Х) =1. Медиану Ме(Х) найдем из условия . Для этого вначале найдем функцию распределения :

Если , то

Если , то

Если , то

Таким образом,

Уравнение равносильно уравнению , откуда .

Пример 8.12. Случайная величина Х задана плотностью распределения

Найти математическое ожидание функции (не находя предварительно плотности распределения ).

Решение. Воспользовавшись формулой для вычисления математического ожидания функции от случайного аргумента Х

Где А и B — концы интервала, в котором заключены возможные значения Х, получим

Пример 8.13. Случайная величина Х задана плотностью распределения

Найти моду, математическое ожидание и медиану величины Х.

Решение. Так как , то отсюда видно, что при Х = 4 плотность распределения достигает максимума и, следовательно, М0(Х) = 4 (можно было найти максимум методами дифференциального исчисления).

Кривая распределения симметрична относительно прямой Х = 4, поэтому М(Х) = Ме(Х) = 4.

< Предыдущая		Следующая >

matica.org.ua