Решение пределов по правилу Лопиталя
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов функций является использование правила Лопиталя. Оно позволяет раскрывать неопределенности вида 0/0 или ∞/∞ в конечной или бесконечно удаленной точке, которую мы обозначим как x0. Правило Лопиталя заключается в том, что мы находим производные числителя и знаменателя дроби. Если существует предел , то существует равный ему предел .
Если после дифференцирования мы опять получаем неопределенность, то процесс можно повторить, то есть применить правило Лопиталя уже к пределу . И так далее, до раскрытия неопределенности.
Для применения этого правила, должна существовать такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и функция в знаменателе и ее производная не обращается в нуль.
Применение правила Лопиталя состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 или ∞/∞. Для этого, если требуется, выполняем преобразования и делаем замену переменной. В результате получаем предел вида .
2) Убеждаемся, что существует такая проколотая окрестность точки x0, на которой функции в числителе и знаменателе являются дифференцируемыми и знаменатель и его производная не обращаются в нуль.
3) Находим производные числителя и знаменателя.
4) Если имеется конечный или бесконечный предел , то задача решена: .
5) Если предела не существует, то это не означает, что не существует исходного предела. Это означает, что данную задачу решить с помощью правила Лопиталя нельзя. Нужно применить другой метод (см. пример ниже).
6) Если в пределе вновь возникает неопределенность, то к нему также можно применить правило Лопиталя, начиная с пункта 2).
Как указывалось выше, применение правила Лопиталя может привести к функции, предела которой не существует. Однако это не означает, что не существует исходного предела. Рассмотрим следующий пример.
.
Применяем правило Лопиталя. , .
Однако предела не существует. Не смотря на это, исходная функция имеет предел:
.
Правило Лопиталя. Формулировки теорем
Здесь мы приводим формулировки теорем, на которых основывается раскрытие неопределенностей по правилу Лопиталя.
Теорема о раскрытии неопределенности 0/0
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точки , причем не равна нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Примеры
Далее мы приводим подробные решения следующих пределов с помощью правила Лопиталя.
⇓, ⇓, ⇓,
⇓, ⇓, ⇓.
Пример 1
Показать, что экспонента растет быстрее любой степенной функции, а логарифм – медленнее. То есть показать, что
А) ;
Б) ,
где .
Решение
Рассмотрим предел А). При . Это неопределенность вида . Для ее раскрытия применим правило Лопиталя. Пусть
.
Находим производные. . Тогда
.
Если , то неопределенность исчезает, поскольку при . По правилу Лопиталя,
.
Если , то применяем правило Лопиталя n раз, где – целая часть числа b.
;
.
Поскольку , то . Хотя мы привыкли читать слева направо, но эту серию равенств следует читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему предел . И так далее, пока не дойдем до предела .
Теперь рассмотрим предел Б):
. Сделаем замену переменной . Тогда ; при ; .
Пример 2
Найти предел с помощью правила Лопиталя:
.
Решение
Это неопределенность вида 0/0. Находим по правилу Лопиталя.
.
Здесь, после первого применения правила мы снова получили неопределенность. Поэтому применили правило Лопиталя второй раз. Эту серию равенств нужно читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Ответ
Пример 3
Вычислить предел, используя правило Лопиталя.
.
Решение
Найдем значения числителя и знаменателя при :
;
.
Числитель и знаменатель равны нулю. Мы имеем неопределенность вида 0/0. Для ее раскрытия, применим правило Лопиталя.
.
Ответ
Пример 4
Решить предел с помощью правила Лопиталя.
.
Решение
Здесь мы имеем неопределенность вида (+0)+0. Преобразуем ее к виду +∞/+∞. Для этого выполняем преобразования.
.
Находим предел в показателе степени, применяя правило Лопиталя.
.
Поскольку экспонента – непрерывная функция для всех значений аргумента, то
.
Ответ
.
Пример 5
Найти предел используя правило Лопиталя:
.
Решение
Здесь мы имеем неопределенность вида ∞ – ∞. Приводя дроби к общему знаменателю, приведем ее к неопределенности вида 0/0:
.
Применяем правило Лопиталя.
;
;
.
Здесь у нас снова неопределенность вида 0/0. Применяем правило Лопиталя еще раз.
;
;
.
Окончательно имеем:
.
Как и во всех пределах, вычисляемых с помощью правила Лопиталя, читать нужно с конца. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Можно упростить вычисления, если воспользоваться теоремой о замене функций эквивалентными в пределе частного. Согласно этой теореме, если функция является дробью или произведением множителей, то множители можно заменить на эквивалентные функции. Поскольку при , то
.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Вычисление пределов по правилу Лопиталя
 — Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида
— Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида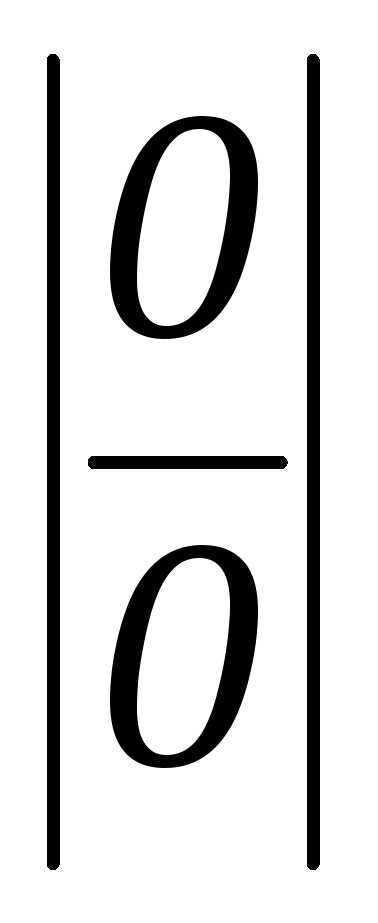 или
или можно сформулировать в виде теоремы.
можно сформулировать в виде теоремы.
— Теорема. Пусть
однозначные функции 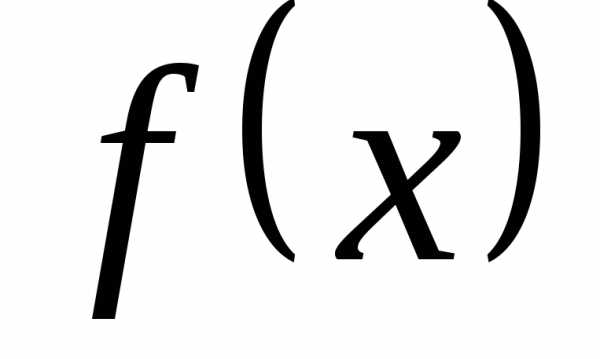 и
и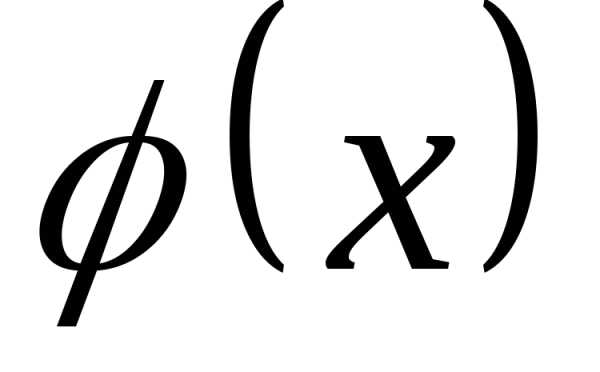 дифференцируемы в некоторой окрестности
точки
дифференцируемы в некоторой окрестности
точки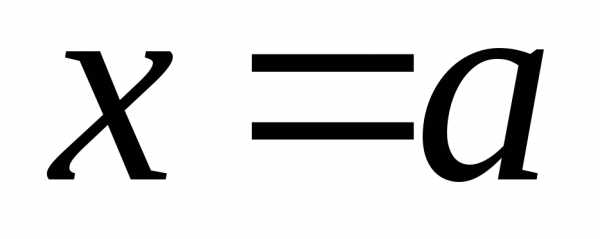 ,
причем
,
причем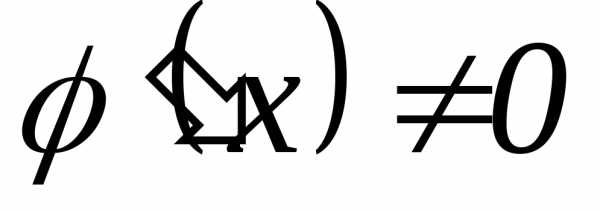 .
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.
.
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.
— Обратите внимание: именно существование предела отношений производных гарантирует существование предела отношения функций, но не наоборот! Предел отношения функций может существовать и при отсутствии предела отношения производных.
Однако на практике это правило применяют в обратном порядке: предел отношения функций приравнивают пределу отношения производных.
Пример – иллюстрирует случай неприменимости правила Лопиталя.
Пусть , найдем пределы отношения функций: ;
и их производных: — не существует.
Правило Лопиталя применять нельзя.
— и
Правило Лопиталя можно применять несколько раз подряд, если неопределенность после очередного применения не раскрыта.
Неопределенные выражения вида с помощью тождественных преобразований приводят к виду
и применяют правило Лопиталя.
Желательно совмещать применение правила Лопиталя с применением эквивалентных бесконечно малых величин. При этом следует строго придерживаться теоремы: заменять эквивалентными можно только в произведении (частном) !
После каждого применения правила Лопиталя следует проверять, сохранилось ли неопределенное выражение. Если при проверке находятся сомножители, предел которых конечен и не равен нулю (равен числу, отличному от нуля),их сразу заменяют соответствующими пределами.
Примеры
Вычислить пределы по правилу Лопиталя.
| Применять
эквивалентные бесконечно малые
величины нельзя, т.к. |
= | Первое применение правила Лопиталя дает конечный предел. |
| Применять эквивалентные бесконечно малые величины нельзя, выполним тождественные |
= | преобразования, чтобы можно было применить правило Лопиталя. Первое применение правила Лопиталя не устраняет неопределенное выражение, |
но проверка пределов сомножителей показывает, что некоторые из них имеют конечные пределы, которыми они и заменяются. | |
Еще раз применяется правило Лопиталя. | |
Полученный в результате предел бесконечен. |
— При вычислении пределов сомножителей используются известные величины:
 — Раскрытие степенных неопределенных
выражений вида
— Раскрытие степенных неопределенных
выражений вида
.
Допустим,
существует конечный или бесконечный
предел степенно-показательной функции 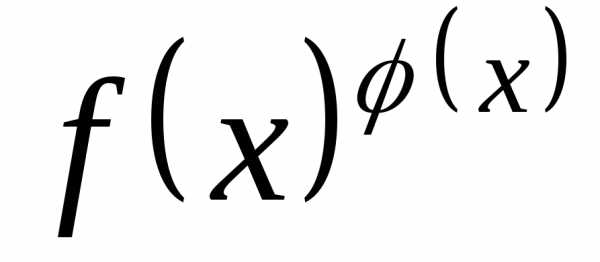 (см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
(см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
.
Прологарифмируем данное выражение и применим правило предельного перехода под знаком непрерывной функции (см. раздел о непрерывности функции, тема 4).
Логарифмируем по основанию е. | |||
| Используем свойства логарифмов (см. приложение) и правило предельного перехода. | ||
Степень числа е вычисляется как предел. | |||
, где | Окончательно получим формулы, по которым можно вычислять пределы степенно-показательных функций. | ||
— Часто при вычислении А применяют правило Лопиталя, поэтому полученные формулы для раскрытия степенно-показательной неопределенности иногда называют вторым правилом Лопиталя.
ПРИМЕР
Вычислить предел по второму правилу Лопиталя.
Допустим
нужный предел существует и обозначим
его | |||
Теперь вычислим показатель степени А. Преобразуем выражение под знаком предела, чтобы можно было применить правило Лопиталя. | |||
| |||
Преобразуем полученное выражение и проверяем неопределенность. Она не устранена. | |||
Заменяем | |||
Окончательный ответ. | |||
Еще примеры вычисления пределов по правилу Лопиталя приведены в разделе «Примеры выполнения обязательных заданий по теме 5».
57
studfiles.net
правило лопиталя
Правило Лопиталя | |||
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или. Пустьa является некоторым конечным действительным числом или равно бесконечности.
Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенностиможно свести к типуилис помощью алгебраических преобразований. А неопределенностисводятся к типус помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов. | |||
Пример 1 | |||
Вычислить предел . Решение. Дифференцируя числитель и знаменатель, находим значение предела:
| |||
Пример 2 | |||
Вычислить предел . Решение. Поскольку прямая подстановка приводит к неопределенности типа , применяем правило Лопиталя.
| |||
| Пример 3 | |||
Вычислить предел . Решение. Здесь мы имеем дело с неопределенностью типа . После простых преобразований, получаем
| |||
Пример 4 | |||
Найти предел . Решение. Используя правило Лопиталя, можно записать
| |||
Пример 5 | |||
Найти предел . Решение. Здесь мы встречаемся с неопределенностью типа . Обозначим. После логарифмирования получаем
Далее, по правилу Лопиталя, находим
Соответственно,
| |||
Пример 6 |
15. Правила Лопиталя*
Швейцарский математик Иоганн I Бернулли (1667-1748) после успешного окончания Базельского университета, путешествуя по Европе, в 1690 году приезжает в Париж. В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691-1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691-1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.
Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Пусть конечно. По выберем : в интервале выполняется неравенство
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .
В случае, когда бесконечно, неравенство (1) заменяется на
или
в зависимости от знака . В остальном доказательство не меняется.
Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
Имеем
при . Применим к отрезку теорему Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) – на неравенство
имеющим место при , достаточно близких к a в силу (3).
Аналогично рассматривается случай .
studfiles.net
Вычисление пределов по правилу Лопиталя
Эффективным способом вычисления пределов функций, имеющих особенности типа бесконечность на
бесконечность или ноль на ноль является применение правила Лопиталя: предел отношения двух
бесконечно малых или двух бесконечно больших функций равен пределу отношения их производных,
если такие существуют
Раскрытие неопределенностей сводится предварительно рассмотренным выше неопределенностей. Если , а при , то применяем преобразование
В случае трех последних неопределенностей нужно применять преобразования
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика»на
применение правила Лопиталя.
————————————
Пример 1. Найти пределы.
1) (5. 626)
2) (6. 629)
3) (6. 634)
4) (4. 639)
5) (4. 645)
6) (4. 668)
Решение. 1) Подстановкой устанавливаем что имеем неопределенность вида ноль на ноль . Для избавления от
нее применим правило Лопиталя
2) Как и в предыдущем примере мы имеем неопределенность . По правилу Лопиталя находим
3) Учитывая неопределенность применяем предыдущее правило
4) Раскрываем неопределенность вида
Числитель и знаменатель преобразуем к сумме синусов на основе правила
В результате получим
Подставим найденные значения
Опять получили неопределенность вида и повторно применяем правило Лопиталя
Здесь учтено, что косинус функция стремится к единице при .
5) Есть неопределенность вида бесконечность на бесконечность .
Найдем производные
6) Применим последнее правило сведения к второй замечательной границы
Применение правила Лопиталя показало все возможности при раскрытии неопределенностей.
Пользуйтесь им на практике и Вам не будет трудно находить подобные границы в обучении.
————————————
Посмотреть материалы:
yukhym.com
2.4.3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «Правило Лопиталя»
Задача 1.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Решение
Ответ:
Задача 2.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 3.
Задача 3.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 0.
Задача 4.
Вычислить предел
Указание
Преобразуйте функцию к виду
Тогда предел показателя степени можно вычислить по правилу Лопиталя.
Решение
Ответ: 1.
Задача 5.
Вычислить предел
Указание
Преобразуйте функцию, стоящую под знаком предела:
Решение
Ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Правило Лопиталя раскрытия неопределенностей 0/0 и ∞/∞ (Лекция №8)
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
| (1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти . Этот предел существует . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
- .
- .
- .
Обозначим .
Прологарифмируем это равенство . Найдем .
Так как lny функция непрерывная, то . Следовательно, или .
ФОРМУЛА ТЕЙЛОРА
Пусть функция y= f(x) задана на (a, b) и x0 Î (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой задачей вычисления значений P(x).
Пусть искомый многочлен имеет степень n P(x) = Pn(x). Будем искать его в виде
| (1) |
В этом равенстве нам нужно найти коэффициенты .
Для того чтобы этот многочлен был «близок» к функции f(x) потребуем выполнения следующих равенств:
Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты многочлена Pn(x) исходя из условия равенства производных.
Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.
Подставим в (1) x = x0 и найдем , но с другой стороны . Поэтому
Далее найдем производную и вычислим Следовательно, .
Учитывая третье условие и то, что
,
получим , т.е. .
Далее . Значит, , т.е. .
Очевидно, что и для всех последующих коэффициентов будет верна формула
Подставляя найденные значения коэффициентов в формулу (1), получим искомый многочлен:
Обозначим и назовем эту разность n-ым остаточным членом функции f(x) в точке x0. Отсюда и, следовательно, если остаточный член будет мал.
Оказывается, что если x0 Î (a, b) при всех x Î (a, b) существует производная f (n+1)(x), то для произвольной точки x Î (a, b) существует точка, лежащая между x0 и x такая, что остаток можно представить в виде:
Это так называемая формула Лагранжа для остаточного члена.
Формула
где x Î (x0, x) называется формулой Тейлора.
Если в этой формуле положить x0 = 0, то она запишется в виде
где x Î ( x0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.
РАЗЛОЖЕНИЕ ПО ФОРМУЛЕ МАКЛОРЕНА НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- Рассмотрим функцию f(x)=ex. Представим ее по формуле
МакЛорена в виде суммы многочлена и некоторого остатка. Для этого найдем
производные до (n+1) порядка:
Таким образом, получаем
Используя эту формулу и придавая x различные значения, мы сможем вычислить значение ex.
Например, при x=1, ограничиваясь n=8, получим формулу, позволяющую найти приближенное значение числа e:
причем остаток
Отметим, что для любого x Î R остаточный член
Действительно, так как ξ Î (0; x), то величина eξ ограничена при фиксированном x. При x> 0 eξ < ex. Докажем, что при фиксированном x
Имеем
Если x зафиксировано, то существует натуральное число N такое, что |x|<N.
Обозначим Заметив, что 0<q<1, при n>N можем написать
Но , не зависящая от n, а так как q<1. Поэтому Следовательно,
Таким образом, при любом x, взяв достаточное число слагаемых, мы можем вычислить ex с любой степенью точности.
- Выпишем разложение по
формуле МакЛорена для функции f(x)=sin x.
Найдем последовательные производные от функции f(x)=sin x.

Подставляя полученные значения в формулу МакЛорена, получим разложение:
Несложно заметить, что преобразовав n-й член ряда, получим
.
Так как , то аналогично разложению ex можно показать, что для всех x.
Пример. Применим полученную формулу для приближенного вычисления sin 20°. При n=3 будем иметь:
Оценим сделанную погрешность, которая равна остаточному члену:
Таким образом, sin 20°= 0,342 с точностью до 0,001.
- f(x) = cos x. Аналогично предыдущему
разложению можно вывести следующую формулу:
Здесь также для всех x. Докажите формулу самостоятельно.
- f(x)=ln (1+x). Заметим, что
область определения этой функции D(y)=(–1; +∞).
Найдем формулу МакЛорена для данной функции.
Подставим все найденные производные в ряд МакЛорена.
Можно доказать, что если x Î (–1;1],то , т.е. выведенная формула справедлива при x Î ( –1;1].
- f(x) = (1+x)m, где m Î R, m≠0.
При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:
И следовательно,
Можно показать, что при |x|<1
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ
Вспомним сначала определения возрастающей и убывающей функций.
Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x1 < x2, то f(x1) < f(x2).
Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x1 < x2, то f(x1) > f(x2).
Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.
Функция y=f(x) называется постоянной на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.
Рассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.
(-∞, a), (c, +∞) – убывает;
(a, b) – постоянная;
(b, c) – возрастает.
Применим понятие производной для исследования возрастания и убывания функции.
Теорема 1. (Необходимое и достаточное условия возрастания функции)
- Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f ‘(x)≥ 0.
- Обратно. Если
функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b)
и ее производная положительна на этом отрезке,f ‘ (x)≥ 0 для a<x<b, то f(x) возрастает
на[a, b].
Доказательство.
- Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке
произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению
возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) — f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
Переходя в этом равенстве к пределу при Δx→0, получим , то есть f ‘(x)≥0.
- Докажем вторую часть теоремы. Пусть f ‘(x)>0при всех x Î (a,b). Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По теореме Лагранжа существует такое число c Î (x1, x2), что . По условию f ‘(x)>0, x1 – x2>0Þ , а это и значит, что f(x) – возрастающая функция.
Аналогичная теорема имеет место и для убывающих функций.
Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].
Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f ‘(x)≥0.
Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f ‘(x)>0 – для возрастания или f ‘(x)<0 – для убывания.
Примеры. Определить интервалы монотонности функции.
- . Область определения заданной функции D(y) = (-∞; 0)È(0; +∞).
. Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).
-
Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
-
.
Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).
- Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке
произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению
возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) — f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
toehelp.ru
Вычислить предел, используя правило Лопиталя
Поиск ЛекцийПервое правило Лопиталя
Рассмотрим функции , которые бесконечно малЫв некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел тоже должен существовать, в противном случае правило не применимо.
Что следует из вышесказанного?
Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)
Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!
И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .
Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат:
К неопределённости 0:0 применим первое правило Лопиталя:
Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!
Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах:
На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).
Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.
Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности.
Второе правило Лопиталя
Брат-2 борется с двумя спящими восьмёрками . Аналогично:
Если существует предел отношения бесконечно большихв точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел должен существовать
Опять же, в различных практических примерах значениеможет быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость .
Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:
Однако для Примера №2 той же статьи проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить предел
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:
Таким образом, линейная функцияболее высокого порядка роста, чем логарифм с основанием бОльшим единицы( и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её график является более пологим относительно того же «икса».
Пример 2
Вычислить предел
Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:
Показательная функция, с основанием, бОльшим единицы( и т.д.)более высокого порядка роста, чем степенная функция с положительной степенью.
Похожие пределы встречаются в ходе полного исследования функции, а именно, при нахождении асимптот графиков. Также замечаются они и в некоторых задачах по теории вероятностей. Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.
Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел.
Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:
Вычислить предел, используя правило Лопиталя
Пример 3
Вычислить предел по правилу Лопиталя
Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .
Пример 4
Вычислить предел по правилу Лопиталя
Пример 4
Пример 5
Вычислить предел, используя правило Лопиталя
Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:
После дифференцирования настоятельно рекомендуюизбавляться от многоэтажности дробии проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.
Пример 6
Вычислить предел, используя правило Лопиталя
Пример 6
Пример 7
Вычислить предел, используя правило Лопиталя
Пример 7
Пример 8
Вычислить предел, используя правило Лопиталя
Поехали:
Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Вычислить предел функции, используя правило Лопиталя
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .
Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов. Давайте для проформы ещё один:
Пример 10
Вычислить предел функции, используя правило Лопиталя
На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:
Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость тоже не сопротивляется превращению в или :
Пример 11
Вычислить предел функции с помощью правила Лопиталя
Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций. Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.
Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:
Готово.
Исходный предел можно было попытаться свести к двум бубликам:
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.
Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».
В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен:
Пример 12
Вычислить предел функции с помощью правила Лопиталя
Для устранения неопределённости используем основное логарифмическое тождество: . В данном случае :
На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).
Чтобы не мельчить, вычислим предел показателя отдельно:
С неопределённостью разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость , к которой применимо правило Лопиталя:
Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:
Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:
В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость :
Пример 13
Вычислить предел по правилу Лопиталя
Очередной папуас тоже сдаётся перед формулой . В данном случае :
В результате сразу получена неопределённость , что облегчает задачу. Предел показателя для удобства вычислим отдельно:
В итоге:
Аналогичное задание для самостоятельного решения:
Пример 14
Вычислить предел по правилу Лопиталя
Полное решение и ответ в конце урока.
Предел с неопределённостью по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:
Пример 15
Вычислить с помощью правила Лопиталя
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru

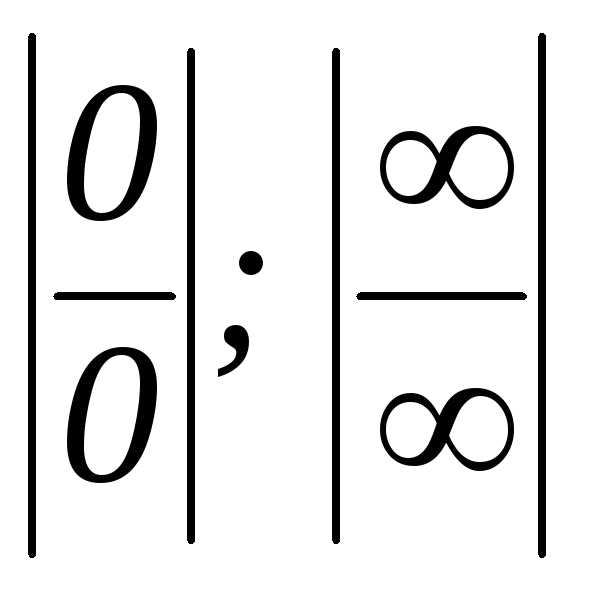
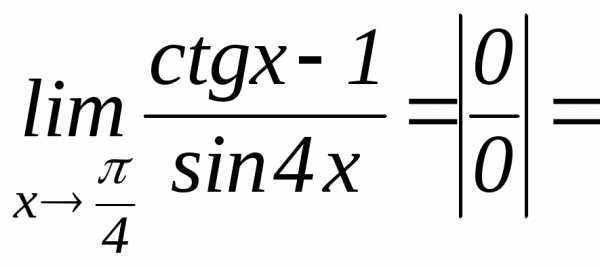
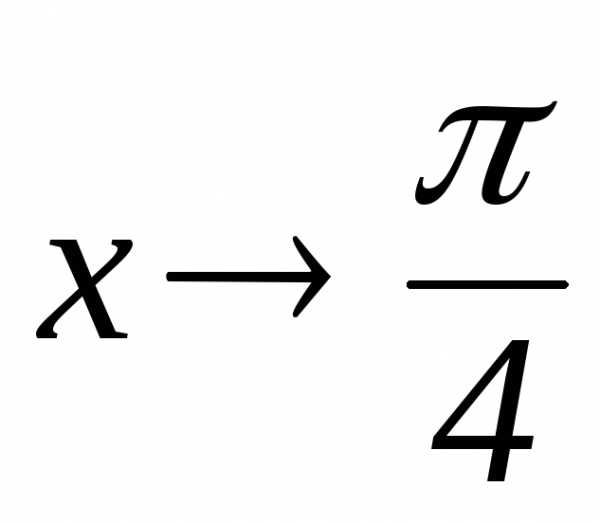
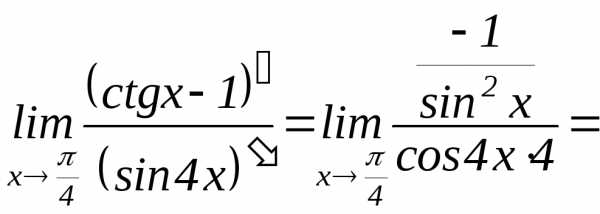
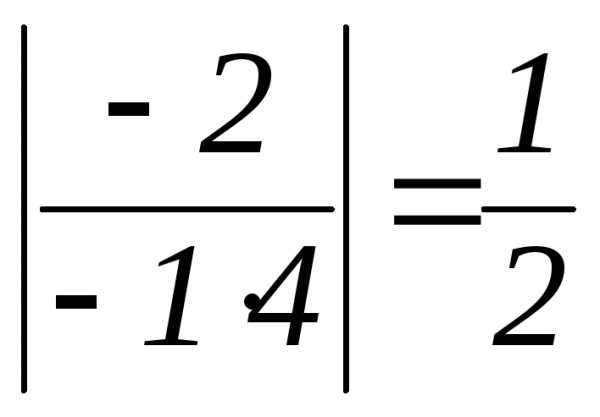


 .
.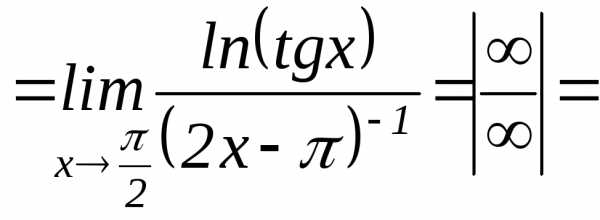
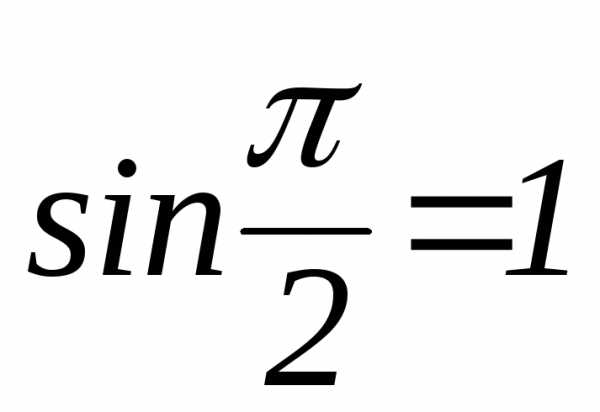 и снова применяем правило Лопиталя.
и снова применяем правило Лопиталя.
