Точки разрыва функции — онлайн справочник для студентов
ОПРЕДЕЛЕНИЕ
Если в точке x=a функция> не является непрерывной, то эта точка называется точкой разрыва функции. Классификация точек разрыва функции
Точка x=a называется точкой устранимого разрыва функции ,если в этой точке односторонние пределы конечны и равны между собой, но не равны значению функции в этой точке; или функция в точке x=a не определена (рис. 1).
Рис. 1
Точка x=a называется точкой разрыва первого рода функции , если в этой точке односторонние пределы конечны и не равны между собой (рис. 2).
Рис. 2
Модуль разности значений односторонних пределов называется скачком функции.
Пример. На рисунке 2 скачок функции равен
Точка x=a называется точкой разрыва второго рода функции , если в этой точке, по крайней мере, один из односторонних пределов равен бесконечности или не существует (рис. 3).
Рис. 3
Примеры решения задач
ПРИМЕР
Задание
Исследовать функцию на непрерывность и классифицировать точки разрыва.
Решение
Функция является непрерывной как отношение двух непрерывных функций (многочленов), разрыв может быть лишь в точках, в которых знаменатель обращается в нуль, то есть
Итак, если разрыв есть, то он может быть лишь в точках . Исследуем функцию на непрерывность в этих точках. Для этого найдем односторонние пределы:
аналогично
Поскольку односторонние пределы бесконечны, то в точке функция имеет разрыв второго рода.
Аналогично для второй точки :
то есть и точка – точка разрыва другого роду.
Ответ
Функция терпит разрыв второго рода в точках (
ПРИМЕР
Задание
Исследовать функцию на непрерывность и сделать схематический чертеж.
Решение
На каждом из промежутков функция задается элементарными функциями, поэтому разрыв может быть только лишь на концах промежутков, а именно в точке x=2. Исследуем функцию на непрерывность в этой точке. Найдем односторонние пределы:
Так як , то точка x=2 является точкой разрыва первого рода.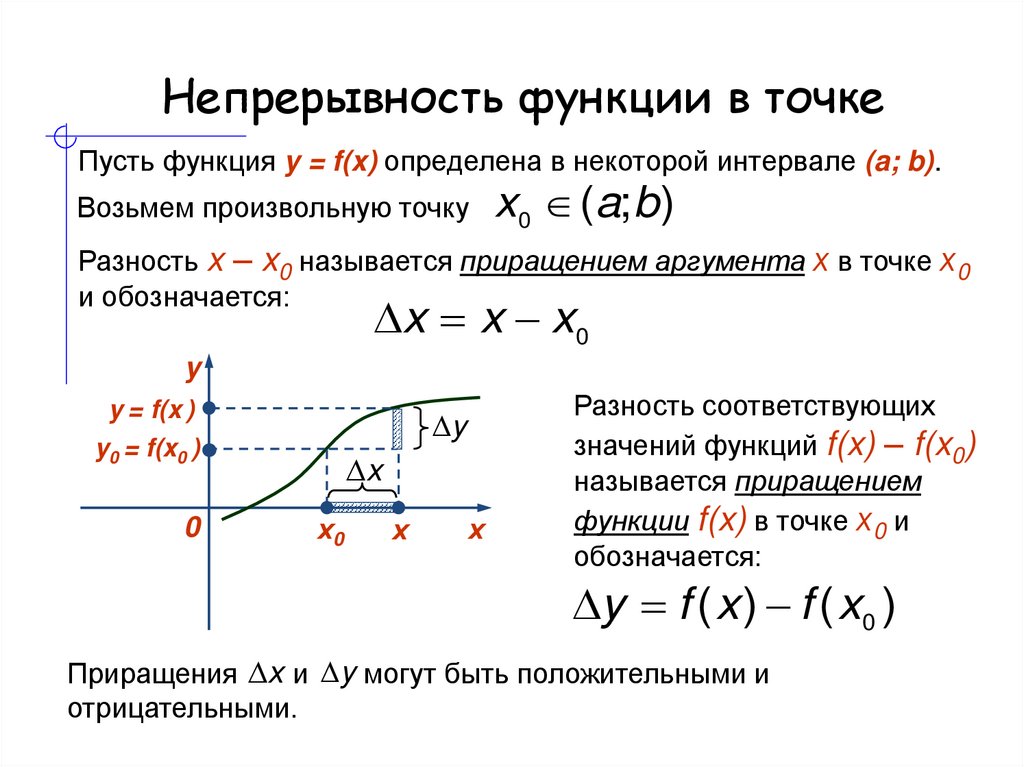
Сделаем схематический чертеж (рис. 4).
Рис. 4
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Длина волны Ограниченные последовательности Числовая последовательность и ее предел Основные теоремы о пределах функции Таблица эквивалентности пределов
Узнать цену работы
Узнай цену
своей работы
Принимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Исследовать функцию на непрерывность, определить характер разрыва.
 Контрольные онлайн
Контрольные онлайн
Образовательные онлайн сервисы: теория и практика
- Главная
- Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика
- Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование. Методы оптимизации
- Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика - Другое
- Контакты
Полезные материалы:
- Учебники
- Справочники
- Онлайн калькуляторы
- Помощь в решении
- Онлайн занятия в Zoom
Исследовать функцию на непрерывность, определить характер разрыва.

Пример 1.
Функция не определена в точках , уже нарушено первое условие непрерывности, следовательно, в этих точках функция испытывает разрыв.
Для выяснения характера разрыва нужно вычислить односторонние пределы в точках .
.
.
Так как левый предел в точке равен бесконечности, то в ней разрыв II рода.
;
.
Так как правый предел в точке равен бесконечности, то в ней разрыв II рода.Пример 2 Функция определена на всей числовой прямой, но при этом она не является непрерывной, так как , , , т.е. правый и левый пределы в нуле не равны между собой и не равны значению функции в нуле, нарушены 2 и 3 условия непрерывности. Так как правый и левый пределы в нуле существуют и конечны, то это разрыв I рода.
Пример 3 Функция неопределена в нуле, следовательно , – точка разрыва.Так как и , то это устранимый разрыв, функцию можно в нуле доопределить “по непрерывности”, положив равной единице.
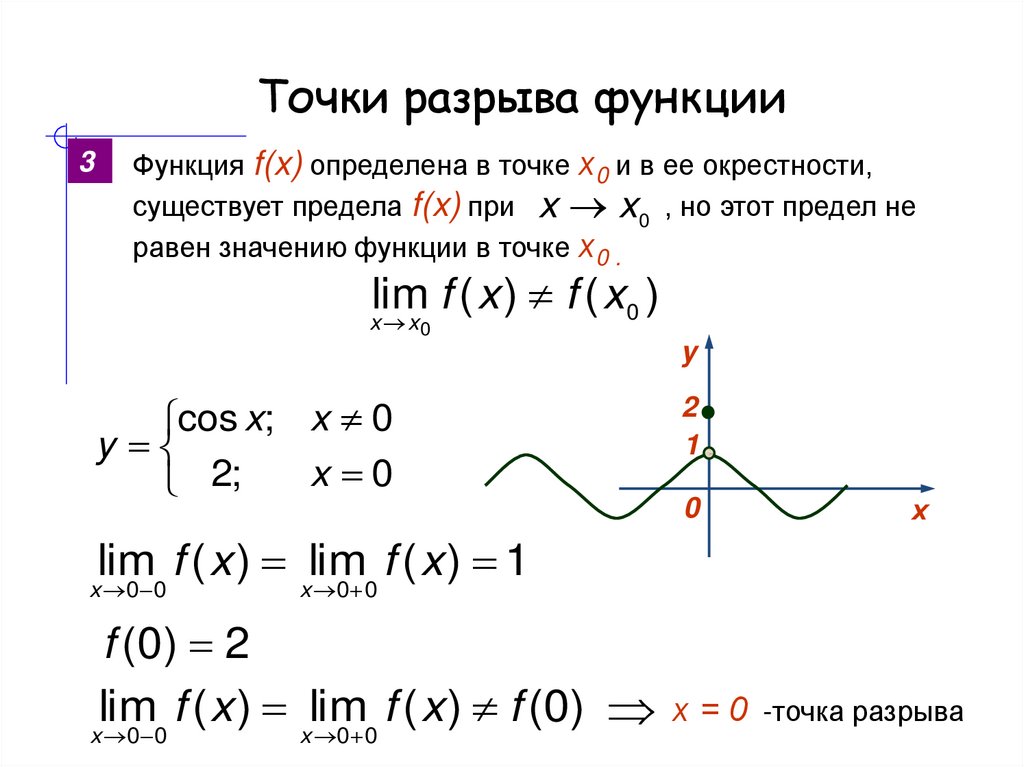
Пример 4
Функция является элементарной, поэтому она непрерывна в области её определения. В область определения не входят точки , , , следовательно, они являются точками разрыва данной функции.
Определим тип точек разрыва.
1) .
;
.
Так как , то точка является точкой
разрыва второго рода функции .
2) .
;
.
Односторонние пределы функции в точке равны, но функция при не определена, следовательно, является устранимой точкой разрыва первого рода.
Так как заданная функция является четной функцией, то, очевидно, что
, и является точкой разрыва второго рода функции .
Для построения эскиза графика функции исследуем поведение функции при
и . Так как функция четная, то
.
Построим эскиз графика функции .
Задать вопрос
Заказать помощь
Отзывы
+7-911-7987704
vk. com/id286009794
com/id286009794
Написать в Whatsapp
Написать в Viber
@matem96
Skype: matem96.ru
Калькулятор непрерывности
Введите функцию, выберите переменную, введите точку и нажмите кнопку вычислить , чтобы оценить непрерывность функции с помощью калькулятора непрерывности
Содержание:
- Калькулятор непрерывности
- Что такое непрерывность?
- Как рассчитать непрерывность?
Дайте нам отзыв
✎
✉
Калькулятор непрерывности
Калькулятор непрерывности определяет, является ли функция непрерывной или прерывистой. Этот непрерывный калькулятор находит результат шагами за пару секунд.
Что такое непрерывность?
В исчислении непрерывность — это термин, используемый для проверки того, является ли функция непрерывной или нет на заданном интервале. Непрерывность можно определить так, как если бы график функции не имел ни дыры, ни обрыва. Если в графике есть дыра или разрыв, то он должен быть прерывистым.
Если в графике есть дыра или разрыв, то он должен быть прерывистым.
Концепция непрерывности очень важна в исчислении, поскольку дифференциал применим только тогда, когда функция непрерывна в точке. Если функция не непрерывна, то дифференцирование невозможно.
Математически функция должна быть непрерывной в точке x = a, если она удовлетворяет следующим условиям.
- f(a) существует (функция должна быть определена в «a»)
- lim x→a f(x) существует (должен существовать предел функции в «a»)
- f(a) = limx→a f(x)
Если выполняются все три условия, то функция непрерывна, в противном случае она разрывна.
Как рассчитать непрерывность?
Вот решенный пример непрерывности, чтобы научиться вычислять его вручную. Пример 1
Шаг 1: Проверка определена функция или нет при x = 2.
f(2) = 3(2) 2 + 4(2) + 5
= 3(4) + 4(2) + 5
= 12 + 8 + 5
= 25
Следовательно, функция определена при x = 2.
Шаг 2: Оцените предел данной функции.
lim x→2 [3x 2 + 4x + 5] = lim x→2 [3x 2 ] + lim x→2 [4x] + lim 900 41 х→2 [5 ]
= 3lim x→2 [x 2 ] + 4lim x→2 [x] + lim
= 3[22] + 4[2] + [ 5]
= 3(4) + 4(2) + 505
= 25
Следовательно, предел функции существует.
Шаг 3: Проверьте третье условие непрерывности.
f(2) = limx→2 f(x)
25 = 25
Следовательно, функция непрерывна, так как все условия выполнены.
Пример 2:
Проверить, является ли заданная функция непрерывной или нет при x = 0,
Решение
Шаг 1: Проверить, определена ли функция при x = 0.
