Непрерывная функция — определение, примеры
Непрерывная функция, как следует из ее названия, — это функция, график которой непрерывен без каких-либо разрывов или скачков. т. е. если мы можем нарисовать кривую (график) функции, даже не отрывая карандаша, то мы говорим, что функция непрерывна. Изучение непрерывности функции действительно важно в исчислении, поскольку функция не может быть дифференцируемой, если она не является непрерывной.
Давайте узнаем больше о непрерывности функции, зная определение непрерывной функции, а также множество других примеров.
| 1. | Что такое непрерывная функция? |
| 2. | Непрерывность в примерах исчисления |
| 3. | Свойства непрерывности |
| 4. | Теоремы о непрерывной функции |
| 5. | НЕ Непрерывная функция |
| 6. | Часто задаваемые вопросы о непрерывной работе |
Что такое непрерывная функция?
Функция f(x) называется непрерывной функцией в исчислении в точке x = a, если кривая функции НЕ разрывается в точке x = a.
Математическое определение непрерывности функции выглядит следующим образом. Функция f(x) непрерывна в точке x = a, если существует
- f(a);
- limₓ → ₐ f(x) существует;
[т.е. limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x)] и - Оба вышеуказанных значения равны. т. е. limₓ → ₐ f(x) = f(a) .
Действительно ли это определение означает, что функция не должна иметь разрыва в точке x = a? Давайте посмотрим. «limₓ → ₐ f(x) существует» означает, что функция должна приближаться к одному и тому же значению как слева, так и справа от значения x = a, а «limₓ → ₐ f(x) = f(a)» означает, что предел функции при x = a такой же, как f (a). Вместе эти два условия сделают функцию непрерывной (без разрыва) в этой точке. Вы можете понять это из следующего рисунка.
Функция называется непрерывной на интервале, если она непрерывна в каждой точке интервала. т. е. на этом интервале график функции не должен ломаться или прыгать.
Непрерывность в примерах исчисления
Вот несколько примеров функций, которые имеют непрерывность . Все приведенные ниже функции непрерывны в соответствующих областях.
В приведенных выше примерах обратите внимание на одну особенность непрерывности: «если граф не имеет дырок или асимптот в какой-либо точке, он всегда непрерывен в этой точке».
Свойства непрерывности
Вот некоторые свойства непрерывности функции. Если две функции f(x) и g(x) непрерывны при x = a, то
- f + g, f — g и fg непрерывны при x = a.
- Если f непрерывна в точке g(a), то функция композиции (fo g) также непрерывна в точке x = a.
- Все полиномиальные функции непрерывны на множестве всех действительных чисел.
- Функция абсолютного значения |x| непрерывна над множеством всех действительных чисел.
- Экспоненциальные функции непрерывны во всех действительных числах.
- Функции sin x и cos x непрерывны во всех действительных числах.
- Функции tan x, cosec x, sec x и cot x непрерывны в своих областях определения.
- Такие функции, как log x, ln x, √x и т. д., непрерывны в соответствующих областях.
Теоремы о непрерывной функции
Существует несколько теорем о непрерывной функции. Вот самые важные теоремы.
- Теорема 1: Все полиномиальные функции непрерывны на (-∞, ∞).
- Теорема 2: Функции e x , sin x, cos x и arctan x непрерывны на (-∞, ∞).
- Теорема 3: Если две функции f и g непрерывны на отрезке [a, b], то алгебра функций: f+g, f-g и fg непрерывна на [a, b]. Но f/g непрерывна на [a, b] при условии, что f/g НЕ равно нулю нигде в интервале.
- Теорема 4: Рациональная функция непрерывна, кроме вертикальных асимптот.
НЕ Непрерывная функция
Функция, которая НЕ является непрерывной, называется прерывистой функцией.
- В отверстиях возникает устранимая несплошность.
- На вертикальных асимптотах возникает бесконечный разрыв.
Разрыв скачка
limₓ → ₐ₋ f(x) и limₓ → ₐ₊ f(x) существуют, но они НЕ равны. Это называется «скачковым разрывом» (или) «неустранимым разрывом».
Устранимый разрыв
limₓ → ₐ f(x) существует (т. е. limₓ → ₐ₋ f(x) = limₓ → ₐ₊ f(x)), но НЕ равен f(a). Это называется «устранимый разрыв».
Бесконечный разрыв
Значения одного или обоих пределов limₓ → ₐ₋ f(x) и limₓ → ₐ₊ f(x) равны ± ∞. Это называется «бесконечный разрыв».
Важные примечания о непрерывности:
Вот несколько моментов, на которые следует обратить внимание в отношении непрерывности функции.
- Функция непрерывна в точке x = a тогда и только тогда, когда limₓ → ₐ f(x) = f(a).
- Это означает, что для того, чтобы функция имела непрерывность в какой-то точке, она не должна прерываться в этой точке.
- Чтобы функция была дифференцируемой, она должна быть непрерывной.
- Все полиномы непрерывны.
- Функции НЕ являются непрерывными на вертикальных асимптотах.
- Функции НЕ непрерывны в отверстиях.
☛ Связанные темы:
Вот некоторые темы, которые могут вас заинтересовать при изучении непрерывных функций.
- Исчисление
- Производные формулы
- Дифференциальные уравнения
- Интеграция
Примеры непрерывной работы
Пример 1: Проверить непрерывность функции f(x) = 3x — 7 при x = 7.
Решение:
Метод 1:
Учитывая, что f(x) = 3x — 7 и х = 7 = а.
Найдем limₓ → ₐ f(x) и f(a).
limₓ → ₐ f(x) = limₓ → ₇ (3x — 7) = 3(7) — 7 = 21 — 7 = 14,
f(a) = f(7) = 3(7) — 7 = 21 — 7 = 14.
Следовательно, limₓ → ₐ f(x) = f(a). Таким образом, f(x) непрерывна при x = 7.
Метод 2:
Мы знаем, что полиномиальная функция непрерывна всюду.
Здесь f(x) = 3x — 7 является полиномиальной функцией и, следовательно, непрерывна всюду и, следовательно, при x = 7.
Ответ: Функция f(x) = 3x — 7 непрерывна при x = 7.
Пример 2: Докажите, что следующая функция НЕ является непрерывной при x = 2, и проверьте то же самое, используя ее график. Также укажите тип разрыва. f (x) = \(\ left \ {\ begin {array} {l} x-3, \ text { if } x \ leq 2 \\ 8, \ text { if } x> 2 \ end {array} \ справа.\)
Решение:
Дано, что a = 2.
Данная функция является кусочной функцией. Таким образом, мы должны найти левый и правый пределы отдельно.
Обратите внимание, что- х → 2- ⇒ х < 2 ⇒ f (х) = х - 3 и
- х → 2+ ⇒ х > 2 ⇒ f(x) = 8.
Теперь мы вычислим пределы.
limₓ → ₂₋ f(x) = limₓ → ₂ (x — 3) = 2 — 3 = -1
limₓ → ₂₊ f(x) = limₓ → ₂ 8 = 8
₂ ₋ f(x) ≠ limₓ → ₂₊ f(x).
Таким образом, limₓ → ₂ f(x) НЕ существует и, следовательно, f(x) НЕ является непрерывной при x = 2.
Проверка по графику:
Функция имеет скачкообразный разрыв.
Ответ: Мы доказали, что функция f(x) алгебраически и графически является разрывной и имеет скачкообразный разрыв.
Пример 3: Найдите связь между a и b, если следующая функция непрерывна в точке x = 4. \(f(x)=\left\{\begin{array}{ll}a x-3, & \ text { if } x \leq 4 \\ b x+8, & \text { if } x>
Решение:
f(x) — непрерывная функция при x = 4. По уравнению непрерывности
limₓ → ₄₋ f(x) = limₓ → ₄₊ f(x) = f(4)
limₓ → ₄ (ax — 3) = limₓ → ₄ (bx + 8) = а(4) — 3
а(4) — 3 = b(4) + 8 = а(4) — 3
Из первых двух выражений
4а — 3 = 4б + 8 : Отношение между a и b равно 4a — 4b = 11.
Обратите внимание, что
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по непрерывным функциям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о непрерывной работе
Что такое определение непрерывной функции?
Непрерывная функция – это функция, график которой нигде не прерывается. Математически f (x) называется непрерывным в точке x = a тогда и только тогда, когда limₓ → ₐ f (x) = f (a).
Пример непрерывной функции? 9{3} & \text { if } x
<-2 \\8 & \text { if } x\geq-2\end{array}\right.\) — кусочно-непрерывная функция.Что такое
Определение непрерывности ? Для непрерывности функции f(x) в точке x = a должны быть выполнены следующие 3 условия.
- f(a) существует
- limₓ → ₐ f(x) существует и
- limₓ → ₐ f(x) = f(a)
Что является примером НЕ непрерывной функции?
Функция f(x) = [x] (целая часть x) НЕ является непрерывной для любого действительного числа. Другой пример НЕ непрерывной функции: f(x) = \(\left\{\begin{array}{l}x-3, \text { if } x \leq 2 \\ 8, \text {if } x>2\end{массив}\right.\)
Опишите непрерывность функции извлечения квадратного корня.
График функции квадратного корня представляет собой гладкую кривую без изломов, отверстий или асимптот по всей области определения. Следовательно, функция квадратного корня непрерывна в своей области определения.
Какая функция всегда непрерывна?
Чтобы функция всегда была непрерывной, на ее графике не должно быть разрывов. Например, f(x) = |x| непрерывна всюду.
Что такое формула непрерывной функции?
Функция f(x) непрерывна при x = a, если ее предел существует при x = a и равен значению функции при x = a.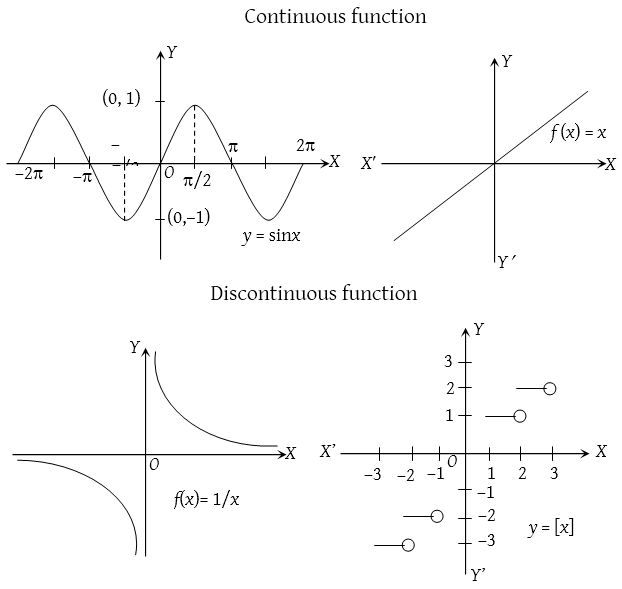
т. е. limₓ → ₐ f(x) = f(a)
Являются ли экспоненциальные функции непрерывными?
Да, экспоненциальные функции непрерывны, поскольку они не имеют изломов, дыр и вертикальных асимптот.
Скачать БЕСПЛАТНЫЕ учебные материалы
ЛИСТКИ
Непрерывные функции и разрывы
Непрерывные функции и разрывы
| 2-1 &\textrm{if} x \neq 2\\ 1 & \textrm{если} х = 2 \end{массив} \right.$$ |
В первом примере фактическое значение $f(2)$ совпадает с нашим «ожидаемым значением», $\lim_{x \rightarrow 2} f(x)$. Также обратите внимание, что в первом примере функция может быть нарисована одним непрерывным росчерком пера (во всяком случае, около $x=2$).
Во втором случае $f(2)$ даже не существует ($x=2$ не находится в области определения второй функции), поэтому она никак не может совпадать с нашим «ожидаемым значением», $\lim_{ х \rightarrow 2} f(x)$. Кроме того, может показаться, что рисование этой функции требует, чтобы мы на мгновение оторвали перо от бумаги в точке $x=2$, учитывая наличие там «дыры».
Таким образом, мы не можем нарисовать эту функцию одним непрерывным штрихом.
Аналогично, в третьем примере $f(2)$ существует, но отличается по значению от $\lim_{x \rightarrow 2} f(x)$. Это снова приводит к «дыре» в функции, из-за которой мы поднимаем перо, когда пытаемся нарисовать эту функцию. Следовательно, мы не можем нарисовать эту функцию вблизи $x=2$ одним непрерывным штрихом.
Точно так же, если мы посмотрим на три функции, где $\lim_{x \rightarrow c} f(x)$ не существует, мы увидим в каждом случае функции, которые нельзя нарисовать одним непрерывным росчерком пера вокруг $х=с$. ( По общему признанию, за последней функцией может быть сложнее следить, но, конечно, вы должны согласиться с тем, что рисовать эту функцию вокруг $x=0$ сложно! )
| $$y=f(x), \quad c=2$$ | $$y=g(x), \quad c=1$$ | $$y=h(x), \quad c=0$$ |
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, мы не можем иметь $\lim_{x \rightarrow c} f(x) = f(c)$.
Таким образом, из этих примеров может показаться, что мы можем нарисовать график $y=f(x)$ около некоторого $x=c$ одним непрерывным штрихом только в том случае, если происходят три вещи:
$\lim_{x \rightarrow c} f(x)$ существует,
$f(c)$ существует (т. е. $c$ находится в области определения $f(x)$), и
- 9+} f(x)$ ВСЕ существуют и совпадают по значению.
Существует множество вариаций на тему, когда речь заходит о словоблудии, используемой в разговоре о непрерывных функциях. Например:
Мы говорим, что функция непрерывна всюду , если она непрерывна при каждом действительном значении $c$.
Мы также можем сказать, что функция непрерывна в своей области определения , если она непрерывна при каждом действительном значении $c$, попадающем в область определения рассматриваемой функции. 9-} f(x) = f(c)}$.
Обратите внимание, что функции могут быть прерывистыми по-разному (все, кроме одного из приведенных выше маленьких рисунков, в какой-то момент были прерывистыми).
Если $\lim_{x \rightarrow c} f(x)$ существует, но по какой-то другой причине не является непрерывным в точке $x=c$ (т. е. либо $f(c)$ не существует, либо не равно значение этого предела), мы говорим, что $f(x)$ имеет устранимых разрывов при $x=c$ .
Можно думать о функциях с устранимыми разрывами как о функциях, непрерывность которых легко «починить» в определенном смысле. То есть, если просто определить (или переопределить) значение функции при $x=c$, разрыв можно устранить. Следующие два графика имеют устранимые разрывы при $x=2$. 92-1 &\textrm{if} x \neq 2\\ 1 & \textrm{если} х = 2 \end{массив} \right.$$
Как видно выше, устранимые разрывы представляются графически как « отверстий » в функциях.
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, то определения или переопределения значения $f(x)$ при $x=c$ будет недостаточно для устранения разрыва. Мы говорим в этой ситуации, что $f(x)$ имеет неустранимых разрывов в точке $x=c$}.
9+} f(x)$ (см. график D ниже)
Мы говорим, что имеем вертикальную асимптоту , когда $\lim_{x \rightarrow c} f(x)$ или один из связанных с ней односторонних пределов не существует, поскольку он бесконечен. (см. диаграмму E ниже)
Какие функции являются непрерывными?
Примеров непрерывных функций множество. Например, рассмотрим полиномиальную функцию $p(x)$. Мы знаем, что область определения $p(x)$ — это множество всех вещественных чисел. Это в сочетании с одним из наших предельных законов, «$\lim_{x \rightarrow c} p(x) = p(c)$ всякий раз, когда $p(x)$ является полиномиальной функцией», говорит нам, что $\lim_{ x \rightarrow c} p(x)$ и $p(x)$ существуют и совпадают по значению для каждого действительного числа $c$. Таким образом, все полиномиальные функции непрерывны всюду (т.