Неравенства 2 класс: «Равенства и неравенства» Уравнения 2 класс

Конспект урока по математике на тему Равенства и неравенства

Тема: Равенства и неравенства.

Цель: знакомство с терминами « равенство», « неравенство».

Задачи:

-формировать знания о равенствах и неравенствах;

-формировать умения сравнивать числа и числовые выражения;

-учить распознавать среди математических записей равенства и неравенства, составлять равенства и неравенства;

Планируемые образовательные результаты

Предметные УУД:

Знать термины «равенство», «неравенство».

Уметь сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно».

Метапредметные УУД.

Познавательные:

уметь анализировать, сравнивать и обобщать полученную информацию на уроке.

Регулятивные:

уметь ставить учебные задачи и самостоятельно формулировать выводы;

уметь слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.

Личностные:

осуществлять сотрудничество в парах, группах при выполнении учебных задач.

Коммуникативные:

вступать в учебное сотрудничество с одноклассниками; участвовать в совместной деятельности;

участвовать в диалоге, в общей беседе, взаимопомощь; осуществлять взаимоконтроль;

проявлять доброжелательное отношение к партнёрам.

Фрагмент урока

Получение новых знаний

— Ребята, давайте вместе с вами выясним, что такое равенство и неравенство, и поможем в этом разобраться Незнайке.

— Сколько синих квадратов? (3)

— Сколько красных квадратов? (3)

– Что можно сказать о количестве синих и красных? (Их поровну. Столько же.)

– Какой знак поставим между цифрами? (Равно.)

Учитель записывает на доске 3=3.

— Кто прочитает это выражение.

— Значит это равенство.

— Как думаете, почему мы называем это выражение равенство? ( Если количество равное, то такое математическое выражение называется равенством)

— Сколько синих треугольников? (3)

— Сколько зеленых треугольников? (2)

– Что можно сказать о количестве синих и зеленых треугольников? (Синих треугольников больше. )

– Какой знак поставим между цифрами? (Больше.)

Учитель записывает на доске 3>2.

— Кто прочитает это выражение.

— Ребята, это неравенство.

— Как думаете, почему мы называем это выражение неравенство? (Если количество неравное, то математическое выражение называется неравенством.)

– Какой вывод можно сделать? (Если между числами или числовыми выражениями стоит знак «равно», то это равенство, если между числами или числовыми выражениями стоит знак « > » или « < », то это – неравенство.)

Закрепление изученного материала

Запишите число 3 ч\з клеточку снова 3

— Какой знак надо поставить?( =)

— Как называется это выражение? Равенство.

— Снова: 3 ч\з клеточку снова 3

-Что мы можем сделать с правой стороной, чтобы получилось неравенство?

Варианты

3 > 3 – 1 или 3 < 3+ 1

— Как прочитаем эти выражения?

1.Игра.

Показываю карточки (2=2, 4>2, 4=4,1<3,1=1,4>3). Если показываю равенство, вы стоите ровно, если неравенство, делаете наклон вправо.

Самостоятельная работа.

— Ребята Незнайка не знает какие нужно поставить знаки. А вы можете выполнить это задание?

(У каждого учащегося карточка с заданием)

Поставьте знаки сравнения:

4-3 4-2 Какой знак поставили?( знак меньше < )

1+2 3+2

2+2 3+1

Проверка работы.

— Прочтите равенства.

— Какой математический знак используется при записи равенства?(знак равно)

— Прочтите неравенства.

— Какие математические знаки используются при записи неравенств?(знаки больше или меньше)

Работа у доски

— У Незнайки был друг Почемучка. Почемучка любит задавать вопросы. Он спрашивает: «А как сравнить число и выражение». Давайте попробуем вместе с вами ответить на этот вопрос.

— Сколько звездочек слева? Запишите. (2)

— Сколько справа красных? А желтых? (2 красные и 2 желтые)

— Какое выражение запишем? (2+2)

— Как сравнить число и выражение? (Надо сначала найти значение выражения и сравнить полученные числа)

— Сколько всего звездочек справа?

— Какой знак поставим? 2<2+2

— Как называется это выражение? (неравенство)

— Почему называем это выражение неравенством? (Стоит знак меньше)

— Сколько солнышек? (3)-показать.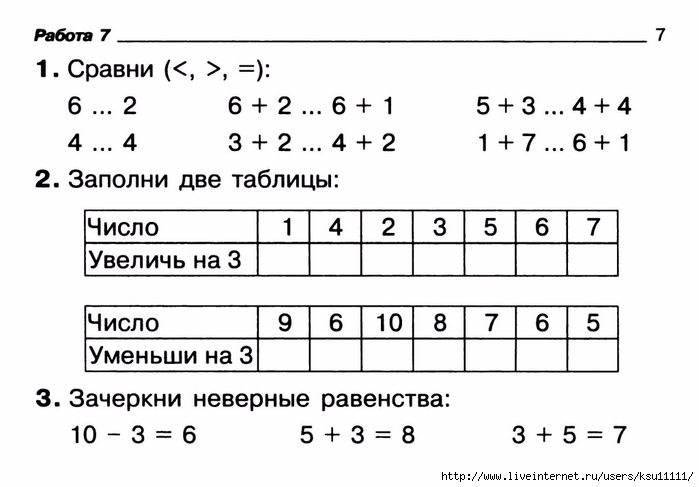 Запишите.

— Сколько было тучек?(4) Одну тучку убрали.

— Какое выражение запишем? (4-1)

— Сравните. Какой знак поставим? (3=4-1)

— Как называется это выражение? (равенство)

— Почему это выражение называется равенством? (Стоит знак равно)

Подведение итогов

-С какими математическими выражениями мы познакомились сегодня на уроке?

-Я благодарю вас за работу на уроке. Поднимите руки, положите на головки и погладьте себя. Все вы молодцы! А теперь покажите мне, пожалуйста, с каким настроением вы уходите с урока.

-Если все получалось и вы довольны собой, нарисуйте улыбку.

-Если недовольны собой и у вас ничего не получалось, нарисуйте грустного человечка.

-Поднимите свои рисунки. У нас много улыбок, а это значит, что мы все на уроке потрудились очень хорошо и еще сможем многое. МОЛОДЦЫ!

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/419498-konspekt-uroka-po-matematike-na-temu-ravenstv

40.Числовые равенства и неравенства как высказывание.

Технология формирования у учащихся этих понятий

В соответсвиии с действующимей программой учащ 1-3 классов должны получить первоначальные сведения о математич выражениях, числовых равенствах и неравенствах, ознакомиться с буквеннной символикой, с переменной, научиться решат неслож уравнения и неравеснства, приобрести умения решать некоторые простые и составные задачи с помощью уравнений. Понятия о равенствах неравенствах и уравнениях раскрываются во взаимосвязи. Работа над ними ведется с 1 класса, сочетаясь с изуч арифм материала. Программа по мат для 1-3 кл ставит задачу выполн сравнение чисел, а также сранвение выражений с целью установления отношений больше меньше равно, научить записывать результаты сравнения с помощью знаков и читать полученные равенства и неравенства. Исловые равенства и неравенства учащ получают в результате сравнения заданных чисел или арифм выражений. Поэтому знаками больше, меньше, равно соединяются не любые 2 числа, не любые 2 выражения а лишь те между которыми существ указанные отношения.

У младших школьников формируются понятия только о верных равенствах и неравенствах. Ознакомл с равен и нерав в нач кл связывается с изуч нумерации и арифм действий. Сравнение чисел осущ сначала на основе сравнения множеств. Этому способу сравн множ учат деетй в подготов период и в начале изуч нумерации чисел первого десятка. В дальнейшем при сравн чисел учащ опираются на ихх место в натур ряду. Установленные отношения запис с помощью знаков ….. учащ упражняются в чтении и записи равенств и неравенств. Сравнение величин выполн с опорой на сравнение самих предметов по данному свойству а потом на основе сравнения числовых значений величин. Сравнение величин вызывает трудности у учащ поэтому чтобы научить этой операции, надо предлагать разноораз упражнения: подберите равную величину, подберите числовые значения величин так, чтобы запись была верной, вставте наименования у величин так чтобы запись была верной. Переход к сравнению выражений осуществл постепенно. Сначала в процессе изуч сложения и вычитания в пределах 10 дети упражн в сранвении выражения и числа. Первые неравенства вида 3+1 болше 3, 3-1 меньше 3 полезно получать из равенства 3=3 сопровождая преобразования соответ операциями над множествами. В дальнейшем выражение и число учащ сравнивают не прибегая к операции над мноествами находят значение выражения и сравнивают его с заданным числом (5+3 больше 5, 8 больше 5) . После знакомства с названиями выраж учащ читают равенства и неравенста так: сумма чисел больше чем число, число .. менььше чем разность чисел и т.п. Упражн на сравнение выраж т числа закрепляют умения читать выраж и способствуют выработке вычислит навыков. Сравнить 2 выраж – значит сравнить их значения.Сравн выраж впервые включ уже в конце изуч слож и вычит в пределах 10. При изуч действий в других концентрах упражн на сравн выраж усложн: учащ предлаг вставить в одно из выраж подходящее число так, чтобы получить верные равенства или нерав, проверить верные ли равеснвта даны,изменить знак отношения или число в одном из выраж. Неравенства с переменной вида: х+3<7, 10-х>5, х-4>12, 72: х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а «окошечком» (квадратом), например: ? >0, 6+4> ?, 7+ ? <10 и т.д. Учащимся предлагается подобрать такое число, чтобы получить верную запись. При выполнении таких упражнений учитель должен побуждать детей к подстановке различных чисел; например, в неравенстве ? >0 можно подставить число 1 (1>?), можно 2 (2>?), можно З (3>?) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).

Рассматривая во II классе, например, неравенство х+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х+3 меньше, чем 10. В каждом таком задании дается множество чисел — значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.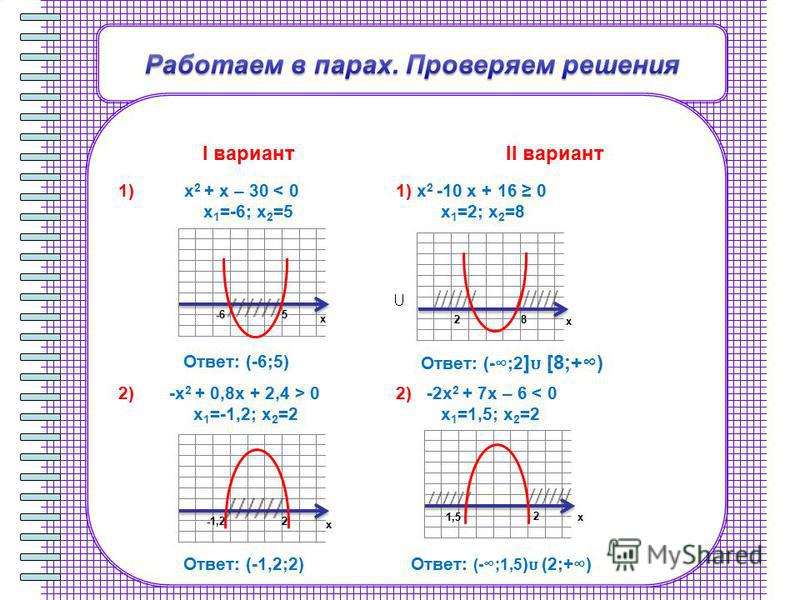 Термины «решить неравенство», «решение неравенства» не вводятся в начальных классах, поскольку во многих случаях ограничиваются подбором только нескольких значений переменной, при которых получается верное неравенство.

Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами подбирают их. Такие упражнения, как правило, выполняются под руководством учителя.

Можно ознакомить детей с таким приемом подбора значений переменной в неравенстве. Пусть дано неравенство 7Чk<70. Сначала устанавливают, при каком значении k данное произведение равно 70 (при k=10). Чтобы произведение было меньше, чем 70, следует множитель брать меньше, чем 10. Учащиеся выполняют подстановку чисел 9, 8 и т.д. до нуля, вычисляют и сравнивают полученные значения выражения с заданным (70) и называют ответ. Упражнения с неравенствами закрепляют вычислительные навыки, а также помогают усвоению арифметических знаний. Например, подставляя различные числовые значения компонентов, дети накапливают наблюдения об изменении результатов действий в зависимости от изменения одного из компонентов. Здесь уточняются знания детей о конкретном смысле каждого действия (так, подставляя значения вычитаемого, дети убеждаются в том, что вычитаемое не больше уменьшаемого и т.п.). Подбирая значения буквы в неравенствах и равенствах вида: 5+х=5, 5-х=5; 10Чх=10, 10Чх<10, учащиеся закрепляют знания особых случаев вычислений. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе.

Математика, 7 класс, алгебраические рассуждения, решение и построение графиков неравенств#GoOpenNC

Обзор

Учащиеся узнают, чем свойства сложения и умножения неравенства отличаются от свойств сложения и умножения равенства.

Учащиеся используют свойства сложения и умножения неравенства для решения неравенства. Они изображают свои решения на числовой прямой.

На этом уроке учащиеся расширяют свои знания о неравенствах, начиная с 6-го класса. В 6-м классе учащиеся узнали, что решение неравенства означает определение того, какие значения делают неравенство верным.

Студенты использовали замену, чтобы определить, делает ли данное значение неравенство верным. Они также использовали числовую прямую для построения графиков решений неравенств. Нанеся эти решения на числовую прямую, они увидели, что неравенство имеет бесконечное число решений.

Теперь, в 7 классе, учащиеся работают с неравенствами, которые также содержат отрицательные числа, и учатся решать и строить графики решений для таких неравенств, как −2 x − 4 < 5. Прежде всего, это включает в себя понимание того, чем свойства неравенства отличаются от свойств свойства равенства. При умножении (или делении) обеих частей неравенства на одно и то же отрицательное число соотношение между двумя частями неравенства меняется, поэтому необходимо изменить направление знака неравенства, чтобы неравенство осталось верным. Как только учащиеся поймут это, они могут применить те же шаги, которые они использовали для решения уравнений для решения неравенств, но не забывая менять направление знака неравенства при умножении или делении обеих частей неравенства на отрицательное число.

• Доступ к предварительным знаниям о том, как решить неравенство.
• Обратите внимание, что при умножении или делении обеих частей неравенства на одно и то же отрицательное число знак неравенства должен изменить направление.
• Решение и неравенство графика формы PX + Q > R или PX + Q < R , где P , Q и R — это специфические номера R Q и R — это специфические номера R и R . .

Учащиеся работают в парах, чтобы выяснить, что произойдет, если к обеим частям неравенства прибавить одно и то же число (положительное или отрицательное). Они также выясняют, что происходит, когда обе части неравенства умножаются на одно и то же число (положительное или отрицательное).

Учащиеся должны обнаружить, что если они прибавят одно и то же число (положительное или отрицательное) к обеим частям неравенства, неравенство останется верным. Когда они умножают обе части неравенства на положительное число, неравенство остается верным. Но когда они умножают обе части на отрицательное число, направление знака неравенства должно измениться на противоположное.

Чтобы проверить это свойство, вы можете предоставить дополнительные образцы. Например, вы можете предоставить неравенство 8 > −4 и предложить учащимся использовать следующие операции с обеих сторон: добавить 7, добавить −7, умножить на 7 и умножить на −7.

ELL: Используйте любую возможность, чтобы учащиеся могли практиковать свои навыки математического мышления. Это задание также дает вам возможность смоделировать эффективные устные и письменные языковые структуры, необходимые для развития языка. Явно научите студентов, как заявить, является ли неравенство истинным или ложным.

Открытие

Вы использовали свойства сложения и умножения равенства, чтобы помочь вам решать уравнения.

Свойство равенства сложения
Вы можете добавить любое число к обеим частям уравнения, и результатом будет истинное уравнение.

Свойство равенства умножения
Вы можете умножить обе части уравнения на любое число, и результатом будет истинное уравнение.

Сегодня вы будете работать с неравенствами. Для неравенства –3 < 4 обсудите, что происходит, когда вы складываете или умножаете, как указано.

• Добавьте по 2 с каждой стороны.
• Добавьте –2 к каждой стороне.
• Умножить каждую сторону на 2.
• Умножить каждую сторону на –2.

Обсудить математическую миссию. Учащиеся узнают, чем похожи и чем отличаются процессы решения неравенств и уравнений.

Открытие

Узнайте, чем похожи и чем отличаются процессы решения неравенств и уравнений.

Предложите учащимся работать в парах.

Студент не знает правил вычисления с целыми числами.

• Можете ли вы смоделировать эту операцию с помощью числовой прямой?
• Можете ли вы смоделировать эту операцию с помощью чертежа?

Учащийся не может определить стороны неравенства.

• Думайте о символе неравенства как о стене, разделяющей обе стороны неравенства.

Студент приходит к выводу, что знак должен быть изменен, когда задействована любая операция с отрицательным числом.

• Попробуйте еще раз. Начните с −4 < 2. Что получится, если вы прибавите −2 к обеим частям?
• Что получится, если вычесть −2 из обеих частей?

• −5 < 2
  При вычитании положительного числа неравенство остается верным.
• −1 < 6
  При вычитании отрицательного числа неравенство остается верным.
• −32 < 2
  При делении на положительное число неравенство останется верным.
• 32 > −2
  При делении на отрицательное число символ неравенства должен изменить направление, чтобы неравенство оставалось верным.

Рабочее время

Снова начните с –3 < 4. Для каждой задачи предскажите, останется ли неравенство верным. Затем проверьте свои прогнозы.

• Вычтите 2 с обеих сторон.
• Вычесть –2 с обеих сторон.
• Разделите обе стороны на 2.
• Разделите обе стороны на –2.

Предложите учащимся работать в парах. Учащиеся используют интерактив для построения графика решения неравенства на числовой прямой. Убедитесь, что учащиеся поняли задание.

SWD: Создайте обучающую таблицу для неравенств с письменными определениями <, >, ≤ и ≥ и примерами каждого из них.

Учащийся не умеет рисовать неравенство.

• Поскольку решение x > 7, где на числовой прямой вы найдете значения больше 7?

• Обе части неравенства делятся на 7 (или умножаются на 17).
• Ответы будут разными.

Рабочее время

Посмотрите на это решение.

2 x > 14

x > 7

• Объясните каждый шаг поиска решения.
• Нарисуйте неравенство на числовой прямой.
• Проверьте свою работу, используя значения из числовой строки исходного неравенства.

ИНТЕРАКТИВ: Постройте график неравенства

Подсказка:

Подумайте, какой круг должен быть на графике: замкнутый круг или открытый круг.

Предложите учащимся продолжить работу в парах.

Студент не может обосновать шаги.

• Что можно сделать с обеими частями неравенства, чтобы перейти от неравенства в первой строке к неравенству во второй строке?

• На первом этапе к обеим частям неравенства было добавлено 6. На втором шаге обе части неравенства делились на 3 (или умножались на 13).
• Ответы будут разными.

Рабочее время

Посмотрите на это решение.

3 x − 6 ≥ 15

3 x ≥ 21

x ≥ 7

• . Объясните каждый шаг поиска решения.
• Нарисуйте неравенство на числовой прямой.
• Проверьте свою работу, используя значения из числовой строки исходного неравенства.

РАЗДАТОЧНЫЙ МАТЕРИАЛ: Представление неравенств на числовой прямой
ИНТЕРАКТИВНЫЙ МАТЕРИАЛ: Построение графика неравенства

Предложите учащимся продолжить работу в парах.

Когда одна сторона неравенства сама по себе содержит отрицательное число, а обе части неравенства умножаются на положительное число, учащийся считает, что знак нужно поменять местами.

• Просто подумайте о том, какое число вы выбрали, когда вычисляли обе стороны.

Ученик может спутать умножение или деление на дробь с умножением или делением на отрицательное число.

• Подумайте об умножении или делении обеих частей 8 > 4 на 12.

• На первом шаге к обеим частям неравенства было добавлено -2. На втором этапе обе части неравенства делились на –4 или умножались на –14. Поскольку мы делим на отрицательное число (или умножаем на отрицательное число), знак неравенства меняется на противоположный.
• Ответы будут разными.

Рабочее время

Посмотрите на это решение.

−4 x + 2 > 10

−4 x > 8

x < −2

• Объясните каждый шаг поиска решения.
• Нарисуйте неравенство на числовой прямой.
• Проверьте свою работу, используя значения из числовой строки исходного неравенства.

РАЗДАТОЧНЫЙ МАТЕРИАЛ: Отрицательные коэффициенты
ИНТЕРАКТИВНЫЙ МАТЕРИАЛ: График неравенства

Предложите учащимся продолжить работу в парах.

Студент не может обосновать шаги.

• Что можно сделать с обеими частями неравенства, чтобы перейти с первого шага на второй?
• Как вы можете превратить 12 x в 1 x или x ?

Учащийся не знает, как построить график неравенства.

• Поскольку решение x больше или равно –10, где бы вы разместили замкнутый круг?
• Как показать, что x больше –10?

Студент использует 0 для проверки своей работы.

• Какое число можно подставить в неравенство, чтобы проверить его?
• Стоит ли пробовать числа с обеих сторон от –10?

• На первом шаге к обеим частям неравенства было добавлено -4. На втором шаге обе части неравенства умножаются на 2 (или делятся на 12). Так как мы умножили (или поделили) на положительное число, то знак неравенства не меняется.
• Ответы будут разными.

Рабочее время

Посмотрите на это решение.

12x+4≥−112x≥−5x≥−10

 

• Объясните каждый шаг поиска решения.
• Нарисуйте неравенство на числовой прямой.
• Проверьте свою работу, используя значения из числовой строки исходного неравенства.

РАЗДАТОЧНЫЙ МАТЕРИАЛ: Дроби в неравенствах
ИНТЕРАКТИВНЫЙ МАТЕРИАЛ: График неравенства

 

Ищите учеников, которые могут ошибаться и делать неправильные выводы, а также учеников, которые делают правильные открытия. Например, распространенное заблуждение состоит в том, что учащиеся ошибочно предполагают, что любая операция с отрицательным числом приведет к необходимости изменить знак неравенства на противоположный. Когда учащиеся делают обобщение, предложите им попробовать другие примеры, чтобы проверить свое обобщение.

Ищите учащихся, которые не уверены в том, чем > и ≥ похожи и чем отличаются. Вы можете включить объяснение символов в обсуждение «Пути мышления».

Определите пары учащихся, которые решают задачу-вызов.

SWD: Плакаты помогают учащимся, способствуя групповой работе и взаимному обучению. Учащиеся могут представлять концепции визуально, помогая им обсуждать и уточнять свои идеи и понимание.

Математическая практика 3: Создание убедительных аргументов и критика рассуждений других.

Учащиеся анализируют, что происходит, когда операции применяются к обеим частям неравенства. Для этого им нужно уметь разбивать ситуацию на случаи (сложение положительного числа, сложение отрицательного числа, вычитание положительного числа и т. д.), а затем приступать к рассмотрению каждого случая отдельно. Чтобы обосновать свои выводы, им нужно будет привести примеры и контрпримеры. Оценивая аргументы других, им нужно будет определить, когда аргумент ошибочен.

Ответ

3x−7≤5x+123x−3x−7≤5x−3x+12−7−12≤2x+12−12−19≤2x−192≤2×2−912≤x  или  x≥−912

 

Рабочее время

• Обобщите свои знания о работе с неравенствами.
• Подтвердите свои выводы примерами своей работы.

Решите это неравенство:

• 3x−7≤5x+12

Подсказка:

Подумайте, как связаны сложение и вычитание и как связаны умножение и деление.

Организуйте обсуждение, чтобы помочь учащимся понять математику урока в неформальной обстановке. Предложите учащимся объяснить свои ответы. Задайте вопросы, например, следующие:

• Что означает решение неравенства?
• Почему вы изменили направление знака неравенства?
• Как вы решаете, должен ли график быть открытым кругом или закрытым кругом?
• Чем отличается умножение или деление на отрицательное число?
• Как складывается или вычитается то же самое?
• Если бы символ неравенства был знаком равенства, каким был бы ваш ответ? Как это будет по-другому?
• Что произойдет с неравенством, если к обеим его частям прибавить или вычесть одно и то же число? Почему?
• Что произойдет с неравенством, если обе его части умножить или разделить на одно и то же положительное число? Почему?
• Что произойдет с неравенством, если обе его части умножить или разделить на одно и то же отрицательное число? Почему?

Если какие-либо учащиеся пытались решить задачу-вызов, попросите их поделиться своими решениями, независимо от того, правильны ли их решения. Это неравенство отличается от тех, которые только что решили учащиеся, потому что оно имеет переменную с обеих сторон неравенства. Цель состоит в том, чтобы получить одну переменную с одной стороны и число с другой стороны.

Эл.: Предоставьте ELL рамки предложений, чтобы помочь им в построении аргументов и критике. Примерами могут быть: «Я думаю, что неравенство верно, потому что…» или «Мои рассуждения, лежащие в основе моих решений, таковы…»

Примерами критических замечаний могут быть: «Я не совсем понимаю, как вы пришли к выводу, что…. поскольку…» или «Пожалуйста, объясните мне, как вы пришли к такому выводу, поскольку я сам этого не вижу».

Performance Task

Делайте заметки об объяснениях ваших одноклассников по решению каждого неравенства и обобщайте их в свойствах неравенств.

Подсказка:

В присутствии одноклассников задайте такие вопросы, как:

• Что означает для решения неравенства в смысле?
• Почему вы изменили направление знака?
• Как вы решили, закрашивать кружок на числовой строке или нет?
• Если бы символом неравенства был знак равенства, каким был бы ваш ответ? Как это будет по-другому?

Предложите учащимся прочитать свойство сложения неравенства и свойство неравенства умножения. Попросите нескольких добровольцев привести примеры каждого свойства. Затем попросите студентов работать индивидуально, чтобы решить неравенства. Дайте время для проверки работы, подставив в исходное неравенство три значения: значение, которое делает обе стороны равными, на одно значение меньше этого и на одно значение больше этого. После того, как они закончат, попросите учащихся представить свои решения партнеру.

Рабочее время

Свойство сложения неравенства
Вы можете добавить любое число к обеим частям неравенства, и результат будет верным.

Свойство умножения неравенства
Вы можете умножить обе части неравенства на любое положительное число, и результат будет верным. Если вы умножите обе части неравенства на отрицательное число, вам нужно будет изменить направление знака неравенства, чтобы неравенство было верным.

Решите каждое неравенство и изобразите его на графике. Проверьте свое решение, проверив значения.

1. x + 6> 3
2. −4 x ≥ 12
3. 4 — 2 x <12
4. 3 x + 4 ≥ 15

9004.

Подумайте, как вы можете проверить свою работу, используя решение на числовой прямой.

Пусть каждый учащийся напишет краткий обзор математики на этом уроке, а затем напишет краткий обзор класса. Когда закончите, если вы считаете, что резюме полезно, поделитесь им с классом.

ELL: Задавая эти вопросы, если вовлеченный учащийся является ELL, говорите в подходящем темпе и предоставьте достаточное время ожидания для вдумчивого ответа. Задайте вопросы и ответы в письменной форме.

Вы можете решать уравнения, используя свойства сложения и умножения равенства. Эти свойства позволяют прибавлять любое число к обеим частям уравнения или умножать обе части уравнения на одно и то же число и по-прежнему иметь истинное уравнение.

Вы можете решать неравенства, используя свойства сложения и умножения неравенства. Разница в том, что для неравенств свойство умножения позволяет умножить обе части неравенства на положительное число и при этом получить истинное неравенство. Но если вы умножите обе части неравенства на отрицательное число, вы должны изменить направление знака неравенства, чтобы неравенство было истинным.

При решении уравнений и неравенств цель одна: получить переменную саму по себе с одной стороны и число с другой.

Формирующее оценивание

Напишите краткое изложение того, что вы узнали о свойствах неравенства.

Подсказка:

Объясните, чем решение неравенств похоже и чем отличается от решения уравнений?

Пусть каждый учащийся напишет краткое размышление перед окончанием урока. Просмотрите размышления, чтобы понять, что учащиеся узнали о концепциях, связанных с решением неравенств.

Рабочее время

Напишите размышления об идеях, обсуждавшихся сегодня в классе. Используйте приведенный ниже образец предложения, если он окажется вам полезным.

Что-то новое, что я узнал сегодня, это…

Мистер Нуссбаум Математика Признаки неравенства Действия

13.11 — Учителя — Подпишитесь на MrN 365 и используйте код купона «снег», чтобы получить 20-процентную скидку от годовой цены в 49 долларов! Получите доступ ко всем моим действиям и многому другому! https://mrn365.com

Главная > Математика > Признаки неравенства

Этот раздел содержит мероприятия и ресурсы, связанные с признаками неравенства

Genius Boxing- Онлайн игра

Описание: Думаешь, ты хорошо разбираешься в математике? Докажите это самым известным математическим мыслителям в истории. В Genius Boxing вы должны победить Альберта Эйнштейна, Пифагора, Галилея, Билла Гейтса, Леонардо да Винчи, Николая Копернюка, Архимеда и сэра Исаака Ньютона в боксе, используя свои математические способности. Посмотрите на числовое уравнение, которое появляется в нижней части экрана. Нажмите <, > или =, чтобы числовое уравнение стало верным. Будьте осторожны, каждый раунд становится намного сложнее!

Тип: Математическая игра

Формат: игра

Уровни оценок: 2, 3, 4

Стандарты СС:

Ланг. Стандарты искусства:

Hungry, Hungry Gators — Онлайн игра

Описание: Сначала введите свое ПЕРВОЕ имя, затем выберите аллигатора «больше чем» или «меньше чем». Если вы выберете аллигатор «больше чем», вы будете стремиться поймать большее из двух чисел или уравнений, которые дают более крупные ответы, падающие с неба. Если вы выберете крокодила «меньше чем», вы сделаете обратное. Будь осторожен! Каждый раунд становится немного сложнее. Когда вы закончите раунд, вы получите код для ввода, так что вам никогда не придется начинать все сначала. Посмотрите видео, чтобы узнать больше.

Тип: Математическая игра

Формат: игра

Уровни оценок: 1, 2, 3

Стандарты СС:

Ланг. Стандарты искусства:

Сравнение чисел на основе разрядных значений с использованием признаков неравенства — онлайн

Описание: Это задание требует, чтобы учащиеся использовали признаки неравенства для сравнения чисел, разбитых на разрядные значения. Например 34 сотни, 19 десятков, 3 единицы > 35 сотен, 6 десятков, 4 единицы

Тип: Математическая тренировка

Формат: онлайн-активность

Уровни оценок: 4, 5, 6

Стандарты СС:

Ланг. Стандарты искусства:

Дроби — Сравнение дробей по признакам неравенства и = — Онлайн

Описание. В этом упражнении учащиеся должны использовать знаки <, > и = для сравнения дробей.

Тип: Математическая тренировка

Формат: онлайн-активность

Уровни оценок: 3, 4, 5, 6

Стандарты СС:

Ланг. Стандарты искусства:

Используйте в качестве оценки в Google Classroom.

ОБНОВЛЕНИЕ ДО MRN365.COM

Подробнее

Не хотите обновляться?

Вы все еще можете купить этот ресурс по отдельности на Учителя платят учителям за .

Нажмите здесь, чтобы купить.

ОБНОВЛЕНИЕ ДО MRN365.