Решение неравенств методом интервалов. Решите неравенство (2x-1)/(x+3)
© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
Главная → Видеоуроки → Алгебра. 8 класс. Квадратные неравенства. Описание видеоурока: Решение дробно-рациональных неравенств методом интервалов. Решите неравенство (2x — 1) / (x + 3) < 0 Валерий Волков 6 29.05.2017 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс.Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
неравенства | Справочник по математике
Разделив неравенства второй степени на коэффициент при x2, мы приведем его к одному из видов
x2+px+q < 0, (1)
x2+px+q > 0, (2)
Перенесем свободный член в правую часть и прибавим к обеим частям (p/2)2.
(x+(p/2))2 < (p/2)2-q, (1a)
(x+(p/2))2 > (p/2)2-q. (2a)
Если обозначить x+(p/2) через z, а (p/2)2-q через m, то мы получим простейшие неравенства
z2 < m, (1b)
z2 > m. (2b)
Решение этих неравенств было дано в предыдущем параграфе. Зная его, найдем решение неравенства (1) или (2).
Пример 1. Решить неравенство -2x2+14x-20 > 0. Разделив обе части на -2 (§ 53, п.3), найдем x2-7x+10 < 0. Перенеся свободный член 10 вправо и прибавим к обеим частям (7/2)2
, получим (x-(7/2))2 < 9/4.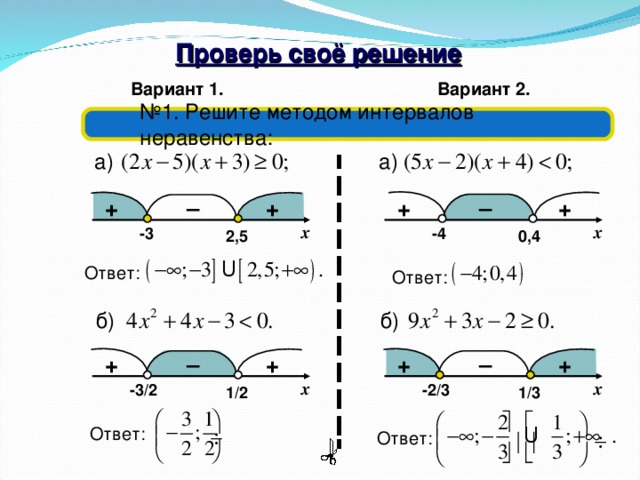 Отсюда (§ 57, п.1)
Отсюда (§ 57, п.1)-(3/2) < x-(7/2) < 3/2.
Прибавляя 7/2, находим -(3/2)+(7/2) < x < (3/2)+(7/2), т.е.
2 < x < 5.
Пример 2. Решить неравенство –2x2+14x-20 < 0. Выполнив те же преобразования, получим неравенство (x-(7/2))2 > 9/4. Отсюда (§ 57, п.2) находим, что наше неравенство справедливо, во-первых, при x-(7/2) > 3/2, т.е. при x > 5, и, во-вторых, при x-(7/2) < -3/2, т.е. при x < 2.
Пример 3. Решить неравенство x2+6x+15 < 0. Перенося свободный член вправо и прибавляя к обеим частям
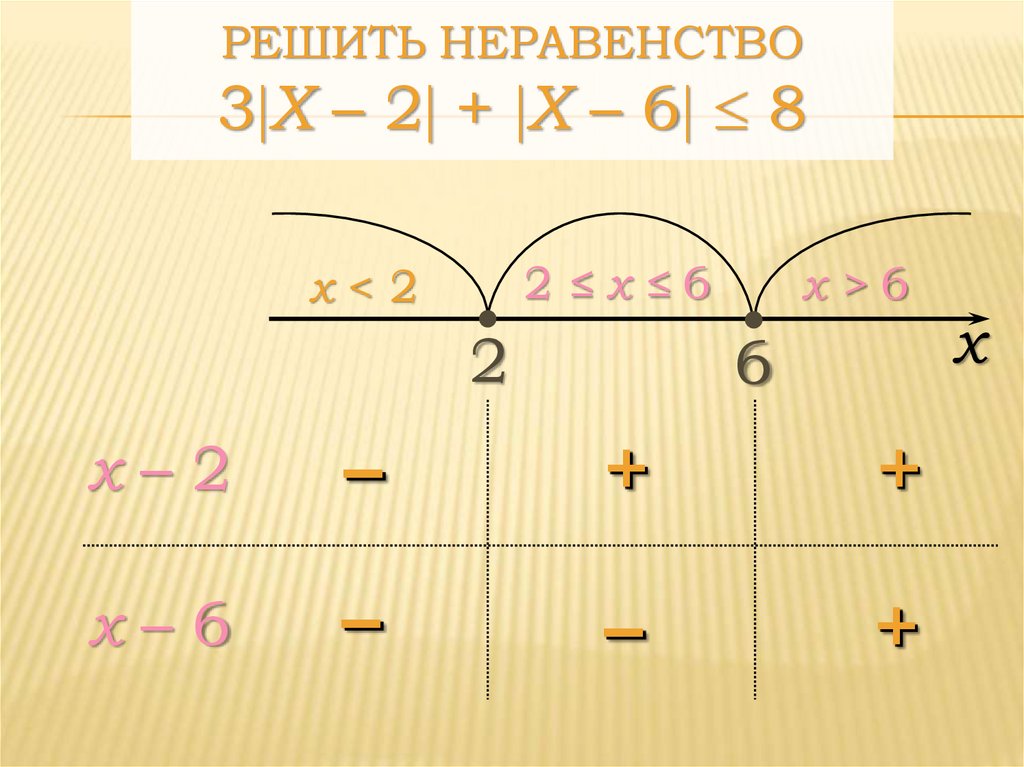 Значит, не имеет решений и данное неравенство.
Значит, не имеет решений и данное неравенство.Пример 4. Решить неравенство x2+6x+15 > 0. Как в примере 3, найдем (x+3)2 > -6. Это неравенство (§ 57, п.2) тождественное. Значит, и данное неравенство тождественное.
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.1. Неравенства x2 < m. (1)
Если m > 0, то решение есть
-√m < x < √m. (1a)
Если m ≤ 0, то решения нет (квадрат действительного числа не может быть отрицательным).
2. Неравенство x2 > m. (2)
Если m > 0, то неравенство (2) справедливо, во-первых, при всех значениях x, больших чем √m, и, во-вторых, при всех значениях x, меньших чем -√m.
x > √m или x < -√m (2a)
Если m=0, то неравенство (2) справедливо при все x, кроме x=0;
x > 0 или x < 0. (2б)
Если m < 0, то неравенство (2) тождественное.
Пример 1. Неравенство x2 < 9 имеет решение -3 < x < 3
Пример 2. Неравенство x2 < -9 не имеет решений.
Пример 3. Неравенство x2 > 9 имеет решением совокупность всех чисел , больших чем 3, и всех чисел, меньших чем -3.
Пример 4. Неравенство x2 > -9 тождественно.
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.Неравенство первой степени с одним неизвестным можно привести к виду
ax > b
Решением будет:
x > (b/a), если a > 0,
и
x < (b/a), если a < 0.
Пример 1. Решить неравенство 5х-3 > 8x+1.
Решение. 5х-8х > 3+1;
-3x > 4;
x < (-4/3).
Пример 2. Решить неравенство 5x + 2 < 7x+6.
Решение. 5x-7x < 6-2;
-2x < 4;
x > -2.
Пример 3. Решить неравенство (x-1)2 < x2+8.
Решение. x2+2x+ 1 < x2+8;
-2x < 7;
x > (-7/2).
Замечание
Пример 1. Дано неравенство 2(3х-5) < 3(2x-1)+5. Оно равносильно неравенству 6x-10 < 6x+2, а последнее приводится к числовому (тождественному) -10 < 2. Значит, исходное неравенство – тождественное.
Пример 2. Неравенство 2(3х-5) > 3(2x-1)+5 приводится к бессмысленному числовому неравенству -10 > 2. Значит, исходное неравенство не имеет решений.
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.Неравенства, содержащие неизвестные величины, подразделяются на алгебраические и трансцендентные; алгебраические неравенства подразделяются на неравенства первой, второй и т.д. степени. Эта классификация производится так же, как и для уравнений (§ 19).
Пример 1. Неравенства 3x2-2x+5 > 3x(x-2) алгебраическое, второй степени.
Пример 2. Неравенство 2x > x+4 трансцендентное.
Пример 3. Неравенство 3x2-2x+5 > 3x(x-2) алгебраическое, первой степени, потому что оно приводится к неравенству 4x+5 > 0.
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они верны при одних и тех же значениях этих неизвестных.
Так же определяется равносильность двух систем неравенств.
Пример 1. Неравенства 3х+1 > 2x+4 и 3x > 2x+3 равносильны, так как оба верны при x > 3 и оба неверны, когда x ≤ 3
Пример 2. Неравенства 2x ≤ 6 и x2 ≤ 9 не равносильны, так как решение первого есть x ≤ 3, а решение второго -3x ≤ x ≤ 3, так что, например x = -4 первое верно, а второе неверно.
Процесс решения неравенства заключается в основном в замене данного неравенства (или данной системы неравенств) другими равносильными1. При решении неравенств применяются следующие основные приемы (ср. § 18).
1. Замена одного выражения другим, тождественно ему равным.
2. Перенос слагаемого из одной части неравенства в другую с заменой знака на противоположный (в силу § 50, п. 3).
3).
3. Умножение или деление обеих частей неравенства на одну и ту же числовую величину (не равную нулю). При этом если множитель положителен, то знак неравенства остается тем же, если же отрицателен, то знак неравенства меняется на противоположный (§ 50, п.6).
Каждое их этих преобразований дает неравенство, равносильное исходному.
Пример. Дано неравенство (2x-3)2 < 4x2+2. Заменяем левую часть тождественно равным выражением 4x2-12x+9. Получаем 4x2-12x+9 < 4x2+2. Переносим из правой части член 4x2в левую, а из левой части член 9 в правую часть. После приведения подобных членов получаем -12x(7/12).
Умножать (а также делить) неравенство на нуль нельзя. Умножая или деля обе части неравенства на буквенные выражения, мы получаем неравенство, которое, как правило, не равносильно исходному.
Пример. Дано неравенство (x-2)x < x-2. Если разделить обе его части на x-2, то получим x < 1. Но это неравенство не равносильно исходному, так как, например, значение x=0 не удовлетворяет неравенству (x-2)x < x-2. Неравенство x < 1 тоже не равносильно исходному, так как, например, значение x=3 неравенству (x-2)x
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.Два выражения, числовые или буквенные, соединенные знаком «больше» (>) или знаком «меньше» (, образуют неравенство (числовое или буквенное).
Всякое верное числовое неравенство, а также всякое буквенное неравенство, справедливое при всех числовых действительных значениях входящих в него букв, называется тождественным.
Пример 1. Числовое неравенство 2*3 – 5 (оно верно!) есть тождественное неравенство.
Пример 2. Буквенное неравенство a2 > – 2 тождественно, так как при всяком числовом (действительном) значении а величина a2 положительна или равна нулю и, значит, всегда больше, чем – 2.
Два выражения соединяются также знаками ≤ («меньше и или равно») и ≥ («больше или равно»). Так, запись 2а ≥ 3b означает, что величина 2а либо больше величины 3b, либо равна ей. Такие записи также именуются неравенствами.
Буквенные величины, входящие в неравенство, могут подразделяться на известные и неизвестные. Какие из букв представляют известные, а какие неизвестные величины, должно быть отдельно указано. Обычно для этого неизвестные величины обозначаются последними буквами латинского алфавита х, у, v, υ и т. д.
д.
Решить неравенство – значит указать границы, в которых должны заключаться (действительные) значения неизвестныx величин, чтобы неравенство было верным.
Если дано несколько неравенств, то решить систему этих неравенств – значит указать границы, в которых должны заключаться значения неизвестных величин, чтобы все данные неравенства были верными.
Пример 3. Решить неравенство х24. Это неравенство верно, если |х| , т. е. если х заключено в границах между – 2 и + 2. Решение имеет вид: – 2 .
Пример 4. Решить неравенство 2х > 8. Решение имеет вид х > 4. Здесь х ограничено только с одной стороны.
Пример 5. Неравенство (х – 2) (х – 3) > 0 верно, если х > 3 (тогда оба сомножителя (х – 2), (х – 3) положительны), а также при х (тогда оба сомножителя отрицательны), в неверно, когда х заключено в границах между 2 и 3 (а также при х = 2 и при х = 3). Поэтому решение представляется двумя неравенствами:
Поэтому решение представляется двумя неравенствами:
х>3; х.
Пример 6. Неравенство х2 не имеет решений (ср. пример 2).
Запись опубликована автором admin в рубрике Алгебра с метками алгебра, неравенства.1. Если a > b, то b < a; наоборот, если а < b, то b > a.
Пример. Если 5х – 1 > 2x + 1, то 2х +1< 5x – 1.
2. Если a > b и b > с, то а > с. Точно так же, а < b и b < с, то a < с.
Пример. Из неравенств x > 2у, 2y > 10 следует, что x >10.
3. Если a > b, то a + c > b + с и a – c > b – c. Если же а < b, то а + с<b+c и a – c<b – c, т.е. к обеим частям неравенства можно прибавить (или вычесть) одну и ту же величину
Пример 1. Дано неравенство х + 8>3. Вычитая из обеих частей неравенства число 8, находим х > – 5.
Пример 2. Дано неравенство х – 6 < – 2. Прибавляя обеим частям 6, находим х < 4.
4. Если a > b и с > d, то a + c >b + d; точно так же если а < b и с < d, то a + с < b + d, т. е. два неравенства одинакового смысла ) можно почленно складывать. Это справедливо и для любого числа неравенств, например, если a1 > b1, a2 > b2, a3 > b3, то a1 + a2 + a3 > b1+b2 +b3.
Пример 1. Неравенства – 8 > – 10 и 5 > 2 верны. Складывая их почленно, находим верное неравенство – 3 > – 8.
Пример 2. Дана система неравенств (1/2)х + (1/2)у < 18; (1/2)х – (1/2)у < 4. Складывая их почленно, находим x < 22.
Замечание. Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 10 > 8 почленно вычесть неравенство 2 > 1, то получим верное неравенство 8 > 7 но если из того же неравенства 10 > 8 почленно вычесть неравенство 6 > 1, то получим нелепость. Сравнить следующий пункт.
5. Если a > b и c < d, то а – с > b – d; если а < b и с – d, то а – с < b – d, т.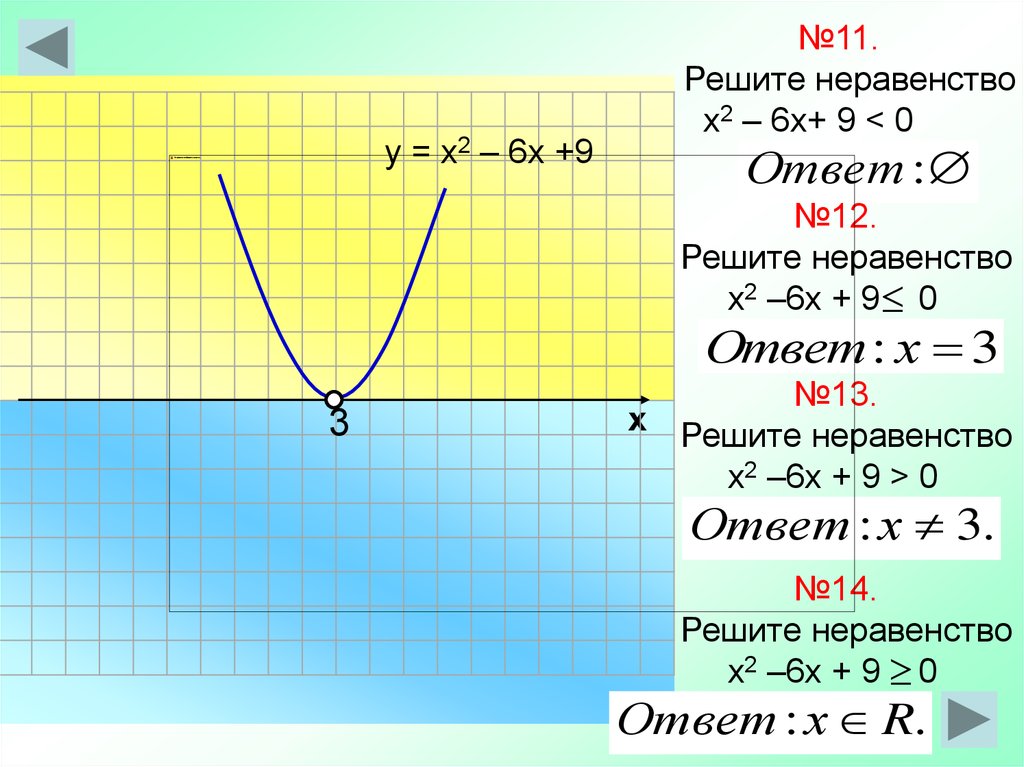 е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла ), оставляя знак того неравенства, из которого вычиталось другое.
е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла ), оставляя знак того неравенства, из которого вычиталось другое.
Пример 1. Неравенства 12 < 20 и 15 > 7 верны. Вычитая почленно второе из первого и оставляя знак первого, получаем верное неравенство – 3 < 13. Вычитая почленно первое из второго и оставляя знак второго, находим верное неравенство 3 > – 13.
Пример 2. Дана система неравенств (1/2)х + (1/2)у < 18; (1/2)х – (1/2)у > 8. Вычитая из первого неравенства второе, находим y < 10.
6. Если а > b и m — положительное число, то ma > mb и a/n > b/n, т. е. обе части неравенства можно разделить или умножить на одно и то же положительное число (знак неравенства остается тем же). Если же a > b и n – отрицательное число, то na < nb и a/n < b/n, т. е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при том знак неравенства нужно изменить на противоположный.
Если же a > b и n – отрицательное число, то na < nb и a/n < b/n, т. е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при том знак неравенства нужно изменить на противоположный.
Пример 1. Разделив обе части верного неравенства 25 > 20 на 5, получим верное неравенство 5 > 4. Если же мы делим обе части неравенства 25 > 20 на – 5, то нужно переменить знак > на < , и тогда получим верное неравенство – 5 < – 4.
Пример 2. Из неравенства 2х < 12 следует, что х < 6.
Пример 3. Из неравенства -(1/3)х – (1/3)х > 4 следует, что x < – 12.
Пример 4. Дано неравенство х/к > у/l; из него следует, что lx > ky, если знаки чисел l и k одинаковы, и что lx < ky, если знаки чисел l и k противоположны.
Дано неравенство х/к > у/l; из него следует, что lx > ky, если знаки чисел l и k одинаковы, и что lx < ky, если знаки чисел l и k противоположны.
Свежие записи
- Умножение двузначных чисел, оканчивающихся на 1
- Фигурные числа
- Многочлен
- Признаки делимости на 2,3,4,5,6,7,8,9,10,11,25,100,1000
- Математические софизмы. Логические парадоксы
Архивы
- Ноябрь 2020
- Апрель 2020
- Май 2018
- Сентябрь 2017
- Октябрь 2015
- Сентябрь 2015
- Июль 2015
- Апрель 2015
- Март 2015
- Октябрь 2014
- Сентябрь 2014
Рубрики
- GIFки
- Алгебра
- Арифметика
- Геометрия
- Загадки
- Как посчитать
- Новости
- Тригонометрия
- Функции и графики
- Энциклопедия
неравенств — Как решить систему из $2$ неравенств $xy0$
Задавать вопрос
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 379 раз
$\begingroup$
Как найти все решения следующей системы неравенств при положительных и действительных $x$ и $y$?
$$xy<1$$ $$2 + x(y-1)>0$$
Я изменил первое неравенство, чтобы получить $y<\frac{1}{x}$, и решил второе неравенство для $y$, чтобы получить $y>1 -\frac{2}{x}$
Таким образом, $\frac{1}{x} \ge 1- \frac{2}{x} \Rightarrow x \le 3$ и первое дает $y< \ дробь{1}{3}$.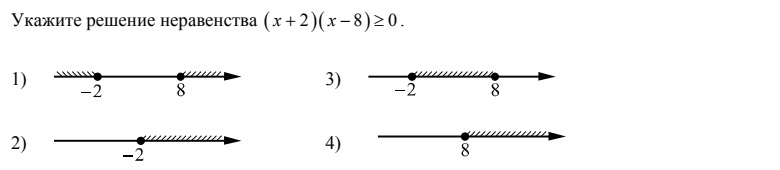
Аналогичным образом решение второго уравнения для $x$ дает $x> \frac{2}{1-y}$, поэтому, предполагая, что $y \ne 1$, мы получаем $\frac{1}{y} \ge \frac {2}{1-y}$, а затем $y \le \frac{1}{3}$, и первый дает $x<3$.
Предположим теперь, что $y=1$, мы получаем $x<1$.
Итак, найдены следующие решения:
$$x \le 3 \text{ AND } y< \frac{1}{3}$$ $$x<3 \text{ AND } y \le \frac{1}{3}$$ $$x <1 \text{ AND } y=1$$
Это кажется хорошим методом, но я пропустил решение $x=1,y<1$
Как решить такую систему, чтобы включить все решения? Спасибо.
- неравенство
$\endgroup$
2
$\begingroup$
Вы решаете каждое неравенство относительно $y$:
$$\begin{cases}y<\frac1x \\ y>1-\frac{2}{x} \end{cases}$$
Нарисуйте допустимую область для каждого неравенства и найдите перекрывающуюся допустимую область. Поскольку допустимая область не является прямоугольной, вы не можете выразить решение численно. Вы можете написать две простые области следующим образом:
$$(0
Поскольку допустимая область не является прямоугольной, вы не можете выразить решение численно. Вы можете написать две простые области следующим образом:
$$(0
$\endgroup$
1
$\begingroup$
Если вы решите оба неравенства относительно $y$, то каждое неравенство можно представить как площадь под (или над) графиком двух функций $y=f(x)$, $y=g(x)$. Поскольку эти функции непрерывны на $(0,\infty)$, приравняем их друг к другу, чтобы найти, где они пересекаются. На каждом интервале вокруг точек пересечения будут верны либо оба неравенства, либо хотя бы одно ложно. Подключите контрольную точку к каждой функции, чтобы определить это. Теперь неравенство будет верным на тех промежутках, для которых оно было верным для вашей контрольной точки.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Решение квадратных неравенств: примеры
Решение Квадратные неравенства: примеры (стр. 2 из 3)
Два связанных двухпеременных
уравнения в этом случае y = 2 х 2 + 4 х и и = х 2 х 6.
Как видите, это
трудно сказать где зеленая линия ( у = 2 х 2 + 4 х )
находится выше синей линии Это последнее неравенство
проще иметь дело, потому что теперь все, что мне нужно сделать, это найти нули
из и = х 2 + 5 х + 6
(что несложно), а затем выбрать правильные интервалы, основываясь только на
одна парабола (что тоже легко). я упростил «2 x 2 + 4 х > x 2 x 6 дюймов чтобы получить « х 2 + 5 x + 6 > 0″. Соответствующее уравнение с двумя переменными: y = х 2 + 5 х + 6. Во-первых, я найду нули (то есть x -перехваты): Эти два перехвата
разделить числовую строку на три интервала, а именно x < 3, 3 < x < 2,
и х > 2. Тогда решение: х < 3 или x > 2 Почему было ли это решение «или равным», а не просто «больше чем» или «меньше чем»? Потому что исходное неравенство было «или равно», поэтому граничные точки являются нулями или х — перехваты, входят в решение. Авторские права Элизабет Стапель 2002-2011 Все права защищены
Первый, Я найду нули: Хм… Поскольку внутри квадратного корня есть минус, не должно быть любые x -перехваты. То есть этот квадрат должен быть либо всегда выше оси x или всегда ниже, потому что он никогда не может пересекать ось или касаться ее.
приведенное выше решение также может быть указано как «все действительные числа» или
записывается как интервал «от отрицательной бесконечности до положительной бесконечности».
Это выглядит так же, как предыдущая проблема, за исключением того, что теперь я ищу где парабола ниже оси. Я уже знаю, что есть нет x — перехваты. Кроме того, поскольку это парабола с правой стороной вверх, я знаю, что график всегда выше оси. Так где же г = х 2 + х + 1 меньше нуля? Нигде! Тогда решение: нет х вышеприведенное решение также может быть указано как «нет решения» или как « пустой набор», представленный символом «». Всякий раз, когда
у вас есть квадратное неравенство, где соответствующее квадратное уравнение
не имеет действительных решений (т. е. там, где соответствующая парабола не имеет
не пересекать x -ось),
решение неравенства будет либо «все x »
или «нет x «,
в зависимости от того, находится ли парабола на стороне оси, которую вы
необходимость. |

 5 класс.
5 класс. 10 — 11 класс.
10 — 11 класс.
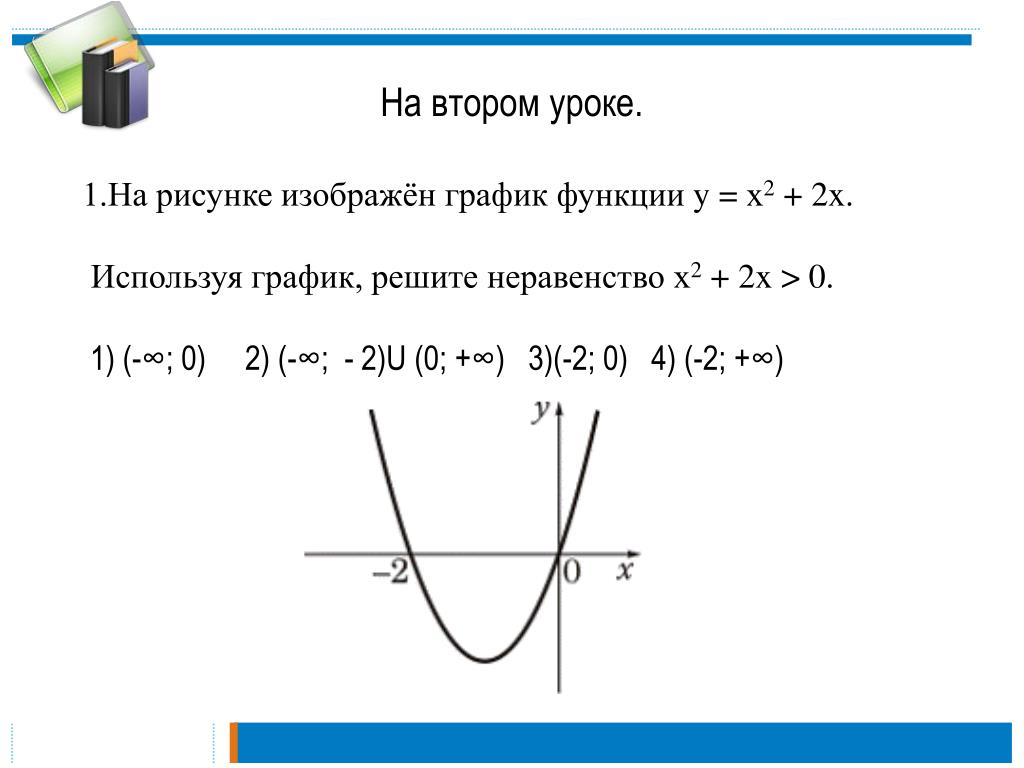 То есть проще сравнить
одна парабола с осью x чем сравнивать две параболы друг с другом. Но так как одна парабола
( г = х 2 + 5 х + 6)
произошло от объединения двух первоначальных парабол («парабол»?),
решение более простого неравенства одной параболы будет таким же
как решение исходного неравенства двух парабол. Поскольку решения
будет то же самое, я буду работать с более простым случаем.
То есть проще сравнить
одна парабола с осью x чем сравнивать две параболы друг с другом. Но так как одна парабола
( г = х 2 + 5 х + 6)
произошло от объединения двух первоначальных парабол («парабол»?),
решение более простого неравенства одной параболы будет таким же
как решение исходного неравенства двух парабол. Поскольку решения
будет то же самое, я буду работать с более простым случаем. На каком
из этих трех интервалов y = х 2 + 5 х + 6
над осью x ?
С по гг.
= х 2 + 5 х + 6
графики в виде параболы с правой стороной вверх, квадратичная функция находится над осью
на концах:
На каком
из этих трех интервалов y = х 2 + 5 х + 6
над осью x ?
С по гг.
= х 2 + 5 х + 6
графики в виде параболы с правой стороной вверх, квадратичная функция находится над осью
на концах: 

